Published online by Cambridge University Press: 22 April 2005
A vector autoregression with deterministic terms and with no restrictions to its characteristic roots is considered. Strong consistency results for the least squares statistics are presented. This extends earlier results where deterministic terms have not been considered. In addition the convergence rates are improved compared with earlier results.Comments from S. Johansen are gratefully acknowledged.
The strong consistency of least squares estimators in a vector autoregression with deterministic terms is studied. Autoregressions generally have three types of asymptotic behavior in that they may be stationary, a random walk type process, or an explosive process. For the econometric analysis of nonexplosive time series it usually suffices to use weak consistency and weak convergence arguments as in the work by Phillips (1991) and Johansen (1995). When a time series has explosive features it is mathematically more natural to use strong consistency arguments exploiting that explosive processes tend to follow persistent trajectories with probability one.
The first results showing consistency for explosive first-order autoregressions were due to Rubin (1950) and Anderson (1959), with some generalizations by, for instance, Fuller, Hasza, and Goebel (1981) and Jeganathan (1988). A general strong consistency result for vector autoregressions was given by Lai and Wei (1985), and this is generalized here to a situation with deterministic terms as seen in econometric models. The techniques employed are to a large extent based on methods presented by Lai and Wei (1982, 1983a, 1983b, 1985) and Wei (1992).
The paper is organized so that Section 2 presents the model and an overview of the main results. The proofs follow in Section 3–10 and will be outlined in Section 2.
The following notation is used throughout the paper. For a matrix α let α[otimes ]2 = αα′, whereas α [otimes ] β is the Kronecker product and equals for example (α11 β,α12 β) if α ∈ R1×2. Further diag(α1,…,αn) is a block diagonal matrix with diagonal blocks αj. When α is symmetric then λmin(α) and λmax(α) are the smallest and the largest eigenvalue, respectively. The choice of norm is the spectral norm ∥α∥ = [λmax(α[otimes ]2)]1/2, implying that ∥α−1∥ = [λmin(α[otimes ]2)]−1/2. Whereas
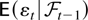
is a conditional expectation, the notation (Yt|Zt) denotes the residual of the least squares regression of Yt on Zt. The abbreviation a.s. is used for properties holding almost surely.
The model in this paper is for a p-dimensional time series, X1−k,…,X0,…,XT satisfying a kth-order vector autoregressive equation
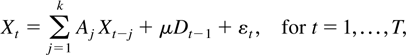
where Dt−1 is a deterministic term and εt an innovation term.
The innovations are required to satisfy the local Marcinkiewicz–Zygmund conditions for convergence of explosive processes introduced by Lai and Wei (1983a). These are that (εt) is a martingale difference sequence with respect to an increasing sequence of σ-fields
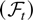
with the properties that some conditional moments of higher order are bounded and that the conditional variance has positive definite limit points.

Each of the Assumptions 2.1 and 2.2 excludes the possibility that the innovations could be autoregressive conditional heteroskedastic (ARCH) as proposed by Engle (1982). Therefore these conditions would probably be perceived as too strong for nonexplosive situations, but for general autoregressions they are convenient.
The deterministic term Dt is a vector of terms such as a constant, a linear trend, or periodic functions such as seasonal dummies. Inspired by Johansen (2000) the deterministic terms are required to satisfy the difference equation
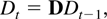
where D has characteristic roots on the complex unit circle. For example
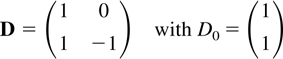
will generate a constant and a dummy for a biannual frequency. The deterministic term Dt is assumed to have linearly independent coordinates, which is formalized as follows.
Assumption 2.3. |eigen(D)| = 1 and rank(D1,…,Ddim D) = dim D.
With this type of deterministic term the time series can be written conveniently in companion form. The stacked process Xt−1 = (Xt−1′,…,Xt−k′)′ satisfies
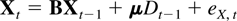
when defining matrices B and μ and a process eX,t as

whereas St = (Xt′,Dt′)′, which combines Xt with the deterministic process Dt, satisfies
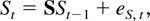
where S and eS,t are defined as
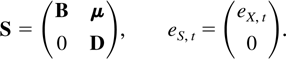
The main object of interest is the least squares estimator for the parameters A1,…,Ak,μ, which has the form
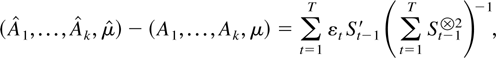
where St−1[otimes ]2 is the outer product St−1 St−1′. The partial estimator for the dynamic parameters A1,…,Ak can correspondingly be written in terms of the residuals (Xt|Dt) from regressing the companion vector Xt on the deterministic terms Dt as
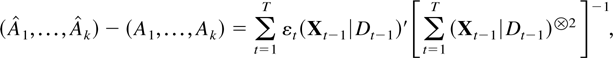
whereas the least squares variance estimator satisfies
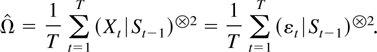
The first main result gives a bound for a studentized version of the joint estimator.
THEOREM 2.4. Suppose Assumptions 2.1–2.3 are satisfied. Then
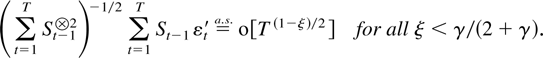
The remainder term can be decomposed as a sum of the following terms:

Special cases have been proved by Pötscher (1989, Lemma A.1) for dim D = 0 and ξ = 0 and by Nielsen (2001a), who proves a univariate version holding in probability.
The proof of Theorem 2.4 relies on a separation of the stochastic and deterministic components using that
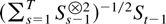
can be rewritten as
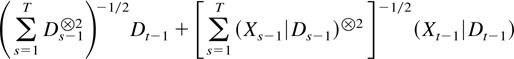
by partitioned inversion. For the least squares estimator itself a more complete understanding of the interaction between the deterministic components and unit root processes appearing in the denominator matrix is needed. Such results are not available as yet, and the following consistency results are therefore only partial although they do represent some improvement over previous results and include a complete description of the pure stationary and purely explosive cases where |eigen(B)| ≠ 1.
THEOREM 2.5. Suppose Assumptions 2.1–2.3 are satisfied. Then
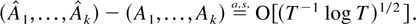
If B and D have no common eigenvalues then
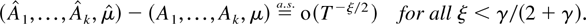
The issue of consistency of the least squares estimator was first discussed for a univariate, explosive, Gaussian first-order autoregression, with dim X = 1, dim D = 0, by Rubin (1950) and Anderson (1959). Lai and Wei (1985, Theorem 4) studied strong consistency for the special case without deterministic terms, so dim D = 0, and gave a weaker result with ξ = 0. A related generalization has previously been presented by Duflo, Senoussi, and Touati (1991, Theorem 1) in the case where the explosive roots have multiplicity one, whereas their Theorem 2 seems false in suggesting that the least square estimator for B otherwise is inconsistent.
A direct consequence of Theorem 2.4 concerning the studentized least squares estimator is that the least squares variance estimator can be estimated consistently.
COROLLARY 2.6: Suppose Assumptions 2.1–2.3 are satisfied. Then
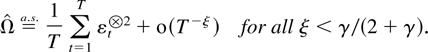
Although Assumptions 2.1 and 2.2 suffice to ensure that the sequence
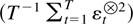
is relatively compact with positive definite limit points as argued by Lai and Wei (1985), some further structure is needed to get convergence to an interpretable matrix. In light of Assumptions 2.1 and 2.2 it is convenient to apply the following sufficient condition used by Chan and Wei (1988).
Assumption 2.7.
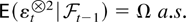
where Ω is positive definite.
This gives rise to the following convergence result.
THEOREM 2.8. Suppose Assumptions 2.1 and 2.7 are satisfied. Then
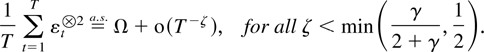
Corollary 2.6 and Theorem 2.8 lead to an immediate result for the least squares variance estimator.
COROLLARY 2.9. Suppose Assumptions 2.1, 2.3, and 2.7 are satisfied. Then
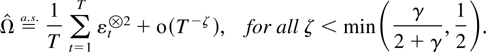
There is potential for many other econometric applications of Theorem 2.4. An example is lag length determination, where it is conceptually important to establish the lag length before determining the location of the characteristic roots; see Pötscher (1989), Wei (1992), and Nielsen (2001b). Other examples are unit root testing (Nielsen 2001a) and cointegration analysis (Nielsen, 2000), where the asymptotic inference results also can be used without knowledge about the characteristic roots.
The remainder of the paper gives the proofs of these results. To a large extent the proofs follow those of Lai and Wei (1983b and 1985) but with many modifications because of the deterministic term. The proofs are outlined as follows. In Section 3 the process Xt is decomposed into autoregressive components Ut,Vt,Wt with characteristic roots outside, on, and inside the unit circle, respectively. The order of magnitude of the deterministic process, Dt, and the process itself, Xt, is discussed in Sections 4 and 5, respectively. The next sections are concerned with the order of magnitude of the denominator matrix
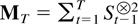
. As a first step the sample correlation of Ut and Dt is considered in Section 6. The order of magnitude of the largest and the smallest eigenvalue of MT is then discussed in Sections 7 and 8, respectively. The next step is to discuss sample correlations of all possible combinations of the processes Ut,Vt,Wt,Dt in Section 9, and finally the main results are proved in Section 10.
The process Xt is decomposed in two ways to facilitate the subsequent asymptotic analysis. The first decomposition concerns the stochastic part of the process whereas the second decomposition disentangles deterministic and stochastic parts of the process.
The first decomposition separates the eigenvalues of the companion matrix B for the stochastic part of the process. Following Herstein (1975, p. 308) there exists a regular, real matrix M that transforms B into a real block diagonal matrix with blocks U, V, and W having eigenvalues with absolute value less than one, equal to one, and larger than one, respectively. That is,

For the purpose of proving the results of Section 2 it can be assumed without loss of generality that B = diag(U,V,W) is block diagonal and St = (Ut′,Vt′,Wt′,Dt′)′.
The second decomposition seeks to separate the stochastic and deterministic components and is based on two arguments. The processes Ut,Wt,Dt are first separated by a similarity transformation using that the matrices U, W, and D have no common eigenvalues, whereas the processes Vt,Dt have to be discussed in more detail because the matrices V and D may in general have common eigenvalues.
The processes Ut,Wt are linear functions of the deterministic process Dt, and they are first shown to satisfy the relationships

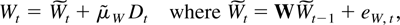
with
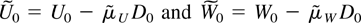
. The argument is the same in both cases. Taking Ut as an example consider the companion matrix for the vector (Ut′,Dt′) and apply a similarity transformation of the form
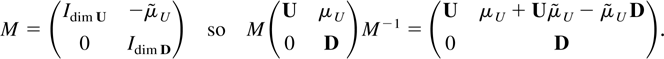
The result (3.1) then follows by arguing that
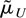
can be chosen so
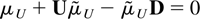
. Because the matrices U and D have no common eigenvalues a unique solution

can be found according to Gantmacher (2000, p. 225).
In the special case where B has no eigenvalues in common with D the same argument can be made for the entire process Xt as for the Ut,Wt processes. That is,
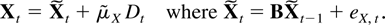
When it comes to the general situation where V and D are allowed to have common eigenvalues it is convenient first to discuss the special case where V and D have their eigenvalues at one and are both Jordan matrices

with (Λ,E) = (1,1). In that situation Vt will be shown to satisfy
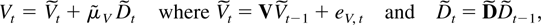
with
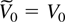
and where
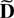
is of the form (3.4) with
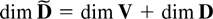
. To see this write the process (Vt,Dt) in companion form as
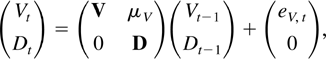
which has the solution
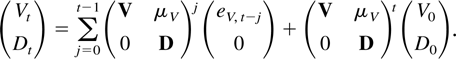
The result (3.5) is therefore a consequence of the following two properties:
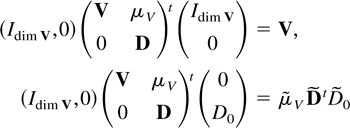
for some matrices
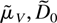
. The second property is proved as follows. Because V and D are both Jordan blocks of the form (3.4) with eigenvalues at one a real matrix M exists so that
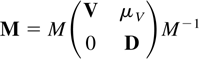
is a block diagonal matrix with diagonal elements that are Jordan blocks of the form (3.4) with (Λ,E) = (1,1). The left-hand side of (3.7) can then be written as a sum:
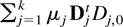
for some matrices μj,Dj,0 and Jordan blocks Dj. Writing the vector Dj,0 as T(0,1)′ where T is an upper triangular band matrix and noting that upper triangular band matrices commute then μjDjtDj,0 = μjDjtT(0,1)′ = μjTDjt(0,1)′. This in turn can be written as
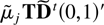
, ensuring the desired result (3.7) with
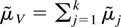
.
In general V and D can have eigenvalues anywhere on the unit circle. Suppose these occur at l distinct complex pairs exp(iθj) and exp(−iθj) for 0 ≤ θj ≤ π, which of course reduce to a single eigenvalue of 1 or −1 if θj equals 0 or π. Following Herstein (1975, p. 308) and using Assumption 2.3 to D there exist regular, real similarity transformations MV and MD that block-diagonalize V and D as
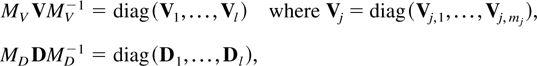
where the subblocks Vj,m and Dj are real Jordan matrices of the form (3.4) and where (Λ,E) is one of the pairs
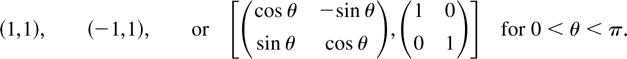
Using the same argument as before it therefore holds in general that Vt has representation (3.5) where
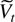
has subcomponents
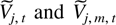
of dimension dim Vj and dim Vj,m, respectively, and
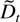
has subcomponents
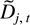
of dimension
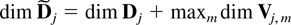
.
Combining the results (3.1), (3.2), and (3.5) with the notation
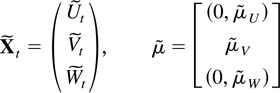
shows that the process without loss of generality can be represented as
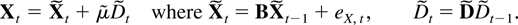
It is convenient also to introduce the dimensions
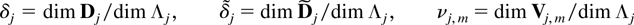
and also the maxima
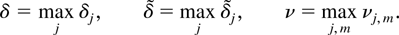
In the following discussion the order of magnitude of the deterministic process Dt and the denominator matrix
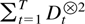
will be described.
The main result is formulated using normalization matrices
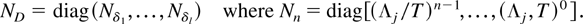
THEOREM 4.1. Suppose Assumption 2.3 is satisfied. Then it holds that

Two lemmas concerning the order of
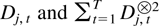
are needed.
LEMMA 4.2. Let Dj,1,0 denote the last element of the initial vector Dj,0. Then
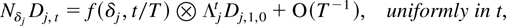
where f is the polynomial vector f(n + 1,u) = [un/(n!),…,u0/(0!)]′.
Proof of Lemma 4.2. The process Dj,t satisfies Dj,t = DjtDj,0 where
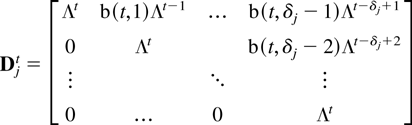
and b(·,·) is the binomial coefficient. The desired result then follows by noting that
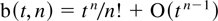
uniformly in t whereas ∥Λn∥ ≤ ∥Λ∥n = 1. █
LEMMA 4.3.

Proof of Lemma 4.3. (i) By Lemma 4.2 the cross-product satisfies
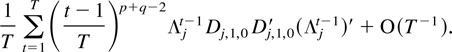
Trigonometric identities show that ΛjtDj,1,0 Dj,1,0′(Λjt)′ equals Ej∥Dj,1,0∥2/dim Λj + Rj where Rj = 0 for dim Λj = 1 and Rj = cos(2θt)A + sin(2θt)B for some constant matrices A,B when dim Λj = 2. When dim Λj = 1 the desired result follows immediately, whereas when dim Λj = 2 it follows from the result
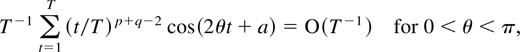
for any constant a; see Gradshteyn and Ryzhik (1965, 2.633.2).
(ii) Note that the vector f (n,u) can be expressed as a nonsingular linear transformation of the first n Legendre polynomials, p(n,u), say, which have the property that
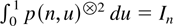
giving the positive definiteness.
(iii) Use the same type of arguments as in (i), noting that ΛjtDj,1,0 Dm,1,0′(Λmt)′ equals cos(2θt)A + sin(2θt)B for some constant matrices A,B. █
Proof of Theorem 4.1.
(i)The result follows from Lemma 4.2 by stacking the processes Nδj Dj,t and using the triangle inequality.
(ii) Lemma 4.3 implies that
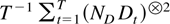
converges to a block diagonal matrix with positive definite diagonal elements.
(iii) The desired result follows from (i) and (ii) and replacing each Dt with ND Dt. █
In the following discussion the order of magnitude of the process Xt is investigated. This is a generalization of Lai and Wei (1985, Theorem 1) where the case without deterministic components is considered. Subsequently a convergence result is given for the explosive component Wt.
To describe the order of magnitude of Xt let λj denote the distinct eigenvalues of B whereas mj is the multiplicity of λj. Define the multiplicity of the largest eigenvalue as
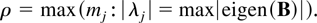
The following result then holds.
THEOREM 5.1. Suppose Assumptions 2.1 and 2.3 are satisfied. Then, for ξ < γ/(2 + γ),

Proof of Theorem 5.1. By (3.9) it holds that
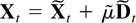
. Lai and Wei (1985, Theorem 1) show the results for the purely stochastic component

, whereas the order of the deterministic component
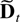
follows from Lemma 4.2. █
When studying the process
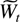
Lai and Wei (1985) use the following generalization of the Marcinkiewicz–Zygmund theorem.
THEOREM 5.2 (Lai and Wei, 1983a, Corollaries 3 and 4). Suppose Assumptions 2.1 and 2.2 are satisfied. Then for any sequence of matrices At the series
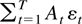
converges a.s. if and only if the series

converges. If this holds, and At ≠ 0 for infinitely many t, then
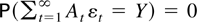
for any variable Y that is
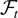
-measurable for some t.
This result yields a more precise statement about the order of magnitude of the explosive component.
COROLLARY 5.3. Suppose Assumptions 2.1–2.3 are satisfied. Then

Proof of Corollary 5.3.

One major difference between the results presented here and the work of Lai and Wei (1985) is that deterministic terms are included in the model. Before turning to the question of how big the denominator matrix can be in Section 7 it is convenient to consider the asymptotic order of magnitude of correlations between the zero mean process with roots smaller than one,
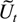
, and the deterministic component, Dt.
As a first step toward discussing the sample correlation of
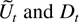
, results of Lai and Wei concerning the matrices
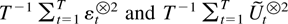
are stated. The results give conditions for relative compactness of sequences of such matrices. Recalling that the relative compactness of a sequence is the property that the limit points fall in a compact set, this enables a discussion of the order of magnitude of the sequence under weak assumptions. In particular, a condition is given ensuring that the limit points are bounded away from zero.
THEOREM 6.1 (Lai and Wei, 1985, Theorem 2, equation (3.7), Example 3). Suppose Assumption 2.1 is satisfied. Then, with probability one, the matrix sequences
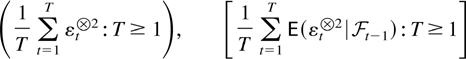
are relatively compact with the same limit points.
If in addition Assumption 2.2 is satisfied, the limit points are positive definite.
Because eU,t is a linear combination of εt the sequence
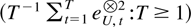
is therefore relatively compact. In addition the following results can be shown.
THEOREM 6.2 (Lai and Wei, 1985, Theorem 2, Example 3). Suppose Assumptions 2.1 and 2.2 are satisfied. Then it holds with probability one that

and also it holds that

Before turning to the sample correlation of
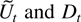
it is useful to cite the following univariate result by Wei (1985).
LEMMA 6.3 (Wei 1985, Lemma 2). Suppose Assumption 2.1 is satisfied. Let (xt) be a sequence of random variables adapted to
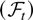
with
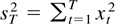
. Assume
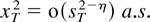
for some η > 0. Then
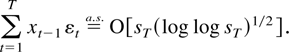
The result for the sample correlation of
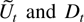
can now be stated and proved.
THEOREM 6.4. Suppose Assumptions 2.1–2.3 are satisfied. Then, for all η > 0,
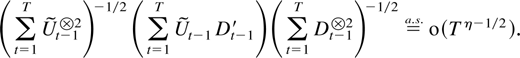
Proof of Theorem 6.4. Theorem 6.2 shows that
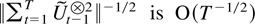
, so it suffices to show that
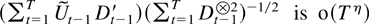
.
The main contribution arises from the sum
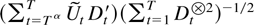
for an α satisfying 1 > α > 0. With this in mind and using
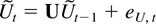
the object of interest can be written as
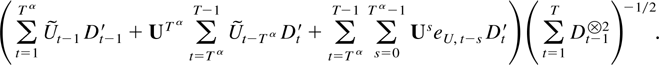
The first two terms in (6.1) are o(Tη). To see this bound their norm by
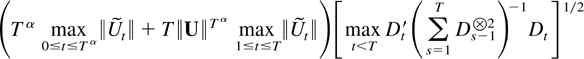
and use Theorems 4.1 and 5.1 and that ∥U∥Tα decreases exponentially.
The third term in (6.1) is o(Tη). To see this use Dt = DsDt−s and the normalization ND given in (4.1) to rewrite it as
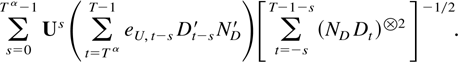
The norm of this expression is bounded by
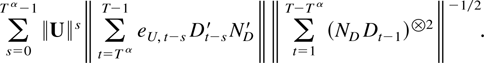
Because the sum

converges it suffices to show that the last two components can be approximated uniformly by a variable that is o(Tη).
The sum
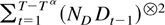
is approximately equal to
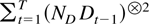
, which converges to a positive definite matrix; see Theorem 4.1. The norm of the approximation error,

, is bounded by
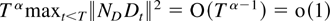
, because of Theorem 4.1.
In a similar way
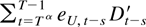
is approximately
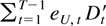
, which is not dependent on s. Considering each element of this matrix and applying Lemma 6.3 shows that this is o(TηND−1). The approximation error can be bounded by
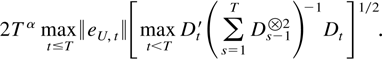
Using Theorems 4.1 and 5.1 this is seen to be o(Tα−ξ/2), which is o(1) for a small α. █
Some immediate consequences of these results are the following examples.
Suppose Assumptions 2.1 and 2.7 are satisfied. Then Theorems 6.1 and 6.2 imply
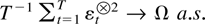
and in particular
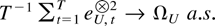
for some matrix ΩU, so
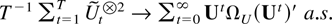
Suppose Assumptions 2.1–2.3 are satisfied. Then Theorems 6.2 and 6.4 and equation (3.1) imply that the sequence of matrices
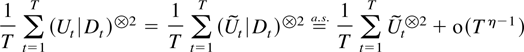
is relatively compact with positive definite limit points. Moreover, this series converges almost surely if
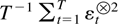
is convergent. According to Example 6.5 this is for instance the case if, in addition, Assumption 2.7 is satisfied.
The order of magnitude of the largest eigenvalue of the denominator matrix
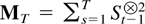
can now be described. This is followed by a convergence result for the purely explosive case and a bound for the rate of convergence of sum of powers of
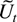
.
First, the largest eigenvalue of MT is considered in the following generalization of Lai and Wei (1985, Corollary 1).
THEOREM 7.1. Suppose Assumptions 2.1–2.3 are satisfied. Then

Proof of Theorem 7.1. If max|eigen(B)| < 1 then
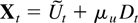
by (3.1). Lai and Wei (1985, Corollary 1) show
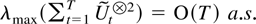
and the result then follows from Theorems 4.1 and 6.4. If max|eigen(B)| ≥ 1 the result follows directly from Theorem 5.1. █
For the explosive part of the process the following generalization of Lai and Wei (1985, Corollary 2) can be established.
COROLLARY 7.2. Suppose Assumptions 2.1–2.3 are satisfied and min|eigen(B)| > 1 so
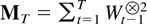
and recall the definition of W in Corollary 5.3. Then
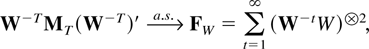
where FW is positive definite a.s.; hence
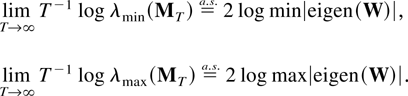
Proof of Corollary 7.2. Let RT denote the difference between the matrices
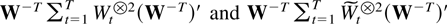
. The decomposition (3.2) shows
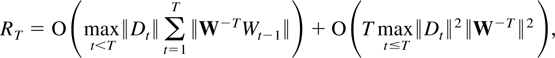
which vanishes for large T because of Theorem 4.1(i) and Corollary 5.3(i). The desired result is then a direct consequence of Lai and Wei (1983b, Theorem 2). █
Whereas Theorem 7.1 gives a bound for the sum of squares of the process, the following result gives a bound for sums of higher order powers of the stationary component.
THEOREM 7.3. Suppose Assumption 2.1 is satisfied. Then, for all η > 0 and ζ < γ,
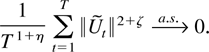
Proof of Theorem 7.3. For notational convenience define
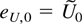
. Using Hölder's inequality it follows that
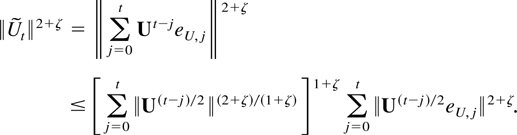
Summation over t then gives the following bound:
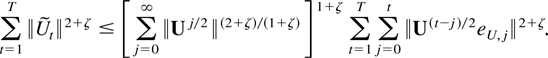
Changing summation index in the double sum, this can be bounded further by
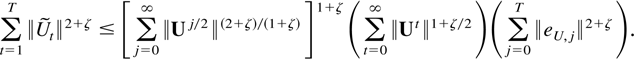
The first two sums converge, whereas the third term can be decomposed as
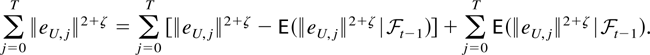
The latter term is of order O(T) = o(T1+η) by Assumption 2.1. The first term is a martingale. Normalized by T1+η it converges to zero a.s. on the set where

see Hall and Heyde (1980, Theorem 2.18). Minkowski's inequality shows that this sum is finite if the sum
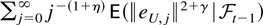
is finite. Assumption 2.1 ensures that this is the case. █
Three results are given concerning the order of the inverse of the denominator matrix,
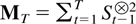
, of the least square estimator in the nonexplosive case. Using the techniques of Chan and Wei (1988) it can be proved that T−1MT is bounded from below in a weak convergence sense. The first result goes some way toward an almost sure version of this result in showing that the partial denominator matrix
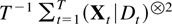
is bounded from below, whereas the second result shows that the joint matrix T−1MT is bounded from below in the special case where B and D have no common eigenvalues. In combination these results can be used to establish the third result concerning the order of maxTα≤t≤T St′MT−1St without actually establishing the order of MT−1, and this will suffice to prove the main theorems.
The first result concerns the partial denominator matrix
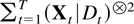
and is related to Lai and Wei (1985, Theorem 3).
THEOREM 8.1. Suppose Assumptions 2.1–2.3 are satisfied and |eigen(B)| ≤ 1. Then
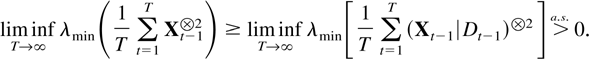
To prove Theorem 8.1 the following lemma is needed. This lemma ensures that Lai and Wei (1982, Lemma 1) concerning the order of magnitude of normalized least squares estimators can be used.
LEMMA 8.2. Suppose Assumptions 2.1–2.3 are satisfied. Then
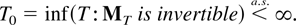
Proof of Lemma 8.2. It suffices to show that u′MTu > 0 for all u ∈ Rdim S so u ≠ 0 and some T. Because
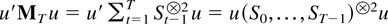
it is equivalent that (S0,…,ST−1)R spans Rdim S for some invertible matrix R.
The decomposition (3.9) shows that
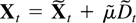
where
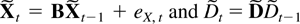
. The Cayley–Hamilton theorem (see Herstein, 1975, p. 334) implies that if
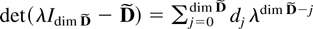
with d0 = 1 is the characteristic polynomial of
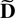
then
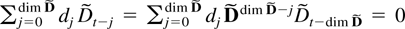
and in particular
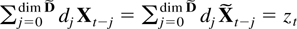
, say. Define
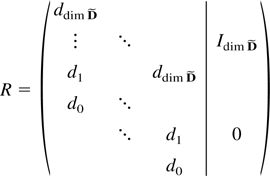
and partition R as a (2 × 2)-block matrix so the upper right block is a dim
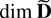
-dimensional square matrix. The preceding properties then show that (S1,…,ST)R is an upper triangular (2 × 2)-block matrix. The lower right block is
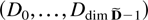
, which spans Rdim D by Assumption 2.3. It is left to prove that the upper left block
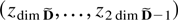
spans Rdim X. The process zt is a linear combination of the process
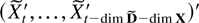
that satisfies a first-order autoregression without deterministic terms. The desired result then follows from Lai and Wei (1985, Theorem 3) using Assumptions 2.1 and 2.2. █
Proof of Theorem 8.1. Let m = dim X. Using the model equation (2.3) and that Dt−1−j = D−1−jDt the process Xt can be rewritten as
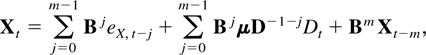
where eX,0 = X0, eX,−t = −μDt−1, and X−t = 0 for t > 0. It follows that

It is now argued that the lower bound in (8.1) satisfies
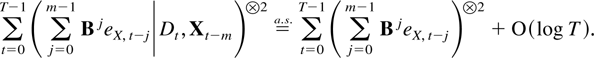
The norm of the difference between the left-hand side and the first term on the right is bounded by

The first sum is finite, so when normalized by the denominator term it is seen to be O(1) as a result of Lemma 8.2. The normalized second term is O[(log T)1/2] as a result of Lai and Wei (1982, Lemma 1), which can be used because of Lemma 8.2.
Using Lai and Wei (1982, Lemma 1) once again in combination with Theorem 6.2 shows that, for j < k,
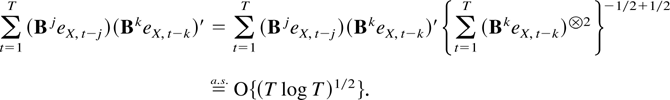
This in turn implies that
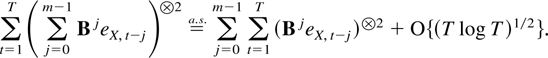
The proof is completed by combining (8.2), (8.3), and Theorem 6.2. █
When B and D have no common eigenvalues Theorem 8.1 can be extended.
THEOREM 8.3. Suppose Assumptions 2.1–2.3 are satisfied and B and D have no common eigenvalues. Then lim infT→∞ λmin(T−1MT) > 0 a.s.
Proof of Theorem 8.3. Because of the representation
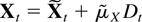
given in (3.3) it suffices to show the result for sums of squares of
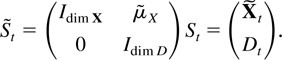
If
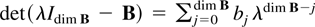
is the characteristic polynomial of B the Cayley–Hamilton theorem (see Herstein, 1975, p. 334) implies
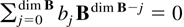
, and hence
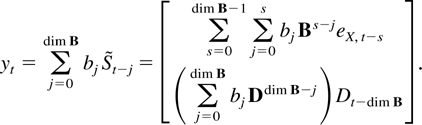
Because B and D have no common eigenvalues then
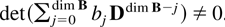
. It follows that
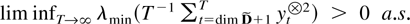
using Theorems 4.1, 6.2, and 6.4 and Lai and Wei (1985, equation (3.19)). The argument is finished as in the proof of Lai and Wei (1985, Theorem 3). █
The final and more technical result addresses the order of St′MT−1St. Lai and Wei (1985, Lemma 4) show that maxt≤T St′MT−1St vanishes when |eigen(B)| ≤ 1 and dim D = 0. For the subsequent analysis it suffices to take a maximum over just Tα ≤ t ≤ T for some 0 < α < 1 requiring that 0 < |eigen(B)| but allowing dim D > 0.
THEOREM 8.4. Suppose Assumptions 2.1–2.3 are satisfied and that 0 < |eigen(B)| ≤ 1. Then
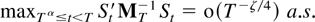
for all α,ζ so 0 < α < 1 and ζ < min[γ/(2 + γ),½].
Theorem 8.4 will be proved in a few steps following Lai and Wei (1983b). The first step is to strengthen their Lemma 3.
LEMMA 8.5. Let (at) be a sequence of nonnegative numbers satisfying the following conditions.

Then aT = o(T−ρ) for all ρ < min(1,κ/2).
Proof of Lemma 8.5. Condition (i) implies that for every 0 < ρ < 1 it holds that minT>t≥T−Tρ at ≥ aT − 2CTρ−κ for all large T. In particular, choosing ρ to satisfy 0 < ρ < min(1,κ/2), it is seen that
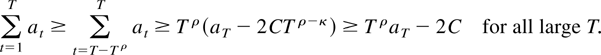
Combining this with (ii) it follows that
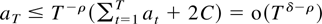
. Because δ can be chosen arbitrarily small this proves the desired result. █
The second step is to generalize Lai and Wei (1983b, Lemma 6ii).
LEMMA 8.6. Suppose Assumptions 2.1–2.3 are satisfied and max|eigen(B)| ≤ 1. Define T0 as in Lemma 8.2. Then
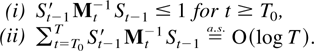
Proof of Lemma 8.6. The proof is the same as that of Lai and Wei (1983b, Lemma 6ii) using the generalizations of their Theorem 3 and Lemma 6i presented previously in Theorem 7.1 and Lemma 8.2. █
The third step is to generalize Lai and Wei (1983b, Lemma 7).
LEMMA 8.7. Suppose Assumptions 2.1–2.3 are satisfied and that 0 < |eigen(B)| ≤ 1. Then

Proof of Lemma 8.7. (i) Using Lai and Wei (1983b, Lemma 5i) in the same way as in the proof of Lai and Wei (1983b, Lemma 7i) it holds that
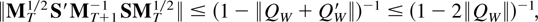
where
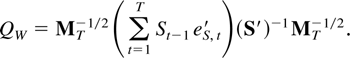
This expression can be rewritten using the identities
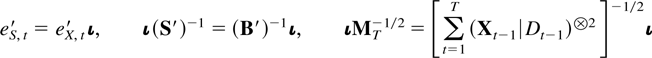
for ι = (Idim X,0). The desired result follows by noting that
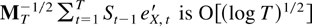
according to Lai and Wei (1982, Lemma 1), which can be used because of Lemma 8.2, whereas the term
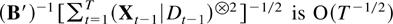
by Theorem 8.1.
(ii) Noting that ST = SST−1 + eS,T it holds that
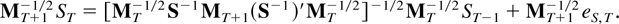
The norm of the first term is less than
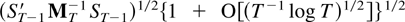
by (i). This is in turn bounded by
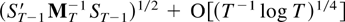
because of Lemma 8.6(i). The second term equals

according to the identities (8.4) and is seen to be o(T−ξ/2) by Theorems 5.1 and 8.1. █
Theorem 8.4 can now be proved.
Proof of Theorem 8.4. Lemmas 8.6(ii) and 8.7(ii) show that the conditions of Lemma 8.5 are satisfied for the sequence St′Mt−1St with κ = ζ/2 and therefore tζ/4St′Mt+1−1St = o(1) for large t. For t > T0 then Mt−1 > Mt+1−1 so that St′MT−1St ≤ St′Mt+1−1St, and thus for all ε > 0 and almost every outcome a T1 exists so that for all t,T so that T > t ≥ T1 it holds that St′MT−1St ≤ St′Mt+1−1St < ε. This in turn implies that for all ε > 0 and almost every outcome a T1 exists so that for all T so that T > T1 it holds that maxTα≤t<T St′MT−1St ≤ St′Mt+1−1St < ε as desired. █
It has already been established in Section 6 that the sample correlation of
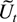
and Dt vanishes asymptotically. In the following discussion the remaining sample correlations of pairs of the processes
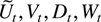
are studied. A first result concerns the sample correlation of Wt and Ut,Dt.
THEOREM 9.1. Suppose Assumptions 2.1–2.3 are satisfied. Then

The bound for the sample correlation of
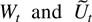
should be viewed in light of the results of Anderson (1959). He found that
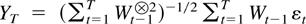
is convergent when the innovations εt are independent, identically distributed, but in general divergent. The stated result combined with Theorem 6.1 shows that the order of YT is at most o[T(1−ξ)/2] for martingale difference sequence innovations.
Proof of Theorem 9.1. The norms of the two expression are bounded by
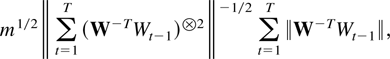
where m is either of
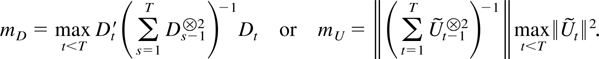
The last two terms of (9.1) are convergent according to Corollaries 5.3 and 7.2. It holds that mD = O(T−1) by Theorem 4.1, whereas mU = o(T−ξ) because Theorem 5.1 shows
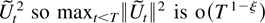
, whereas the denominator term is O(T−1) by Example 6.6. █
For the sample correlation between Wt and St=(Vt′,Dt′)′ a different type of proof is needed using the results of Section 8. This is because the order of the smallest eigenvalue of

is unknown.
THEOREM 9.2. Suppose Assumptions 2.1–2.3 are satisfied. Then, for all ζ < min[γ/(2 + γ),½], it holds that
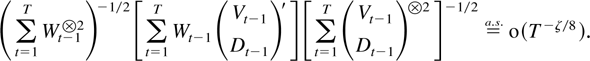
Proof of Theorem 9.2. For convenience define

Because
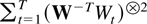
is convergent according to Corollary 7.2 it suffices to show that

. Follow Anderson (1959, Theorem 2.2) in writing
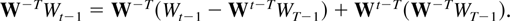
Because
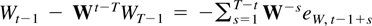
it follows, for any 0 < α < 1, that

The first two terms in (9.3) vanish exponentially fast. Their norm is less than
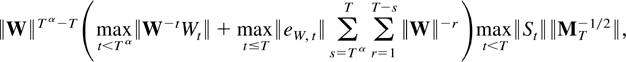
where ∥W∥Tα−T vanishes exponentially, MT−1 = O(1) by Lemma 8.2, and the remaining terms are of polynomial order according to Theorem 5.1 and Corollary 5.3.
The final term in (9.3) is o(T−ζ/8). Its norm is less than
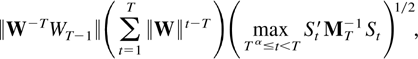
where the first two components converge (see Corollary 5.3) and the last component is o(T−ζ/8) by Theorem 8.4. █
Remark 9.3. The bottleneck in the proof of Theorem 9.2 is the order of magnitude of maxTα<t≤T St′MT−1St. By extending the weak convergence results of Chan and Wei (1988) it can be proved that this term is
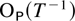
when |eigen(B)| ≤ 1, implying that the sample correlation between Wt and (Vt′,Dt′) is
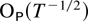
.
Wei (1992, Theorem A.1) considers the sample correlation between Ut and Vt in the univariate case dim X = 1 when Dt is absent and εt is a martingale difference sequence satisfying Assumptions 2.1 and 2.7. That result can be generalized and strengthened by a proof resembling that of Theorem 6.4.
THEOREM 9.4. Suppose Assumptions 2.1–2.3 are satisfied. Then, for all ξ < γ/(2 + γ),
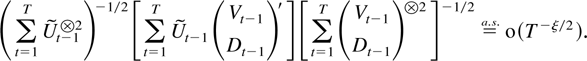
Proof of Theorem 9.4. Define St, S, eS,t, and MT as in (9.2). Theorem 6.2 shows that
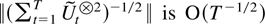
, so it suffices to show that
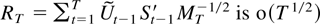
. Inspired by the proof of Theorem 6.4 and Wei (1992, Theorem A.1) write
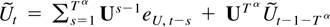
for some 0 < α < 1 so that
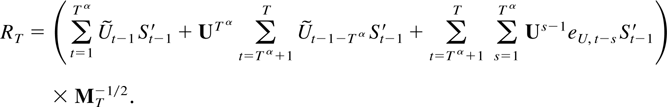
The first term in (9.4) is o[T(1−ξ)/2]. The norm of the sum
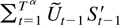
is bounded by
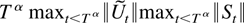
, which is of the desired order when α is chosen small enough and using Theorem 5.1, whereas MT−1/2 is bounded as a result of the positive definiteness of MT stated in Lemma 8.2.
The second term in (9.4) is o(1). By Cauchy–Schwarz inequality its norm is bounded by
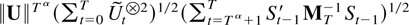
where ∥U∥Tα vanishes exponentially and the other terms are O[(T log T)1/2] as a result of Theorem 6.2 and Lemma 8.6(ii).
The third term of (9.4) is o[T(1−ξ)/2]. Its norm is bounded by
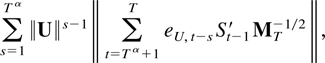
according to the triangle inequality. Hölder's inequality implies
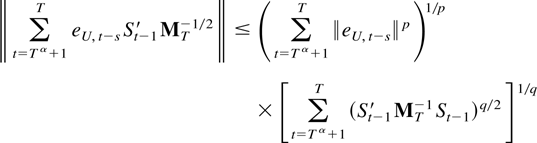
for 2 < p < 2 + γ and p−1 + q−1 = 1. Because q/2 < 1 and Tα > T0 for large T, then (St′MT−1St)q/2 ≤ St′MT−1St ≤ St′Mt−1St, so the last term is o(Tη) for all η > 0 according to Lemma 8.6(ii). Because of Theorem 7.3 then
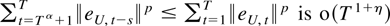
uniformly in s. Overall the sum in t is therefore o[T(1−ξ)/2] uniformly in s. The desired result then follows because
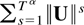
converges. █
Tables 1 and 2 give an overview of the sample correlation results of Theorems 6.4, 9.1, 9.2, and 9.4. All pairs of
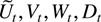
have been considered except for Vt,Dt, which has nonnegligible sample correlation when V and D have common characteristic roots. To produce these tables it is used that the marginal sample correlation, C(x,y), of processes xt,yt relates to joint correlations by
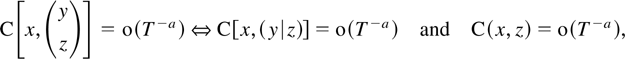
according to the formula for partitioned inversion, and also by
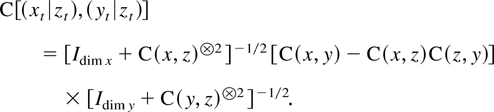
Order of pairwise sample correlations, with η > 0 and ξ < γ/(2 + γ)

Order of pairwise sample correlations, with η > 0 and ξ < γ/(2 + γ)

As a consequence of the results summarized in Table 2 the condition |eigen(B)| ≤ 1 can be eliminated in Theorem 8.1 concerning the lower bound for
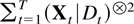
.
COROLLARY 9.5. Suppose Assumptions 2.1–2.3 are satisfied. Then
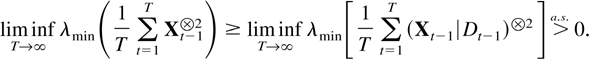
Proof of Corollary 9.5. Let Rt = (Ut′,Vt′)′. Using a similarity transformation M as described in Section 3 and the results in Table 2 shows that
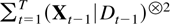
equals
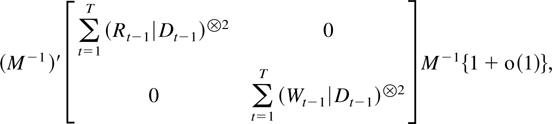
a.s. Apply Theorem 8.1 to the upper left block and Corollary 7.2 and Theorem 9.1 to the lower left block. █
The proofs of the main results in Theorems 2.4, 2.5, and 2.8 now follow. The first of these results concerns the studentized least squares estimator.
Proof of Theorem 2.4. The process St is a linear combination of Rt = (Ut′,Vt′,Dt′)′ and Wt. As a consequence of Theorems 9.1 and 9.4 the sample correlation of Rt and Wt vanishes asymptotically; see also Table 1. The vector of interest therefore equals
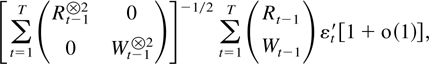
so the nonexplosive and explosive components can be considered separately.
For the explosive component note that the norm of
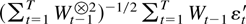
is bounded by
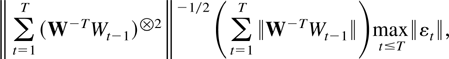
where the first two terms are convergent because of Corollaries 7.2 and 5.3. The order of the last term is given in Theorem 5.1.
For the nonexplosive part with max|eigen(B)| = 1 Lai and Wei (1982, Lemma 1) together with Theorem 7.1 shows the desired result.
For max|eigen(B)| < 1 then Lemma 6.3 combined with Theorems 4.1, 6.2, and 6.4 shows the result. █
By combining Theorem 2.4 with results for the denominator matrix established in Sections 7 and 8 the strong consistency result for the least squares estimator can now be proved.
Proof of Theorem 2.5. Consider first the partial estimator. Transforming Xt into (Rt′,Wt′) with Rt = (Ut′,Vt′)′ using a similarity transformation M as described in Section 3 shows that
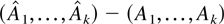
equals
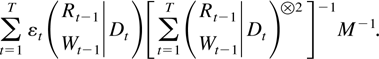
The sample correlation between (Rt−1|Dt) and (Wt−1|Dt) vanishes asymptotically, so it suffices to prove the result for the two special cases where max|eigen(B)| ≤ 1 so dim W = 0 and where min|eigen(B)| > 1 so dim R = 0. In the first case the desired order follows from Theorems 2.4 and 8.1 whereas in the second case the statistic vanishes exponentially fast as a result of Theorem 2.4 and Corollary 7.2.
The second result for the full estimator when B and D have no common eigenvalues follows from Theorems 2.4 and 8.3. █
Proof of Theorem 2.8. Assumption 2.7 shows that mt = a′(εt2 − Ω)b for arbitrary dim X-vectors a and b. Hall and Heyde (1980, Theorem 2.18) show that if 1 ≤ p ≤ 2 then
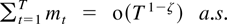
on the set
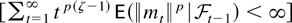
. This set has probability one if p ≤ 1 + γ/2 and p(ζ − 1) < −1 according to Assumption 2.1. These restrictions are satisfied when ζ < min[γ/(2 + γ),½]. █

Order of pairwise sample correlations, with η > 0 and ξ < γ/(2 + γ)

Order of pairwise sample correlations, with η > 0 and ξ < γ/(2 + γ)