Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-11T12:18:51.040Z Has data issue: false hasContentIssue false
  • English
  • Français

REDUCING BIAS OF MLE IN A DYNAMIC PANEL MODEL

Published online by Cambridge University Press:  15 March 2006

Jinyong Hahn  and
Hyungsik Roger Moon
Jinyong Hahn
Affiliation:
UCLA
Hyungsik Roger Moon
Affiliation:
University of Southern California
Rights & Permissions [Opens in a new window]

Abstract

This paper investigates a simple dynamic linear panel regression model with both fixed effects and time effects. Using “large n and large T” asymptotics, we approximate the distribution of the fixed effect estimator of the autoregressive parameter in the dynamic linear panel model and derive its asymptotic bias. We find that the same higher order bias correction approach proposed by Hahn and Kuersteiner (2002, Econometrica 70, 1639–1659) can be applied to the dynamic linear panel model even when time specific effects are present.We thank Peter Phillips and three anonymous referees for helpful comments. The first author gratefully acknowledges financial support from NSF grant SES-0313651. The second author appreciates the Faculty Development Awards of USC for research support.

Type
MISCELLANEA
Information
Econometric Theory , Volume 22 , Issue 3 , June 2006 , pp. 499 - 512
Copyright
© 2006 Cambridge University Press

1. INTRODUCTION

One of the advantages of panel data is that they allow the possibility of controlling for unobserved individual heterogeneity. Failure to control for such heterogeneity can result in misleading inferences. Although it is intuitive to deal with the unobserved individual effect by treating each such effect as a separate parameter to be estimated, such estimators are typically subject to the incidental parameters problem noted by Neyman and Scott (1948). In a simple dynamic linear panel regression model, the fixed effect estimator of the autoregressive coefficient is severely biased when the cross-sectional dimension is large but the time series dimension is small.1

Various alternative methods, including the generalized method of moments (GMM) approach with first differenced data, have been proposed. For a survey on recent developments of these methods, one can refer to Arellano and Honoré (2001).

See Nickell (1981), Kiviet (1995), Alvarez and Arellano (2003), and Phillips and Sul (2003b). Phillips and Sul (2003a) investigate the median unbiased estimation method for various dynamic linear panel regression models.

Adopting a perspective that such bias can be understood as a higher order time series bias, Hahn and Kuersteiner (2002, 2003) propose a method that reduces the bias of the fixed effects estimator. Using alternative asymptotics where both n and T are large, they establish that a simpler form of the higher order bias can be derived. The alternative asymptotics, where both n and T grow to infinity,2

In other words, the alternative asymptotics are joint asymptotics, not sequential asymptotics. For discussion on the difference between the two, see, for example, Phillips and Moon (1999).

can be quite convenient, especially for nonlinear panel models. See Hahn and Newey (2004) and Hahn and Kuersteiner (2003).

The panel models considered by Hahn and Kuersteiner (2003) and Hahn and Newey (2004) do not include any time effect, mainly because of analytical difficulties in nonlinear models. As argued in Hahn and Kuersteiner (2003), the alternative asymptotics can be understood as a simpler form of higher order time series asymptotics with fixed n. When time effects are not present, higher order time series asymptotics is straightforward, although tedious. Unfortunately, time effects create an incidental parameter problem in the time series domain, because the number of time effects grows to infinity as T → ∞, which explains the analytic difficulty there.3

The GMM approach based on fixed T assumption can easily handle models with time effects. See, for example, Holtz-Eakin, Newey, and Rosen (1988), and Ahn, Lee, and Schmidt (2001). These papers, in fact, consider more general models where the time effects are individually heterogeneous.

In this paper, we make a contribution to understanding the bias of fixed effects estimators in models with time effects. We establish the asymptotic distribution of the fixed effect estimator (or Gaussian quasi maximum likelihood estimator [QMLE]) of the autoregressive parameter when both n and T are large. In particular, we derive the asymptotic bias of the fixed effect estimator and propose an estimator that corrects for the asymptotic bias. We find that the asymptotic bias is the same as the one in the panel model of Hahn and Kuersteiner (2002) without the time effect. It follows that the same higher order bias correction approach as in Hahn and Kuersteiner (2002) can be adopted even when time effects are present. We should stress that such robustness is limited only to linear models. For more general models, we expect that estimation of time effects would lead to biases in addition to the biases due to estimation of individual effects. Because these two biases need to be analyzed simultaneously, it is not trivial to extend the analysis of Hahn and Kuersteiner (2003) or Hahn and Newey (2004) to nonlinear models with both time effects and individual effects.

This paper is organized as follows. In Section 2 we introduce a linear dynamic panel regression model with both individual effects and time effects and assumptions. The main results are summarized in Theorems 1 and 2. Section 3 concludes the paper. All the technical proofs and derivations are collected in the Appendix.

2. MAIN RESULT

We consider a simple dynamic panel regression model with fixed individual effects and time specific effects,

where yit are m-dimensional observables, εit are mean zero scalar error terms, θ is an m × m matrix of parameters of interest, i denotes the cross-sectional unit, and t denotes the time index.4

The panel vector autoregression (VAR) model may be understood as a completion of the univariate dynamic panel AR(1) model with additional regressors. If we write yit = (Yit,Xit+1′)′, then the first component of the model (1) can be rewritten as

where ci, gt, and (β,γ′) denote the first components of (Im − θ)αi, ft, and the first row of θ, respectively. This implies that, under the special circumstances where Xit follows a first-order VAR, we can regard model (1) as a completion of this model. Under this interpretation, model (1) encompasses panel models with further regressors such as this model.

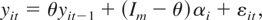
We denote n and T to be the dimensions of cross section and time series, respectively, of the panel. In model (1), the parameter αi (m × 1) signifies fixed individual effects, and ft (m × 1) represents time specific effects. The dynamic panel model in (1) extends the conventional dynamic panel model with fixed effects,

where the dynamics of the panel data yit does not include time effects. In many empirical applications, the time effect ft is included to model a simple form of nonstationarity in the time series of yit or to represent an aggregate shock (e.g., a common macro shock) that is common to all the cross-section units. In the latter case, when the common shock ft is random, the cross-sectional observations yit have cross-sectional dependence.5

Recently Bai and Ng (2004), Moon and Perron (2004), and Phillips and Sul (2003a) have used a dynamic factor model to model cross-sectional dependence. The time effect model in (1) may correspond to a special case of the factor model with known homogeneous factor loading coefficients.

Before we proceed, we introduce a set of regularity conditions that will be used in deriving the main results in the following section. These conditions are the same as Conditions 1–3 in Hahn and Kuersteiner (2002).

Condition 1. (i) εit is independent and identically distributed (i.i.d.) across i and strictly stationary in t for each i, E [εit] = 0 for all i and t, E [εitεis′] = Ω for t = s and E [εitεis′] = 0 for t ≠ s, and has finite eighth moments; (ii) both n and T tend to infinity jointly under the restriction n/T → c, where 0 < c < ∞; (iii) limn→∞ θn = 0; (iv)

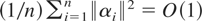
; (v)

.

The individual effect αi and the initial observations yi0 are assumed to be deterministic sequences. It is in principle possible to treat αi and yi0 as random, but we can avoid specifying their joint distribution by focusing our attention on the distribution of y's conditional on αi and yi0. Therefore, the distribution of the y's is in fact a conditional distribution. The time specific effect can be either a deterministic or a random sequence. When it is random, it does not have to be stationary. The fixed effects and the initial conditions are deterministic. Condition 1(ii) means that we adopt the “large n, T” asymptotics. Finally, notice that Condition 1(iii) excludes a possibility of unit roots in the panel. Our analysis fails to carry over to the case when the largest characteristic root of θ is one, which suggests that our approximation may not be accurate when yit has the largest root near unity, which was confirmed by the Monte Carlo study in Hahn and Kuersteiner (2002) for the simpler model without time effects. For a nonstationary dynamic panel model, see Moon and Phillips (2004), Moon and Perron (2004), and Phillips and Sul (2003a).

The next two conditions restrict the higher order serial dependence of the error term εit and its moments. For this, define

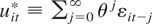
, which is well defined under Conditions 1(i) and (iii). Also, define zit = (Im [otimes ] uit−1*)εit.

Condition 2. (i)

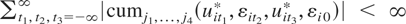
, and (ii)

, for all i and j1,…,j4 ∈ {1,…,m}, where cumj1,…,j4(·,·,·,·) is defined as in Brillinger (1981).

The estimator we consider in this paper is a fixed effect estimator. Let

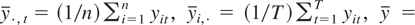
. Similarly, we define α, ε·,t, εi,·, and ε. For notational simplicity, write

. The estimator is defined as

It can be shown that

is the Gaussian maximum likelihood estimator (MLE) (see, e.g., Hsiao, 2003). The main purposes of the paper are (i) to find an asymptotic bias of the fixed effect estimator

as n,T → ∞ with n/T → c, where 0 < c < ∞ and (ii) to consider an estimator that corrects for the asymptotic bias.

Because

by definition, we have

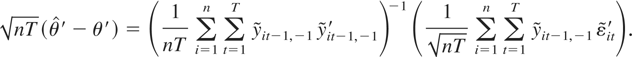
The following theorem finds the limiting distribution of

.

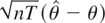
THEOREM 1. Suppose that Conditions 1 and 2 hold. Then,

where

According to Theorem 1, as n,T → ∞ with n/T → c, the fixed effects estimator

has a normal limiting distribution with an asymptotic bias −(1/T) (Im [otimes ] ϒ)−1(Im [otimes ] Im − (Im [otimes ] θ))−1 vec(Ω). This bias is the same as the bias found by Hahn and Kuersteiner (2002) with the linear dynamic panel regression with fixed effects in (2). Unlike the conventional model in (2), our model (1) assumes incidental parameters in both cross-section and time series. Theorem 1 shows that the incidental parameters in the time series, ft, do not contribute to the asymptotic bias of the fixed effect estimator and it is the αi, the cross-sectional incidental parameters, that cause the asymptotic bias.

To understand the different roles of the two incidental parameters, it is useful to consider a simple case where yit is univariate and εit are i.i.d. First, notice that QMLE estimation eliminates the individual effect αi through the following time series filtering:

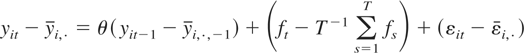
and then eliminates the time effect ft through the following cross-sectional filtering:6

The filtering sequence is chosen for convenience of explanation.

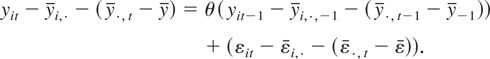
The covariance between the filtered regressor yit−1 − yi,·,−1 − (y·,t−1 − y−1) and the filtered error term εit − εi,· − (ε·,t − ε) can be shown

7

See equation (A.3) in the Appendix.

to consist of the following four covariances: (i) the correlation between yit−1 and εit, (ii) the correlation between yi,·,−1 and εi,·, (iii) the correlation between y·,t−1 and ε·,t, and (iv) the correlation between y−1 and ε. The second correlation is generated by the time series filtering in (3), and the third and fourth correlations are due to the cross-sectional filtering eliminating ft in (4). Now, because of the weak exogeneity of yit−1, it is easy to see that the first correlation is zero. Second, according to Hahn and Kuersteiner (2002), the second correlation times

, the convergence rate of the fixed effects estimator, does not vanish even though T → ∞ and remains as a bias in the limit distribution, if n,T → ∞ with n/T → c, where 0 < c < ∞. As for the third correlation, we observe that because the time series of yit−1 is weakly exogeneous and the cross section is independent, the time series of the cross section aggregate y·,t−1 is also weakly exogeneous with respect to the time series of the cross section aggregate ε·,t. Therefore, we expect that the third correlation is zero. Finally, we expect that the fourth correlation is negligible in large n and T samples. As a consequence, the additional filtering in (4) to eliminate the time effect does not have the same effect of the time series filtering in (3), which is why the asymptotic bias in Theorem 1 is identical to that in Hahn and Kuersteiner (2002) where only αi are assumed present.

In view of the limiting distribution of

in Theorem 1, to fix the asymptotic bias in

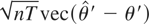
, we can use the same bias correction formula as in Hahn and Kuersteiner (2002). Define the following bias corrected estimator:

where

We can easily see that the bias corrected estimator

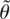
is asymptotically centered at zero:

8

The proof of Theorem 2 is straightforward and we omit it.

THEOREM 2. Under Conditions 1 and 2, we have

To assess the effectiveness of bias correction as discussed in Theorem 2, we conducted a small-scale Monte Carlo study for the simple case when yit is a scalar and the error term εit is i.i.d. with constant variance, which is summarized in Table 1. Note that the limiting distribution of

in Theorem 1 simplifies to

. For this simple situation, we may use the bias correction formula

as in Hahn and Kuersteiner (2002). This estimator may be intuitively understood by observing that the bias of

is approximately equal to

, which may be estimated by

, and as a consequence, the asymptotic distribution of

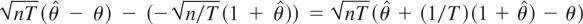
is centered at zero. For this bias corrected estimator, we find that the performance is almost identical whether the time effect is present in the model or not.

Performance of bias corrected maximum likelihood estimators

3. CONCLUSION

This paper investigates a simple dynamic linear panel regression model with both fixed effects and time effects. Using large n and T asymptotics, we approximate the distribution of the fixed effect estimator of the autoregressive parameter in the dynamic linear panel model and derive its asymptotic bias. As main results, we find that the asymptotic bias is the same as the one in the panel model of Hahn and Kuersteiner (2002) without the time effect, and we show that the same higher order bias correction approach proposed by Hahn and Kuersteiner (2002) can be applied to the dynamic linear panel model with both fixed effects and time effects. However, as mentioned in the introduction, we stress that the robustness of the bias correction approach of Hahn and Kuersteiner (2002) to the time effects model is limited only to a linear model so far.

APPENDIX

Before we start the proof of Theorem 1, we introduce the following notation. Define Θt−1 = (Im + θ + ··· + θt−2)(Im − θ) = (Im − θt−1), Ft−1 = ft−1 + θft−2 + ··· + θt−2f1, and uit−1 = εit−1 + θεit−2 + ··· + θt−2εi1, where t = 2,…,T. For notational convenience, define Θ0 = 0, F0 = 0, and ui0 = 0. We let

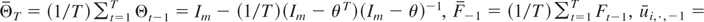
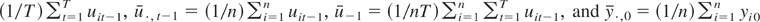
. By definition, then, we have

Therefore, we have

where

.

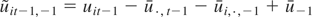
It will be convenient to define another process such that Yi0 = yi0 and

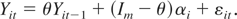
Note that

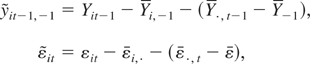
so that

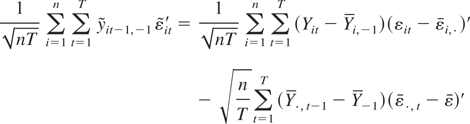
and

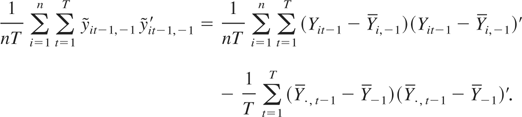
This is because

But because

we have the desired simplification. We note that Conditions 1 and 2 are identical to Conditions 1–3 in Hahn and Kuersteiner (2002). We also note that Yit is the same process considered there. Therefore, we can conclude that their Lemmas 6 and 7 are satisfied for Yit.

LEMMA 1 (Hahn and Kuersteiner, 2002, Lem. 6). Under Conditions 1 and 2, we have

LEMMA 2 (Hahn and Kuersteiner 2002, Lem. 7). Under Conditions 1 and 2, we have

In light of Lemmas 1 and 2, we can show that

by proving

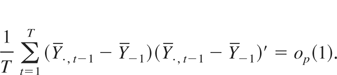
Because

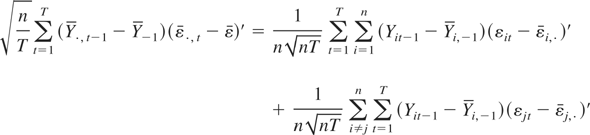
and the first term is of order Op(n−1) = op(1) by Lemma 1, it suffices to prove that

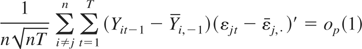
to establish (A.5). On the other hand, because

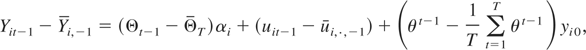
we can establish (A.7) by showing that

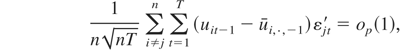
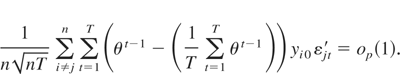
As for (A.6), we note that

and establish (A.6) by showing that

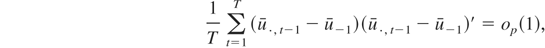
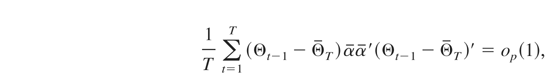
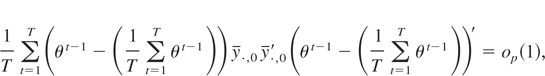
noting that the cross-product terms will all be of order op(1) by Cauchy–Schwartz.

We first show (A.8). Note that

The first term on the right has mean zero and variance equal to

The second term on the right also has mean zero and variance equal to

and is of the same order as (T/n)E [ui,·,−1ui,·,−1′]. But because

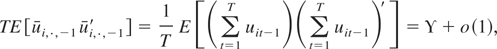
the second term is of order op(1) also. Therefore, we obtain (A.8).

As for (A.9), we note that

has mean zero and variance equal to

from which we obtain (A.9). Likewise, we can establish (A.10).

As for (A.11), we note that

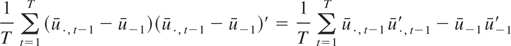
and that

from which we obtain

As for (A.12), we note that

and that (A.13) can be similarly established.

References

REFERENCES

Ahn, S.C., Y.H. Lee, & P. Schmidt (2001) GMM estimation of linear panel data models with time-varying individual effects. Journal of Econometrics 101, 219–255.Google Scholar
Alvarez, J. & M. Arellano (2003) The time series and cross-section asymptotics of dynamic panel data estimators. Econometrica 71, 1121–1160.Google Scholar
Arellano, M. & B. Honoré (2001) Panel data models: Some recent developments. In J. Heckman & E. Leamer (eds.), Handbook of Econometrics, vol. 5, pp. 3229–3296. Elsevier Science.
Bai, J. & S. Ng (2004) A PANIC attack on unit roots and cointegration. Econometrica 72, 1127–1177.Google Scholar
Brillinger, D. (1981) Time Series: Data Analysis and Theory. Holden-Day.
Hahn, J. & G. Kuersteiner (2002) Asymptotically unbiased inference for a dynamic panel model with fixed effects when both n and T are large. Econometrica 70, 1639–1659.Google Scholar
Hahn, J. & G. Kuersteiner (2003) Bias Reduction for Dynamic Nonlinear Panel Models with Fixed Effects. Mimeo, UCLA.
Hahn, J. & W. Newey (2004) Jackknife and analytical bias reduction for nonlinear panel models. Econometrica 72, 1295–1319.Google Scholar
Holtz-Eakin, D., W. Newey, & H. Rosen (1988) Estimating vector autoregressions with panel data. Econometrica 56, 1371–1395.Google Scholar
Hsiao, C. (2003) Analysis of Panel Data, 2nd ed. Cambridge University Press.
Kiviet, J. (1995) On bias, inconsistency, and efficiency of various estimators in dynamic panel data models. Journal of Econometrics 68, 53–78.Google Scholar
Moon, H.R. & B. Perron (2004) Testing for a unit root in panels with dynamic factors. Journal of Econometrics 122, 81–126.Google Scholar
Moon, H.R. & P.C.B. Phillips (2004) GMM estimation of autoregressive roots near unity with panel data. Econometrica 72, 467–522.Google Scholar
Neyman, J. & E. Scott (1948) Consistent estimates based on partially consistent observations. Econometrica 16, 1–31.Google Scholar
Nickell, S.J. (1981) Biases in dynamic models with fixed effects. Econometrica 49, 1417–1426.Google Scholar
Phillips, P.C.B. & H.R. Moon (1999) Linear regression limit theory for nonstationary panel data. Econometrica 67, 1057–1111.Google Scholar
Phillips, P.C.B. & D. Sul (2003a) Dynamic panel estimation and homogeneity testing under cross section dependence. Econometric Journal 6, 217–259.Google Scholar
Phillips, P.C.B. & D. Sul (2003b) Bias in Dynamic Panel Estimation with Fixed Effects, Incidental Trends and Cross Section Dependence. Mimeo, Yale University and University of Auckland.
Figure 0

Performance of bias corrected maximum likelihood estimators