Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-05T23:52:25.301Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE PRODUCT AND RATIO OF GAMMA AND WEIBULL RANDOM VARIABLES

Published online by Cambridge University Press:  09 February 2006

Saralees Nadarajah  and
Samuel Kotz
Saralees Nadarajah
Affiliation:
University of Nebraska
Samuel Kotz
Affiliation:
George Washington University
Rights & Permissions [Opens in a new window]

Abstract

The distributions of products and ratios of random variables are of interest in many areas of the sciences. In this note, the exact distributions of the product XY and the ratio X/Y are derived when X and Y are gamma and Weibull random variables distributed independently of each other.The authors thank the referee and the editor for carefully reading the paper and for their help in improving the paper.

Type
NOTES AND PROBLEMS
Information
Econometric Theory , Volume 22 , Issue 2 , April 2006 , pp. 338 - 344
Copyright
© 2006 Cambridge University Press

1. INTRODUCTION

For given random variables X and Y, the distributions of the product XY and the ratio X/Y are of interest in many areas of the sciences.

In traditional portfolio selection models certain cases involve the product of random variables. The best examples of this are in the case of investment in a number of different overseas markets. In portfolio diversification models (see, e.g., Grubel, 1968) not only are prices of shares in local markets uncertain, but also the exchange rates are uncertain, and so the value of the portfolio in domestic currency is related to a product of random variables. Similarly in models of diversified production by multinationals (see, e.g., Rugman, 1979) there are local production uncertainty and exchange rate uncertainty, and so profits in home currency are again related to a product of random variables. An entirely different example is drawn from the econometric literature. In making a forecast from an estimated equation Feldstein (1971) pointed out that both the parameter and the value of the exogenous variable in the forecast period could be considered random variables. Hence the forecast was proportional to a product of random variables.

An important example of ratios of random variables is the stress-strength model in the context of reliability. It describes the life of a component that has a random strength Y and is subjected to random stress X. The component fails at the instant that the stress applied to it exceeds the strength, and the component will function satisfactorily whenever Y > X. Thus, Pr(X < Y) is a measure of component reliability. It has many applications, especially in engineering concepts such as structures, deterioration of rocket motors, static fatigue of ceramic components, fatigue failure of aircraft structures, and the aging of concrete pressure vessels.

The distributions of XY and X/Y have been studied by several authors, especially when X and Y are independent random variables and come from the same family. With respect to products of random variables, see Sakamoto (1943) for uniform family, Harter (1951) and Wallgren (1980) for Student's t family, Springer and Thompson (1970) for normal family, Stuart (1962) and Podolski (1972) for gamma family, Steece (1976), Bhargava and Khatri (1981), and Tang and Gupta (1984) for beta family, AbuSalih (1983) for power function family, and Malik and Trudel (1986) for exponential family (for a comprehensive review of known results, see also Rathie and Rohrer, 1987). With respect to ratios of random variables, see Marsaglia (1965) and Korhonen and Narula (1989) for normal family, Press (1969) for Student's t family, Basu and Lochner (1971) for Weibull family, Shcolnick (1985) for stable family, Hawkins and Han (1986) for noncentral chi-squared family, Provost (1989) for gamma family, and Pham-Gia (2000) for beta family.

There is relatively little work of the preceding kind when X and Y belong to different families (the only work known to the authors is that by Nadarajah and Ali, 2004, and Nadarajah and Gupta, 2005). In the applications mentioned before, it is quite possible that X and Y could arise from different but similar distributions. In this note, we study the exact distributions of XY and X/Y when X and Y are independent random variables having the gamma and Weibull distributions with probability density functions (p.d.f.s)

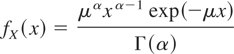
and

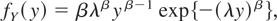
respectively, for x > 0, y > 0, α > 0, β > 0, λ > 0, and μ > 0. The calculations involve the incomplete gamma function defined by

and the Gauss hypergeometric function defined by

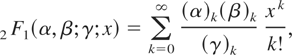
where (e)k = e(e + 1)…(e + k − 1) denotes the ascending factorial (also known as Pochhammer's symbol). Further properties of the preceding special functions can be found in Prudnikov, Brychkov, and Marichev (1986) and Gradshteyn and Ryzhik (2000).

2. PRODUCT

Theorem 1 expresses the cumulative distribution function (c.d.f.) of XY as an infinite sum of elementary functions.

THEOREM 1. Suppose X and Y are distributed according to (1) and (2), respectively. The c.d.f. of Z = XY can be expressed as

for z > 0.

Proof. The c.d.f. corresponding to (1) is 1 − Γ(α,μx)/Γ(α). Thus, one can write the c.d.f. of XY as

where we have set w = 1/y. Application of equation (2.10.1.12) in Prudnikov et al. (1986, vol. 2) shows that the integral I can be calculated as

The result of the theorem follows by substituting (5) and (4). █

Figure 1 illustrates possible shapes of the p.d.f. of XY for selected values of α and β. The four curves in each plot correspond to selected values of α. The effect of the parameters is evident.

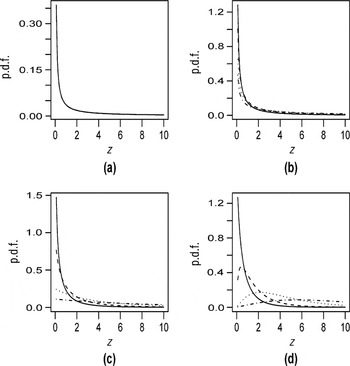
Plots of the p.d.f. of (3) for λ = 1, μ = 1, α = 1, 2, 5, 10, and (a) β = 0.1, (b) β = 0.5, (c) β = 1, and (d) β = 2. The four curves in each plot are the solid curve (α = 1), the curve of dots (α = 2), the curve of lines (α = 5), and the curve of dots and lines (α = 10).

3. RATIO

Theorem 2 expresses the c.d.f. of X/Y as an infinite sum of elementary functions.

THEOREM 2. Suppose X and Y are distributed according to (1) and (2), respectively. The c.d.f. of Z = X/Y can be expressed as

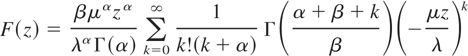
for β > 1,

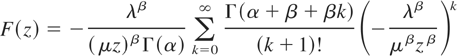
for β < 1, and

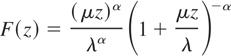
for β = 1.

Proof. Because 1 − Γ(α,μx)/Γ(α) is the c.d.f. corresponding to (1), one can write the c.d.f. of X/Y as

Application of equation (2.10.1.5) in Prudnikov et al. (1986, vol. 2) shows that the integral I can be calculated as

Note that the hypergeometric term in (10) simplifies as

The result of the theorem follows by substituting (10) into (9). █

Figure 2 illustrates possible shapes of the p.d.f. of X/Y for selected values of α and β. The four curves in each plot correspond to selected values of α. The effect of the parameters is evident.

Plots of the p.d.f. of (6)–(8) for λ = 1, μ = 1, α = 1, 2, 5, 10, and (a) β = 0.1, (b) β = 0.5, (c) β = 1, and (d) β = 2. The four curves in each plot are the solid curve (α = 1), the curve of dots (α = 2), the curve of lines (α = 5), and the curve of dots and lines (α = 10).

References

REFERENCES

AbuSalih, M.S. (1983) Distributions of the product and the quotient of power-function random variables. Arab Journal of Mathematics 4, 77–90.Google Scholar
Basu, A.P. & R.H. Lochner (1971) On the distribution of the ratio of two random variables having generalized life distributions. Technometrics 13, 281–287.CrossRefGoogle Scholar
Bhargava, R.P. & C.G. Khatri (1981) The distribution of product of independent beta random variables with application to multivariate analysis. Annals of the Institute of Statistical Mathematics 33, 287–296.CrossRefGoogle Scholar
Feldstein, M.S. (1971) The error of forecast in econometric models when the forecast-period exogenous variables are stochastic. Econometrica 39, 55–60.CrossRefGoogle Scholar
Gradshteyn, I.S. & I.M. Ryzhik (2000) Table of Integrals, Series, and Products, 6th ed. Academic Press.
Grubel, H.G. (1968) Internationally diversified portfolios: Welfare gains capital flows. American Economic Review 58, 1299–1314.Google Scholar
Harter, H.L. (1951) On the distribution of Wald's classification statistic. Annals of Mathematical Statistics 22, 58–67.CrossRefGoogle Scholar
Hawkins, D.L. & C.-P. Han (1986) Bivariate distributions of some ratios of independent noncentral chi-square random variables. Communications in Statistics—Theory and Methods 15, 261–277.CrossRefGoogle Scholar
Korhonen, P.J. & S.C. Narula (1989) The probability distribution of the ratio of the absolute values of two normal variables. Journal of Statistical Computation and Simulation 33, 173–182.CrossRefGoogle Scholar
Malik, H.J. & R. Trudel (1986) Probability density function of the product and quotient of two correlated exponential random variables. Canadian Mathematical Bulletin 29, 413–418.CrossRefGoogle Scholar
Marsaglia, G. (1965) Ratios of normal variables and ratios of sums of uniform variables. Journal of the American Statistical Association 60, 193–204.CrossRefGoogle Scholar
Nadarajah, S. & M.M. Ali (2004) On the product and ratio of t and logistic random variables. Calcutta Statistical Association Bulletin 55, 1–14.Google Scholar
Nadarajah, S. & A.K. Gupta (2005) Products of random variables with Cauchy kernel. Pan American Journal of Mathematics 15, 47–56.Google Scholar
Pham-Gia, T. (2000) Distributions of the ratios of independent beta variables and applications. Communications in Statistics—Theory and Methods 29, 2693–2715.CrossRefGoogle Scholar
Podolski, H. (1972) The distribution of a product of n independent random variables with generalized gamma distribution. Demonstratio Mathematica 4, 119–123.Google Scholar
Press, S.J. (1969) The t ratio distribution. Journal of the American Statistical Association 64, 242–252.CrossRefGoogle Scholar
Provost, S.B. (1989) On the distribution of the ratio of powers of sums of gamma random variables. Pakistan Journal of Statistics 5, 157–174.Google Scholar
Prudnikov, A.P., Y.A. Brychkov, & O.I. Marichev (1986) Integrals and Series, vols. 1–3. Gordon and Breach.
Rathie, P.N. & H.G. Rohrer (1987) The exact distribution of products of independent random variables. Metron 45, 235–245.Google Scholar
Rugman, A.M. (1979) International Diversification and the Multinational Enterprise. Lexington Books.
Sakamoto, H. (1943) On the distributions of the product and the quotient of the independent and uniformly distributed random variables. Tohoku Mathematical Journal 49, 243–260.Google Scholar
Shcolnick, S.M. (1985) On the ratio of independent stable random variables. In Stability Problems for Stochastic Models, Lecture Notes in Mathematics 1155, pp. 349–354. Springer-Verlag.
Springer, M.D. & W.E. Thompson (1970) The distribution of products of beta, gamma and Gaussian random variables. SIAM Journal on Applied Mathematics 18, 721–737.CrossRefGoogle Scholar
Steece, B.M. (1976) On the exact distribution for the product of two independent beta-distributed random variables. Metron 34, 187–190.Google Scholar
Stuart, A. (1962) Gamma-distributed products of independent random variables. Biometrika 49, 564–565.CrossRefGoogle Scholar
Tang, J. & A.K. Gupta (1984) On the distribution of the product of independent beta random variables. Statistics and Probability Letters 2, 165–168.CrossRefGoogle Scholar
Wallgren, C.M. (1980) The distribution of the product of two correlated t variates. Journal of the American Statistical Association 75, 996–1000.Google Scholar
Figure 0

Plots of the p.d.f. of (3) for λ = 1, μ = 1, α = 1, 2, 5, 10, and (a) β = 0.1, (b) β = 0.5, (c) β = 1, and (d) β = 2. The four curves in each plot are the solid curve (α = 1), the curve of dots (α = 2), the curve of lines (α = 5), and the curve of dots and lines (α = 10).

Figure 1

Plots of the p.d.f. of (6)–(8) for λ = 1, μ = 1, α = 1, 2, 5, 10, and (a) β = 0.1, (b) β = 0.5, (c) β = 1, and (d) β = 2. The four curves in each plot are the solid curve (α = 1), the curve of dots (α = 2), the curve of lines (α = 5), and the curve of dots and lines (α = 10).