1. INTRODUCTION
Over the past decade important advances have been made in the study of
dynamic panel data models where both the time dimension (T) and
the cross-sectional dimension (N) are large. See, for example,
the surveys by Baltagi and Kao (2000) and
Phillips and Moon (2000) and the references
cited therein. In this paper we are concerned with the more traditional
panel literature where N is large and T is short
(typically 10 or less), which remains the prevalent setting for the
majority of empirical microeconometric research.1
For references to much of this empirical work see, for
example, Baltagi (2001).
However, this
literature has primarily focused on single equation dynamic panel data
models, whereas there are many applications that ideally require a
simultaneous treatment of the decision problems faced by households,
firms, and institutions. A natural starting point is vector autoregressive
models (VARs), which have been extensively studied in the time-series
literature. An early analysis of panel VARs (PVARs) with a short
T was provided by Holtz-Eakin, Newey, and Rosen (
1988). The fact that
T is short does not mean
that the underlying data could not have arisen from nonstationary
and/or cointegrated processes. The slope homogeneity and cross-section
independence assumptions of the traditional panel literature may allow
researchers to make inferences about the long-term properties of the model
even when
T is short. Moreover, the analysis of cointegration
provides a natural starting point for introducing cross-equation
restrictions into PVAR models.
As in single equation dynamic panel data models there are two main
issues that need to be addressed in the study of PVARs. (i) The fact that
T is fixed necessitates the modeling of the initial
observations.2
For discussions of the initial
observations in the single equation context see, for example, Anderson and
Hsiao (1981, 1982),
Bhargava and Sargan (1983), Blundell and Smith
(1991), and Nerlove (1999).
(ii) Presence of cross-sectional
heterogeneity poses the important question of how to best model the
unobserved individual-specific effects.
3 Dealing with possible slope coefficient heterogeneity poses
further complications and might not be feasible in dynamic panels where
T is very short. See, for example, Hsiao, Pesaran, and
Tahmiscioglu (1999).
Here we shall
consider both the random and fixed effects specifications. The fixed
effects specification has the advantage of being robust to possible
misspecification of the distribution of the individual effects. But it is
subject to the classical incidental parameters problem as in Neyman and
Scott (
1948), violating the regularity
conditions needed for the consistency of the conventional quasi maximum
likelihood (QML) estimator.
4 See, for
example, Anderson and Hsiao (1981) and Nickell
(1981) for a discussion of this issue in the
context of single equation models.
To overcome this problem generalized method of moments (GMM)
estimation has been suggested in the literature. It is useful to
distinguish between the “standard” GMM estimators proposed by
Holtz-Eakin et al. (1988) and Arellano and Bond
(1991) and their subsequent extensions by, for
example, Ahn and Schmidt (1995), Arellano and
Bover (1995), and Blundell and Bond (1998). The “standard” GMM estimators are
based on orthogonality conditions that interact the lagged values of the
endogenous variables with first differences of the model's
disturbances, whereas the “extended” GMM estimators augment
these orthogonality conditions with additional moment conditions implied
by homoskedasticity and initialization restrictions.
This paper develops random and fixed effects QML estimators (RE-QMLE
and FE-QMLE, respectively) when it is not known a priori whether the
underlying series are stationary, have unit roots, or are cointegrated. It
contributes to the discussion of the initialization of dynamic models with
a fixed T by generalizing the stationarity restrictions proposed
in the literature to settings involving unit roots and cointegration. New
panel unit root and cointegration tests are proposed for panels with short
T. Under certain regularity conditions it is shown that the QML
estimators are consistent and asymptotically normally distributed (as
N → ∞, with T fixed and short), irrespective
of whether the underlying time series are (trend) stationary, integrated
of order one, I(1), or I(1) and cointegrated. The paper also provides a
generalization of the extended GMM estimators to PVARs and presents a
comparative analysis of these estimation procedures in terms of their
asymptotic properties and also their finite-sample performances using
Monte Carlo experiments. The RE-QMLE is more efficient than the FE-QMLE,
but it imposes moment homogeneity restrictions on the initial observations
and requires the individual effects to be random draws from probability
distributions with finite fourth-order moments. The standard and extended
GMM estimators are also shown to impose restrictions on the distribution
of the individual effects not needed under the fixed effects
specification. It is shown that the asymptotic variance of the standard
and extended GMM estimators conditional on the variance of the model
disturbances increases as a function of the variance of the individual
effects. This is an important result and shows that in dynamic panels the
performance of the GMM estimators could be adversely affected, possibly
substantially, when the individual effects exhibit considerable
variations. By contrast, the FE-QMLE is by construction invariant to the
variation of the individual effects and hence is not subject to the same
problem. The importance of the variance of the individual effects for
comparisons of the FE-QMLE and GMM estimators is also investigated by
means of Monte Carlo experiments. It is documented that the FE-QMLE
performs well under a variety of parameter configurations (including unit
roots) and nonnormal errors.
The remainder of this paper is organized as follows. Section 2
introduces the PVAR model. Sections 3 and 4 develop the QML estimators
under random and fixed effects specifications, respectively. Section 5
proposes new tests for unit roots and cointegration in panels with short
time dimension. Section 6 discusses GMM estimation of the PVAR model.
Monte Carlo simulation results regarding the finite-sample performance of
the QML and GMM estimators are presented in Section 7, and Section 8
concludes and provides some suggestions for future research. The Appendix
provides a proof of the dependence of the asymptotic variance of the
standard GMM estimator on the variance of the individual effects.
2. A PVAR MODEL
Let wit be an m × 1 vector
of random variables for the ith cross-sectional unit at time
t and suppose that the wit's
are generated by the following PVAR model of order one, PVAR(1):
for i = 1,2,…,N and t =
1,2,…,T, where Φ denotes an m
× m matrix of slope coefficients,
μi is an m × 1 vector of
individual-specific effects, εit is an
m × 1 vector of disturbances, and
Im denotes the identity matrix of dimension
m × m. For simplicity we restrict our exposition
to first-order PVAR models.
We shall consider both random and fixed effects specifications of the
individual-specific effects in the remainder of this paper, highlighting
their differences and the implications these differences have for
estimation and inference. However, for both the random and fixed effects
specifications we make the following general assumptions.
Assumption (G1). The available observations are
wi0,wi1,…,wiT,
with T ≥ 2 but fixed as N → ∞.
Assumption (G2). The disturbances
εit, t ≤ T, are
independently and identically distributed (i.i.d.) for all i and
t with E(εit) =
0 and Var(εit) =
Ωε,
Ωε being a positive definite
matrix.
For panels with N and T sufficiently large and under
certain conditions it is possible to relax the cross-sectional
independence assumption; see, for example, Conley (1999), Phillips and Sul (2003), Bai and Ng (2004),
Moon and Perron (2004), and Pesaran (2003, 2004). Exploring the
issue of cross-sectional dependence in the context of the PVAR model with
T fixed is beyond the scope of the present paper.
Let ξit =
wit −
μi and note that (2.1) can also be
written as
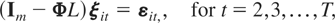
with
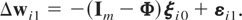
When T is fixed, it is necessary to consider the
initialization of the wit-process for
estimation and inference. We make the following assumption.
Assumption (G3). The initial deviations,
ξi0, are i.i.d. across i, with
zero means and the constant nonsingular variance,
E(ξi0ξi0′)
= Ψξ0.
Under Assumption (G3), if all eigenvalues of Φ fall
inside the unit circle, then the process (2.1) can either start from an
infinite past or a finite past. If some of the eigenvalues of Φ are
equal to unity, then the nonstationary direction can only start from a
finite past.
The PVAR(1) model (2.1) is the generalization of the univariate
dynamic panel data model considered, for example, in Ahn and Schmidt
(1995) to the multivariate context,
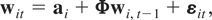
which would be equivalent to (2.1) when all eigenvalues of
Φ fall inside the unit circle. However, in the presence of
unit roots the two specifications (2.1) and (2.3) will have different
trend properties, with the unrestricted intercepts specification (2.3)
exhibiting linear trends whereas the restricted specification (2.1) does
not. In what follows we adopt (2.1) as the data generating mechanism,
although for estimation purposes it is often more convenient to work with
(2.3).
3. RANDOM EFFECTS SPECIFICATION
In this case the general assumptions, (G1)–(G3), need to be
supplemented with additional assumptions on the individual-specific
effects, μi. In particular, we make the
following assumption.
Assumption (R1).
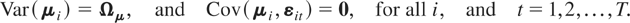
This is a standard assumption for the random effects model and
together with the general assumptions (G1)–(G3) yields
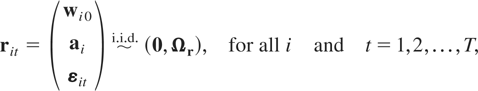
where ai =
(Im −
Φ)μi,
Ωa =
(Im −
Φ)Ωμ(Im
− Φ)′, Ω0a =
Cov(wi0,ai), and
Ω0 and Ωa are,
respectively, positive definite and nonnegative definite matrices.5
Assumption (R1) could be relaxed, for example,
to allow the individual effects μi to
have a common nonzero mean. Nonzero correlations between the disturbances
εit and the initial observations
wi0/the individual effects
μi could also be allowed for, but they
will not be considered here because in general it is not possible to test
whether these correlations are zero or nonzero. See Ahn and Schmidt (1995) for more detailed discussion of this in the
single equation setting.
Assumption (R2). All elements of the cross-product matrices
ritrit′,
t = 1,2,…,T, have finite second-order
moments.
Denote the [2m2 + 3m(m +
1)/2] × 1 vector of unknown coefficients by
θ,
where φ = vec(Φ),
σε =
vech(Ωε),
σa =
vech(Ωa), σ0 =
vech(Ω0), and
σ0a =
vec(Ω0a).
Assumption (R3). θ ∈ Θ, where
Θ is a compact subset of
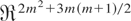
and the true parameter vector, θ0, falls in the
interior of Θ.
Assumption (R1) can be derived from more primitive assumptions
concerning the initialization of the wit
process. For example, in the case when wit is
stationary and has started in the infinite past we have6
For further details see Binder, Hsiao, and Pesaran (2004).
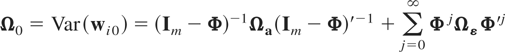
and
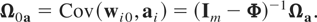
Let
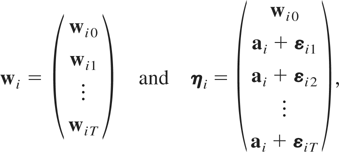
and note that ηi =
Rwi, where R is a matrix of
dimension m(T + 1) × m(T + 1)
given by
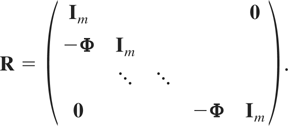
The RE-QML estimator of θ is derived by maximizing the
following log-likelihood function, which assumes normally distributed
errors, as the criterion function:
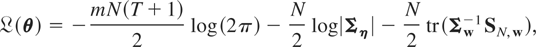
where7
Notice that
Ση is nonsingular even if
initialization restrictions such as Ωa =
0 and Ω0a = 0 that
follow under Φ = Im are
imposed. To allow the possibility of nonstationarity of initial
observations and/or the case where the process is stationary but had
not started from an infinite past, in our estimation setup
Ωa and
Ω0a will be treated as unrestricted
coefficient matrices.
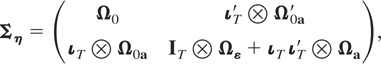
with ιT being a T × 1
vector of ones, and
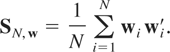
We then have the following proposition.8
A proof can be established using familiar techniques as
reviewed, for example, in White (1994).
PROPOSITION 3.1. Under assumptions (G1)–(G3), and
(R1)–(R3), and assuming that (2.1) holds, then as N →
∞, SN,w converges almost
surely to the nonstochastic matrix
Σw, and the RE-QMLE of
θ, defined by maximizing (3.3), is consistent.
Furthermore, under these assumptions
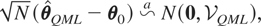
where
with
being a positive definite matrix.
Remark 3.1. If time-specific effects are present, and
wit is generated by9
The presence of N cross-sectional units allows us to
consider a nonparametrically specified common trend for all
cross-sectional units.
where δt is an m × 1
vector of time-specific effects, then upon redefining for estimation
purposes
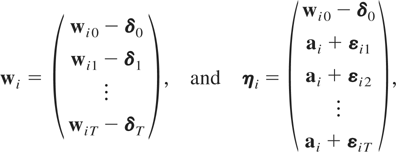
the log-likelihood function is again given by (3.3). It can be shown
that the RE-QMLE of δt is given by
In the special case where δt =
δt, t = 0,1,…,T, the
RE-QMLE of δ can be obtained using the following weighted
average of the unrestricted estimates,
:
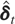
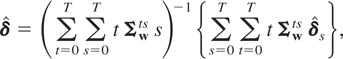
where we have partitioned
Σw−1 into (T +
1)2 blocks of dimension m × m,
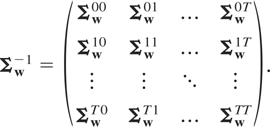
The RE-QMLE of the remaining parameters, θ, can be
computed using the concentrated log-likelihood function.
4. FIXED EFFECTS SPECIFICATION
Under the fixed effects specification no restrictions need to be
placed on the probability distribution function generating the
individual-specific effects μi in (2.1)
(or, in unrestricted form, ai in (2.3)). In
particular, Assumptions (R1) and (R2) are no longer required. It can then
be allowed, for example, that (i) the individual effects are dependently
distributed, (ii) the individual effects are heteroskedastic, (iii) the
individual effects are (more generally) characterized by a joint
probability distribution function with the number of unknown parameters
increasing at the same rate as the number of cross-sectional observations
in the panel, (iv) the individual effects do not have moments, and (v) the
individual effects and the disturbances are correlated.
Following standard practice the
μi's can be eliminated by
first-differencing (2.1), namely,10
Hsiao,
Pesaran, and Tahmiscioglu (2002) in the
univariate context show that the QML estimator is invariant to the choice
of the T × (T + 1) transformation matrix
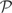
that is of rank T and eliminates the individual-specific
effects, namely, that has the property that
,
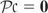
with
being a vector of constants of dimension (T + 1) × 1. The
argument in Hsiao et al. (2002) readily extends
to the multivariate setting considered here.
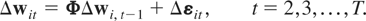
To obtain a consistent QML estimator one needs to work with the
unconditional joint probability distribution of
(Δwi1,Δwi2,…,ΔwiT),
or the distribution of
(Δwi2,Δwi3,…,ΔwiT)
conditional on Δwi1, and ensure that
these distributions are free of the incidental parameters problem. The
latter condition is obviously satisfied if the unconditional distribution
of Δwi1 does not depend on any incidental
parameters. Therefore, for the fixed effects specification we shall
supplement Assumptions (G1)–(G3) with the following assumption.
Assumption (F1). The following moment restrictions are satisfied:
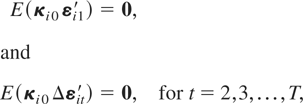
where κi0 =
(Im −
Φ)ξi0.
Combining this assumption with Assumptions (G1)–(G3) and using
(2.2) we now have11
Assumptions (G3) and
(F1) can be relaxed to allow for κi0 to
have a constant nonzero mean and for
Cov(κi0,
εi1) and
Cov(κi0,Δεit),
for t = 2,3,…,T, to be nonzero and possibly
time-varying (but still homogeneous across i).
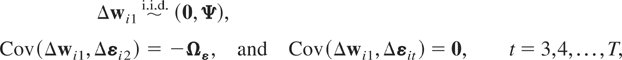
where
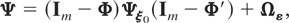
with Ψξ0 already
defined in Assumption (G3).
Remark 4.1. The first-differencing operation simultaneously deals with
the incidental parameters and unit root problems. Unlike in time-series
models, first-differencing in panels with T fixed still allows
identification and estimation of the long-run (level) relations that are
of economic interest irrespective of the unit root and cointegrating
properties of the wit process.
Remark 4.2. It is important to note that Assumption (F1) imposes
homogeneity restrictions on a linear combination of the initial
deviations, (Im −
Φ)ξi0, and the initial
error terms, εi1, for all i, without
imposing any such restrictions on the individual effects,
μi, themselves.
The following moment and parameter space assumptions will also be
needed.
Assumption (F2). The second moments of the cross-product matrix
Δrit
Δrit′, t =
2,3,…,T, with
exist.
Denote the [m2 + m(m +
1)] × 1 vector of unknown coefficients by ρ,
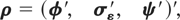
where φ = vec(Φ),
σε =
vech(Ωε), and ψ =
vech(Ψ).
Assumption (F3). ρ ∈ Ξ, where
Ξ is a compact subset of
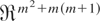
and the true parameter vector, ρ0, lies in the
interior of Ξ.
Let
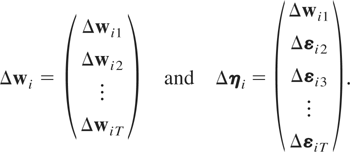
It follows that Δηi =
RΔwi, where R is given
by (3.2), but its dimension now is mT × mT,
with
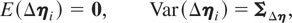
and
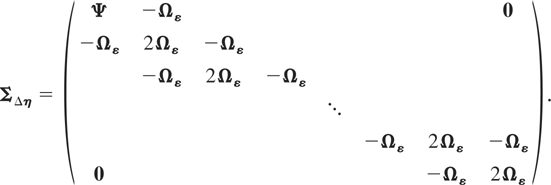
The QML estimator of ρ is obtained by maximizing the
following log-likelihood function based on the joint probability
distribution of (Δwi1,
Δwi2,…,ΔwiT)
under the normality assumption:12
The
likelihood function (4.4) holds whether T is finite or approaches
infinity. However, if T → ∞, one can estimate
μi consistently, and hence one may apply
QML estimation to (2.1) instead of working with (4.4).
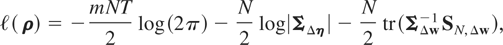
where
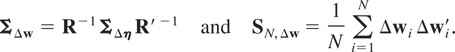
PROPOSITION 4.1. Under assumptions (G1)–(G3), and
(F1)–(F3), and assuming that (2.1) holds, then as N →
∞, SN,Δw converges
almost surely to the nonstochastic matrix
ΣΔw, and the FE-QMLE of
ρ, defined by maximizing (4.4), is consistent.
Furthermore, under these assumptions
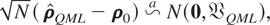
where
with H[ell ] being a positive definite
matrix.
Remark 4.3. If wit is generated by the
fixed effects counterpart of (3.4), so that time-specific effects are
present, we have that
with γt =
Δδt. Upon redefining
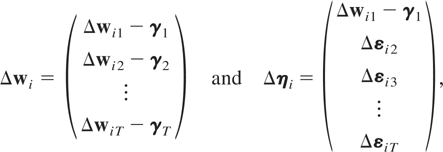
the log-likelihood function is again given by (4.4). Using similar
derivations as in the random effects setting, it can be shown that the
FE-QMLE of γt is given by
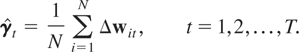
In the restricted case of γt =
γ, t = 1,2,…,T, we have
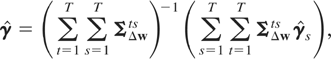
where ΣΔw−1 is
partitioned into m × m-dimensional blocks
ΣΔwts,
t,s = 1,2,…,T, analogous to the
partition in (3.5).
Remark 4.4. Computation of the FE-QMLE is complicated by the fact that
the matrix ΣΔη will often be
high-dimensional. However, to compute the determinant and inverse of
ΣΔη, one may make use of the
block-tridiagonal structure of
ΣΔη. Applying the block
LDL′ factorization to
ΣΔη, the latter may be
factorized as
,
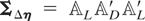
where
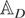
is a block-diagonal matrix with jth diagonal block given by
,
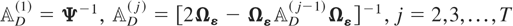
and where
,
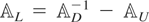
with
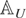
being a block-subdiagonal matrix with all subdiagonal blocks equal to
Ωε.
13 For further details see, for example, Binder and Pesaran
(2000), who in the context of the solution of
multivariate linear rational expectations models discuss the block
LDU factorization, of which the block LDL′
factorization is a special case.
It then follows that
To compute the inverse of
ΣΔη, a computationally efficient
scheme is to adapt the recursions based on Bowden's procedure in
Binder and Pesaran (2000), which yields
and
where
ΣΔη,jl−1
denotes the jlth block of
ΣΔη−1,
j,l = 1,2,…,T. Further details of our
numerical algorithm that renders computation of the FE-QMLE practically
feasible even for high-dimensional systems are described in a note
available upon request.
Because under the fixed effects specification no restrictions are
placed on the distribution generating the individual effects
μi, by default the FE-QMLE allows for the
possibility of cross-sectional heteroskedasticity in the combined error
components, (Im −
Φ)μi +
εit. Furthermore, the preceding
analysis can readily accommodate intertemporal error variance
heteroskedasticity. This can be done by relaxing Assumption (G2) so that
the disturbances εit are distributed
i.i.d. for all i and independently for all t with
Var(εit) =
Ωεt,
Ωεt being
positive definite matrices for all t. In this case
ΣΔη defined by (4.3) generalizes
to
The FE-QMLE can now be derived under suitable parameterization of the
error variance matrices
Ωεt, for
t = 1,2,…,T.
Finally, it is also worth noting that under the random effects
specification considered in Section 3 there are m(T +
1)(T + 2)/2 exploitable moment conditions, whereas under the
fixed effects specification there are mT(T + 1)/2
moment conditions, or m(T + 1) fewer moment
restrictions. Therefore, in general one would expect the RE-QMLE to be
asymptotically more efficient than the FE-QMLE. The finite-sample
importance of these additional moment conditions will be addressed in
Section 7, where the RE-QMLE and FE-QMLE will be compared. Nevertheless,
it should be clear that, in general, FE-QMLE is preferable to RE-QMLE,
unless prior information is available that the individual effects are
cross-sectionally homoskedastic and have finite moments of up to the
fourth order.
5. UNIT ROOTS AND COINTEGRATION IN
PVARs
Although the focus of this paper is on short panel, the fact that
T is short does not necessarily mean that the underlying data are
stationary or not cointegrated. One of the advantages of using panel data
is that under the homogeneity assumption, one can test for nonstationarity
or the presence of “long-run equilibrium” with short
T. In this section we demonstrate how one may use panel data to
test for unit roots and cointegration rank even if T is small.
The asymptotic properties of the QML estimators set out previously hold
irrespective of the location of the eigenvalues of Φ and the
size of T, and one may, therefore, use the results of Sections 3
and 4 for this purpose.
To be able to interpret the rank of the matrix Π as the
number of linearly independent cointegrating relations, it is necessary to
know whether each of the variables in wit
follows an I(1) process. Our framework can be easily adapted to test for
unit roots in short panel univariate autoregressive models. For m
= 1 the equation to be estimated is
where wit is now a scalar variable.14
As for unit root testing in the time-series
context, the appropriate order of augmentation of
wit is important for the validity of the
test. In practice one may therefore need to consider higher order cases
also. Here we confine ourselves to p = 1 for simplicity of
exposition.
The unit root hypothesis
can now be tested under both the random and fixed effects
specifications. Denoting the QML estimator of the slope coefficient under
either model specification as
,
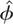
a Wald-type statistic of testing H0 versus
H1 will be
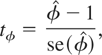
where
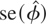
denotes the standard error of
.
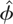
Under the null hypothesis tφ is asymptotically
distributed as a standard normal variate as N → ∞, for
a fixed T ≥ 3. The alternative hypothesis considered is
homogeneous and one-sided. This test can be extended to models with
serially correlated errors (to models with p > 1), so long as
the slope homogeneity assumption is maintained. Unit root tests for panels
with slope heterogeneity and more complicated dynamics have been proposed
in the literature but require large N and T panels and
are not valid when the time dimension is short.
15 See, for example, Maddala and Wu (1999), Levin, Lin, and Chu (2002), and Im, Pesaran, and Shin (2003). Extensions of these tests to models with
cross-section dependence have been considered by Pesaran (2003), Phillips and Sul (2003), Moon and Perron (2004), and Bai and Ng (2004).
A short
T panel unit root
test has been proposed by Harris and Tzavalis (
1999) but requires bias corrections and could be
difficult to extend to models with serially correlated errors.
The natural next step after the unit root tests have been carried out
is to test for cointegration. Consider again the PVAR(1) model in the
m variables wit, now assumed to be
I(1). The hypothesis that wit −
μi is cointegrated with rank r
versus rank r + 1, r = 0,1,…,m −
1, can be formulated as
where αr and
βr are m × r
matrices of full column rank r. Because
;
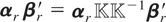
for any r × r nonsingular matrix
,
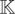
one needs, in the absence of short-run restrictions, r
restrictions on each of the r columns of
βr.
16 For a
more detailed discussion see, for example, Pesaran and Shin (2002). Also note that the extrema of the QML criterion
function under rank(Π) = r are invariant to the
choice of
.
A convenient procedure for the identification of
βr is to let
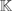
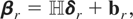
where
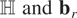
are, respectively, m × q and m ×
r matrices, both with known coefficients, and δ is a
q × r matrix with unknown coefficients. For
example, if one chooses (as we shall do in what follows) the Phillips
(1991) exact identification restriction that
,
where
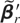
is an r × (m − r) matrix with
unrestricted coefficients, then
.
The QML estimators restricting the rank of the matrix Π can
now be set out as before, noting that in the random effects case the
unknown coefficients are now given by
and in the fixed effects case are defined by
.
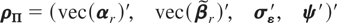
The likelihood ratio test statistic of Hr
versus Hr+1 is asymptotically chi-square
distributed with (m − r)2 −
(m − r − 1)2 = 2(m
− r) − 1 degrees of freedom. (Imposing Π
to be of rank r leaves m2 − (m
− r)2 unrestricted coefficients in
Π.)
Additional parameter restrictions or overidentifying restrictions can
be formulated in terms of
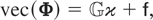
where
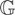
is an m2 × q matrix and an
m2 × 1 vector, both with known elements, and
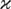
is a q × 1 vector of free parameters. A likelihood ratio
test of (5.1) will be asymptotically chi-square distributed with
m2 − q degrees of freedom.
6. GMM ESTIMATION
There now exists an extensive literature on the GMM estimation of
univariate dynamic panel data models (e.g., Arellano
and Bond, 1991; Ahn and Schmidt, 1995,
1997; Arellano and Bover,
1995; Blundell and Bond, 1998; Alonso-Borrego and Arellano, 1999). However, just as
three stage least squares estimation of a system of equations can be more
efficient than the single equation–based two stage least squares, in
this section we shall generalize GMM estimation to a systems context and
show that if the PVAR model (2.1) contains unit roots, then the standard
GMM approach (e.g., Arellano and Bond, 1991) of
using lagged level variables as instruments that are orthogonal to the
disturbances of the first-differenced form of the model breaks down. We
then discuss how this problem may be overcome using additional moment
conditions implied by homoskedasticity and initialization restrictions of
the type suggested in the case of univariate models by Ahn and Schmidt
(1995), Arellano and Bover (1995), and Blundell and Bond (1998).
6.1. Standard GMM and Its Breakdown under Unit
Roots
The standard GMM estimator of Arellano and Bond (1991) employs instruments that are orthogonal to the
disturbances of the first-differenced form of the model. For the PVAR(1)
model (2.1), such instruments are given by levels of the dependent
variables, wit, lagged two or more periods.
The resulting orthogonality conditions may be written as
where qit is the m(t
− 1) × 1 vector defined by
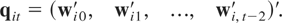
To derive the standard GMM estimator of Φ based on the
moment conditions (6.1), it will be useful to rewrite these moment
conditions in stacked form as
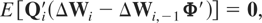
where Qi′ is a matrix of dimension
mT(T − 1)/2 × (T − 1)
given by
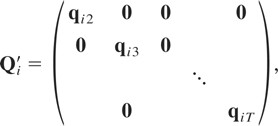
and ΔWi and
ΔWi,−1 are (T − 1)
× m-dimensional matrices,
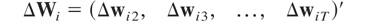
and
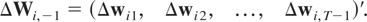
The standard GMM estimator of φ = vec(Φ)
is now given by17
An alternative estimator
of
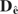
also used in the literature is given by
.
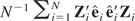
See, for example, Arellano and Honoré (2001) and Baltagi (2001).
However, our Monte Carlo experiments suggest
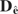
to be preferable in the settings we consider, particularly for purposes
of hypothesis testing. Arellano and Honoré (2001) also discuss how auxiliary assumptions can be
used to impose further restrictions on
.
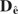
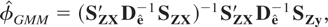
where
and
,
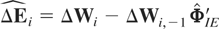
where
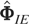
is an initial consistent estimate of Φ such as the
generalized instrumental variables estimator obtained using the formula
(6.4) but with
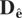
replaced by ΛQ [otimes ]
Im, where
and
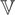
is the (T − 1) × (T − 1) matrix,
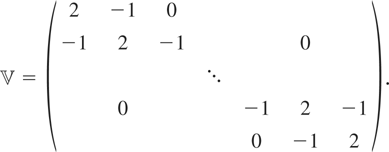
Because the resultant instrumental variables estimator is invariant to
the choice of Ωε, without loss of
generality the estimator may be computed replacing
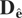
by ΛQ [otimes ]
Im. Using the standard formula, a consistent
estimate of the variance matrix of
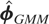
can be obtained as
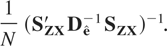
The standard GMM estimator is consistent if all eigenvalues of
Φ fall inside the unit circle but breaks down if some
eigenvalues of Φ are equal to unity. Note that a necessary
condition for the GMM estimator (6.4) to exist is that
rank(Qi′ΔWi,−1)
= m as N → ∞. In the case where
Φ = Im,
rank(Qi′ΔWi,−1)
as N → ∞ is less than m, however. This is
because when Φ = Im, for
t = 2,3,…,T we have
Δwit =
εit, and
wit = wi0 +
sit, with
,
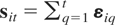
and thus it follows that for t = 2,3,…,T,
l = 0,1,…,t − 2, as N →
∞
where
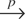
denotes convergence in probability. In other words, when Φ
= Im, the elements of
qit, although still uncorrelated with the
equation errors, are also uncorrelated with the regressors.
18 The same conclusion holds for PVAR(p)
models, with more complicated derivation. A note containing a detailed
argument is available from the authors upon request.
The
situation is analogous to that of Phillips (
1989) on partial identification.
6.2. Extended GMM
Nevertheless, a consistent GMM-type estimator may be obtained by
making use of additional moment conditions. One possibility is the
estimator proposed by Ahn and Schmidt (1995,
1997), which augments the standard moment
conditions with those implied by homoskedasticity assumptions as in
Assumption (G2). These are legitimate instruments regardless of the unit
root and cointegrating properties of wit
− μi. In the context of (2.1) and
under homoskedasticity (over time) of the
εit's we have the following
additional sets of moment conditions:
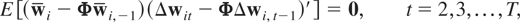
and
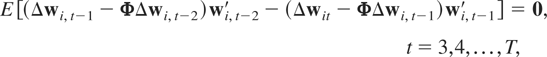
where
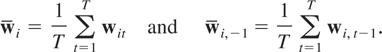
Arellano and Bover (1995) and Blundell and
Bond (1998) proposed an additional set of moment
conditions that in the case of model (2.1) can be written as
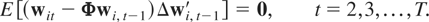
It is readily seen that these conditions require that
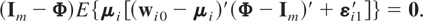
Thus, unless Φ = Im, the
moment conditions (6.10) involve restrictions on the distribution of the
initial observations, wi0, and assume that
the individual effects and the disturbances are uncorrelated. The Ahn and
Schmidt (1995, 1997)
homoskedasticity implied moment restrictions (equations (6.7) and (6.8)),
and the Arellano and Bover (1995) and Blundell
and Bond (1998) initialization restrictions
implied moment conditions (equation (6.10)), can now be combined, after
eliminating redundant conditions, to yield the following moment conditions
that are linear in Φ:
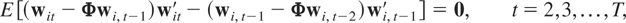
together with the conditions set out in (6.10).
The extended GMM estimator of Φ can now be based on the
moment conditions (6.1), (6.10), and (6.11), which we write in stacked
form as
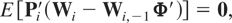
where Pi′ is a matrix of dimension
[mT(T − 1)/2 + 2m(T
− 1)] × T,
with P1i a matrix of dimension
mT(T − 1)/2 × T given by
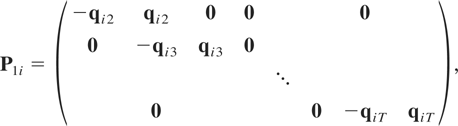
P2i a matrix of dimension
m(T − 1) × T given by
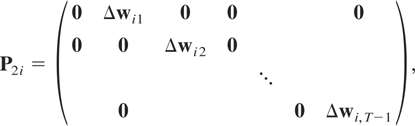
P3i a matrix of dimension
m(T − 1) × T given by
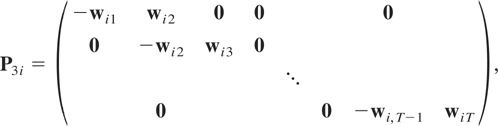
and Wi and
Wi,−1 are T ×
m-dimensional matrices,
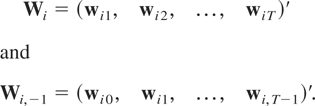
The extended GMM estimator of φ = vec(Φ)
is now given by
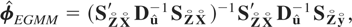
where
and
,
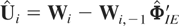
where
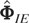
is an initial consistent estimator of Φ, for example, the
generalized instrumental variables estimator based on (6.12), but with
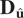
replaced by ΛP [otimes ]
Im, where
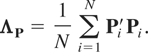
Using the standard formula, a consistent estimate of the
variance-covariance matrix of the extended GMM estimator (6.12) can be
obtained as
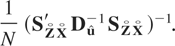
Remark 6.1. The GMM estimators (6.4) and (6.12) require that the
second moments of μi exist. For
asymptotic normality of these estimators it will also be required that the
fourth moments of μi exist. The existence
of these moments is not implied by any of the assumptions we had invoked
for QML estimation under the fixed effects specification. Moreover, the
number of moment conditions for GMM increases at the order of
T2, whereas the orthogonality conditions for QML
estimation remain the same as T increases, which can have
implications for the finite-sample performance of the two types of
estimators.
Remark 6.2. The efficiency of the GMM estimators depends on the
correlations between the instruments,
wi0,wi1,…,wi,t−2,
and the regressors,
Δwi,t−1. We show in the
Appendix that in the stationary case the asymptotic variance of the
standard GMM estimator is an increasing function of
Ωμ, the variance matrix of the
individual effects, relative to the variance matrix of
,
Ωξ, in the sense that for any two
variance matrices, Ωμ(1)
and Ωμ(2), conditional on
a given choice of Ωξ,
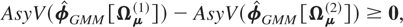
if Ωμ(1) −
Ωμ(2) ≥ 0,
and vice versa, where ≥ stands for a positive semidefinite matrix.19
In Binder et al. (2004, Appendix B), we show that in the pure unit root
case the asymptotic variance of the extended GMM estimator similarly is an
increasing function of Ωμ relative
to Ωε.
In particular, in
the special case where
Ωμ =
τ
Ωε the precision of the GMM
estimators deteriorates with τ. In contrast, the asymptotic variance
of the FE-QMLE discussed in Section 4 by construction does not depend on
Ωμ.
Remark 6.3. To ensure that the efficiency of GMM does not depend on
the nuisance parameters, Ωμ, one may
reformulate standard GMM using
Δwi,t−2,
Δwi,t−3,…,Δwi1
as instruments (an estimator that might be referred to as FE-GMM).
However, such a FE-GMM estimator still cannot be as efficient as QMLE as
the former uses linear combinations of
Δwi,t−2,Δwi,t−3,…,Δwi1
as instruments whereas the latter uses linear combinations of
Δwi,t−1,
Δwi,t−2,…,
Δwi1 as instruments for
Δwi,t−1. Moreover, if one
or more characteristic roots of the underlying PVAR are close to unity,
the correlations between
Δwi,t−1 and
Δwi,t−2,Δwi,t−3,…
would be small; hence GMM using lagged first-differenced variables may be
highly inefficient. On the other hand the efficiency of FE-QMLE is not
affected by the value of the characteristic roots because
Δwi,t−1 is one of the
instruments for
Δwi,t−1.
Remark 6.4. As is well known from the instrumental variables
literature, asymptotic efficiency results in any case need not carry over
to small or even moderate sized samples, particularly when the number of
moment conditions is large relative to the number of observations. The
extended GMM estimators seem to be subject to such a shortcoming. This is
because in the absence of prior information on the unit root properties of
wit all moment conditions could be
informative,20
In the single equation
context, Wansbeek and Bekker (1996) argue the
importance of using all applicable moment conditions; Hahn (1999) argues that the information content of the
homoskedasticity implied moment conditions is significantly augmented if
initialization restrictions are imposed.
and as a result the
extended GMM estimators tend to use moment conditions well in excess of
the number of unknown parameters.
21 The use
of more moment conditions can lead to an increase in the bias of the GMM
estimators in finite sample; for example, see Ziliak (1997).
We thus turn next to an examination of the finite-sample properties of
the QML estimators and also standard and extended GMM estimators by means
of Monte Carlo experiments.22
In the single
equation context Monte Carlo studies of the finite-sample properties of
various GMM estimators include Kiviet (1995),
Blundell and Bond (1998), and Alonso-Borrego and
Arellano (1999).
7. FINITE-SAMPLE EVIDENCE
Although we consider a fairly broad range of model specifications,23
A number of model specifications not
considered in this section, together with the case of nonnormal errors,
are available in Binder et al. (2004).
our Monte Carlo analysis as reported in this section is, given the scope
of the paper, necessarily limited in nature. Nevertheless, we conjecture
that our conclusions are likely to be of general validity.
7.1. Monte Carlo Design
We consider three types of designs for the matrix of slope
coefficients, Φ. These designs distinguish between
stationary, pure unit root, and cointegrated PVAR models. In the case of
stationary designs we consider three subcases with Φ having
maximum eigenvalues equal to 0.6, 0.8, and 0.95. For all designs we set
m = 2, and to make the Monte Carlo results from the various
designs comparable, we specify (where appropriate) different error
variance matrices for different designs so as to obtain similar population
R2 values for both equations of the PVAR model and
across all designs.
Design 1a: Stationary PVAR with maximum eigenvalue
of Φ equal to 0.6
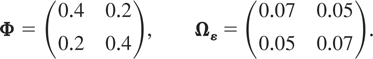
The other eigenvalue of Φ is 0.2, and the population
R2 values are given by
R[utri ]wlit2 =
0.2364, l = 1,2, i = 1,2,…,N, and
t = 2,3,…,T, where
with
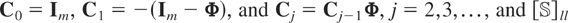
denoting the element in the lth row and lth column of
the matrix
.
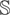
24 See Pesaran, Shin, and Smith (2000) for a discussion of the computation of
R2 values for (possibly cointegrated)
VARs.
Design 1b: Stationary PVAR with maximum eigenvalue
of Φ equal to 0.8
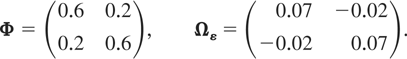
The other eigenvalue of Φ is 0.4, and the population
R2 values are given by
R[utri ]wlit2 =
0.2396, l = 1,2, t = 2,3,…,T, where
R[utri ]wlit2
are computed as in (7.1).
Design 1c: Stationary PVAR with maximum eigenvalue
of Φ equal to 0.95
The other eigenvalue of Φ is 0.45, and the population
R2 values are given by
R[utri ]wlit2 =
0.2383, l = 1,2, t = 2,3,…,T, where
R[utri ]wlit2
are computed as in (7.1).
Design 2: PVAR with unit roots (but
noncointegrated)
Design 3: Cointegrated PVAR
The eigenvalues of Φ in this case are given by 1 and
0.6, and the implied vectors/matrices α, β,
and Π are given by
The population R2 values are given by
R[utri ]wlit2 =
0.2381, l = 1,2, t = 2,3,…,T, where
R[utri ]wlit2
are computed as in (7.1).
The baseline settings across all five designs for the remaining model
parameters are as follows. We take the
εit's to be normally distributed,
and we generate the individual-specific effects as
with
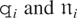
being distributed independently of εit
for all i and t. In this way the individual effects will
not be normally distributed. Clearly, the particular way that the
individual effects are generated has no consequence for the FE-QMLE but
could be important for the GMM-type estimators. For τ we consider two
values, τ = 1 and 5. It should be recalled that τ measures the
degree of cross-section to time-series variations, which can be large in
economic applications (for some evidence, see, e.g., the estimates
provided in Tables I–IV of Lee, Pesaran, and Smith, 1997, and the figures in Hsiao,
Shen, and Fujiki, forthcoming). The Monte Carlo studies of GMM
estimators in the univariate context typically set τ = 1. The
properties of the FE-QMLE do not depend on τ.
The wit's were generated using (2.1)
and the initialization
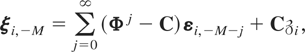
with C =
β⊥(α⊥′
β⊥)−1α⊥′
and where α⊥ and
β⊥ are m × (m
− r) matrices of full column rank such that
α′α⊥ = 0 and
β′β⊥ = 0; also
.
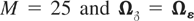
Under this initialization we have that
R[utri ]wli12 =
R[utri ]wlit2,
for t = 2,3,…,T, and l = 1,2.
25 See Binder et al. (2004) for further discussion of this initialization
scheme, which ensures that the same processes generating the stationary
components of
{ξit}t=1T
also generate those of ξi0, and the same
processes generating the common stochastic trend components of
{ξit}t=1T
also generate those of ξi0.
We
set
N = (50, 250),
T = (3, 10), and carry out 1,000
replications for all baseline experiments, computing the FE-QMLE in
addition to the standard and extended GMM estimators.
In further experiments we consider a couple of deviations from the
baseline scenario. As a partial analysis of the performance of the QML
estimator under nonnormal disturbances we consider the cases of t- and chi
square distributed disturbances (see Binder, Hsiao, and
Pesaran, 2004). Also, as a partial analysis of the information
content of the moment conditions available under the random but not the
fixed effects specification, we compare the FE-QMLE and RE-QMLE under
cross-sectionally homoskedastic individual-specific effects, generating
the latter as
,
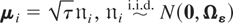
with
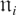
again being distributed independently of
εit for all i and t,
and τ = (1, 5).
In what follows we compare the various estimators in terms of their
biases and root mean square errors (RMSEs). We also investigate the
finite-sample performance of a number of tests based on these estimators.
For Designs 1 and 2 we compute the various estimators with Π
unrestricted, and for Design 3 we compute the QML estimator both with and
without imposing rank restrictions on Π. In what follows we
refer to the GMM estimator that uses only the orthogonality and
initialization restrictions implied moment conditions as the extended GMM
estimator I and to the GMM estimator that uses only the orthogonality and
homoskedasticity implied moment conditions as the extended GMM estimator
II. Finally, the GMM estimator that uses the orthogonality, initialization
restrictions, and homoskedasticity implied moment conditions will be
referred to as the extended GMM estimator III. A summary of the
computational details is provided in Binder et al. (2004).
7.2. The Results
The evidence on the finite-sample properties of the various estimators
in the case of normally distributed disturbances and when no rank
restrictions are imposed on the matrix Π are summarized in
Tables 1 and 2.
Performance of each estimator is evaluated according to the familiar four
criteria, namely, bias, RMSE, size, and power. Table
1 reports the bias and RMSEs of the various estimators. To
economize on space we focus on the results for the elements in the first
column of Φ, namely, φ11 and
φ21. The results for φ12 and
φ22 are qualitatively similar and are available upon
request. Size and power of the tests are reported in Tables 2a, 2b, 2c, and 2d. The nominal
size is set to 5%. Once again to save space Tables 2a, 2b, 2c, and 2d only report the
results for Designs 1a and 3. For the GMM-type estimators we report the
results for τ = 1 and 5.
Bias and RMSE of alternative estimators of panel VAR
Size and power properties of tests for φ11 under
alternative estimators of panel VAR, λmax =
0.6
Size and power properties of tests for φ21 under
alternative estimators of panel VAR, λmax =
0.6
Size and power properties of tests for φ11 under
alternative estimators of panel VAR, λmax =
1
Size and power properties of tests for φ21 under
alternative estimators of panel VAR, λmax =
1
The results in Tables 1 and 2 clearly show that the performance of the GMM-type
estimators tends to deteriorate with increases in τ, except in the
pure unit root case. These simulation results are in line with our
theoretical derivations discussed in Remark 6.2 and will not disappear if
larger sample sizes are considered. The FE-QMLE is invariant to changes in
τ, and its finite-sample performance is therefore unaffected by the
choice of τ. The dependence of the GMM-type estimators on τ
and/or on whether Φ = I2 complicates
the comparison of the various estimators. However, our Monte Carlo results
suggest that even when τ is relatively small, τ = 1, the FE-QMLE
tends to perform significantly better than the GMM-type estimators,
possibly with the exception of the extended GMM estimators in the pure
unit root case. Although for a small number of scenarios with τ = 1
one or more of the extended GMM estimators on a subset of our four
evaluation criteria perform slightly better than the FE-QMLE, the
differences in performance in those cases tend to be small and are
outweighed or at least offset by reverse ranking on one or more of the
other evaluation criteria.26
At the
suggestion of a referee, we also carried out a Monte Carlo study of the
FE-GMM estimator discussed in Remark 6.3. This estimator performed
considerably worse than the standard GMM estimator, and to save space we
are not including it in the result tables.
The results in Tables 1 and 2 also confirm the breakdown of the standard GMM
estimator in the presence of unit roots and document its deterioration as
the eigenvalues of Φ approach unity, even for the relatively
large sample size of N = 250, T = 10. None of the
extended GMM estimators suffers from this problem. In fact, ceteris
paribus the extended GMM estimators perform best in the pure unit root
case. Of the various extended GMM estimators, the one using the
homoskedasticity but not the initialization restrictions (extended GMM
estimator II) is least sensitive to changes in τ. The tests based on
extended GMM estimators I and III suffer from a considerable degree of
overrejection when T = 10, particularly as τ is increased.
This finding should not be too surprising given that the standard
orthogonality conditions and also the initialization restrictions implied
moment conditions involve interaction terms involving both levels and
first differences, whereas the homoskedasticity implied moment conditions
only involve levels terms. The finding that the extended GMM estimator II
is relatively robust to changes in τ is unfortunately of limited use
for empirical analysis, however, as the extended GMM estimator II performs
worse than the other two extended GMM estimators when smaller values of
τ are considered. Also, it is worth noting that although for τ = 1
the extended GMM estimators outperform the standard GMM estimator, as
τ increases this ranking is reversed in some instances. Finally, the
results show that the performance of the GMM-type estimators need not
improve as T is increased. This is due to the rapid increase in
the number of legitimate instruments with T, and it stands in
contrast to the FE-QMLE, whose performance invariably improves with
T. In summary, the Monte Carlo results suggest that the GMM
estimators are likely to perform well if prior knowledge is available
regarding the location of the eigenvalues of Φ and/or if
it is known that τ is small (so that the most suitable moment
conditions could be picked). However, even in cases where the GMM
estimators perform reasonably well in terms of bias and RMSE, they tend to
be outperformed by the FE-QMLE in terms of size and power of the tests,
except in the pure unit root case. The extended GMM estimators, however,
provide useful consistent initial estimates for the QML estimation
iterations.27
We also followed up on a
further suggestion of a referee and considered GMM estimators with
randomly selected moment conditions. We examined a number of alternative
moment selection procedures. But none of these GMM estimators outperformed
the corresponding GMM estimators based on all the valid moment conditions.
However, a comprehensive examination of the subset moment selection
procedure as a possible means of improving the finite-sample performance
of the various GMM estimators is beyond the scope of this
paper.
Overall, the results show that the FE-QMLE performs well and is
remarkably robust to the time-series properties of the underlying
variables. In particular, the performance of the FE-QMLE is generally
unaffected by whether the maximal eigenvalue of Φ is
moderately sized, close to, or equal to unity.
Table 3 presents evidence on the
finite-sample properties of the FE-QMLE in the case of a cointegrated PVAR
model (Design 3). We did not compute any of the GMM estimators for this
design: the main virtue of the GMM estimators, their computational
simplicity, is lost in the presence of rank restrictions on
Π, as in such cases the GMM estimators would have to be
computed using iterative optimization techniques. The results in Table 3 show that the FE-QMLE continues to perform
reasonably well under rank restrictions on Π. Nevertheless,
it should be noted that in the smallest sample (N = 50,
T = 3) the RMSEs for the FE-QMLE tend to be larger than for the
other designs and the test of cointegration rank is undersized. For larger
sample sizes featuring a larger N and/or T, bias and
RMSE diminish rather rapidly, however, and size and power properties of
the tests improve considerably.
Table 3a. Bias and RMSE of fixed effects QML estimator of
cointegrated panel VAR
Table 3b. Size and power properties of cointegration rank
tests based on fixed effects QML estimator
Table 3c. Size and power properties of tests for
α1 under fixed effects QML estimator of cointegrated panel
VAR
Table 3d. Size and power properties of tests for
α2 under fixed effects QML estimator of cointegrated panel
VAR
Table 3e. Size and power properties of tests for
β2 under fixed effects QML estimator of cointegrated panel
VAR
We have also carried out Monte Carlo studies on the performance of the
FE-QMLE under two types of departures from normally distributed
disturbances, namely, when the disturbances are t(5) or
χ2(1) distributed.28
Because
these two types of departure from normality cover both the possibility of
fat tails and the possibility of an asymmetric/skewed shock
distribution, it is very likely that the results could be of greater
generality.
For the case of t(5) distributed disturbances the
FE-QMLE on all four evaluation criteria performed just about the same as
under normally distributed disturbances. For χ
2(1)
distributed disturbances the same tended to be true, specifically for bias
and RMSE, except that there was significant evidence of overrejection when
T = 3.
29 We also obtained broadly
similar results for the various GMM estimators.
The size did
quickly tend toward its nominal value as
T increased, though.
Considering the size of the tests when normality is (erroneously) assumed
in the computation of the standard errors, with one exception the results
did not favor the use of robust estimation of the variance matrix. The
exception was that under χ
2(1) distributed disturbances,
when
T is small (
T = 3) and
N relatively large
(
N = 250), the use of the sandwich formula helps in correcting
the overrejection problem.
All of the preceding arguments carry over to the random effects
setting. Our Monte Carlo studies revealed that under the random effects
model the FE-QMLE performs on a par with the RE-QMLE even for the smallest
sample size (N = 50, T = 3). The differences between the
two estimators are very small across all the four evaluation criteria,
often even favoring the FE-QMLE. Thus, the argument often advanced
concerning the efficiency loss involved in the first-differencing
operation that underlies the FE-QMLE as compared to the RE-QMLE does not
appear to be important for the estimation of PVARs using finite samples.
The RE-QMLE, however, remains the estimator of choice if the primary
purpose of the analysis is the identification and estimation of the
effects of time-invariant variables in short panels. In that case great
caution must be exercised because the random effects model imposes strong
assumptions on the distribution of the individual-specific effects. For
the identification and estimation of the effects of time-varying variables
our findings favor the use of FE-QMLE on grounds of its robustness to any
form of specification of the distribution generating the
individual-specific effects.
8. CONCLUSION
In this paper, we have extended the analysis of linear dynamic panel
data models with short time dimension in a number of respects. We have
generalized the extended GMM estimators, hitherto studied in the
literature in a single equation context, to a multivariate PVAR setting.
We have derived random and fixed effects QML estimators and have shown
that the QML estimators are consistent and asymptotically normally
distributed when the cross-sectional dimension of the panel approaches
infinity, irrespective of whether the underlying time series are (trend)
stationary, pure I(1), or I(1) and cointegrated. Furthermore, we have
proposed new QML-based procedures for conducting tests for unit roots and
cointegration rank in panels with short time dimension and have shown that
the limiting distributions of the relevant test statistics follow standard
chi square and normal distributions.
The applicability of the various GMM estimators requires that certain
assumptions on the unobserved individual effects are satisfied. From the
perspective of empirical analysis, these assumptions could be restrictive.
In addition, the Monte Carlo evidence presented in Section 7 favors the
FE-QMLE over the various GMM estimators, even under important departures
from normally distributed disturbances. The finite-sample performance of
the various GMM estimators depends critically on a ratio reflecting
unobserved cross-section variation in the data relative to unobserved
time-series variation, but even if this ratio is relatively small the GMM
estimators are outperformed in finite sample by the QML estimators. A
theoretical rationale is also provided for this result whereby it is shown
that the asymptotic variance of the GMM estimators is an increasing
function of the variance of the individual effects, whereas the
distribution of the FE-QMLE is invariant to the size of this variance.
The use of likelihood-based procedures for estimation and inference in
VAR models is standard in the time-series literature. This paper has
provided both theoretical and operational arguments for the application of
likelihood-based methods to PVAR models, whether the underlying time
series are stationary, integrated, or cointegrated. The ultimate test of
our approach lies in the application of the proposed techniques to
substantive economic problems. This is the next stage of our research and
hopefully that of others. The likelihood approach can also be used to
address other theoretical issues of interest, such as model selection and
conditional estimation and inference in PVARs.
APPENDIX: The Asymptotic Variance Matrix of
the Standard GMM Estimator
In this Appendix we derive the asymptotic variance of
,
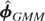
the standard GMM estimator defined by (6.4), as N →
∞, and show that it is an increasing function of
Ωμ, the variance matrix of the
individual effects, μi, in the sense that
if Ωμ(1) −
Ωμ(2) is a positive
semidefinite matrix, so will be
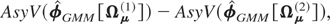
where Ωμ(j),
j = 1,2, are two different variance matrices for the individual
effects. (The more complicated case of the dependence of extended GMM on
Ωμ can be derived similarly noting
that wit −
Φwi,t−1 =
(I − Φ)μi +
εit and making use of the relations
(6.10) and (6.11).)
The asymptotic variance of
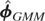
is given by (also see (6.6))
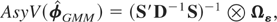
where Ωε =
E(εitεit′),
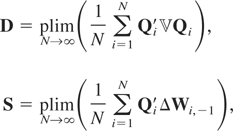
and
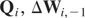
are defined by (6.2), (6.3), and (6.5), respectively.
To simplify the derivations we suppose that Assumptions (G1), (G2),
and (R1) hold, that all eigenvalues of Φ fall inside the
unit circle, and that the wit process has
started in the infinite past. Under these assumptions (the results will be
qualitatively unaffected if one considers other initializations of the
wit process discussed in Binder et al., 2004)
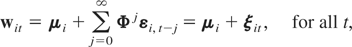
and it is easily seen that
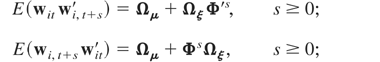
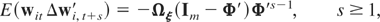
where
.
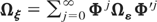
Also under Assumption (G2)
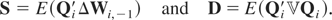
Using (A.1) and (A.2) we have
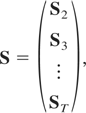
with St, for t =
2,3,…,T, a matrix of dimension m(t
− 1) × m given by
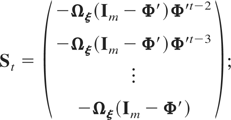
furthermore we have
where
is a matrix of dimension T(T − 1)/2 ×
T(T − 1)/2 given by
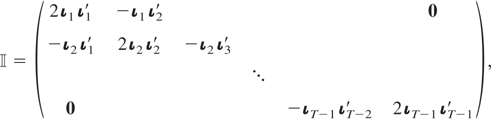
ιt being a vector of ones of
dimension t × 1, for t = 1,2,…,T
− 1, and where H is a matrix of dimension
mT(T − 1)/2 × mT(T
− 1)/2 given by
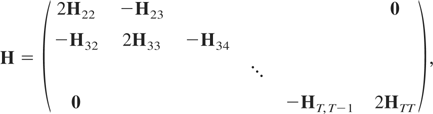
with Htt, for t =
2,3,…,T, a matrix of dimension m(t
− 1) × m(t − 1) given by
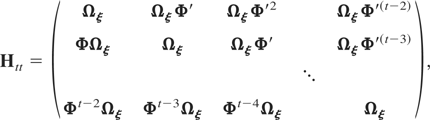
Ht,t+1, for s =
2,3,…,T, a matrix of dimension m(t
− 1) × m(t − 1) given by
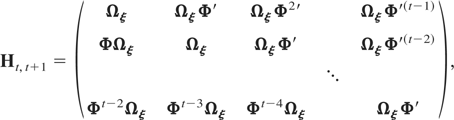
and Ht+1,t, for s =
2,3,…,T, a matrix of dimension m(t
− 1) × m(t − 1) given by
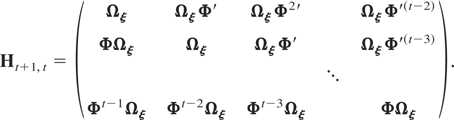
It is clear that
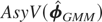
will depend on Ωμ only through the
matrix D, and for any two variance matrices,
Ωμ(j),
j = 1,2,
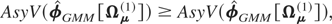
if
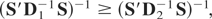
where
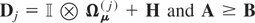
denotes that A − B is a positive semidefinite
matrix. This condition implies
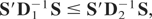
and because S does not depend on
Ωμ(j), using
(A.3) the condition (A.4) will be satisfied if
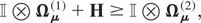
or if Ωμ(1) ≥
Ωμ(2). The preceding
sequence can be reversed to show that if
Ωμ(1) ≥
Ωμ(2) then (A.4) will
follow.
In the simple case where m = 1 and T = 3, we
have
and after some algebra it follows that
where τ =
σμ2/σε2.
It is interesting to note that
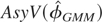
depends on the ratio τ and not the error variances
σμ2 and
σε2 separately. It is also easily
established that
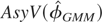
is an increasing function of τ, for all values of
|φ| < 1 and τ > 0.
