Consider the basic linear regression model with heteroskedasticity, y_i = x_i′ β + e_i, with i = 1,…, n, where e_i is a zero-mean random variable distributed independently from all x_i and all e_j with i ≠ j. The variance of e_i is σ_i², where all σ_i², i = 1,…, n may be different. The “true” generalized least squares estimator (GLSE)

of β is obtained as the ordinary least squares estimator (OLSE) from the regression of the y_i /σ_i on the x_i /σ_i. When, as usual, the σ_i are unknown, we might instead be tempted to use the absolute value of the residual

, with b the OLSE from the regression of the y_i on the x_i, and obtain a “feasible” GLSE

, say, by regressing the

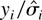
on the

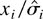
. Intuitively, this is not a sensible approach, but one is hard put to find an argument in the literature. What are the (finite or asymptotic) distributional properties of

? (One might conjecture that

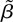
is consistent and asymptotically normal.) Is there any sense in which

constitutes an improvement over b?