Published online by Cambridge University Press: 08 February 2005
Infinite order vector autoregressive (VAR) models have been used in a number of applications ranging from spectral density estimation, impulse response analysis, and tests for cointegration and unit roots, to forecasting. For estimation of such models it is necessary to approximate the infinite order lag structure by finite order VARs. In practice, the order of approximation is often selected by information criteria or by general-to-specific specification tests. Unlike in the finite order VAR case these selection rules are not consistent in the usual sense, and the asymptotic properties of parameter estimates of the infinite order VAR do not follow as easily as in the finite order case. In this paper it is shown that the parameter estimates of the infinite order VAR are asymptotically normal with zero mean when the model is approximated by a finite order VAR with a data dependent lag length. The requirement for the result to hold is that the selected lag length satisfies certain rate conditions with probability tending to one. Two examples of selection rules satisfying these requirements are discussed. Uniform rates of convergence for the parameters of the infinite order VAR are also established.Very helpful comments by the editor and two referees led to a substantial improvement of the manuscript. I am particularly indebted to one of the referees for pointing out an error in the proofs. All remaining errors are my own. Financial support from NSF grant SES−0095132 is gratefully acknowledged.
Infinite order vector autoregressive (VAR(∞)) models are appealing nonparametric specifications for the covariance structure of stationary processes because they can be justified under relatively weak restrictions on the Wold representation of a stationary process. In practice, the VAR(∞) specification needs to be approximated, usually by a VAR(h) model where the truncation parameter h increases with sample size n. This approach was proposed by Akaike (1969) and Parzen (1974) for the estimation of spectral densities.
Approximations to VAR(∞) models have received renewed interest in recent years in a number of econometric applications. Lütkepohl and Saikkonen (1997) consider impulse response functions in infinite order cointegrated systems. Cointegration tests and inference in systems with infinite order dynamics are considered by Saikkonen and Luukkonen (1997) and Saikkonen and Lütkepohl (1996). Ng and Perron (1995, 2001) use flexible autoregressive specifications in augmented Dickey–Fuller (ADF) unit root tests to improve size properties of these tests. Lütkepohl and Poskitt (1996) construct tests for causality using infinite order vector autoregressive processes. Paparoditis (1996), Inoue and Kilian (2002), and Goncalves and Kilian (2003) propose bootstrap procedures for VAR(∞) models. Finally, den Haan and Levin (2000) use prewhitening procedures and VAR(∞) approximations to estimate heteroskedasticity and autocovariance consistent (HAC) covariance matrices for robust inference. They use Akaike and Bayesian information criteria (AIC and BIC) to select the order of the approximating VAR and report evidence that applying standard kernel based smoothing to estimate spectral densities from the prewhitened residuals does not lead to improvements over estimates that are entirely based on the VAR specification.
The lag length h is the key design parameter in implementing procedures that approximate VAR(∞) models. The results of Berk (1974) and Lewis and Reinsel (1985) establish rates of convergence necessary for consistency and asymptotic normality. A number of papers using VAR(h) approximations do not go beyond listing these restrictions on rates as conditions for their results. In practice, such restrictions however can not be used to construct automated procedures because the lower bound for the expansion rate of h depends on unknown properties of the data. Moreover, conditions on the growth rate of h as a function of the sample size n are not sufficient to choose h in a finite sample. What is called for are data-dependent rules where h is chosen based on information in the sample.
Hannan and Kavalieris (1986) and Hannan and Deistler (1988) analyze the stochastic properties of feasible rules

based on the AIC and BIC criteria. The AIC information criterion has been shown to possess minimal mean squared error properties for the estimation of parameters in AR(∞) models and minimal integrated mean squared error properties for the estimation of approximations to the spectral density of AR(∞) models by Shibata (1980, 1981). Ng and Perron (1995) point out that the AIC criterion violates the conditions on h obtained by Berk (1974) and Lewis and Reinsel (1985). This leads to expansion rates for h that are too slow to eliminate biases that result in shifts of the asymptotic limit distribution of the parameters.
Infinite dimensional models have a long tradition in econometric theory. The work of Sargan (1975) is an early example. The problem of biases caused by parameter spaces that grow in dimension with the sample size has recently been discussed in econometrics by Bekker (1994). Similar effects can be found in various contexts, for example, in the work of Donald and Newey (2001), Hahn and Kuersteiner (2002, 2003), and Kuersteiner (2002).
Especially in time series applications finite sample biases can be substantial and may have a dominating effect on inference. Kilian (1998) shows that bootstrap confidence intervals for impulse response functions are severely affected by finite sample biases in the estimates of the underlying autoregressions. He proposes a bias correction to overcome severe distortions in coverage rates. In panel models with lagged dependent variables Hahn, Hausman, and Kuersteiner (2000) and Hahn and Kuersteiner (2002) document the predominant effect of finite sample biases on the mean squared error of parameter estimates.
Ng and Perron (1995) propose a general-to-specific testing approach to select the approximate lag order in ADF tests where the underlying model is a VAR(∞). Their work extends results of Hall (1994) for lag order selection in ADF tests when the underlying model is a finite order VAR to the infinite order case. Ng and Perron (1995) advocate general-to-specific selection rules to overcome the problems of AIC and BIC in selecting the lag length in VAR(∞) approximations described previously although their focus is on the performance of unit root tests and not on the estimation of the VAR(∞) parameters. They show that distributional properties of ADF tests are not affected by biases induced by AIC and BIC but report simulation evidence demonstrating the advantages in terms of finite sample size of the ADF tests when parametrized with their lag selection procedure.
In this paper the results of Ng and Perron (1995) are extended to estimation and inference in VAR(∞) models. It is argued that the convergence properties of
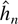
based on model selection procedures typically are not strong enough to apply the arguments of Eastwood and Gallant (1991) for admissible estimation. This is true for the general-to-specific approach of Ng and Perron (1995) and also for conventional model selection methods based on information criteria. In fact, in infinite dimensional parameter spaces adaptiveness of selection rules, a concept that has appeared in the literature and will be defined more precisely in Section 2, is hard to show. Moreover, the results of Shibata (1980, 1981) do not establish the asymptotic distribution of parameter estimates in an
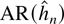
model when
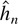
is selected by AIC. Such a result seems to be missing in the literature to this date.
Here, the arguments do not rely on adaptiveness properties of the selection rule. An alternative proof, based on the work of Lewis and Reinsel (1985), is used to show that h can be replaced by
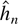
determined by the general-to-specific approach of Ng and Perron (1995) without affecting the limiting distribution of the parameters in the VAR(h) approximation. This leads to fully automated approximations to the VAR(∞) model that do not suffer from higher order biases as approximations using AIC and BIC generally would. Nevertheless, in the special case where the underlying process is a vector autoregressive moving average (VARMA) model, a modification of AIC also can be used without affecting the limiting distribution, a result that is discussed at the end of Section 2. Uniform rates of convergence for the parameters of the
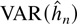
approximation are also obtained. These rates in turn can be used to establish rates for functionals of the VAR parameters such as the spectral density matrix.
The main results of the paper are presented in Section 2, Section 3 contains some conclusions, and all the proofs are collected in Section 4.
Let

be a strictly stationary time series with an infinite order moving average representation
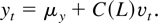
Here,

is a constant and vt is a strictly stationary and conditionally homoskedastic martingale difference sequence. The lag polynomial C(L) is defined as
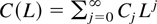
where L is the lag operator.
Assumption A. Let
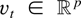
be strictly stationary and ergodic, with
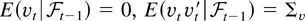
where Σv is a positive definite symmetric matrix of constants. Let vti be the ith element of

, and v = (vt1i1,…,vtkik) such that φi1,…,ik,t1,…,tk(ξ) = Eeiξ′v is the joint characteristic function with corresponding joint kth order cumulant function defined as cumi1,…,ik*(t1,…,tk) = (∂u1 + ··· + uk/∂ξ1u1…∂ξkuk)|ξ=0 ln φi1,…,ik,t1,…,tk(ξ) where ui are nonnegative integers such that u1 + ··· + uk = k. By stationarity it is enough to define cumi1,…,ik(t1,…,tk−1) = cumi1,…,ik*(t1,…,tk−1,0). Assume that
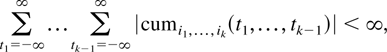
where the sum converges for all k ≤ 4 and all ij ∈ {1,…,p} with j ∈ {1,…,k}.
Assumption A is weaker than the assumptions imposed in Lewis and Reinsel (1985), where independence of the innovations is assumed, but is somewhat stronger than the assumptions in Hannan and Deistler (1988, Theorem 7.4.8), which also allows for the more general heteroskedastic case that is excluded here by the requirement that

. Recently, Goncalves and Kilian (2003) have obtained explicit formulas for the norming constant when the innovations are conditionally heteroskedastic. The summability assumption (2.2) is quite common in the literature on HAC estimation. Andrews (1991), for example, uses a similar condition and shows that (2.2) is implied by a mixing condition.
Assumption B. The lag polynomial C(L) with coefficient matrices Cj satisfies
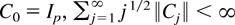
where ∥A∥2 = tr AA′ for a square matrix A and det C(z) ≠ 0 for |z| ≤ 1 where

.
Assumption C. For Cj as defined in Assumption B it holds that

and det C(z) ≠ 0 for |z| ≤ 1.
The summability restriction on the impulse coefficients Cj in Assumptions B and C is stronger than the condition imposed by Lewis and Reinsel (1985), where only

is required. It is needed here to achieve similar flexibility in the central limit theorem as Lewis and Reinsel (1985). Assumption B implies that yt has an infinite order VAR representation given by
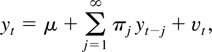
where μ = C(1)−1μy and C(L)−1 = π(L) with
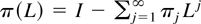
. The impulse response function C(L) of yt is thus a functional of π(L) defined by C(L) = π(L)−1. Another functional of interest is the spectral density fy(λ) of yt where fy(λ) = (2π)−1π(eiλ)−1Σv(π(e−iλ)−1)′. For inferential purposes we are often interested in fy(0), the spectral density at frequency zero.
The VAR(∞) representation in (2.3) needs to be approximated in practice by a model with a finite number of parameters, in the case considered here a VAR(h) model. The approximate model with VAR coefficient matrices π1,h,…,πh,h is thus given by

where Σv,h = Evt,h vt,h′ is the mean squared prediction error of the approximating model.
It was shown by Berk (1974) and Lewis and Reinsel (1985) that the parameters (π1,h,…,πh,h) are root-n consistent and asymptotically normal for π(h) = (π1,…,πh) in an appropriate sense to be made explicit later if h does not increase too quickly, that is, if h is chosen such that h3/n → 0. At the same time h must not increase too slowly to avoid asymptotic biases. Berk (1974) shows that h needs to increase such that

. In practice such rules are difficult to implement as they only determine rates of expansion for h and do not lead directly to feasible selection criteria for h. Ng and Perron (1995) argue that information criteria such as the Akaike criterion do not satisfy
1A special case where a version of AIC satisfies Berk's conditions is discussed at the end of this section.

then bias terms due to asymptotic misspecification of the model are of order n−1/2. These biases are more severe than the usual finite sample biases, which are typically of order n−1.
To avoid the problems that arise from using information criteria to select the order of the approximating model we use the sequential testing procedure analyzed in Ng and Perron (1995). Let π(h) = (π1′,…,πh′)′, Yt,h = (yt′ − y′,…,yt−h+1′ − y′)′ where
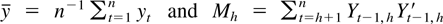
. Define Mh−1(1) to be the lower-right p × p block of Mh−1. Let Γh be the hp × hp matrix whose (m,n)th block is Γn−myy and Γ1,h′ = [Γ−1yy,…,Γ−hyy] where Γj−iyy = Cov(yt−i,yt−j′). The coefficients of the approximate model satisfy the equations (π1,h,…,πh,h) = Γ1,hΓh−1. Let
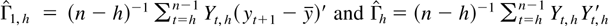
. The estimated error covariance matrix is
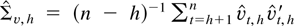
where
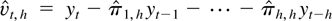
with coefficients
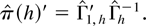
Under Assumptions A and B it follows from Hannan and Deistler (1988, Theorem 7.4.6) that
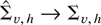
uniformly in h ≤ hmax and hmax = o((n/log n)1/2). A Wald test for the null hypothesis that the coefficients of the last lag h are jointly 0 is then, in Ng and Perron's notation,
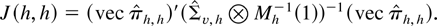
The following lag order selection procedure from Ng and Perron (1995) is adopted.
DEFINITION 2.1. The general-to-specific procedure chooses (i)
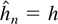
if, at significance level α, J(h,h) is the first statistic in the sequence J(i,i),{i = hmax,…,1}, which is significantly different from zero or (ii)

if J(i,i) is not significantly different from zero for all i = hmax,…,1 where hmax is such that
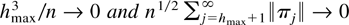
as n → ∞.
Implementation of the general-to-specific procedure may be difficult in practice because the critical values depend on complicated conditional densities that are not Gaussian in the parameters and therefore not χ2 for the test statistics. This seems to be the case even though the underlying joint and marginal densities can be assumed to be Gaussian with easily estimated coefficients.2
I am grateful to one of the referees for pointing out this fact.
To illustrate the problems with establishing results that allow substituting h with
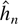
in
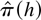
we consider the lag order estimate
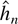
based on the AIC and BIC criteria. The lag order estimate is defined as
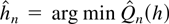
with
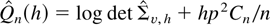
where Cn = 2 for AIC and Cn = log n for BIC. Hannan and Deistler (1988, Theorem 7.4.7) show under slightly different assumptions than here that
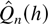
can be essentially replaced by Qn(h) = hp2/n(Cn − 1) + tr(Σ−1(Σv,h − Σ)). Shibata (1980)
3Hannan and Deistler (1988, p. 317) discuss this interpretation.
Abadir, Hadri, and Tzavalis (1999) analyze nonstationary VARs where the asymptotic limiting distribution of ordinary least squares estimators is also shifted away from the origin. They find an explicit relation between the dimension p and the bias. The situation there is however quite different from the one considered here where bias is due to misspecification.
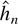
is selected by AIC or BIC then
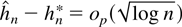
. Eastwood and Gallant (1991) and Ng and Perron (1995) define the concept of adaptive selection rules. A sequence of random variables
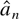
is an adaptive selection rule if there is a deterministic rule an such that
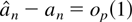
. The discussion of AIC and BIC based selection rules

shows that these rules are not adaptive for hn* in the sense of Eastwood and Gallant (1991) and Ng and Perron (1995).
Similarly, the results of Ng and Perron (1995) imply that
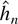
selected by the procedure in Definition 2.1 satisfies
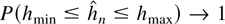
as n → 0 for any sequence hmin such that hmin ≤ hmax and hmax − hmin → ∞. Such a result again is not strong enough to guarantee that
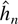
is adaptive for Mhmax where M is an arbitrary positive constant. Any argument that relies on the adaptiveness property of selection rules to establish that
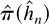
has the same asymptotic properties as
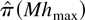
therefore can not be applied. It may be possible to prove adaptiveness properties of selection rules, but such results do not seem to be readily available in the literature.
For this reason an alternative proof strategy is chosen here. The following weaker consequence of Lemma 5.2 of Ng and Perron (1995) that follows directly from their proof turns out to be sufficient to establish the feasibility of a fully automatic approximation to the VAR(∞) model.
LEMMA 2.2. Let
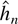
be given by Definition 2.1. Let hmin be any sequence such that hmax ≥ hmin, hmax − hmin → ∞, and

. Then
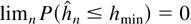
.
The following two main results of this paper establish that the results in Lewis and Reinsel (1985) essentially remain valid if in
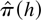
, h is replaced by
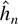
. The proofs establish uniform convergence of

over a set Hn of values h such that

is contained in Hn with probability tending to one. First, an asymptotic normality result is established for an arbitrary but absolutely summable linear transformation l(h) of the parameters into the real line. In particular this result implies that arbitrary finite linear combinations of elements in
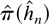
are asymptotically normal. By the Cramér–Wold theorem this also implies that any finite combination of elements in
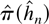
is jointly asymptotically normal.
THEOREM 2.3. Let
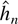
be given by Definition 2.1. (i) Let Assumptions A and B hold. Let l(h) = (l1′,…,lh′)′ be the p2h × 1 section of an infinite dimensional vector l such that for some constants
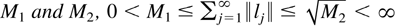
. Let ωh = l(h)′(Γh−1 [otimes ] Σv)l(h). Then limh→∞ ωh = ω exists and is bounded and
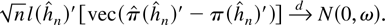
(ii) Instead of Assumption B let Assumption C hold. Let hmax be as in Definition 2.1, let hmin be defined as in Lemma 2.2 with Δn ≡ hmax − hmin → ∞, Δn = O(nδ) for 0 < δ < 1/3, and assume that there exists some h such that h ≤ hmin, Δn /(hmin − h) → 0 and h → ∞, some h** such that
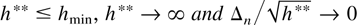
, and a sequence l(h) = (l1,h′,…,lh,h′)′ of p2h × 1 vectors partitioned into p2 × 1 vectors lj,h such that for some constants M1 and M2, 0 < M1 ≤ ∥l(h)∥2 = l(h)′l(h) ≤ M2 < ∞ for all h = 1,2,…, and

and also
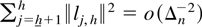
for all h → ∞, hmin ≤ h ≤ hmax. Then
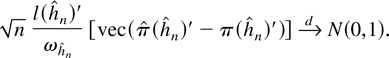
Remark 1. The rate at which Δn → ∞ can essentially be arbitrarily slow. Thus the restrictions on h** and h are quite weak.
Remark 2. Note that the tail summability conditions in the second part of the theorem are automatically satisfied for the fixed vectors l with l′l < ∞ that satisfy the additional constraint
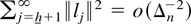
for some h → ∞. The second part allows for more general limit theorems where l(h) fluctuates except in the “tails.”
Remark 3. Although the theorem essentially provides the same results as Lewis and Reinsel (1985) for many cases of practical interest it nevertheless requires somewhat stronger assumptions both on Ci and l(h). A different proof strategy may lead to different and maybe less restrictive conditions, but it seems unlikely that a result at the same level of generality as in Lewis and Reinsel (1985) can be shown without establishing adaptiveness of
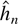
.
Remark 4. For (i) it also follows that
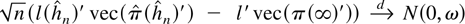
because
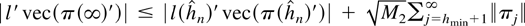
with
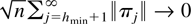
.
The next result is a refined version of Theorem 1 of Lewis and Reinsel (1985). It establishes a uniform rate of convergence for the parameter estimates when the lag length is chosen by the general-to-specific approach of Ng and Perron (1995).
THEOREM 2.4. Let Assumptions A and B hold. Let

be given by Definition 2.1. Then
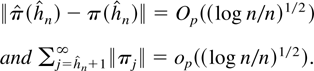
The result in Theorem 2.4 is particularly useful to establish consistency and convergence rates of functionals of π(L) such as the spectral density matrix of yt. The result presented here is stronger than a corresponding result for nonstochastic lag order selection presented in Lewis and Reinsel (1985, Theorem 1) where only uniform consistency is established without specifying the convergence rate. Theorem 2.4 complements results in Hannan and Deistler (1988, Theorem 7.4.5) where the case of nonstochastic h sequences is analyzed.
Theorems 2.3 and 2.4 do not rely on a specific model selection procedure. All that is required for the theorems to apply is that there are sequences hmin and hmax satisfying the conditions stated previously and a data-dependent rule
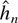
such that
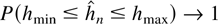
as n → ∞. It is thus quite plausible that feasibility can be established for a broader class of selection procedures than the one considered here.
Under more restrictive assumptions this can even be done for AIC based procedures. In fact for VARMA models
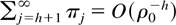
where ρ0 is the modulus of a zero of C(z) nearest |z| = 1. Hannan and Deistler (1988, Theorem 6.6.4 and p. 334) show that
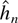
selected by AIC satisfies
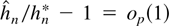
for hn* = log n/(2 log ρ0). It thus follows that
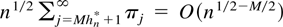
, which is o(1) for M > 1. This suggests that at least for VARMA systems AIC could be used as an automatic order selection criterion for autoregressive approximations.
5I am grateful to one of the referees for pointing out this fact, which is discussed in Hannan and Deistler (1988, p. 262).

selected by AIC, the rule
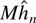
can be used instead of the general-to-specific procedure if the underlying model is a VARMA model.
In this paper data-dependent selection rules for the specification of VAR(h) approximations to VAR(∞) models are analyzed. It is shown that the method of Ng and Perron (1995) can be used to produce a data-dependent selection rule

such that the parameters of the approximating VAR(h) model are asymptotically normal for the parameters of the underlying VAR(∞) model. The asymptotic normality result does only hold on essentially finite subsets of the parameter space. Uniform rates of convergence for the VAR(∞) parameters are thus obtained in addition.
The results presented here extend the existing literature, where so far model selection has been carried out mostly in terms of information criteria. Such criteria are known to result in sizable higher order biases. On the other hand, the selection criteria analyzed here do not suffer from these biases. The paper also reconsiders some existing proof strategies in the context of infinite dimensional parameter spaces where the concept of consistent model selection is hard to apply.
The following lemmas are used in the proof of Theorem 2.3. The matrix norm ∥A∥22 = supl≠0 l′A′Al/l′l, known as the two-norm, is adopted from Lewis and Reinsel (1985, p. 396), where the less common notation ∥.∥1 is used. There it is also shown that for two matrices A and B, the inequalities ∥AB∥2 ≤ ∥A∥22∥B∥2 and ∥AB∥2 ≤ ∥A∥2∥B∥22 hold. First it is shown that the mean of yt can be replaced by an estimate without affecting the asymptotics.
LEMMA 4.1. Let

and let
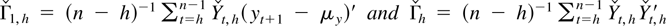
. Let
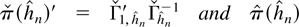
is defined in Section 2. Then

.
Proof. Choose δ such that 0 < δ < 1/3 and pick a sequence hmin* such that hmax ≥ hmin*, hmax − hmin* → ∞, hmax − hmin* = O(nδ), and
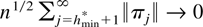
. Define
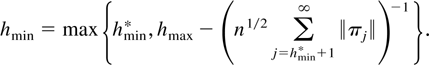
It follows that hmin ≤ hmax and
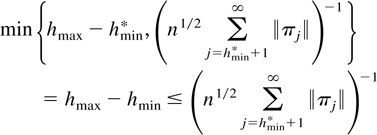
such that hmax − hmin → ∞. Because hmax − hmin* = O(nδ) it follows that hmax − hmin = O(nδ). Because hmin ∈ [hmin*,hmax] it also follows that

. Let Hn = {h|hmin ≤ h ≤ hmax}. Note that from Lemma 2.2 it follows that
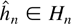
with probability tending to one. Consider
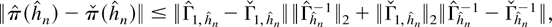
where

It now can be established that

Furthermore,
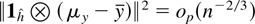
such that
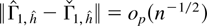
by the Markov inequality and Lemma 2.2. In the same way,

such that
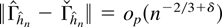
. By the arguments in the proof of Theorem 1 in Lewis and Reinsel (1985) it then also follows that
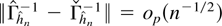
. █
LEMMA 4.2. If yt has typical element a denoted by yta and wt,i = (yt − μy)(yt−i − μy)′ then
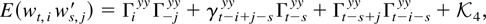
where the scalar coefficient γt−syy is defined as γt−syy = E(yt − μy)′(ys − μy) and
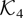
is a p × p matrix with typical element (a,b) denoted by [·]a,b and given as
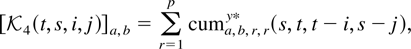
where cuma,b,r,ry*(s,t,t − i,s − j) is defined as

with cja,b = [Cj]a,b. It also follows that
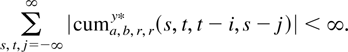
Proof. Without loss of generality assume μy = 0. Then the matrix

has typical element (a,b) equal to
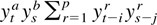
. The result follows from applying E(wxyz) = E(wx)E(yz) + E(wy)E(xz) + E(wz)E(xy) + cum*(x,y,w,z) for any set of scalar random variables x,y,w,z with E(x) = 0 and E|x|4 < ∞ with the same conditions on y, w, and z. It thus follows that

For the summability of the cumulant note that
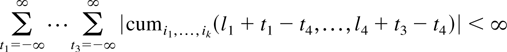
uniformly in l1,…,l4 by Assumption A. The result then follows from the absolute summability of cja,b for a,b ∈ {1,…,p}. █
COROLLARY 4.3. Let Kpp be the p2 × p2 commutation matrix
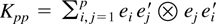
where ei is the ith unit p-vector. If yt is a vector of p random variables then
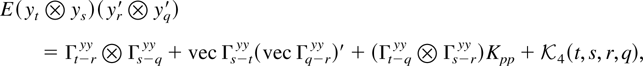
where
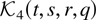
is a matrix with
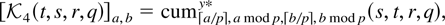
[lceil ]a[rceil ] is the smallest integer larger than a, and a mod p = 0 is interpreted as a mod p = p with
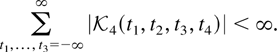
Proof. Note that (yt yr′ [otimes ] ys yq′) = vec ys yt′(vec yq yr′)′ = vec ys yt′(vec yr yq′)′Kpp = (yt yq′ [otimes ] ys yr′)Kpp. █
LEMMA 4.4. Let Hn be defined as in the proof of Lemma 4.1 and let Assumptions A hold. Then
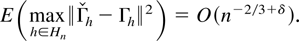
Proof. Without loss of generality assume that μy = 0. Then

because

by Lemma 4.2 █
LEMMA 4.5. Let Assumption A hold and assume that
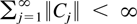
. Then ∥Γh∥2 < ∞ and ∥Γh−1∥2 < ∞ uniformly in h. Let
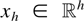
with lim suph∥xh∥ < ∞. Then ∥Γh xh∥ < ∞ and ∥Γh−1xh∥ < ∞. Let Γhj,k be the j,kth block of Γh−1. Then,
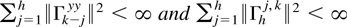
uniformly in k,h. Moreover, supj,k∥Γhj,k ∥ < ∞ uniformly in h.
Proof. The properties ∥Γh∥2 < ∞ and ∥Γh−1∥2 < ∞ follow from Berk (1974, p. 493) and Lewis and Reinsel (1985, p. 397). Then, ∥Γh xh∥ ≤ ∥xh∥∥Γh∥2 < ∞ and ∥Γh−1xh∥ ≤ ∥xh∥∥Γh−1∥2 < ∞. For the last statement take ek,h′ = (0p,…,0p,Ip,0p,…)′ where the p × p identity matrix Ip is at the kth block. It follows that ∥ek,h∥2 = p, which is uniformly bounded in h,
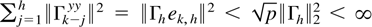
with a similar argument holding for
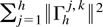
. The last assertion follows from ∥Γhj,k ∥ = ∥ej,h′Γh−1ek,h∥ ≤ p∥Γh−1∥2 < ∞ for any j,k uniformly in h. █
LEMMA 4.6. Let Assumptions A and C hold. Then,
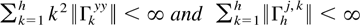
uniformly in j,h.
Proof. The first statement follows immediately from Assumption C. The second result follows from Hannan and Deistler (1988, Theorem 6.6.11). █
LEMMA 4.7. Let Assumptions A and C and the conditions of Theorem 2.3 hold. Then,
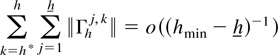
for all h*,h such that h ≥ hmin ≥ h* ≥ h, h* − h = O(hmin − h), hmin − h* = O(hmin − h), and h → ∞. If instead of C, Assumption B holds then for any fixed constant k0 < ∞ and for hmin,hmax as defined in Lemma 4.1 it follows that

as n → ∞ where the sum is assumed to be zero for all n where k0 ≥ hmin.
Proof. Let Γ∞ be the infinite dimensional matrix with j,kth block Γk−jyy for j,k = 1,2,… and Γ∞−1 the inverse of Γ∞ with j,kth block denoted by Γ∞j,k . From Lewis and Reinsel (1985, p. 401) and Hannan and Deistler (1988, Theorem 7.4.2) it follows that

where πj = 0 for j < 0. Next use the bound ∥Γhj,k ∥ ≤ ∥Γ∞j,k ∥ + ∥Γhj,k − Γ∞j,k ∥. From Lewis and Reinsel (1985, p. 402) it follows that

where the last term is o((h* − h)−1) because
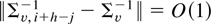
and the same argument as in (4.2) applies. Next, note that

where the second term again is o((h* − h)−1) because of the uniform bound in (4.3), which follows. From Hannan and Deistler (1988, Theorem 6.6.12 and p. 336) it follows that

where the bound holds uniformly in i = 1,2,…. Similarly, for all i < j,
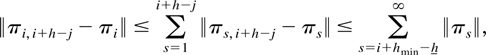
where the first inequality follows from the fact that h − j ≥ 0 for all h ∈ Hn and j ≤ h and the second inequality follows from h ≥ hmin and Hannan and Deistler (1988, Theorem 6.6.12 and p. 336). Substituting for ∥πi,i+h−j − πi∥ it can then be seen that uniformly for j ≤ h,

This shows that
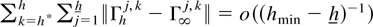
.
For the second part note that

uniformly in h. Also, note that

such that
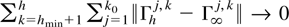
uniformly in h by the same arguments as before. █
LEMMA 4.8. Let Assumptions A and C hold, define
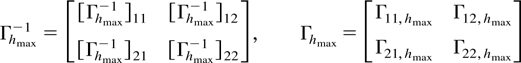
such that [Γhmax−1]11 is the right upper hp × hp block of Γhmax−1 and similarly for Γ11,hmax, and let A = Γ12,hmaxΓ22,hmax−1Γ21,hmax with typical p × p block (a,b) denoted by Aa,b. Then

for any sequence h* such that hmin − h* → ∞ as h → ∞.
Proof. Note that
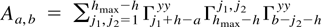
because Γ22,hmax = Γ11,hmax−h by the Toeplitz structure of the covariance matrix. Then it follows by Lemma 4.6 that

where
uniformly in h. █
Proof of Theorem 2.3. The proof is identical for parts (i) and (ii) unless otherwise stated. Define hmin and Hn as in the proof of Lemma 4.1. In view of Lemma 4.1 we can assume that μy = 0. We therefore set y = 0. Let
. Note that
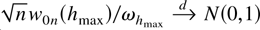
by Hannan and Deistler (1988, Theorem 7.4.8). Then

where ωh is uniformly bounded from below and above by Lewis and Reinsel (1985, p. 400) such that

is bounded from below and above with probability one. It is thus enough to show that
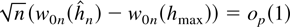
and
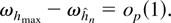
Next note that for any η > 0,
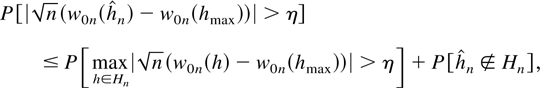
where the second probability goes to zero by Lemma 2.2.
Let
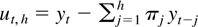
. From Lewis and Reinsel (1985, equation (2.7)) it follows that
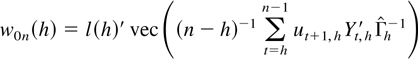
such that

where w4n,…,w7n are defined in the obvious way. First, consider

To establish a bound for maxh∈Hn|w4n| we consider
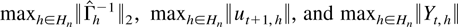
in turn.
From Lewis and Reinsel (1985, p. 397) we have
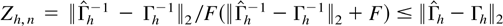
where F is a constant such that ∥Γh−1∥2 ≤ F uniformly in
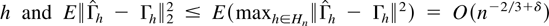
by Lemma 4.4 such that maxh∈Hn Zh,n = op(n−1/3+δ/2). Then,
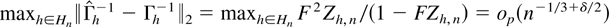
and
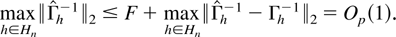
For maxh∈Hn∥ut+1,h∥ consider

such that maxh∈Hn∥ut+1,h∥ = Op(1) by the Markov inequality. Finally,
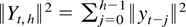
such that
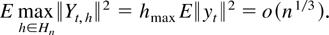
These results show that
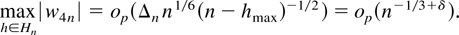
For |w5n| consider w5n = w51n + w52n where

For w51n consider
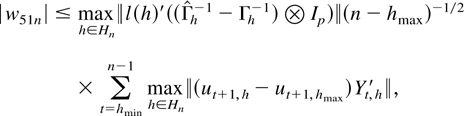
where
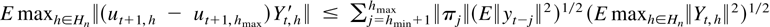
with supt E∥yt∥2 ≤ c < ∞ and
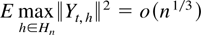
from before such that

Also,

such that w51n = op(1).
Use the notation l(h) = (l1,h′,…,lh,h′)′ where lj,h is a p2 × 1 vector with lj,h = lj for part (i) and Γhjk is the j,kth block of Γh−1 and note that

From Corollary 4.3 it follows that

For the first term note that

because
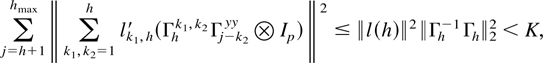
where Γh is a matrix with k,lth element Γl+h−k+1yy and K is a generic bounded constant that does not depend on h. Then

where the inequality follows from (4.1). For the second term consider the following term of equal order:
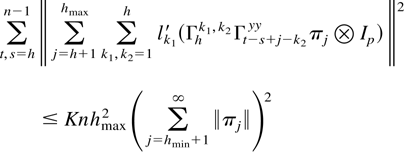
that only differs by Kpp. The inequality holds because

such that the second term is of smaller order than the first term. Note that here
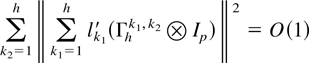
because ∥l(h)′(Γh−1 [otimes ] Ip)∥ ≤ ∥l(h)∥∥Γh−1∥2 is uniformly bounded in h. Finally, turning to the third term,

such that the third term is also of smaller order than the first. Finally, the fourth-order cumulant term is of smaller order by Corollary 4.3. Therefore, w52n = op(1).
For |w6n| note
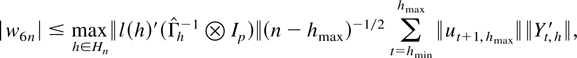
where
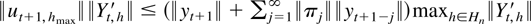
and
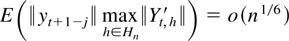
by previous arguments such that the last term in (4.7) is bounded in expectation by

and thus |w6n| = op(1).
Finally, consider |w7n|. We distinguish the following terms:

where w71n,…,w73n are defined in the obvious way and

and
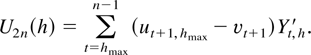
For the term w72n the proof of Theorem 2 in Lewis and Reinsel (1985) can be applied to show that w72n = op(1). For w71n and w73n we need additional uniformity arguments. For w71 consider
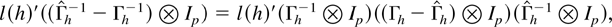
where the vector a(h) ≡ l(h)′(Γh−1 [otimes ] Ip) satisfies ∥a(h)∥2 < ∞ for all h. Then
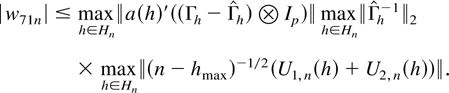
Using the result in (4.6) it follows that

. Next consider
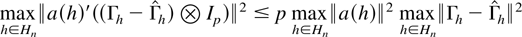
such that it follows from Lemma 4.4 that
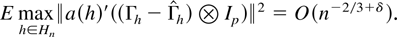
Next, consider
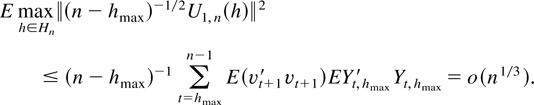
Finally,
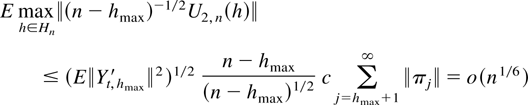
with supt(E∥yt2∥)1/2 ≤ c < ∞. This shows maxh∈Hn|w71n| = op(n−1/3+δ/2 × n1/6) = op(1).
Next, let ζt,h = l(h)′(Γh−1Yt,h [otimes ] Ip) such that
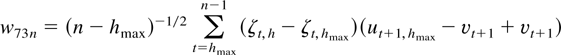
and E∥ζt,h∥2 = l(h)′(Γh−1 [otimes ] Ip)l(h) ≤ C < ∞ by Lewis and Reinsel (1985, p. 399). Then

where E maxh∈Hn∥(ζt,h − ζt,hmax)∥2 = o(1) by the analysis that follows and

where we have used stationarity and the fact that
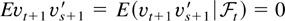
for t > s and

.
At this point the proof for Theorem 2.3 (i) and (ii) proceeds separately. First turn to (i). Because h ≤ hmax,

where supt E∥yt∥2 ≤ c < ∞. By Hannan and Deistler (1988, Theorem 6.6.11) there exists a constant c1 such that
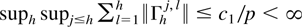
. By the second part of Lemma 4.7 and for any ε > 0 there exists a constant k0 < ∞ such that
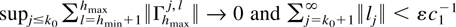
. Then

Also
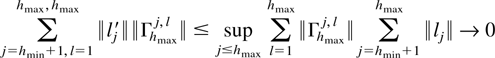
by the assumptions on l. Now define constants
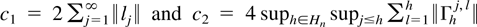
. For any ε > 0 fix integer constants k0,k1 such that

and

where the last inequality holds for some k1 and any k0 and all n ≥ n0 for some positive integer n0 < ∞ by Lemma 4.7. Then

because for fixed k0, k1, suph∈Hn∥Γhj,l − Γhmaxj,l ∥ → 0 by Lewis and Reinsel (1985, p. 402) and Hannan and Deistler (1988, Theorem 6.6.12) such that maxh∈Hn∥ζt,h − ζt,hmax∥ = op(1).
Now turn to the proof for Theorem 2.3 (ii). Partition

where
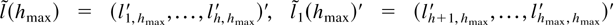
. Consider
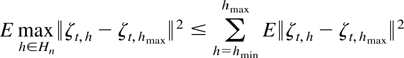
with

Note that for any sequence h** → ∞ such that
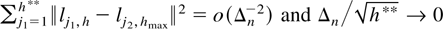
,

because
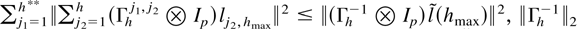
is uniformly bounded by Lewis and Reinsel (1985, p. 397) and
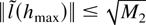
uniformly in h. Because also

the second term is o(Δn−1) too. Finally, consider

where Γhmax−1 and Γhmax are partitioned as in Lemma 4.8, where the notation for the blocks of the inverse [Γhmax−1]ij and the blocks Γij,hmax of Γhmax is introduced. Then,
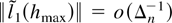
uniformly in h because by assumption ∃h ≤ hmin such that
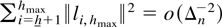
. Then,
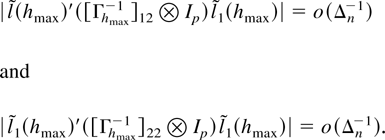
For the first term define
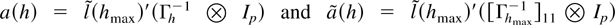
where

uniformly in h. Let A be defined as in Lemma 4.8. Write Γh−1 − [Γhmax−1]11 = −Γh−1A[Γhmax−1]11 by the partitioned inverse formula. Now for h* = h + (hmin − h)/2 such that h ≤ h* ≤ hmin with h* − h = (hmin − h)/2 and hmin − h* = (hmin − h)/2 it follows that

where the second term is o(Δn−1) uniformly in h by the assumptions on the sequence l(h) and the fact that
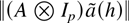
is uniformly bounded in h. For the first term consider

where the order of the error term follows again from

and

where
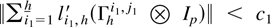
is uniformly bounded,
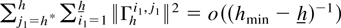
by Lemma 4.7,

because
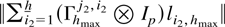
is uniformly bounded, and
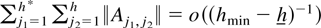
by Lemma 4.8. It now follows that
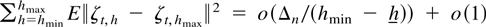
such that |w73n| = op(1) uniformly in h ∈ Hn.
To show (4.5) note that

so that the same arguments used to show E∥ζt,h − ζt,hmax∥2 → 0 apply. For part (i) of the theorem, note that
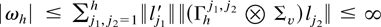
uniformly in h such that it follows from absolute convergence arguments that
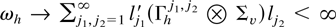
. The statement of part (i) of the theorem then follows from applying the continuous mapping theorem to
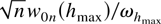
. █
Proof of Theorem 2.4. Let cn = (log n/n)1/2. For all
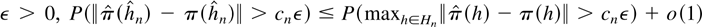
. Because h ∈ Hn implies that

it follows from An, Chen, and Hannan (1982, p. 936) and Hannan and Kavalieris (1986, Theorem 2.1) that
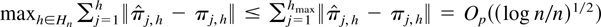
. To see this note that as in the proof of Theorem 2.1 in Hannan and Kavalieris (1986, p. 39), we have
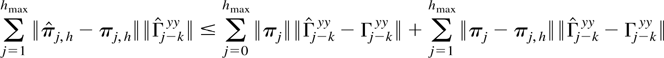
for k = 1,…,hmax where
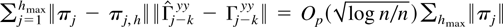
by Hannan and Kavalieris (1986). Again, by Hannan and Deistler (1988, Theorem 7.4.3) it follows that
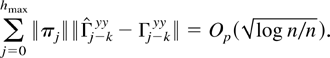
Because
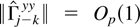
uniformly by the same result it follows that
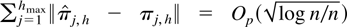
. Moreover,
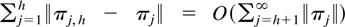
by Hannan and Deistler (1988, Theorem 6.6.12). Because h ≥ hmin and hmin satisfies
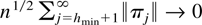
the result follows. █