1. INTRODUCTION
The primary feature of the autoregressive conditional
heteroskedasticity (ARCH) model, as proposed by Engle (1982), is that the conditional variance of the
errors varies over time. Such conditional variances have been strongly
supported by a huge body of empirical research, especially in stock
returns, interest rates, and foreign exchange markets. Following
Engle's pathbreaking idea, many alternatives have been proposed to
model conditional variances, forming an immense ARCH family; see, for
example, the surveys of Bollerslev, Chou, and Kroner (1992), Bollerslev, Engle, and Nelson (1994), and Li, Ling, and McAleer (2002). Of these models, the most popular is
undoubtedly the generalized autoregressive conditional
heteroskedasticity (GARCH) model of Bollerslev (1986). Some multivariate extensions of these models
have been proposed; see, for example, Engle, Granger, and Kraft (1984), Bollerslev, Engle, and Wooldridge (1988), Engle and Rodrigues (1989), Ling and Deng (1993), Engle and Kroner (1995), Wong and Li (1997), and Li, Ling, and Wong (2001), among others. However, apart from Ling and
Deng (1993) and Li, Ling, and Wong (2001), it seems that no asymptotic theory of the
estimators has been established for these multivariate ARCH-type
models. In most of these multivariate extensions, the primary purpose
has been to investigate the structure of the model, as in Engle and
Kroner (1995), and to report empirical
findings.
In this paper, we propose a vector autoregressive moving
average–GARCH (ARMA-GARCH) model that includes the multivariate
GARCH model of Bollerslev (1990) as a special
case. The sufficient conditions for the strict stationarity and
ergodicity, and a causal representation of the vector ARMA-GARCH model,
are obtained as extensions of Ling and Li (1997). Based on Tweedie (1988), a simple sufficient condition for the higher
order moments of the model is also obtained.
The main part of this paper investigates the asymptotic theory of the
quasi-maximum-likelihood estimator (QMLE) for the vector ARMA-GARCH
model. Consistency of the QMLE is proved under only the second-order
moment condition. Jeantheau (1998) proves
consistency for the constant conditional mean drift model with vector
GARCH errors. His result is based on a modified result in Pfanzagl
(1969), in which it is assumed that the
initial values consisting of the infinite past observations are known.
In practice, of course, this is not possible.
In the univariate case, the QMLE based on any fixed initial values
has been investigated by Weiss (1986),
Pantula (1989), Lee and Hansen (1994), Lumsdaine (1996),
and Ling and Li (1997). Weiss (1986) and Ling and Li (1997) use the conditions of Basawa, Feign, and
Heyde (1976), whereby their consistency
results rely on the assumption that the fourth-order moments exist. Lee
and Hansen (1994) and Lumsdaine (1996) use the conditions of Amemiya (1985, pp. 106–111), but their methods are
only valid for the simple GARCH(1,1) model and cannot be extended to
more general cases. Moreover, the conditional errors, that is,
η0t when m = 1 in equation (2.3) in
the next section, are required to have the (2 + κ)th (κ > 0)
finite moment by Lee and Hansen (1994) and
the 32nd finite moment by Lumsdaine (1996).
The consistency result in this paper is based on a uniform
convergence as a modification of a theorem in Amemiya (1985, p. 116). Moreover, the consistency of the
QMLE for the vector ARMA-GARCH model is obtained only under the
second-order moment condition. This result is new, even for the
univariate ARCH and GARCH models. For the univariate GARCH(1,1) model,
our consistency result also avoids the requirement of the higher order
moment of the conditional errors, as in Lee and Hansen (1994) and Lumsdaine (1996).
This paper also investigates the asymptotic normality of the QMLE.
For the vector ARCH model, asymptotic normality requires only the
second-order moment of the unconditional errors and the finite
fourth-order moment of the conditional errors. The corresponding result
for univariate ARCH requires the fourth-order moment, as in Weiss
(1986) and Pantula (1989). The conditions for asymptotic normality of
the GARCH(1,1) model in Lee and Hansen (1994)
and Lumsdaine (1996) are quite weak. However,
their GARCH(1,1) model explicitly excludes the special case of the
ARCH(1) model because they assume that B1 ≠ 0
(see equation (2.7) in Section 2) for purposes of identifiability.
Under additional moment conditions, the asymptotic normality of the
QMLE for the general vector ARMA-GARCH model is also obtained. Given
the uniform convergence result, the proof of asymptotic normality does
not need to explore the third-order derivative of the quasi-likelihood
function. Hence, our method is simpler than those in Weiss (1986), Lee and Hansen (1994), Lumsdaine (1996),
and Ling and Li (1997).
It is worth emphasizing that, unlike Lumsdaine (1996) and Ling and Li (1997), Lee and Hansen (1994) do not assume that the conditional errors
η0t are independently and identically
distributed (i.i.d) instead of a series of strictly stationary and
ergodic martingale differences. Although it is possible to use this
weaker assumption for our model, for simplicity we use the i.i.d.
assumption.
The paper is organized as follows. Section 2 defines the vector
ARMA-GARCH model and investigates its properties. Section 3 presents
the quasi-likelihood function and gives a uniform convergence result.
Section 4 establishes the consistency of the QMLE, and Section 5
develops its asymptotic normality. Concluding remarks are offered in
Section 6. All proofs are given in Appendixes A and B.
Throughout this paper, we use the following notation. The term
|·| denotes the absolute value of a univariate
variable or the determinant of a matrix; ∥·∥ denotes the
Euclidean norm of a matrix or vector; A′ denotes the
transpose of the matrix or vector A; O(1) (or
o(1)) denotes a series of nonstochastic variables that are
bounded (or converge to zero); Op(1) (or
op(1)) denotes a series of random
variables that are bounded (or converge to zero) in probability;
→p
denotes convergence in probability (or in distribution); ρ(A)
denotes the eigenvalue of the matrix A with largest absolute
value.
2. THE MODEL AND ITS PROPERTIES
Bollerslev (1990) presents an
m-dimensional multivariate conditional covariance model,
namely,
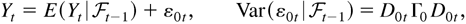
where
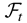
is the past information available up to time t,
D0t =
diag(h01t1/2,…,h0mt1/2),
and
in which σ0ij = σ0ji.
The main feature of this model is that the conditional correlation
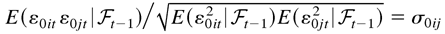
is constant over time, where i ≠ j and
ε0it is the ith element of
ε0t. By assuming
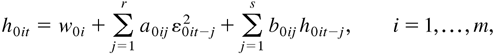
that is, with only i-specific effects, Bollerslev (1990) models the exchange rates of the German mark,
French franc, and British pound against the U.S. dollar. His results
provide evidence that the assumption of constant correlations is
adequate. Tse (2000) has developed the
Lagrange multiplier test for the hypothesis of constant correlation in
Bollerslev's model and provides evidence that the hypothesis is
adequate for spot and futures prices and for foreign exchange rates.
It is possible to provide a straightforward explanation for the
hypothesis of constant correlation. Suppose that
h0it captures completely the past
information, with Eh0it =
Eε0it2. Then
η0it = ε0it
h0it−1/2 will be
independent of the past information. Thus, for each i,
{η0it,t =
0,±1,±2,…} will be a sequence of i.i.d. random
variables, with zero mean and variance one. In general,
η0it and η0jt are
correlated for i ≠ j, and hence it is natural to
assume that η0t =
(η01t,…,η0mt)′
is a sequence of i.i.d. random vectors, with zero mean and covariance
Γ0. Thus, we can write
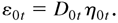
Obviously, ε0t in (2.1) has the same
conditional covariance matrix as that in (2.3).
Now, the remaining problem is how to define
h0it so that it can capture completely the
past information. It is obvious that h0it
may have as many different forms as in the univariate case. In the
multivariate case, h0it should contain
some past information, not only from ε0it but
also from ε0jt. Hence, a simple specification
such as (2.2) is likely to be inadequate. In particular, if it is
desired to explain the relationships of the volatilities across
different markets, it would be necessary to accommodate some
interdependence of the ε0it,
ε0jt, h0it, and
h0jt in the model. Note that
D0t depends only on
(h01t,…,h0mt)′,
denoted by H0t. It is natural to define
H0t in the form of (2.5), which follows,
which has also been used by Jeantheau (1998).
Specifying the conditional mean part as the vector ARMA model, we
define the vector ARMA-GARCH model as follows:
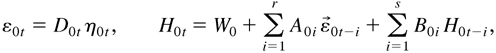
where D0t and
η0t are defined as in (2.3),
Φ0(L) = Im
− Φ01 L − ···
− Φ0p Lp
and Ψ0(L) = Im +
Ψ01 L + ··· +
Ψ0q Lq are
polynomials in L, Ik is the
k × k identity matrix, and
.
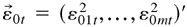
The true parameter vector is denoted by λ0 =
(φ0′,δ0′,σ0′)′,
where φ0 =
vec(μ0,Φ01,…,Φ0p,Ψ01,…,Ψ0q),
δ0 =
vec(W0,A01,…,A0r,
B01,…,B0s), and
σ0 =
(σ021,…,σ0m,1,σ032,…,σ0m,2,…,σ0m,m−1)′.
This model was used to analyze the Hang Seng index and Standard and
Poor's 500 Composite index by Wong, Li, and Ling (2000). They found that the off-diagonal elements in
A01 are significantly different from zero and hence
can be used to explain the volatility relationship between the two
markets.
The model for the unknown parameter λ =
(φ′,δ′,σ′)′, with φ, δ,
and σ defined in a similar manner to φ0,
δ0, and σ0, respectively, is
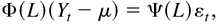
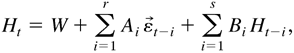
where
,
and Φ(L) and Ψ(L) are defined in a similar
manner to Φ0(L) and Ψ0(L),
respectively. First, the εt are computed from the
observations Y1,…,Yn,
from (2.6), with initial value Y0 =
(Y0,…,Y1−p,ε0,…,ε1−q).
Then Ht can be calculated from (2.7), with
initial values
.
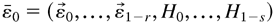
We assume that the parameter space Θ is a compact subspace of
Euclidean space, such that λ0 is an interior point in
Θ and, for each λ ∈ Θ, we make the following
assumptions.
Assumption 1. All the roots of |Φ(L)| = 0
and all the roots of |Ψ(L)| = 0 are outside the
unit circle.
Assumption 2. The terms Φ(L) and Ψ(L) are left
coprime (i.e., if Φ(L) =
U(L)Φ1(L) and
Ψ(L) =
U(L)Ψ1(L), then
U(L) is unimodular with constant determinant) and
satisfy other identifiability conditions given in Dunsmuir and Hannan
(1976).
Assumption 3. The matrix Γ is a finite and positive definite symmetric
matrix, with the elements on the diagonal being 1 and ρ(Γ) having a
positive lower bound over Θ; all the elements of
Ai and Bj are
nonnegative, i = 1,…,r, j =
1,…,s; each element of W has positive lower and
upper bounds over Θ; and all the roots of
are outside the unit circle.
Assumption 4.
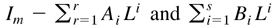
are left coprime and satisfy other identifiability conditions given in
Jeantheau (1998) (see also Dunsmuir and Hannan, 1976).
In Assumptions 2 and 4, we use the identifiability conditions in
Dunsmuir and Hannan (1976) and Jeantheau
(1998). These conditions may be too strong.
Alternatively, we can use other identifiability conditions, such as the
final form or echelon form in Lütkepohl (1993, Ch. 7), under which the results in this paper
for consistency and asymptotic normality will still hold with some
minor modifications. These identifiability conditions are sufficient
for the proofs of (B.3) and (B.6) in Appendix B.
Note that, under Assumption 4, Bs ≠ 0
and hence the ARCH and GARCH models are nonnested. We define the
ARMA-ARCH model as follows:
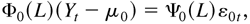
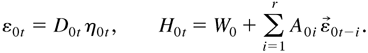
Similarly, under Assumption 2, it is not allowed that all the
coefficients in the ARMA model are zero, so that the ARMA-ARCH model
does not include the following ARCH model as a special case:
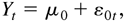
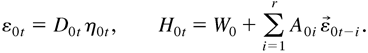
In models (2.8) and (2.9) and (2.10) and (2.11), we assume that all
the components of A0i, i =
1,…,r, are positive. In practice, this assumption may
be too strong. If the parameter matrices
Ai are assumed to have the nested
reduced-rank form, as in Ahn and Reinsel (1988), then the results in this and the following
sections will still hold with some minor modifications.
The unknown parameter ARCH and ARMA-ARCH models are defined similarly
to models (2.6) and (2.7). The true parameter λ0 =
(φ0′,δ0′,σ0′)′,
with δ0 =
vec(W0,A01,…,A0r),
σ0 being defined as in models (2.4) and (2.5), and
φ0 being defined as in models (2.4) and (2.5) for
models (2.8) and (2.9), and φ0 = μ0 for
models (2.10) and (2.11). Similarly, define the unknown parameter λ
and the parametric space Θ, with 0 <
aijkl ≤
aijk ≤
aijku < ∞,
where aijk is the
(j,k)th component of Ai,
aijkl and
aijku are independent
of λ, i = 1,…,r, and j,k
= 1,…,m.1
For models (2.8)
and (2.9) and (2.10) and (2.11), Bi in
Assumption 3 reduces to the zero matrix, where i =
1,…,s.
The following theorem gives some basic properties of models (2.4) and
(2.5). When m = 1, the result in Theorem 2.1 reduces to that
in Ling and Li (1997) and the result in
Theorem 2.2 reduces to Theorem 6.2 in Ling (1999) (see also Ling and McAleer, 2002a, 2002b). When the
ARMA model is replaced by a constant mean drift, the second-order
stationarity and ergodicity condition in Theorem 2.1 appears to be the
same as Proposition 3.1 in Jeantheau (1998).
Our proof is different from that in his paper and provides a useful
causal expansion. Also note that, in the following theorems,
Assumptions 2 and 4 are not imposed and hence these results hold for
models (2.8) and (2.9) and models (2.10) and (2.11). However, for these
two special cases, the matrix
,
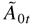
which follows, can simply be replaced by its (1,1) block.
THEOREM 2.1. Under Assumptions 1 and 3, models (2.4) and (2.5)
possess an
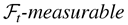
second-order stationary solution
{Yt,ε0t,H0t},
which is unique, given the η0t,
where
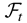
is a σ-field generated by {η0k
: k ≤ t}. The solutions
{Yt} and
{H0t} have the following causal
representations:
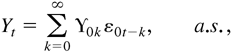
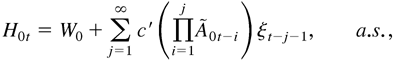
where
,
that is, the subvector consisting of the first m components is
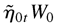
and the subvector consisting of the (rm + 1)th to
(r + 1)mth components is
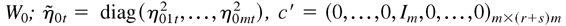
with the subvector consisting of the (rm + 1)th to
(r + 1)mth columns being Im; and
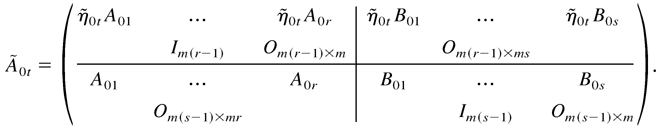
Hence,
{Yt,ε0t,H0t}
are strictly stationary and ergodic.
THEOREM 2.2. Suppose that the assumptions of Theorem 2.1 hold. If
,
with k being a strictly positive integer, then the 2kth moments
of {Yt,ε0t}
are finite, where
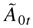
is defined as in Theorem 2.1 and A[otimes ]k
is the Krönecker product of the k matrices A.
3. QUASI-MAXIMUM-LIKELIHOOD ESTIMATOR
The estimators of the parameters in models (2.4) and (2.5) are
obtained by maximizing, conditional on
(Y0,ε0),
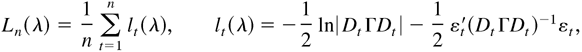
where Ln(λ) takes the form of the
Gaussian log-likelihood and Dt =
diag(h1t1/2,
…,hmt1/2). Because
we do not assume that η0t is normal, the
estimators from (3.1) are the QMLEs. Note that the processes
εi and Di,
i ≤ 0, are unobserved and hence they are only some chosen
constant vectors. Thus, Ln(λ) is the
likelihood function that is not conditional on the true
(Y0,ε0) and, in
practice, we work with this likelihood function.
For convenience, we introduce the unobserved process
{(εtε,Htε)
: t = 0,±1,±2,…}, which satisfies
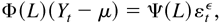
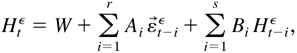
where
.
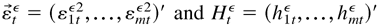
Denote Y0 =
(Y0,Y−1,…). The
unobserved log-likelihood function conditional on Y0
is
where Dtε =
diag(h1tε,…,hmtε).
When λ = λ0, we have
εtε =
ε0t,
Htε =
H0t, and
Dtε =
D0t. The primary difference in the
likelihoods (3.1) and (3.4) is that (3.1) is conditional on any initial
values, whereas (3.4) is conditional on the infinite past observations.
In practice, the use of (3.4) is not possible. Jeantheau (1998) investigates the likelihood (3.4) for models
(2.4) and (2.5) with p = q = 0, that is, with the
conditional mean part identified as the constant drift. By modifying a
result in Pfanzagl (1969), he proves the
consistency of the QMLE for a special case of models (2.4) and (2.5).
An improvement on his result requires only the second-order moment
condition. However, the method of his proof is valid only for the
log-likelihood function (3.4), and it is not clear whether his result
also holds for the likelihood (3.1).
The likelihood function Ln(λ) and
the unobserved log-likelihood function
Lnε(λ) for models
(2.8) and (2.9) and models (2.10) and (2.11) are similarly defined as
in (3.1) and (3.4).
The following uniform convergence theorem is a modification of
Theorem 4.2.1 in Amemiya (1985). This
theorem, and also Lemma 4.5 in the next section, makes it possible to
prove the consistency of the QMLE from the likelihood (3.1) under only
a second-order moment condition.
THEOREM 3.1.
2 The co-editor has
suggested that this theorem may not be new, consisting of Lemma 2.4 and
footnote 18 of Newey and McFadden (1994).
(
y,θ)
be a measurable function of
y in Euclidean space for each
θ ∈ Θ, a compact subset of
Rm (Euclidean
m-space), and a
continuous function of θ ∈ Θ for each
y.
Suppose that
yt is a sequence of strictly
stationary and ergodic time series, such that
Eg(
yt,θ) = 0 and
E
sup
θ∈Θ|
g(
yt,θ)|
< ∞. Then
.
4. CONSISTENCY OF THE QMLE
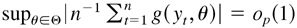
In (3.4), Dtε is
evaluated by an infinite expansion of (3.3). We need to show that such
an expansion is convergent. In general, all the roots of
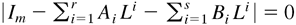
lying outside the unit circle does not ensure that all the roots of
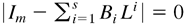
are outside the unit circle. However, because all the elements of
Ai and Bi are
negative, we have the following lemma.
LEMMA 4.1. Under Assumption 3, all the roots of
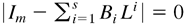
are outside the unit circle.
We first present five lemmas. Lemma 4.2 ensures the identification of
λ0. Lemmas 4.3, 4.4, and 4.6 ensure that the likelihood
Ln(λ) of the ARMA-GARCH, ARMA-ARCH,
and ARCH models converges uniformly in the whole parameter space, with
its limit attaining a unique maximum at λ0. Lemma 4.5 is
important for the proof of Lemma 4.6 under the second-order moment
condition.
LEMMA 4.2. Suppose that Yt is generated
by models (2.4) and (2.5) satisfying Assumptions 1–4, or models
(2.8) and (2.9) satisfying Assumptions 1–3, or models (2.10) and
(2.11) satisfying Assumption 3. Let cφ and
c be constant vectors, with the same dimensions as φ and
δ, respectively. Then
cφ′(∂εtε′/∂φ)
= 0 a.s. only if cφ = 0, and
c′(∂Htε′/∂δ)
= 0 a.s. only if c = 0.
LEMMA 4.3. Define L(λ) = E
[ltε(λ)].
Under the assumptions of Lemma 4.2, L(λ) exists for all
λ ∈ Θ and
supλ∈Θ|Lnε(λ)
− L(λ)| =
op(1).
LEMMA 4.4. Under the assumptions of Lemma 4.2, L(λ)
achieves a unique maximum at λ0.
LEMMA 4.5. Let Xt be a strictly
stationary and ergodic time series, with
E|Xt| < ∞,
and ξt be a sequence of random variables
such that
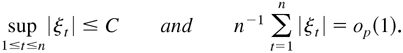
Then
.
LEMMA 4.6. Under the assumptions of Lemma 4.2,
supλ∈Θ|Lnε(λ)
− Ln(λ)| =
op(1).
Based on the preceding lemmas, we now have the following consistency
theorem.
THEOREM 4.1. Denote
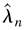
as the solution to maxλ∈Θ
Ln(λ). Under the assumptions of Lemma
4.2,
.
5. ASYMPTOTIC NORMALITY OF THE QMLE
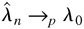
To prove the asymptotic normality of the QMLE, it is inevitable to
explore the second derivative of the likelihood. The method adopted by
Weiss (1986), Lee and Hansen (1994), Lumsdaine (1996),
and Ling and Li (1997) uses the third
derivative of the likelihood. By using Theorem 3.1, our method requires
only the second derivative of the likelihood, which simplifies the
proof and reduces the requirement for higher order moments.
For the general models (2.4) and (2.5), the asymptotic normality of
the QMLE would require the existence of the sixth moment. However, for
models (2.8) and (2.9) or models (2.10) and (2.11), the moment
requirements are weaker. Now we can state some basic results.
LEMMA 5.1. Suppose that Yt is generated
by models (2.4) and (2.5) satisfying Assumptions 1–4, or models
(2.8) and (2.9) satisfying Assumptions 1–3, or models (2.10) and
(2.11) satisfying Assumption 3. Then, it follows that
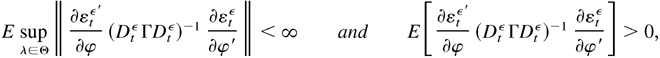
where a matrix A > 0 means that A is positive
definite.
LEMMA 5.2. Suppose that Yt is generated
by models (2.4) and (2.5) satisfying Assumptions 1–4 and
E∥Yt∥4 <
∞, or models (2.8) and (2.9) satisfying Assumptions 1–3 and
E∥Yt∥4 <
∞, or models (2.10) and (2.11) satisfying Assumption 3 and
E∥η0t∥4 <
∞. Then Ω0 = E
[(∂l0tε
/∂λ)(∂l0tε/∂λ′)]
is finite. Furthermore, if
Ω0 > 0, then
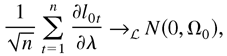
where
∂l0tε/∂λ =
∂ltε/∂λ|λ0
and ∂l0t /∂λ =
∂lt
/∂λ|λ0.
LEMMA 5.3. Suppose that Yt is generated
by models (2.4) and (2.5) satisfying Assumptions 1–4 and
E∥Yt∥6 <
∞, or models (2.8) and (2.9) satisfying Assumptions 1–3 and
E∥Yt∥4 <
∞, or models (2.10) and (2.11) satisfying Assumption 3. Then,
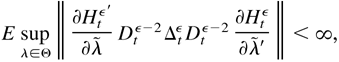
where
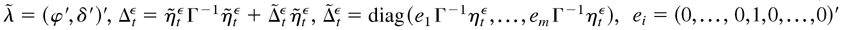
of which the ith element is 1,
.
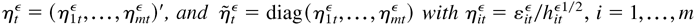
LEMMA 5.4. Under the assumptions of Lemma 5.3,
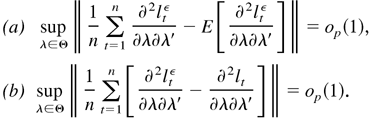
By straightforward calculation, we can show that
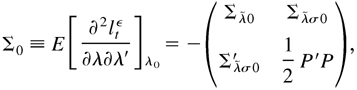
m × m matrix with the (i,i)th
component being 1 and the other components zero,
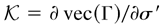
is a constant matrix, and C = Γ0−1
[odot ] Γ0 + Im, where A
[odot ] B = (aij
bij) for two matrices A =
(aij) and B =
(bij). In practice, Σ0 is
evaluated by
LEMMA 5.5. Under the assumptions of Lemma 5.3,
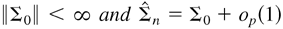
for any sequence λn, such that
λn − λ0 =
op(1). If
Γ0−1 [odot ] Γ0 ≥
Im, then −Σ0 >
0.
From the proof, we can see that the sixth-order moment in models
(2.4) and (2.5) is required only for Lemma 5.4(a), whereas the
fourth-order moment is sufficient for Lemma 5.4(b). If we can show that
the convergent rate of the QMLE is
Op(n−1/2),
then the fourth-order moment is sufficient for models (2.4) and (2.5).
However, it would seem that proving the rate of convergence is quite
difficult.
LEMMA 5.6. Under the assumptions of Lemma 5.2, if
,
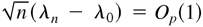
then
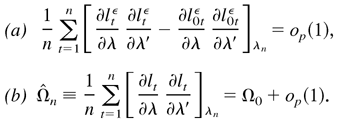
THEOREM 5.1. Suppose that Yt is
generated by models (2.4) and (2.5) satisfying Assumptions 1–4
and E∥Yt∥6
< ∞, or models (2.8) and (2.9) satisfying Assumptions
1–3 and
E∥Yt∥4 <
∞, or models (2.10) and (2.11) satisfying Assumption 3 and
E∥η0t∥4 <
∞. If Ω0 > 0 and
Γ0−1 [odot ] Γ0 ≥
Im, then
.
Furthermore, Σ0 and Ω0
can be estimated consistently by
,
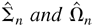
respectively.
When m = 1 or 2, we can show that
Γ0−1 [odot ] Γ0 ≥
Im, and hence, in this case,
−Σ0 > 0. However, it is difficult to prove
Γ0−1 [odot ] Γ0 ≥
Im for the general case. When
Γ0 = Im, it is
straightforward to show that −Σ0 > 0 and
Ω0 are positive definite. When
η0t follows a symmetric distribution,
where Σδ0 = E
[∂H0tε′/∂δD0t−2CD0t−2∂H0tε/∂δ′]/4
and Σδσ0 = E
[∂H0tε′/
∂δD0t−2]C1
P/2. Furthermore, if η0t is
normal, it follows that −Σ0 = Ω0.
Note that the QMLE here is the global maximum over the whole parameter
space. The requirement of the sixth-order moment is quite strong for
models (2.4) and (2.5) and is used only because we need to verify the
uniform convergence of the second derivative of the log-likelihood
function, that is, Lemma 5.4(a). If we consider only the local QMLE,
then the fourth-order moment is sufficient. For univariate cases, such
proofs can be found in Ling and Li (1998) and
Ling and McAleer (2003).
6. CONCLUSION
This paper presented the asymptotic theory for a vector ARMA-GARCH
model. An explanation of the proposed model was offered. Using a
similar idea, different multivariate models such as E-GARCH, threshold
GARCH, and asymmetric GARCH can be proposed for modeling multivariate
conditional heteroskedasticity. The conditions for the strict
stationarity and ergodicity of the vector ARMA-GARCH model were
obtained. A simple sufficient condition for the higher order moments of
the model was also provided. We established a uniform convergence
result by modifying a theorem in Amemiya (1985). Based on the uniform convergence result, the
consistency of the QMLE was obtained under only the second-order moment
condition. Unlike Weiss (1986) and Pantula
(1989) for the univariate case, the
asymptotic normality of the QMLE for the vector ARCH model requires
only the second-order moment of the unconditional errors and the finite
fourth-order moment of the conditional errors. The asymptotic normality
of the QMLE for the vector ARMA-ARCH model was proved using the
fourth-order moment, which is an extension of Weiss (1986) and Pantula (1989).
For the general vector ARMA-GARCH model, the asymptotic normality of
the QMLE requires the assumption that the sixth-order moment exists.
Whether this result will hold under some weaker moment conditions
remains to be proved.
APPENDIX A: PROOFS OF THEOREMS 2.1 AND 2.2
Proof of Theorem 2.1. Multiplying (2.5) by
yields
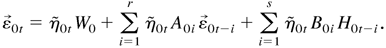
Now rewrite (A.1) in vector form as
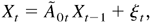
where
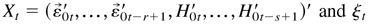
and ξt is defined as in (2.13). Let
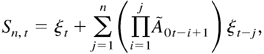
where n = 1,2,…. Denote the kth element of
.
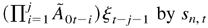
We have
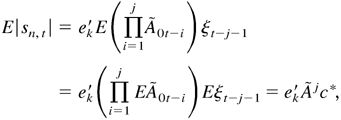
where ek =
(0,…,0,1,0,…,0)m(r+s)×1′
and 1 appears in the kth position, c* =
Eξt is a constant vector, and
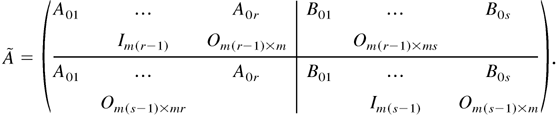
By direct calculation, we know that the characteristic polynomial of
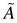
is
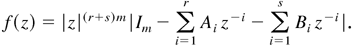
By Assumption 3, it is obvious that all the roots of f
(z) lie inside the unit circle. Thus,
,
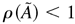
and hence each component of
.
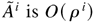
Therefore, the right-hand side of (A.4) is equal to
O(ρj). Note that
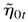
is a sequence of i.i.d. random matrices and each element of
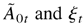
is nonnegative. We know that each component of
Sn,t converges almost surely
(a.s.) as n → ∞, as does
Sn,t. Denote the limit of
Sn,t by
Xt. We have
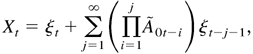
with the first-order moment being finite.
It is easy to verify that Xt satisfies
(A.2). Hence, there exists an
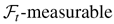
second-order solution ε0t to (2.5) with
ith element
,
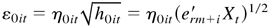
with the representation (2.13).
Now we show that such a solution is unique to (2.5). Let
εt(1) be another
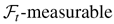
second-order stationary solution of (2.5). As in (A.2), we have
.
Let Ut = Xt
− Xt(1). Then
Ut is first-order stationary and, by
(A.2),
.
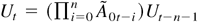
Denote the kth component of Ut as
uk,t. Then, as each element of
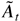
is nonnegative,
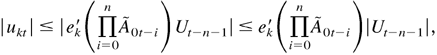
where ek is defined as in (A.4) and
|Ut| is defined as
(|u1t|,…,|u(r+s)m,t|)′.
As Ut is first-order stationary and
,
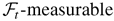
by (A.8), we have
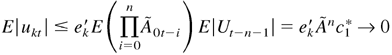
as n → ∞, where c1* =
E|Ut| is a constant
vector. So ukt = 0 a.s., that is,
Xt =
Xt(1) a.s. Thus,
hit =
hit(1) a.s., and hence
ε0t =
ε0t(1) =
η0it
h0it1/2 a.s. That is,
ε0t satisfying (2.5) is unique.
For the unique solution ε0t, by the usual
method, we can show that there exists a unique
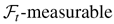
second-order stationary solution Yt satisfying
(2.4), with the expansion given by
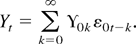
Note that the solution
{Yt,ε0t,H0t}
is a fixed function of a sequence of i.i.d. random vectors
η0t and hence is strictly stationary and
ergodic. This completes the proof. █
The proof of Theorem 2.2 first transforms models (2.4) and (2.5) into
a Markov chain and then uses Tweedie's criterion. Let
{Xt; t = 1,2,…} be a
temporally homogeneous Markov chain with a locally compact completely
separable metric state space
.
The transition probability is P(x,A) =
Pr(Xn ∈
A|Xn−1 =
x), where x ∈ S and
.
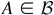
Tweedie's criterion is the following lemma.
LEMMA A.1. (Tweedie, 1988, Theorem 2).
Suppose that {Xt} is a Feller
chain.
(1) If there exist, for some compact set
,
a nonnegative function g and ε > 0
satisfying
then there exists a σ-finite invariant
measure μ for P with 0 < μ(A) <
∞.
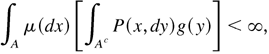
then μ is finite, and hence π =
μ/μ(S) is an invariant
probability.
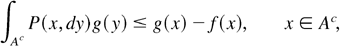
then μ admits a finite f-moment, that
is,
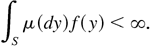
The following two lemmas are preliminary results for the proof of
Theorem 2.2.
LEMMA A.2. Suppose that
.
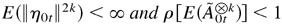
Then there exists a vector M > 0 such that
,
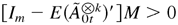
where a vector B > 0 means that each element of
B is positive.
Proof. From the condition given,
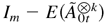
is invertible. Because each element of
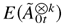
is nonnegative, we can choose a vector L1 > 0
such that
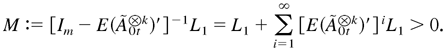
Thus,
.
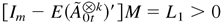
This completes the proof. █
LEMMA A.3. Suppose that there is a vector M > 0 such
that
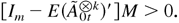
Then there exists a compact set
,
a function g1(x), and κ > 0
such that the function g, defined by g(x) = 1 +
(x[otimes ]k)′M, satisfies
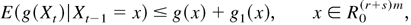
and
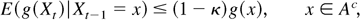
where Ac =
R(r+s)m −
A, xi is the ith component of x,
maxx∈A
g1(x) < C0,
Xt is defined as in (A.2), and
C0, κ, and Δ are positive constants not
depending on x.
Proof. We illustrate the proof for k = 3. The technique
for k ≠ 3 is analogous.
For any x ∈
R0(r+s)m, by
straightforward algebra, we can show that
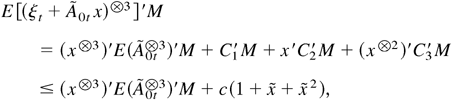
where C1, C2, and
C3 are some constant vectors or matrices with
nonnegative elements, which do not depend on x, and c
= maxk{all components of
C1′M,
C2′M, and
C3′M}.
By (A.2) and (A.18), we have
Denote
It is obvious that A is a compact set on
R0(r+s)m.
Because M*,M > 0, it follows that
c1,c2,c3
> 0. From (A.19), we can show that
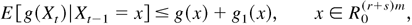
where maxx∈A
g1(x) < C0(Δ)
and C0(Δ) is a constant not depending on
x.
Let Δ > max{1/c2,1}. When x
∈ Ac,
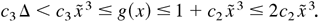
Thus,
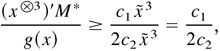
and furthermore, because
,
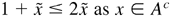
we can show that
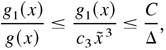
where C is a positive constant not depending on x
and Δ. By (A.19), (A.22), and (A.23), as x ∈
Ac,
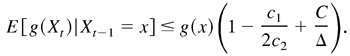
Provided 0 < c1 /4c2
< κ < c1 /2c2 and
Δ > max{1, 1/c2,
C/(c1 /2c2
− κ)}, then E
[g(Xt)|Xt−1
= x] ≤ g(x)(1 − κ). This
completes the proof. █
Proof of Theorem 2.2. Obviously, Xt
defined as in (A.2) is a Markov chain with state space
R0(r+s)m. It
is straightforward to prove that, for each bounded continuous function
g on
R0(r+s)m,
E
[g(Xt)|Xt−1
= x] is continuous in x, that is,
{Xt} is a Feller chain. In a similar
manner to Lemma A.3, in the following discussion we illustrate only
that the conditions (A.11)–(A.13) are satisfied for k =
3.
From Lemmas A.2 and A.3, we know that there exists a vector
M > 0, a compact set
,
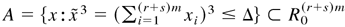
and κ > 0 such that the function defined by g(x) =
1 + (x[otimes ]3)′M satisfies
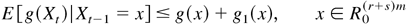
and
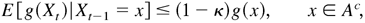
where maxx∈A
g1(x) < C0 and
C0, κ, and Δ are positive constants not
depending on x.
Because g(x) ≥ 1, it follows that E
[g(Xt)|Xt−1
= x] ≤ g(x) − κ. By Lemma
A.1, there exists a σ-finite invariant measure μ for P
with 0 < μ(A) < ∞.
Denote c2 = max{all components of M} and
c3 = min{all components of M}. From
(A.24), as x ∈ A, it is easy to show that
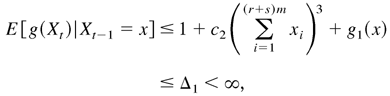
where Δ1 is a constant not depending on x.
Hence,
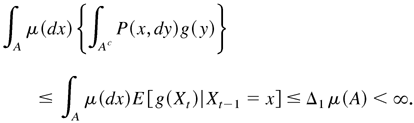
This shows that {Xt} has a finite
invariant measure μ and hence π =
μ/μ(R0(r+s)m)
is an invariant probability measure of
{Xt}; that is, there exists a strictly
stationary solution satisfying (A.2), still denoted by
Xt.
Let f (x) be the function on
R0(r+s)m
defined by
.
Then, by (A.25), as x ∈ Ac, we
have
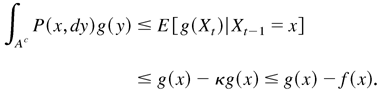
By Lemma A.1(3), we know that
,
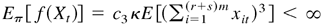
where π is the stationary distribution of
{Xt}, where xit
is the ith component of Xt. Thus,
Eπ1∥ε0t∥6
< ∞, where π1 are the stationary distributions
of {ε0t}. Now, because
Eπ1∥ε0t∥6
< ∞, it is easy to show that
Eπ2∥Yt∥6
< ∞, where π2 is the stationary distribution of
Yt.
By Hölder's inequality,
Eπ1∥ε0t∥2
<
(Eπ1∥ε0t∥2k)1/k
< ∞. Similarly, we have
Eπ2∥Yt∥2
< ∞. Thus,
{Yt,ε0t} is a
second-order stationary solution of models (2.4) and (2.5).
Furthermore, by Theorem 2.1, the solution
{Yt,ε0t} is
unique and ergodic. Thus, the process
{Yt,ε0t}
satisfying models (2.4) and (2.5) has a finite 2kth moment.
This completes the proof. █
APPENDIX B: PROOFS OF RESULTS IN SECTIONS
3–5
Proof of Theorem 3.1. The proof is similar to that of Theorem
4.2.1 in Amemiya (1985), except that the Kolmogorov
law of large numbers is replaced by the ergodic theorem. This completes the
proof. █
Proof of Lemma 4.1. Note that
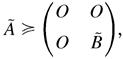
where
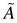
is defined as in (A.5),
,
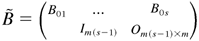
and here “the matrix A [sccue ] the matrix
B” means that each component of A is larger
than or equal to the corresponding component of B. Thus, we
have
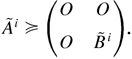
By Assumption 3,
converges to a finite limit as k → ∞. By (B.1),
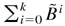
also converges to a finite limit as k → ∞, and hence
,
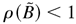
which is equivalent to all the roots of
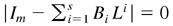
lying outside the unit circle. This completes the proof. █
In the following discussion, we prove Lemmas 4.2–4.4, Lemma
4.6, and Theorem 4.1 only for models (2.4) and (2.5). The proofs for
models (2.8) and (2.9) and (2.10) and (2.11) are similar and simpler
and hence are omitted.
Proof of Lemma 4.2. First, by (3.2),
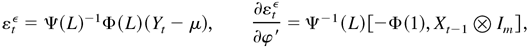
where Xt−1 =
(Yt−1′ −
μ′,…,Yt−p+1′
−
μ′,εt−1ε′,…,εt−q+1ε′)
and the preceding vector differentiation follows rules in
Lütkepohl (1993, Appendix A). Denote
Ut =
∂εtε/∂φ′
and Vt =
[−Φ(1),Xt−1 [otimes ]
Im] . Then
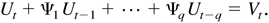
If Ut cφ = 0
a.s., then Vt cφ
= 0 a.s. Let c1 be the vector consisting of the
first m elements of cφ, whereas
c2 is the vector consisting of the remaining
elements of cφ. Then
−Φ(1)c1 +
(Xt−1 [otimes ]
Im)c2 = 0. Because
Xt−1 is not degenerate,
(Xt−1 [otimes ]
Im)c2 = 0 and
Φ(1)c1 = 0. By Assumption 1, Φ(1) is of
full rank, and hence c1 = 0. By Assumption 2, we
can show that c2 = 0. Thus,
cφ = 0.
Next, by (3.3),
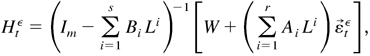
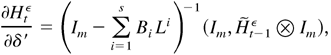
where
,
we have the following recursive equation:
If U1t c = 0 a.s., then
V1t c = 0 a.s. By Assumptions 3
and 4, in a similar manner to Vt
cφ = 0, we can conclude c = 0 (also
refer to Jeantheau, 1998, the proof of
Proposition 3.4). This completes the proof. █
Proof of Lemma 4.3. As the parameter space Θ is compact,
all the roots of Φ(L) lie outside the unit circle, and the
roots of a polynomial are continuous functions of its coefficients, there
exist constants c0,c1 > 0 and 0
< ϱamp; < 1, independent of all λ ∈ Θ, such that
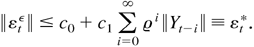
Thus, E
supλ∈Θ∥εtε∥2
< ∞ by Theorem 2.1. Note that, by Assumption 3,
|DtεΓDtε|
has a lower bound uniformly over Θ. We have E
supλ∈Θ[εtε′(DtεΓDtε)−1εtε]
< ∞. By Assumption 3 and Lemma 4.1, we can show that
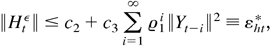
where c2,c3 > 0 and 0 <
ϱamp;1 < 1 are constants independent of all λ
∈ Θ. Thus, E
supλ∈Θ∥Htε∥
< ∞, and hence E
supλ∈Θ|DtεΓDtε|
< ∞. By Jensen's inequality, E
supλ∈Θ|ln|DtεΓDtε||
< ∞. Thus,
E|ltε(λ)|
< ∞ for all λ ∈ Θ. Let
g(Yt,λ) =
ltε −
Eltε, where
Yt =
(Yt,Yt−1,…).
Then E
supλ∈Θ|g(Yt,λ)|
< ∞. Furthermore, because
g(Yt,λ) is strictly
stationary with Eg(Yt,λ) =
0, by Theorem 3.1,
.
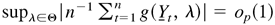
This completes the proof. █
Proof of Lemma 4.4. First,
The term L2(λ) obtains its maximum at zero,
and this occurs if and only if
εtε =
ε0t. Thus,
By Lemma 4.2, we know that equation (B.10) holds if and only if
φ = φ0.
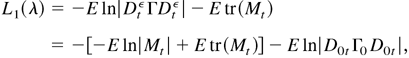
where tr(Mt) =
trace(Mt) and
Mt =
(DtεΓDtε)−1/2(D0tΓ0
D0t)(DtεΓDtε)−1/2.
Note that, for any positive definite matrix M,
−f (M) ≡
−ln|M| + tr M ≥ m
(see Johansen, 1995, Lemma A.6), and hence
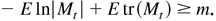
When Mt =
Im, we have f
(Mt) = f
(Im) = −m. If
Mt ≠ Im,
then f (Mt) < f
(Im), so that Ef
(Mt) ≤ Ef
(Im) with equality only if
Mt = Im with
probability one. Thus, L1(λ) reaches its
maximum −m − E
ln(D0tΓ0
D0t), and this occurs if and only if
DtεΓDtε
= D0tΓ0
D0t. From the definition of Γ, we have
hit = h0it,
and hence Γ = Γ0. Note that
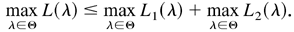
The expression maxλ∈Θ L(λ) =
−m − E
ln(D0tΓ0
D0t) if and only if
maxλ∈Θ L2(λ) = 0 and
maxλ∈Θ L1 (λ) =
−m − E
ln(D0tΓ0
D0t), which occurs if and only if φ =
φ0, Γ = Γ0, and
hit = h0it.
From φ = φ0 and hit =
h0it, we have
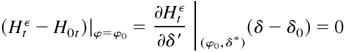
with probability one, where δ* lies between δ and
δ0. By Lemma 4.2, (B.13) holds if and only if δ =
δ0. Thus, L(λ) is uniquely maximized at
λ0. This completes the proof. █
Proof of Lemma 4.5. First, for any positive constant
M,
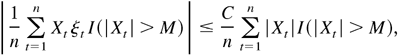
where I(·) is the indicator function. For any small
ε,κ > 0, because
E|Xt| < ∞,
there exists a constant M0 such that
where F(x) is the distribution of
Xt. For such a constant
M0, by the given condition, there exists a positive
integer N such that, when n > N,
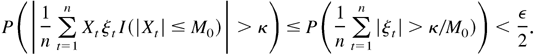
By (B.15) and (B.16), as
.
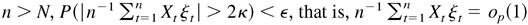
This completes the proof. █
Proof of Lemma 4.6. For convenience, let the initial values be
Y0 = 0 and ε0 = 0. When
the initial values are not equal to zero, the proof is similar. By Assumption
1, εtε and
εt have the expansions
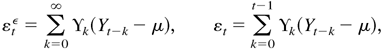
where
.
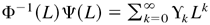
By (B.17),
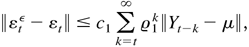
where 0 < ϱamp;1 < 1 and c1
and ϱamp;1 are constants independent of the parameter
λ. By Assumption 3 and Lemma 4.1, we have
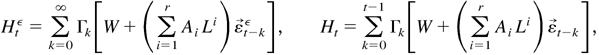
where
.
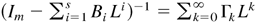
By (B.19)
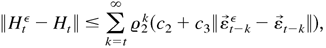
where 0 < ϱamp;2 < 1 and
c2, c3, and
ϱamp;2 are constants independent of the parameter
λ. By (B.18) and (B.20), we have
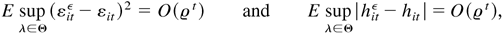
where i = 1,…,m, 0 < ϱamp; < 1,
and O(·) holds uniformly in all t. Because
hit has a lower bound, by (B.21), it
follows that
Again, because hitε and
hit have a lower bound uniformly in all
t, i, and λ,
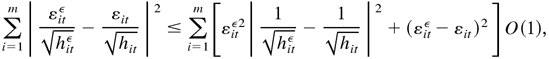
where O(1) holds uniformly in all t. We have
where O(1) holds uniformly in all t and the second
inequality comes from (B.23). By (B.7) and (B.21), it is easy to show
that
.
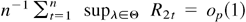
Thus, it is sufficient to show that
.
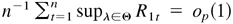
Let Xt
= εt*2 and ξt =
supλ∈Θ|hitε−1/2
−
hit−1/2|2,
where εt* is defined by (B.7). Then,
Xt is a strictly stationary and ergodic
time series, with EXt < ∞ and
|ξt| ≤ C, a constant.
Furthermore, by (B.21),
By Lemma 4.5,
.
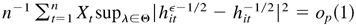
Similarly, we can show that
.
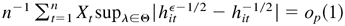
Thus,
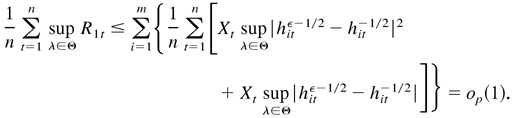
This completes the proof. █
Proof of Theorem 4.1. First, the space Θ is compact and
λ0 is an interior point in Θ. Second,
Ln(λ) is continuous in λ ∈ Θ
and is a measurable function of Yt, t =
1,…,n for all λ ∈ Θ. Third, by Lemmas 4.3 and
4.4, Lnε(λ)
→p L(λ) uniformly in Θ. From
Lemma 4.6, we have
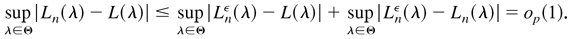
Fourth, Lemma 4.4 showed that L(λ) has a unique maximum
at λ0. Thus, we have established all the conditions for
consistency in Theorem 4.1.1 in Amemiya (1985). This completes the proof. █
Proof of Lemma 5.1. In the proof of Lemma 4.3, we have shown that
E
supλ∈Θ∥εtε∥2
< ∞. With the same argument, it can be shown that E
supλ∈Θ∥(∂εtε′/
∂φ)∥2 < ∞. Because
DtεΓDtε
has a lower bound uniformly for all λ ∈ Θ, we have
E
supλ∈Θ∥(∂εtε′/∂φ)(DtεΓDtε)−1(∂εtε/∂φ′)∥
< ∞. Let c be any constant vector with the same
dimension as φ. If c′E
[(∂εtε′/∂φ)(DtεΓDtε)−1(∂εtε/∂φ′)]c
= 0, then
c′(∂εtε′/∂φ)(DtεΓDtε)−1/2
= 0 a.s., and hence
c′∂εtε′/∂φ
= 0 a.s. By Lemma 4.2, c = 0. Thus E
[(∂εtε′/∂φ)(DtεΓDtε)−1
(∂εtε/∂φ′)]
> 0. This completes the proof. █
Proof of Lemma 5.2. First,
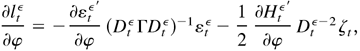
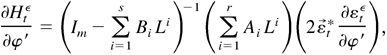
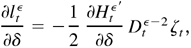
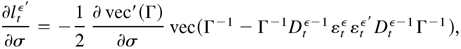
where
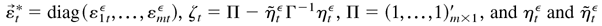
are defined as in Lemma 5.3. When λ = λ0,
ηtε =
η0t and, in this case, we denote
,
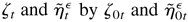
respectively.
For models (2.10) and (2.11),
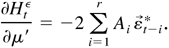
Because
|εjt−iε2|
≤
hjtε/αiij
and αiij ≥
aiijl > 0,
j = 1,…,m and i =
1,…,r, we have
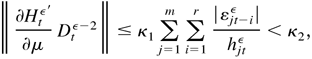
where κ1 and κ2 are some constants
independent of λ. Furthermore, because all the terms in
∂hit /∂δ appear in
hitε,
∥(∂Htε′/∂δ)
Dtε−2∥ <
M, a constant independent of λ. Because
Eη0it4 < ∞ and
E∥ζ0t∥2 <
∞, it follows that Ω0 < ∞.
For models (2.4) and (2.5), because (B.25) and (B.26),
E∥ζ0t∥2 <
∞,
E∥Yt∥4 <
∞, and D0t has a lower bound, we
have
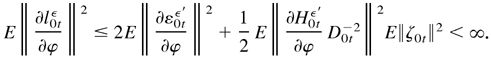
Similarly, we can show that
E∥∂l0tε/∂δ∥2
is finite. It is obvious that
E∥∂l0tε/∂σ∥2
< ∞. Thus, we also have Ω0 < ∞. In a
similar manner, it can be shown that Ω0 < ∞
for models (2.8) and (2.9).
Let
,
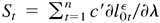
where c is a constant vector with the same dimension as λ.
Then Sn is a martingale array with respect to
.
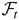
By the given assumptions, ESn /n =
c′E
[∂l0tε/∂λ∂l0tε/∂λ′]c
> 0. Using the central limit theorem of Stout (1974),
n−1/2Sn
converges to N(0,c′Ω0
c) in distribution. Finally, by the Cramér–Wold
device,
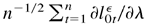
converges to N(0,Ω0) in distribution.
In a similar manner to the proof of Lemma 4.6, we can show that
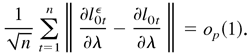
Thus,
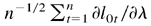
converges to N(0,Ω0) in distribution. This
completes the proof. █
Proof of Lemma 5.3. For models (2.10) and (2.11), from the proof
of Lemma 5.2, we have shown that
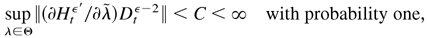
where C is a nonrandom constant. Furthermore,
where εt* is defined as in (B.7). Thus,
.
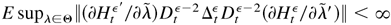
For models (2.8) and (2.9),
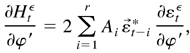
where
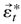
is defined as in (B.26). Thus, with probability one,
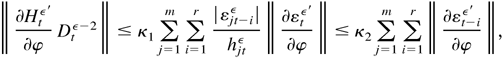
where κ1 and κ2 are constants
independent of λ. Because all the components in
∂Htε′/∂δ
also appear in Dtε2, we
have
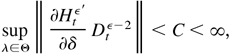
where C is a nonrandom constant independent of λ. By
(B.31) and (B.32), it is easy to show that, if
.
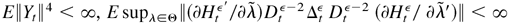
For models (2.4) and (2.5), because
E∥Yt∥6 <
∞,
where C is a nonrandom constant independent of λ. This
completes the proof. █
Proof of Lemma 5.4. By direct differentiation of (B.25) and (B.27)
and (B.28), we have
and
,
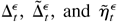
are defined as in Lemma 5.3. By Lemmas 5.1 and 5.3, we have E
supλ∈Θ
Rt(1) < ∞ and
E supλ∈Θ
Rt(2) < ∞. Similarly,
we can show that E supλ∈Θ
Rt(3) < ∞. Thus, by
(B.33),
.
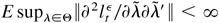
Furthermore,
In a similar manner, it is straightforward to show that E
supλ∈Θ∥∂2ltε/∂φ∂σ′∥
< ∞, E
supλ∈Θ∥∂2ltε/∂δ∂σ′∥
< ∞, and E
supλ∈Θ∥∂2ltε/∂σ∂σ′∥
< ∞. Finally, by the triangle inequality, we can show that
E
supλ∈Θ∥∂2ltε/∂λ∂λ′∥
< ∞. By Theorem 3.1, (a) holds. The proof of (b) is similar to
that of Lemma 4.6, and hence the details are omitted. This completes
the proof. █
Proof of Lemma 5.5. By Lemmas 5.1 and 5.3, we know
∥Σ0∥ < ∞. By Lemma 5.4, we have
Σn = Σ0 +
op(1).
Let c be a constant vector with the same dimension as δ.
If c′E
[∂H0tε′/∂δD0t−4∂
H0tε/∂δ′]c
= 0, then
c′(∂H0tε′/∂δ)D0t−2
= 0 and hence
c′∂H0tε′/∂δ
= 0. By Lemma 4.2, c = 0. Thus, E
[∂H0tε′/∂δD0t−4∂H0tε/∂δ′]
> 0.
Denote
By the condition given, C ≥
2Im. Thus, it is easy to show that
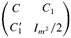
is positive by Theorem 14.8.5 in Harville (1997).
Because
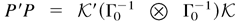
and E
[∂H0tε′/∂δD0t−4∂H0tε/∂δ′]
are positive, we know that Σδ0 is positive.
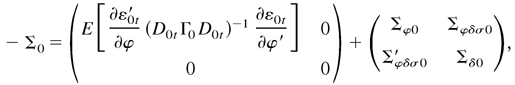
where Σφ0 = E
[(∂H0tε′/∂φ)D0t−2CD0t−2(∂H0tε/∂φ′)]/4,
Σφδσ0 =
(Σφδ0,Σφσ0),
Σφδ0 = E
[(∂H0tε′/∂φ)D0t−2CD0t−2(∂H0tε/∂δ′)]/4,
and Σφσ0 = E
[(∂H0tε′/∂φ)D0t−2]
C1 P/2. Let c =
(c1′,c2′)′ be
any constant vector with the same dimension as λ and let
c1 have the same dimension as φ, that is,
m + (p + q)m2 for models
(2.4) and (2.5) and (2.8) and (2.9) and m for models (2.10)
and (2.11). If −c′Σ0 c =
0, then c1′E
[(∂ε0t′/∂φ)(D0tΓ0
D0t)−1
(∂ε0t
/∂φ′)]c1 = 0. By Lemma
5.1, c1 = 0. Thus,
c2′Σδ0
c2 = 0. As we have shown that
Σδ0 is positive definite, c2 =
0. Thus, −Σ0 is positive definite. This completes
the proof. █
Proof of Lemma 5.6. We only present the proof for models (2.4)
and (2.5). The proofs for models (2.8) and (2.9) and models (2.10) and (2.11)
are similar, except that (B.29) and (B.30) are used to avoid the requirement
of moments. In the following, ci and
ρi are some constants independent of λ,
with 0 < ρi < 1. By (B.2), we can show
that
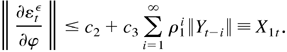
Because X1t is a strictly stationary
time series with EX1t2 <
∞, we have (see Chung, 1968, p. 93)
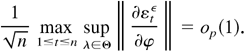
By (B.5), (B.7), (B.8), and (B.26), it follows that
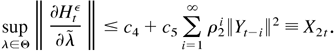
Because X2t is a strictly stationary
time series with EX2t2 <
∞, we have
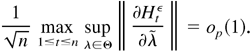
In the following discussion, ζt is defined as
in (B.27) and
are defined as in Lemma 5.3. Denote
,
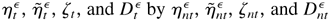
respectively, when λ = λn. By (B.35) and
(B.37),
where op(1) holds uniformly in all
t, i = 1,…,m, and
λ1n* and λ2n* lie
between λ0 and λn. From (B.38),
we have
where op(1) holds uniformly in all
t. By (B.37),
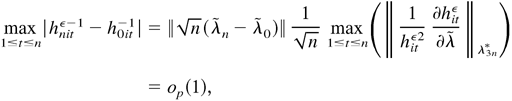
where λ3n* lies in between λ0
and λn. By (B.39) and (B.40),
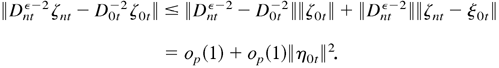
By (B.41),
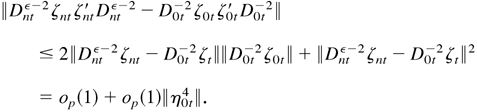
In a similar manner to (B.37), we can show that
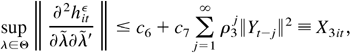
where i = 1,…,m. By (B.42) and (B.43), we
can show that
where Op(1) and
op(1) hold uniformly in all t.
Note that Xt*(1 +
∥η0t∥4) is strictly
stationary, with E [Xt*(1 +
∥η0t∥4)] =
EXt*E(1 +
∥η0t∥4) < ∞. By
the ergodic theorem, we have
.
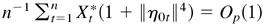
Thus, by (B.44), we have
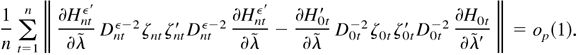
Similarly, we can show that
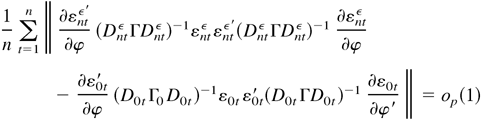
and
Thus, by (B.45)–(B.47) and the triangle inequality, we can show
that
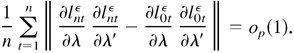
Thus, (a) holds. In a similar manner to the proof of Lemma 4.6, we
can show that
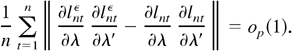
Note that
(∂l0tε/∂λ)(∂l0tε/∂λ′)
is strictly stationary and ergodic with
E∥(∂l0tε/∂λ)
(∂l0tε/∂λ′)∥
< ∞. By the ergodic theorem, we have
.
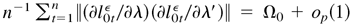
Furthermore, by (B.48) and (B.49), (b) holds. This completes the proof.
█
Proof of Theorem 5.1. We need only to verify the conditions of
Theorem 4.1.3 in Amemiya (1985). First, by Theorem
4.1, the QMLE
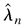
of λ0 is consistent. Second,
exists and is continuous in Θ. Third, by Lemmas 5.4 and 5.5, we
can immediately obtain that
converges to Σ0 > 0 for any sequence
λn, such that λn →
λ0 in probability. Fourth, by Lemma 5.2,
converges to N(0,Ω0) in distribution. Thus, we
have established all the conditions in Theorem 4.1.3 in Amemiya (1985), and hence
converges to
N(0,Σ0−1Ω0Σ0−1).
Finally, by Lemmas 5.5 and 5.6, Σ0 and
Ω0 can be estimated consistently by
,
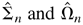
respectively. This completes the proof. █
