The problem falls in the framework of two-step generalized method of moments estimators (GMM estimators) as described in Newey and McFadden (1994, Sec. 6). Their general results may be applied; here, however, we give a direct derivation of the asymptotic variance. For simplicity, assume that consistency of

has already been proved. We choose our parameter space as Θ = {θ|β + γ < 1} to ensure that the second moment exists. Let θ₀ and σ₀² denote the true parameter values and let

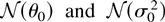
, respectively, denote (shrinking) neighborhoods of these.

By a standard Taylor expansion,

for some

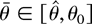
and

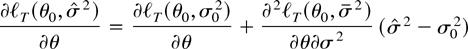
for some

. If

we have that

If ε_t are normally distributed,

is larger than the variance of the full maximum likelihood estimator (MLE) of θ₀, but in the absence of normality the comparison could go either way. If σ² were known instead of estimated, then the asymptotic variance would simplify to H_θθ⁻¹Σ_θθ H_θθ⁻¹.

In the following we show that (i)–(iii) hold: First, derive the first and second derivatives of [ell ]_T:

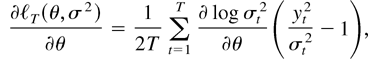
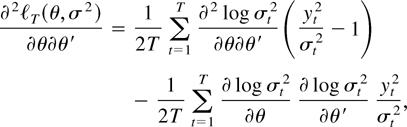
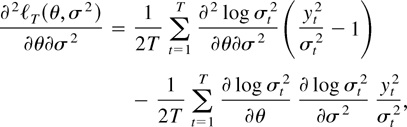
where σ_t² = σ_t²(θ,σ²). The derivative of log σ_t² with respect to α = (θ,σ²) is given by ∂ log σ_t²/∂α = ∂σ_t²/∂α·σ_t⁻² where

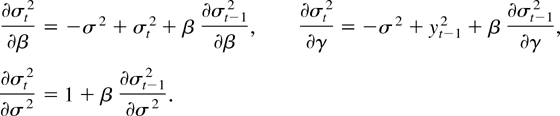
Iterating the preceding expressions yields

where we have taken σ_t²|_t=0 to be given. From these expressions, one can check that (see Lee and Hansen, 1994, Lemmas 8 and 10)

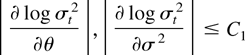
uniformly over

for some constant C₁ < ∞. Also, there exists C₂ < ∞ such that

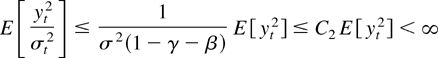
uniformly over

. This proves that (4) and (5) both are uniformly bounded by functions with finite expectations. They are furthermore continuous in (θ,σ²), so by standard results concerning uniform convergence (see, e.g., Tauchen, 1985) (ii) and (iii) follow.

To show (i), we first observe that under (1), we have that {y_t,σ_t²(θ₀,σ₀²)} is β-mixing with exponentially decaying mixing coefficients (cf. Carrasco and Chen, 2002). A standard central limit theorem (CLT) for mixing sequences may therefore be applied to obtain the desired result given that Σ exists. Note that the weak convergence of

alone can be proved using martingale arguments, but

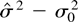
is not a martingale so we have to appeal to CLT for mixing sequences instead. The asymptotic variance matrix is given by

Using the inequalities established earlier, it is easily seen that Σ_θθ is well defined if E [ε_t⁴] < ∞. But for Σ_σσ to be finite we must require E [y_t⁴] < ∞. A necessary and sufficient condition for this is ν₄ ≡ E [ε_t⁴] < ∞ and

(cf. He and Teräsvirta, 1999). This is a stronger condition than (1). In effect, we need to restrict our parameter space Θ further to obtain asymptotic normality.

As a result of the correlation structure, explicit expressions for Σ will require tedious and rather lengthy algebra, and the resulting expressions will most likely be very complicated. But we are still able to derive a simple estimator of the asymptotic variance: we have already found consistent estimators of H_θθ and H_θσ, so we only need to find an estimator of Σ. Here, we use the general covariance estimator proposed by Newey and West (1987) and check that their conditions are satisfied in our case. Define the function

that satisfies

We then apply the conditions of Newey and West (1987, Theorem 2) on m, which are as follows: (i) There exists a function m such that ∥m_t(θ,σ²)∥ ≤ m(y_t,y_t−1) uniformly over

and E [m(y_t,y_t−1)²] < ∞; (ii) E [∥m_t(θ₀,σ₀²)∥^4(1+δ)] < ∞ for some δ > 0; and (iii) {y_t} is φ-mixing with mixing coefficients of size 2r/(2r − 1) for some r > 1. If these are satisfied, we may choose

as an estimator of the variance of Σ where w_j(N_T) are weights and N_T is an increasing sequence. Under certain conditions on w_j(N_T) and N_T (see Newey and West, 1987, p. 705),

is consistent. By the inequalities established in (6) and (7) together with the assumption that E [y_t⁴] < ∞, ∥m_t(θ,σ²)∥ ≤ m_t uniformly over

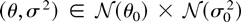
for some random variable with E [m_t²] < ∞, which proves (i). If E [y_t^8(1+δ)] < ∞ for some δ > 0 then (ii) is satisfied. Finally, (iii) holds by the aforementioned result of Carrasco and Chen (2002).

We conclude that if E [y_t⁴] < ∞, we have asymptotic normality of

; if furthermore E [y_t^8(1+δ)] < ∞, we may estimate its asymptotic variance by

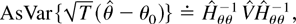
where

and with

given previously.