A solution to the problem is to calculate the greatest lower bound for the asymptotic variance of GMM estimators based on moment function h(i;β) = (y_t − βx_t)x_t−i, i = 0,1,2,…. To do so, we apply Hansen (1985). In the sequel, we will denote h(i) the moment functions h(i;β₀). Let L²(h) be the linear space spanned by {h(i) : i = 0,1,…}; it is made of elements

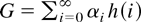
for any real α_i. Note that {h(i) : i = 0,1,…} are martingale difference sequences. Moreover, they are linearly independent and in that sense are complete in L²(h).

We are looking for the solution of equation (4.8) of Hansen (1985). That is, we are looking for the element G in L²(h) (if it exists) such that

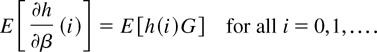
Or, equivalently, we are looking for the constants α_j solutions of

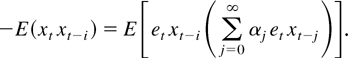
Note that the solution may not exist in L²(h), but there is always a solution in the closure of L²(h). If a solution in L²(h) exists, it is unique because {h(i) : i = 0,1,…} is complete. Let α_j = 0, for j = 1,2,…; equation (2) becomes

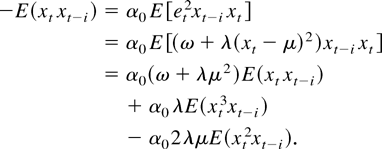
Using the fact that η_t are i.i.d. standard normal, we have

Hence, Equation (2) becomes

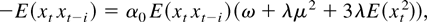
which is satisfied for

Therefore, we found a solution to (1), which is G₀ = α₀ x_t e_t with α₀ as in (3). By Lemma 4.3 of Hansen (1985), the greatest lower bound is given by

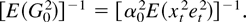
Note that α₀ can be rewritten as

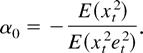
Therefore, the GMM efficiency bound is

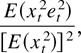
which corresponds to the asymptotic variance of the OLS estimator.

We have shown that the OLS estimator is not only as efficient as any GMM estimator that uses an arbitrary fixed number of instruments from {x_t, x_t−1,…} but also as efficient as any GMM estimator that uses an infinity of instruments from {x_t, x_t−1,…}.