1. Introduction
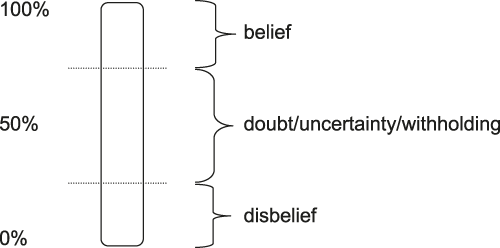
According to the Threshold View of belief and confidence, belief is nothing other than sufficiently high confidence. Put a different way, belief is confidence that exceeds the relevant threshold in the confidence spectrum, as illustrated in Figure 1.

Figure 1 The Confidence Spectrum with Belief and Disbelief Thresholds
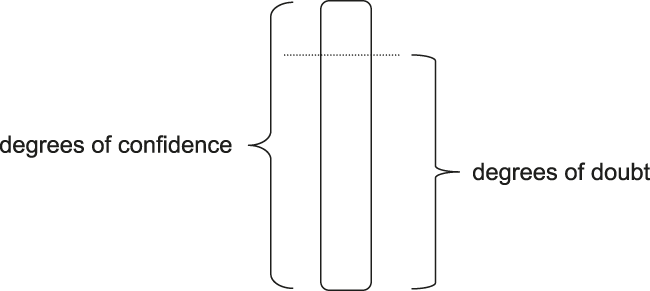
Figure 2 The Doubt and Confidence Spectra
If you know how sure I am of a proposition’s truth, and you know how high the threshold is, you have all the information you need to determine whether I believe the proposition in question.
The Threshold View is alluring for the tidy picture of the relationship between belief and confidence that it offers. And those who deny the Threshold View have some explaining to do. If belief isn’t simply a high degree of confidence, then why does certainty (maximal confidence) seem sufficient for belief while deep uncertainty seems sufficient for non-belief? Why does repeated diminution of confidence seem inevitably to lead in the long run to loss of belief? Footnote 1 And why do we so readily substitute high confidence for belief in explaining human action? Footnote 2 The Threshold View represents a simple and fruitful theory of the relationship between belief and confidence.
Suppose we formulate the Threshold View in the following straightforward way:
Naïve Threshold View: There is a degree of confidence T B such that you believe a proposition if and only if your confidence in that proposition’s truth is higher than T B .
A proponent of the Naïve Threshold View might, for example, set the threshold T B at 99% confidence. On that version of the view, you believe all and only those things of which you are more than 99% sure. Whatever the choice of threshold, the Naïve Threshold View provides a tidy account of the relationship between the binary notion of belief and the graded notion of confidence.
As elegant as the thesis is, no prominent advocate of the Threshold View has endorsed the Naïve Threshold View. Footnote 3 For there is a well-known objection to the Naïve Threshold View—what I will call the ‘Arbitrariness Objection.’ Brian Weatherson puts the objection this way:
[A]ny number [T B ] is bound to seem arbitrary. Unless these numbers are made salient by the environment, there is no special difference between believing p to degree 0.9786 and believing it to degree 0.9875. But if [T B ] is 0.98755, this will be the difference between believing p and not believing it, which is an important difference. Footnote 4
The Naïve Threshold View does not commit one to any particular value for the belief threshold T B . But it does commit one to saying that there is a threshold T B . The trouble is that there is no plausible value for T B to take.
T B = 1 is implausible because it would imply that there is no belief without absolute certainty. There are at least two problems with identifying belief with absolute certainty. First, assuming knowledge entails rational belief, a Threshold View that sets T B = 1 would have the consequence that we possess knowledge only when our epistemic situation is strong enough to make absolute certainty rational for us. But surely we know more than that. Second, we are more confident of some things we believe than of others. (I am, for instance, more confident that 2 + 2 = 4 than that I am registered to vote in my county, though I do believe both.) But, if we are more confident of some things we believe than of others, then we must believe some things with less than maximal confidence.
It is also implausible to set the threshold T B at or below 0.5 (i.e., 50% confidence). Having T B ≤ 0.5 would imply that you can’t suspend judgment on p whenever you are even slightly more confident that p than that not-p. But suppose I see someone walk by with a fork, a spoon, and a knife, and then hear (behind me) one of the utensils clatter on the floor. If I am no good at distinguishing the clatter of one utensil from that of another, I will (purely on the basis of the probability) be more than 50% confident that it was something other than the knife that fell. But I will not believe that it was something other than the knife; I would suspend judgment, since it’s quite possible (though somewhat improbable) that it was the knife.
So a proponent of the Naïve Threshold View must say that T B has some value between 0.5 and 1, exclusive. But pick any value n in that interval. It is implausible that anyone with credence n – 0.001 in p does not believe that p, while anyone with credence n + 0.001 in p does believe that p. Belief and non-belief are different from each other in a way that does not square with the sharp boundary that the Naïve Threshold View requires.
Proponents of the Threshold View have typically dealt with the Arbitrariness Objection by maintaining that ‘believes’ is vague and the belief/withholding threshold fuzzy. Footnote 5 The situation is much as with baldness: there are clear cases of baldness and clear cases of non-baldness, but there is no sharp cutoff between them. Rather, one finds ‘borderline’ cases of baldness in-between the clear cases of baldness and the clear cases of non-baldness. Just so, proponents of the Threshold View contend, there are clear cases of belief (those at the high end of the confidence spectrum) and clear cases of non-belief (those falling at or below the middle of the confidence spectrum), and there are borderline cases in-between.
Weatherson, however, finds this move unsatisfactory. The endorsement of fuzzy thresholds can succeed only if there is some suitable theory of vagueness in the offing. But Weatherson contends that no plausible theory of vagueness will support the fuzzy-threshold response. The fuzzy-threshold response will therefore not save the Threshold View.
In this paper, I do three things. First, I identify a way in which one might defend the Threshold View against the Arbitrariness Objection without recourse to fuzzy thresholds. Second, I formulate a version of the Threshold View that posits a fuzzy threshold, without committing proponents to controversial claims about vagueness. Footnote 6 And third, I show what is wrong with Weatherson’s objection to the fuzzy-threshold response to the Arbitrariness Objection.
I carry out the first of these tasks in §2. The explanation of the proposal is followed by an objection and a gesture (nothing more) at a way of meeting the objection. In §3, I reformulate the Threshold View to accommodate a fuzzy threshold. I lay out Weatherson’s objection to the fuzzy-threshold response to the Arbitrariness Objection in §4. And in §5, I explain what is wrong with Weatherson’s objection.
2. A Sharp Response to the Arbitrariness Objection
Proponents of the Threshold View are not forced to maintain that the belief/withholding threshold is fuzzy. Not that they should be shy about doing so (see §5 below). But, in this section, I will indicate another avenue they might pursue.
Suppose you learn that Andrew is more doubtful that p than Beata is. Who, then, is more confident that p? The answer is obvious: Beata. Or suppose you learn that Andrew is more doubtful that p than that q. Of which proposition is Andrew more confident? q, obviously. And it does not appear to matter whether Andrew is in extreme doubt or only very mild doubt. If Andrew is more doubtful that p than that q, then he is more confident that q than that p. All degrees of doubt, it seems, are degrees of confidence.
The reverse does not seem to be the case, however. I have no doubt my grandmother is presently in Georgia. She lives in Georgia and never leaves her town, much less the state. I also have no doubt that 2 + 2 = 4. Here we have two propositions of which I have no doubt: (i) my grandmother is in Georgia, and (ii) 2 + 2 = 4. I am not more doubtful of the one than of the other; I have no doubt about either one. Yet I am more confident of the latter than of the former. It is not, after all, even conceivable that 2 + 2 ≠ 4. It is conceivable that my grandmother may not be in Georgia, even though the possibility is so remote as not to be ‘live’ for me and thus occasions no doubt.
One might therefore propose a picture like this:
The doubt spectrum is a proper part of the confidence spectrum. Some degrees of confidence are also degrees of doubt. But the highest levels of confidence are not tinged with doubt; they are purely ‘positive.’
If this picture is correct, the confidence spectrum may be as fine grained as you like, and there will still be a qualitative difference between the highest levels of confidence that are within the doubt spectrum and the lowest levels of confidence that are beyond it. The latter involve not the slightest bit of the negativity that is characteristic of doubt; the former all have it, even if only a miniscule quantity of it. Footnote 7 If the doubt/non-doubt threshold in the confidence spectrum is also the belief/withholding threshold, then there is a plausible answer to the Arbitrariness Objection. Footnote 8
The main difficulty I see for this way of addressing the Arbitrariness Objection is how to answer the question of where on the scale from 0% confidence to 100% confidence doubt ends and ‘pure’ confidence—and belief—begins. 100% is too high; as noted above, it is implausible that 100% confidence should be required for belief. But any place short of 100% confidence would seem to imply doubt. If someone claims to be 99% confident, we take her to imply that she has doubt, even if very faint doubt.
I’ll just suggest one angle from which this issue might be approached. I might say I’m 99% sure that my laptop is in my office when I recall putting it there several hours ago and have no memory of taking it out again. Once I poke my head in and spot my laptop on the desk, all doubt is removed. Yet it is still not the case that I have attained the highest possible level of confidence with respect to the proposition that my laptop is on my desk. I am more confident still that I exist and that 2 + 2 = 4. And I recognise the remote possibility of certain sceptical scenarios (e.g., the laptop on my desk is not mine but a duplicate). So I do not report being 100% confident—which I understand as maximal confidence—that my laptop is in my office. Do I express my confidence with some number above 99% and below 100%? No, I probably wouldn’t do that either, since that might still sound like an expression of a degree of doubt, and I don’t have any. I wouldn’t know what number to report. What are we to make of this?
A hypothesis: once upon a time (or once upon a place) numerical degrees of confidence were used to report absence of doubt—you report a lower degree of confidence to the extent that you doubt, a higher degree to the extent that you lack doubt. ‘100% confidence’ meant no doubt; it didn’t mean maximal confidence. Later (or elsewhere) ‘100% confidence’ was defined in some context to mean maximal confidence. And now the two have been run together. We use values below 100% to report the extent to which we lack doubt; we use ‘100%’ to report maximal confidence. But this is a mashup of two different scales! We have left ourselves without a way of numerically expressing levels of confidence that are doubt-free but non-maximal.
I would not insist on this hypothesis, but I do insist that there is something to be explained: why is it that, once I have checked and seen my laptop on the desk, no confidence rating seems correct? 100% seems too high; everything else seems too low. This odd phenomenon suggests that there is a problem with the scale we are using to describe confidence states. But then the question of where on this scale doubt ends and pure confidence begins may not be a fair question. The matter bears further exploration. Footnote 9
But my purpose here is simply to show that the proponent of the Threshold View has room to maneuver. The Arbitrariness Objection cannot by itself compel her to endorse a fuzzy threshold. Nevertheless, I devote the rest of this paper to removing obstacles to the fuzzy-threshold approach.
3. The Threshold View Reformulated
As mentioned above, none of the most prominent proponents of the Threshold View has endorsed the Naïve Threshold View. They have generally been cognisant of arbitrariness worries and have allowed the belief/withholding threshold to be fuzzy. How might we formulate the view they are defending?
We first need to be clear about what we mean by a ‘fuzzy’ threshold. Fuzziness in the sense at issue here is the opposite of ‘sharpness.’ Fuzziness and sharpness are properties of boundaries, and the type of boundary at issue here is the boundary between cases to which a predicate (‘believes’) applies and cases to which it does not apply.
Philosophers who study vagueness distinguish between predicates that have ‘fuzzy boundaries’ and predicates that admit of ‘borderline cases.’ Footnote 10 Suppose I drive up in an aqua-coloured car, and you say, ‘You have a blue car.’ Your statement is neither clearly true nor clearly false. Footnote 11 And we cannot settle the question of whether your statement is true by taking a closer look at the car, or by comparing its colour to other shades. No amount of inquiry will settle the question of whether it is true that my car is blue. Footnote 12 My car is a borderline case with respect to the predicate ‘blue.’
Fuzzy boundaries are features of ‘sorites’ series. In a box, there is a heap (Greek sorites) consisting of 1 million grains of sand. In the next box, there is a heap consisting of 999,999 grains of sand. And in each subsequent box there is a heap with one grain fewer than the one before. Clearly, there is a heap in the first box. Clearly, there is no heap in the millionth box. But, plausibly, for any box in the row, if there is a heap in that box, then there is a heap in the next box. The boundary between heaps and non-heaps is fuzzy.
When a boundary is fuzzy, there are borderline cases. If we had a sorites series and none of the objects in the series were a borderline case, then at some point there would be an object that is clearly an F (e.g., a heap) followed by an object that is clearly not an F (e.g., a non-heap). But if there’s such an abrupt change from clear cases of Fs to clear cases of non-Fs, then the boundary between Fs and non-Fs isn’t fuzzy—it’s sharp. So fuzzy boundaries require borderline cases.
It might be tempting to think we could express a fuzzy Threshold View this way:
Thick Threshold View: There is an interval [T W , T B ] (where T W < T B ) such that, for any proposition p, any degree of confidence below T W in p is a clear case of not believing that p, any degree of confidence above T B in p is a clear case of believing that p, and any degree of confidence in p in the interval [T W , T B ] is a borderline case of belief.
The Thick Threshold View posits a thick threshold consisting of borderline cases. But there is reason to think that the Thick Threshold View is not quite right. Suppose for illustration that T W = 0.75 and T B = 0.95. That is, any credence below 0.75 is a clear case of non-belief, any credence above 0.95 is a clear case of belief, and any credence in-between is a borderline case. But now consider credence 0.95 and credence 0.951. Is it really plausible that credence 0.951 is a clear case of belief, but credence 0.95 isn’t?
In fact, one can generate a sorites series for clear cases of belief. Credence 1.0 is a clear case of belief if anything is. For any n, if credence n is a clear case of belief, then credence n – 0.001 is a clear case of belief. But credence 0.5 isn’t a clear case of belief. The predicate ‘clear case of belief’ seems just as good a candidate for having a fuzzy boundary as ‘belief’ is.
As many philosophers have observed, there seems to be higher-order vagueness. There are shades that are clearly borderline cases of blue (e.g., aqua), but also shades that are borderline cases of borderline cases of blue (e.g., turquoise). And if there are credences that are borderline cases of belief, there may well be some credences that are clearly borderline cases and others that are borderline borderline cases of belief. It will not do to reject a sharp belief threshold, only to assume a sharp cutoff between clear cases and borderline cases of belief.
It would be best, then, to formulate the Threshold View in a way that does not beg the question against those who admit higher-order vagueness. Here is a more suitable formulation:
Sophisticated Threshold View: (i) Some degrees of confidence are clear cases of belief, some are clear cases of non-belief, and some are borderline cases of belief/non-belief, (ii) if any degree of confidence in p is a clear case of believing that p, then every higher degree of confidence in p is a clear case of believing that p, and (iii) if any degree of confidence in p is a clear case of not believing that p, then every lower degree of confidence in p is a clear case of not believing that p. Footnote 13
The Sophisticated Threshold View asserts that there are credences that make for clear cases of belief, credences that make for clear cases of non-belief, and credences that make for borderline cases of belief. And it asserts further that the clear cases of belief are congregated on one side of the fuzzy boundary and the clear cases of non-belief are congregated on the opposite side of the fuzzy boundary. For any credence that makes for a clear case of belief, all higher credences also make for clear cases of belief. For any credence that makes for a clear case of non-belief, all lower credences also make for clear cases of non-belief. The Sophisticated Threshold View asserts nothing about the transition from clear cases of non-belief to borderline cases of belief, nor the transition from borderline cases of belief to clear cases of belief. For all the Sophisticated Threshold View says, there could be higher-order sharpness or higher-order fuzziness. The Sophisticated Threshold View posits a fuzzy threshold but is neutral on the matter of higher-order vagueness. It thus better represents the view of flesh-and-blood proponents of the Threshold View than does the Naïve Threshold View or the Thick Threshold View.
4. Weatherson’s Worry
According to the Arbitrariness Objection, the Threshold View is implausible because any choice of credence as the belief/withholding threshold would be intolerably arbitrary. After all, for any credence n, there is no special difference between n + 0.001 and n – 0.001—or, not special in the way that the difference between belief and non-belief is special. (Anyway, that is so of any choice other than 0.5 and 1, which, as we saw in §1, are unacceptable as threshold values for other reasons.) I said at the beginning that the standard response is to posit a fuzzy threshold. And the Sophisticated Threshold View formulated in the previous section posits just such a threshold.
The Sophisticated Threshold View makes possible the following response to the Arbitrariness Objection. There is a special difference between clear cases of belief and clear cases of non-belief. But, the difference between two borderline cases of belief need be no more special than the difference between two borderline cases of courage or intelligence or wealth. And the Sophisticated Threshold View allows there to be significant separation between the clear cases of belief and the clear cases of non-belief. So the Sophisticated Threshold View does not have the consequence that invites the Arbitrariness Objection. One might even say (if one finds the proposals of §2 unattractive): the significance of the Arbitrariness Objection is not that it defeats the Threshold View, but that it points us toward the appropriately nuanced version of the Threshold View that we find in the Sophisticated Threshold View.
But Weatherson has voiced dissatisfaction with this response. Here is his complaint:
[I]t’s not clear how this helps. On an epistemic theory of vagueness, there is still a number such that degrees of belief above that count, and degrees below that do not, and any such number is bound to seem unimportant. On supervaluational theories, the same is true. There won’t be a determinate number, to be sure, but there will be a number, and that seems false. My preferred degree of belief theory of vagueness as set out in Weatherson (Reference Weatherson2005) has the same consequence. Hunter [(Reference Hunter1996)] defends a version of the threshold view combined with a theory of vagueness based around fuzzy logic, which seems to be the only theory that could avoid the arbitrariness objection. But as Williamson (Reference Williamson1994: Ch. 4) showed, there are deep and probably insurmountable difficulties with that position. So I think the vagueness response to the arbitrariness objection is (a) the only prima facie plausible response and (b) unsuccessful. Footnote 14
While positing a fuzzy threshold may look, on the face of it, like a good response to the Arbitrariness Objection, Weatherson thinks the devil is in the details. The proponent of the Sophisticated Threshold View needs there to be some plausible account of vagueness that renders this response to the Arbitrariness Objection viable. And Weatherson is sceptical that any account of vagueness can do the job.
Consider for illustration the epistemic theory of vagueness—‘epistemicism’—that Weatherson mentions. The epistemicist holds that vagueness is merely a matter of ignorance. Our ability to set boundaries by linguistic practice outstrips our ability to discover those boundaries. There is a sharp boundary between blue and green, but we’ll never discover which side of the boundary aqua falls on. There is a precise number of hairs (or proportion of scalp coverage) that makes the difference between baldness and non-baldness, but we’ll never identify it. On the epistemicist view, then, asserting that ‘believes’ is vague does not let us do away with a sharp threshold between belief and non-belief. The Sophisticated Threshold View, then, does not allow us to escape the Arbitrariness Objection.
Supervaluationism—one of the main rivals to epistemicism—has the same consequence. The supervaluationist holds that, in borderline cases, the predication of a vague term is neither true nor false. Every vague predicate has a set of ‘admissible precisifications.’ We can think of a precisification as simply a function that maps each object in the world either to ‘True’ or to ‘False,’ leaving no objects unmapped. For a vague predicate F, each admissible precisification F i maps to ‘True’ every object that is clearly F and maps to ‘False’ every object that is clearly not-F. If a predicate had only a single borderline case, it would have only two admissible precisifications—one mapping the borderline case to ‘True,’ the other mapping the borderline case to ‘False.’ Typical vague predicates will have many admissible precisifications. One further requirement for an admissible precisification F i for a predicate F is that F i never maps a better candidate for an F to ‘False’ while mapping a worse candidate for an F to ‘True.’ For example, if Barney and Fred are borderline bald, but Barney is balder than Fred, then no admissible precisification of ‘bald’ will map Barney to ‘False’ and Fred to ‘True.’ With the notion of admissible precisifications in hand, the supervaluationist claims that a sentence is true if and only if it is true for all admissible precisifications of its vague predicates, false if and only if it is false for all admissible precisifications of its vague predicates, and neither true nor false otherwise. For example, if you have a car that is solid royal blue, it will be true on every admissible precisification of ‘blue’ that your car is blue. So, according to the supervaluationist, it is true that your car is blue. If I have a car that is aqua, it will be true on some admissible precisifications of ‘blue’ that my car is blue and false on others. So, according to the supervaluationist, it is neither true nor false that my car is blue.
Weatherson points out that the supervaluationist is committed to saying that belief has a sharp threshold in the confidence spectrum. Consider the sentence ‘There is some degree of confidence such that every higher degree of confidence is a case of belief and every degree of confidence that is not higher is a case of non-belief.’ The sentence asserts a sharp boundary between belief and non-belief. But, by the supervaluationist’s lights, the sentence is true. Keep in mind that it is a constraint on an admissible precisification B i of ‘believes’ that B i never maps a better candidate for belief to ‘False’ while mapping a worse candidate for belief to ‘True.’ And every precisification B i for ‘believes’ maps each degree of confidence either to ‘True’ or to ‘False.’ So every admissible precisification B i for ‘believes’ will impose a sharp boundary between degrees of confidence that are cases of belief and degrees of confidence that aren’t. But, then it is true on every admissible precisification that some degree of confidence is such that every higher degree of confidence is a case of belief and every degree of confidence that is not higher is a case of non-belief. The supervaluationist is thus committed to a sharp threshold.
Weatherson does concede that a viable fuzzy logic would enable proponents of the Threshold View to elude the Arbitrariness Objection. Fuzzy logic allows sentences to be assigned degrees of truth. An assignment of truth-values to the sentences of a language can assign any number from 0 to 1 to represent the degree to which a sentence is true. Fuzzy logic suggests a way of dealing with vagueness. When a sentence predicates some vague term F of an object, the sentence’s degree of truth will be a function of the degree to which the object is a good candidate for an F. If your car is solid royal blue and mine is aqua, then ‘Your car is blue’ (out of my mouth when speaking to you) will be assigned a higher degree of truth than ‘My car is blue’ (out of my mouth).
Suppose credence c B is no better a candidate for belief than for non-belief. Then, using the apparatus of fuzzy logic, we might say that it is only 50% true that c B is a case of belief and 50% true that c B is a case of non-belief. Footnote 15 It will be truer of higher degrees of confidence that they are cases of belief, less true of lower degrees of confidence. As we move up the confidence spectrum, there is no sharp boundary where cases of non-belief give way to cases of belief. Instead, we have a smooth transition from cases that are not at all truly describable as cases of belief to cases that are perfectly truly describable as cases of belief.
But Weatherson follows Timothy Williamson in thinking that this sort of account of vagueness is hopeless. Weatherson does not rehearse Williamson’s criticisms of the fuzzy-logic approach to vagueness, and those criticisms need not detain us either. Footnote 16 We can just concede for the sake of argument that the fuzzy-logic approach is hopeless and assume with Weatherson that the correct account of vagueness is epistemicism or supervaluationism or some other account on which even the Sophisticated Threshold View has the consequence that there is a sharp cutoff between belief and non-belief. What, then, can be said on behalf of the Sophisticated Threshold View?
5. Response to Weatherson’s Worry
Epistemicists and supervaluationists and others who reject the fuzzy-logic approach to vagueness must already endorse such claims as the following:
-
(1) In any conversational context, there is a particular number n such that ‘I am bald’ is true when uttered in that context by anyone with fewer than n hairs on her head and false when uttered in that context by anyone with more than n hairs on her head.
-
(2) In any conversational context, there is a particular number of seconds such that ‘I am old’ is true when uttered in that context by anyone who has lived more than that number of seconds and false when uttered in that context by anyone who has lived fewer than that number of seconds.
-
(3) In any conversational context, there is a particular number such that ‘I am tall’ is true when uttered in that context by anyone whose height in millimeters exceeds that number and false when uttered in that context by anyone whose height in millimeters does not exceed that number.
-
(4) In any conversational context, there is a particular number such that “It is hot in here” is true when uttered in that context if the room temperature in degrees Celsius exceeds that number and false when uttered in that context if the room temperature in degrees Celsius does not exceed that number.
Such statements are the stuff of philosophical comedy, and it is not easy to take seriously a view that has such consequences. But for the sake of argument we are taking such views seriously. We are conceding to Weatherson that the fuzzy-logic approach to vagueness is unacceptable and that the correct account of vagueness is one on which (1)-(4) and many similarly absurd-sounding statements must be true.
If such an account of vagueness is true, as Weatherson maintains, then the world is a strange place. There are sharp cutoffs for baldness, oldness, tallness, hotness, and many other properties. The following thus seems a perfectly fair response to Weatherson’s complaint: ‘What’s one more sharp cutoff in a world replete with them?’ If Weatherson could stomach the other bizarre consequences of epistemicism, supervaluationism, and their ilk, why does he find the idea of a sharp belief threshold so upsetting?
The best hint I find is his assertion that the difference between believing a proposition and not believing is an important difference. Footnote 17 The worry seems to be that we forfeit the importance of the difference between belief and non-belief if we suppose one level of confidence to be a case of belief and an abutting level of confidence to be a case of non-belief. The difference between two abutting levels of confidence is just too trivial to underwrite the importance of the difference between belief and non-belief.
But, if there is an issue here, the same issue could be raised for a host of other properties whose presence makes an important difference. Being courageous, for instance, is importantly different from not being courageous. Yet courage comes in degrees, and it is vague how much courage one must have to qualify as being ‘courageous.’ Epistemicism, supervaluationism, and their ilk would have the consequence that there is some sharp boundary between levels of courage that would qualify one as being ‘courageous’ and abutting levels of courage that would not. And the same is true of many other important qualities (intelligence, happiness, etc.).
So, if Weatherson is correct in his view about which accounts of vagueness are live options, there is no special problem for the belief threshold; we get the same surprising consequences for a multitude of important qualities that represent the high end of some spectrum or other. I take it that the lesson is not that we should reject a threshold view of these qualities. Perhaps the lesson is that we have further reason to question epistemicism, supervaluationism, and their ilk. Or perhaps the lesson is just that there is one more way in which the world is strange—not one dissimilar from the ways in which epistemicists and supervaluationists and others have already admitted the world to be strange, but simply one that had gone unnoticed. In any case, we do not have good reason here to reject the Threshold View. Footnote 18
6. Conclusion
Recent literature on the Threshold View has been largely unfriendly. Footnote 19 Often as not the treatment goes like this: the Threshold View is mentioned; a handful of objections are enumerated; the Threshold View is dismissed as too problematic to salvage. One gets the impression that the objections are piling up and the threshold paradigm is breaking under the weight.
My own assessment is that none of the objections to the Threshold View are very good and that even the whole pile of objections has little weight. But I have not tried to substantiate that general claim here. Footnote 20 The focus has been on just one of the standard objections: the Arbitrariness Objection. We have seen that the proponent of the Threshold View is not forced to go in for fuzzy thresholds to meet the Arbitrariness Objections. There are other lines of resistance that might be developed. But we have also seen that there is no reason—at least none arising from the need for a suitable account of vagueness—to be embarrassed about embracing the fuzzy-threshold approach. The Threshold View can be rigorously formulated to posit a fuzzy belief/withholding threshold, without begging any significant questions about vagueness. And Weatherson’s challenge to this version of the Threshold View proves too much. If that challenge were successful, then it would be a matter of indifference whether you are courageous, intelligent, attractive, and pleasant. Your vanity should prompt you to side here with the proponents of the Threshold View, if nothing else does.
Acknowledgements:
For feedback on and discussion of the material in this paper, I am grateful to Robert Audi, Michael R. DePaul, Vincent Gregoire, Jean-Baptiste Guillon, Daniel Immerman, Michael Papazian, Bradley Rettler, Jeff Speaks, Leopold Stubenberg, and two anonymous referees for this journal.