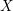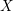1 Introduction
This paper touches on several topics in the étale cohomology of nonarchimedean analytic spaces. On the one hand, we prove an analogue of the Artin–Grothendieck vanishing theorem.Footnote 1 This involves the class of so-called Zariski-constructible étale sheaves on rigid analytic spaces, which we define and study in this paper. On the other hand, as part of this study, we prove some new comparison theorems for étale cohomology, both for affinoid rings and for schemes over affinoid rings. Using these comparison results, we prove a strong structure theorem for Zariski-constructible sheaves on characteristic-zero affinoid rigid spaces, and show that Zariski-constructibility is preserved under certain of the six functor operations.
1.1 Artin–Grothendieck vanishing
Let ![]() $X\subset \mathbf{C}^{m}$ be a smooth affine variety over
$X\subset \mathbf{C}^{m}$ be a smooth affine variety over ![]() $\mathbf{C}$, or more generally any complex Stein manifold. According to a classical theorem of Andreotti and Frankel [Reference Andreotti and FrankelAF59],
$\mathbf{C}$, or more generally any complex Stein manifold. According to a classical theorem of Andreotti and Frankel [Reference Andreotti and FrankelAF59], ![]() $X$ has the homotopy type of a CW complex of real dimension
$X$ has the homotopy type of a CW complex of real dimension ![]() ${\leqslant}\text{dim}\,X$ . In particular, the cohomology groups
${\leqslant}\text{dim}\,X$ . In particular, the cohomology groups ![]() $H^{i}(X,A)$ vanish for any abelian group
$H^{i}(X,A)$ vanish for any abelian group ![]() $A$ and any
$A$ and any ![]() $i>\text{dim}\,X$. This vanishing theorem was significantly generalized by Artin and Grothendieck, who proved the following striking result.
$i>\text{dim}\,X$. This vanishing theorem was significantly generalized by Artin and Grothendieck, who proved the following striking result.
Theorem 1.1 [Reference Artin, Grothendieck and VerdierSGA4, Corollaire XIV.3.2].
Let ![]() $X$ be an affine variety over a separably closed field
$X$ be an affine variety over a separably closed field ![]() $k$ and let
$k$ and let ![]() $\mathscr{F}$ be any torsion abelian sheaf on the étale site of
$\mathscr{F}$ be any torsion abelian sheaf on the étale site of ![]() $X$. Then
$X$. Then
for all ![]() $i>\text{dim}\,X$.
$i>\text{dim}\,X$.
We remind the reader that for a general ![]() $k$-variety
$k$-variety ![]() $X$, the groups
$X$, the groups ![]() $H_{\acute{\text{e}}\text{t}}^{i}(X,\mathscr{F})$ vanish in degrees
$H_{\acute{\text{e}}\text{t}}^{i}(X,\mathscr{F})$ vanish in degrees ![]() $i>2\,\text{dim}\,X$, and this bound is sharp.
$i>2\,\text{dim}\,X$, and this bound is sharp.
It is natural to wonder whether there is a rigid analytic analogue of the Artin–Grothendieck vanishing theorem.Footnote 2 Again, we have a general sharp vanishing theorem due to Berkovich and Huber (cf. [Reference BerkovichBer93, Corollary 4.2.6] and [Reference HuberHub96, Corollary 2.8.3]): for any quasicompact and quasiseparatedFootnote 3 rigid space ![]() $X$ over a complete algebraically closed nonarchimedean field
$X$ over a complete algebraically closed nonarchimedean field ![]() $C$, and any torsion abelian sheaf
$C$, and any torsion abelian sheaf ![]() $\mathscr{F}$ on
$\mathscr{F}$ on ![]() $X_{\acute{\text{e}}\text{t}}$, the cohomology group
$X_{\acute{\text{e}}\text{t}}$, the cohomology group ![]() $H_{\acute{\text{e}}\text{t}}^{i}(X,\mathscr{F})$ vanishes for all
$H_{\acute{\text{e}}\text{t}}^{i}(X,\mathscr{F})$ vanishes for all ![]() $i>2\,\text{dim}\,X$. Now in rigid geometry the affinoid spaces play the role of basic affine objects, and the most naive guess for an analogue of Artin–Grothendieck vanishing would be that
$i>2\,\text{dim}\,X$. Now in rigid geometry the affinoid spaces play the role of basic affine objects, and the most naive guess for an analogue of Artin–Grothendieck vanishing would be that ![]() $H_{\acute{\text{e}}\text{t}}^{i}(X,\mathscr{F})$ vanishes for all affinoids
$H_{\acute{\text{e}}\text{t}}^{i}(X,\mathscr{F})$ vanishes for all affinoids ![]() $X/C$, all torsion abelian sheaves
$X/C$, all torsion abelian sheaves ![]() $\mathscr{F}$ on
$\mathscr{F}$ on ![]() $X_{\acute{\text{e}}\text{t}}$, and all
$X_{\acute{\text{e}}\text{t}}$, and all ![]() $i>\text{dim}\,X$.
$i>\text{dim}\,X$.
Unfortunately, after some experimentation, one discovers that this fails miserably: there are plenty of torsion abelian sheaves on the étale site of any ![]() $d$-dimensional affinoid with nonzero cohomology in all degrees
$d$-dimensional affinoid with nonzero cohomology in all degrees ![]() $i\in [0,2d]$. For example, let
$i\in [0,2d]$. For example, let ![]() $X/C$ be any (reduced)
$X/C$ be any (reduced) ![]() $d$-dimensional affinoid, and let
$d$-dimensional affinoid, and let ![]() $j:U\rightarrow X$ be the open inclusion of any small
$j:U\rightarrow X$ be the open inclusion of any small ![]() $d$-dimensional affinoid ball with
$d$-dimensional affinoid ball with ![]() $U$ strictly contained in
$U$ strictly contained in ![]() $X$. Set
$X$. Set ![]() $\mathscr{F}=j_{!}\mathbf{Z}/n\mathbf{Z}$ for some
$\mathscr{F}=j_{!}\mathbf{Z}/n\mathbf{Z}$ for some ![]() $n$ prime to the residue characteristic of
$n$ prime to the residue characteristic of ![]() $C$. Then
$C$. Then ![]() $H_{\acute{\text{e}}\text{t}}^{i}(X,\mathscr{F})=H_{c,\acute{\text{e}}\text{t}}^{i}(U,\mathbf{Z}/n\mathbf{Z})$, and the latter group is Poincaré dual to
$H_{\acute{\text{e}}\text{t}}^{i}(X,\mathscr{F})=H_{c,\acute{\text{e}}\text{t}}^{i}(U,\mathbf{Z}/n\mathbf{Z})$, and the latter group is Poincaré dual to ![]() $H_{\acute{\text{e}}\text{t}}^{2d-i}(U,\mathbf{Z}/n\mathbf{Z})$, which is nonzero when
$H_{\acute{\text{e}}\text{t}}^{2d-i}(U,\mathbf{Z}/n\mathbf{Z})$, which is nonzero when ![]() $i=2d$. In particular,
$i=2d$. In particular, ![]() $H_{\acute{\text{e}}\text{t}}^{2d}(X,\mathscr{F})\neq 0$.
$H_{\acute{\text{e}}\text{t}}^{2d}(X,\mathscr{F})\neq 0$.
In this example, the sheaf ![]() $\mathscr{F}$ is constructible in a certain weak sense [Reference HuberHub96, Definition 2.7.2], but it is far from the type of constructible étale sheaves one traditionally encounters in algebraic geometry, which are locally constant after passing to some locally closed strata in the Zariski topology. In particular, the formulation of the following conjecture rules out counterexamples like this, and seems to be a reasonable salvage of Artin–Grothendieck vanishing.
$\mathscr{F}$ is constructible in a certain weak sense [Reference HuberHub96, Definition 2.7.2], but it is far from the type of constructible étale sheaves one traditionally encounters in algebraic geometry, which are locally constant after passing to some locally closed strata in the Zariski topology. In particular, the formulation of the following conjecture rules out counterexamples like this, and seems to be a reasonable salvage of Artin–Grothendieck vanishing.
Conjecture 1.2. Let ![]() $X$ be an affinoid rigid space over a complete algebraically closed nonarchimedean field
$X$ be an affinoid rigid space over a complete algebraically closed nonarchimedean field ![]() $C$, and let
$C$, and let ![]() $\mathscr{G}$ be any Zariski-constructible sheaf of
$\mathscr{G}$ be any Zariski-constructible sheaf of ![]() $\mathbf{Z}/n\mathbf{Z}$-modules on
$\mathbf{Z}/n\mathbf{Z}$-modules on ![]() $X_{\acute{\text{e}}\text{t}}$ for some
$X_{\acute{\text{e}}\text{t}}$ for some ![]() $n$ prime to the residue characteristic of
$n$ prime to the residue characteristic of ![]() $C$. Then
$C$. Then
for all ![]() $i>\text{dim}\,X$.
$i>\text{dim}\,X$.
Here for a given rigid space ![]() $X$ and Noetherian coefficient ring
$X$ and Noetherian coefficient ring ![]() $\unicode[STIX]{x1D6EC}$, we say that a sheaf
$\unicode[STIX]{x1D6EC}$, we say that a sheaf ![]() $\mathscr{G}$ of
$\mathscr{G}$ of ![]() $\unicode[STIX]{x1D6EC}$-modules on
$\unicode[STIX]{x1D6EC}$-modules on ![]() $X_{\acute{\text{e}}\text{t}}$ is Zariski-constructible if
$X_{\acute{\text{e}}\text{t}}$ is Zariski-constructible if ![]() $X$ admits a locally finite stratification into subspaces
$X$ admits a locally finite stratification into subspaces ![]() $Z_{i}\subset X$, each locally closed for the Zariski topology on
$Z_{i}\subset X$, each locally closed for the Zariski topology on ![]() $X$, such that
$X$, such that ![]() $\mathscr{G}|_{Z_{i,\acute{\text{e}}\text{t}}}$ is a locally constant sheaf of
$\mathscr{G}|_{Z_{i,\acute{\text{e}}\text{t}}}$ is a locally constant sheaf of ![]() $\unicode[STIX]{x1D6EC}$-modules of finite type for each
$\unicode[STIX]{x1D6EC}$-modules of finite type for each ![]() $i$. We denote the category of such sheaves by
$i$. We denote the category of such sheaves by![]() $\text{Sh}_{zc}(X,\unicode[STIX]{x1D6EC})$. We will see that
$\text{Sh}_{zc}(X,\unicode[STIX]{x1D6EC})$. We will see that ![]() $\text{Sh}_{zc}(X,\unicode[STIX]{x1D6EC})$ is a thick abelian subcategory of the category
$\text{Sh}_{zc}(X,\unicode[STIX]{x1D6EC})$ is a thick abelian subcategory of the category ![]() $\text{Sh}(X,\unicode[STIX]{x1D6EC})$ of all sheaves of
$\text{Sh}(X,\unicode[STIX]{x1D6EC})$ of all sheaves of ![]() $\unicode[STIX]{x1D6EC}$-modules on
$\unicode[STIX]{x1D6EC}$-modules on ![]() $X_{\acute{\text{e}}\text{t}}$. In the derived setting, we say that a complex of étale sheaves
$X_{\acute{\text{e}}\text{t}}$. In the derived setting, we say that a complex of étale sheaves ![]() $A\in D(X,\unicode[STIX]{x1D6EC})$ is Zariski-constructible if it has Zariski-constructible cohomology sheaves; such objects form a saturated triangulated subcategory
$A\in D(X,\unicode[STIX]{x1D6EC})$ is Zariski-constructible if it has Zariski-constructible cohomology sheaves; such objects form a saturated triangulated subcategory ![]() $D_{zc}(X,\unicode[STIX]{x1D6EC})$. Note that Zariski-constructible sheaves are overconvergent, and so it is immaterial whether one interprets their étale cohomology in the framework of Berkovich spaces or adic spaces (cf. [Reference HuberHub96, Theorem 8.3.5]).
$D_{zc}(X,\unicode[STIX]{x1D6EC})$. Note that Zariski-constructible sheaves are overconvergent, and so it is immaterial whether one interprets their étale cohomology in the framework of Berkovich spaces or adic spaces (cf. [Reference HuberHub96, Theorem 8.3.5]).
The first main result of this paper confirms Conjecture 1.2 in the case where ![]() $C$ has characteristic zero and the pair
$C$ has characteristic zero and the pair ![]() $(X,\mathscr{G})$ arises via base extension from a discretely valued nonarchimedean field.
$(X,\mathscr{G})$ arises via base extension from a discretely valued nonarchimedean field.
Theorem 1.3. Let ![]() $X$ be an affinoid rigid space over a complete discretely valued nonarchimedean field
$X$ be an affinoid rigid space over a complete discretely valued nonarchimedean field ![]() $K$ of characteristic zero, and let
$K$ of characteristic zero, and let ![]() $\mathscr{F}$ be any Zariski-constructible sheaf of
$\mathscr{F}$ be any Zariski-constructible sheaf of ![]() $\mathbf{Z}/n\mathbf{Z}$-modules on
$\mathbf{Z}/n\mathbf{Z}$-modules on ![]() $X_{\acute{\text{e}}\text{t}}$ for some
$X_{\acute{\text{e}}\text{t}}$ for some ![]() $n$ prime to the residue characteristic of
$n$ prime to the residue characteristic of ![]() $K$. Then the cohomology groups
$K$. Then the cohomology groups ![]() $H_{\acute{\text{e}}\text{t}}^{i}(X_{\widehat{\overline{K}}},\mathscr{F})$ are finite for all
$H_{\acute{\text{e}}\text{t}}^{i}(X_{\widehat{\overline{K}}},\mathscr{F})$ are finite for all ![]() $i$, and
$i$, and
for all ![]() $i>\text{dim}\,X$.
$i>\text{dim}\,X$.
For a slightly more general result, see Corollary 3.4. As far as we know, this is the first progress on Conjecture 1.2 since Berkovich [Reference BerkovichBer96] treated some cases where ![]() $\mathscr{F}=\mathbf{Z}/n\mathbf{Z}$ is constant and
$\mathscr{F}=\mathbf{Z}/n\mathbf{Z}$ is constant and ![]() $X$ is assumed algebraizable in a certain sense. In particular, using a deep algebraization theorem of Elkik [Reference ElkikElk73, Théorème 7], Berkovich proved Conjecture 1.2 when
$X$ is assumed algebraizable in a certain sense. In particular, using a deep algebraization theorem of Elkik [Reference ElkikElk73, Théorème 7], Berkovich proved Conjecture 1.2 when ![]() $\mathscr{F}$ is constant and
$\mathscr{F}$ is constant and ![]() $X$ is smooth, which might give one some confidence in the general conjecture.
$X$ is smooth, which might give one some confidence in the general conjecture.
Our proof of Theorem 1.3 does not explicitly use any algebraization techniques. Instead, we reduce to the special case where ![]() $\mathscr{F}$ is constant. In this situation, it turns out we can argue directly, with fewer assumptions on
$\mathscr{F}$ is constant. In this situation, it turns out we can argue directly, with fewer assumptions on ![]() $K$, as follows.
$K$, as follows.
Theorem 1.4. Let ![]() $X$ be an affinoid rigid space over a complete discretely valued nonarchimedean field
$X$ be an affinoid rigid space over a complete discretely valued nonarchimedean field ![]() $K$. Then
$K$. Then
for all ![]() $i>\text{dim}\,X$ and all
$i>\text{dim}\,X$ and all ![]() $n$ prime to the residue characteristic of
$n$ prime to the residue characteristic of ![]() $K$.
$K$.
The proof of this theorem uses a number of ingredients, including some theorems of Greco and Valabrega on excellent rings, a remarkable formula of Huber for the stalks of the nearby cycle sheaves ![]() $R^{q}\unicode[STIX]{x1D706}_{\ast }(\mathbf{Z}/n\mathbf{Z})$ on
$R^{q}\unicode[STIX]{x1D706}_{\ast }(\mathbf{Z}/n\mathbf{Z})$ on ![]() $\text{Spec}(A^{\circ }/\unicode[STIX]{x1D71B})_{\text{et}}$, a special case of Gabber’s delicate ‘affine Lefschetz theorem’ for quasi-excellent schemes, and the classical Artin–Grothendieck vanishing theorem. We note that the proof of Gabber’s theorem makes heavy use of algebraization techniques.
$\text{Spec}(A^{\circ }/\unicode[STIX]{x1D71B})_{\text{et}}$, a special case of Gabber’s delicate ‘affine Lefschetz theorem’ for quasi-excellent schemes, and the classical Artin–Grothendieck vanishing theorem. We note that the proof of Gabber’s theorem makes heavy use of algebraization techniques.
The reduction step involves an ingredient which seems interesting in its own right. To explain this, we make the following definition.
Definition 1.5. Let ![]() $X$ be a normal rigid space. A cover of
$X$ be a normal rigid space. A cover of ![]() $X$ is a finite surjective map
$X$ is a finite surjective map ![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X$ from a normal rigid space
$\unicode[STIX]{x1D70B}:Y\rightarrow X$ from a normal rigid space ![]() $Y$, such that there exists some closed nowhere-dense analytic subset
$Y$, such that there exists some closed nowhere-dense analytic subset ![]() $Z\subset X$ with
$Z\subset X$ with ![]() $\unicode[STIX]{x1D70B}^{-1}(Z)$ nowhere-dense and such that
$\unicode[STIX]{x1D70B}^{-1}(Z)$ nowhere-dense and such that ![]() $Y\smallsetminus \unicode[STIX]{x1D70B}^{-1}(Z)\rightarrow X\smallsetminus Z$ is finite étale.
$Y\smallsetminus \unicode[STIX]{x1D70B}^{-1}(Z)\rightarrow X\smallsetminus Z$ is finite étale.
We then have the following result, which seems to be new.
Theorem 1.6. Let ![]() $X$ be a normal rigid space over a complete nonarchimedean field
$X$ be a normal rigid space over a complete nonarchimedean field ![]() $K$ and let
$K$ and let ![]() $Z\subset X$ be any closed nowhere-dense analytic subset. Then the restriction functor
$Z\subset X$ be any closed nowhere-dense analytic subset. Then the restriction functor
 $$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}c@{}}\text{covers of }X\\ \acute{\text{e}}\text{tale over }X\smallsetminus Z\end{array}\right\} & \rightarrow & \displaystyle \left\{\begin{array}{@{}c@{}}\text{finite }\acute{e} \text{tale covers}\\ \text{of }X\smallsetminus Z\end{array}\right\}\nonumber\\ \displaystyle Y & \mapsto & \displaystyle Y\times _{X}(X\smallsetminus Z)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}c@{}}\text{covers of }X\\ \acute{\text{e}}\text{tale over }X\smallsetminus Z\end{array}\right\} & \rightarrow & \displaystyle \left\{\begin{array}{@{}c@{}}\text{finite }\acute{e} \text{tale covers}\\ \text{of }X\smallsetminus Z\end{array}\right\}\nonumber\\ \displaystyle Y & \mapsto & \displaystyle Y\times _{X}(X\smallsetminus Z)\nonumber\end{eqnarray}$$ is fully faithful. Moreover, if ![]() $K$ has characteristic zero, it is an equivalence of categories; in other words, any finite étale cover of
$K$ has characteristic zero, it is an equivalence of categories; in other words, any finite étale cover of ![]() $X\smallsetminus Z$ extends uniquely to a cover of
$X\smallsetminus Z$ extends uniquely to a cover of ![]() $X$.
$X$.
We remind the reader that in the schemes setting, the analogue of the equivalence in Theorem 1.6 is an easy exercise in taking normalizations, and holds essentially whenever the base scheme ![]() $X$ is Nagata, while for complex analytic spaces the problem was solved by Stein and Grauert–Remmert in the 1950s; cf. [Reference Dethloff and GrauertDG94].
$X$ is Nagata, while for complex analytic spaces the problem was solved by Stein and Grauert–Remmert in the 1950s; cf. [Reference Dethloff and GrauertDG94].
Let us say something about the proof. Full faithfulness is an easy consequence of Bartenwerfer’s rigid analytic version of Riemann’s Hebbarkeitssatz, which says that bounded functions on normal rigid spaces extend uniquely across nowhere-dense closed analytic subsets. Essential surjectivity in characteristic zero is more subtle; indeed, it provably fails in positive characteristic. When ![]() $X$ is smooth and
$X$ is smooth and ![]() $Z$ is a strict normal crossings divisor, however, essential surjectivity was proved by Lütkebohmert in his work [Reference LütkebohmertLüt93] on Riemann’s existence problem.Footnote 4 We reduce the general case to Lütkebohmert’s result using recent work of Temkin on embedded resolution of singularities for quasi-excellent schemes in characteristic zero.
$Z$ is a strict normal crossings divisor, however, essential surjectivity was proved by Lütkebohmert in his work [Reference LütkebohmertLüt93] on Riemann’s existence problem.Footnote 4 We reduce the general case to Lütkebohmert’s result using recent work of Temkin on embedded resolution of singularities for quasi-excellent schemes in characteristic zero.
We also note that our argument for the reduction of Theorems 1.3–1.4 reduces Conjecture 1.2 to the special case where ![]() $\mathscr{F}$ is constant, at least for
$\mathscr{F}$ is constant, at least for ![]() $C$ of characteristic zero. With Theorem 1.4 in hand, this might put the general characteristic-zero case of Conjecture 1.2 within reach of some approximation argument.
$C$ of characteristic zero. With Theorem 1.4 in hand, this might put the general characteristic-zero case of Conjecture 1.2 within reach of some approximation argument.
We also note that Conjecture 1.2 may well still hold true without restricting to ![]() $n$ coprime to the residue characteristic, but our evidence in this case is rather weaker, and
$n$ coprime to the residue characteristic, but our evidence in this case is rather weaker, and ![]() $p$-adic étale cohomology of affinoids over
$p$-adic étale cohomology of affinoids over ![]() $p$-adic fields behaves rather badly. As such, we have chosen not to explicitly formulate the conjecture in that generality.
$p$-adic fields behaves rather badly. As such, we have chosen not to explicitly formulate the conjecture in that generality.
1.2 Comparison theorems and applications
The next main result in this paper is the following theorem, which gives some further justification for the definition of Zariski-constructible sheaves.
Theorem 1.7. Let ![]() $S=\text{Spa}\,A$ be an affinoid rigid space over some characteristic-zero nonarchimedean field
$S=\text{Spa}\,A$ be an affinoid rigid space over some characteristic-zero nonarchimedean field ![]() $K$, and write
$K$, and write ![]() ${\mathcal{S}}=\text{Spec}\,A$, so there is a natural map of sites
${\mathcal{S}}=\text{Spec}\,A$, so there is a natural map of sites ![]() $\unicode[STIX]{x1D707}_{S}:S_{\acute{\text{e}}\text{t}}\rightarrow {\mathcal{S}}_{\acute{\text{e}}\text{t}}$. Let
$\unicode[STIX]{x1D707}_{S}:S_{\acute{\text{e}}\text{t}}\rightarrow {\mathcal{S}}_{\acute{\text{e}}\text{t}}$. Let ![]() $\unicode[STIX]{x1D6EC}$ be a Noetherian coefficient ring killed by some positive integer, such that either
$\unicode[STIX]{x1D6EC}$ be a Noetherian coefficient ring killed by some positive integer, such that either ![]() $\#\unicode[STIX]{x1D6EC}$ is finite or the residue characteristic of
$\#\unicode[STIX]{x1D6EC}$ is finite or the residue characteristic of ![]() $K$ is invertible in
$K$ is invertible in ![]() $\unicode[STIX]{x1D6EC}$. Let
$\unicode[STIX]{x1D6EC}$. Let ![]() $\text{Sh}_{c}({\mathcal{S}},\unicode[STIX]{x1D6EC})$ denote the category of constructible sheaves of
$\text{Sh}_{c}({\mathcal{S}},\unicode[STIX]{x1D6EC})$ denote the category of constructible sheaves of ![]() $\unicode[STIX]{x1D6EC}$-modules on
$\unicode[STIX]{x1D6EC}$-modules on ![]() ${\mathcal{S}}_{\acute{\text{e}}\text{t}}$.
${\mathcal{S}}_{\acute{\text{e}}\text{t}}$.
Then the functor
is an equivalence of categories.
Note that we still expect full faithfulness in positive characteristic, but essential surjectivity definitely fails. For an explicit counterexample, take ![]() $K=\mathbf{F}_{p}((t))$ and
$K=\mathbf{F}_{p}((t))$ and ![]() $S=\text{Spa}\,K\langle T\rangle$. Write
$S=\text{Spa}\,K\langle T\rangle$. Write ![]() $j:S^{\times }=S\smallsetminus \{T=0\}\rightarrow S$ for the inclusion of the punctured disk. Then (for any
$j:S^{\times }=S\smallsetminus \{T=0\}\rightarrow S$ for the inclusion of the punctured disk. Then (for any ![]() $\unicode[STIX]{x1D6EC}$) there exists a locally constant constructible sheaf
$\unicode[STIX]{x1D6EC}$) there exists a locally constant constructible sheaf ![]() $\mathscr{F}$ on
$\mathscr{F}$ on ![]() $S^{\times }$ such that
$S^{\times }$ such that ![]() $j_{!}\mathscr{F}$ is not in the essential image of
$j_{!}\mathscr{F}$ is not in the essential image of ![]() $\unicode[STIX]{x1D707}_{S}^{\ast }$: precisely, one can choose an Artin–Schreier cover
$\unicode[STIX]{x1D707}_{S}^{\ast }$: precisely, one can choose an Artin–Schreier cover ![]() $\unicode[STIX]{x1D70B}:U\rightarrow S^{\times }$ defined by an equation
$\unicode[STIX]{x1D70B}:U\rightarrow S^{\times }$ defined by an equation ![]() $T^{p}-T-f$ for some well-chosen
$T^{p}-T-f$ for some well-chosen ![]() $f\in {\mathcal{O}}(S^{\times })$, such that
$f\in {\mathcal{O}}(S^{\times })$, such that ![]() $\mathscr{F}=\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6EC}$ gives an example of the desired shape. The point is to choose an
$\mathscr{F}=\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6EC}$ gives an example of the desired shape. The point is to choose an ![]() $f$ which has an especially bad essential singularity at
$f$ which has an especially bad essential singularity at ![]() $T=0$. This counterexample is closely related to the failure of Theorem 1.6 in positive characteristic.
$T=0$. This counterexample is closely related to the failure of Theorem 1.6 in positive characteristic.
Although intuitively reasonable, Theorem 1.7 is definitely not trivial to prove. The main tools in the proof are Theorem 1.6 together with two new comparison theorems for étale cohomology. To state the latter results, fix an affinoid ![]() $S=\text{Spa}\,A$ over some nonarchimedean field
$S=\text{Spa}\,A$ over some nonarchimedean field ![]() $K$, and let
$K$, and let ![]() ${\mathcal{S}}=\text{Spec}\,A$ and
${\mathcal{S}}=\text{Spec}\,A$ and ![]() $\unicode[STIX]{x1D707}_{S}$ be as above. Recall that for any locally finite-type
$\unicode[STIX]{x1D707}_{S}$ be as above. Recall that for any locally finite-type ![]() ${\mathcal{S}}$-scheme
${\mathcal{S}}$-scheme ![]() ${\mathcal{X}}$, there is a functorially associated rigid space
${\mathcal{X}}$, there is a functorially associated rigid space ![]() $X={\mathcal{X}}^{\text{an}}$ over
$X={\mathcal{X}}^{\text{an}}$ over ![]() $S$ together with a morphism
$S$ together with a morphism ![]() $X\rightarrow {\mathcal{X}}$ of locally ringed spaces characterized by a simple universal property, and again there is a functorial map of sites
$X\rightarrow {\mathcal{X}}$ of locally ringed spaces characterized by a simple universal property, and again there is a functorial map of sites ![]() $\unicode[STIX]{x1D707}_{X}:X_{\acute{\text{e}}\text{t}}\rightarrow {\mathcal{X}}_{\acute{\text{e}}\text{t}}$. We then have the following relative comparison theorem.
$\unicode[STIX]{x1D707}_{X}:X_{\acute{\text{e}}\text{t}}\rightarrow {\mathcal{X}}_{\acute{\text{e}}\text{t}}$. We then have the following relative comparison theorem.
Theorem 1.8 (Relative comparison theorem).
Assume that ![]() $\text{char}(K)=0$, and let
$\text{char}(K)=0$, and let ![]() $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ be a finite-type morphism between
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ be a finite-type morphism between ![]() ${\mathcal{S}}$-schemes locally of finite type, with analytification
${\mathcal{S}}$-schemes locally of finite type, with analytification ![]() $f^{\text{an}}:X\rightarrow Y$. Let
$f^{\text{an}}:X\rightarrow Y$. Let ![]() $\unicode[STIX]{x1D6EC}$ be a Noetherian coefficient ring killed by some positive integer, such that either
$\unicode[STIX]{x1D6EC}$ be a Noetherian coefficient ring killed by some positive integer, such that either ![]() $\#\unicode[STIX]{x1D6EC}$ is finite or the residue characteristic of
$\#\unicode[STIX]{x1D6EC}$ is finite or the residue characteristic of ![]() $K$ is invertible in
$K$ is invertible in ![]() $\unicode[STIX]{x1D6EC}$. Then, for any
$\unicode[STIX]{x1D6EC}$. Then, for any ![]() $F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$, the natural comparison map
$F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$, the natural comparison map
is an isomorphism in ![]() $D(Y,\unicode[STIX]{x1D6EC})$.
$D(Y,\unicode[STIX]{x1D6EC})$.
In the special cases where ![]() $f$ is proper or
$f$ is proper or ![]() ${\mathcal{S}}=\text{Spec}\,K$ is a point, this was proved by Berkovich and Huber in the 1990s (see [Reference BerkovichBer93, Corollaries 7.1.4 and 7.5.4] and [Reference HuberHub96, Theorems 3.7.2 and 3.8.1]).
${\mathcal{S}}=\text{Spec}\,K$ is a point, this was proved by Berkovich and Huber in the 1990s (see [Reference BerkovichBer93, Corollaries 7.1.4 and 7.5.4] and [Reference HuberHub96, Theorems 3.7.2 and 3.8.1]).
On the other hand, we also prove an ‘absolute’ comparison theorem for affinoid adic spaces.
Theorem 1.9 (Affinoid comparison theorem).
Let ![]() $(A,A^{+})$ be any strongly Noetherian Tate–Huber pair, with
$(A,A^{+})$ be any strongly Noetherian Tate–Huber pair, with ![]() $S=\text{Spa}(A,A^{+})$ the associated affinoid adic space. Write
$S=\text{Spa}(A,A^{+})$ the associated affinoid adic space. Write ![]() ${\mathcal{S}}=\text{Spec}\,A$, so there is a map of sites
${\mathcal{S}}=\text{Spec}\,A$, so there is a map of sites ![]() $\unicode[STIX]{x1D707}_{S}:S_{\acute{\text{e}}\text{t}}\rightarrow {\mathcal{S}}_{\acute{\text{e}}\text{t}}$ as above. Then for any torsion abelian sheaf
$\unicode[STIX]{x1D707}_{S}:S_{\acute{\text{e}}\text{t}}\rightarrow {\mathcal{S}}_{\acute{\text{e}}\text{t}}$ as above. Then for any torsion abelian sheaf ![]() $\mathscr{F}$ on
$\mathscr{F}$ on ![]() ${\mathcal{S}}_{\acute{\text{e}}\text{t}}$, the natural comparison map
${\mathcal{S}}_{\acute{\text{e}}\text{t}}$, the natural comparison map
is an isomorphism for all ![]() $n$.
$n$.
When ![]() $\mathscr{F}$ is a constant sheaf, this is proved in Huber’s book, and one might hope to reduce to this case by a trick. This turns out to be surprisingly easy.
$\mathscr{F}$ is a constant sheaf, this is proved in Huber’s book, and one might hope to reduce to this case by a trick. This turns out to be surprisingly easy.
The proof of Theorem 1.8 is somewhat more involved. The rough idea is to reduce the general case by a series of dévissages to the very special case where ![]() ${\mathcal{Y}}$ is regular,
${\mathcal{Y}}$ is regular, ![]() $f$ is a dense open immersion, and
$f$ is a dense open immersion, and ![]() $F=\text{}\underline{M}$ is a constant constructible sheaf of
$F=\text{}\underline{M}$ is a constant constructible sheaf of ![]() $\unicode[STIX]{x1D6EC}$-modules. This special case is handled by a completely straightforward adaptation of the final stages in the proof of [Reference Artin, Grothendieck and VerdierSGA4, Theorem XVI.4.1], making crucial use of a cohomological purity theorem due to Huber; the latter theorem is where the conditions on
$\unicode[STIX]{x1D6EC}$-modules. This special case is handled by a completely straightforward adaptation of the final stages in the proof of [Reference Artin, Grothendieck and VerdierSGA4, Theorem XVI.4.1], making crucial use of a cohomological purity theorem due to Huber; the latter theorem is where the conditions on ![]() $\unicode[STIX]{x1D6EC}$ in Theorem 1.8 arise. The reduction steps use a number of ingredients, including Temkin’s results on resolution of singularities, Gabber’s results on the étale cohomology of quasi-excellent schemes, and the truth of Theorem 1.8 for proper
$\unicode[STIX]{x1D6EC}$ in Theorem 1.8 arise. The reduction steps use a number of ingredients, including Temkin’s results on resolution of singularities, Gabber’s results on the étale cohomology of quasi-excellent schemes, and the truth of Theorem 1.8 for proper ![]() $f$. We note that Huber already suggested in his book that Theorem 1.8 should be true and provable along these lines; cf. [Reference HuberHub96, p. 162].
$f$. We note that Huber already suggested in his book that Theorem 1.8 should be true and provable along these lines; cf. [Reference HuberHub96, p. 162].
Putting these comparison theorems together, we get the following very useful result.
Theorem 1.10. Let ![]() ${\mathcal{S}}=\text{Spec}\,A$ be the spectrum of a characteristic-zero affinoid, and let
${\mathcal{S}}=\text{Spec}\,A$ be the spectrum of a characteristic-zero affinoid, and let ![]() $f:{\mathcal{X}}\rightarrow {\mathcal{S}}$ be an
$f:{\mathcal{X}}\rightarrow {\mathcal{S}}$ be an ![]() ${\mathcal{S}}$-scheme of finite type with analytification
${\mathcal{S}}$-scheme of finite type with analytification ![]() $f^{\text{an}}:X\rightarrow S=\text{Spa}\,A$. Let
$f^{\text{an}}:X\rightarrow S=\text{Spa}\,A$. Let ![]() $\unicode[STIX]{x1D6EC}$ be a Noetherian coefficient ring killed by some positive integer, such that either
$\unicode[STIX]{x1D6EC}$ be a Noetherian coefficient ring killed by some positive integer, such that either ![]() $\#\unicode[STIX]{x1D6EC}$ is finite or the residue characteristic of
$\#\unicode[STIX]{x1D6EC}$ is finite or the residue characteristic of ![]() $K$ is invertible in
$K$ is invertible in ![]() $\unicode[STIX]{x1D6EC}$. Then:
$\unicode[STIX]{x1D6EC}$. Then:
(i) for any
 $F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$, the natural map
$F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$, the natural map  $R\unicode[STIX]{x1D6E4}({\mathcal{X}},F)\rightarrow R\unicode[STIX]{x1D6E4}(X,\unicode[STIX]{x1D707}_{X}^{\ast }F)$ is an isomorphism. Moreover, the natural adjunction map
$R\unicode[STIX]{x1D6E4}({\mathcal{X}},F)\rightarrow R\unicode[STIX]{x1D6E4}(X,\unicode[STIX]{x1D707}_{X}^{\ast }F)$ is an isomorphism. Moreover, the natural adjunction map  $F\rightarrow R\unicode[STIX]{x1D707}_{X\ast }\unicode[STIX]{x1D707}_{X}^{\ast }F$ is an isomorphism;
$F\rightarrow R\unicode[STIX]{x1D707}_{X\ast }\unicode[STIX]{x1D707}_{X}^{\ast }F$ is an isomorphism;(ii) the functor
 $\unicode[STIX]{x1D707}_{X}^{\ast }:D_{c}^{b}({\mathcal{X}},\unicode[STIX]{x1D6EC})\rightarrow D(X,\unicode[STIX]{x1D6EC})$ is fully faithful. More generally, there is a natural isomorphism for any
$\unicode[STIX]{x1D707}_{X}^{\ast }:D_{c}^{b}({\mathcal{X}},\unicode[STIX]{x1D6EC})\rightarrow D(X,\unicode[STIX]{x1D6EC})$ is fully faithful. More generally, there is a natural isomorphism for any $$\begin{eqnarray}\text{Hom}_{D(X,\unicode[STIX]{x1D6EC})}(\unicode[STIX]{x1D707}_{X}^{\ast }G,\unicode[STIX]{x1D707}_{X}^{\ast }F)\cong \text{Hom}_{D({\mathcal{X}},\unicode[STIX]{x1D6EC})}(G,F)\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{D(X,\unicode[STIX]{x1D6EC})}(\unicode[STIX]{x1D707}_{X}^{\ast }G,\unicode[STIX]{x1D707}_{X}^{\ast }F)\cong \text{Hom}_{D({\mathcal{X}},\unicode[STIX]{x1D6EC})}(G,F)\end{eqnarray}$$ $F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$ and
$F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$ and  $G\in D^{-}({\mathcal{X}},\unicode[STIX]{x1D6EC})$.
$G\in D^{-}({\mathcal{X}},\unicode[STIX]{x1D6EC})$.
Note that even if ![]() ${\mathcal{X}}={\mathcal{S}}$, the proof of Theorem 1.10 requires the full power of the relative comparison theorem, since one needs to compare the étale cohomology of
${\mathcal{X}}={\mathcal{S}}$, the proof of Theorem 1.10 requires the full power of the relative comparison theorem, since one needs to compare the étale cohomology of ![]() ${\mathcal{U}}$ and
${\mathcal{U}}$ and ![]() ${\mathcal{U}}^{\text{an}}$ for an arbitrary quasicompact étale map
${\mathcal{U}}^{\text{an}}$ for an arbitrary quasicompact étale map ![]() ${\mathcal{U}}\rightarrow {\mathcal{S}}$, in which case
${\mathcal{U}}\rightarrow {\mathcal{S}}$, in which case ![]() ${\mathcal{U}}^{\text{an}}$ is typically never affinoid. This was our original motivation for proving the relative comparison theorem.
${\mathcal{U}}^{\text{an}}$ is typically never affinoid. This was our original motivation for proving the relative comparison theorem.
Finally, we take some first steps towards showing that Zariski-constructibility interacts well with the six operations in the étale cohomology of rigid spaces. We caution the reader that unless ![]() $f$ is proper, the functors
$f$ is proper, the functors ![]() $Rf_{\ast }$ and
$Rf_{\ast }$ and ![]() $Rf_{!}$ typically destroy Zariski-constructibility, even if
$Rf_{!}$ typically destroy Zariski-constructibility, even if ![]() $f$ is the inclusion of a Zariski-open subset.Footnote 5 However, we expect that this is more or less the only thing that goes wrong.
$f$ is the inclusion of a Zariski-open subset.Footnote 5 However, we expect that this is more or less the only thing that goes wrong.
Theorem 1.11. Let ![]() $S$ be a characteristic-zero affinoid space over a nonarchimedean field
$S$ be a characteristic-zero affinoid space over a nonarchimedean field ![]() $K$, and set
$K$, and set ![]() $\unicode[STIX]{x1D6EC}=\mathbf{Z}/n\mathbf{Z}$ for some
$\unicode[STIX]{x1D6EC}=\mathbf{Z}/n\mathbf{Z}$ for some ![]() $n$ prime to the residue characteristic of
$n$ prime to the residue characteristic of ![]() $K$. Let
$K$. Let ![]() $g:S\rightarrow \text{Spa}K$ be the structure map and let
$g:S\rightarrow \text{Spa}K$ be the structure map and let ![]() $\unicode[STIX]{x1D714}_{S}=Rg^{!}\unicode[STIX]{x1D6EC}$ be the dualizing complex. Then:
$\unicode[STIX]{x1D714}_{S}=Rg^{!}\unicode[STIX]{x1D6EC}$ be the dualizing complex. Then:
(i) if
 $j:U\rightarrow S$ is the inclusion of a Zariski-open subspace and
$j:U\rightarrow S$ is the inclusion of a Zariski-open subspace and  $\mathscr{F}\in \text{Sh}(U,\unicode[STIX]{x1D6EC})$ is locally constant constructible, then
$\mathscr{F}\in \text{Sh}(U,\unicode[STIX]{x1D6EC})$ is locally constant constructible, then  $Rj_{\ast }\mathscr{F}$ is Zariski-constructible;
$Rj_{\ast }\mathscr{F}$ is Zariski-constructible;(ii) if
 $\mathscr{F},\mathscr{G}\in D^{-}(S,\unicode[STIX]{x1D6EC})$ are Zariski-constructible, then so is
$\mathscr{F},\mathscr{G}\in D^{-}(S,\unicode[STIX]{x1D6EC})$ are Zariski-constructible, then so is  $\mathscr{F}\otimes _{\unicode[STIX]{x1D6EC}}^{\mathbf{L}}\mathscr{G}$;
$\mathscr{F}\otimes _{\unicode[STIX]{x1D6EC}}^{\mathbf{L}}\mathscr{G}$;(iii) the Verdier duality functor
sends $$\begin{eqnarray}\mathbf{D}_{S}(-)=R\mathscr{H}\text{om}_{S}(-,\unicode[STIX]{x1D714}_{S})\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{D}_{S}(-)=R\mathscr{H}\text{om}_{S}(-,\unicode[STIX]{x1D714}_{S})\end{eqnarray}$$ $D^{\pm }(S,\unicode[STIX]{x1D6EC})$ into
$D^{\pm }(S,\unicode[STIX]{x1D6EC})$ into  $D^{\mp }(S,\unicode[STIX]{x1D6EC})$ and, if
$D^{\mp }(S,\unicode[STIX]{x1D6EC})$ and, if  $\mathscr{F}\in D(S,\unicode[STIX]{x1D6EC})$ is Zariski-constructible, then the Verdier dual
$\mathscr{F}\in D(S,\unicode[STIX]{x1D6EC})$ is Zariski-constructible, then the Verdier dual  $\mathbf{D}_{S}\mathscr{F}$ is Zariski-constructible as well. In particular, the dualizing complex
$\mathbf{D}_{S}\mathscr{F}$ is Zariski-constructible as well. In particular, the dualizing complex  $\unicode[STIX]{x1D714}_{S}$ is Zariski-constructible. Moreover, if
$\unicode[STIX]{x1D714}_{S}$ is Zariski-constructible. Moreover, if  $\mathscr{F}\in D(S,\unicode[STIX]{x1D6EC})$ is Zariski-constructible, then it is reflexive: the natural biduality map
$\mathscr{F}\in D(S,\unicode[STIX]{x1D6EC})$ is Zariski-constructible, then it is reflexive: the natural biduality map  $\mathscr{F}\rightarrow \mathbf{D}_{S}\mathbf{D}_{S}\mathscr{F}$ is an isomorphism;
$\mathscr{F}\rightarrow \mathbf{D}_{S}\mathbf{D}_{S}\mathscr{F}$ is an isomorphism;(iv) if
 $\mathscr{F}\in D^{-}(S,\unicode[STIX]{x1D6EC})$ and
$\mathscr{F}\in D^{-}(S,\unicode[STIX]{x1D6EC})$ and  $\mathscr{G}\in D^{+}(S,\unicode[STIX]{x1D6EC})$ are Zariski-constructible, then so is
$\mathscr{G}\in D^{+}(S,\unicode[STIX]{x1D6EC})$ are Zariski-constructible, then so is  $R\mathscr{H}\text{om}_{S}(\mathscr{F},\mathscr{G})$;
$R\mathscr{H}\text{om}_{S}(\mathscr{F},\mathscr{G})$;(v) if
 $f:T\rightarrow S$ is any map of affinoid rigid spaces and
$f:T\rightarrow S$ is any map of affinoid rigid spaces and  $\mathscr{F}\in D(S,\unicode[STIX]{x1D6EC})$ is Zariski-constructible, then so is
$\mathscr{F}\in D(S,\unicode[STIX]{x1D6EC})$ is Zariski-constructible, then so is  $Rf^{!}\mathscr{F}$.
$Rf^{!}\mathscr{F}$.
The irritating restriction to affinoid spaces here would disappear if one could settle the following fundamental problem.
Conjecture 1.12. Zariski-constructibility is an étale-local property. More precisely, if ![]() $f:Y\rightarrow X$ is any surjective étale map of rigid spaces and
$f:Y\rightarrow X$ is any surjective étale map of rigid spaces and ![]() $\mathscr{F}\in \text{Sh}(X,\unicode[STIX]{x1D6EC})$ is any étale sheaf such that
$\mathscr{F}\in \text{Sh}(X,\unicode[STIX]{x1D6EC})$ is any étale sheaf such that ![]() $f^{\ast }\mathscr{F}$ is Zariski-constructible, then
$f^{\ast }\mathscr{F}$ is Zariski-constructible, then ![]() $\mathscr{F}$ is Zariski-constructible.
$\mathscr{F}$ is Zariski-constructible.
We note that Huber has also defined a notion of Zariski-constructible sheaves on rigid spaces: a sheaf is Zariski-constructible in his sense if it is étale-locally Zariski-constructible in our sense. In particular, Conjecture 1.12 implies that Huber’s definition coincides with ours. Conjecture 1.12 also implies (upon combining it with Theorem 1.7) that sheaves which are Zariski-constructible in our sense coincide with the constructible sheaves defined by Berkovich in [Reference BerkovichBer15, § 1], at least in characteristic zero.
Conjecture 1.12 can be deduced from the following conjecture, which looks very plausible.
Conjecture 1.13. Let ![]() $\mathscr{F}\in \text{Sh}(X,\unicode[STIX]{x1D6EC})$ be a Zariski-constructible sheaf on an affinoid rigid space
$\mathscr{F}\in \text{Sh}(X,\unicode[STIX]{x1D6EC})$ be a Zariski-constructible sheaf on an affinoid rigid space ![]() $X$, and let
$X$, and let ![]() ${\mathcal{U}}_{X}(\mathscr{F})$ denote the largest open subset
${\mathcal{U}}_{X}(\mathscr{F})$ denote the largest open subset ![]() $U\subset X$ such that
$U\subset X$ such that ![]() $\mathscr{F}|U$ is locally constant. Then
$\mathscr{F}|U$ is locally constant. Then ![]() ${\mathcal{U}}_{X}(\mathscr{F})\subset X$ is Zariski-open.
${\mathcal{U}}_{X}(\mathscr{F})\subset X$ is Zariski-open.
We end this introduction with one more tantalizing problem, which seems to really require a new idea.
Conjecture 1.14. Let ![]() $f:X\rightarrow Y$ be a proper morphism of rigid spaces. If
$f:X\rightarrow Y$ be a proper morphism of rigid spaces. If ![]() $F\in D^{+}(X,\unicode[STIX]{x1D6EC})$ is Zariski-constructible, then so is
$F\in D^{+}(X,\unicode[STIX]{x1D6EC})$ is Zariski-constructible, then so is ![]() $Rf_{\ast }F$.
$Rf_{\ast }F$.
Remarks on terminology and conventions
Our convention is that a ‘nonarchimedean field’ is a topological field whose topology is defined by a nontrivial nonarchimedean valuation of rank one. If ![]() $K$ is any nonarchimedean field, we regard rigid analytic spaces over
$K$ is any nonarchimedean field, we regard rigid analytic spaces over ![]() $K$ as a full subcategory of the category of adic spaces locally of topologically finite type over
$K$ as a full subcategory of the category of adic spaces locally of topologically finite type over ![]() $\text{Spa}(K,K^{\circ })$. If
$\text{Spa}(K,K^{\circ })$. If ![]() $A$ is any topological ring, we write
$A$ is any topological ring, we write ![]() $A^{\circ }$ for the subset of power-bounded elements; if
$A^{\circ }$ for the subset of power-bounded elements; if ![]() $A$ is a Huber ring, we write
$A$ is a Huber ring, we write ![]() $\text{Spa }A$ for
$\text{Spa }A$ for ![]() $\text{Spa}(A,A^{\circ })$. Unless explicitly stated otherwise, all sheaves are étale sheaves, all derived categories are derived categories of étale sheaves, all cohomology groups are étale cohomology groups, etc.
$\text{Spa}(A,A^{\circ })$. Unless explicitly stated otherwise, all sheaves are étale sheaves, all derived categories are derived categories of étale sheaves, all cohomology groups are étale cohomology groups, etc.
We use the terms ‘Zariski-closed subset’ and ‘closed analytic subset’ interchangeably, and we always regard Zariski-closed subsets of rigid spaces as rigid spaces via the induced reduced structure. Finally, we remind the reader that in rigid geometry the phrases ‘dense Zariski-open subset’ and ‘Zariski-dense open subset’ have very different meanings.
2 Preliminaries
2.1 Zariski-constructible sheaves on rigid spaces
In this section we discuss some basics on Zariski-constructible étale sheaves on rigid spaces. For simplicity we fix a nonarchimedean field ![]() $K$ and a Noetherian coefficient ring
$K$ and a Noetherian coefficient ring ![]() $\unicode[STIX]{x1D6EC}$; until further notice, roman letters
$\unicode[STIX]{x1D6EC}$; until further notice, roman letters ![]() $X,Y,\ldots$ denote rigid spaces over
$X,Y,\ldots$ denote rigid spaces over ![]() $K$, and ‘Zariski-constructible’ means a Zariski-constructible sheaf of
$K$, and ‘Zariski-constructible’ means a Zariski-constructible sheaf of ![]() $\unicode[STIX]{x1D6EC}$-modules, as defined in the introduction, on the étale site of some rigid space
$\unicode[STIX]{x1D6EC}$-modules, as defined in the introduction, on the étale site of some rigid space ![]() $X$ over
$X$ over ![]() $K$.
$K$.
Proposition 2.1. Let ![]() $\mathscr{F}$ be a Zariski-constructible sheaf on a rigid space
$\mathscr{F}$ be a Zariski-constructible sheaf on a rigid space ![]() $X$.
$X$.
(i) If
 $f:Y\rightarrow X$ is any morphism of rigid spaces, then
$f:Y\rightarrow X$ is any morphism of rigid spaces, then  $f^{\ast }\mathscr{F}$ is Zariski-constructible.
$f^{\ast }\mathscr{F}$ is Zariski-constructible.(ii) If
 $i:X\rightarrow W$ is a closed immersion, then
$i:X\rightarrow W$ is a closed immersion, then  $i_{\ast }\mathscr{F}$ is Zariski-constructible.
$i_{\ast }\mathscr{F}$ is Zariski-constructible.(iii) If
 $j:X\rightarrow V$ is a Zariski-open immersion and
$j:X\rightarrow V$ is a Zariski-open immersion and  $\mathscr{F}$ is locally constant, then
$\mathscr{F}$ is locally constant, then  $j_{!}\mathscr{F}$ is Zariski-constructible.
$j_{!}\mathscr{F}$ is Zariski-constructible.
Proof. This is trivial. ◻
We will often verify Zariski-constructibility via the following dévissage, which is a trivial consequence of the previous proposition.
Proposition 2.2. Let ![]() $X$ be any rigid space and let
$X$ be any rigid space and let ![]() $\mathscr{F}$ be a sheaf of
$\mathscr{F}$ be a sheaf of ![]() $\unicode[STIX]{x1D6EC}$-modules on
$\unicode[STIX]{x1D6EC}$-modules on ![]() $X_{\acute{\text{e}}\text{t}}$. The following are equivalent.
$X_{\acute{\text{e}}\text{t}}$. The following are equivalent.
(i)
 $\mathscr{F}$ is Zariski-constructible.
$\mathscr{F}$ is Zariski-constructible.(ii) There is some dense Zariski-open subset
 $j:U\rightarrow X$ with closed complement
$j:U\rightarrow X$ with closed complement  $i:Z\rightarrow X$ such that
$i:Z\rightarrow X$ such that  $i^{\ast }\mathscr{F}$ is Zariski-constructible and
$i^{\ast }\mathscr{F}$ is Zariski-constructible and  $j^{\ast }\mathscr{F}$ is locally constant of finite type.
$j^{\ast }\mathscr{F}$ is locally constant of finite type.
Note that one cannot weaken the hypotheses in (ii) here to the condition that ![]() $j^{\ast }\mathscr{F}$ is Zariski-constructible; this is related to the fact that the Zariski topology in the rigid analytic world is not transitive.
$j^{\ast }\mathscr{F}$ is Zariski-constructible; this is related to the fact that the Zariski topology in the rigid analytic world is not transitive.
Proposition 2.3. If ![]() $f:X^{\prime }\rightarrow X$ is a finite morphism and
$f:X^{\prime }\rightarrow X$ is a finite morphism and ![]() $\mathscr{F}$ is a Zariski-constructible sheaf on
$\mathscr{F}$ is a Zariski-constructible sheaf on ![]() $X^{\prime }$, then
$X^{\prime }$, then ![]() $f_{\ast }\mathscr{F}$ is Zariski-constructible.
$f_{\ast }\mathscr{F}$ is Zariski-constructible.
We note in passing that if ![]() $f:X\rightarrow Y$ is a finite morphism, or more generally any quasicompact separated morphism with finite fibers, then
$f:X\rightarrow Y$ is a finite morphism, or more generally any quasicompact separated morphism with finite fibers, then ![]() $f_{\ast }:\text{Sh}(X_{\acute{\text{e}}\text{t}},\unicode[STIX]{x1D6EC})\rightarrow \text{Sh}(Y_{\acute{\text{e}}\text{t}},\unicode[STIX]{x1D6EC})$ is an exact functor; cf. [Reference HuberHub96, Proposition 2.6.4 and Lemma 1.5.2].
$f_{\ast }:\text{Sh}(X_{\acute{\text{e}}\text{t}},\unicode[STIX]{x1D6EC})\rightarrow \text{Sh}(Y_{\acute{\text{e}}\text{t}},\unicode[STIX]{x1D6EC})$ is an exact functor; cf. [Reference HuberHub96, Proposition 2.6.4 and Lemma 1.5.2].
Proof. We treat the case where ![]() $X^{\prime }=\text{Spa}\,A^{\prime }$ and
$X^{\prime }=\text{Spa}\,A^{\prime }$ and ![]() $X=\text{Spa}\,A$ are affinoid, which is all we will need later. We can assume that they are reduced and that
$X=\text{Spa}\,A$ are affinoid, which is all we will need later. We can assume that they are reduced and that ![]() $f$ is surjective. If
$f$ is surjective. If ![]() $i:Z\rightarrow X$ is Zariski-closed and nowhere dense, then
$i:Z\rightarrow X$ is Zariski-closed and nowhere dense, then ![]() $\text{dim}\,Z<\text{dim}\,X$; setting
$\text{dim}\,Z<\text{dim}\,X$; setting ![]() $Z^{\prime }=Z\times _{X}X^{\prime }$ and writing
$Z^{\prime }=Z\times _{X}X^{\prime }$ and writing ![]() $f^{\prime }:Z^{\prime }\rightarrow Z$ and
$f^{\prime }:Z^{\prime }\rightarrow Z$ and ![]() $i^{\prime }:Z^{\prime }\rightarrow X^{\prime }$ for the evident morphisms, we can assume that
$i^{\prime }:Z^{\prime }\rightarrow X^{\prime }$ for the evident morphisms, we can assume that ![]() $i^{\ast }f_{\ast }\mathscr{F}\cong f_{\ast }^{\prime }{i^{\prime }}^{\ast }\mathscr{F}$ is Zariski-constructible by induction on
$i^{\ast }f_{\ast }\mathscr{F}\cong f_{\ast }^{\prime }{i^{\prime }}^{\ast }\mathscr{F}$ is Zariski-constructible by induction on ![]() $\text{dim}\,X$. By dévissage, it now suffices to find a dense Zariski-open subset
$\text{dim}\,X$. By dévissage, it now suffices to find a dense Zariski-open subset ![]() $j:U\rightarrow X$ such that
$j:U\rightarrow X$ such that ![]() $j^{\ast }f_{\ast }\mathscr{F}$ is locally constant. To do this, choose a dense Zariski-open subset
$j^{\ast }f_{\ast }\mathscr{F}$ is locally constant. To do this, choose a dense Zariski-open subset ![]() $V\subset X^{\prime }$ such that
$V\subset X^{\prime }$ such that ![]() $\mathscr{F}|_{V}$ is locally constant. Then
$\mathscr{F}|_{V}$ is locally constant. Then ![]() $W=X\smallsetminus f(X^{\prime }\smallsetminus V)$ is a dense Zariski-open subset of
$W=X\smallsetminus f(X^{\prime }\smallsetminus V)$ is a dense Zariski-open subset of ![]() $X$, and
$X$, and ![]() $\mathscr{F}$ is locally constant after pullback along the open immersion
$\mathscr{F}$ is locally constant after pullback along the open immersion ![]() $W^{\prime }=W\times _{X}X^{\prime }\rightarrow X^{\prime }$. If
$W^{\prime }=W\times _{X}X^{\prime }\rightarrow X^{\prime }$. If ![]() $\text{char}(K)=0$, we now conclude by taking
$\text{char}(K)=0$, we now conclude by taking ![]() $U$ to be any dense Zariski-open subset contained in
$U$ to be any dense Zariski-open subset contained in ![]() $W$ such that
$W$ such that ![]() $U^{\prime }=U\times _{X}X^{\prime }\rightarrow U$ is finite étale; if
$U^{\prime }=U\times _{X}X^{\prime }\rightarrow U$ is finite étale; if ![]() $\text{char}(K)=p$, we instead choose
$\text{char}(K)=p$, we instead choose ![]() $U$ so that
$U$ so that ![]() $U^{\prime }\rightarrow U$ factors as the composition of a universal homeomorphism followed by a finite étale map. (For the existence of such a
$U^{\prime }\rightarrow U$ factors as the composition of a universal homeomorphism followed by a finite étale map. (For the existence of such a ![]() $U$, look at the map of schemes
$U$, look at the map of schemes ![]() $\text{Spec}\,A^{\prime }\rightarrow \text{Spec}\,A$; this morphism has the desired structure over all generic points of the target, and these structures then spread out over a dense Zariski-open subset of
$\text{Spec}\,A^{\prime }\rightarrow \text{Spec}\,A$; this morphism has the desired structure over all generic points of the target, and these structures then spread out over a dense Zariski-open subset of ![]() $\text{Spec}\,A$. One then concludes by analytifying.)◻
$\text{Spec}\,A$. One then concludes by analytifying.)◻
Proposition 2.4. Let ![]() $X$ be a rigid space.
$X$ be a rigid space.
(i) Let
 $0\rightarrow \mathscr{F}\rightarrow \mathscr{G}\rightarrow \mathscr{H}\rightarrow 0$ be a short exact sequence of étale sheaves of
$0\rightarrow \mathscr{F}\rightarrow \mathscr{G}\rightarrow \mathscr{H}\rightarrow 0$ be a short exact sequence of étale sheaves of  $\unicode[STIX]{x1D6EC}$-modules on
$\unicode[STIX]{x1D6EC}$-modules on  $X$. If two of the three sheaves
$X$. If two of the three sheaves  $\{\mathscr{F},\mathscr{G},\mathscr{H}\}$ are Zariski-constructible, then so is the third.
$\{\mathscr{F},\mathscr{G},\mathscr{H}\}$ are Zariski-constructible, then so is the third.(ii) Let
 $f:\mathscr{F}\rightarrow \mathscr{G}$ be any map of Zariski-constructible sheaves. Then
$f:\mathscr{F}\rightarrow \mathscr{G}$ be any map of Zariski-constructible sheaves. Then  $\ker f$,
$\ker f$,  $\text{im}f$, and
$\text{im}f$, and  $\text{coker}\,f$ are Zariski-constructible.
$\text{coker}\,f$ are Zariski-constructible.(iii) Let
 $F\rightarrow G\rightarrow H\overset{[1]}{\rightarrow }$ be a distinguished triangle in
$F\rightarrow G\rightarrow H\overset{[1]}{\rightarrow }$ be a distinguished triangle in  $D(X,\unicode[STIX]{x1D6EC})$. If two of the three objects
$D(X,\unicode[STIX]{x1D6EC})$. If two of the three objects  $F,G,H$ are Zariski-constructible, then so is the third.
$F,G,H$ are Zariski-constructible, then so is the third.
We often refer to parts (i) and (iii) as the ‘two-out-of-three property’.
Proof. For (i), by induction on ![]() $\text{dim}\,X$ and dévissage, it suffices to find some dense Zariski-open subset
$\text{dim}\,X$ and dévissage, it suffices to find some dense Zariski-open subset ![]() $j:U\rightarrow X$ such that all three sheaves are locally constant after restriction to
$j:U\rightarrow X$ such that all three sheaves are locally constant after restriction to ![]() $U$. By assumption, we can choose
$U$. By assumption, we can choose ![]() $U$ such that two of the three sheaves have this property. Looking at the exact sequence
$U$ such that two of the three sheaves have this property. Looking at the exact sequence ![]() $0\rightarrow \mathscr{F}|_{U}\rightarrow \mathscr{G}|_{U}\rightarrow \mathscr{H}|_{U}\rightarrow 0$, [Reference HuberHub96, Lemma 2.7.3] implies that all three sheaves are constructible (in the sense of [Reference HuberHub96]). By [Reference HuberHub96, Lemma 2.7.11], it now suffices to check that all three sheaves are overconvergent. But if
$0\rightarrow \mathscr{F}|_{U}\rightarrow \mathscr{G}|_{U}\rightarrow \mathscr{H}|_{U}\rightarrow 0$, [Reference HuberHub96, Lemma 2.7.3] implies that all three sheaves are constructible (in the sense of [Reference HuberHub96]). By [Reference HuberHub96, Lemma 2.7.11], it now suffices to check that all three sheaves are overconvergent. But if ![]() $\overline{x}{\rightsquigarrow}\overline{y}$ is any specialization of geometric points, this follows immediately by applying the snake lemma to the diagram
$\overline{x}{\rightsquigarrow}\overline{y}$ is any specialization of geometric points, this follows immediately by applying the snake lemma to the diagram

since by assumption two of the three vertical arrows are isomorphisms.
For (ii), we first show that ![]() $\text{coker}\,f$ is Zariski-constructible. As in the argument for (i), it suffices to find some dense Zariski-open subset
$\text{coker}\,f$ is Zariski-constructible. As in the argument for (i), it suffices to find some dense Zariski-open subset ![]() $j:U\rightarrow X$ such that
$j:U\rightarrow X$ such that ![]() $\text{coker}\,f|_{U}$ is locally constant. Choose
$\text{coker}\,f|_{U}$ is locally constant. Choose ![]() $U$ such that
$U$ such that ![]() $\mathscr{F}|_{U}$ and
$\mathscr{F}|_{U}$ and ![]() $\mathscr{G}|_{U}$ are locally constant, so
$\mathscr{G}|_{U}$ are locally constant, so ![]() $\text{coker}\,f|_{U}$ is constructible. Then for
$\text{coker}\,f|_{U}$ is constructible. Then for ![]() $\overline{x}{\rightsquigarrow}\overline{y}$ any specialization of geometric points of
$\overline{x}{\rightsquigarrow}\overline{y}$ any specialization of geometric points of ![]() $U$, the first two vertical maps in the diagram
$U$, the first two vertical maps in the diagram

are isomorphisms by assumption, so the map ![]() $(\text{coker}\,f)_{\overline{y}}\rightarrow (\text{coker}\,f)_{\overline{x}}$ is an isomorphism by the five lemma. Thus,
$(\text{coker}\,f)_{\overline{y}}\rightarrow (\text{coker}\,f)_{\overline{x}}$ is an isomorphism by the five lemma. Thus, ![]() $\text{coker}\,f|_{U}$ is overconvergent and constructible and hence locally constant by [Reference HuberHub96, Lemma 2.7.11].
$\text{coker}\,f|_{U}$ is overconvergent and constructible and hence locally constant by [Reference HuberHub96, Lemma 2.7.11].
The remaining parts of (ii) now follow from the exact sequences ![]() $0\rightarrow \text{im}f\rightarrow \mathscr{G}\rightarrow \text{coker}\,f\rightarrow 0$ and
$0\rightarrow \text{im}f\rightarrow \mathscr{G}\rightarrow \text{coker}\,f\rightarrow 0$ and ![]() $0\rightarrow \ker f\rightarrow \mathscr{F}\rightarrow \text{im}f\rightarrow 0$ by successive applications of (i).
$0\rightarrow \ker f\rightarrow \mathscr{F}\rightarrow \text{im}f\rightarrow 0$ by successive applications of (i).
For (iii), we can assume (possibly after a shift) that ![]() $F$ and
$F$ and ![]() $H$ are Zariski-constructible. The result then follows from parts (i) and (ii), by looking at the exact sequences
$H$ are Zariski-constructible. The result then follows from parts (i) and (ii), by looking at the exact sequences
◻
Corollary 2.5. For any rigid space ![]() $X$,
$X$, ![]() $\text{Sh}_{zc}(X,\unicode[STIX]{x1D6EC})$ is a thick abelian subcategory of
$\text{Sh}_{zc}(X,\unicode[STIX]{x1D6EC})$ is a thick abelian subcategory of ![]() $\text{Sh}(X,\unicode[STIX]{x1D6EC})$.
$\text{Sh}(X,\unicode[STIX]{x1D6EC})$.
2.2 Extending covers across closed subsets
In this section we prove a slight strengthening of Theorem 1.6. We will freely use basic facts about irreducible components of rigid spaces, as developed in [Reference ConradCon99], without any comment. The following result of Bartenwerfer [Reference BartenwerferBar76, § 3] is also crucial for our purposes.
Theorem 2.6 (Bartenwerfer).
Let ![]() $X$ be a normal rigid space, and let
$X$ be a normal rigid space, and let ![]() $Z\subset X$ be a nowhere-dense closed analytic subset, with
$Z\subset X$ be a nowhere-dense closed analytic subset, with ![]() $j:X\smallsetminus Z\rightarrow X$ the inclusion of the open complement. Then
$j:X\smallsetminus Z\rightarrow X$ the inclusion of the open complement. Then ![]() ${\mathcal{O}}_{X}^{+}\overset{{\sim}}{\rightarrow }j_{\ast }{\mathcal{O}}_{X\smallsetminus Z}^{+}$ and
${\mathcal{O}}_{X}^{+}\overset{{\sim}}{\rightarrow }j_{\ast }{\mathcal{O}}_{X\smallsetminus Z}^{+}$ and ![]() ${\mathcal{O}}_{X}\overset{{\sim}}{\rightarrow }(j_{\ast }{\mathcal{O}}_{X\smallsetminus Z}^{+})[\frac{1}{\unicode[STIX]{x1D71B}}]$. In particular, if
${\mathcal{O}}_{X}\overset{{\sim}}{\rightarrow }(j_{\ast }{\mathcal{O}}_{X\smallsetminus Z}^{+})[\frac{1}{\unicode[STIX]{x1D71B}}]$. In particular, if ![]() $X$ is affinoid and
$X$ is affinoid and ![]() $f\in {\mathcal{O}}_{X}(X\smallsetminus Z)$ is bounded, then
$f\in {\mathcal{O}}_{X}(X\smallsetminus Z)$ is bounded, then ![]() $f$ extends uniquely to an element of
$f$ extends uniquely to an element of ![]() ${\mathcal{O}}_{X}(X)$, so
${\mathcal{O}}_{X}(X)$, so ![]() ${\mathcal{O}}_{X}(X)\cong {\mathcal{O}}_{X}^{+}(X\smallsetminus Z)[\frac{1}{\unicode[STIX]{x1D71B}}]$.
${\mathcal{O}}_{X}(X)\cong {\mathcal{O}}_{X}^{+}(X\smallsetminus Z)[\frac{1}{\unicode[STIX]{x1D71B}}]$.
Corollary 2.7. If ![]() $X$ is a connected normal rigid space and
$X$ is a connected normal rigid space and ![]() $Z\subset X$ is a nowhere-dense closed analytic subset, then
$Z\subset X$ is a nowhere-dense closed analytic subset, then ![]() $X\smallsetminus Z$ is connected.
$X\smallsetminus Z$ is connected.
Proof. Any idempotent in ![]() ${\mathcal{O}}_{X}(X\smallsetminus Z)$ is power-bounded, so this is immediate from the previous theorem.◻
${\mathcal{O}}_{X}(X\smallsetminus Z)$ is power-bounded, so this is immediate from the previous theorem.◻
Proposition 2.8. Let ![]() $X$ be a normal rigid space and let
$X$ be a normal rigid space and let ![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X$ be a cover of
$\unicode[STIX]{x1D70B}:Y\rightarrow X$ be a cover of ![]() $X$. Then each irreducible component of
$X$. Then each irreducible component of ![]() $Y$ maps surjectively onto some irreducible component of
$Y$ maps surjectively onto some irreducible component of ![]() $X$. Moreover, if
$X$. Moreover, if ![]() $V\subset X$ is any closed nowhere-dense analytic subset, then
$V\subset X$ is any closed nowhere-dense analytic subset, then ![]() $\unicode[STIX]{x1D70B}^{-1}(V)$ is nowhere-dense.
$\unicode[STIX]{x1D70B}^{-1}(V)$ is nowhere-dense.
Proof. We immediately reduce to the case where ![]() $X$ is connected. Let
$X$ is connected. Let ![]() $Z\subset X$ be as in the definition of a cover, and let
$Z\subset X$ be as in the definition of a cover, and let ![]() $Y_{i}$ be any connected component of
$Y_{i}$ be any connected component of ![]() $Y$, so then
$Y$, so then ![]() $Y_{i}\cap \unicode[STIX]{x1D70B}^{-1}(Z)$ is closed and nowhere-dense in
$Y_{i}\cap \unicode[STIX]{x1D70B}^{-1}(Z)$ is closed and nowhere-dense in ![]() $Y_{i}$ and
$Y_{i}$ and ![]() $Y_{i}\smallsetminus Y_{i}\cap \unicode[STIX]{x1D70B}^{-1}(Z)\rightarrow X\smallsetminus Z$ is finite étale. Then
$Y_{i}\smallsetminus Y_{i}\cap \unicode[STIX]{x1D70B}^{-1}(Z)\rightarrow X\smallsetminus Z$ is finite étale. Then
is a nonempty open and closed subset of ![]() $X\smallsetminus Z$, so it coincides with
$X\smallsetminus Z$, so it coincides with ![]() $X\smallsetminus Z$ by the previous corollary. In particular,
$X\smallsetminus Z$ by the previous corollary. In particular, ![]() $\unicode[STIX]{x1D70B}(Y_{i})$ contains a dense subset of
$\unicode[STIX]{x1D70B}(Y_{i})$ contains a dense subset of ![]() $X$. On the other hand,
$X$. On the other hand, ![]() $\unicode[STIX]{x1D70B}(Y_{i})$ is a closed analytic subset of
$\unicode[STIX]{x1D70B}(Y_{i})$ is a closed analytic subset of ![]() $X$ since
$X$ since ![]() $\unicode[STIX]{x1D70B}$ is finite. Therefore,
$\unicode[STIX]{x1D70B}$ is finite. Therefore, ![]() $\unicode[STIX]{x1D70B}(Y_{i})=X$.
$\unicode[STIX]{x1D70B}(Y_{i})=X$.
For the second claim, note that if ![]() $V$ is a closed analytic subset of a connected normal space
$V$ is a closed analytic subset of a connected normal space ![]() $X$, then
$X$, then ![]() $V\subsetneq X$ if and only if
$V\subsetneq X$ if and only if ![]() $V$ is nowhere-dense if and only if
$V$ is nowhere-dense if and only if ![]() $\text{dim}\,V<\text{dim}\,X$. Since
$\text{dim}\,V<\text{dim}\,X$. Since
for any irreducible component ![]() $Y_{i}$ of
$Y_{i}$ of ![]() $Y$, this gives the claim.◻
$Y$, this gives the claim.◻
Proposition 2.9. Let ![]() $X$ be a normal rigid space and let
$X$ be a normal rigid space and let ![]() $Z\subset X$ be any closed nowhere-dense analytic subset. Then the restriction functor
$Z\subset X$ be any closed nowhere-dense analytic subset. Then the restriction functor
is fully faithful.
Proof. If ![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X$ is any cover and
$\unicode[STIX]{x1D70B}:Y\rightarrow X$ is any cover and ![]() $U\subset X$ is any open affinoid, then
$U\subset X$ is any open affinoid, then ![]() $\unicode[STIX]{x1D70B}^{-1}(U)$ is affinoid as well, and
$\unicode[STIX]{x1D70B}^{-1}(U)$ is affinoid as well, and ![]() $\unicode[STIX]{x1D70B}^{-1}(Z\cap U)$ is nowhere-dense in
$\unicode[STIX]{x1D70B}^{-1}(Z\cap U)$ is nowhere-dense in ![]() $U$ by the previous proposition. But then
$U$ by the previous proposition. But then ![]() ${\mathcal{O}}_{Y}(\unicode[STIX]{x1D70B}^{-1}(U))\cong {\mathcal{O}}_{Y}^{+}(\unicode[STIX]{x1D70B}^{-1}(U\smallsetminus U\cap Z))[\frac{1}{\unicode[STIX]{x1D71B}}]$ by Theorem 2.6, so
${\mathcal{O}}_{Y}(\unicode[STIX]{x1D70B}^{-1}(U))\cong {\mathcal{O}}_{Y}^{+}(\unicode[STIX]{x1D70B}^{-1}(U\smallsetminus U\cap Z))[\frac{1}{\unicode[STIX]{x1D71B}}]$ by Theorem 2.6, so ![]() ${\mathcal{O}}_{Y}(U)$ only depends on
${\mathcal{O}}_{Y}(U)$ only depends on ![]() $Y\times _{X}(X\smallsetminus Z)$. This immediately gives the result.◻
$Y\times _{X}(X\smallsetminus Z)$. This immediately gives the result.◻
It remains to prove the following result.
Theorem 2.10. Let ![]() $X$ be a normal rigid space over a characteristic-zero complete nonarchimedean field
$X$ be a normal rigid space over a characteristic-zero complete nonarchimedean field ![]() $K$ and let
$K$ and let ![]() $Z\subset X$ be any closed nowhere-dense analytic subset. Then the restriction functor
$Z\subset X$ be any closed nowhere-dense analytic subset. Then the restriction functor
 $$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}c@{}}\text{covers of }X\\ \acute{\text{e}}\text{tale over }X\smallsetminus Z\end{array}\right\} & \rightarrow & \displaystyle \left\{\begin{array}{@{}c@{}}\text{finite }\acute{e} \text{tale covers}\\ \text{of }X\smallsetminus Z\end{array}\right\}\nonumber\\ \displaystyle Y & \mapsto & \displaystyle Y\times _{X}(X\smallsetminus Z)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}c@{}}\text{covers of }X\\ \acute{\text{e}}\text{tale over }X\smallsetminus Z\end{array}\right\} & \rightarrow & \displaystyle \left\{\begin{array}{@{}c@{}}\text{finite }\acute{e} \text{tale covers}\\ \text{of }X\smallsetminus Z\end{array}\right\}\nonumber\\ \displaystyle Y & \mapsto & \displaystyle Y\times _{X}(X\smallsetminus Z)\nonumber\end{eqnarray}$$is essentially surjective.
In other words, given a (surjective) finite étale cover ![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X\smallsetminus Z$, we need to find a cover
$\unicode[STIX]{x1D70B}:Y\rightarrow X\smallsetminus Z$, we need to find a cover ![]() $\tilde{\unicode[STIX]{x1D70B}}:{\tilde{Y}}\rightarrow X$ and an open immersion
$\tilde{\unicode[STIX]{x1D70B}}:{\tilde{Y}}\rightarrow X$ and an open immersion ![]() $Y\rightarrow {\tilde{Y}}$ such that the diagram
$Y\rightarrow {\tilde{Y}}$ such that the diagram

is cartesian. We refer to this as the problem of extending ![]() $Y$ to a cover of
$Y$ to a cover of ![]() $X$. Note that by the full faithfulness proved above, we are always free to work locally on
$X$. Note that by the full faithfulness proved above, we are always free to work locally on ![]() $X$ when extending a given cover of
$X$ when extending a given cover of ![]() $X\smallsetminus Z$.
$X\smallsetminus Z$.
Until further notice, fix ![]() $K$ of characteristic zero. The key special case is the following result.
$K$ of characteristic zero. The key special case is the following result.
Theorem 2.11 (Lütkebohmert).
If ![]() $X$ is a smooth rigid space and
$X$ is a smooth rigid space and ![]() $D\subset X$ is a strict normal crossings divisor, then any finite étale cover of
$D\subset X$ is a strict normal crossings divisor, then any finite étale cover of ![]() $X\smallsetminus D$ extends to a cover of
$X\smallsetminus D$ extends to a cover of ![]() $X$.
$X$.
This is more or less an immediate consequence of the arguments in § 3 in Lütkebohmert’s paper [Reference LütkebohmertLüt93] (and is implicit in the proof of Theorem 3.1 thereof). For the convenience of the reader, we explain the deduction in detail. Let ![]() $\mathbf{B}^{r}=~\text{Spa }K\langle X_{1},\ldots ,X_{r}\rangle$ denote the
$\mathbf{B}^{r}=~\text{Spa }K\langle X_{1},\ldots ,X_{r}\rangle$ denote the ![]() $r$-dimensional closed affinoid ball.
$r$-dimensional closed affinoid ball.
Lemma 2.12 [Reference LütkebohmertLüt93, Lemma 3.3].
Let ![]() $S$ be a smooth
$S$ be a smooth ![]() $K$-affinoid space and let
$K$-affinoid space and let ![]() $r\geqslant 1$ be any integer. If
$r\geqslant 1$ be any integer. If ![]() $Y_{0}$ is a cover of
$Y_{0}$ is a cover of ![]() $S\times (\mathbf{B}^{r}\smallsetminus V(X_{1},\ldots ,X_{r}))$ which is étale over
$S\times (\mathbf{B}^{r}\smallsetminus V(X_{1},\ldots ,X_{r}))$ which is étale over ![]() $S\times (\mathbf{B}^{r}\smallsetminus V(X_{1}\cdots X_{r}))$, then
$S\times (\mathbf{B}^{r}\smallsetminus V(X_{1}\cdots X_{r}))$, then ![]() $Y_{0}$ extends to a cover
$Y_{0}$ extends to a cover ![]() ${\tilde{Y}}$ of
${\tilde{Y}}$ of ![]() $S\times \mathbf{B}^{r}$.
$S\times \mathbf{B}^{r}$.
We also need a result of Kiehl on the existence of ‘tubular neighbourhoods’ of strict normal crossings divisors in smooth rigid spaces.
Lemma 2.13. If ![]() $D\subset X$ is a strict normal crossings divisor in a smooth rigid space, then for any (adic) point
$D\subset X$ is a strict normal crossings divisor in a smooth rigid space, then for any (adic) point ![]() $x$ in
$x$ in ![]() $X$ contained in exactly
$X$ contained in exactly ![]() $r$ irreducible components
$r$ irreducible components ![]() $D_{1},\ldots ,D_{r}$ of
$D_{1},\ldots ,D_{r}$ of ![]() $D$, we can find some small open affinoid
$D$, we can find some small open affinoid ![]() $U\subset X$ containing
$U\subset X$ containing ![]() $x$ together with a smooth affinoid
$x$ together with a smooth affinoid ![]() $S$ and an isomorphism
$S$ and an isomorphism ![]() $U\simeq S\times \mathbf{B}^{r}$, under which the individual components
$U\simeq S\times \mathbf{B}^{r}$, under which the individual components ![]() $D_{i}\cap U$ containing
$D_{i}\cap U$ containing ![]() $x$ identify with the zero loci of the coordinate functions
$x$ identify with the zero loci of the coordinate functions ![]() $X_{i}\in {\mathcal{O}}(\mathbf{B}^{r})$.
$X_{i}\in {\mathcal{O}}(\mathbf{B}^{r})$.
Proof. This follows from a careful reading of [Reference KiehlKie67b, Theorem 1.18] (cf. also [Reference MitsuiMit09, Theorem 2.11]). ◻
Granted these results, we deduce Theorem 2.11 as follows. By full faithfulness we can assume that ![]() $X$ is quasicompact, or even affinoid. We now argue by induction on the maximal number
$X$ is quasicompact, or even affinoid. We now argue by induction on the maximal number ![]() $\unicode[STIX]{x1D704}(D)$ of irreducible components of
$\unicode[STIX]{x1D704}(D)$ of irreducible components of ![]() $D$ passing through any individual point of
$D$ passing through any individual point of ![]() $X$. If
$X$. If ![]() $\unicode[STIX]{x1D704}(D)=1$, then
$\unicode[STIX]{x1D704}(D)=1$, then ![]() $D$ is smooth, so arguing locally around any point in
$D$ is smooth, so arguing locally around any point in ![]() $D$, Lemma 2.13 puts us exactly in the situation covered by the case
$D$, Lemma 2.13 puts us exactly in the situation covered by the case ![]() $r=1$ of Lemma 2.12. If
$r=1$ of Lemma 2.12. If ![]() $\unicode[STIX]{x1D704}(D)=n,$ then locally on
$\unicode[STIX]{x1D704}(D)=n,$ then locally on ![]() $X$ we can assume that
$X$ we can assume that ![]() $D$ has (at most)
$D$ has (at most) ![]() $n$ smooth components
$n$ smooth components ![]() $D_{1},D_{2},\ldots ,D_{n}$. By the induction hypothesis, any finite étale cover
$D_{1},D_{2},\ldots ,D_{n}$. By the induction hypothesis, any finite étale cover ![]() $Y$ of
$Y$ of ![]() $X\smallsetminus D$ extends to a cover
$X\smallsetminus D$ extends to a cover ![]() $Y_{i}$ of
$Y_{i}$ of ![]() $X\smallsetminus D_{i}$ for each
$X\smallsetminus D_{i}$ for each ![]() $1\leqslant i\leqslant n$, since
$1\leqslant i\leqslant n$, since ![]() $\unicode[STIX]{x1D704}(D\smallsetminus D_{i})\leqslant n-1$ for
$\unicode[STIX]{x1D704}(D\smallsetminus D_{i})\leqslant n-1$ for ![]() $D\smallsetminus D_{i}$ viewed as a strict normal crossings divisor in
$D\smallsetminus D_{i}$ viewed as a strict normal crossings divisor in ![]() $X\smallsetminus D_{i}$. By full faithfulness the
$X\smallsetminus D_{i}$. By full faithfulness the ![]() $Y_{i}$ glue to a cover
$Y_{i}$ glue to a cover ![]() $Y_{0}$ of
$Y_{0}$ of ![]() $X\smallsetminus \bigcap _{1\leqslant i\leqslant n}D_{i}$, and locally around any point in
$X\smallsetminus \bigcap _{1\leqslant i\leqslant n}D_{i}$, and locally around any point in ![]() $\bigcap _{1\leqslant i\leqslant n}D_{i}$ Lemma 2.13 again puts us in the situation handled by Lemma 2.12, so
$\bigcap _{1\leqslant i\leqslant n}D_{i}$ Lemma 2.13 again puts us in the situation handled by Lemma 2.12, so ![]() $Y_{0}$ extends to a cover
$Y_{0}$ extends to a cover ![]() ${\tilde{Y}}$ of
${\tilde{Y}}$ of ![]() $X$, as desired.
$X$, as desired.
Proof of Theorem 2.10.
We can assume that ![]() $X=\text{Spa}\,A$ is an affinoid rigid space, so
$X=\text{Spa}\,A$ is an affinoid rigid space, so ![]() $Z=\text{Spa}\,B$ is also affinoid, and we get a corresponding closed immersion of schemes
$Z=\text{Spa}\,B$ is also affinoid, and we get a corresponding closed immersion of schemes ![]() ${\mathcal{Z}}=\text{Spec}\,B\rightarrow {\mathcal{X}}=\text{Spec}\,A$. These are quasi-excellent schemes over
${\mathcal{Z}}=\text{Spec}\,B\rightarrow {\mathcal{X}}=\text{Spec}\,A$. These are quasi-excellent schemes over ![]() $\mathbf{Q}$, so, according to [Reference TemkinTem17, Theorem 1.11], we can find a projective birational morphism
$\mathbf{Q}$, so, according to [Reference TemkinTem17, Theorem 1.11], we can find a projective birational morphism ![]() $f:{\mathcal{X}}^{\prime }\rightarrow {\mathcal{X}}$ such that
$f:{\mathcal{X}}^{\prime }\rightarrow {\mathcal{X}}$ such that ![]() ${\mathcal{X}}^{\prime }$ is regular and
${\mathcal{X}}^{\prime }$ is regular and ![]() $f^{-1}({\mathcal{Z}})^{\text{red}}$ is a strict normal crossings divisor, and such that
$f^{-1}({\mathcal{Z}})^{\text{red}}$ is a strict normal crossings divisor, and such that ![]() $f$ is an isomorphism away from
$f$ is an isomorphism away from ![]() ${\mathcal{Z}}\cup {\mathcal{X}}^{\text{sing}}$. Analytifying, we get a proper morphism of rigid spaces
${\mathcal{Z}}\cup {\mathcal{X}}^{\text{sing}}$. Analytifying, we get a proper morphism of rigid spaces ![]() $g:X^{\prime }\rightarrow X$ with
$g:X^{\prime }\rightarrow X$ with ![]() $X^{\prime }$ smooth such that
$X^{\prime }$ smooth such that ![]() $g^{-1}(Z)^{\text{red}}$ is a strict normal crossings divisor.
$g^{-1}(Z)^{\text{red}}$ is a strict normal crossings divisor.
Suppose now that we are given a finite étale cover ![]() $Y\rightarrow X\smallsetminus Z$. Base changing along
$Y\rightarrow X\smallsetminus Z$. Base changing along ![]() $g$, we get a finite étale cover of
$g$, we get a finite étale cover of ![]() $X^{\prime }\smallsetminus g^{-1}(Z)$, which then extends to a cover
$X^{\prime }\smallsetminus g^{-1}(Z)$, which then extends to a cover ![]() $h:Y^{\prime }\rightarrow X^{\prime }$ by Theorem 2.11. Now, since
$h:Y^{\prime }\rightarrow X^{\prime }$ by Theorem 2.11. Now, since ![]() $g\circ h$ is proper, the sheaf
$g\circ h$ is proper, the sheaf ![]() $(g\circ h)_{\ast }{\mathcal{O}}_{Y^{\prime }}$ defines a sheaf of coherent
$(g\circ h)_{\ast }{\mathcal{O}}_{Y^{\prime }}$ defines a sheaf of coherent ![]() ${\mathcal{O}}_{X}$-algebras by [Reference KiehlKie67a]. Taking the normalization of the affinoid space associated with the global sections of this sheaf, we get a normal affinoid
${\mathcal{O}}_{X}$-algebras by [Reference KiehlKie67a]. Taking the normalization of the affinoid space associated with the global sections of this sheaf, we get a normal affinoid ![]() $Y^{\prime \prime }$ together with a finite map
$Y^{\prime \prime }$ together with a finite map ![]() $Y^{\prime \prime }\rightarrow X$ and a canonical isomorphism
$Y^{\prime \prime }\rightarrow X$ and a canonical isomorphism ![]() $Y^{\prime \prime }|_{(X\smallsetminus Z)^{\text{sm}}}\cong Y|_{(X\smallsetminus Z)^{\text{sm}}}$. The cover
$Y^{\prime \prime }|_{(X\smallsetminus Z)^{\text{sm}}}\cong Y|_{(X\smallsetminus Z)^{\text{sm}}}$. The cover ![]() ${\tilde{Y}}\rightarrow X$ we seek can then be defined as the Zariski closure of
${\tilde{Y}}\rightarrow X$ we seek can then be defined as the Zariski closure of ![]() $Y^{\prime \prime }|_{(X\smallsetminus Z)^{\text{sm}}}$ in
$Y^{\prime \prime }|_{(X\smallsetminus Z)^{\text{sm}}}$ in ![]() $Y^{\prime \prime }$; note that this is just a union of irreducible components of
$Y^{\prime \prime }$; note that this is just a union of irreducible components of ![]() $Y^{\prime \prime }$, so it is still normal, and it is easy to check that
$Y^{\prime \prime }$, so it is still normal, and it is easy to check that ![]() ${\tilde{Y}}$ is a cover of
${\tilde{Y}}$ is a cover of ![]() $X$. Finally, since
$X$. Finally, since ![]() ${\tilde{Y}}$ and
${\tilde{Y}}$ and ![]() $Y$ are canonically isomorphic after restriction to
$Y$ are canonically isomorphic after restriction to ![]() $(X\smallsetminus Z)^{\text{sm}}$, the full faithfulness argument shows that this isomorphism extends to an isomorphism
$(X\smallsetminus Z)^{\text{sm}}$, the full faithfulness argument shows that this isomorphism extends to an isomorphism ![]() ${\tilde{Y}}|_{X\smallsetminus Z}\cong Y$, since
${\tilde{Y}}|_{X\smallsetminus Z}\cong Y$, since ![]() $(X\smallsetminus Z)^{\text{sm}}$ is a dense Zariski-open subset of
$(X\smallsetminus Z)^{\text{sm}}$ is a dense Zariski-open subset of ![]() $X\smallsetminus Z$. This concludes the proof.◻
$X\smallsetminus Z$. This concludes the proof.◻
For completeness, we state the following mild generalization of Theorem 2.10.
Theorem 2.14. Let ![]() $X$ be a normal rigid space over a characteristic-zero complete nonarchimedean field
$X$ be a normal rigid space over a characteristic-zero complete nonarchimedean field ![]() $K$ and let
$K$ and let ![]() $V\subset X$ be any closed nowhere-dense analytic subset. Suppose that
$V\subset X$ be any closed nowhere-dense analytic subset. Suppose that ![]() $Y\rightarrow X\smallsetminus V$ is a cover, and that there is some closed nowhere-dense analytic set
$Y\rightarrow X\smallsetminus V$ is a cover, and that there is some closed nowhere-dense analytic set ![]() $W\subset X\smallsetminus V$ such that
$W\subset X\smallsetminus V$ such that ![]() $V\cup W$ is an analytic set in
$V\cup W$ is an analytic set in ![]() $X$ and such that
$X$ and such that
is finite étale. Then ![]() $Y$ extends to a cover
$Y$ extends to a cover ![]() ${\tilde{Y}}\rightarrow X$.
${\tilde{Y}}\rightarrow X$.
Proof. Apply Theorem 2.10 with ![]() $Z=V\cup W$ to construct
$Z=V\cup W$ to construct ![]() ${\tilde{Y}}\rightarrow X$ extending
${\tilde{Y}}\rightarrow X$ extending
and then use full faithfulness to deduce that ![]() ${\tilde{Y}}|_{X\smallsetminus V}\cong Y$.◻
${\tilde{Y}}|_{X\smallsetminus V}\cong Y$.◻
Combining this extension theorem with classical Zariski–Nagata purity, we get a purity theorem for rigid analytic spaces.
Corollary 2.15. Let ![]() $X$ be a smooth rigid analytic space over a characteristic-zero complete nonarchimedean field and let
$X$ be a smooth rigid analytic space over a characteristic-zero complete nonarchimedean field and let ![]() $Z\subset X$ be any closed analytic subset which is everywhere of codimension
$Z\subset X$ be any closed analytic subset which is everywhere of codimension ![]() ${\geqslant}2$. Then finite étale covers of
${\geqslant}2$. Then finite étale covers of ![]() $X$ are equivalent to finite étale covers of
$X$ are equivalent to finite étale covers of ![]() $X\smallsetminus Z$.
$X\smallsetminus Z$.
We also get the following equivalence, which plays an important role in the proof of Theorem 1.7.
Corollary 2.16. Let ![]() $S=\text{Spa}\,A$ be a characteristic-zero affinoid. Set
$S=\text{Spa}\,A$ be a characteristic-zero affinoid. Set ![]() ${\mathcal{S}}=\text{Spec}\,A$, and let
${\mathcal{S}}=\text{Spec}\,A$, and let ![]() ${\mathcal{U}}\subset {\mathcal{S}}$ be any normal dense open subscheme, with
${\mathcal{U}}\subset {\mathcal{S}}$ be any normal dense open subscheme, with ![]() $U\subset S$ the corresponding dense Zariski-open subspace of
$U\subset S$ the corresponding dense Zariski-open subspace of ![]() $S$. Then analytification induces an equivalence of categories
$S$. Then analytification induces an equivalence of categories ![]() ${\mathcal{U}}_{\text{f}\acute{\text{e}}\text{t}}\cong U_{\text{f}\acute{\text{e}}\text{t}}$.
${\mathcal{U}}_{\text{f}\acute{\text{e}}\text{t}}\cong U_{\text{f}\acute{\text{e}}\text{t}}$.
Note that ![]() ${\mathcal{U}}$ is normal if and only if
${\mathcal{U}}$ is normal if and only if ![]() $U$ is normal; this follows from [Reference Bosch, Güntzer and RemmertBGR84, Proposition 7.3.2/8.i].
$U$ is normal; this follows from [Reference Bosch, Güntzer and RemmertBGR84, Proposition 7.3.2/8.i].
Proof. The essential point is to construct the functor ![]() $U_{\text{f}\acute{\text{e}}\text{t}}\mapsto {\mathcal{U}}_{\text{f}\acute{\text{e}}\text{t}}$. For this, let
$U_{\text{f}\acute{\text{e}}\text{t}}\mapsto {\mathcal{U}}_{\text{f}\acute{\text{e}}\text{t}}$. For this, let ![]() $Y\rightarrow U$ be any finite étale cover. Letting
$Y\rightarrow U$ be any finite étale cover. Letting ![]() $S^{\unicode[STIX]{x1D708}}$ and
$S^{\unicode[STIX]{x1D708}}$ and ![]() ${\mathcal{S}}^{\unicode[STIX]{x1D708}}$ denote the normalizations of
${\mathcal{S}}^{\unicode[STIX]{x1D708}}$ denote the normalizations of ![]() $S$ and
$S$ and ![]() ${\mathcal{S}}$, the map
${\mathcal{S}}$, the map ![]() $U\rightarrow S$ factors canonically over a dense Zariski-open immersion
$U\rightarrow S$ factors canonically over a dense Zariski-open immersion ![]() $U\rightarrow S^{\unicode[STIX]{x1D708}}$, and similarly for
$U\rightarrow S^{\unicode[STIX]{x1D708}}$, and similarly for ![]() ${\mathcal{U}}$. By Theorem 2.10,
${\mathcal{U}}$. By Theorem 2.10, ![]() $Y\rightarrow U$ extends to a cover
$Y\rightarrow U$ extends to a cover ![]() ${\tilde{Y}}\rightarrow S^{\unicode[STIX]{x1D708}}$. Since
${\tilde{Y}}\rightarrow S^{\unicode[STIX]{x1D708}}$. Since ![]() ${\tilde{Y}}\rightarrow S^{\unicode[STIX]{x1D708}}$ is finite,
${\tilde{Y}}\rightarrow S^{\unicode[STIX]{x1D708}}$ is finite, ![]() ${\tilde{Y}}=\text{Spa}\,B$ for
${\tilde{Y}}=\text{Spa}\,B$ for ![]() $B$ some module-finite
$B$ some module-finite ![]() $A^{\unicode[STIX]{x1D708}}$-algebra. Then
$A^{\unicode[STIX]{x1D708}}$-algebra. Then ![]() ${\mathcal{Y}}=\text{Spec}\,B\times _{{\mathcal{S}}^{\unicode[STIX]{x1D708}}}{\mathcal{U}}\rightarrow {\mathcal{U}}$ is the desired algebraization of
${\mathcal{Y}}=\text{Spec}\,B\times _{{\mathcal{S}}^{\unicode[STIX]{x1D708}}}{\mathcal{U}}\rightarrow {\mathcal{U}}$ is the desired algebraization of ![]() $Y\rightarrow U$.◻
$Y\rightarrow U$.◻
3 Vanishing theorems
3.1 The reduction step
In this section we deduce Theorem 1.3 from Theorem 1.4. For clarity we focus on the vanishing statement in the theorem; it is easy to see that the following argument also reduces the finiteness of the groups ![]() $H_{\acute{\text{e}}\text{t}}^{i}(X_{\widehat{\overline{K}}},\mathscr{F})$ to finiteness in the special case where
$H_{\acute{\text{e}}\text{t}}^{i}(X_{\widehat{\overline{K}}},\mathscr{F})$ to finiteness in the special case where ![]() $\mathscr{F}=\mathbf{Z}/n\mathbf{Z}$ is constant, and finiteness in the latter case follows from [Reference BerkovichBer15, Theorem 1.1.1].
$\mathscr{F}=\mathbf{Z}/n\mathbf{Z}$ is constant, and finiteness in the latter case follows from [Reference BerkovichBer15, Theorem 1.1.1].
Proof of Theorem 1.3.
Fix a nonarchimedean field ![]() $K$ and a coefficient ring
$K$ and a coefficient ring ![]() $\unicode[STIX]{x1D6EC}=\mathbf{Z}/n\mathbf{Z}$ as in the theorem. In what follows, ‘sheaf’ is shorthand for ‘étale sheaf of
$\unicode[STIX]{x1D6EC}=\mathbf{Z}/n\mathbf{Z}$ as in the theorem. In what follows, ‘sheaf’ is shorthand for ‘étale sheaf of ![]() $\unicode[STIX]{x1D6EC}$-modules’. For nonnegative integers
$\unicode[STIX]{x1D6EC}$-modules’. For nonnegative integers ![]() $d,i$, consider the following statement.
$d,i$, consider the following statement.
Statement ![]() ${\mathcal{T}}_{d,i}$: ‘For all
${\mathcal{T}}_{d,i}$: ‘For all ![]() $K$-affinoids
$K$-affinoids ![]() $X$ of dimension
$X$ of dimension ![]() ${\leqslant}d$, all Zariski-constructible sheaves
${\leqslant}d$, all Zariski-constructible sheaves ![]() $\mathscr{F}$ on
$\mathscr{F}$ on ![]() $X$, and all integers
$X$, and all integers ![]() $j>i$, we have
$j>i$, we have ![]() $H_{\acute{\text{e}}\text{t}}^{j}(X_{\widehat{\overline{K}}},\mathscr{F})=0$’.
$H_{\acute{\text{e}}\text{t}}^{j}(X_{\widehat{\overline{K}}},\mathscr{F})=0$’.
We are trying to prove that ![]() ${\mathcal{T}}_{d,d}$ is true for all
${\mathcal{T}}_{d,d}$ is true for all ![]() $d\geqslant 0$. The idea is to argue by ascending induction on
$d\geqslant 0$. The idea is to argue by ascending induction on ![]() $d$ and descending induction on
$d$ and descending induction on ![]() $i$. More precisely, it clearly suffices to assume the truth of
$i$. More precisely, it clearly suffices to assume the truth of ![]() ${\mathcal{T}}_{d-1,d-1}$ and then show that
${\mathcal{T}}_{d-1,d-1}$ and then show that ![]() ${\mathcal{T}}_{d,i+1}$ implies
${\mathcal{T}}_{d,i+1}$ implies ![]() ${\mathcal{T}}_{d,i}$ for any
${\mathcal{T}}_{d,i}$ for any ![]() $i\geqslant d$; as noted in the introduction,
$i\geqslant d$; as noted in the introduction, ![]() ${\mathcal{T}}_{d,2d}$ is true for any
${\mathcal{T}}_{d,2d}$ is true for any ![]() $d\geqslant 0$, which gives a starting place for the descending induction.
$d\geqslant 0$, which gives a starting place for the descending induction.
We break the details into several steps.
Step one.
Suppose that ![]() ${\mathcal{T}}_{d-1,d-1}$ holds. Then, for any
${\mathcal{T}}_{d-1,d-1}$ holds. Then, for any ![]() $d$-dimensional affinoid
$d$-dimensional affinoid ![]() $X$, any Zariski-constructible sheaf
$X$, any Zariski-constructible sheaf ![]() $\mathscr{F}$ on
$\mathscr{F}$ on ![]() $X$, and any dense Zariski-open subset
$X$, and any dense Zariski-open subset ![]() $j:U\rightarrow X$, the natural map
$j:U\rightarrow X$, the natural map ![]() $H_{\acute{\text{e}}\text{t}}^{i}(X_{\widehat{\overline{K}}},j_{!}j^{\ast }\mathscr{F})\rightarrow H_{\acute{\text{e}}\text{t}}^{i}(X_{\widehat{\overline{K}}},\mathscr{F})$ is surjective for
$H_{\acute{\text{e}}\text{t}}^{i}(X_{\widehat{\overline{K}}},j_{!}j^{\ast }\mathscr{F})\rightarrow H_{\acute{\text{e}}\text{t}}^{i}(X_{\widehat{\overline{K}}},\mathscr{F})$ is surjective for ![]() $i=d$ and bijective for
$i=d$ and bijective for ![]() $i>d$.
$i>d$.
Letting ![]() $i:Z\rightarrow X$ denote the closed complement, this is immediate by looking at the long exact sequence
$i:Z\rightarrow X$ denote the closed complement, this is immediate by looking at the long exact sequence
associated with the short exact sequence
and then applying ![]() ${\mathcal{T}}_{d-1,d-1}$ to control the outer terms.
${\mathcal{T}}_{d-1,d-1}$ to control the outer terms.
Step two.
For any ![]() $d,i$,
$d,i$, ![]() ${\mathcal{T}}_{d,i}$ holds if and only if it holds for all normal affinoids.
${\mathcal{T}}_{d,i}$ holds if and only if it holds for all normal affinoids.
One direction is trivial. For the other direction, note that by Noether normalization for affinoids [Reference Bosch, Güntzer and RemmertBGR84, Corollary 6.1.2/2], any ![]() $d$-dimensional affinoid
$d$-dimensional affinoid ![]() $X$ admits a finite map
$X$ admits a finite map
and ![]() $\unicode[STIX]{x1D70F}_{\ast }=R\unicode[STIX]{x1D70F}_{\ast }$ preserves Zariski-constructibility by Proposition 2.3.
$\unicode[STIX]{x1D70F}_{\ast }=R\unicode[STIX]{x1D70F}_{\ast }$ preserves Zariski-constructibility by Proposition 2.3.
Step three.
Footnote 6 Suppose that ![]() ${\mathcal{T}}_{d-1,d-1}$ holds. Then, for any
${\mathcal{T}}_{d-1,d-1}$ holds. Then, for any ![]() $d$-dimensional normal affinoid
$d$-dimensional normal affinoid ![]() $X$, any dense Zariski-open subset
$X$, any dense Zariski-open subset ![]() $j:U\rightarrow X$, and any locally constant constructible sheaf
$j:U\rightarrow X$, and any locally constant constructible sheaf ![]() $\mathscr{H}$ on
$\mathscr{H}$ on ![]() $U$, we can find a Zariski-constructible sheaf
$U$, we can find a Zariski-constructible sheaf ![]() $\mathscr{G}$ on
$\mathscr{G}$ on ![]() $X$ together with a surjection
$X$ together with a surjection ![]() $s:\mathscr{G}\rightarrow j_{!}\mathscr{H}$, such that moreover
$s:\mathscr{G}\rightarrow j_{!}\mathscr{H}$, such that moreover ![]() $H_{\acute{\text{e}}\text{t}}^{i}(X_{\widehat{\overline{K}}},\mathscr{G})=0$ for all
$H_{\acute{\text{e}}\text{t}}^{i}(X_{\widehat{\overline{K}}},\mathscr{G})=0$ for all ![]() $i>d$.
$i>d$.
To prove this, suppose that we are given ![]() $X,\,U$, and
$X,\,U$, and ![]() $\mathscr{H}$ as in the statement. By definition, we can find a finite étale cover
$\mathscr{H}$ as in the statement. By definition, we can find a finite étale cover ![]() $\unicode[STIX]{x1D70B}:Y\rightarrow U$ such that
$\unicode[STIX]{x1D70B}:Y\rightarrow U$ such that ![]() $\unicode[STIX]{x1D70B}^{\ast }\mathscr{H}$ is constant, i.e. such that there exists a surjection
$\unicode[STIX]{x1D70B}^{\ast }\mathscr{H}$ is constant, i.e. such that there exists a surjection ![]() $\unicode[STIX]{x1D6EC}_{Y}^{n}\rightarrow \unicode[STIX]{x1D70B}^{\ast }\mathscr{H}$ for some
$\unicode[STIX]{x1D6EC}_{Y}^{n}\rightarrow \unicode[STIX]{x1D70B}^{\ast }\mathscr{H}$ for some ![]() $n$; fix such a surjection. This is adjoint to a surjection
$n$; fix such a surjection. This is adjoint to a surjection ![]() $\unicode[STIX]{x1D70B}_{!}(\unicode[STIX]{x1D6EC}_{Y}^{n})\rightarrow \mathscr{H}$,Footnote 7 which extends by zero to a surjection
$\unicode[STIX]{x1D70B}_{!}(\unicode[STIX]{x1D6EC}_{Y}^{n})\rightarrow \mathscr{H}$,Footnote 7 which extends by zero to a surjection ![]() $s:j_{!}\unicode[STIX]{x1D70B}_{!}(\unicode[STIX]{x1D6EC}_{Y}^{n})\rightarrow j_{!}\mathscr{H}$. We claim that the sheaf
$s:j_{!}\unicode[STIX]{x1D70B}_{!}(\unicode[STIX]{x1D6EC}_{Y}^{n})\rightarrow j_{!}\mathscr{H}$. We claim that the sheaf ![]() $\mathscr{G}=j_{!}\unicode[STIX]{x1D70B}_{!}(\unicode[STIX]{x1D6EC}_{Y}^{n})$ has the required properties. Zariski-constructibility is clear from the identification
$\mathscr{G}=j_{!}\unicode[STIX]{x1D70B}_{!}(\unicode[STIX]{x1D6EC}_{Y}^{n})$ has the required properties. Zariski-constructibility is clear from the identification ![]() $\unicode[STIX]{x1D70B}_{!}=\unicode[STIX]{x1D70B}_{\ast }$ and Proposition 2.3. For the vanishing statement, we apply Theorem 1.6 to extend
$\unicode[STIX]{x1D70B}_{!}=\unicode[STIX]{x1D70B}_{\ast }$ and Proposition 2.3. For the vanishing statement, we apply Theorem 1.6 to extend ![]() $Y\rightarrow U$ to a cover
$Y\rightarrow U$ to a cover ![]() $\tilde{\unicode[STIX]{x1D70B}}:{\tilde{Y}}\rightarrow X$ sitting in a cartesian diagram
$\tilde{\unicode[STIX]{x1D70B}}:{\tilde{Y}}\rightarrow X$ sitting in a cartesian diagram

where ![]() ${\tilde{Y}}$ is a normal affinoid and
${\tilde{Y}}$ is a normal affinoid and ![]() $h$ is a dense Zariski-open immersion. By proper base change and the finiteness of
$h$ is a dense Zariski-open immersion. By proper base change and the finiteness of ![]() $\tilde{\unicode[STIX]{x1D70B}}$, we get isomorphisms
$\tilde{\unicode[STIX]{x1D70B}}$, we get isomorphisms
so ![]() $H_{\acute{\text{e}}\text{t}}^{i}(X_{\widehat{\overline{K}}},\mathscr{G})\cong H_{\acute{\text{e}}\text{t}}^{i}({\tilde{Y}}_{\widehat{\overline{K}}},h_{!}\unicode[STIX]{x1D6EC}_{Y})^{\oplus n}$.
$H_{\acute{\text{e}}\text{t}}^{i}(X_{\widehat{\overline{K}}},\mathscr{G})\cong H_{\acute{\text{e}}\text{t}}^{i}({\tilde{Y}}_{\widehat{\overline{K}}},h_{!}\unicode[STIX]{x1D6EC}_{Y})^{\oplus n}$. ![]() $$Now, writing
$$Now, writing ![]() $i:V\rightarrow {\tilde{Y}}$ for the closed complement of
$i:V\rightarrow {\tilde{Y}}$ for the closed complement of ![]() $Y$, we get exact sequences
$Y$, we get exact sequences
for all ![]() $i$. Examining this sequence for any fixed
$i$. Examining this sequence for any fixed ![]() $i>d$, we see that the rightmost term vanishes by Theorem 1.4, while the leftmost term vanishes by the assumption that
$i>d$, we see that the rightmost term vanishes by Theorem 1.4, while the leftmost term vanishes by the assumption that ![]() ${\mathcal{T}}_{d-1,d-1}$ holds.Footnote 8 Therefore,
${\mathcal{T}}_{d-1,d-1}$ holds.Footnote 8 Therefore, ![]() $H_{\acute{\text{e}}\text{t}}^{i}({\tilde{Y}}_{\widehat{\overline{K}}},h_{!}\unicode[STIX]{x1D6EC}_{Y})=0$ for
$H_{\acute{\text{e}}\text{t}}^{i}({\tilde{Y}}_{\widehat{\overline{K}}},h_{!}\unicode[STIX]{x1D6EC}_{Y})=0$ for ![]() $i>d$, as desired.
$i>d$, as desired.
Step four.
Suppose that ![]() ${\mathcal{T}}_{d-1,d-1}$ holds. Then
${\mathcal{T}}_{d-1,d-1}$ holds. Then ![]() ${\mathcal{T}}_{d,i+1}$ implies that
${\mathcal{T}}_{d,i+1}$ implies that ![]() ${\mathcal{T}}_{d,i}$ for any
${\mathcal{T}}_{d,i}$ for any ![]() $i\geqslant d$.
$i\geqslant d$.
Fix ![]() $d$ and
$d$ and ![]() $i\geqslant d$ as in the statement, and assume that
$i\geqslant d$ as in the statement, and assume that ![]() ${\mathcal{T}}_{d,i+1}$ is true. Let
${\mathcal{T}}_{d,i+1}$ is true. Let ![]() $X$ be a
$X$ be a ![]() $d$-dimensional affinoid and let
$d$-dimensional affinoid and let ![]() $\mathscr{F}$ be a Zariski-constructible sheaf on
$\mathscr{F}$ be a Zariski-constructible sheaf on ![]() $X$. We need to show that
$X$. We need to show that ![]() $H_{\acute{\text{e}}\text{t}}^{i+1}(X_{\widehat{\overline{K}}},\mathscr{F})=0$. By Step two, we can assume that
$H_{\acute{\text{e}}\text{t}}^{i+1}(X_{\widehat{\overline{K}}},\mathscr{F})=0$. By Step two, we can assume that ![]() $X$ is normal (or even that
$X$ is normal (or even that ![]() $X$ is the
$X$ is the ![]() $d$-dimensional affinoid ball). By Step one, it suffices to show that
$d$-dimensional affinoid ball). By Step one, it suffices to show that ![]() $H_{\acute{\text{e}}\text{t}}^{i+1}(X_{\widehat{\overline{K}}},j_{!}j^{\ast }\mathscr{F})=0$, where
$H_{\acute{\text{e}}\text{t}}^{i+1}(X_{\widehat{\overline{K}}},j_{!}j^{\ast }\mathscr{F})=0$, where ![]() $j:U\rightarrow X$ is the inclusion of any dense Zariski-open subset. Fix a choice of such a
$j:U\rightarrow X$ is the inclusion of any dense Zariski-open subset. Fix a choice of such a ![]() $U$ with the property that
$U$ with the property that ![]() $j^{\ast }\mathscr{F}$ is locally constant. By Step three, we can choose a Zariski-constructible sheaf
$j^{\ast }\mathscr{F}$ is locally constant. By Step three, we can choose a Zariski-constructible sheaf ![]() $\mathscr{G}$ on
$\mathscr{G}$ on ![]() $X$ and a surjection
$X$ and a surjection ![]() $s:\mathscr{G}\rightarrow j_{!}j^{\ast }\mathscr{F}$ such that
$s:\mathscr{G}\rightarrow j_{!}j^{\ast }\mathscr{F}$ such that ![]() $H_{\acute{\text{e}}\text{t}}^{n}(X_{\widehat{\overline{K}}},\mathscr{G})=0$ for all
$H_{\acute{\text{e}}\text{t}}^{n}(X_{\widehat{\overline{K}}},\mathscr{G})=0$ for all ![]() $n>d$. By Proposition 2.4, the sheaf
$n>d$. By Proposition 2.4, the sheaf ![]() $\mathscr{K}=\ker s$ is Zariski-constructible. Now, looking at the exact sequence
$\mathscr{K}=\ker s$ is Zariski-constructible. Now, looking at the exact sequence
we see that the leftmost term vanishes by the construction of ![]() $\mathscr{G}$, while the rightmost term vanishes by the induction hypothesis. Therefore,
$\mathscr{G}$, while the rightmost term vanishes by the induction hypothesis. Therefore,
as desired. ◻
3.2 Constant coefficients
In this section we prove Theorem 1.4. The following technical lemma plays an important role in the argument.
Lemma 3.1. Let ![]() $K$ be a complete discretely valued nonarchimedean field and let
$K$ be a complete discretely valued nonarchimedean field and let ![]() $A$ be a reduced
$A$ be a reduced ![]() $K$-affinoid algebra. Then
$K$-affinoid algebra. Then ![]() $A^{\circ }$ is an excellent Noetherian ring. Moreover, the strict Henselization of any localization of
$A^{\circ }$ is an excellent Noetherian ring. Moreover, the strict Henselization of any localization of ![]() $A^{\circ }$ is excellent as well.
$A^{\circ }$ is excellent as well.
Proof. By Noether normalization for affinoids and [Reference Bosch, Güntzer and RemmertBGR84, Corollary 6.4.1/6], ![]() $A^{\circ }$ can be realized as a module-finite integral extension of
$A^{\circ }$ can be realized as a module-finite integral extension of ![]() ${\mathcal{O}}_{K}\langle T_{1},\ldots ,T_{n}\rangle$ with
${\mathcal{O}}_{K}\langle T_{1},\ldots ,T_{n}\rangle$ with ![]() $n=\text{dim}\,A$. By a result of Valabrega (cf. [Reference ValabregaVal75, Proposition 7] and [Reference ValabregaVal76, Theorem 9]), the convergent power series ring
$n=\text{dim}\,A$. By a result of Valabrega (cf. [Reference ValabregaVal75, Proposition 7] and [Reference ValabregaVal76, Theorem 9]), the convergent power series ring ![]() ${\mathcal{O}}_{K}\langle T_{1},\ldots ,T_{n}\rangle$ is excellent for any complete discrete valuation ring
${\mathcal{O}}_{K}\langle T_{1},\ldots ,T_{n}\rangle$ is excellent for any complete discrete valuation ring ![]() ${\mathcal{O}}_{K}$. Since excellence propagates along finite-type ring maps and localizations, cf. [Sta17, Tag 07QU], we see that
${\mathcal{O}}_{K}$. Since excellence propagates along finite-type ring maps and localizations, cf. [Sta17, Tag 07QU], we see that ![]() $A^{\circ }$ and any localization thereof are excellent. Now, by a result of Greco [Reference GrecoGre76, Corollary 5.6(iii)], the strict Henselization of any excellent local ring is excellent, which gives what we want.◻
$A^{\circ }$ and any localization thereof are excellent. Now, by a result of Greco [Reference GrecoGre76, Corollary 5.6(iii)], the strict Henselization of any excellent local ring is excellent, which gives what we want.◻
We also need the following extremely powerful theorem of Gabber.
Theorem 3.2 (Gabber).
Let ![]() $B$ be a quasi-excellent strictly Henselian local ring and let
$B$ be a quasi-excellent strictly Henselian local ring and let ![]() $U\subset \text{Spec}\,B$ be an affine open subscheme. Then
$U\subset \text{Spec}\,B$ be an affine open subscheme. Then ![]() $H_{\acute{\text{e}}\text{t}}^{i}(U,\mathbf{Z}/n\mathbf{Z})=0$ for any
$H_{\acute{\text{e}}\text{t}}^{i}(U,\mathbf{Z}/n\mathbf{Z})=0$ for any ![]() $i>\text{dim}\,B$ and any integer
$i>\text{dim}\,B$ and any integer ![]() $n$ invertible in
$n$ invertible in ![]() $B$.
$B$.
Proof. This is a special case of Gabber’s affine Lefschetz theorem for quasi-excellent schemes; cf. [Reference Illusie, Laszlo and OrgogozoILO14, Corollaire XV.1.2.4]. ◻
Finally, we recall the following strong form of the Artin–Grothendieck vanishing theorem [Reference Artin, Grothendieck and VerdierSGA4, § XIV.3].
Theorem 3.3 (Artin–Grothendieck).
Let ![]() $X$ be an affine variety over a separably closed field
$X$ be an affine variety over a separably closed field ![]() $k$ and let
$k$ and let ![]() $\mathscr{F}$ be a torsion abelian sheaf on
$\mathscr{F}$ be a torsion abelian sheaf on ![]() $X_{\acute{\text{e}}\text{t}}$. Set
$X_{\acute{\text{e}}\text{t}}$. Set
Then ![]() $H_{\acute{\text{e}}\text{t}}^{i}(X,\mathscr{F})=0$ for all
$H_{\acute{\text{e}}\text{t}}^{i}(X,\mathscr{F})=0$ for all ![]() $i>\unicode[STIX]{x1D6FF}(\mathscr{F})$.
$i>\unicode[STIX]{x1D6FF}(\mathscr{F})$. ![]() $\phantom{}$
$\phantom{}$
Proof of Theorem 1.4.
Let ![]() $X=\text{Spa}\,A$ be a
$X=\text{Spa}\,A$ be a ![]() $K$-affinoid as in the theorem. After replacing
$K$-affinoid as in the theorem. After replacing ![]() $K$ by
$K$ by ![]() $\widehat{K^{\text{nr}}}$ and
$\widehat{K^{\text{nr}}}$ and ![]() $X$ by
$X$ by ![]() $X_{\widehat{K^{\text{nr}}}}^{\text{red}}$, we can assume that
$X_{\widehat{K^{\text{nr}}}}^{\text{red}}$, we can assume that ![]() $A$ is reduced and that
$A$ is reduced and that ![]() $K$ has separably closed residue field
$K$ has separably closed residue field ![]() $k$. By an easy induction we can also assume that
$k$. By an easy induction we can also assume that ![]() $n=l$ is prime. For notational simplicity we give the remainder of the proof in the case where
$n=l$ is prime. For notational simplicity we give the remainder of the proof in the case where ![]() $\text{char}(k)=p>0$; the equal characteristic-zero case is only easier.
$\text{char}(k)=p>0$; the equal characteristic-zero case is only easier.
By e.g. [Reference BerkovichBer93, Corollary 2.4.6], ![]() $\text{Gal}_{\overline{K}/K}$ sits in a short exact sequence
$\text{Gal}_{\overline{K}/K}$ sits in a short exact sequence
where ![]() $P$ is pro-
$P$ is pro-![]() $p$. In particular, if
$p$. In particular, if ![]() $L\subset \overline{K}$ is any finite extension of
$L\subset \overline{K}$ is any finite extension of ![]() $K$, then
$K$, then
For any such ![]() $L$, look at the Cartan–Leray spectral sequence
$L$, look at the Cartan–Leray spectral sequence
The group ![]() $\bigoplus _{j\geqslant 0}H_{\acute{\text{e}}\text{t}}^{j}(X_{\widehat{\overline{K}}},\mathbf{Z}/l\mathbf{Z})$ is finite by vanishing in degrees
$\bigoplus _{j\geqslant 0}H_{\acute{\text{e}}\text{t}}^{j}(X_{\widehat{\overline{K}}},\mathbf{Z}/l\mathbf{Z})$ is finite by vanishing in degrees ![]() ${>}2\,\text{dim}\,X$ together with [Reference BerkovichBer15, Theorem 1.1.1], so all the Galois actions in the
${>}2\,\text{dim}\,X$ together with [Reference BerkovichBer15, Theorem 1.1.1], so all the Galois actions in the ![]() $E_{2}$-page are trivial for any large enough
$E_{2}$-page are trivial for any large enough ![]() $L$,Footnote 9 in which case we can rewrite the spectral sequence as
$L$,Footnote 9 in which case we can rewrite the spectral sequence as
Now if ![]() $d$ is the largest integer such that
$d$ is the largest integer such that ![]() $H_{\acute{\text{e}}\text{t}}^{d}(X_{\widehat{\overline{K}}},\mathbf{Z}/l\mathbf{Z})\neq 0$, then the
$H_{\acute{\text{e}}\text{t}}^{d}(X_{\widehat{\overline{K}}},\mathbf{Z}/l\mathbf{Z})\neq 0$, then the ![]() $E_{2}^{1,d}$ term survives the spectral sequence, so
$E_{2}^{1,d}$ term survives the spectral sequence, so ![]() $H_{\acute{\text{e}}\text{t}}^{d+1}(X_{L},\mathbf{Z}/l\mathbf{Z})\neq 0$. Since the residue field of
$H_{\acute{\text{e}}\text{t}}^{d+1}(X_{L},\mathbf{Z}/l\mathbf{Z})\neq 0$. Since the residue field of ![]() $L$ is still separably closed, it thus suffices to prove the following statement.
$L$ is still separably closed, it thus suffices to prove the following statement.
(†) For any reduced affinoid
 $X=\text{Spa}\,A$ over a complete discretely valued nonarchimedean field
$X=\text{Spa}\,A$ over a complete discretely valued nonarchimedean field  $K$ with separably closed residue field
$K$ with separably closed residue field  $k$ of characteristic
$k$ of characteristic  $p>0$, we have
$p>0$, we have  $H_{\acute{\text{e}}\text{t}}^{i}(X,\mathbf{Z}/l\mathbf{Z})=0$ for all
$H_{\acute{\text{e}}\text{t}}^{i}(X,\mathbf{Z}/l\mathbf{Z})=0$ for all  $i>1+\text{dim}\,X$ and all primes
$i>1+\text{dim}\,X$ and all primes  $l\neq p$.
$l\neq p$.
Fix a uniformizer ![]() $\unicode[STIX]{x1D71B}\in {\mathcal{O}}_{K}$. Set
$\unicode[STIX]{x1D71B}\in {\mathcal{O}}_{K}$. Set ![]() ${\mathcal{X}}=\text{Spec}\,A^{\circ }$ and
${\mathcal{X}}=\text{Spec}\,A^{\circ }$ and ![]() ${\mathcal{X}}_{s}=\text{Spec}\,A^{\circ }/\unicode[STIX]{x1D71B}$, so
${\mathcal{X}}_{s}=\text{Spec}\,A^{\circ }/\unicode[STIX]{x1D71B}$, so ![]() ${\mathcal{X}}_{s}$ is an affine variety over
${\mathcal{X}}_{s}$ is an affine variety over ![]() $k$. As in [Reference HuberHub96, § 3.5] or [Reference BerkovichBer94], there is a natural map of sites
$k$. As in [Reference HuberHub96, § 3.5] or [Reference BerkovichBer94], there is a natural map of sites ![]() $\unicode[STIX]{x1D706}:X_{\acute{\text{e}}\text{t}}\rightarrow {\mathcal{X}}_{s,\acute{\text{e}}\text{t}}$, corresponding to the natural functor
$\unicode[STIX]{x1D706}:X_{\acute{\text{e}}\text{t}}\rightarrow {\mathcal{X}}_{s,\acute{\text{e}}\text{t}}$, corresponding to the natural functor
given by (uniquely) deforming an étale map ![]() ${\mathcal{U}}\rightarrow {\mathcal{X}}_{s}$ to a
${\mathcal{U}}\rightarrow {\mathcal{X}}_{s}$ to a ![]() $\unicode[STIX]{x1D71B}$-adic formal scheme étale over
$\unicode[STIX]{x1D71B}$-adic formal scheme étale over ![]() $\text{Spf}\,A^{\circ }$ and then passing to rigid generic fibers. (We follow Huber’s notation in writing
$\text{Spf}\,A^{\circ }$ and then passing to rigid generic fibers. (We follow Huber’s notation in writing ![]() $\unicode[STIX]{x1D706}$ – Berkovich denotes this map by
$\unicode[STIX]{x1D706}$ – Berkovich denotes this map by ![]() $\unicode[STIX]{x1D6E9}$.) For any abelian étale sheaf
$\unicode[STIX]{x1D6E9}$.) For any abelian étale sheaf ![]() $\mathscr{F}$ on
$\mathscr{F}$ on ![]() $X$, the derived pushforward along
$X$, the derived pushforward along ![]() $\unicode[STIX]{x1D706}$ gives rise to the so-called nearby cycle sheaves
$\unicode[STIX]{x1D706}$ gives rise to the so-called nearby cycle sheaves ![]() $R^{j}\unicode[STIX]{x1D706}_{\ast }\mathscr{F}$ on
$R^{j}\unicode[STIX]{x1D706}_{\ast }\mathscr{F}$ on ![]() ${\mathcal{X}}_{s,\acute{\text{e}}\text{t}}$, which can be calculated as the sheafifications of the presheaves
${\mathcal{X}}_{s,\acute{\text{e}}\text{t}}$, which can be calculated as the sheafifications of the presheaves ![]() ${\mathcal{U}}\mapsto H_{\acute{\text{e}}\text{t}}^{j}(\unicode[STIX]{x1D702}({\mathcal{U}}),\mathscr{F})$, and there is a spectral sequence
${\mathcal{U}}\mapsto H_{\acute{\text{e}}\text{t}}^{j}(\unicode[STIX]{x1D702}({\mathcal{U}}),\mathscr{F})$, and there is a spectral sequence
cf. [Reference BerkovichBer94, Proposition 4.1 and Corollary 4.2(iii)]. Taking ![]() $\mathscr{F}=\mathbf{Z}/l\mathbf{Z}$, we see that to prove
$\mathscr{F}=\mathbf{Z}/l\mathbf{Z}$, we see that to prove ![]() $(\dagger )$ it is enough to show that
$(\dagger )$ it is enough to show that ![]() $H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{X}}_{s},R^{j}\unicode[STIX]{x1D706}_{\ast }\mathbf{Z}/l\mathbf{Z})=0$ for any
$H_{\acute{\text{e}}\text{t}}^{i}({\mathcal{X}}_{s},R^{j}\unicode[STIX]{x1D706}_{\ast }\mathbf{Z}/l\mathbf{Z})=0$ for any ![]() $j\geqslant 0$ and any
$j\geqslant 0$ and any ![]() $i>1+\text{dim}\,X-j$. By the strong form of the Artin–Grothendieck vanishing theorem recalled above, we are reduced to proving that if
$i>1+\text{dim}\,X-j$. By the strong form of the Artin–Grothendieck vanishing theorem recalled above, we are reduced to proving that if ![]() $x\in {\mathcal{X}}_{s}$ is any point such that
$x\in {\mathcal{X}}_{s}$ is any point such that
then ![]() $\text{tr.deg}\,k(x)/k\leqslant 1+\text{dim}\,X-j$.
$\text{tr.deg}\,k(x)/k\leqslant 1+\text{dim}\,X-j$.
We check this by a direct computation. So, let ![]() $x\in {\mathcal{X}}_{s}$ be any point and let
$x\in {\mathcal{X}}_{s}$ be any point and let ![]() $\mathfrak{p}_{x}\subset A^{\circ }$ be the associated prime ideal. Crucially, we have a ‘purely algebraic’ description of the stalk
$\mathfrak{p}_{x}\subset A^{\circ }$ be the associated prime ideal. Crucially, we have a ‘purely algebraic’ description of the stalk ![]() $(R^{j}\unicode[STIX]{x1D706}_{\ast }\mathbf{Z}/l\mathbf{Z})_{\overline{x}}$: letting
$(R^{j}\unicode[STIX]{x1D706}_{\ast }\mathbf{Z}/l\mathbf{Z})_{\overline{x}}$: letting ![]() ${\mathcal{O}}_{{\mathcal{X}},\overline{x}}$ denote the strict Henselization of
${\mathcal{O}}_{{\mathcal{X}},\overline{x}}$ denote the strict Henselization of ![]() ${\mathcal{O}}_{{\mathcal{X}},x}=(A^{\circ })_{\mathfrak{p}_{x}}$ as usual, then
${\mathcal{O}}_{{\mathcal{X}},x}=(A^{\circ })_{\mathfrak{p}_{x}}$ as usual, then
This is a special case of [Reference HuberHub96, Theorem 3.5.10], and it is remarkable that we have a description like this which does not involve taking some completion. By Lemma 3.1, ![]() ${\mathcal{O}}_{{\mathcal{X}},\overline{x}}$ is excellent, so Theorem 3.2 implies that
${\mathcal{O}}_{{\mathcal{X}},\overline{x}}$ is excellent, so Theorem 3.2 implies that ![]() $H_{\acute{\text{e}}\text{t}}^{j}(U,\mathbf{Z}/l\mathbf{Z})=0$ for any open affine subscheme
$H_{\acute{\text{e}}\text{t}}^{j}(U,\mathbf{Z}/l\mathbf{Z})=0$ for any open affine subscheme ![]() $U\subset \text{Spec}\,{\mathcal{O}}_{{\mathcal{X}},\overline{x}}$ and any
$U\subset \text{Spec}\,{\mathcal{O}}_{{\mathcal{X}},\overline{x}}$ and any ![]() $j>\text{dim}\,{\mathcal{O}}_{{\mathcal{X}},\overline{x}}$. In particular, taking
$j>\text{dim}\,{\mathcal{O}}_{{\mathcal{X}},\overline{x}}$. In particular, taking ![]() $U=\text{Spec}\,{\mathcal{O}}_{{\mathcal{X}},\overline{x}}[\frac{1}{\unicode[STIX]{x1D71B}}]$ and applying Huber’s formula (
$U=\text{Spec}\,{\mathcal{O}}_{{\mathcal{X}},\overline{x}}[\frac{1}{\unicode[STIX]{x1D71B}}]$ and applying Huber’s formula (![]() $\ast$) above, we see that if
$\ast$) above, we see that if ![]() $j$ is an integer such that
$j$ is an integer such that ![]() $(R^{j}\unicode[STIX]{x1D706}_{\ast }\mathbf{Z}/l\mathbf{Z})_{\overline{x}}\neq 0$, then necessarily
$(R^{j}\unicode[STIX]{x1D706}_{\ast }\mathbf{Z}/l\mathbf{Z})_{\overline{x}}\neq 0$, then necessarily
where the first equality follows from e.g. [Sta17, Tag 06LK]. Writing ![]() $R=A^{\circ }/\unicode[STIX]{x1D71B}$ and
$R=A^{\circ }/\unicode[STIX]{x1D71B}$ and ![]() $\overline{\mathfrak{p}_{x}}=\mathfrak{p}_{x}/\unicode[STIX]{x1D71B}\subset R$, we then have
$\overline{\mathfrak{p}_{x}}=\mathfrak{p}_{x}/\unicode[STIX]{x1D71B}\subset R$, we then have
 $$\begin{eqnarray}\displaystyle j+\text{tr.deg}\,k(x)/k & {\leqslant} & \displaystyle \text{ht}\,\mathfrak{p}_{x}+\text{tr.deg}\,k(x)/k\nonumber\\ \displaystyle & = & \displaystyle 1+\text{ht}\,\overline{\mathfrak{p}_{x}}+\text{tr}.\text{deg}\,k(x)/k\nonumber\\ \displaystyle & = & \displaystyle 1+\text{dim}\,R_{\overline{\mathfrak{p}_{x}}}+\text{dim}\,R/\overline{\mathfrak{p}_{x}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 1+\text{dim}\,R\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 1+\text{dim}\,X.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle j+\text{tr.deg}\,k(x)/k & {\leqslant} & \displaystyle \text{ht}\,\mathfrak{p}_{x}+\text{tr.deg}\,k(x)/k\nonumber\\ \displaystyle & = & \displaystyle 1+\text{ht}\,\overline{\mathfrak{p}_{x}}+\text{tr}.\text{deg}\,k(x)/k\nonumber\\ \displaystyle & = & \displaystyle 1+\text{dim}\,R_{\overline{\mathfrak{p}_{x}}}+\text{dim}\,R/\overline{\mathfrak{p}_{x}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 1+\text{dim}\,R\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 1+\text{dim}\,X.\nonumber\end{eqnarray}$$ Here the second line follows from the fact that ![]() $\unicode[STIX]{x1D71B}\in \mathfrak{p}_{x}$ is part of a system of parameters of
$\unicode[STIX]{x1D71B}\in \mathfrak{p}_{x}$ is part of a system of parameters of ![]() $(A^{\circ })_{\mathfrak{p}_{x}}$, so
$(A^{\circ })_{\mathfrak{p}_{x}}$, so ![]() $\text{ht}\,\overline{\mathfrak{p}_{x}}=\text{dim}\,R_{\overline{\mathfrak{p}_{x}}}=\text{dim}\,(A^{\circ })_{\mathfrak{p}_{x}}-1$; the third line is immediate from the equality
$\text{ht}\,\overline{\mathfrak{p}_{x}}=\text{dim}\,R_{\overline{\mathfrak{p}_{x}}}=\text{dim}\,(A^{\circ })_{\mathfrak{p}_{x}}-1$; the third line is immediate from the equality ![]() $\text{tr}.\text{deg}\,k(x)/k=\text{dim}\,R/\overline{\mathfrak{p}_{x}}$, which is a standard fact about domains of finite type over a field; the fourth line is trivial; and the fifth line follows from the fact that
$\text{tr}.\text{deg}\,k(x)/k=\text{dim}\,R/\overline{\mathfrak{p}_{x}}$, which is a standard fact about domains of finite type over a field; the fourth line is trivial; and the fifth line follows from the fact that ![]() $R$ is module-finite over
$R$ is module-finite over ![]() $k[T_{1},\ldots ,T_{n}]$ with
$k[T_{1},\ldots ,T_{n}]$ with ![]() $n=\text{dim}\,X$. But then
$n=\text{dim}\,X$. But then
as desired. ◻
3.3 Stein spaces
We end this section with the following slightly more general version of the vanishing theorem.
Corollary 3.4. Let ![]() $X$ be a rigid space over a characteristic-zero complete discretely valued nonarchimedean field
$X$ be a rigid space over a characteristic-zero complete discretely valued nonarchimedean field ![]() $K$ which is weakly Stein in the sense that it admits an admissible covering
$K$ which is weakly Stein in the sense that it admits an admissible covering ![]() $X=\bigcup _{n\geqslant 1}U_{n}$ by a nested sequence of open affinoid subsets
$X=\bigcup _{n\geqslant 1}U_{n}$ by a nested sequence of open affinoid subsets ![]() $U_{1}\subset U_{2}\subset U_{3}\subset \cdots \,$. Let
$U_{1}\subset U_{2}\subset U_{3}\subset \cdots \,$. Let ![]() $\mathscr{F}$ be any Zariski-constructible sheaf of
$\mathscr{F}$ be any Zariski-constructible sheaf of ![]() $\mathbf{Z}/n\mathbf{Z}$-modules on
$\mathbf{Z}/n\mathbf{Z}$-modules on ![]() $X_{\acute{\text{e}}\text{t}}$ for some
$X_{\acute{\text{e}}\text{t}}$ for some ![]() $n$ prime to the residue characteristic of
$n$ prime to the residue characteristic of ![]() $K$. Then
$K$. Then
for all ![]() $i>\text{dim}\,X$.
$i>\text{dim}\,X$.
Proof. By [Reference HuberHub96, Lemma 3.9.2], we have a short exact sequence
But the groups ![]() $H_{\acute{\text{e}}\text{t}}^{j}(U_{i,\widehat{\overline{K}}},\mathscr{F})$ are finite, so the
$H_{\acute{\text{e}}\text{t}}^{j}(U_{i,\widehat{\overline{K}}},\mathscr{F})$ are finite, so the ![]() $\text{lim}^{1}$ term vanishes, and the result now follows from Theorem 1.3.◻
$\text{lim}^{1}$ term vanishes, and the result now follows from Theorem 1.3.◻
This argument also shows that Conjecture 1.2, for a fixed choice of ![]() $C$, is equivalent to the apparently more general conjecture that the cohomology of any Zariski-constructible sheaf on any weakly Stein space
$C$, is equivalent to the apparently more general conjecture that the cohomology of any Zariski-constructible sheaf on any weakly Stein space ![]() $X$ over
$X$ over ![]() $C$ vanishes in all degrees
$C$ vanishes in all degrees ![]() ${>}\text{dim}\,X$.
${>}\text{dim}\,X$.
4 Comparison theorems
4.1 The affinoid comparison theorem
In this section we prove Theorem 1.9. Note that when ![]() $\mathscr{F}$ is a constant sheaf of torsion abelian groups, this theorem is already in Huber’s book [Reference HuberHub96], and we will eventually reduce to this case.
$\mathscr{F}$ is a constant sheaf of torsion abelian groups, this theorem is already in Huber’s book [Reference HuberHub96], and we will eventually reduce to this case.
Let ![]() ${\mathcal{S}}$ and
${\mathcal{S}}$ and ![]() $S$ be as in the statement of the theorem. Before continuing, we note for later use that if
$S$ be as in the statement of the theorem. Before continuing, we note for later use that if ![]() $j:{\mathcal{U}}\rightarrow {\mathcal{S}}$ is any open immersion with closed complement
$j:{\mathcal{U}}\rightarrow {\mathcal{S}}$ is any open immersion with closed complement ![]() $i:{\mathcal{Z}}\rightarrow {\mathcal{S}}$, the four functors
$i:{\mathcal{Z}}\rightarrow {\mathcal{S}}$, the four functors ![]() $j_{!},j^{\ast }$,
$j_{!},j^{\ast }$, ![]() $i_{\ast }$,
$i_{\ast }$, ![]() $i^{\ast }$, and their analytifications can be canonically and functorially commuted with the appropriate
$i^{\ast }$, and their analytifications can be canonically and functorially commuted with the appropriate ![]() $\unicode[STIX]{x1D707}^{\ast }$ in the evident sense. Indeed, for
$\unicode[STIX]{x1D707}^{\ast }$ in the evident sense. Indeed, for ![]() $j^{\ast }$ and
$j^{\ast }$ and ![]() $i^{\ast }$ this is obvious (by taking adjoints of the obvious equivalences
$i^{\ast }$ this is obvious (by taking adjoints of the obvious equivalences ![]() $j_{\ast }\unicode[STIX]{x1D707}_{U\ast }\cong \unicode[STIX]{x1D707}_{S\ast }j_{\ast }^{\text{an}}$ and
$j_{\ast }\unicode[STIX]{x1D707}_{U\ast }\cong \unicode[STIX]{x1D707}_{S\ast }j_{\ast }^{\text{an}}$ and ![]() $i_{\ast }\unicode[STIX]{x1D707}_{Z\ast }\cong \unicode[STIX]{x1D707}_{X\ast }i_{\ast }^{\text{an}}$), for
$i_{\ast }\unicode[STIX]{x1D707}_{Z\ast }\cong \unicode[STIX]{x1D707}_{X\ast }i_{\ast }^{\text{an}}$), for ![]() $j_{!}$ it follows by taking adjoints of the equivalence
$j_{!}$ it follows by taking adjoints of the equivalence ![]() $j^{\ast }\unicode[STIX]{x1D707}_{S\ast }\cong \unicode[STIX]{x1D707}_{U\ast }j^{\text{an}\ast }$ (which holds by ‘base change for a slice’), and for
$j^{\ast }\unicode[STIX]{x1D707}_{S\ast }\cong \unicode[STIX]{x1D707}_{U\ast }j^{\text{an}\ast }$ (which holds by ‘base change for a slice’), and for ![]() $i_{\ast }$ it is a very special case of [Reference HuberHub96, Theorem 3.7.2]. Moreover, if
$i_{\ast }$ it is a very special case of [Reference HuberHub96, Theorem 3.7.2]. Moreover, if ![]() $f:{\mathcal{Y}}\rightarrow {\mathcal{S}}$ is any finite morphism with analytification
$f:{\mathcal{Y}}\rightarrow {\mathcal{S}}$ is any finite morphism with analytification ![]() $f^{\text{an}}:Y=\text{Spa}\,B\rightarrow X$, then
$f^{\text{an}}:Y=\text{Spa}\,B\rightarrow X$, then ![]() $\unicode[STIX]{x1D707}_{X}^{\ast }f_{\ast }\cong f_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{Y}^{\ast }$ (by [Reference HuberHub96, Theorem 3.7.2 and Proposition 2.6.4] again) and
$\unicode[STIX]{x1D707}_{X}^{\ast }f_{\ast }\cong f_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{Y}^{\ast }$ (by [Reference HuberHub96, Theorem 3.7.2 and Proposition 2.6.4] again) and ![]() $\unicode[STIX]{x1D707}_{Y}^{\ast }f^{\ast }\cong f^{\text{an}\ast }\unicode[STIX]{x1D707}_{X}^{\ast }$ (by taking adjoints to the obvious equivalence
$\unicode[STIX]{x1D707}_{Y}^{\ast }f^{\ast }\cong f^{\text{an}\ast }\unicode[STIX]{x1D707}_{X}^{\ast }$ (by taking adjoints to the obvious equivalence ![]() $\unicode[STIX]{x1D707}_{X\ast }f_{\ast }^{\text{an}}\cong f_{\ast }\unicode[STIX]{x1D707}_{Y\ast }$). We will use all of these compatibilities without further comment.
$\unicode[STIX]{x1D707}_{X\ast }f_{\ast }^{\text{an}}\cong f_{\ast }\unicode[STIX]{x1D707}_{Y\ast }$). We will use all of these compatibilities without further comment.
Proof of Theorem 1.9.
First, observe that all functors involved in the statement of the theorem commute with filtered colimits: for ![]() $H_{\acute{\text{e}}\text{t}}^{n}({\mathcal{S}},-)$ this is standard, for
$H_{\acute{\text{e}}\text{t}}^{n}({\mathcal{S}},-)$ this is standard, for ![]() $H_{\acute{\text{e}}\text{t}}^{n}(S,-)$ this follows from [Reference HuberHub96, Lemma 2.3.13], and for
$H_{\acute{\text{e}}\text{t}}^{n}(S,-)$ this follows from [Reference HuberHub96, Lemma 2.3.13], and for ![]() $\unicode[STIX]{x1D707}_{S}^{\ast }$ it is trivial (because
$\unicode[STIX]{x1D707}_{S}^{\ast }$ it is trivial (because ![]() $\unicode[STIX]{x1D707}_{S}^{\ast }$ is a left adjoint). Writing
$\unicode[STIX]{x1D707}_{S}^{\ast }$ is a left adjoint). Writing ![]() $\mathscr{F}$ as the filtered colimit of its
$\mathscr{F}$ as the filtered colimit of its ![]() $m$-torsion subsheaves, we therefore reduce to the case where
$m$-torsion subsheaves, we therefore reduce to the case where ![]() $\mathscr{F}$ is killed by some integer
$\mathscr{F}$ is killed by some integer ![]() $m\geqslant 1$. Since
$m\geqslant 1$. Since ![]() ${\mathcal{S}}$ is qcqs, we can write any sheaf of
${\mathcal{S}}$ is qcqs, we can write any sheaf of ![]() $\mathbf{Z}/m\mathbf{Z}$-modules on
$\mathbf{Z}/m\mathbf{Z}$-modules on ![]() ${\mathcal{S}}_{\acute{\text{e}}\text{t}}$ as a filtered colimit of constructible sheaves of
${\mathcal{S}}_{\acute{\text{e}}\text{t}}$ as a filtered colimit of constructible sheaves of ![]() $\mathbf{Z}/m\mathbf{Z}$-modules, cf. [Sta17, Tag 03SA], which reduces us further to the case where
$\mathbf{Z}/m\mathbf{Z}$-modules, cf. [Sta17, Tag 03SA], which reduces us further to the case where ![]() $\mathscr{F}$ is a constructible sheaf of
$\mathscr{F}$ is a constructible sheaf of ![]() $\mathbf{Z}/m\mathbf{Z}$-modules.
$\mathbf{Z}/m\mathbf{Z}$-modules.
Next, by repeated application of [Reference Artin, Grothendieck and VerdierSGA4, Proposition IX.2.14(ii)], we may choose a resolution
where each sheaf ![]() $\mathscr{G}^{i}$ is isomorphic to a finite direct sum of sheaves of the form
$\mathscr{G}^{i}$ is isomorphic to a finite direct sum of sheaves of the form ![]() $\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M}$, where
$\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M}$, where ![]() $\unicode[STIX]{x1D70B}:{\mathcal{S}}^{\prime }\rightarrow {\mathcal{S}}$ is a finite morphism and
$\unicode[STIX]{x1D70B}:{\mathcal{S}}^{\prime }\rightarrow {\mathcal{S}}$ is a finite morphism and ![]() $M$ is a finite
$M$ is a finite ![]() $\mathbf{Z}/n\mathbf{Z}$-module. By Lemma 4.1, it then suffices to prove that
$\mathbf{Z}/n\mathbf{Z}$-module. By Lemma 4.1, it then suffices to prove that ![]() $H_{\acute{\text{e}}\text{t}}^{n}({\mathcal{S}},\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M})\rightarrow H_{\acute{\text{e}}\text{t}}^{n}(S,\unicode[STIX]{x1D707}_{S}^{\ast }\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M})$ is an isomorphism for any such
$H_{\acute{\text{e}}\text{t}}^{n}({\mathcal{S}},\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M})\rightarrow H_{\acute{\text{e}}\text{t}}^{n}(S,\unicode[STIX]{x1D707}_{S}^{\ast }\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M})$ is an isomorphism for any such ![]() $\unicode[STIX]{x1D70B}$ and
$\unicode[STIX]{x1D70B}$ and ![]() $M$, and any
$M$, and any ![]() $n$. Using the exactness of
$n$. Using the exactness of ![]() $\unicode[STIX]{x1D70B}_{\ast }$ and
$\unicode[STIX]{x1D70B}_{\ast }$ and ![]() $\unicode[STIX]{x1D70B}_{\ast }^{\text{an}}$ and their compatibility with
$\unicode[STIX]{x1D70B}_{\ast }^{\text{an}}$ and their compatibility with ![]() $\unicode[STIX]{x1D707}$-pullback, one immediately reduces further to the case of constant sheaves, which is exactly [Reference HuberHub96, Corollary 3.2.3].◻
$\unicode[STIX]{x1D707}$-pullback, one immediately reduces further to the case of constant sheaves, which is exactly [Reference HuberHub96, Corollary 3.2.3].◻
In the previous argument we used the following lemma, which is less trivial than it appears. The reader may wish to skip the proof.
Lemma 4.1. Let ![]() $f:{\mathcal{D}}\rightarrow {\mathcal{C}}$ be a morphism of sites and let
$f:{\mathcal{D}}\rightarrow {\mathcal{C}}$ be a morphism of sites and let ![]() $\mathscr{F}^{\bullet }$ be a bounded-below complex of abelian sheaves on
$\mathscr{F}^{\bullet }$ be a bounded-below complex of abelian sheaves on ![]() ${\mathcal{C}}$. Then there is a map of spectral sequences
${\mathcal{C}}$. Then there is a map of spectral sequences
 $$\begin{eqnarray}\displaystyle E_{1}^{i,j}=H^{j}({\mathcal{C}},\mathscr{F}^{i}) & \Rightarrow & \displaystyle H^{i+j}({\mathcal{C}},\mathscr{F}^{\bullet })\nonumber\\ \displaystyle & \Downarrow & \displaystyle \nonumber\\ \displaystyle E_{1}^{\prime i,j}=H^{j}({\mathcal{D}},f^{-1}\mathscr{F}^{i}) & \Rightarrow & \displaystyle H^{i+j}({\mathcal{D}},f^{-1}\mathscr{F}^{\bullet }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{1}^{i,j}=H^{j}({\mathcal{C}},\mathscr{F}^{i}) & \Rightarrow & \displaystyle H^{i+j}({\mathcal{C}},\mathscr{F}^{\bullet })\nonumber\\ \displaystyle & \Downarrow & \displaystyle \nonumber\\ \displaystyle E_{1}^{\prime i,j}=H^{j}({\mathcal{D}},f^{-1}\mathscr{F}^{i}) & \Rightarrow & \displaystyle H^{i+j}({\mathcal{D}},f^{-1}\mathscr{F}^{\bullet }),\nonumber\end{eqnarray}$$ which is given on the ![]() $E_{1}$-page and abutment by the canonical maps
$E_{1}$-page and abutment by the canonical maps ![]() $H^{j}({\mathcal{C}},\mathscr{F}^{i})\rightarrow H^{j}({\mathcal{D}},f^{-1}\mathscr{F}^{i})$ and
$H^{j}({\mathcal{C}},\mathscr{F}^{i})\rightarrow H^{j}({\mathcal{D}},f^{-1}\mathscr{F}^{i})$ and ![]() $H^{j}({\mathcal{C}},\mathscr{F}^{\bullet })\rightarrow H^{j}({\mathcal{D}},f^{-1}\mathscr{F}^{\bullet })$, respectively.
$H^{j}({\mathcal{C}},\mathscr{F}^{\bullet })\rightarrow H^{j}({\mathcal{D}},f^{-1}\mathscr{F}^{\bullet })$, respectively.
Proof. Filter ![]() $\mathscr{F}^{\bullet }$ by the subcomplexes
$\mathscr{F}^{\bullet }$ by the subcomplexes ![]() $F^{i}\mathscr{F}^{\bullet }=[\mathscr{F}^{i}\rightarrow \mathscr{F}^{i+1}\rightarrow \cdots \,]$. By [Sta17, 0BKI], we can choose a filtered complex
$F^{i}\mathscr{F}^{\bullet }=[\mathscr{F}^{i}\rightarrow \mathscr{F}^{i+1}\rightarrow \cdots \,]$. By [Sta17, 0BKI], we can choose a filtered complex ![]() $\mathscr{G}^{\bullet }$ of abelian sheaves on
$\mathscr{G}^{\bullet }$ of abelian sheaves on ![]() ${\mathcal{C}}$ together with a filtered quasi-isomorphism
${\mathcal{C}}$ together with a filtered quasi-isomorphism ![]() $\unicode[STIX]{x1D6FC}:\mathscr{F}^{\bullet }\rightarrow \mathscr{G}^{\bullet }$ such that (for all
$\unicode[STIX]{x1D6FC}:\mathscr{F}^{\bullet }\rightarrow \mathscr{G}^{\bullet }$ such that (for all ![]() $j$)
$j$) ![]() $\mathscr{G}^{\bullet }$ and
$\mathscr{G}^{\bullet }$ and ![]() $\text{gr}^{j}\mathscr{G}^{\bullet }$ are K-injective complexes of injective sheaves and
$\text{gr}^{j}\mathscr{G}^{\bullet }$ are K-injective complexes of injective sheaves and
is a quasi-isomorphism. Unwinding definitions, one checks that the upper spectral sequence in question coincides with the spectral sequence associated with the filtered complex ![]() $\unicode[STIX]{x1D6E4}({\mathcal{C}},\mathscr{G}^{\bullet })$.
$\unicode[STIX]{x1D6E4}({\mathcal{C}},\mathscr{G}^{\bullet })$.
Applying [Sta17, 0BKI] again, we can choose a filtered complex ![]() $\mathscr{H}^{\bullet }$ of abelian sheaves on
$\mathscr{H}^{\bullet }$ of abelian sheaves on ![]() ${\mathcal{D}}$ together with a filtered quasi-isomorphism
${\mathcal{D}}$ together with a filtered quasi-isomorphism ![]() $\unicode[STIX]{x1D6FD}:f^{-1}\mathscr{G}^{\bullet }\rightarrow \mathscr{H}^{\bullet }$ such that (for all
$\unicode[STIX]{x1D6FD}:f^{-1}\mathscr{G}^{\bullet }\rightarrow \mathscr{H}^{\bullet }$ such that (for all ![]() $j$)
$j$) ![]() $\mathscr{H}^{\bullet }$ and
$\mathscr{H}^{\bullet }$ and ![]() $\text{gr}^{j}\mathscr{H}^{\bullet }$ are K-injective complexes of injective sheaves and
$\text{gr}^{j}\mathscr{H}^{\bullet }$ are K-injective complexes of injective sheaves and ![]() $\text{gr}^{j}\unicode[STIX]{x1D6FD}$ is a quasi-isomorphism. Again, one checks directly that the lower spectral sequence identifies with the spectral sequence associated with the filtered complex
$\text{gr}^{j}\unicode[STIX]{x1D6FD}$ is a quasi-isomorphism. Again, one checks directly that the lower spectral sequence identifies with the spectral sequence associated with the filtered complex ![]() $\unicode[STIX]{x1D6E4}({\mathcal{D}},\mathscr{H}^{\bullet })$. By construction, we have filtered maps of filtered complexes
$\unicode[STIX]{x1D6E4}({\mathcal{D}},\mathscr{H}^{\bullet })$. By construction, we have filtered maps of filtered complexes
where the left-hand map exists by general nonsense and the right-hand map is induced by ![]() $\unicode[STIX]{x1D6FD}$. The composition of these maps induces the desired map of spectral sequences.◻
$\unicode[STIX]{x1D6FD}$. The composition of these maps induces the desired map of spectral sequences.◻
4.2 The relative comparison theorem
In this section we prove Theorem 1.8. Fix ![]() $S$,
$S$, ![]() ${\mathcal{S}}$, and
${\mathcal{S}}$, and ![]() $\unicode[STIX]{x1D6EC}$ as in the theorem. In what follows we will write
$\unicode[STIX]{x1D6EC}$ as in the theorem. In what follows we will write ![]() ${\mathcal{X}},{\mathcal{Y}},{\mathcal{U}}$, etc., for schemes locally of finite type over
${\mathcal{X}},{\mathcal{Y}},{\mathcal{U}}$, etc., for schemes locally of finite type over ![]() ${\mathcal{S}}$, and
${\mathcal{S}}$, and ![]() $X,Y,U$, etc., for the corresponding rigid analytic spaces over
$X,Y,U$, etc., for the corresponding rigid analytic spaces over ![]() $S$. If
$S$. If ![]() $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ is a finite-type morphism as in the theorem, then for any
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ is a finite-type morphism as in the theorem, then for any ![]() $F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$ we write
$F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$ we write ![]() $\text{comp}(f,F)$ for the natural base change map
$\text{comp}(f,F)$ for the natural base change map ![]() $\unicode[STIX]{x1D707}_{Y}^{\ast }Rf_{\ast }F\rightarrow Rf_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{X}^{\ast }F$. For brevity, we will say that ‘
$\unicode[STIX]{x1D707}_{Y}^{\ast }Rf_{\ast }F\rightarrow Rf_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{X}^{\ast }F$. For brevity, we will say that ‘![]() $\text{comp}(f)$ is an isomorphism’ if the map
$\text{comp}(f)$ is an isomorphism’ if the map ![]() $\text{comp}(f,F)$ is an isomorphism in
$\text{comp}(f,F)$ is an isomorphism in ![]() $D(Y,\unicode[STIX]{x1D6EC})$ for every
$D(Y,\unicode[STIX]{x1D6EC})$ for every ![]() $F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$. (In general, it is not true that the base change map
$F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$. (In general, it is not true that the base change map ![]() $\unicode[STIX]{x1D707}_{Y}^{\ast }Rf_{\ast }\rightarrow Rf_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{X}^{\ast }$ is a natural isomorphism of functors.)
$\unicode[STIX]{x1D707}_{Y}^{\ast }Rf_{\ast }\rightarrow Rf_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{X}^{\ast }$ is a natural isomorphism of functors.)
Before beginning the proof, we collect some preliminary observations. We will freely use the following result, which is well known to experts.
Proposition 4.2 (Grothendieck, Gabber).
Let ![]() $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ be a finite-type morphism between quasi-excellent Noetherian schemes, and let
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ be a finite-type morphism between quasi-excellent Noetherian schemes, and let ![]() $\unicode[STIX]{x1D6EC}$ be a Noetherian ring killed by some positive integer invertible on
$\unicode[STIX]{x1D6EC}$ be a Noetherian ring killed by some positive integer invertible on ![]() ${\mathcal{Y}}$. Then the functor
${\mathcal{Y}}$. Then the functor ![]() $Rf_{\ast }:D({\mathcal{X}},\unicode[STIX]{x1D6EC})\rightarrow D({\mathcal{Y}},\unicode[STIX]{x1D6EC})$ preserves constructibility; more precisely, it carries
$Rf_{\ast }:D({\mathcal{X}},\unicode[STIX]{x1D6EC})\rightarrow D({\mathcal{Y}},\unicode[STIX]{x1D6EC})$ preserves constructibility; more precisely, it carries ![]() $D_{c}^{b}({\mathcal{X}},\unicode[STIX]{x1D6EC})$ into
$D_{c}^{b}({\mathcal{X}},\unicode[STIX]{x1D6EC})$ into ![]() $D_{c}^{b}({\mathcal{Y}},\unicode[STIX]{x1D6EC})$.
$D_{c}^{b}({\mathcal{Y}},\unicode[STIX]{x1D6EC})$.
Proof. Cover ![]() ${\mathcal{X}}$ by open affines
${\mathcal{X}}$ by open affines ![]() ${\mathcal{X}}_{i},0\leqslant i\leqslant n$; for any
${\mathcal{X}}_{i},0\leqslant i\leqslant n$; for any ![]() $0\leqslant i_{1}<\cdots <i_{p}\leqslant n$, set
$0\leqslant i_{1}<\cdots <i_{p}\leqslant n$, set ![]() ${\mathcal{X}}_{i_{1}<\cdots <i_{p}}=\bigcap _{1\leqslant j\leqslant p}{\mathcal{X}}_{i_{j}}$, so each
${\mathcal{X}}_{i_{1}<\cdots <i_{p}}=\bigcap _{1\leqslant j\leqslant p}{\mathcal{X}}_{i_{j}}$, so each ![]() ${\mathcal{X}}_{i_{1}<\cdots <i_{p}}$ is a separated open subscheme of
${\mathcal{X}}_{i_{1}<\cdots <i_{p}}$ is a separated open subscheme of ![]() ${\mathcal{X}}$. Let
${\mathcal{X}}$. Let ![]() $f_{i_{1}<\cdots <i_{p}}:{\mathcal{X}}_{i_{1}<\cdots <i_{p}}\rightarrow {\mathcal{Y}}$ be the evident morphism. Looking at the Čech spectral sequence
$f_{i_{1}<\cdots <i_{p}}:{\mathcal{X}}_{i_{1}<\cdots <i_{p}}\rightarrow {\mathcal{Y}}$ be the evident morphism. Looking at the Čech spectral sequence
it suffices to show that each ![]() $R(f_{i_{1}<\cdots <i_{p}})_{\ast }$ sends
$R(f_{i_{1}<\cdots <i_{p}})_{\ast }$ sends ![]() $D_{c}^{b}({\mathcal{X}}_{i_{1}<\cdots <i_{p}},\unicode[STIX]{x1D6EC})$ into
$D_{c}^{b}({\mathcal{X}}_{i_{1}<\cdots <i_{p}},\unicode[STIX]{x1D6EC})$ into ![]() $D_{c}^{b}({\mathcal{Y}},\unicode[STIX]{x1D6EC})$. In particular, it suffices to consider the case where
$D_{c}^{b}({\mathcal{Y}},\unicode[STIX]{x1D6EC})$. In particular, it suffices to consider the case where ![]() ${\mathcal{X}}$ is separated. Since
${\mathcal{X}}$ is separated. Since ![]() $f$ is then separated, by Nagata’s compactification theorem we may choose a factorization
$f$ is then separated, by Nagata’s compactification theorem we may choose a factorization ![]() $f=\overline{f}\circ j$, where
$f=\overline{f}\circ j$, where ![]() $\overline{f}:{\mathcal{X}}^{\prime }\rightarrow {\mathcal{Y}}$ is proper and
$\overline{f}:{\mathcal{X}}^{\prime }\rightarrow {\mathcal{Y}}$ is proper and ![]() $j:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }$ is an open immersion. Combining [Reference Illusie, Laszlo and OrgogozoILO14, Theorem XIII.1.1.1] and [Reference Illusie, Laszlo and OrgogozoILO14, Proposition XVII.7.6.7], we see that
$j:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }$ is an open immersion. Combining [Reference Illusie, Laszlo and OrgogozoILO14, Theorem XIII.1.1.1] and [Reference Illusie, Laszlo and OrgogozoILO14, Proposition XVII.7.6.7], we see that ![]() $Rj_{\ast }$ sends
$Rj_{\ast }$ sends ![]() $D_{c}^{b}({\mathcal{X}},\unicode[STIX]{x1D6EC})$ into
$D_{c}^{b}({\mathcal{X}},\unicode[STIX]{x1D6EC})$ into ![]() $D_{c}^{b}({\mathcal{X}}^{\prime },\unicode[STIX]{x1D6EC})$. By [Reference Artin, Grothendieck and VerdierSGA4, Theorem XIV.1.1],
$D_{c}^{b}({\mathcal{X}}^{\prime },\unicode[STIX]{x1D6EC})$. By [Reference Artin, Grothendieck and VerdierSGA4, Theorem XIV.1.1], ![]() $R\overline{f}_{\ast }$ sends
$R\overline{f}_{\ast }$ sends ![]() $D_{c}^{b}({\mathcal{X}}^{\prime },\unicode[STIX]{x1D6EC})$ into
$D_{c}^{b}({\mathcal{X}}^{\prime },\unicode[STIX]{x1D6EC})$ into ![]() $D_{c}^{b}({\mathcal{Y}},\unicode[STIX]{x1D6EC})$. Since
$D_{c}^{b}({\mathcal{Y}},\unicode[STIX]{x1D6EC})$. Since ![]() $Rf_{\ast }\cong R\overline{f}_{\ast }Rj_{\ast }$, this gives the result.◻
$Rf_{\ast }\cong R\overline{f}_{\ast }Rj_{\ast }$, this gives the result.◻
Proposition 4.3. Let ![]() $h:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ and
$h:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ and ![]() $g:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$ be finite-type morphisms of locally finite-type
$g:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$ be finite-type morphisms of locally finite-type ![]() ${\mathcal{S}}$-schemes.
${\mathcal{S}}$-schemes.
(i) If
 $\text{comp}(h)$ and
$\text{comp}(h)$ and  $\text{comp}(g)$ are isomorphisms, then so is
$\text{comp}(g)$ are isomorphisms, then so is  $\text{comp}(g\circ h)$.
$\text{comp}(g\circ h)$.(ii) If
 $\text{comp}(h)$ and
$\text{comp}(h)$ and  $\text{comp}(g\circ h)$ are isomorphisms, then
$\text{comp}(g\circ h)$ are isomorphisms, then  $\text{comp}(g,Rh_{\ast }F)$ is an isomorphism for every
$\text{comp}(g,Rh_{\ast }F)$ is an isomorphism for every  $F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$.
$F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$.(iii) (2-out-of-3 property) If
 $F_{1}\rightarrow F_{2}\rightarrow F_{3}\rightarrow$ is a distinguished triangle in
$F_{1}\rightarrow F_{2}\rightarrow F_{3}\rightarrow$ is a distinguished triangle in  $D({\mathcal{X}},\unicode[STIX]{x1D6EC})$ such that two of the three maps
$D({\mathcal{X}},\unicode[STIX]{x1D6EC})$ such that two of the three maps  $\text{comp}(h,F_{i})$ are isomorphisms, then so is the third.
$\text{comp}(h,F_{i})$ are isomorphisms, then so is the third.
Proof. Part (i) is a special case of the composability of base change maps; cf. [Sta17, Tag 0E46]. For (ii), consider the composition
where the first arrow is ![]() $\text{comp}(g,Rh_{\ast }F)$ and the second arrow is
$\text{comp}(g,Rh_{\ast }F)$ and the second arrow is ![]() $Rg_{\ast }^{\text{an}}\text{comp}(h,F)$. By the composability of base change maps, this composition is the comparison map
$Rg_{\ast }^{\text{an}}\text{comp}(h,F)$. By the composability of base change maps, this composition is the comparison map ![]() $\text{comp}(g\circ h,F)$. By our assumptions, the second arrow and the composition of both arrows are isomorphisms. We then conclude by observing that if
$\text{comp}(g\circ h,F)$. By our assumptions, the second arrow and the composition of both arrows are isomorphisms. We then conclude by observing that if ![]() $A\overset{s}{\rightarrow }B\overset{t}{\rightarrow }C$ is any pair of morphisms in any category such that
$A\overset{s}{\rightarrow }B\overset{t}{\rightarrow }C$ is any pair of morphisms in any category such that ![]() $t$ and
$t$ and ![]() $t\circ s$ are isomorphisms, then
$t\circ s$ are isomorphisms, then ![]() $s$ is an isomorphism as well.
$s$ is an isomorphism as well.
Part (iii) is an easy exercise, using the fact that the three maps ![]() $\text{comp}(h,F_{i})$ define a morphism between the evident distinguished triangles.◻
$\text{comp}(h,F_{i})$ define a morphism between the evident distinguished triangles.◻
Proposition 4.4. Suppose that ![]() $\text{comp}(j)$ is an isomorphism for all open immersions
$\text{comp}(j)$ is an isomorphism for all open immersions ![]() $j:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ of locally finite-type
$j:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ of locally finite-type ![]() ${\mathcal{S}}$-schemes. Then Theorem 1.8 is true.
${\mathcal{S}}$-schemes. Then Theorem 1.8 is true.
Proof. First, we show that if ![]() $\text{comp}(j)$ is an isomorphism for all open immersions, then
$\text{comp}(j)$ is an isomorphism for all open immersions, then ![]() $\text{comp}(f)$ is an isomorphism for all separated maps. For this, let
$\text{comp}(f)$ is an isomorphism for all separated maps. For this, let ![]() $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ be as in Theorem 1.8 and suppose that
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ be as in Theorem 1.8 and suppose that ![]() $f$ is separated. We can argue locally on
$f$ is separated. We can argue locally on ![]() ${\mathcal{Y}}$, so we can assume that
${\mathcal{Y}}$, so we can assume that ![]() ${\mathcal{Y}}$ is affine. By Nagata’s compactification theorem, we may choose a factorization
${\mathcal{Y}}$ is affine. By Nagata’s compactification theorem, we may choose a factorization ![]() $f=\overline{f}\circ j$, where
$f=\overline{f}\circ j$, where ![]() $\overline{f}:{\mathcal{X}}^{\prime }\rightarrow {\mathcal{Y}}$ is proper and
$\overline{f}:{\mathcal{X}}^{\prime }\rightarrow {\mathcal{Y}}$ is proper and ![]() $j:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }$ is an open immersion. Then
$j:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }$ is an open immersion. Then ![]() $\text{comp}(j)$ is an isomorphism by assumption, and
$\text{comp}(j)$ is an isomorphism by assumption, and ![]() $\text{comp}(\overline{f})$ is an isomorphism by Berkovich and Huber’s proof of the proper case. We then conclude by part (i) of the previous proposition.
$\text{comp}(\overline{f})$ is an isomorphism by Berkovich and Huber’s proof of the proper case. We then conclude by part (i) of the previous proposition.
For the general case, we can assume that ![]() ${\mathcal{Y}}$ is affine, so
${\mathcal{Y}}$ is affine, so ![]() ${\mathcal{X}}$ is quasicompact. We now argue by induction on the minimal number
${\mathcal{X}}$ is quasicompact. We now argue by induction on the minimal number ![]() $s({\mathcal{X}})$ of separated open subschemes required to cover
$s({\mathcal{X}})$ of separated open subschemes required to cover ![]() ${\mathcal{X}}$. Choose an open cover
${\mathcal{X}}$. Choose an open cover ![]() ${\mathcal{X}}={\mathcal{U}}\cup {\mathcal{V}}$, where
${\mathcal{X}}={\mathcal{U}}\cup {\mathcal{V}}$, where ![]() ${\mathcal{U}}$ is separated and
${\mathcal{U}}$ is separated and ![]() $s({\mathcal{V}})=s({\mathcal{X}})-1$. Note that
$s({\mathcal{V}})=s({\mathcal{X}})-1$. Note that ![]() ${\mathcal{U}}\cap {\mathcal{V}}$ is separated. Let
${\mathcal{U}}\cap {\mathcal{V}}$ is separated. Let ![]() $j_{{\mathcal{U}}}:{\mathcal{U}}\rightarrow {\mathcal{X}}$,
$j_{{\mathcal{U}}}:{\mathcal{U}}\rightarrow {\mathcal{X}}$, ![]() $j_{{\mathcal{V}}}:{\mathcal{V}}\rightarrow {\mathcal{X}}$, and
$j_{{\mathcal{V}}}:{\mathcal{V}}\rightarrow {\mathcal{X}}$, and ![]() $j_{{\mathcal{U}}\cap {\mathcal{V}}}:{\mathcal{U}}\cap {\mathcal{V}}\rightarrow {\mathcal{X}}$ be the evident open inclusions, so we get a functorial distinguished triangle
$j_{{\mathcal{U}}\cap {\mathcal{V}}}:{\mathcal{U}}\cap {\mathcal{V}}\rightarrow {\mathcal{X}}$ be the evident open inclusions, so we get a functorial distinguished triangle
for any ![]() $F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$. Applying
$F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$. Applying ![]() $Rf_{\ast }$, the comparison maps
$Rf_{\ast }$, the comparison maps ![]() $\text{comp}(f,-)$ fit together into a morphism
$\text{comp}(f,-)$ fit together into a morphism

of distinguished triangles. For each ![]() $\bullet \in \{{\mathcal{U}},{\mathcal{V}},{\mathcal{U}}\cap {\mathcal{V}}\}$, the maps
$\bullet \in \{{\mathcal{U}},{\mathcal{V}},{\mathcal{U}}\cap {\mathcal{V}}\}$, the maps ![]() $\text{comp}(j_{\bullet })$ are isomorphisms by assumption; by induction on
$\text{comp}(j_{\bullet })$ are isomorphisms by assumption; by induction on ![]() $s$, the maps
$s$, the maps ![]() $\text{comp}(f\circ j_{\bullet })$ are isomorphisms as well. Applying part (ii) of the previous proposition with
$\text{comp}(f\circ j_{\bullet })$ are isomorphisms as well. Applying part (ii) of the previous proposition with ![]() $g=f$ and
$g=f$ and ![]() $h=j_{\bullet }$, we see that the maps
$h=j_{\bullet }$, we see that the maps ![]() $(2)$ and
$(2)$ and ![]() $(3)$ are both isomorphisms. By the 2-out-of-3 property, the morphism
$(3)$ are both isomorphisms. By the 2-out-of-3 property, the morphism ![]() $(1)$ is therefore an isomorphism, as desired.◻
$(1)$ is therefore an isomorphism, as desired.◻
Proposition 4.5. Suppose that ![]() $\text{comp}(h,\text{}\underline{M})$ is an isomorphism for any open immersion
$\text{comp}(h,\text{}\underline{M})$ is an isomorphism for any open immersion ![]() $h:{\mathcal{U}}\rightarrow {\mathcal{V}}$ of locally finite-type
$h:{\mathcal{U}}\rightarrow {\mathcal{V}}$ of locally finite-type ![]() ${\mathcal{S}}$-schemes and any constant constructible sheaf of
${\mathcal{S}}$-schemes and any constant constructible sheaf of ![]() $\unicode[STIX]{x1D6EC}$-modules
$\unicode[STIX]{x1D6EC}$-modules ![]() $\text{}\underline{M}$ on
$\text{}\underline{M}$ on ![]() ${\mathcal{U}}$. Then Theorem 1.8 is true.
${\mathcal{U}}$. Then Theorem 1.8 is true.
Proof. By the previous proposition, it suffices to deduce under these assumptions that ![]() $\text{comp}(j,F)$ is an isomorphism for any open immersion
$\text{comp}(j,F)$ is an isomorphism for any open immersion ![]() $j:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ and any
$j:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ and any ![]() $F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$. We can clearly assume that
$F\in D_{c}^{+}({\mathcal{X}},\unicode[STIX]{x1D6EC})$. We can clearly assume that ![]() ${\mathcal{Y}}$ is affine and that
${\mathcal{Y}}$ is affine and that ![]() $j$ has dense image. We can also assume that
$j$ has dense image. We can also assume that ![]() $F=\mathscr{F}$ is a constructible sheaf (placed in degree zero). As in the proof of Theorem 1.9, we may choose an isomorphism
$F=\mathscr{F}$ is a constructible sheaf (placed in degree zero). As in the proof of Theorem 1.9, we may choose an isomorphism
where each sheaf ![]() $\mathscr{G}^{i}$ is isomorphic to a finite direct sum of sheaves of the form
$\mathscr{G}^{i}$ is isomorphic to a finite direct sum of sheaves of the form ![]() $\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M}$, where
$\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M}$, where ![]() $\unicode[STIX]{x1D70B}:{\mathcal{U}}\rightarrow {\mathcal{X}}$ is a finite morphism and
$\unicode[STIX]{x1D70B}:{\mathcal{U}}\rightarrow {\mathcal{X}}$ is a finite morphism and ![]() $\text{}\underline{M}$ is a constant constructible sheaf of
$\text{}\underline{M}$ is a constant constructible sheaf of ![]() $\unicode[STIX]{x1D6EC}$-modules on
$\unicode[STIX]{x1D6EC}$-modules on ![]() ${\mathcal{U}}$. By an easy variant of the spectral sequence argument used in the proof of Theorem 1.9, it suffices to prove that
${\mathcal{U}}$. By an easy variant of the spectral sequence argument used in the proof of Theorem 1.9, it suffices to prove that ![]() $\text{comp}(j,\mathscr{G}^{i})$ is an isomorphism for all
$\text{comp}(j,\mathscr{G}^{i})$ is an isomorphism for all ![]() $i$. In particular, it suffices to prove that
$i$. In particular, it suffices to prove that ![]() $\text{comp}(j,\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M})$ is an isomorphism for any finite morphism
$\text{comp}(j,\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M})$ is an isomorphism for any finite morphism ![]() $\unicode[STIX]{x1D70B}:{\mathcal{U}}\rightarrow {\mathcal{X}}$ and any constant constructible sheaf
$\unicode[STIX]{x1D70B}:{\mathcal{U}}\rightarrow {\mathcal{X}}$ and any constant constructible sheaf ![]() $\text{}\underline{M}$ as above.
$\text{}\underline{M}$ as above.
Fix such a ![]() $\unicode[STIX]{x1D70B}$ and
$\unicode[STIX]{x1D70B}$ and ![]() $\text{}\underline{M}$. By Zariski’s main theorem, we can choose a commutative diagram
$\text{}\underline{M}$. By Zariski’s main theorem, we can choose a commutative diagram

where ![]() $h$ is an open immersion and
$h$ is an open immersion and ![]() $\unicode[STIX]{x1D70F}$ is finite. In what follows, we freely use the facts that
$\unicode[STIX]{x1D70F}$ is finite. In what follows, we freely use the facts that ![]() $\unicode[STIX]{x1D70B}_{\ast }=R\unicode[STIX]{x1D70B}_{\ast }$ and
$\unicode[STIX]{x1D70B}_{\ast }=R\unicode[STIX]{x1D70B}_{\ast }$ and ![]() $\unicode[STIX]{x1D70F}=R\unicode[STIX]{x1D70F}_{\ast }$, and likewise for
$\unicode[STIX]{x1D70F}=R\unicode[STIX]{x1D70F}_{\ast }$, and likewise for ![]() $\unicode[STIX]{x1D70B}^{\text{an}}$ and
$\unicode[STIX]{x1D70B}^{\text{an}}$ and ![]() $\unicode[STIX]{x1D70F}^{\text{an}}$; we also freely use the fact that
$\unicode[STIX]{x1D70F}^{\text{an}}$; we also freely use the fact that ![]() $\text{comp}(\unicode[STIX]{x1D70B})$ is an isomorphism for any finite morphism
$\text{comp}(\unicode[STIX]{x1D70B})$ is an isomorphism for any finite morphism ![]() $\unicode[STIX]{x1D70B}$. Consider the sequence of canonical isomorphisms
$\unicode[STIX]{x1D70B}$. Consider the sequence of canonical isomorphisms
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{Y}^{\ast }Rj_{\ast }\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M} & \cong & \displaystyle \unicode[STIX]{x1D707}_{Y}^{\ast }R(j\circ \unicode[STIX]{x1D70B})_{\ast }\text{}\underline{M}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D707}_{Y}^{\ast }R(\unicode[STIX]{x1D70F}\circ h)_{\ast }\text{}\underline{M}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D707}_{Y}^{\ast }\unicode[STIX]{x1D70F}_{\ast }Rh_{\ast }\text{}\underline{M}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70F}_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{V}^{\ast }Rh_{\ast }\text{}\underline{M}\nonumber\\ \displaystyle & \overset{(\ast )}{\cong } & \displaystyle \unicode[STIX]{x1D70F}_{\ast }^{\text{an}}Rh_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{U}^{\ast }\text{}\underline{M}\nonumber\\ \displaystyle & \cong & \displaystyle Rj_{\ast }^{\text{an}}\unicode[STIX]{x1D70B}_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{U}^{\ast }\text{}\underline{M}\nonumber\\ \displaystyle & \cong & \displaystyle Rj_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{X}^{\ast }\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{Y}^{\ast }Rj_{\ast }\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M} & \cong & \displaystyle \unicode[STIX]{x1D707}_{Y}^{\ast }R(j\circ \unicode[STIX]{x1D70B})_{\ast }\text{}\underline{M}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D707}_{Y}^{\ast }R(\unicode[STIX]{x1D70F}\circ h)_{\ast }\text{}\underline{M}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D707}_{Y}^{\ast }\unicode[STIX]{x1D70F}_{\ast }Rh_{\ast }\text{}\underline{M}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70F}_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{V}^{\ast }Rh_{\ast }\text{}\underline{M}\nonumber\\ \displaystyle & \overset{(\ast )}{\cong } & \displaystyle \unicode[STIX]{x1D70F}_{\ast }^{\text{an}}Rh_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{U}^{\ast }\text{}\underline{M}\nonumber\\ \displaystyle & \cong & \displaystyle Rj_{\ast }^{\text{an}}\unicode[STIX]{x1D70B}_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{U}^{\ast }\text{}\underline{M}\nonumber\\ \displaystyle & \cong & \displaystyle Rj_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{X}^{\ast }\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M},\nonumber\end{eqnarray}$$ where the starred isomorphism is the map ![]() $\unicode[STIX]{x1D70F}_{\ast }^{\text{an}}\text{comp}(h,\text{}\underline{M})$. One checks directly that the composition of these maps coincides with
$\unicode[STIX]{x1D70F}_{\ast }^{\text{an}}\text{comp}(h,\text{}\underline{M})$. One checks directly that the composition of these maps coincides with ![]() $\text{comp}(j,\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M})$, so the latter is an isomorphism, as desired.◻
$\text{comp}(j,\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{M})$, so the latter is an isomorphism, as desired.◻
Proposition 4.6. Suppose that ![]() $\text{comp}(h,\text{}\underline{M})$ is an isomorphism for any open immersion
$\text{comp}(h,\text{}\underline{M})$ is an isomorphism for any open immersion ![]() $h:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ of regular finite-type
$h:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ of regular finite-type ![]() ${\mathcal{S}}$-schemes and any constant constructible sheaf
${\mathcal{S}}$-schemes and any constant constructible sheaf ![]() $\text{}\underline{M}$ of
$\text{}\underline{M}$ of ![]() $\unicode[STIX]{x1D6EC}$-modules. Then Theorem 1.8 is true.
$\unicode[STIX]{x1D6EC}$-modules. Then Theorem 1.8 is true.
Proof. By the previous proposition, it suffices to show that the hypothesis of the proposition implies that ![]() $\text{comp}(j,F)$ is an isomorphism for any open immersion
$\text{comp}(j,F)$ is an isomorphism for any open immersion ![]() $j:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ of finite-type
$j:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ of finite-type ![]() ${\mathcal{S}}$-schemes and any constant constructible sheaf
${\mathcal{S}}$-schemes and any constant constructible sheaf ![]() $\text{}\underline{M}$ on
$\text{}\underline{M}$ on ![]() ${\mathcal{X}}$.
${\mathcal{X}}$.
Fix such a choice of ![]() $j$ and
$j$ and ![]() $\text{}\underline{M}$. We can clearly assume that
$\text{}\underline{M}$. We can clearly assume that ![]() ${\mathcal{Y}}$ is affine. By the topological invariant of the étale site, we can also assume that
${\mathcal{Y}}$ is affine. By the topological invariant of the étale site, we can also assume that ![]() ${\mathcal{Y}}$ and
${\mathcal{Y}}$ and ![]() ${\mathcal{X}}$ are reduced. Choose a dense open regular subscheme
${\mathcal{X}}$ are reduced. Choose a dense open regular subscheme ![]() $g:{\mathcal{U}}\rightarrow {\mathcal{X}}$ with closed complement
$g:{\mathcal{U}}\rightarrow {\mathcal{X}}$ with closed complement ![]() $i:{\mathcal{Z}}\rightarrow {\mathcal{X}}$, so we get a distinguished triangle
$i:{\mathcal{Z}}\rightarrow {\mathcal{X}}$, so we get a distinguished triangle
By induction on ![]() $\text{dim}\,\text{supp}$, we can assume that
$\text{dim}\,\text{supp}$, we can assume that ![]() $\text{comp}(j,i_{\ast }i^{!}\text{}\underline{M})$ is an isomorphism. By the 2-out-of-3 property, it now suffices to prove that
$\text{comp}(j,i_{\ast }i^{!}\text{}\underline{M})$ is an isomorphism. By the 2-out-of-3 property, it now suffices to prove that ![]() $\text{comp}(j,Rg_{\ast }g^{\ast }\text{}\underline{M})$ is an isomorphism. By another application of Proposition 4.3(ii), we observe that the latter map is an isomorphism if both
$\text{comp}(j,Rg_{\ast }g^{\ast }\text{}\underline{M})$ is an isomorphism. By another application of Proposition 4.3(ii), we observe that the latter map is an isomorphism if both ![]() $\text{comp}(g,g^{\ast }\text{}\underline{M})$ and
$\text{comp}(g,g^{\ast }\text{}\underline{M})$ and ![]() $\text{comp}(j\circ g,g^{\ast }\text{}\underline{M})$ are isomorphisms. In particular, we are reduced to showing that
$\text{comp}(j\circ g,g^{\ast }\text{}\underline{M})$ are isomorphisms. In particular, we are reduced to showing that ![]() $\text{comp}(h,\text{}\underline{M})$ is an isomorphism for any open immersion
$\text{comp}(h,\text{}\underline{M})$ is an isomorphism for any open immersion ![]() $h:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ of reduced finite-type
$h:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ of reduced finite-type ![]() ${\mathcal{S}}$-schemes with
${\mathcal{S}}$-schemes with ![]() ${\mathcal{X}}$ regular.
${\mathcal{X}}$ regular.
Since ![]() ${\mathcal{Y}}$ is regular, by applying the results of [Reference TemkinTem17] we can choose a commutative diagram
${\mathcal{Y}}$ is regular, by applying the results of [Reference TemkinTem17] we can choose a commutative diagram

where ![]() $\tilde{h}$ is a dense open embedding of regular finite-type
$\tilde{h}$ is a dense open embedding of regular finite-type ![]() ${\mathcal{S}}$-schemes and
${\mathcal{S}}$-schemes and ![]() $f$ is a proper birational morphism. In particular,
$f$ is a proper birational morphism. In particular, ![]() $\text{comp}(f)$ is an isomorphism. By the hypotheses of the proposition,
$\text{comp}(f)$ is an isomorphism. By the hypotheses of the proposition, ![]() $\text{comp}(\tilde{h},\text{}\underline{M})$ is an isomorphism as well. Arguing as in the proof of Proposition 4.3(ii), one deduces that
$\text{comp}(\tilde{h},\text{}\underline{M})$ is an isomorphism as well. Arguing as in the proof of Proposition 4.3(ii), one deduces that ![]() $\text{comp}(h,\text{}\underline{M})$ is an isomorphism.◻
$\text{comp}(h,\text{}\underline{M})$ is an isomorphism.◻
Proposition 4.7. Let ![]() $S$,
$S$, ![]() ${\mathcal{S}}$, and
${\mathcal{S}}$, and ![]() $\unicode[STIX]{x1D6EC}$ be as in the statement of Theorem 1.8. Then for any open immersion
$\unicode[STIX]{x1D6EC}$ be as in the statement of Theorem 1.8. Then for any open immersion ![]() $h:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ of regular finite-type
$h:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ of regular finite-type ![]() ${\mathcal{S}}$-schemes and any constant constructible sheaf of
${\mathcal{S}}$-schemes and any constant constructible sheaf of ![]() $\unicode[STIX]{x1D6EC}$-modules
$\unicode[STIX]{x1D6EC}$-modules ![]() $\text{}\underline{M}$, the map
$\text{}\underline{M}$, the map ![]() $\text{comp}(h,\text{}\underline{M})$ is an isomorphism.
$\text{comp}(h,\text{}\underline{M})$ is an isomorphism.
Proof. This follows exactly as in the final stages of the proof of [Reference Artin, Grothendieck and VerdierSGA4, Theorem XVI.4.1], with the appeal to results in [Reference Artin, Grothendieck and VerdierSGA4, § XVI.3] replaced by Huber’s cohomological purity theorem [Reference HuberHub96, Theorem 3.9.1]. ◻
Putting together the previous two propositions, Theorem 1.8 follows.
4.3 Applications
Proof of Theorem 1.10.
For the first part of (i), we compute that
 $$\begin{eqnarray}\displaystyle R\unicode[STIX]{x1D6E4}({\mathcal{X}},F) & \overset{(1)}{\cong } & \displaystyle R\unicode[STIX]{x1D6E4}({\mathcal{S}},Rf_{\ast }F)\nonumber\\ \displaystyle & \overset{(2)}{\cong } & \displaystyle R\unicode[STIX]{x1D6E4}(S,\unicode[STIX]{x1D707}_{S}^{\ast }Rf_{\ast }F)\nonumber\\ \displaystyle & \overset{(3)}{\cong } & \displaystyle R\unicode[STIX]{x1D6E4}(S,Rf_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{X}^{\ast }F)\nonumber\\ \displaystyle & \overset{(4)}{\cong } & \displaystyle R\unicode[STIX]{x1D6E4}(X,\unicode[STIX]{x1D707}_{X}^{\ast }F),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R\unicode[STIX]{x1D6E4}({\mathcal{X}},F) & \overset{(1)}{\cong } & \displaystyle R\unicode[STIX]{x1D6E4}({\mathcal{S}},Rf_{\ast }F)\nonumber\\ \displaystyle & \overset{(2)}{\cong } & \displaystyle R\unicode[STIX]{x1D6E4}(S,\unicode[STIX]{x1D707}_{S}^{\ast }Rf_{\ast }F)\nonumber\\ \displaystyle & \overset{(3)}{\cong } & \displaystyle R\unicode[STIX]{x1D6E4}(S,Rf_{\ast }^{\text{an}}\unicode[STIX]{x1D707}_{X}^{\ast }F)\nonumber\\ \displaystyle & \overset{(4)}{\cong } & \displaystyle R\unicode[STIX]{x1D6E4}(X,\unicode[STIX]{x1D707}_{X}^{\ast }F),\nonumber\end{eqnarray}$$ where (1) and (4) are the evident Leray isomorphisms, (2) follows from Theorem 1.9, and (3) follows from Theorem 1.8. For the second part of (i), it suffices to assume that ![]() $F=\mathscr{F}[0]$ is a sheaf. In this case, we need to prove that
$F=\mathscr{F}[0]$ is a sheaf. In this case, we need to prove that ![]() $\mathscr{F}\overset{{\sim}}{\rightarrow }\unicode[STIX]{x1D707}_{X\ast }\unicode[STIX]{x1D707}_{X}^{\ast }\mathscr{F}$ and that
$\mathscr{F}\overset{{\sim}}{\rightarrow }\unicode[STIX]{x1D707}_{X\ast }\unicode[STIX]{x1D707}_{X}^{\ast }\mathscr{F}$ and that ![]() $R^{i}\unicode[STIX]{x1D707}_{X\ast }\unicode[STIX]{x1D707}_{X}^{\ast }\mathscr{F}=0$ for all
$R^{i}\unicode[STIX]{x1D707}_{X\ast }\unicode[STIX]{x1D707}_{X}^{\ast }\mathscr{F}=0$ for all ![]() $i\geqslant 1$. By definition,
$i\geqslant 1$. By definition, ![]() $R^{i}\unicode[STIX]{x1D707}_{X\ast }\unicode[STIX]{x1D707}_{X}^{\ast }\mathscr{F}$ is the sheafification of the presheaf sending any finite-type
$R^{i}\unicode[STIX]{x1D707}_{X\ast }\unicode[STIX]{x1D707}_{X}^{\ast }\mathscr{F}$ is the sheafification of the presheaf sending any finite-type ![]() ${\mathcal{S}}$-scheme
${\mathcal{S}}$-scheme ![]() ${\mathcal{U}}$ with an étale map
${\mathcal{U}}$ with an étale map ![]() $g:{\mathcal{U}}\rightarrow {\mathcal{X}}$ to
$g:{\mathcal{U}}\rightarrow {\mathcal{X}}$ to ![]() $H_{\acute{\text{e}}\text{t}}^{i}(U,g^{\text{an}\ast }\unicode[STIX]{x1D707}_{X}^{\ast }\mathscr{F})$, where of course
$H_{\acute{\text{e}}\text{t}}^{i}(U,g^{\text{an}\ast }\unicode[STIX]{x1D707}_{X}^{\ast }\mathscr{F})$, where of course ![]() $U={\mathcal{U}}^{\text{an}}$ is the analytification of
$U={\mathcal{U}}^{\text{an}}$ is the analytification of ![]() ${\mathcal{U}}$. But then
${\mathcal{U}}$. But then
where the second isomorphism follows from the first part of (i), so the result follows from the locality of cohomology (cf. [Sta17, Tag 01FW]).
For (ii), note that
where the first isomorphism follows from the adjointness of ![]() $\unicode[STIX]{x1D707}_{X}^{\ast }$ and
$\unicode[STIX]{x1D707}_{X}^{\ast }$ and ![]() $R\unicode[STIX]{x1D707}_{X\ast }$, and the second isomorphism follows from part (i).◻
$R\unicode[STIX]{x1D707}_{X\ast }$, and the second isomorphism follows from part (i).◻
Next, we prove the structure theorem.
Proof of Theorem 1.7.
Full faithfulness is immediate from Theorem 1.10(ii) together with the natural identification ![]() $\text{Hom}_{{\mathcal{A}}}(M,N)=\text{Hom}_{D({\mathcal{A}})}(M,N)$, which holds for any abelian category
$\text{Hom}_{{\mathcal{A}}}(M,N)=\text{Hom}_{D({\mathcal{A}})}(M,N)$, which holds for any abelian category ![]() ${\mathcal{A}}$.
${\mathcal{A}}$.
For essential surjectivity, we argue as follows. By the topological invariance of étale sites, we can assume that ![]() $A$ is reduced. Fix
$A$ is reduced. Fix ![]() $\mathscr{F}\in \text{Sh}_{zc}(S,\unicode[STIX]{x1D6EC})$. Pick a dense Zariski-open subset
$\mathscr{F}\in \text{Sh}_{zc}(S,\unicode[STIX]{x1D6EC})$. Pick a dense Zariski-open subset ![]() $j:U\rightarrow S$ such that
$j:U\rightarrow S$ such that ![]() $U$ is normal and
$U$ is normal and ![]() $j^{\ast }\mathscr{F}$ is locally constant, and let
$j^{\ast }\mathscr{F}$ is locally constant, and let ![]() $i:Z\rightarrow S$ be the inclusion of the closed complement. Let
$i:Z\rightarrow S$ be the inclusion of the closed complement. Let ![]() $j^{\text{alg}}:{\mathcal{U}}\rightarrow {\mathcal{S}}$ and
$j^{\text{alg}}:{\mathcal{U}}\rightarrow {\mathcal{S}}$ and ![]() $i^{\text{alg}}:{\mathcal{Z}}\rightarrow {\mathcal{S}}$ be the associated open and closed subschemes of
$i^{\text{alg}}:{\mathcal{Z}}\rightarrow {\mathcal{S}}$ be the associated open and closed subschemes of ![]() ${\mathcal{S}}$. By induction on
${\mathcal{S}}$. By induction on ![]() $\text{dim}\,\text{supp}\,\mathscr{F}$, we can assume that
$\text{dim}\,\text{supp}\,\mathscr{F}$, we can assume that ![]() $i_{\ast }i^{\ast }\mathscr{F}\simeq \unicode[STIX]{x1D707}_{S}^{\ast }{\mathcal{G}}$ for some constructible sheaf
$i_{\ast }i^{\ast }\mathscr{F}\simeq \unicode[STIX]{x1D707}_{S}^{\ast }{\mathcal{G}}$ for some constructible sheaf ![]() ${\mathcal{G}}$. By Corollary 2.16, analytification induces an equivalence of categories
${\mathcal{G}}$. By Corollary 2.16, analytification induces an equivalence of categories ![]() ${\mathcal{U}}_{\text{f}\acute{\text{e}}\text{t}}\cong U_{\text{f}\acute{\text{e}}\text{t}}$. Since (on individual connected components of
${\mathcal{U}}_{\text{f}\acute{\text{e}}\text{t}}\cong U_{\text{f}\acute{\text{e}}\text{t}}$. Since (on individual connected components of ![]() $U$)
$U$) ![]() $j^{\ast }\mathscr{F}$ corresponds to a representation of
$j^{\ast }\mathscr{F}$ corresponds to a representation of ![]() $\unicode[STIX]{x1D70B}_{1}(U,\overline{x})\cong \unicode[STIX]{x1D70B}_{1}({\mathcal{U}},\overline{x})$, we immediately see that
$\unicode[STIX]{x1D70B}_{1}(U,\overline{x})\cong \unicode[STIX]{x1D70B}_{1}({\mathcal{U}},\overline{x})$, we immediately see that ![]() $j^{\ast }\mathscr{F}\simeq \unicode[STIX]{x1D707}_{U}^{\ast }{\mathcal{F}}^{\prime }$ for some locally constant constructible sheaf
$j^{\ast }\mathscr{F}\simeq \unicode[STIX]{x1D707}_{U}^{\ast }{\mathcal{F}}^{\prime }$ for some locally constant constructible sheaf ![]() ${\mathcal{F}}^{\prime }$ on
${\mathcal{F}}^{\prime }$ on ![]() ${\mathcal{U}}$, so then
${\mathcal{U}}$, so then
where we have set ![]() ${\mathcal{F}}=j_{!}^{\text{alg}}{\mathcal{F}}^{\prime }$. Thus,
${\mathcal{F}}=j_{!}^{\text{alg}}{\mathcal{F}}^{\prime }$. Thus, ![]() $\mathscr{F}$ sits in a short exact sequence
$\mathscr{F}$ sits in a short exact sequence
To conclude, recall that for any abelian category ![]() ${\mathcal{A}}$, there is a canonical identification
${\mathcal{A}}$, there is a canonical identification ![]() $\text{Ext}_{{\mathcal{A}}}^{i}(B,A)=\text{Hom}_{D({\mathcal{A}})}(B,A[i])$ for any objects
$\text{Ext}_{{\mathcal{A}}}^{i}(B,A)=\text{Hom}_{D({\mathcal{A}})}(B,A[i])$ for any objects ![]() $A,B$ in
$A,B$ in ![]() ${\mathcal{A}}$; cf. [Sta17, Tag 06XP]. Combining this observation with Theorem 1.10(ii), we conclude that
${\mathcal{A}}$; cf. [Sta17, Tag 06XP]. Combining this observation with Theorem 1.10(ii), we conclude that ![]() $\unicode[STIX]{x1D707}_{S}^{\ast }$ induces a bijection
$\unicode[STIX]{x1D707}_{S}^{\ast }$ induces a bijection
on Yoneda Ext groups. Therefore, ![]() $\mathscr{F}\simeq \unicode[STIX]{x1D707}_{S}^{\ast }{\mathcal{H}}$ for some constructible sheaf
$\mathscr{F}\simeq \unicode[STIX]{x1D707}_{S}^{\ast }{\mathcal{H}}$ for some constructible sheaf ![]() ${\mathcal{H}}$ on
${\mathcal{H}}$ on ![]() ${\mathcal{S}}$, as desired.◻
${\mathcal{S}}$, as desired.◻
Finally, we prove Theorem 1.11.
Proof of Theorem 1.11.
For part (i), let ![]() $j^{\text{alg}}:{\mathcal{U}}\rightarrow {\mathcal{S}}$ be the evident open immersion with analytification
$j^{\text{alg}}:{\mathcal{U}}\rightarrow {\mathcal{S}}$ be the evident open immersion with analytification ![]() $j$. By Theorem 1.7, we can write
$j$. By Theorem 1.7, we can write ![]() $\mathscr{F}\simeq \unicode[STIX]{x1D707}_{U}^{\ast }{\mathcal{F}}$ for some
$\mathscr{F}\simeq \unicode[STIX]{x1D707}_{U}^{\ast }{\mathcal{F}}$ for some ![]() ${\mathcal{F}}\in \text{Sh}_{c}({\mathcal{U}},\unicode[STIX]{x1D6EC})$. (Precisely, Theorem 1.7 produces a sheaf
${\mathcal{F}}\in \text{Sh}_{c}({\mathcal{U}},\unicode[STIX]{x1D6EC})$. (Precisely, Theorem 1.7 produces a sheaf ![]() ${\mathcal{G}}\in \text{Sh}_{c}({\mathcal{S}},\unicode[STIX]{x1D6EC})$ with
${\mathcal{G}}\in \text{Sh}_{c}({\mathcal{S}},\unicode[STIX]{x1D6EC})$ with ![]() $j_{!}\mathscr{F}\simeq \unicode[STIX]{x1D707}_{S}^{\ast }{\mathcal{G}}$; we then take
$j_{!}\mathscr{F}\simeq \unicode[STIX]{x1D707}_{S}^{\ast }{\mathcal{G}}$; we then take ![]() ${\mathcal{F}}=j^{\text{alg}\ast }{\mathcal{G}}$.) By Proposition 4.2,
${\mathcal{F}}=j^{\text{alg}\ast }{\mathcal{G}}$.) By Proposition 4.2, ![]() $Rj_{\ast }^{\text{alg}}{\mathcal{F}}$ is constructible, so
$Rj_{\ast }^{\text{alg}}{\mathcal{F}}$ is constructible, so
is Zariski-constructible by Theorem 1.8.
For part (ii), the spectral sequence
shows that any given cohomology sheaf ![]() $\mathscr{H}^{n}(\mathscr{F}\otimes _{\unicode[STIX]{x1D6EC}}^{\mathbf{L}}\mathscr{G})$ is unchanged if we replace
$\mathscr{H}^{n}(\mathscr{F}\otimes _{\unicode[STIX]{x1D6EC}}^{\mathbf{L}}\mathscr{G})$ is unchanged if we replace ![]() $\mathscr{F}$ by
$\mathscr{F}$ by ![]() $\unicode[STIX]{x1D70F}^{{\geqslant}-n}\mathscr{F}$ for some large
$\unicode[STIX]{x1D70F}^{{\geqslant}-n}\mathscr{F}$ for some large ![]() $n\gg 0$. This reduces us to the case where
$n\gg 0$. This reduces us to the case where ![]() $\mathscr{F}$ is bounded, and then (by an easy induction using the two-out-of-three property) to the case where
$\mathscr{F}$ is bounded, and then (by an easy induction using the two-out-of-three property) to the case where ![]() $\mathscr{F}$ is a sheaf. Repeating this argument, we can also assume that
$\mathscr{F}$ is a sheaf. Repeating this argument, we can also assume that ![]() $\mathscr{G}$ is a sheaf. Going to a stratification
$\mathscr{G}$ is a sheaf. Going to a stratification ![]() $S=\coprod S_{i}$ such that
$S=\coprod S_{i}$ such that ![]() $\mathscr{F}$ and
$\mathscr{F}$ and ![]() $\mathscr{G}$ are locally constant on each stratum, we reduce to the case where both sheaves are locally constant, which is easy.
$\mathscr{G}$ are locally constant on each stratum, we reduce to the case where both sheaves are locally constant, which is easy.
For part (iii), note that ![]() $\mathscr{H}^{n}(\mathbf{D}_{S}\mathscr{F})$ is the sheafification of the presheaf sending any quasicompact separated étale map
$\mathscr{H}^{n}(\mathbf{D}_{S}\mathscr{F})$ is the sheafification of the presheaf sending any quasicompact separated étale map ![]() $j:U\rightarrow S$ to the module
$j:U\rightarrow S$ to the module
Our assumptions on ![]() $K$ and
$K$ and ![]() $\unicode[STIX]{x1D6EC}$ guarantee that
$\unicode[STIX]{x1D6EC}$ guarantee that ![]() $R\unicode[STIX]{x1D6E4}_{c}(U,-)$ sends
$R\unicode[STIX]{x1D6E4}_{c}(U,-)$ sends ![]() $D^{[a,b]}(U,\unicode[STIX]{x1D6EC})$ into
$D^{[a,b]}(U,\unicode[STIX]{x1D6EC})$ into ![]() $D^{[a,b+N]}(\unicode[STIX]{x1D6EC})$ for some
$D^{[a,b+N]}(\unicode[STIX]{x1D6EC})$ for some ![]() $N$ depending only on the pair
$N$ depending only on the pair ![]() $(S,\unicode[STIX]{x1D6EC})$, and that
$(S,\unicode[STIX]{x1D6EC})$, and that ![]() $R\mathscr{H}\text{om}_{\unicode[STIX]{x1D6EC}}(-,\unicode[STIX]{x1D6EC})$ sends
$R\mathscr{H}\text{om}_{\unicode[STIX]{x1D6EC}}(-,\unicode[STIX]{x1D6EC})$ sends ![]() $D^{[a,b]}(\unicode[STIX]{x1D6EC})$ into
$D^{[a,b]}(\unicode[STIX]{x1D6EC})$ into ![]() $D^{[-b,-a+\text{dim}\,\unicode[STIX]{x1D6EC}]}(\unicode[STIX]{x1D6EC})$. This shows that
$D^{[-b,-a+\text{dim}\,\unicode[STIX]{x1D6EC}]}(\unicode[STIX]{x1D6EC})$. This shows that ![]() $\mathbf{D}_{S}$ exchanges the boundedness conditions as claimed, and that any given cohomology sheaf
$\mathbf{D}_{S}$ exchanges the boundedness conditions as claimed, and that any given cohomology sheaf ![]() $\mathscr{H}^{n}(\mathbf{D}_{S}\mathscr{F})$ depends only on the truncation
$\mathscr{H}^{n}(\mathbf{D}_{S}\mathscr{F})$ depends only on the truncation ![]() $\unicode[STIX]{x1D70F}^{{\leqslant}b}\unicode[STIX]{x1D70F}^{{\geqslant}a}\mathscr{F}$ for some large
$\unicode[STIX]{x1D70F}^{{\leqslant}b}\unicode[STIX]{x1D70F}^{{\geqslant}a}\mathscr{F}$ for some large ![]() $a\ll 0\ll b$. For the Zariski-constructibility of
$a\ll 0\ll b$. For the Zariski-constructibility of ![]() $\mathbf{D}_{S}\mathscr{F}$, we can therefore assume that
$\mathbf{D}_{S}\mathscr{F}$, we can therefore assume that ![]() $\mathscr{F}$ is bounded, and then that
$\mathscr{F}$ is bounded, and then that ![]() $\mathscr{F}$ is a sheaf. Pick a smooth dense Zariski-open
$\mathscr{F}$ is a sheaf. Pick a smooth dense Zariski-open ![]() $j:U\rightarrow S$ with closed (affinoid) complement
$j:U\rightarrow S$ with closed (affinoid) complement ![]() $i:Z\rightarrow X$, so
$i:Z\rightarrow X$, so ![]() $j^{\ast }\unicode[STIX]{x1D714}_{S}=\unicode[STIX]{x1D714}_{U}$ is locally constant up to a shift and twist. Shrinking
$j^{\ast }\unicode[STIX]{x1D714}_{S}=\unicode[STIX]{x1D714}_{U}$ is locally constant up to a shift and twist. Shrinking ![]() $U$ further, if necessary, we can also assume that
$U$ further, if necessary, we can also assume that ![]() $j^{\ast }\mathscr{F}$ is locally constant, so
$j^{\ast }\mathscr{F}$ is locally constant, so
is locally constant constructible, up to a shift and twist. Dualizing the distinguished triangle
and using the habitual isomorphisms ![]() $\mathbf{D}_{S}j_{!}\cong Rj_{\ast }\mathbf{D}_{U}$ and
$\mathbf{D}_{S}j_{!}\cong Rj_{\ast }\mathbf{D}_{U}$ and ![]() $\mathbf{D}_{S}i_{\ast }i^{\ast }\cong i_{\ast }\mathbf{D}_{Z}i^{\ast }$, we get a distinguished triangle
$\mathbf{D}_{S}i_{\ast }i^{\ast }\cong i_{\ast }\mathbf{D}_{Z}i^{\ast }$, we get a distinguished triangle
By induction on ![]() $\text{dim}\,S$, the first term in this triangle is Zariski-constructible. Since
$\text{dim}\,S$, the first term in this triangle is Zariski-constructible. Since ![]() $\mathbf{D}_{U}j^{\ast }\mathscr{F}$ is locally constant, the third term is Zariski-constructible by part (i). The result now follows from the two-out-of-three property. Finally, for the reflexivity of
$\mathbf{D}_{U}j^{\ast }\mathscr{F}$ is locally constant, the third term is Zariski-constructible by part (i). The result now follows from the two-out-of-three property. Finally, for the reflexivity of ![]() $\mathscr{F}$, we can again assume that
$\mathscr{F}$, we can again assume that ![]() $\mathscr{F}$ is a sheaf, in which case the desired result is [Reference HansenHan17, Theorem B.1.2].
$\mathscr{F}$ is a sheaf, in which case the desired result is [Reference HansenHan17, Theorem B.1.2].
For part (iv), note that we have isomorphisms
where the first comes from the reflexivity of ![]() $\mathscr{G}$ proved in (iii), and the second is an easy exercise in tensor–hom adjunction. The result now follows from parts (ii) and (iii).
$\mathscr{G}$ proved in (iii), and the second is an easy exercise in tensor–hom adjunction. The result now follows from parts (ii) and (iii).
For part (v), the habitual isomorphism ![]() $Rf^{!}\mathbf{D}_{S}\cong \mathbf{D}_{T}f^{\ast }$ together with the reflexivity of
$Rf^{!}\mathbf{D}_{S}\cong \mathbf{D}_{T}f^{\ast }$ together with the reflexivity of ![]() $\mathscr{F}$ gives isomorphisms
$\mathscr{F}$ gives isomorphisms
so the result now follows from part (iii). ◻
Acknowledgements
Several years ago, Giovanni Rosso and John Welliaveetil asked me whether anything was known about the ![]() $l$-cohomological dimension of affinoid rigid spaces, and I would like to thank them very heartily for this crucial initial stimulation. Johan de Jong listened to some of my early ideas about these problems and pointed me to the ‘Travaux de Gabber’ volumes in response to my desperate search for tools. Christian Johansson planted in my head the usefulness of the excellence property for convergent power series rings. Peter Scholze read a rough initial draft and pointed out that certain arguments worked without change in equal characteristic zero; Scholze also inadvertently inspired a crucial trick (cf. Footnote 9). Brian Conrad offered several helpful comments and corrections on a later draft. The anonymous referee gave some perceptive suggestions for clarifications and improvements. To all of these mathematicians, I am very grateful.
$l$-cohomological dimension of affinoid rigid spaces, and I would like to thank them very heartily for this crucial initial stimulation. Johan de Jong listened to some of my early ideas about these problems and pointed me to the ‘Travaux de Gabber’ volumes in response to my desperate search for tools. Christian Johansson planted in my head the usefulness of the excellence property for convergent power series rings. Peter Scholze read a rough initial draft and pointed out that certain arguments worked without change in equal characteristic zero; Scholze also inadvertently inspired a crucial trick (cf. Footnote 9). Brian Conrad offered several helpful comments and corrections on a later draft. The anonymous referee gave some perceptive suggestions for clarifications and improvements. To all of these mathematicians, I am very grateful.