Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-14T09:54:09.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of products of equivalence relations

Part of: Selfadjoint operator algebras Ergodic theory

Published online by Cambridge University Press:  17 August 2018

Amine Marrakchi
Amine Marrakchi*
Affiliation:
Laboratoire de Mathématiques d’Orsay, Université Paris-Sud, CNRS, Université Paris-Saclay, 91405 Orsay, France email amine.marrakchi@math.u-psud.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

An ergodic probability measure preserving (p.m.p.) equivalence relation 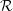${\mathcal{R}}$ is said to be stable if ${\mathcal{R}}\cong {\mathcal{R}}\times {\mathcal{R}}_{0}$ where 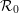${\mathcal{R}}_{0}$ is the unique hyperfinite ergodic type 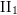$\text{II}_{1}$ equivalence relation. We prove that a direct product 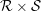${\mathcal{R}}\times {\mathcal{S}}$ of two ergodic p.m.p. equivalence relations is stable if and only if one of the two components 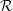${\mathcal{R}}$ or 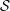${\mathcal{S}}$ is stable. This result is deduced from a new local characterization of stable equivalence relations. The similar question on McDuff 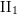$\text{II}_{1}$ factors is also discussed and some partial results are given.

Keywords

stable equivalence relationdirect productfull groupMcDuff factorvon Neumann algebratensor productcentral sequencemaximality argument

MSC classification

Primary: 37A20: Orbit equivalence, cocycles, ergodic equivalence relations 46L10: General theory of von Neumann algebras 46L36: Classification of factors
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 9 , September 2018 , pp. 2005 - 2019
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is supported by ERC Starting Grant GAN 637601.

References

Connes, A., Classification of injective factors. Cases II1 , II ∞ , III𝜆 , 𝜆≠1 , Ann. of Math. (2) 74 (1976), 73–115.Google Scholar
Connes, A., Factors of type III1 , property L 𝜆 ′ and closure of inner automorphisms , J. Operator Theory 14 (1985), 189–211.Google Scholar
Connes, A. and Stormer, E., Homogeneity of the state space of factors of type III1 , J. Funct. Anal. 28 (1976), 187–196.Google Scholar
Feldman, J. and Moore, C. C., Ergodic equivalence relations, cohomology, and von Neumann algebras. I, II , Trans. Amer. Math. Soc. 234 (1977), 289–324; 325–359.Google Scholar
Haagerup, U., A new proof of the equivalence of injectivity and hyperfiniteness for factors on a separable Hilbert space , J. Funct. Anal. 62 (1985), 160–201.Google Scholar
Haagerup, U., Connes’ bicentralizer problem and uniqueness of the injective factor of type III1 , Acta Math. 69 (1986), 95–148.Google Scholar
Houdayer, C., Marrakchi, A. and Verraedt, P., Fullness and Connes’ 𝜏 invariant of type III tensor product factors , J. Math. Pures Appl. , to appear. Preprint (2016), arXiv:1611.07914.Google Scholar
Houdayer, C., Marrakchi, A. and Verraedt, P., Strongly ergodic equivalence relations: spectral gap and type III invariants , Ergodic Theory Dynam. Systems , to appear.Google Scholar
Ioana, A. and Vaes, S., Spectral gap for inclusions of von Neumann algebras. Appendix to the article Cartan subalgebras of amalgamated free product II1 factors by A. Ioana , Ann. Sci. Éc. Norm. Supér. 48 (2015), 71–130.Google Scholar
Jones, V. F. R. and Schmidt, K., Asymptotically invariant sequences and approximate finiteness , Amer. J. Math. 109 (1987), 91–114.Google Scholar
McDuff, D., Central sequences and the hyperfinite factor , Proc. Lond. Math. Soc. (3) 21 (1970), 443–461.Google Scholar
Marrakchi, A., Spectral gap characterization of full type III factors , J. Reine Angew. Math. , to appear. Preprint (2016), arXiv:1605.09613.Google Scholar
Marrakchi, A., Strongly ergodic actions have local spectral gap , Proc. Amer. Math. Soc. 146 (2018), 3887–3893.Google Scholar
Murray, F. and von Neumann, J., Rings of operators. IV , Ann. of Math. (2) 44 (1943), 716–808.Google Scholar
Popa, S., A short proof that injectivity implies hyperfiniteness for finite von Newmann algebras , J. Operator Theory 16 (1986), 261–272.Google Scholar
Popa, S., The commutant modulo the set of compact operators of a von Neumann algebra , J. Funct. Anal. 712 (1987), 393–408.Google Scholar
Popa, S., Free-independent sequences in type $\text{II}_{1}$ factors and related problems, Astérisque 232 (1995), 187–202; Recent advances in operator algebras (Orléans, 1992).Google Scholar
Popa, S., On spectral gap rigidity and Connes’ invariant 𝜒(M) , Proc. Amer. Math. Soc. 138 (2010), 3531–3539.Google Scholar
Popa, S., Independence properties in subalgebras of ultraproduct II1 factors , J. Funct. Anal. 266 (2014), 5818–5846.Google Scholar
Wu, W. and Yuan, W., A remark on central sequence algebras of the tensor product of II1 factors , Proc. Amer. Math. Soc. 142 (2014), 2829–2835.Google Scholar