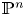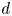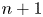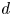Introduction
We will consider in this paper smooth hypersurfaces ![]() $X_f\subset \mathbb {P}^{n}$ of degree
$X_f\subset \mathbb {P}^{n}$ of degree ![]() $d$ defined by a homogeneous polynomial equation
$d$ defined by a homogeneous polynomial equation ![]() $f$. By the Lefschetz theorem on hyperplane sections, only the degree
$f$. By the Lefschetz theorem on hyperplane sections, only the degree ![]() $n-1$ cohomology group
$n-1$ cohomology group ![]() $H^{n-1}(X_f,\mathbb {Z})$ carries a nontrivial Hodge structure, and its primitive part
$H^{n-1}(X_f,\mathbb {Z})$ carries a nontrivial Hodge structure, and its primitive part ![]() $H^{n-1}(X_f,\mathbb {Z})_{\rm prim}:={\rm Ker}\,(H^{n-1}(X_f,\mathbb {Z})\rightarrow H^{n+1}(\mathbb {P}^{n},\mathbb {Z}))$ carries a Hodge structure polarized by the cup-product
$H^{n-1}(X_f,\mathbb {Z})_{\rm prim}:={\rm Ker}\,(H^{n-1}(X_f,\mathbb {Z})\rightarrow H^{n+1}(\mathbb {P}^{n},\mathbb {Z}))$ carries a Hodge structure polarized by the cup-product ![]() $\langle \,,\,\rangle _X$ (the two groups agree when
$\langle \,,\,\rangle _X$ (the two groups agree when ![]() $n-1$ is odd, otherwise they differ by
$n-1$ is odd, otherwise they differ by ![]() $\mathbb {Z}h^{{(n-1)}/{2}}$, where
$\mathbb {Z}h^{{(n-1)}/{2}}$, where ![]() $h=c_1(\mathcal {O}_X(1))$). The global Torelli problem for hypersurfaces thus asks whether the existence of an isomorphism of polarized Hodge structures
$h=c_1(\mathcal {O}_X(1))$). The global Torelli problem for hypersurfaces thus asks whether the existence of an isomorphism of polarized Hodge structures
(extending to an isomorphism of Hodge structures ![]() $H^{n-1}(X_f,\mathbb {Z})\cong H^{n-1}(X_{f'},\mathbb {Z})$ preserving the classes
$H^{n-1}(X_f,\mathbb {Z})\cong H^{n-1}(X_{f'},\mathbb {Z})$ preserving the classes ![]() $h^{{(n-1)}/{2}}$ on both sides when
$h^{{(n-1)}/{2}}$ on both sides when ![]() $n-1$ is even) implies that
$n-1$ is even) implies that ![]() $X_f\cong X_{f'}$. There are very few cases where this statement is known. For plane curves, we can apply the Torelli theorem for curves. For quartic surfaces, the global Torelli theorem is proved by Piateski-Shapiro and Shafarevich [Reference Piateski-Shapiro and ShafarevichPS71]. For cubic threefolds, the global Torelli theorem is proved by Clemens and Griffiths [Reference Clemens and GriffithsCG72] and Beauville [Reference BeauvilleBea82], and for cubic fourfolds it was first proved in [Reference VoisinVoi86] (alternative proofs are now available, see e.g. [Reference Huybrechts and RennemoHR19]).
$X_f\cong X_{f'}$. There are very few cases where this statement is known. For plane curves, we can apply the Torelli theorem for curves. For quartic surfaces, the global Torelli theorem is proved by Piateski-Shapiro and Shafarevich [Reference Piateski-Shapiro and ShafarevichPS71]. For cubic threefolds, the global Torelli theorem is proved by Clemens and Griffiths [Reference Clemens and GriffithsCG72] and Beauville [Reference BeauvilleBea82], and for cubic fourfolds it was first proved in [Reference VoisinVoi86] (alternative proofs are now available, see e.g. [Reference Huybrechts and RennemoHR19]).
The generic Torelli theorem for hypersurfaces of degree ![]() $d$ and dimension
$d$ and dimension ![]() $n-1$ is the following statement that we will study in this paper.
$n-1$ is the following statement that we will study in this paper.
Let ![]() $X_f$ be a very general smooth hypersurface of degree
$X_f$ be a very general smooth hypersurface of degree ![]() $d$ in
$d$ in ![]() $\mathbb {P}^{n}$. Then any smooth hypersurface
$\mathbb {P}^{n}$. Then any smooth hypersurface ![]() $X_{f'}$ of degree
$X_{f'}$ of degree ![]() $d$ in
$d$ in ![]() $\mathbb {P}^{n}$ such that there exists an isomorphism of Hodge structures
$\mathbb {P}^{n}$ such that there exists an isomorphism of Hodge structures
is isomorphic to ![]() $X_f$.
$X_f$.
We will explain in § 1.1 why the ‘very general’ assumption is natural in this statement. This is related to the Cattani–Deligne–Kaplan theorem [Reference Cattani, Deligne and KaplanCDK95] which implies that the set of pairs ![]() $(f,\,{f'})$ such that an isomorphism as in (1) exists is a countable union of closed algebraic subsets in
$(f,\,{f'})$ such that an isomorphism as in (1) exists is a countable union of closed algebraic subsets in ![]() $U_{d,n}\times U_{d,n}$, where
$U_{d,n}\times U_{d,n}$, where ![]() $U_{d,n}$ is the moduli space of smooth hypersurfaces of degree
$U_{d,n}$ is the moduli space of smooth hypersurfaces of degree ![]() $d$ in
$d$ in ![]() $\mathbb {P}^{n}$.
$\mathbb {P}^{n}$.
Remark 0.1 The Torelli theorem is usually stated for the isomorphisms of polarized Hodge structures. However, using infinitesimal arguments (see [Reference VoisinVoi03, 6.3.1]) we can see that, except in the case of cubic surfaces, the Hodge structure on the primitive cohomology of ![]() $X_f$ has a unique polarization (up to a scalar) for very general
$X_f$ has a unique polarization (up to a scalar) for very general ![]() $X_f$. So the polarized and nonpolarized statements are equivalent.
$X_f$. So the polarized and nonpolarized statements are equivalent.
In the case of cubic surfaces, the generic Torelli theorem is clearly wrong, since they have moduli, while their variation of Hodge structure is trivial. The case of plane quartics is also a counterexample to the generic Torelli theorem with rational coefficients, since in genus ![]() $3$, a general curve is not determined by the isogeny class of its Jacobian. Donagi proved in [Reference DonagiDon83] the following beautiful result.
$3$, a general curve is not determined by the isogeny class of its Jacobian. Donagi proved in [Reference DonagiDon83] the following beautiful result.
Theorem 0.2 The generic Torelli theorem holds for smooth hypersurfaces of degree ![]() $d$ in
$d$ in ![]() $\mathbb {P}^{n}$, with
$\mathbb {P}^{n}$, with ![]() $n\geq 3$,
$n\geq 3$, ![]() $(d,n)\not =(3,3)$ and the following possible exceptions:
$(d,n)\not =(3,3)$ and the following possible exceptions:
(1)
 $d$ divides
$d$ divides  $n+1$;
$n+1$;(2)
 $d=4$,
$d=4$,  $n=4m+1$, with
$n=4m+1$, with  $m\geq 1$;
$m\geq 1$;(3)
 $d=6$,
$d=6$,  $n=6m+2$, with
$n=6m+2$, with  $m\geq 1$.
$m\geq 1$.
Remark 0.3 The Torelli theorem is usually stated for integral Hodge structures, and Donagi's original statement indeed concerned integral Hodge structures. In fact, his proof works as well for rational Hodge structures, since it relies on the study of the (complex!) variation of Hodge structure for hypersurfaces of given degree and dimension and its local invariants. Another instance where a generic Torelli theorem has been proved for rational Hodge structures is the case of curves of genus ![]() $g\geq 4$ which is treated in [Reference Bardelli and PirolaBP89]. In this case, Bardelli and Pirola prove that a very general curve of genus at least
$g\geq 4$ which is treated in [Reference Bardelli and PirolaBP89]. In this case, Bardelli and Pirola prove that a very general curve of genus at least ![]() $4$ is determined by the isogeny class of its Jacobian.
$4$ is determined by the isogeny class of its Jacobian.
Remark 0.4 The Cattani–Deligne–Kaplan algebraicity theorem mentioned above appeared much later than [Reference DonagiDon83], so that Theorem 0.2 is in fact a slightly strengthened version of Donagi's theorem, taking into account [Reference Cattani, Deligne and KaplanCDK95].
Cox and Green solved in [Reference Cox and GreenCG90] the case (3), that is ![]() $d=6$, but the two infinite series (1) and (2) essentially remained open. The starting point of Donagi's proof is the description due to Griffiths [Reference GriffithsGri69] and Carlson and Griffiths [Reference Carlson, Griffiths and BeauvilleCG80] of the infinitesimal variation of Hodge structure of a smooth hypersurface. Denote by
$d=6$, but the two infinite series (1) and (2) essentially remained open. The starting point of Donagi's proof is the description due to Griffiths [Reference GriffithsGri69] and Carlson and Griffiths [Reference Carlson, Griffiths and BeauvilleCG80] of the infinitesimal variation of Hodge structure of a smooth hypersurface. Denote by ![]() $S^{*} =\mathbb {C}[X_0,\ldots,X_n]$ the graded polynomial ring of
$S^{*} =\mathbb {C}[X_0,\ldots,X_n]$ the graded polynomial ring of ![]() $\mathbb {P}^{n}$ and by
$\mathbb {P}^{n}$ and by ![]() $R_f^{*}=S^{*}/J_f^{*}$ the Jacobian ring of
$R_f^{*}=S^{*}/J_f^{*}$ the Jacobian ring of ![]() $f$, where
$f$, where
is the Jacobian ideal of ![]() $f$, generated by the partial derivatives of
$f$, generated by the partial derivatives of ![]() $f$. The infinitesimal variation of Hodge structure on the primitive cohomology of degree
$f$. The infinitesimal variation of Hodge structure on the primitive cohomology of degree ![]() $n-1$ of
$n-1$ of ![]() $X_f$ is given, according to Griffiths [Reference GriffithsGri69], see also [Reference VoisinVoi03, 6.1.3], by linear maps
$X_f$ is given, according to Griffiths [Reference GriffithsGri69], see also [Reference VoisinVoi03, 6.1.3], by linear maps
for ![]() $p+q=n-1$. Here, the space
$p+q=n-1$. Here, the space ![]() $R^{d}_f$ is naturally identified with the first-order deformations of
$R^{d}_f$ is naturally identified with the first-order deformations of ![]() $X_f$ in
$X_f$ in ![]() $\mathbb {P}^{n}$ modulo the infinitesimal action of
$\mathbb {P}^{n}$ modulo the infinitesimal action of ![]() ${\rm PGL}(n+1)$. It also identifies via the Kodaira–Spencer map to the subspace
${\rm PGL}(n+1)$. It also identifies via the Kodaira–Spencer map to the subspace ![]() $H^{1}(X_f,T_{X_f})_0\subset H^{1}(X_f,T_{X_f})$ of deformations of
$H^{1}(X_f,T_{X_f})_0\subset H^{1}(X_f,T_{X_f})$ of deformations of ![]() $X_f$ induced by a deformation of
$X_f$ induced by a deformation of ![]() $f$. Griffiths constructs residue isomorphisms
$f$. Griffiths constructs residue isomorphisms
and the paper [Reference Carlson, Griffiths and BeauvilleCG80] in turn describes (3) using the isomorphisms (4) as follows.
Theorem 0.5 Via the isomorphisms (4), the maps (3) identify up to a scalar coefficient with the map
induced by multiplication in ![]() $R_f^{*}$. In other words, the following diagram is commutative up to a coefficient.
$R_f^{*}$. In other words, the following diagram is commutative up to a coefficient.

Furthermore, the Serre pairing between ![]() $H^{n-1-q,q}(X_f)_{{\rm prim}}$ and
$H^{n-1-q,q}(X_f)_{{\rm prim}}$ and ![]() $H^{q,n-1-q}(X_f)_{{\rm prim}}$ identifies with the Macaulay pairing
$H^{q,n-1-q}(X_f)_{{\rm prim}}$ identifies with the Macaulay pairing
given by the product in ![]() $R_f^{*}$.
$R_f^{*}$.
Donagi's proof starts with the observation that Theorem 0.2 is implied by the following result.
Theorem 0.6 Let ![]() $X$ be a smooth hypersurface of degree
$X$ be a smooth hypersurface of degree ![]() $d$ in
$d$ in ![]() $\mathbb {P}^{n}$, with
$\mathbb {P}^{n}$, with ![]() $n\geq 3$. Assume
$n\geq 3$. Assume ![]() $(d,n)\not =(3,3)$ and we are not in the cases (1), (2), (3) listed in Theorem 0.2. Then
$(d,n)\not =(3,3)$ and we are not in the cases (1), (2), (3) listed in Theorem 0.2. Then ![]() $X$ is determined by the data (5) for all
$X$ is determined by the data (5) for all ![]() $q$ and the Macaulay pairings (7), hence, using Theorem 0.5, by its polarized infinitesimal variation of Hodge structure.
$q$ and the Macaulay pairings (7), hence, using Theorem 0.5, by its polarized infinitesimal variation of Hodge structure.
Concretely, Theorem 0.6 says that if ![]() $X_f$ and
$X_f$ and ![]() $X_{f'}$ are two smooth hypersurfaces of degree
$X_{f'}$ are two smooth hypersurfaces of degree ![]() $d$ and dimension
$d$ and dimension ![]() $n-1$ such that there exist isomorphisms,
$n-1$ such that there exist isomorphisms,
compatible with the Macaulay pairing (7) for ![]() $f$ and
$f$ and ![]() $f'$, and such that the following diagram commutes,
$f'$, and such that the following diagram commutes,

then ![]() $X_f$ is isomorphic to
$X_f$ is isomorphic to ![]() $X_{f'}$.
$X_{f'}$.
Donagi's proof of Theorem 0.6 consists in recovering from the data (5) its polynomial structure (see § 1), and more precisely, reconstructing the whole Jacobian ring of ![]() $f$ from its partial data appearing in (5). He then applies the Mather–Yau theorem (see Proposition 3.2) which says that
$f$ from its partial data appearing in (5). He then applies the Mather–Yau theorem (see Proposition 3.2) which says that ![]() $f$ is determined by
$f$ is determined by ![]() $J_f^{d-1}\subset S^{d-1}$.
$J_f^{d-1}\subset S^{d-1}$.
Donagi's method does not work in the case where ![]() $(d,n)=(4,3)$, that is, quartic
$(d,n)=(4,3)$, that is, quartic ![]() $K3$ surfaces, because Theorem 0.6 is clearly wrong in this case. In fact, Theorem 0.2 is also wrong for quartic surfaces, due to the fact that it is stated for rational Hodge structures. More generally, Donagi's method to recover the polynomial structure, based on the use of the symmetrizer lemma (Proposition 1.1), gives nothing more, when
$K3$ surfaces, because Theorem 0.6 is clearly wrong in this case. In fact, Theorem 0.2 is also wrong for quartic surfaces, due to the fact that it is stated for rational Hodge structures. More generally, Donagi's method to recover the polynomial structure, based on the use of the symmetrizer lemma (Proposition 1.1), gives nothing more, when ![]() $d$ divides
$d$ divides ![]() $n+1$, than the subring
$n+1$, than the subring ![]() $R_f^{*d}\subset R^{*}_f$ defined as the sum of the graded pieces of
$R_f^{*d}\subset R^{*}_f$ defined as the sum of the graded pieces of ![]() $R_f^{*}$ of degree divisible by
$R_f^{*}$ of degree divisible by ![]() $d$. This is why Donagi's method fails to give the result in that case. The goal of this paper is to extend Theorem 0.2 to most families of hypersurfaces not covered by Donagi's theorem.
$d$. This is why Donagi's method fails to give the result in that case. The goal of this paper is to extend Theorem 0.2 to most families of hypersurfaces not covered by Donagi's theorem.
Theorem 0.7
(1) The generic Torelli theorem holds for smooth hypersurfaces of degree
 $d$ in
$d$ in  $\mathbb {P}^{n}$ when
$\mathbb {P}^{n}$ when  $d$ divides
$d$ divides  $n+1$ and
$n+1$ and  $d$ is large enough. In particular, it holds for Calabi–Yau hypersurfaces of degree
$d$ is large enough. In particular, it holds for Calabi–Yau hypersurfaces of degree  $d$ large enough.
$d$ large enough.(2) The generic Torelli theorem holds for smooth hypersurfaces of degree
 $4$ in
$4$ in  $\mathbb {P}^{4m+1}$ for
$\mathbb {P}^{4m+1}$ for  $m$ sufficiently large.
$m$ sufficiently large.
These results combined with Donagi's theorem (Theorem 0.2) and Cox and Green's result in [Reference Cox and GreenCG90] imply the following result.
Corollary 0.8 The generic Torelli theorem holds for hypersurfaces of degree ![]() $d$ in
$d$ in ![]() $\mathbb {P}^{n}$ with finitely many exceptions.
$\mathbb {P}^{n}$ with finitely many exceptions.
The proof of Theorem 0.7(2) will be given in § 2. We will give there an effective estimate for ![]() $m$, which can probably be improved by refining the method. In that case, the method of proof follows closely Donagi's ideas, and in particular passes through a proof of Theorem 0.6, at least for
$m$, which can probably be improved by refining the method. In that case, the method of proof follows closely Donagi's ideas, and in particular passes through a proof of Theorem 0.6, at least for ![]() $X$ generic.
$X$ generic.
Theorem 0.7(1) had been also proved in [Reference Voisin, Hulek, Catanese, Peters and ReidVoi99] in the case of quintic threefolds, the first case which is not covered by Theorem 0.2, by extending Theorem 0.6 to that case. It is quite possible that Theorem 0.6 is true more generally when ![]() $d$ divides
$d$ divides ![]() $n+1$ and
$n+1$ and ![]() $d$ is sufficiently large, but the proof given in [Reference Voisin, Hulek, Catanese, Peters and ReidVoi99] is very technical and ad hoc, hence not encouraging.
$d$ is sufficiently large, but the proof given in [Reference Voisin, Hulek, Catanese, Peters and ReidVoi99] is very technical and ad hoc, hence not encouraging.
Our proof of Theorem 0.7(1) also rests on the algebraic analysis of the finite-order variation of Hodge structure, but it does not pass through a proof of Theorem 0.6. Theorem 0.6 tells that for the given pairs ![]() $(d,n)$, a hypersurface of degree
$(d,n)$, a hypersurface of degree ![]() $d$ and dimension
$d$ and dimension ![]() $n-1$ can be reconstructed from its first order variation of Hodge structure. Instead, our proof will involve the higher-order variation of Hodge structure.
$n-1$ can be reconstructed from its first order variation of Hodge structure. Instead, our proof will involve the higher-order variation of Hodge structure.
We introduce in this paper a main new ingredient, which is the notion of Schiffer variation of a hypersurface (see § 3). These Schiffer variations are of the form
(up to a change of variable ![]() $t$) and we believe they are interesting for their own. The chosen terminology comes from the notion of Schiffer variations for a smooth curve
$t$) and we believe they are interesting for their own. The chosen terminology comes from the notion of Schiffer variations for a smooth curve ![]() $C$. They consist in deforming the complex structure of
$C$. They consist in deforming the complex structure of ![]() $C$ in a way that is supported on a point
$C$ in a way that is supported on a point ![]() $p$ of
$p$ of ![]() $C$. First-order Schiffer variations are in that case the elements
$C$. First-order Schiffer variations are in that case the elements ![]() $u_p\in \mathbb {P}(H^{1}(C,T_C))$ given by
$u_p\in \mathbb {P}(H^{1}(C,T_C))$ given by
First-order Schiffer variations (9) of hypersurfaces ![]() $X_f$ are the tangent directions at
$X_f$ are the tangent directions at ![]() $0$ of Schiffer variations of
$0$ of Schiffer variations of ![]() $f$. They are parameterized by the
$f$. They are parameterized by the ![]() $d$th Veronese embedding of
$d$th Veronese embedding of ![]() $\mathbb {P}(S^{1})$ in
$\mathbb {P}(S^{1})$ in ![]() $\mathbb {P}(S^{d})$ projected to
$\mathbb {P}(S^{d})$ projected to ![]() $\mathbb {P}(R^{d}_f)$ via the linear projection
$\mathbb {P}(R^{d}_f)$ via the linear projection ![]() $\mathbb {P}(S^{d})\dashrightarrow \mathbb {P}(R^{d}_f)$. Although the following result is easy to prove, it is crucial for our strategy.
$\mathbb {P}(S^{d})\dashrightarrow \mathbb {P}(R^{d}_f)$. Although the following result is easy to prove, it is crucial for our strategy.
Proposition 0.9 (cf. Proposition 3.6)
Let ![]() $X_f,\,X_g$ be two smooth hypersurfaces of degree
$X_f,\,X_g$ be two smooth hypersurfaces of degree ![]() ${d\geq 4}$ and dimension
${d\geq 4}$ and dimension ![]() $n-1\geq 3$, with
$n-1\geq 3$, with ![]() $f$ generic. If there exists a linear isomorphism
$f$ generic. If there exists a linear isomorphism ![]() $R_f^{d}\cong R_g^{d}$ mapping the set of first order Schiffer variations of
$R_f^{d}\cong R_g^{d}$ mapping the set of first order Schiffer variations of ![]() $f$ to the set of first-order Schiffer variations of
$f$ to the set of first-order Schiffer variations of ![]() $g$,
$g$, ![]() $X_f$ is isomorphic to
$X_f$ is isomorphic to ![]() $X_g$.
$X_g$.
Our strategy then consists in characterizing Schiffer variations by the formal properties of the variation of Hodge structure along them. An obvious but key point (see Lemma 3.8) is the fact that the structure of the Jacobian ring (hence of the infinitesimal variation of Hodge structure) does not change much along them. This follows from the fact that the Jacobian ideals of ![]() $f$ and
$f$ and ![]() $f_t=f+tx^{d}$ agree modulo the ideal generated by
$f_t=f+tx^{d}$ agree modulo the ideal generated by ![]() $x^{d-1}$. This is a higher-order property since it concerns the variation of the infinitesimal variation of Hodge structures. It would be nice to have a better understanding and a more Hodge-theoretic, less formal, characterization of Schiffer variations.
$x^{d-1}$. This is a higher-order property since it concerns the variation of the infinitesimal variation of Hodge structures. It would be nice to have a better understanding and a more Hodge-theoretic, less formal, characterization of Schiffer variations.
Remark 0.10 Schiffer variations have very special first-order properties mentioned above, as their tangent vector at any point lies in the Veronese variety. However, crucial to our argument is the fact that they also satisfy higher-order conditions, saying that the hypersurface in ![]() $\mathbb {P}^{n-1}$ defined by
$\mathbb {P}^{n-1}$ defined by ![]() $f_{\mid x=0}$ is constant, independent of
$f_{\mid x=0}$ is constant, independent of ![]() $t$.
$t$.
Our main result can be rephrased as follows.
Theorem 0.11 (cf. Claim 4.18)
Let ![]() $d$ be large enough, and
$d$ be large enough, and ![]() $n\geq d$. Let
$n\geq d$. Let ![]() $f\in U_{d,n}$ be generic,
$f\in U_{d,n}$ be generic, ![]() $U\subset U_{d,n}$,
$U\subset U_{d,n}$, ![]() $V\subset U_{d,n}$ be Euclidean open sets with
$V\subset U_{d,n}$ be Euclidean open sets with ![]() $f\in U$, and let
$f\in U$, and let ![]() $i:U\cong V$ be a holomorphic diffeomorphism inducing an isomorphism of complex variations of Hodge structures
$i:U\cong V$ be a holomorphic diffeomorphism inducing an isomorphism of complex variations of Hodge structures
on ![]() $U$. Then for a Schiffer variation
$U$. Then for a Schiffer variation ![]() $(f_t)_{t\in \Delta }$ of
$(f_t)_{t\in \Delta }$ of ![]() $f$ contained in
$f$ contained in ![]() $U$, where
$U$, where ![]() $\Delta$ is a disc, with tangent vector
$\Delta$ is a disc, with tangent vector ![]() $\phi =({df_t}/{dt})_{\mid t=0}\in T_{U,f}$,
$\phi =({df_t}/{dt})_{\mid t=0}\in T_{U,f}$, ![]() $i_*\phi$ is a first order Schiffer variation of
$i_*\phi$ is a first order Schiffer variation of ![]() $f':=i(f)$.
$f':=i(f)$.
This theorem easily implies Theorem 0.7(1) using Proposition 0.9. With more work, it could be improved in two ways.
(1) Under the same assumptions as above, for a general Schiffer variation
 $(f_t)_{t\in \Delta }$ of
$(f_t)_{t\in \Delta }$ of  $f$,
$f$,  $(i(f_t))_{t\in \Delta }$ is a Schiffer variation of
$(i(f_t))_{t\in \Delta }$ is a Schiffer variation of  $f'=i(f)$.
$f'=i(f)$.(2) One should be able to replace the Schiffer variation
 $(f_t)_{t\in \Delta }$ of
$(f_t)_{t\in \Delta }$ of  $f$ parameterized by a disc by a second-order Schiffer variation of
$f$ parameterized by a disc by a second-order Schiffer variation of  $f$.
$f$.
The paper is organized as follows. In § 1, we first explain (see § 1.1) how Theorem 0.6 implies Theorem 0.2 and we next discuss the notion of polynomial structure on the data of an infinitesimal variation of Hodge structure of a hypersurface. We discuss various recipes toward proving uniqueness of the polynomial structure, including Donagi's method. For example, we exhibit a very simple recipe to show that the natural polynomial structure for most hypersurfaces of degree ![]() $d$ dividing
$d$ dividing ![]() $n+1$ is rigid. In § 2, we prove Theorem 0.7(2), that is, degree 4. This proof follows Donagi's argument but provides a different recipe to prove the uniqueness of the polynomial structure of the infinitesimal variation of Hodge structure in these cases.
$n+1$ is rigid. In § 2, we prove Theorem 0.7(2), that is, degree 4. This proof follows Donagi's argument but provides a different recipe to prove the uniqueness of the polynomial structure of the infinitesimal variation of Hodge structure in these cases.
The main new ideas and results of the paper appear starting from § 3 where we introduce Schiffer variations of hypersurfaces and discuss their formal properties. The proof of Theorem 0.7(1) is given in § 4.2, where we give a characterization of Schiffer variations based on the local analysis of the variation of Hodge structure along the corresponding family of hypersurfaces and prove Theorem 0.11 (see Proposition 4.14 and Claim 4.18).
1. Polynomial structure and the Torelli theorem
1.1 Donagi's strategy and reduction to Theorem 0.6
For completeness, and because this argument will be also used in the last section, we explain in this section how Theorem 0.6 implies Theorem 0.2. Assume ![]() $f\in U_{d,n}$ is very general and
$f\in U_{d,n}$ is very general and ![]() $X_{f'}$ is a smooth hypersurface of degree
$X_{f'}$ is a smooth hypersurface of degree ![]() $d$ and dimension
$d$ and dimension ![]() $n-1$ with polarized Hodge structure on
$n-1$ with polarized Hodge structure on ![]() $H^{n-1}(X_{f'},\mathbb {Q})_{{\rm prim}}$, isomorphic to the Hodge structure on
$H^{n-1}(X_{f'},\mathbb {Q})_{{\rm prim}}$, isomorphic to the Hodge structure on ![]() $H^{n-1}(X_f,\mathbb {Q})_{{\rm prim}}$. We claim that this implies, except in the case where
$H^{n-1}(X_f,\mathbb {Q})_{{\rm prim}}$. We claim that this implies, except in the case where ![]() $(d,n)=(3,3)$, that
$(d,n)=(3,3)$, that ![]() $X_{f'}$ is also very general and there is an isomorphism of variations of Hodge structures on respective neighborhoods
$X_{f'}$ is also very general and there is an isomorphism of variations of Hodge structures on respective neighborhoods ![]() $U$,
$U$, ![]() $V$ of
$V$ of ![]() $f$ and
$f$ and ![]() $f'$ in their moduli space
$f'$ in their moduli space ![]() $U_{d,n}$. Indeed, the Hodge locus
$U_{d,n}$. Indeed, the Hodge locus
defined as the set of points ![]() $t,\,t'\in U\times V$ such that the given isomorphism
$t,\,t'\in U\times V$ such that the given isomorphism
induces an isomorphism of Hodge structures
is by the Cattani–Deligne–Kaplan theorem [Reference Cattani, Deligne and KaplanCDK95] the restriction to ![]() $U\times V$ of a closed algebraic subset (that we also denote
$U\times V$ of a closed algebraic subset (that we also denote ![]() $\Gamma _\phi$) of
$\Gamma _\phi$) of ![]() $U_{d,n}\times U_{d,n}$. As
$U_{d,n}\times U_{d,n}$. As ![]() $f$ is very general and in the image of
$f$ is very general and in the image of ![]() ${\rm pr}_1: \Gamma _\phi \rightarrow U_{d,n}$,
${\rm pr}_1: \Gamma _\phi \rightarrow U_{d,n}$, ![]() ${\rm pr}_1$ has to be dominant.
${\rm pr}_1$ has to be dominant.
An important point is the fact that, as an easy consequence of Macaulay theorem [Reference VoisinVoi03, Theorem 6.19], the smooth hypersurfaces of degree ![]() $d$ in
$d$ in ![]() $\mathbb {P}^{n}$, with
$\mathbb {P}^{n}$, with ![]() $(d,n)\not =(3,3)$ satisfy the infinitesimal Torelli theorem. This means that the period map is an immersion at the points
$(d,n)\not =(3,3)$ satisfy the infinitesimal Torelli theorem. This means that the period map is an immersion at the points ![]() $f$ of the open set
$f$ of the open set ![]() $U_{d,n}^{0}\subset U_{d,n}$ parameterizing automorphisms free hypersurfaces, once
$U_{d,n}^{0}\subset U_{d,n}$ parameterizing automorphisms free hypersurfaces, once ![]() $(d,n)\not =(3,3)$. As
$(d,n)\not =(3,3)$. As ![]() $f$ is very general, we can assume that
$f$ is very general, we can assume that ![]() $f$ belongs to
$f$ belongs to ![]() $U_{d,n}^{0}$. It follows that the projection
$U_{d,n}^{0}$. It follows that the projection
must be locally finite since, by definition, the fiber of ![]() ${\rm pr}_2$ over any
${\rm pr}_2$ over any ![]() $t'\in V$ parameterizes points
$t'\in V$ parameterizes points ![]() $t$ with isomorphic Hodge structures on
$t$ with isomorphic Hodge structures on ![]() $H^{n-1}(X_t,\mathbb {Q})_{{\rm prim}}$. In particular,
$H^{n-1}(X_t,\mathbb {Q})_{{\rm prim}}$. In particular, ![]() $f'$ is also very general so we can assume that
$f'$ is also very general so we can assume that ![]() $f'$ is also automorphism free.
$f'$ is also automorphism free.
The two projections ![]() ${\rm pr}_1$,
${\rm pr}_1$, ![]() ${\rm pr_2}$ are thus immersions and dominant morphisms, and hence they must be étale. It thus follows that
${\rm pr_2}$ are thus immersions and dominant morphisms, and hence they must be étale. It thus follows that ![]() $\Gamma _\phi$ induces a local holomorphic diffeomorphism
$\Gamma _\phi$ induces a local holomorphic diffeomorphism ![]() $i$ between
$i$ between ![]() $U$ and
$U$ and ![]() $V$ which, by definition of
$V$ which, by definition of ![]() $\Gamma _\phi$, has the property that the isomorphism
$\Gamma _\phi$, has the property that the isomorphism
of trivial local systems on ![]() $U$ induces an isomorphism of variations of Hodge structures. Here, if
$U$ induces an isomorphism of variations of Hodge structures. Here, if ![]() $\pi :\mathcal {X}_{d,n}\rightarrow U_{d,n}^{0}$ is the universal hypersurface,
$\pi :\mathcal {X}_{d,n}\rightarrow U_{d,n}^{0}$ is the universal hypersurface, ![]() $H^{n-1}_\mathbb {C}$ is the local system
$H^{n-1}_\mathbb {C}$ is the local system ![]() $R^{n-1}\pi _*\mathbb {C}_{{\rm prim}}$ on
$R^{n-1}\pi _*\mathbb {C}_{{\rm prim}}$ on ![]() $U_{d,n}^{0}$. Taking the differential of this isomorphism provides a commutative diagram where the vertical maps are isomorphisms,
$U_{d,n}^{0}$. Taking the differential of this isomorphism provides a commutative diagram where the vertical maps are isomorphisms,

where the vertical map on the left is the differential ![]() $i_*$ at
$i_*$ at ![]() $f\in U$ and the vertical map on the right is induced by the isomorphism of Hodge structures
$f\in U$ and the vertical map on the right is induced by the isomorphism of Hodge structures ![]() $\phi : H^{n-1}(X_f,\mathbb {Q})_{{\rm prim}}\rightarrow H^{n-1}(X_{f'},\mathbb {Q})_{{\rm prim}}$. By Theorem 0.5, we then get a commutative diagram (8) to which Theorem 0.6 applies.
$\phi : H^{n-1}(X_f,\mathbb {Q})_{{\rm prim}}\rightarrow H^{n-1}(X_{f'},\mathbb {Q})_{{\rm prim}}$. By Theorem 0.5, we then get a commutative diagram (8) to which Theorem 0.6 applies.
1.2 Polynomial structure and the symmetrizer lemma
The method used by Donagi to prove Theorem 0.6 consists in applying the ‘symmetrizer lemma’ (Proposition 1.1 below), in order to recover from the data (5) the whole Jacobian ring in degrees divisible by ![]() $l$, where
$l$, where ![]() $l$ is the greatest common denominator of
$l$ is the greatest common denominator of ![]() $n+1$ and
$n+1$ and ![]() $d$. This result proved first in [Reference DonagiDon83] for the Jacobian ring of generic hypersurfaces, and reproved in [Reference Donagi and GreenDG84] for any smooth hypersurface (and more generally quotients
$d$. This result proved first in [Reference DonagiDon83] for the Jacobian ring of generic hypersurfaces, and reproved in [Reference Donagi and GreenDG84] for any smooth hypersurface (and more generally quotients ![]() $R_{f_{\bullet }}$ of the polynomial ring
$R_{f_{\bullet }}$ of the polynomial ring ![]() $S=\mathbb {C}[X_0,\ldots,X_n]$ by a regular sequence
$S=\mathbb {C}[X_0,\ldots,X_n]$ by a regular sequence ![]() $f_{\bullet }=(f_0,\ldots,f_n)$ with
$f_{\bullet }=(f_0,\ldots,f_n)$ with ![]() ${\rm deg}\,f_i=d-1$), is the following statement. Consider the multiplication map
${\rm deg}\,f_i=d-1$), is the following statement. Consider the multiplication map
Proposition 1.1 Let ![]() $N=(n+1)(d\,{-}\,2)$. Then, if
$N=(n+1)(d\,{-}\,2)$. Then, if ![]() $\,{\rm Max}\,(k,N\,{-}\,k')\geq d\,{-}\,1$ and
$\,{\rm Max}\,(k,N\,{-}\,k')\geq d\,{-}\,1$ and ![]() ${N-k-k'>0}$, the multiplication map
${N-k-k'>0}$, the multiplication map
is determined by the multiplication map (11) as follows
Coming back to the case of a Jacobian ring ![]() $R_f$, when
$R_f$, when ![]() $d$ divides
$d$ divides ![]() $n+1$, the infinitesimal variation of Hodge structure (3) of
$n+1$, the infinitesimal variation of Hodge structure (3) of ![]() $X_f$, translated in the form (5), involves only pieces
$X_f$, translated in the form (5), involves only pieces ![]() $R^{k}_f$ of the Jacobian ring of degree
$R^{k}_f$ of the Jacobian ring of degree ![]() $k$ divisible by
$k$ divisible by ![]() $d$. Hence the symmetrizer lemma at best allows us, starting from the infinitesimal variation of Hodge structure (IVHS) of the hypersurface, to reconstruct the Jacobian ring in degrees divisible by
$d$. Hence the symmetrizer lemma at best allows us, starting from the infinitesimal variation of Hodge structure (IVHS) of the hypersurface, to reconstruct the Jacobian ring in degrees divisible by ![]() $d$. At the opposite, when
$d$. At the opposite, when ![]() $d$ and
$d$ and ![]() $n+1$ are coprime, repeated applications of the symmetrizer lemma allow us to reconstruct the whole Jacobian ring. In degree
$n+1$ are coprime, repeated applications of the symmetrizer lemma allow us to reconstruct the whole Jacobian ring. In degree ![]() $< d-1$, the Jacobian ring coincides with the polynomial ring, and hence we directly recover in that case the multiplication map
$< d-1$, the Jacobian ring coincides with the polynomial ring, and hence we directly recover in that case the multiplication map
and its kernel ![]() $J_f^{d}$. The proof of Donagi is then finished by applying Mather and Yau's theorem [Reference Mather and YauMY82] (see also Proposition 3.2).
$J_f^{d}$. The proof of Donagi is then finished by applying Mather and Yau's theorem [Reference Mather and YauMY82] (see also Proposition 3.2).
This leads us to the following definition. Suppose that we have two integers ![]() $d,\ n$ and the partial data of a graded ring structure
$d,\ n$ and the partial data of a graded ring structure ![]() $R^{*}$, namely finite dimensional vector spaces
$R^{*}$, namely finite dimensional vector spaces ![]() $R^{d},\ R^{-(n+1)+id}$ for
$R^{d},\ R^{-(n+1)+id}$ for ![]() $i$ such that
$i$ such that ![]() $-(n+1)+id\geq 0$ with multiplication maps
$-(n+1)+id\geq 0$ with multiplication maps
When ![]() $d$ divides
$d$ divides ![]() $n+1$, we get all the upper-indices divisible by
$n+1$, we get all the upper-indices divisible by ![]() $d$, and an actual ring structure
$d$, and an actual ring structure ![]() $R^{d*}$, but in general (13) is the sort of data provided by the infinitesimal variation of Hodge structure of a hypersurface of degree
$R^{d*}$, but in general (13) is the sort of data provided by the infinitesimal variation of Hodge structure of a hypersurface of degree ![]() $d$ in
$d$ in ![]() $\mathbb {P}^{n}$. Let
$\mathbb {P}^{n}$. Let ![]() $S^{k}$ be the degree
$S^{k}$ be the degree ![]() $k$ part of the polynomial ring in
$k$ part of the polynomial ring in ![]() $n+1$ variables.
$n+1$ variables.
Definition 1.2 A polynomial structure in ![]() $n+1$ variables for the partial data of a graded ring structure
$n+1$ variables for the partial data of a graded ring structure
is the data of a rank ![]() $n+1$ base-point free linear subspace
$n+1$ base-point free linear subspace ![]() $J\subset S^{d-1}$ generating a graded ideal
$J\subset S^{d-1}$ generating a graded ideal ![]() $J^{*}\subset S^{*}$, of a linear isomorphism
$J^{*}\subset S^{*}$, of a linear isomorphism ![]() $S^{d}/J^{d}\cong R^{d}$ and, for all
$S^{d}/J^{d}\cong R^{d}$ and, for all ![]() $i$, of linear isomorphisms
$i$, of linear isomorphisms
compatible with the multiplication maps, i.e. making the following diagrams commutative.

The group ![]() ${\rm GL}(n+1)$ acts in the obvious way on the set of polynomial structures. We will say that the polynomial structure of
${\rm GL}(n+1)$ acts in the obvious way on the set of polynomial structures. We will say that the polynomial structure of ![]() $(R^{d},\,R^{-(n+1)+id},\,\mu _i)$ is unique if all its polynomial structures are conjugate under
$(R^{d},\,R^{-(n+1)+id},\,\mu _i)$ is unique if all its polynomial structures are conjugate under ![]() ${\rm GL}(n+1)$. As explained above, Donagi's Theorem 0.6 has the more precise form that, under some assumptions on
${\rm GL}(n+1)$. As explained above, Donagi's Theorem 0.6 has the more precise form that, under some assumptions on ![]() $(d,n)$, the polynomial structure of the infinitesimal variation of Hodge structure
$(d,n)$, the polynomial structure of the infinitesimal variation of Hodge structure ![]() $(R^{d}_f,\,R^{-(n+1)+id}_f,\,\mu _i)$ of a smooth hypersurface
$(R^{d}_f,\,R^{-(n+1)+id}_f,\,\mu _i)$ of a smooth hypersurface ![]() $X_f$ is unique, and this is sufficient to imply the generic Torelli theorem for hypersurfaces of these degree and dimension. We will prove a similar statement in the case (2) (that is degree
$X_f$ is unique, and this is sufficient to imply the generic Torelli theorem for hypersurfaces of these degree and dimension. We will prove a similar statement in the case (2) (that is degree ![]() $d=4$) of Theorem 0.7, at least for generic
$d=4$) of Theorem 0.7, at least for generic ![]() $f$ and
$f$ and ![]() $n$ large enough.
$n$ large enough.
For the main series of cases not covered by Donagi's theorem, namely when ![]() $d$ divides
$d$ divides ![]() $n+1$, we have not been able to prove the uniqueness of the polynomial structure of
$n+1$, we have not been able to prove the uniqueness of the polynomial structure of ![]() $R^{d*}_f$ (even for generic
$R^{d*}_f$ (even for generic ![]() $f$), although it is likely to be true (and it is proved in [Reference Voisin, Hulek, Catanese, Peters and ReidVoi99] for
$f$), although it is likely to be true (and it is proved in [Reference Voisin, Hulek, Catanese, Peters and ReidVoi99] for ![]() $d=5$,
$d=5$, ![]() $n=4$). We finish this section by the proof of a weaker statement that provides evidence for the uniqueness. We will say that a polynomial structure is rigid if its small deformations are given by its orbit under
$n=4$). We finish this section by the proof of a weaker statement that provides evidence for the uniqueness. We will say that a polynomial structure is rigid if its small deformations are given by its orbit under ![]() ${\rm GL}(n+1)$. We have the following.
${\rm GL}(n+1)$. We have the following.
Proposition 1.3 Assume ![]() $n+1\geq 8$ and
$n+1\geq 8$ and ![]() $d\geq 6$. Let
$d\geq 6$. Let ![]() $f\in S^{d}$ be a generic homogeneous polynomial of degree
$f\in S^{d}$ be a generic homogeneous polynomial of degree ![]() $d$ in
$d$ in ![]() $n+1$ variables and
$n+1$ variables and ![]() $R_{f}^{d*}$ be its Jacobian ring in degrees divisible by
$R_{f}^{d*}$ be its Jacobian ring in degrees divisible by ![]() $d$. Then the natural polynomial structure
$d$. Then the natural polynomial structure
given by the quotient map is rigid.
Remark 1.4 The case where ![]() $d=4$ and
$d=4$ and ![]() $n+1\cong 2$ mod
$n+1\cong 2$ mod ![]() $4$ will be studied in next section. We will prove there, using a different recipe, that the polynomial structure on
$4$ will be studied in next section. We will prove there, using a different recipe, that the polynomial structure on ![]() $R^{2*}_f$ is unique for
$R^{2*}_f$ is unique for ![]() $n$ large enough.
$n$ large enough.
Remark 1.5 Proposition 1.3 implies that the natural polynomial structure of ![]() $R_{f_{\bullet }}^{d*}$ for a generic rank
$R_{f_{\bullet }}^{d*}$ for a generic rank ![]() $n+1$ regular sequence
$n+1$ regular sequence ![]() $f_{\bullet }$ of degree
$f_{\bullet }$ of degree ![]() $d-1$ homogeneous polynomials is rigid.
$d-1$ homogeneous polynomials is rigid.
We will use in fact only the multiplication map in degree ![]() $d$
$d$
Proposition 1.3 will be implied by Proposition 1.8 below. For our original polynomial structure on ![]() $R_f^{d*}$, and for each
$R_f^{d*}$, and for each ![]() $x\in S^{1}$, we get a pair of vector subspaces
$x\in S^{1}$, we get a pair of vector subspaces
which form an ideal in the sense that
It is not hard to see that the multiplication map by ![]() $x$, from
$x$, from ![]() $R^{d-1}_{f}$ to
$R^{d-1}_{f}$ to ![]() $R^{d}_{f}$, is injective for a generic
$R^{d}_{f}$, is injective for a generic ![]() $x\in S^{1}$ when
$x\in S^{1}$ when ![]() $f$ is generic with
$f$ is generic with ![]() $d\geq 4$ and
$d\geq 4$ and ![]() $n\geq 3$ (or
$n\geq 3$ (or ![]() $d\geq 3$ and
$d\geq 3$ and ![]() $n\geq 5$). In fact, we even have the following (statement (ii) will be used only later on).
$n\geq 5$). In fact, we even have the following (statement (ii) will be used only later on).
Lemma 1.6
(i) The multiplication map by
 $x$ is injective on
$x$ is injective on  $R^{2d-1}_{f}$ when
$R^{2d-1}_{f}$ when  $f$ is generic,
$f$ is generic,  $x\in S^{1}$ is generic and
(17)(for example,
$x\in S^{1}$ is generic and
(17)(for example, \begin{equation} 2(2d-1)<(d-2)(n+1) \end{equation}
\begin{equation} 2(2d-1)<(d-2)(n+1) \end{equation} $n+1\geq 5$ and
$n+1\geq 5$ and  $d>8$, or
$d>8$, or  $n+1\geq 6$ and
$n+1\geq 6$ and  $d>4$ work).
$d>4$ work).(ii) The multiplication map by
 $x$ is injective on
$x$ is injective on  $R^{3d-1}_{f}$ when
$R^{3d-1}_{f}$ when  $f$ is generic,
$f$ is generic,  $x\in S^{1}$ is generic and
(for example,
$x\in S^{1}$ is generic and
(for example, \[ 2(3d-1)<(d-2)(n+1) \]
\[ 2(3d-1)<(d-2)(n+1) \] $n+1\geq 5$ and
$n+1\geq 5$ and  $d>8$, or
$d>8$, or  $n+1\geq 6$ and
$n+1\geq 6$ and  $d>4$ work).
$d>4$ work).(iii) The multiplication map by
 $x^{l}$ is injective on
$x^{l}$ is injective on  $R^{k}_{f}$ when
$R^{k}_{f}$ when  $f$ is generic,
$f$ is generic,  $x\in S^{1}$ is generic and
$x\in S^{1}$ is generic and
 \[ 2k+l\leq (d-2)(n+1). \]
\[ 2k+l\leq (d-2)(n+1). \]
Proof. As the dimensions of the vector spaces ![]() $R^{k}_f$ are independent of
$R^{k}_f$ are independent of ![]() $f$ (assumed to define a smooth hypersurface), the conclusions are open properties of
$f$ (assumed to define a smooth hypersurface), the conclusions are open properties of ![]() $f$, and hence it suffices to check them for a particular
$f$, and hence it suffices to check them for a particular ![]() $f$. Take for
$f$. Take for ![]() $f$ the Fermat polynomial
$f$ the Fermat polynomial ![]() $f_{\rm Fermat}=\sum _{i=0}^{n}X_i^{d}$. Then
$f_{\rm Fermat}=\sum _{i=0}^{n}X_i^{d}$. Then ![]() $R_{f_{\rm Fermat}}^{*}$ identifies with the cohomology ring
$R_{f_{\rm Fermat}}^{*}$ identifies with the cohomology ring ![]() $H^{2*}((\mathbb {P}^{d-2})^{n+1},\mathbb {C})$ (indeed, it has generators
$H^{2*}((\mathbb {P}^{d-2})^{n+1},\mathbb {C})$ (indeed, it has generators ![]() $X_i$ and relations
$X_i$ and relations ![]() $X_i^{d-1}=0$) and
$X_i^{d-1}=0$) and ![]() $x=\sum _iX_i$ corresponds to an ample class in
$x=\sum _iX_i$ corresponds to an ample class in ![]() $H^{2}((\mathbb {P}^{d-2})^{n+1},\mathbb {C})$. By the hard Leschetz theorem for
$H^{2}((\mathbb {P}^{d-2})^{n+1},\mathbb {C})$. By the hard Leschetz theorem for ![]() $(\mathbb {P}^{d-2})^{n+1}$, the multiplication by
$(\mathbb {P}^{d-2})^{n+1}$, the multiplication by ![]() $x$ is thus injective on
$x$ is thus injective on ![]() $R^{2d-1}_{f_{\rm Fermat}}$ if
$R^{2d-1}_{f_{\rm Fermat}}$ if ![]() $2(2d-1)<(d-2)(n+1)$, and injective on
$2(2d-1)<(d-2)(n+1)$, and injective on ![]() $R^{3d-1}_{f_{\rm Fermat}}$ if
$R^{3d-1}_{f_{\rm Fermat}}$ if ![]() $2(3d-1)<(d-2)(n+1)$. More generally, the Lefschetz isomorphism for the power
$2(3d-1)<(d-2)(n+1)$. More generally, the Lefschetz isomorphism for the power ![]() $x^{l}$ gives the injectivity of
$x^{l}$ gives the injectivity of ![]() $x^{l}$ on
$x^{l}$ on ![]() $R^{k}_{f_{\rm Fermat}}$ when
$R^{k}_{f_{\rm Fermat}}$ when ![]() $2k+l\leq (d-2)(n+1)$.
$2k+l\leq (d-2)(n+1)$.
Remark 1.7 The estimate in (i) is optimal for dimension reasons. Indeed, the dimensions of the graded pieces ![]() $R^{k}_{f}$ are increasing in the interval
$R^{k}_{f}$ are increasing in the interval ![]() $k\leq {((d-2)(n+1))}/{2}$, and decreasing in the interval
$k\leq {((d-2)(n+1))}/{2}$, and decreasing in the interval ![]() ${((d-2)(n+1))}/{2}\leq k\leq (d-2)(n+1)$.
${((d-2)(n+1))}/{2}\leq k\leq (d-2)(n+1)$.
It follows from Lemma 1.6 that, assuming inequality (17), the space ![]() $I_x^{d}$ defined in (15) has generic dimension
$I_x^{d}$ defined in (15) has generic dimension ![]() $r_{d-1}:={\rm dim}\, R^{d-1}_{f}$, while
$r_{d-1}:={\rm dim}\, R^{d-1}_{f}$, while ![]() $I_x^{2d}$ has generic dimension
$I_x^{2d}$ has generic dimension ![]() $r_{2d-1}:={\rm dim}\, R^{2d-1}_{f}$.
$r_{2d-1}:={\rm dim}\, R^{2d-1}_{f}$.
Proposition 1.8 If ![]() $f$ is generic of degree
$f$ is generic of degree ![]() $d$ in
$d$ in ![]() $n+1$ variables, and
$n+1$ variables, and ![]() $d\geq 6,\ n\geq 9$, then the subset
$d\geq 6,\ n\geq 9$, then the subset ![]() $Z_{\rm ideal}=\{[I^{d}_x]\in G(r_{d-1},R^{d}_{f}),\,x\in S^{1}\}$ of the Grassmannian
$Z_{\rm ideal}=\{[I^{d}_x]\in G(r_{d-1},R^{d}_{f}),\,x\in S^{1}\}$ of the Grassmannian ![]() $G(r_{d-1},R^{d}_{f})$ is a reduced component of the closed algebraic subset
$G(r_{d-1},R^{d}_{f})$ is a reduced component of the closed algebraic subset ![]() $Z\subset G(r_{d-1},R^{d}_{f})$ defined as
$Z\subset G(r_{d-1},R^{d}_{f})$ defined as
Proof. The tangent space to ![]() $Z_{\rm ideal}$ at the point
$Z_{\rm ideal}$ at the point ![]() $[I^{d}_x]\in G(r_{d-1},R^{d}_{f})$ is the image of
$[I^{d}_x]\in G(r_{d-1},R^{d}_{f})$ is the image of ![]() $S^{1}/\langle x\rangle$ in
$S^{1}/\langle x\rangle$ in ![]() ${\rm Hom}(R^{d-1}_{f},R^{d}_{f}/xR^{d-1}_{f})=T_{G(r_{d-1},R^{d}_{f}),[I_x^{d}]}$ given by multiplication by
${\rm Hom}(R^{d-1}_{f},R^{d}_{f}/xR^{d-1}_{f})=T_{G(r_{d-1},R^{d}_{f}),[I_x^{d}]}$ given by multiplication by ![]() $y\in S^{1}/\langle x\rangle$, where we identify
$y\in S^{1}/\langle x\rangle$, where we identify ![]() $I_x^{d}$ with
$I_x^{d}$ with ![]() $R^{d-1}_{f}$ via multiplication by
$R^{d-1}_{f}$ via multiplication by ![]() $x$. Let us now compute the Zariski tangent space to
$x$. Let us now compute the Zariski tangent space to ![]() $Z$ at
$Z$ at ![]() $[I^{d}_x]$ for
$[I^{d}_x]$ for ![]() $f$ and
$f$ and ![]() $x$ generic. As
$x$ generic. As ![]() ${\rm dim}\,I_x^{2d}=r_{2d-1}$ is maximal by the claim above, the condition (18) provides the following infinitesimal conditions:
${\rm dim}\,I_x^{2d}=r_{2d-1}$ is maximal by the claim above, the condition (18) provides the following infinitesimal conditions:
 \begin{align} T_{Z,[I_x^{d}]}&=\bigg\{h\in {\rm Hom}\big(R^{d-1}_{f},R^{d}_{f}/xR^{d-1}_{f}\big),\, \sum_iA_ih(B_i)=0\ {\rm in}\ R^{2d}_{f}/xR^{d-1}_{f},\nonumber\\ &\qquad {\rm for\ any}\ K=\sum_iA_i\otimes B_i\in R^{d}_f\otimes R^{d-1}_{f}\ {\rm such\ that}\ \sum_iA_iB_i=0\ {\rm in} \ R^{2d-1}_{f}\bigg\}. \end{align}
\begin{align} T_{Z,[I_x^{d}]}&=\bigg\{h\in {\rm Hom}\big(R^{d-1}_{f},R^{d}_{f}/xR^{d-1}_{f}\big),\, \sum_iA_ih(B_i)=0\ {\rm in}\ R^{2d}_{f}/xR^{d-1}_{f},\nonumber\\ &\qquad {\rm for\ any}\ K=\sum_iA_i\otimes B_i\in R^{d}_f\otimes R^{d-1}_{f}\ {\rm such\ that}\ \sum_iA_iB_i=0\ {\rm in} \ R^{2d-1}_{f}\bigg\}. \end{align}
Equation (19) says that ![]() $h: R^{d-1}_{f}\rightarrow R^{d}_{f}/xR^{d-1}_{f}$ is a ‘morphism of
$h: R^{d-1}_{f}\rightarrow R^{d}_{f}/xR^{d-1}_{f}$ is a ‘morphism of ![]() $R^{d}_{f}$-modules’, the set of which we will denote by
$R^{d}_{f}$-modules’, the set of which we will denote by ![]() ${\rm Mor}_{R^{d}_f}(R^{d-1}_{f},R^{d}_{f}/xR^{d-1}_{f})$, in the sense that we have a commutative diagram for some
${\rm Mor}_{R^{d}_f}(R^{d-1}_{f},R^{d}_{f}/xR^{d-1}_{f})$, in the sense that we have a commutative diagram for some ![]() $h'\in {\rm Hom}(R^{2d-1}_{f},R^{2d}_{f}/\langle x\rangle )$,
$h'\in {\rm Hom}(R^{2d-1}_{f},R^{2d}_{f}/\langle x\rangle )$,

where the horizontal maps are given by multiplication. The equality ![]() $T_{Z_{\rm ideal}}=T_Z$ at the point
$T_{Z_{\rm ideal}}=T_Z$ at the point ![]() $[I_x^{d}]$ is thus equivalent to the fact that all the ‘
$[I_x^{d}]$ is thus equivalent to the fact that all the ‘![]() $R^{d}_{f}$-modules morphisms’
$R^{d}_{f}$-modules morphisms’ ![]() $h: R^{d-1}_{f}\rightarrow R^{d}_{f}/xR^{d-1}_{f}$, are given by multiplication by some
$h: R^{d-1}_{f}\rightarrow R^{d}_{f}/xR^{d-1}_{f}$, are given by multiplication by some ![]() $y\in S^{1}$, followed by reduction modulo
$y\in S^{1}$, followed by reduction modulo ![]() $x$. This is the statement of the following
$x$. This is the statement of the following
Lemma 1.9 Let ![]() ${f}$ be a generic homogeneous degree
${f}$ be a generic homogeneous degree ![]() $d$ polynomial in
$d$ polynomial in ![]() $n+1$ variables with
$n+1$ variables with ![]() $d \geq 5,\ n\geq 9$ (or
$d \geq 5,\ n\geq 9$ (or ![]() $d\geq 6$ and
$d\geq 6$ and ![]() $n\geq 7$), and let
$n\geq 7$), and let ![]() $x\in S^{1}$ be generic. Then the natural map
$x\in S^{1}$ be generic. Then the natural map ![]() $S^{1}/\langle x\rangle \rightarrow {\rm Mor}_{R_{f}^{d}}(R^{d-1}_{f},R^{d}_{f}/\langle x\rangle )$ is surjective.
$S^{1}/\langle x\rangle \rightarrow {\rm Mor}_{R_{f}^{d}}(R^{d-1}_{f},R^{d}_{f}/\langle x\rangle )$ is surjective.
Proof. The existence of ![]() $h'$ as in (20) says that for any tensor
$h'$ as in (20) says that for any tensor ![]() $\sum _i A_i\otimes B_i\in R^{d}_{f}\otimes R^{d-1}_{f}$ such that
$\sum _i A_i\otimes B_i\in R^{d}_{f}\otimes R^{d-1}_{f}$ such that ![]() $\sum _iA_iB_i=0$ in
$\sum _iA_iB_i=0$ in ![]() $R^{2d-1}_{f}$,
$R^{2d-1}_{f}$, ![]() $\sum _i A_ih(B_i)=0$ in
$\sum _i A_ih(B_i)=0$ in ![]() $R^{2d}_{f}/\langle x\rangle$.
$R^{2d}_{f}/\langle x\rangle$.
Claim 1.10 Under the same assumptions as in Lemma 1.9, for a generic ![]() $q\in R^{d-1}_{f}$, the multiplication map
$q\in R^{d-1}_{f}$, the multiplication map
is injective.
Proof. This is proved again by looking at the Fermat polynomial ![]() $f_{\rm Fermat}=\sum _iX_i^{d}$ and choosing carefully
$f_{\rm Fermat}=\sum _iX_i^{d}$ and choosing carefully ![]() $x$ so that multiplication by
$x$ so that multiplication by ![]() $x$ is injective on
$x$ is injective on ![]() $R^{2d-1}_{f_{\rm Fermat}}$, and multiplication by
$R^{2d-1}_{f_{\rm Fermat}}$, and multiplication by ![]() $q$ is injective on
$q$ is injective on ![]() $R^{d+1}_{f_{\rm Fermat}}/\langle x\rangle$. We write
$R^{d+1}_{f_{\rm Fermat}}/\langle x\rangle$. We write ![]() $f_{\rm Fermat}=f'_{\rm Fermat}+f''_{\rm Fermat}$, where
$f_{\rm Fermat}=f'_{\rm Fermat}+f''_{\rm Fermat}$, where ![]() $f'_{\rm Fermat}=\sum _{i=0}^{4}X_i^{d}$ and
$f'_{\rm Fermat}=\sum _{i=0}^{4}X_i^{d}$ and ![]() $f''_{\rm Fermat}=\sum _{i=5}^{n}X_i^{d}$. We take
$f''_{\rm Fermat}=\sum _{i=5}^{n}X_i^{d}$. We take ![]() $x=\sum _{i=0}^{4}X_i$ and
$x=\sum _{i=0}^{4}X_i$ and ![]() $q=\big (\sum _{i=5}^{N}X_i\big )^{d-1}$. We observe that
$q=\big (\sum _{i=5}^{N}X_i\big )^{d-1}$. We observe that
as graded rings, and that ![]() $x$ acts by multiplication on the left term
$x$ acts by multiplication on the left term ![]() $R_{f'_{\rm Fermat}}^{*}$, while
$R_{f'_{\rm Fermat}}^{*}$, while ![]() $q$ acts by multiplication on the right term
$q$ acts by multiplication on the right term ![]() $R_{f''_{\rm Fermat}}^{*}$. So it suffices to show that multiplication by
$R_{f''_{\rm Fermat}}^{*}$. So it suffices to show that multiplication by ![]() $x$ is injective on
$x$ is injective on ![]() $R_{f'_{\rm Fermat}}^{k}$ for
$R_{f'_{\rm Fermat}}^{k}$ for ![]() $k\leq 2d-1$ and multiplication by
$k\leq 2d-1$ and multiplication by ![]() $q$ is injective on
$q$ is injective on ![]() $R_{f''_{\rm Fermat}}^{k}$ for
$R_{f''_{\rm Fermat}}^{k}$ for ![]() $k\leq d+1$. The first statement follows from Lemma 1.6(i) when
$k\leq d+1$. The first statement follows from Lemma 1.6(i) when ![]() $2(d+1)<5(d-2)$, hence when
$2(d+1)<5(d-2)$, hence when ![]() $d\geq 5$. The second statement holds by Lemma 1.6(iii) when
$d\geq 5$. The second statement holds by Lemma 1.6(iii) when ![]() $2(d+1)+d-1\leq (n-4)(d-2)$, and in particular if
$2(d+1)+d-1\leq (n-4)(d-2)$, and in particular if ![]() $d\geq 6$ and
$d\geq 6$ and ![]() $n\geq 9$.
$n\geq 9$.
We deduce from Claim 1.10 that for any tensor ![]() $\sum _i A_i\otimes B_i\in S^{1}\otimes R^{d-1}_{f}$ such that
$\sum _i A_i\otimes B_i\in S^{1}\otimes R^{d-1}_{f}$ such that ![]() ${\sum _iA_iB_i=0}$ in
${\sum _iA_iB_i=0}$ in ![]() $R^{d}_{f}$, we have
$R^{d}_{f}$, we have
since this becomes true after multiplication by ![]() $q$. It follows now that
$q$. It follows now that ![]() $h$ vanishes on
$h$ vanishes on ![]() $\langle x\rangle$. Indeed, let
$\langle x\rangle$. Indeed, let ![]() $b=xb'$. Then for any
$b=xb'$. Then for any ![]() $y\in S^{1}$, we have
$y\in S^{1}$, we have ![]() $yb=xb''$ with
$yb=xb''$ with ![]() $b''=yb'$. Hence by (21), we get
$b''=yb'$. Hence by (21), we get ![]() $yh(b)=xh(b'')=0$. Hence
$yh(b)=xh(b'')=0$. Hence ![]() $yh(b)=0$ in
$yh(b)=0$ in ![]() $R^{d+1}_f/\langle x\rangle$ for any
$R^{d+1}_f/\langle x\rangle$ for any ![]() $y\in S^{1}$, and it follows, by choosing
$y\in S^{1}$, and it follows, by choosing ![]() $y$ such that multiplication by
$y$ such that multiplication by ![]() $y$ is injective on
$y$ is injective on ![]() $R^{d}_{f}/\langle x\rangle$, that
$R^{d}_{f}/\langle x\rangle$, that ![]() $h(b)=0$ in
$h(b)=0$ in ![]() $R^{d}_{f}/\langle x\rangle$. Thus
$R^{d}_{f}/\langle x\rangle$. Thus ![]() $h$ induces a morphism
$h$ induces a morphism
which also satisfies (21). Assuming ![]() $d\geq 6,\,n\geq 9$, we now show by similar arguments as above that for generic
$d\geq 6,\,n\geq 9$, we now show by similar arguments as above that for generic ![]() $z,\,y\in S^{1}/\langle x\rangle$, the following holds. For any
$z,\,y\in S^{1}/\langle x\rangle$, the following holds. For any ![]() $p,\,q\in R^{d}_{f}/\langle x\rangle$,
$p,\,q\in R^{d}_{f}/\langle x\rangle$,
for some ![]() $r\in R^{d-1}_f/\langle x\rangle$. Furthermore we already know that the multiplication map by
$r\in R^{d-1}_f/\langle x\rangle$. Furthermore we already know that the multiplication map by ![]() $z$ from
$z$ from ![]() $R^{d}_{f}/\langle x\rangle$ to
$R^{d}_{f}/\langle x\rangle$ to ![]() $R^{d+1}_{f}/\langle x\rangle$ is injective. It follows that there exists
$R^{d+1}_{f}/\langle x\rangle$ is injective. It follows that there exists
inducing ![]() $\bar {h}$, that is,
$\bar {h}$, that is,
for any ![]() $p\in R^{d-2}_{f}/ \langle x\rangle$, and any
$p\in R^{d-2}_{f}/ \langle x\rangle$, and any ![]() $a\in S^{1}/\langle x\rangle$. Indeed,
$a\in S^{1}/\langle x\rangle$. Indeed, ![]() $y$ and
$y$ and ![]() $z$ being as above, we have for any
$z$ being as above, we have for any ![]() $p\in R^{d-2}_{f}/ \langle x\rangle$
$p\in R^{d-2}_{f}/ \langle x\rangle$
hence by (21), we get that ![]() $y\bar {h}(zp)-z \bar {h}(yp)=0$ in
$y\bar {h}(zp)-z \bar {h}(yp)=0$ in ![]() $R^{d+1}_{f}/\langle x\rangle$, and by (22), this gives
$R^{d+1}_{f}/\langle x\rangle$, and by (22), this gives ![]() $\bar {h}(zp)=z\bar {h}''(p)$, which defines
$\bar {h}(zp)=z\bar {h}''(p)$, which defines ![]() $\bar {h}''$. One then shows that the map
$\bar {h}''$. One then shows that the map ![]() $\bar {h}''$ so defined does not depend on
$\bar {h}''$ so defined does not depend on ![]() $z$ and satisfies (23), which is easy. To finish the proof, we construct similarly
$z$ and satisfies (23), which is easy. To finish the proof, we construct similarly ![]() $\bar {h}''':R^{d-3}_{f}/\langle x\rangle \rightarrow R^{d-2}_{f}/\langle x\rangle$ inducing
$\bar {h}''':R^{d-3}_{f}/\langle x\rangle \rightarrow R^{d-2}_{f}/\langle x\rangle$ inducing ![]() $\bar {h}''$ and
$\bar {h}''$ and ![]() $\bar {h}^{iv}:R^{d-4}_{f}/\langle x\rangle \rightarrow R^{d-3}_{f}/\langle x\rangle$ inducing
$\bar {h}^{iv}:R^{d-4}_{f}/\langle x\rangle \rightarrow R^{d-3}_{f}/\langle x\rangle$ inducing ![]() $\bar {h}'''$. As
$\bar {h}'''$. As ![]() $R^{i}_{f}/\langle x\rangle =S^{i}/\langle x\rangle$ for
$R^{i}_{f}/\langle x\rangle =S^{i}/\langle x\rangle$ for ![]() $i\leq d-2$, it is immediate to show that
$i\leq d-2$, it is immediate to show that ![]() $\bar {h}^{iv}$ is multiplication by some element of
$\bar {h}^{iv}$ is multiplication by some element of ![]() $S^{1}$, hence also
$S^{1}$, hence also ![]() $\bar {h}$.
$\bar {h}$.
The proof of Proposition 1.8 is thus complete.
Proof Proof of Proposition 1.3
Let ![]() $f$ be generic of degree
$f$ be generic of degree ![]() $d\geq 6$ in
$d\geq 6$ in ![]() $n+1\geq 10$ variables. We first claim that for any
$n+1\geq 10$ variables. We first claim that for any ![]() $x\in S^{1}$, the multiplication map by
$x\in S^{1}$, the multiplication map by ![]() $x:R^{d-1}_{f}\rightarrow R^{d}_{f}$ is injective, and that the morphism
$x:R^{d-1}_{f}\rightarrow R^{d}_{f}$ is injective, and that the morphism
so constructed is an embedding. None of these statements is difficult to prove. The first statement says that if ![]() ${f}$ is a generic homogeneous degree
${f}$ is a generic homogeneous degree ![]() $d$ polynomials in
$d$ polynomials in ![]() $n+1$ variables,
$n+1$ variables, ![]() ${f}$ does not satisfy an equation
${f}$ does not satisfy an equation ![]() $\partial _u(f)_{\mid H}=0$ for some hyperplane
$\partial _u(f)_{\mid H}=0$ for some hyperplane ![]() $H \subset \mathbb {P}^{n}$ and vector field
$H \subset \mathbb {P}^{n}$ and vector field ![]() $u$ on
$u$ on ![]() $\mathbb {P}^{n}$. The obvious dimension count shows that this holds if
$\mathbb {P}^{n}$. The obvious dimension count shows that this holds if ![]() $h^{0}(\mathbb {P}^{n-1},\mathcal {O}(d))>n-1+{(n+1)^{2}}/{2}$, which holds if
$h^{0}(\mathbb {P}^{n-1},\mathcal {O}(d))>n-1+{(n+1)^{2}}/{2}$, which holds if ![]() $d\geq 4,\ n\geq 3$. As for the second statement, suppose that
$d\geq 4,\ n\geq 3$. As for the second statement, suppose that ![]() $xR^{d-1}_f=yR^{d-1}_f$ for some nonproportional
$xR^{d-1}_f=yR^{d-1}_f$ for some nonproportional ![]() $x,\,y\in S^{1}$. Then there is a subspace of dimension
$x,\,y\in S^{1}$. Then there is a subspace of dimension ![]() $\geq {\rm dim}\,S^{d-1}$ of pairs
$\geq {\rm dim}\,S^{d-1}$ of pairs ![]() $(p,q)\in S^{d-1}\times S^{d-1}$ such that
$(p,q)\in S^{d-1}\times S^{d-1}$ such that ![]() $xp=yq$ in
$xp=yq$ in ![]() $R^{d}_f$, that is
$R^{d}_f$, that is ![]() $xp-yq\in J^{d}_f$. As the kernel of the map
$xp-yq\in J^{d}_f$. As the kernel of the map ![]() $x-y: S^{d-1}\times S^{d-1}\rightarrow S^{d}$ is of dimension
$x-y: S^{d-1}\times S^{d-1}\rightarrow S^{d}$ is of dimension ![]() ${\rm dim}\,S^{d-2}$, this would imply that
${\rm dim}\,S^{d-2}$, this would imply that
As ![]() ${\rm dim}\,J_f^{d}=(n+1)^{2}$, (25) is impossible if
${\rm dim}\,J_f^{d}=(n+1)^{2}$, (25) is impossible if ![]() $h^{0}(\mathbb {P}^{n-1},\mathcal {O}(d-1))>(n+1)^{2}$, which holds if
$h^{0}(\mathbb {P}^{n-1},\mathcal {O}(d-1))>(n+1)^{2}$, which holds if ![]() $n\geq 5, d\geq 4$. We have thus proved that the map
$n\geq 5, d\geq 4$. We have thus proved that the map ![]() $\Phi$ of (24) is injective. That it is an immersion follows in the same way because the differential at
$\Phi$ of (24) is injective. That it is an immersion follows in the same way because the differential at ![]() $x$ is given by the multiplication map
$x$ is given by the multiplication map
and ![]() $\mu _y$ is zero if and only if
$\mu _y$ is zero if and only if ![]() $y R^{d-1}_f\subset xR^{d-1}_f$, which has just been excluded. The claim is thus proved.
$y R^{d-1}_f\subset xR^{d-1}_f$, which has just been excluded. The claim is thus proved.
It follows from the claim and from Proposition 1.8 that, if we have a family of polynomial structures
with ![]() $\phi _0$ the natural one, then there is an isomorphism
$\phi _0$ the natural one, then there is an isomorphism
such that for any ![]() $x\in S^{1}$,
$x\in S^{1}$,
Such a projective isomorphism is induced by a linear isomorphism
and composing ![]() $\phi _t$ with the automorphism of
$\phi _t$ with the automorphism of ![]() $S^{d*}$ induced by
$S^{d*}$ induced by ![]() $\tilde {\psi }_t^{-1}$, we conclude that we may assume that for any
$\tilde {\psi }_t^{-1}$, we conclude that we may assume that for any ![]() $x\in S^{1}$,
$x\in S^{1}$,
We claim that this implies ![]() $\phi _t: S^{d}\rightarrow R^{d}_f$ is the natural map of reduction mod
$\phi _t: S^{d}\rightarrow R^{d}_f$ is the natural map of reduction mod ![]() $J_f$. To see this, choose a general
$J_f$. To see this, choose a general ![]() $x$, so that the multiplication map by
$x$, so that the multiplication map by ![]() $x$ is injective on
$x$ is injective on ![]() $R^{2d-1}_f$. The polynomial structure given by
$R^{2d-1}_f$. The polynomial structure given by ![]() $\phi _t$ and satisfying (26) provides two linear maps
$\phi _t$ and satisfying (26) provides two linear maps
such that ![]() $x\phi '_t=\phi _t\circ x: S^{d-1}\rightarrow R^{d}_f$,
$x\phi '_t=\phi _t\circ x: S^{d-1}\rightarrow R^{d}_f$, ![]() $x\phi ''_t=\phi _t\circ x:S^{2d-1}\rightarrow R^{2d}_f$, and the injectivity of the map of multiplication by
$x\phi ''_t=\phi _t\circ x:S^{2d-1}\rightarrow R^{2d}_f$, and the injectivity of the map of multiplication by ![]() $x$ on
$x$ on ![]() $R^{2d-1}_f$ implies that the following diagram commutes, since it commutes after multiplying the maps by
$R^{2d-1}_f$ implies that the following diagram commutes, since it commutes after multiplying the maps by ![]() $x$.
$x$.

The horizontal maps in the diagram above are the multiplication maps. Following Donagi [Reference DonagiDon83], the multiplication map on the bottom line determines the polynomial structure of ![]() $R_f^{*}$, because it determines (for
$R_f^{*}$, because it determines (for ![]() $d\geq 3$)
$d\geq 3$) ![]() $S^{1}$ and the multiplication map
$S^{1}$ and the multiplication map ![]() $S^{1}\otimes R^{d-1}_f\rightarrow R^{d}_f$ by the symmetrizer lemma (Proposition 1.1). The diagram (
$S^{1}\otimes R^{d-1}_f\rightarrow R^{d}_f$ by the symmetrizer lemma (Proposition 1.1). The diagram (
) then says that up to the action of an automorphism ![]() $g$ of
$g$ of ![]() $S^{*}$, the polynomial structure given by
$S^{*}$, the polynomial structure given by ![]() $(\phi '_t,\,\phi _t)$ is the standard one. Finally, as
$(\phi '_t,\,\phi _t)$ is the standard one. Finally, as ![]() $g$ must act trivially on the space
$g$ must act trivially on the space ![]() $Z_{\rm ideal}$ of ideals by (26),
$Z_{\rm ideal}$ of ideals by (26), ![]() $g$ is proportional to the identity.
$g$ is proportional to the identity.
2. The case of degree  $4$
$4$
We explain in this section how to recover the polynomial structure of the infinitesimal variation of Hodge structure of a generic hypersurface of degree ![]() $4$ so as to prove Theorem 0.7(2), namely the cases where
$4$ so as to prove Theorem 0.7(2), namely the cases where ![]() $d=4$,
$d=4$, ![]() $n=4m+1$, with
$n=4m+1$, with ![]() $m$ large. Note that the methods of Schiffer variations that we will develop later would presumably also apply to this case, but it is much more difficult and does not prove Theorem 0.6 (saying that one can recover a hypersurface from its IVHS).
$m$ large. Note that the methods of Schiffer variations that we will develop later would presumably also apply to this case, but it is much more difficult and does not prove Theorem 0.6 (saying that one can recover a hypersurface from its IVHS).
The congruence conditions is equivalent to the fact that we have ![]() ${\rm gcd}(4,n+1)=2$. The infinitesimal variation of Hodge structure (as translated in (5) using Theorem 0.5)
${\rm gcd}(4,n+1)=2$. The infinitesimal variation of Hodge structure (as translated in (5) using Theorem 0.5)
has for smallest degree term the multiplication map
and the symmetrizer lemma (see Proposition 1.1) allows us to reconstruct in these cases the whole ring ![]() $R^{2*}_f$, and in particular the multiplication map
$R^{2*}_f$, and in particular the multiplication map
(Note that ![]() $R^{2}_f=S^{2}$.) We thus only have to explain in both cases how to recover the polynomial structure of (28) from (29), at least for a generic polynomial
$R^{2}_f=S^{2}$.) We thus only have to explain in both cases how to recover the polynomial structure of (28) from (29), at least for a generic polynomial ![]() $f$. We use the notation
$f$. We use the notation ![]() $\mathcal {S}q^{2l}_f\subset R^{2l}_f$ for the set of squares
$\mathcal {S}q^{2l}_f\subset R^{2l}_f$ for the set of squares
This is a closed algebraic subset which is a cone in ![]() $R_f^{2l}$ and we will denote by
$R_f^{2l}$ and we will denote by ![]() $\mathbb {P}(\mathcal {S}q^{2l})$ the corresponding closed algebraic subset of
$\mathbb {P}(\mathcal {S}q^{2l})$ the corresponding closed algebraic subset of ![]() $\mathbb {P}(R^{2l}_f)$. When
$\mathbb {P}(R^{2l}_f)$. When ![]() $d=4,\ d'=2$, (29) determines
$d=4,\ d'=2$, (29) determines ![]() $\mathcal {S}q^{4}_f$. Our proof of Theorem 0.7(2) will be based (following Donagi's strategy described in the previous section) on the following.
$\mathcal {S}q^{4}_f$. Our proof of Theorem 0.7(2) will be based (following Donagi's strategy described in the previous section) on the following.
Claim 2.1 The algebraic subset ![]() $\mathcal {S}q^{2}_f\subset R^{2}_f=S^{2}$ determines the polynomial structure of the even degree Jacobian ring
$\mathcal {S}q^{2}_f\subset R^{2}_f=S^{2}$ determines the polynomial structure of the even degree Jacobian ring ![]() $R^{2*}_f$ of
$R^{2*}_f$ of ![]() $f$.
$f$.
Proof. Indeed, passing to the projectivization of these affine cones, ![]() $\mathbb {P}(\mathcal {S}q^{2}_f)$ is the second Veronese embedding of
$\mathbb {P}(\mathcal {S}q^{2}_f)$ is the second Veronese embedding of ![]() $\mathbb {P}(S^{1})$ in
$\mathbb {P}(S^{1})$ in ![]() $\mathbb {P}(S^{2})$. Thus the positive generator
$\mathbb {P}(S^{2})$. Thus the positive generator ![]() $H$ of
$H$ of ![]() ${\rm Pic}(\mathbb {P}(\mathcal {S}q^{2}_f))$ satisfies the property that
${\rm Pic}(\mathbb {P}(\mathcal {S}q^{2}_f))$ satisfies the property that ![]() $H^{0}(\mathbb {P}(\mathcal {S}q^{2}_f), H)=:V$ has dimension
$H^{0}(\mathbb {P}(\mathcal {S}q^{2}_f), H)=:V$ has dimension ![]() $n+1$ and the restriction map
$n+1$ and the restriction map ![]() $(S^{2})^{*}\rightarrow {\rm Sym}^{2}V$ is an isomorphism. The dual isomorphism gives the desired isomorphism
$(S^{2})^{*}\rightarrow {\rm Sym}^{2}V$ is an isomorphism. The dual isomorphism gives the desired isomorphism ![]() ${\rm Sym}^{2}S^{1}\cong S^{2}$, with
${\rm Sym}^{2}S^{1}\cong S^{2}$, with ![]() ${S^{1}:=V^{*}}$.
${S^{1}:=V^{*}}$.
We observe now that the closed algebraic subset ![]() $\mathcal {S}q^{2}_f\subset R^{2}_f$ has the following property:
$\mathcal {S}q^{2}_f\subset R^{2}_f$ has the following property:
We prove now the following result, which by Claim 2.1 completes the proof of Theorem 0.7(2).
Proposition 2.2 Let ![]() $f$ be a generic homogeneous polynomial of degree
$f$ be a generic homogeneous polynomial of degree ![]() $4$ in
$4$ in ![]() $n+1$ variables, with
$n+1$ variables, with ![]() $n\geq 599$. Then the only subvariety
$n\geq 599$. Then the only subvariety ![]() $T\subset R^{2}_f=S^{2}$ of dimension
$T\subset R^{2}_f=S^{2}$ of dimension ![]() $\geq n+1$ satisfying the condition
$\geq n+1$ satisfying the condition
is ![]() $\mathcal {S}q^{2}_f$.
$\mathcal {S}q^{2}_f$.
Note that in this statement, we can clearly assume that ![]() $T$ is a cone, since the conditions are homogeneous.
$T$ is a cone, since the conditions are homogeneous.
Proof Proof of Proposition 2.2
We observe that by a proper specialization argument, the schematic version of the statement, saying that, furthermore, (30) define, at least generically, the reduced structure of ![]() $\mathcal {S}q^{2}_f$, is an open condition on the set of polynomials
$\mathcal {S}q^{2}_f$, is an open condition on the set of polynomials ![]() $f$ for which
$f$ for which ![]() $R_f^{4}$, or equivalently
$R_f^{4}$, or equivalently ![]() $J^{4}_f$, has the right dimension. We will thus prove this schematic version for one specific
$J^{4}_f$, has the right dimension. We will thus prove this schematic version for one specific ![]() $f$, for which
$f$, for which ![]() $J^{4}_f$ has the right dimension.
$J^{4}_f$ has the right dimension.
Let us first explain the specific polynomials we will use. We will first choose general linear sections ![]() $\mathbb {P}\cap Pf_4$ of the Pfaffian quartic
$\mathbb {P}\cap Pf_4$ of the Pfaffian quartic ![]() $\mathcal {P}f_4\subset \mathbb {P}\big (\bigwedge ^{2} V_8\big )$, where
$\mathcal {P}f_4\subset \mathbb {P}\big (\bigwedge ^{2} V_8\big )$, where ![]() $\mathbb {P}\subset \mathbb {P}\big (\bigwedge ^{2} V_8\big )$ is a linear subspace of dimension
$\mathbb {P}\subset \mathbb {P}\big (\bigwedge ^{2} V_8\big )$ is a linear subspace of dimension ![]() $23$ or
$23$ or ![]() $24$. We get this way polynomials
$24$. We get this way polynomials ![]() $f_i$ of degree
$f_i$ of degree ![]() $4$ in
$4$ in ![]() $24$ or
$24$ or ![]() $25$ variables. In higher dimension, we will then consider polynomials of the form
$25$ variables. In higher dimension, we will then consider polynomials of the form
with ![]() $i_1,\ldots,i_l\in \{24,\,25\}$, which allows us to construct degree
$i_1,\ldots,i_l\in \{24,\,25\}$, which allows us to construct degree ![]() $4$ polynomials with any number
$4$ polynomials with any number ![]() $n+1$ of variables starting from
$n+1$ of variables starting from ![]() $600$.
$600$.
If a degree ![]() $d$ polynomial
$d$ polynomial ![]() $f$ defines a smooth hypersurface
$f$ defines a smooth hypersurface ![]() $X_f$, the Jacobian ideal
$X_f$, the Jacobian ideal ![]() $J_f$ is generated by the regular sequence
$J_f$ is generated by the regular sequence ![]() $J_f^{d-1}$ of degree
$J_f^{d-1}$ of degree ![]() $d-1$ polynomials, and hence, assuming
$d-1$ polynomials, and hence, assuming ![]() $d\geq 3$, we find that the multiplication map
$d\geq 3$, we find that the multiplication map ![]() $S^{1}\otimes J_f^{d-1}\rightarrow J_f^{d}$ is an isomorphism, so that
$S^{1}\otimes J_f^{d-1}\rightarrow J_f^{d}$ is an isomorphism, so that ![]() ${{\rm dim}\,J_f^{d}=(n+1)^{2}}$. In general, assuming
${{\rm dim}\,J_f^{d}=(n+1)^{2}}$. In general, assuming ![]() $X_f$ reduced with regular locus
$X_f$ reduced with regular locus ![]() $X_{f,{\rm reg}}$ and using the normal bundle sequence
$X_{f,{\rm reg}}$ and using the normal bundle sequence
we see that the kernel of the map ![]() $S^{1}\otimes J_f^{d-1}\rightarrow J_f^{d}$ identifies naturally with the set of infinitesimal automorphisms of
$S^{1}\otimes J_f^{d-1}\rightarrow J_f^{d}$ identifies naturally with the set of infinitesimal automorphisms of ![]() $X_f$ induced by an infinitesimal automorphism of
$X_f$ induced by an infinitesimal automorphism of ![]() $\mathbb {P}^{n}$. The hypersurfaces
$\mathbb {P}^{n}$. The hypersurfaces ![]() $X_f$ discussed above are singular. We nevertheless have the following.
$X_f$ discussed above are singular. We nevertheless have the following.
Lemma 2.3 For a polynomial ![]() $f$ of the form above,
$f$ of the form above, ![]() $J_f^{4}$ has the right dimension, i.e.
$J_f^{4}$ has the right dimension, i.e. ![]() $(n+1)^{2}$.
$(n+1)^{2}$.
Proof. One has ![]() $f=\sum _j f_{j}$, where each
$f=\sum _j f_{j}$, where each ![]() $f_{j}$ involves variables
$f_{j}$ involves variables ![]() $X_{j,1},\ldots, X^{j,i_j}$. It is immediate to check that the statement for each
$X_{j,1},\ldots, X^{j,i_j}$. It is immediate to check that the statement for each ![]() $f_{j}$ implies the statement for
$f_{j}$ implies the statement for ![]() $f$. Turning to the
$f$. Turning to the ![]() $f_{j}$, they are either general linear sections of the quartic Pfaffian hypersurface in
$f_{j}$, they are either general linear sections of the quartic Pfaffian hypersurface in ![]() $\mathbb {P}^{27}$ by a
$\mathbb {P}^{27}$ by a ![]() $\mathbb {P}^{n}$,
$\mathbb {P}^{n}$, ![]() $n=23$ or
$n=23$ or ![]() $24$. Let us show that each of them has no infinitesimal automorphism. The automorphism group of the general Pfaffian hypersurface
$24$. Let us show that each of them has no infinitesimal automorphism. The automorphism group of the general Pfaffian hypersurface ![]() $\mathcal {P}f_k\subset \mathbb {P}\big (\bigwedge ^{2}V_{2k}\big )$ is the group
$\mathcal {P}f_k\subset \mathbb {P}\big (\bigwedge ^{2}V_{2k}\big )$ is the group ![]() ${\rm {P}GL}(2k)$. We claim that the automorphism group of a general linear section of dimension
${\rm {P}GL}(2k)$. We claim that the automorphism group of a general linear section of dimension ![]() $>2(2k-2)={\rm dim}\,G(2,V_{2k})$ is also contained in
$>2(2k-2)={\rm dim}\,G(2,V_{2k})$ is also contained in ![]() ${\rm {P}GL}(2k)$. This follows from the fact that after blowing-up
${\rm {P}GL}(2k)$. This follows from the fact that after blowing-up ![]() $\mathcal {P}f_{k}$ along its singular locus, which parameterizes forms of rank
$\mathcal {P}f_{k}$ along its singular locus, which parameterizes forms of rank ![]() $<2k-2$, we get a dominant morphism
$<2k-2$, we get a dominant morphism ![]() $\widetilde {\mathcal {P}f_{k}}\rightarrow G(2,V_{2k})$, which to a degenerate form associates its kernel. If we consider a general linear section
$\widetilde {\mathcal {P}f_{k}}\rightarrow G(2,V_{2k})$, which to a degenerate form associates its kernel. If we consider a general linear section ![]() $X_l$ of
$X_l$ of ![]() $\mathcal {P}f_{2k}$ of dimension
$\mathcal {P}f_{2k}$ of dimension ![]() $>{\rm dim}\,G(2,V_{2k})$ defined by a
$>{\rm dim}\,G(2,V_{2k})$ defined by a ![]() $r$-dimensional vector subspace
$r$-dimensional vector subspace ![]() $W\subset \bigwedge ^{2}V_{2k}^{*}$, the same remains true and we get a morphism
$W\subset \bigwedge ^{2}V_{2k}^{*}$, the same remains true and we get a morphism ![]() $\tilde {X}_l\rightarrow G(2,V_{2k})$ which is dominant with connected fiber of positive dimension. Thus the automorphism group of
$\tilde {X}_l\rightarrow G(2,V_{2k})$ which is dominant with connected fiber of positive dimension. Thus the automorphism group of ![]() $X_l$ has to act on
$X_l$ has to act on ![]() $G(2,V_{2k})$ and it has to identify with the group of automorphisms of
$G(2,V_{2k})$ and it has to identify with the group of automorphisms of ![]() $G(2,V_{2k})$, or automorphisms of
$G(2,V_{2k})$, or automorphisms of ![]() $\mathbb {P}(V_{2k})$ preserving the space
$\mathbb {P}(V_{2k})$ preserving the space ![]() $W\subset \bigwedge ^{2}V_{2k}^{*}$. It is easy to check that this space is zero once
$W\subset \bigwedge ^{2}V_{2k}^{*}$. It is easy to check that this space is zero once ![]() $r\geq 3$. Coming back to our situation where
$r\geq 3$. Coming back to our situation where ![]() $k=d=4$, our choices of
$k=d=4$, our choices of ![]() $r$ are
$r$ are ![]() $r=3$ or
$r=3$ or ![]() $r=4$ for
$r=4$ for ![]() $k=4$. In all cases, the variety
$k=4$. In all cases, the variety ![]() $X_l$ has dimension
$X_l$ has dimension ![]() $>2(2k-2)$ so the analysis above applies.
$>2(2k-2)$ so the analysis above applies.
We now prove Proposition 2.2 for ![]() $f$ as above.
$f$ as above.
Lemma 2.4 Let ![]() $f=\sum _jf_j$ be a polynomial of degree
$f=\sum _jf_j$ be a polynomial of degree ![]() $4$ in
$4$ in ![]() $n+1$ variables as constructed above. Then if
$n+1$ variables as constructed above. Then if ![]() $T\subset S^{2}$ is an algebraic subvariety of dimension
$T\subset S^{2}$ is an algebraic subvariety of dimension ![]() $\geq n+1$ such that
$\geq n+1$ such that
for any ![]() $A,B\in T$,
$A,B\in T$, ![]() $T= \mathcal {S}q^{2}$.
$T= \mathcal {S}q^{2}$.
Proof. Let as above ![]() $f=\sum _l f_{j}$. The singular locus
$f=\sum _l f_{j}$. The singular locus ![]() $Z_f$ of
$Z_f$ of ![]() $X_f=V(f)$ is the join of the singular loci
$X_f=V(f)$ is the join of the singular loci ![]() $Z_{j}$ of
$Z_{j}$ of ![]() $V(f_j)$ in
$V(f_j)$ in ![]() $\mathbb {P}^{i_j}$. This means that, introducing the natural rational projection map
$\mathbb {P}^{i_j}$. This means that, introducing the natural rational projection map ![]() $\pi :\mathbb {P}^{\sum _j i_j-1}\dashrightarrow \prod _l\mathbb {P}^{i_j-1}$, one has
$\pi :\mathbb {P}^{\sum _j i_j-1}\dashrightarrow \prod _l\mathbb {P}^{i_j-1}$, one has ![]() $Z_f=\pi ^{-1}\big (\prod _jZ_{j}\big )$.
$Z_f=\pi ^{-1}\big (\prod _jZ_{j}\big )$.
Claim 2.5 The varieties ![]() $Z_{f}$ are not contained in any quadric.
$Z_{f}$ are not contained in any quadric.
Proof. Consider first the case of the Pfaffian linear sections ![]() $Z_j$. The claim follows in this case because they are general linear sections of the singular locus
$Z_j$. The claim follows in this case because they are general linear sections of the singular locus ![]() $Z$ of the quartic universal Pfaffian
$Z$ of the quartic universal Pfaffian ![]() $\mathcal {P}f_4$ in
$\mathcal {P}f_4$ in ![]() $\mathbb {P}\big (\bigwedge ^{2} V_8\big )$, which is defined by the equations
$\mathbb {P}\big (\bigwedge ^{2} V_8\big )$, which is defined by the equations ![]() $\omega ^{3}=0$, that is, by cubics, and is not contained in any quadric. The last point can be seen by looking at the singular locus of
$\omega ^{3}=0$, that is, by cubics, and is not contained in any quadric. The last point can be seen by looking at the singular locus of ![]() $Z$, which consists of forms of rank
$Z$, which consists of forms of rank ![]() $2$, that is the Grassmannian
$2$, that is the Grassmannian ![]() $G(2,V_8^{*})$. Along this locus, the Zariski tangent space of
$G(2,V_8^{*})$. Along this locus, the Zariski tangent space of ![]() $Z$ is the full Zariski tangent space of
$Z$ is the full Zariski tangent space of ![]() $\mathbb {P}\big (\bigwedge ^{2}V_8\big )$. A quadric containing
$\mathbb {P}\big (\bigwedge ^{2}V_8\big )$. A quadric containing ![]() $Z$ should thus be singular along
$Z$ should thus be singular along ![]() ${\rm Sing}\,Z$. But
${\rm Sing}\,Z$. But ![]() ${\rm Sing}\,Z=G(2,V_8^{*})$ is not contained in any proper linear subspace of
${\rm Sing}\,Z=G(2,V_8^{*})$ is not contained in any proper linear subspace of ![]() $\mathbb {P}\big (\bigwedge ^{2} V_8\big )$. It follows that
$\mathbb {P}\big (\bigwedge ^{2} V_8\big )$. It follows that ![]() $Z$ is not contained in any quadric. It remains to conclude that the same statement is true for the general linear section
$Z$ is not contained in any quadric. It remains to conclude that the same statement is true for the general linear section ![]() $\mathbb {P}^{i_l-1}\cap \mathcal {P}f_4$, with
$\mathbb {P}^{i_l-1}\cap \mathcal {P}f_4$, with ![]() $i_l=24,\ 25$. Its singular locus
$i_l=24,\ 25$. Its singular locus ![]() $Z_l$ is the general linear section
$Z_l$ is the general linear section ![]() $\mathbb {P}^{i_l-1}\cap Z$, and we show inductively that any quadric containing
$\mathbb {P}^{i_l-1}\cap Z$, and we show inductively that any quadric containing ![]() $Z_l$ is the restriction of a quadric containing
$Z_l$ is the restriction of a quadric containing ![]() $Z$. This statement only needs that
$Z$. This statement only needs that ![]() $Z_l$ is nonempty (it has dimension
$Z_l$ is nonempty (it has dimension ![]() $\geq 18$ in our case) and that all the successive linear sections
$\geq 18$ in our case) and that all the successive linear sections ![]() $\mathbb {P}^{j}\cap Z$, with
$\mathbb {P}^{j}\cap Z$, with ![]() $j\geq i_l$, are linearly normal in
$j\geq i_l$, are linearly normal in ![]() $\mathbb {P}^{j}$, which is not hard to prove. Finally we have to show that the same is true for a general
$\mathbb {P}^{j}$, which is not hard to prove. Finally we have to show that the same is true for a general ![]() $f=\sum f_j$. As already mentioned,
$f=\sum f_j$. As already mentioned, ![]() $Z_f$ is then a join
$Z_f$ is then a join ![]() $Z_1*\ldots *Z_l$ and a join of varieties not contained in any quadric is not contained in any quadric.
$Z_1*\ldots *Z_l$ and a join of varieties not contained in any quadric is not contained in any quadric.
We also prove the following.
Claim 2.6
(a) The restriction map
 $S^{1}\rightarrow H^{0}(Z_f,\mathcal {O}_{Z_f}(1))$ is an isomorphism.
$S^{1}\rightarrow H^{0}(Z_f,\mathcal {O}_{Z_f}(1))$ is an isomorphism.(b) The only
 $n$-dimensional family
$n$-dimensional family  $\{D_A\}$ of divisors on
$\{D_A\}$ of divisors on  $Z_f$ such that for some fixed effective divisor
$Z_f$ such that for some fixed effective divisor  $D_0$,
is the family of hyperplane sections of
$D_0$,
is the family of hyperplane sections of \[ 2D_A+ D_0\in |\mathcal{O}_{Z_f}(2)| \]
\[ 2D_A+ D_0\in |\mathcal{O}_{Z_f}(2)| \] $Z_f$.
$Z_f$.
Proof. We know that ![]() $Z_f$ is the join of the
$Z_f$ is the join of the ![]() $Z_j\subset \mathbb {P}^{i_j}$, where each
$Z_j\subset \mathbb {P}^{i_j}$, where each ![]() $Z_j$ is a smooth linear section of the singular locus
$Z_j$ is a smooth linear section of the singular locus ![]() $Z$ of
$Z$ of ![]() $\mathcal {P}f_4$ by either a
$\mathcal {P}f_4$ by either a ![]() $\mathbb {P}^{24}$ or a
$\mathbb {P}^{24}$ or a ![]() $\mathbb {P}^{23}$. Let us first conclude the proof when f is one of the
$\mathbb {P}^{23}$. Let us first conclude the proof when f is one of the ![]() $f_j$ (and thus Z is one of the
$f_j$ (and thus Z is one of the ![]() $Z_j$). We observe that
$Z_j$). We observe that ![]() $Z\subset \mathbb {P}\big (\bigwedge ^{2}V_8\big )$ is the set of
$Z\subset \mathbb {P}\big (\bigwedge ^{2}V_8\big )$ is the set of ![]() $2$-forms of rank
$2$-forms of rank ![]() $\leq 4$ (the generic element of
$\leq 4$ (the generic element of ![]() $Z$ being of rank exactly
$Z$ being of rank exactly ![]() $4$), and has a natural birational model
$4$), and has a natural birational model ![]() $\tilde {Z}\rightarrow Z$, where
$\tilde {Z}\rightarrow Z$, where
 \[ \tilde{Z}\subset G(4,V_8^{*})\times \mathbb{P}\bigg(\bigwedge^{2}V_8\bigg),\quad \tilde{Z}=\{([W_4],\omega),\,W_4\subset {\rm Ker}\,\omega\}. \]
\[ \tilde{Z}\subset G(4,V_8^{*})\times \mathbb{P}\bigg(\bigwedge^{2}V_8\bigg),\quad \tilde{Z}=\{([W_4],\omega),\,W_4\subset {\rm Ker}\,\omega\}. \]
The statement (a) easily follows from the above description of ![]() $\tilde {Z}$ and the fact that the
$\tilde {Z}$ and the fact that the ![]() $Z_j$ are general linear sections of codimension
$Z_j$ are general linear sections of codimension ![]() $3$ or
$3$ or ![]() $4$ of
$4$ of ![]() $Z$. Let us prove (b). The variety
$Z$. Let us prove (b). The variety ![]() $\tilde {Z}$ is smooth and, being a projective bundle fibration over
$\tilde {Z}$ is smooth and, being a projective bundle fibration over ![]() $G(4,V_8^{*})$, has Picard rank
$G(4,V_8^{*})$, has Picard rank ![]() $2$. Its effective cone is very easy to compute: indeed, the line bundle
$2$. Its effective cone is very easy to compute: indeed, the line bundle ![]() $l$ which is pulled-back from the Plücker line bundle on the Grassmannian via the first projection
$l$ which is pulled-back from the Plücker line bundle on the Grassmannian via the first projection ![]() $pr_1$ is clearly one extremal ray of the effective cone since the corresponding morphism has positive dimensional fibers. There is a second extremal ray of the effective cone, which is the class of the divisor
$pr_1$ is clearly one extremal ray of the effective cone since the corresponding morphism has positive dimensional fibers. There is a second extremal ray of the effective cone, which is the class of the divisor ![]() $D$ contracted by the birational map
$D$ contracted by the birational map ![]() $\tilde {Z}\rightarrow Z$ (induced by the second projection
$\tilde {Z}\rightarrow Z$ (induced by the second projection ![]() $pr_2$). One easily computes that this class is
$pr_2$). One easily computes that this class is ![]() $2h-l$, where
$2h-l$, where ![]() $h$ is the pull-back of hyperplane class on
$h$ is the pull-back of hyperplane class on ![]() $\mathbb {P}\big (\bigwedge ^{2}V_8\big )$ by
$\mathbb {P}\big (\bigwedge ^{2}V_8\big )$ by ![]() $pr_2$. We observe that the fibers of
$pr_2$. We observe that the fibers of ![]() $pr_1$ are of dimension
$pr_1$ are of dimension ![]() $5$, so that, when we take a general linear section of
$5$, so that, when we take a general linear section of ![]() $Z$ by a codimension
$Z$ by a codimension ![]() $3$ or
$3$ or ![]() $4$ projective subspace, getting the singular locus
$4$ projective subspace, getting the singular locus ![]() $Z_j$ of
$Z_j$ of ![]() $X_j$, all the properties above remain satisfied, and thus
$X_j$, all the properties above remain satisfied, and thus ![]() ${\rm Pic}\,\tilde {Z}_j=\mathbb {Z} h_j+\mathbb {Z}l_j$, with effective cone generated by
${\rm Pic}\,\tilde {Z}_j=\mathbb {Z} h_j+\mathbb {Z}l_j$, with effective cone generated by ![]() $l_j$ and
$l_j$ and ![]() $2h_j-l_j$. We now finish the argument for
$2h_j-l_j$. We now finish the argument for ![]() $Z_j$: we lift our data
$Z_j$: we lift our data ![]() $\{D_A\},\ D_0$ to
$\{D_A\},\ D_0$ to ![]() $\tilde {Z}_j$. We then have
$\tilde {Z}_j$. We then have
in ![]() ${\rm Pic}\,\tilde {Z}_j$, with
${\rm Pic}\,\tilde {Z}_j$, with ![]() $\tilde {D}_0$ effective and
$\tilde {D}_0$ effective and ![]() ${\rm dim}|\tilde {D}_A|\geq n$, where
${\rm dim}|\tilde {D}_A|\geq n$, where ![]() $n$ is
$n$ is ![]() ${\rm dim}|h_{\mid Z_j}|$ by (a). Let us write
${\rm dim}|h_{\mid Z_j}|$ by (a). Let us write
with ![]() $\alpha,\beta \in 2\mathbb {Z}$. Then the analysis above shows that
$\alpha,\beta \in 2\mathbb {Z}$. Then the analysis above shows that
As ![]() $2h_j-\tilde {D}_0$ is effective, we also have
$2h_j-\tilde {D}_0$ is effective, we also have
As ![]() $\alpha$ is even, we only get the possibilities
$\alpha$ is even, we only get the possibilities ![]() $\alpha =0,\ 2$. If
$\alpha =0,\ 2$. If ![]() $\alpha =2$, we get
$\alpha =2$, we get ![]() $\beta =0$ and thus
$\beta =0$ and thus ![]() $2h_j-\tilde {D}_0=0$, contradicting the assumption
$2h_j-\tilde {D}_0=0$, contradicting the assumption ![]() ${\rm dim}|2h-\tilde {D}_0|\geq n$. If
${\rm dim}|2h-\tilde {D}_0|\geq n$. If ![]() $\alpha =0$, we get from the inequalities above
$\alpha =0$, we get from the inequalities above ![]() $\beta =0$ since
$\beta =0$ since ![]() $\beta$ has to be even, and
$\beta$ has to be even, and ![]() $2h=2\tilde {D}_A$, which proves statement (b) (using the fact that
$2h=2\tilde {D}_A$, which proves statement (b) (using the fact that ![]() ${\rm Pic}\,Z_j$ has no
${\rm Pic}\,Z_j$ has no ![]() $2$-torsion and statement (a)).
$2$-torsion and statement (a)).
We now have to prove the same result for the join ![]() $Z_f=Z_1*Z_2*\ldots * Z_l$, which is done inductively on the number
$Z_f=Z_1*Z_2*\ldots * Z_l$, which is done inductively on the number ![]() $l$, assuming, as this is satisfied in our situation, that the
$l$, assuming, as this is satisfied in our situation, that the ![]() $Z_i$ are simply connected. This way we are reduced to consider only the join
$Z_i$ are simply connected. This way we are reduced to consider only the join ![]() $Z_1*Z_2\subset \mathbb {P}^{n}$, with
$Z_1*Z_2\subset \mathbb {P}^{n}$, with ![]() $n=n_1+n_2+1$, of two linearly normal varieties
$n=n_1+n_2+1$, of two linearly normal varieties ![]() $Z_1\subset \mathbb {P}^{n_1},\ Z_2\subset \mathbb {P}^{n_2}$, which satisfy the properties (a) and (b). We observe that
$Z_1\subset \mathbb {P}^{n_1},\ Z_2\subset \mathbb {P}^{n_2}$, which satisfy the properties (a) and (b). We observe that ![]() $Z_1*Z_2$ is dominated by a
$Z_1*Z_2$ is dominated by a ![]() $\mathbb {P}^{1}$-bundle over
$\mathbb {P}^{1}$-bundle over ![]() $Z_1\times Z_2$, namely
$Z_1\times Z_2$, namely
the two sections being contracted to ![]() $Z_1$, respectively
$Z_1$, respectively ![]() $Z_2$, by the natural morphism to
$Z_2$, by the natural morphism to ![]() $Z_1*Z_2\subset \mathbb {P}^{n}$. The description (32) of the join immediately proves (a) for
$Z_1*Z_2\subset \mathbb {P}^{n}$. The description (32) of the join immediately proves (a) for ![]() $Z_1*Z_2$ once we have it for
$Z_1*Z_2$ once we have it for ![]() $Z_1$ and
$Z_1$ and ![]() $Z_2$. We now turn to (b). Let
$Z_2$. We now turn to (b). Let ![]() $h=\mathcal {O}_{\mathbb {P}(\mathcal {O}_{Z_1}(1)\oplus \mathcal {O}_{Z_2}(1)})$ on
$h=\mathcal {O}_{\mathbb {P}(\mathcal {O}_{Z_1}(1)\oplus \mathcal {O}_{Z_2}(1)})$ on ![]() $\widetilde {Z_1*Z_2}$ and let
$\widetilde {Z_1*Z_2}$ and let ![]() $D_0$ be a fixed effective divisor and
$D_0$ be a fixed effective divisor and ![]() $\{D_A\}$ be a mobile family of divisors on
$\{D_A\}$ be a mobile family of divisors on ![]() $\widetilde {Z_1*Z_2}$ such that
$\widetilde {Z_1*Z_2}$ such that
Then either ![]() $D_0$ or
$D_0$ or ![]() $D_A$ is vertical for
$D_A$ is vertical for ![]() $\pi$. Indeed, they both restrict otherwise to a divisor of degree
$\pi$. Indeed, they both restrict otherwise to a divisor of degree ![]() $\geq 1$ on the fibers of
$\geq 1$ on the fibers of ![]() $\pi$, contradicting (33). Assume
$\pi$, contradicting (33). Assume ![]() $D_0$ is vertical for
$D_0$ is vertical for ![]() $\pi$, that is,
$\pi$, that is, ![]() $D_0=\pi ^{-1}(D'_0)$. The equality
$D_0=\pi ^{-1}(D'_0)$. The equality ![]() $2h-D'_0=2D_A$ says that
$2h-D'_0=2D_A$ says that ![]() $D'_0=2D''_0$ as divisors on
$D'_0=2D''_0$ as divisors on ![]() $Z_1\times Z_2$ and, as
$Z_1\times Z_2$ and, as ![]() $Z_1$ and
$Z_1$ and ![]() $Z_2$ are simply connected,
$Z_2$ are simply connected, ![]() $D''_0\in |pr_1^{*}D''_{0,1}+pr_2^{*}D''_{0,2}|$ and both
$D''_0\in |pr_1^{*}D''_{0,1}+pr_2^{*}D''_{0,2}|$ and both ![]() $2D''_{0,1}, \ 2D''_{0,2}$ are effective. The divisors
$2D''_{0,1}, \ 2D''_{0,2}$ are effective. The divisors ![]() $D''_{0,i}$ on
$D''_{0,i}$ on ![]() $Z_i$ have the property that the linear system
$Z_i$ have the property that the linear system ![]() $|h-pr_1^{*}D''_{0,1}-pr_2^{*}D''_{0,2}|$ on
$|h-pr_1^{*}D''_{0,1}-pr_2^{*}D''_{0,2}|$ on ![]() $\mathbb {P}(\mathcal {O}_{Z_1}(1)\oplus \mathcal {O}_{Z_2}(1))$ has dimension
$\mathbb {P}(\mathcal {O}_{Z_1}(1)\oplus \mathcal {O}_{Z_2}(1))$ has dimension ![]() $\geq n$, which says that
$\geq n$, which says that
As ![]() $2D''_{0,1}$ is effective on
$2D''_{0,1}$ is effective on ![]() $Z_1$ and
$Z_1$ and ![]() $2D''_{0,2}$ is effective on
$2D''_{0,2}$ is effective on ![]() $Z_2$, we conclude that
$Z_2$, we conclude that ![]() $D''_{0,i}=0$ and that the
$D''_{0,i}=0$ and that the ![]() $D_A$ belong to
$D_A$ belong to ![]() $|\mathcal {O}_{Z_1*Z_2}(1)|$, so (b) is proved in this case.
$|\mathcal {O}_{Z_1*Z_2}(1)|$, so (b) is proved in this case.
In the case where ![]() $D_0$ is not vertical, then restricting again to the fibers of
$D_0$ is not vertical, then restricting again to the fibers of ![]() $\pi$,
$\pi$, ![]() $D_0=2h-D'_0$ where
$D_0=2h-D'_0$ where ![]() $D'_0$ is effective and comes from
$D'_0$ is effective and comes from ![]() $Z_1\times Z_2$, and
$Z_1\times Z_2$, and ![]() $D_A$ is vertical,
$D_A$ is vertical, ![]() $D_A=\pi ^{-1}(D'_A)$. Hence we have again
$D_A=\pi ^{-1}(D'_A)$. Hence we have again ![]() $D'_0=2D''_0$, and
$D'_0=2D''_0$, and ![]() ${\rm dim}\,|h-D'_0-D'_A|\geq n$, so the proof finishes as before that
${\rm dim}\,|h-D'_0-D'_A|\geq n$, so the proof finishes as before that ![]() $D'_0=0$ and
$D'_0=0$ and ![]() $D_A=0$ which contradicts (34).
$D_A=0$ which contradicts (34).
We now complete the proof of Lemma 2.4. We have ![]() $J_f\subset I_{Z_f}$, since
$J_f\subset I_{Z_f}$, since ![]() $Z_f$ is contained in
$Z_f$ is contained in ![]() ${\rm Sing}\,X_f$. Let
${\rm Sing}\,X_f$. Let ![]() $T\subset S^{2}$ be a closed algebraic subset satisfying the assumptions of Lemma 2.4 for
$T\subset S^{2}$ be a closed algebraic subset satisfying the assumptions of Lemma 2.4 for ![]() $f$. Then for any
$f$. Then for any ![]() $A,B\in T$,
$A,B\in T$, ![]() $AB_{|Z_f}=M^{2}_{|Z_f}$, for some
$AB_{|Z_f}=M^{2}_{|Z_f}$, for some ![]() $M\in S^{2}$. This implies that the moving part of
$M\in S^{2}$. This implies that the moving part of ![]() ${\rm div}\,A_{\mid Z_f}$ appears with multiplicity
${\rm div}\,A_{\mid Z_f}$ appears with multiplicity ![]() $2$. Hence
$2$. Hence ![]() ${\rm div}\,A_{\mid Z_f}=D_0+2D_A$. We now use Claim 2.5 which implies that the family of divisors
${\rm div}\,A_{\mid Z_f}=D_0+2D_A$. We now use Claim 2.5 which implies that the family of divisors ![]() ${\rm div}\,A_{\mid Z_f}$ is of dimension
${\rm div}\,A_{\mid Z_f}$ is of dimension ![]() $\geq n$, hence also the family
$\geq n$, hence also the family ![]() $\{D_A\}$ of divisors. We then conclude from Claim 2.6 that
$\{D_A\}$ of divisors. We then conclude from Claim 2.6 that ![]() $T\subset \mathcal {S}q^{2}$.
$T\subset \mathcal {S}q^{2}$.
In order to complete the proof of Proposition 2.2, it suffices now to make Lemma 2.4 more precise by analyzing the schematic structure of a closed algebraic subset ![]() $T\subset S^{2}$ satisfying the assumptions of this lemma. We first observe the following.
$T\subset S^{2}$ satisfying the assumptions of this lemma. We first observe the following.
Lemma 2.7 Let ![]() $f$ be as in Lemma 2.4 and let
$f$ be as in Lemma 2.4 and let ![]() $A,B\in S^{1}$ be general. Let
$A,B\in S^{1}$ be general. Let ![]() $M:=AB$ and consider the subspace
$M:=AB$ and consider the subspace ![]() $MS^{2}=MR^{2}_f\subset R^{4}_f$. Then
$MS^{2}=MR^{2}_f\subset R^{4}_f$. Then
where as usual, the notation ![]() $[ MS^{2}:A^{2}]$ is used for
$[ MS^{2}:A^{2}]$ is used for ![]() $\{S\in S^{2},\,SA^{2}\in \langle M\rangle \}$.
$\{S\in S^{2},\,SA^{2}\in \langle M\rangle \}$.
The lemma is obvious, using restriction to ![]() $Z_f$ and using Claim 2.6.
$Z_f$ and using Claim 2.6.
We now complete the proof of Proposition 2.2. We observe that ![]() $MS^{2}$ is the tangent space to
$MS^{2}$ is the tangent space to ![]() $\mathcal {S}q^{4}$ at
$\mathcal {S}q^{4}$ at ![]() $M^{2}$, while
$M^{2}$, while ![]() $BS^{1}\subset S^{2}$ is the tangent space to
$BS^{1}\subset S^{2}$ is the tangent space to ![]() $\mathcal {S}q^{2}$ at
$\mathcal {S}q^{2}$ at ![]() $B^{2}$. Equation (35) thus says that a space
$B^{2}$. Equation (35) thus says that a space ![]() $T\subset S^{2}$ satisfying the assumptions of Lemma 2.4 must be generically the reduced
$T\subset S^{2}$ satisfying the assumptions of Lemma 2.4 must be generically the reduced ![]() $\mathcal {S}q^{2}$. The completion of the proof then follows by a specialization and cycle-theoretic argument, using the fact that these sets
$\mathcal {S}q^{2}$. The completion of the proof then follows by a specialization and cycle-theoretic argument, using the fact that these sets ![]() $T$ above are cones, hence come from closed algebraic subsets
$T$ above are cones, hence come from closed algebraic subsets ![]() $\mathbb {P}(T)$ of
$\mathbb {P}(T)$ of ![]() $\mathbb {P}(S^{2})$.
$\mathbb {P}(S^{2})$.
3. Schiffer variations and Jacobian ideals
Definition 3.1 A Schiffer variation of a homogeneous polynomial ![]() $f$ of degree
$f$ of degree ![]() $d$ in
$d$ in ![]() $n+1$ variables
$n+1$ variables ![]() $X_0,\ldots, X_n$ is a one-parameter family
$X_0,\ldots, X_n$ is a one-parameter family ![]() $f+t x^{d},\ t\in \mathbb {C}$, where
$f+t x^{d},\ t\in \mathbb {C}$, where ![]() $x\in S^{1}$ is a linear form of the variables
$x\in S^{1}$ is a linear form of the variables ![]() $X_0,\ldots, X_n$.
$X_0,\ldots, X_n$.
In the definition above, we are not interested in the linear character of the parameterization, as this does not make sense anymore after projection of this line to the moduli space. We should thus consider more generally one-parameter families of polynomials supported (up to the action of ![]() ${\rm GL}(n+1)$) on a line as above. We can also speak of finite-order Schiffer variations, which consist in looking at a finite-order arc in an affine line as above passing through
${\rm GL}(n+1)$) on a line as above. We can also speak of finite-order Schiffer variations, which consist in looking at a finite-order arc in an affine line as above passing through ![]() $f$. Observe that if
$f$. Observe that if ![]() $g=f+ x^{d}$, then for any
$g=f+ x^{d}$, then for any ![]() $u\in H^{0}(\mathbb {P}^{n},T_{\mathbb {P}^{n}}(-1))=H^{0}(\mathbb {P}^{n}, \mathcal {O}_{\mathbb {P}^{n}}(1))^{*}$ such that
$u\in H^{0}(\mathbb {P}^{n},T_{\mathbb {P}^{n}}(-1))=H^{0}(\mathbb {P}^{n}, \mathcal {O}_{\mathbb {P}^{n}}(1))^{*}$ such that ![]() $\partial _u(x)=0$, one has
$\partial _u(x)=0$, one has ![]() $\partial _u(f)=\partial _u(g)$. It follows that the Jacobian ideals
$\partial _u(f)=\partial _u(g)$. It follows that the Jacobian ideals ![]() $J_f$, respectively
$J_f$, respectively ![]() $J_g$ generated by the partial derivatives of
$J_g$ generated by the partial derivatives of ![]() $f$, respectively
$f$, respectively ![]() $g$, satisfy the condition
$g$, satisfy the condition
It turns out that (36) is in most cases a characterization of Schiffer variations, as shows Proposition 3.4 below. A well-known result due (in various forms) to Carlson and Griffiths [Reference Carlson, Griffiths and BeauvilleCG80], Donagi [Reference DonagiDon83], and Mather and Yau [Reference Mather and YauMY82] says the following.
Proposition 3.2 Let ![]() $f,\ g$ be two homogeneous polynomials in
$f,\ g$ be two homogeneous polynomials in ![]() $n+1$ variables, defining smooth hypersurfaces in
$n+1$ variables, defining smooth hypersurfaces in ![]() $\mathbb {P}^{n}$. If the Jacobian ideals
$\mathbb {P}^{n}$. If the Jacobian ideals ![]() $J_f^{d-1}$ and
$J_f^{d-1}$ and ![]() $J_g^{d-1}$ coincide, then
$J_g^{d-1}$ coincide, then ![]() $f$ and
$f$ and ![]() $g$ are in the same orbit under the group
$g$ are in the same orbit under the group ![]() ${\rm PGL}(n+1)$.
${\rm PGL}(n+1)$.
A nice proof of this statement is given in [Reference DonagiDon83]. The example of the Fermat equation ![]() $f=\sum _iX_i^{d}$ and its variations
$f=\sum _iX_i^{d}$ and its variations ![]() $g=\sum _i \alpha _iX_i^{d}$ shows that one does not always have
$g=\sum _i \alpha _iX_i^{d}$ shows that one does not always have ![]() $f= \mu g$ for some coefficient
$f= \mu g$ for some coefficient ![]() $\mu$, under the assumptions of Proposition 3.2. The Mather–Yau theorem is the following variant which is more precise but works only for
$\mu$, under the assumptions of Proposition 3.2. The Mather–Yau theorem is the following variant which is more precise but works only for ![]() $d$ large enough and
$d$ large enough and ![]() $f$ generic.
$f$ generic.
Proposition 3.3 Let ![]() $f,\ g$ be two homogeneous polynomials of degree
$f,\ g$ be two homogeneous polynomials of degree ![]() $d$ in
$d$ in ![]() $n+1$ variables, defining smooth hypersurfaces in
$n+1$ variables, defining smooth hypersurfaces in ![]() $\mathbb {P}^{n}$. Assume
$\mathbb {P}^{n}$. Assume ![]() $d\geq 4,\ n\geq 4$. If
$d\geq 4,\ n\geq 4$. If ![]() $f$ is generic and the Jacobian ideals
$f$ is generic and the Jacobian ideals ![]() $J_f$ and
$J_f$ and ![]() $J_g$ coincide, then
$J_g$ coincide, then ![]() $f=\mu g$ for some coefficient
$f=\mu g$ for some coefficient ![]() $\mu$.
$\mu$.
Let us prove a closely related statement concerning the case where ![]() $J_f^{d-1}$ and
$J_f^{d-1}$ and ![]() $J_g^{d-1}$ are not equal but almost equal, that is, satisfy (36).
$J_g^{d-1}$ are not equal but almost equal, that is, satisfy (36).
Proposition 3.4 Let ![]() $d,\ n$ be such that
$d,\ n$ be such that
Then for a generic polynomial ![]() $f\in H^{0}(\mathbb {P}^{n},\ \mathcal {O}_{\mathbb {P}^{n}}(d))$, (36) holds if and only if
$f\in H^{0}(\mathbb {P}^{n},\ \mathcal {O}_{\mathbb {P}^{n}}(d))$, (36) holds if and only if ![]() $g$ belongs to a Schiffer variation of
$g$ belongs to a Schiffer variation of ![]() $\lambda f$ for some coefficient
$\lambda f$ for some coefficient ![]() $\lambda$.
$\lambda$.
Note that (37) holds if ![]() $d\geq 4$ and
$d\geq 4$ and ![]() $n\geq 4$.
$n\geq 4$.
Proof Proof of Proposition 3.4
As ![]() $f$ is generic, its Jacobian ideal
$f$ is generic, its Jacobian ideal ![]() $J_f^{d-1}$ has dimension
$J_f^{d-1}$ has dimension ![]() $n+1$. Equation (37) can thus be written in the following form, for adequate choices of linear coordinates
$n+1$. Equation (37) can thus be written in the following form, for adequate choices of linear coordinates ![]() $X_0,\ldots,X_n$ and
$X_0,\ldots,X_n$ and ![]() $Y_0,\ldots,Y_n$ on
$Y_0,\ldots,Y_n$ on ![]() $\mathbb {P}^{n}$
$\mathbb {P}^{n}$
Let us now use the symmetry of partial derivatives:
Combined with (38), it provides, for any ![]() $i,\,j$ between
$i,\,j$ between ![]() $0$ and
$0$ and ![]() $n-1$, the following second-order equations:
$n-1$, the following second-order equations:
Lemma 3.5 Under the numerical assumption (37), a generic polynomial ![]() $f$ of degree
$f$ of degree ![]() $d$ in
$d$ in ![]() $n+1$ variables does not satisfy a nontrivial second-order partial differential equation of the type (39).
$n+1$ variables does not satisfy a nontrivial second-order partial differential equation of the type (39).
Proof. This is a dimension count. The differential equations appearing in (39) are linear second-order equations determined by elements ![]() $U$ of
$U$ of ![]() ${\rm rank}\leq 4$ in
${\rm rank}\leq 4$ in ![]() ${\rm Sym}^{2}H^{0}(\mathbb {P}^{n},\mathcal {O}_{\mathbb {P}^{n}}(1))^{*}$. The nonzero elements
${\rm Sym}^{2}H^{0}(\mathbb {P}^{n},\mathcal {O}_{\mathbb {P}^{n}}(1))^{*}$. The nonzero elements ![]() $U$ of
$U$ of ![]() ${\rm rank}\leq 4$ are parameterized by a variety of dimension
${\rm rank}\leq 4$ are parameterized by a variety of dimension ![]() $4(n-3)+9$. Given a nonzero
$4(n-3)+9$. Given a nonzero ![]() $U$, the differential equation
$U$, the differential equation ![]() $\partial ^{2}_U \phi =0$ determines a linear subspace
$\partial ^{2}_U \phi =0$ determines a linear subspace ![]() $H_U$ of
$H_U$ of ![]() $H^{0}(\mathbb {P}^{n},\mathcal {O}_{\mathbb {P}^{n}}(d))$ of codimension
$H^{0}(\mathbb {P}^{n},\mathcal {O}_{\mathbb {P}^{n}}(d))$ of codimension ![]() $h^{0}(\mathbb {P}^{n},\mathcal {O}_{\mathbb {P}^{n}}(d-2))$ since
$h^{0}(\mathbb {P}^{n},\mathcal {O}_{\mathbb {P}^{n}}(d-2))$ since
is surjective. If (37) holds, the union of the spaces ![]() $H_U$ does not fill-in a Zariski open set of
$H_U$ does not fill-in a Zariski open set of ![]() $H^{0}(\mathbb {P}^{n},\mathcal {O}_{\mathbb {P}^{n}}(d))$.
$H^{0}(\mathbb {P}^{n},\mathcal {O}_{\mathbb {P}^{n}}(d))$.
It follows that all the equations appearing in (39) are trivial, which says equivalently that for any ![]() $i,\ j$
$i,\ j$
These equations exactly say that for some ![]() $\lambda \in \mathbb {C}$,
$\lambda \in \mathbb {C}$,
for ![]() $i=0,\ldots,n-1$. Thus
$i=0,\ldots,n-1$. Thus ![]() $g-\lambda f$ satisfies
$g-\lambda f$ satisfies ![]() $({\partial }/{\partial X_i})(g-\lambda f)=0$ for
$({\partial }/{\partial X_i})(g-\lambda f)=0$ for ![]() $i=0,\ldots,n-1$, and hence
$i=0,\ldots,n-1$, and hence ![]() $g=\lambda f +\alpha X_n^{d}$ for some coefficient
$g=\lambda f +\alpha X_n^{d}$ for some coefficient ![]() $\alpha$, which completes the proof.
$\alpha$, which completes the proof.
We complete this section with the following proposition which shows the relevance of first-order Schiffer variations to our subject.
Proposition 3.6 Let ![]() $f,\ g$ be two degree
$f,\ g$ be two degree ![]() $d$ homogeneous polynomials in
$d$ homogeneous polynomials in ![]() $n+1$ variables defining smooth hypersurfaces
$n+1$ variables defining smooth hypersurfaces ![]() $X_f$,
$X_f$, ![]() $X_g$. Assume
$X_g$. Assume ![]() $d\geq 4,\ n\geq 4$ and
$d\geq 4,\ n\geq 4$ and ![]() $f$ is generic. Then if there exists a linear isomorphism
$f$ is generic. Then if there exists a linear isomorphism ![]() $i: R^{d}_f\cong R^{d}_g$ mapping the set of first-order Schiffer variations of
$i: R^{d}_f\cong R^{d}_g$ mapping the set of first-order Schiffer variations of ![]() $f$ to the set of first-order Schiffer variations of
$f$ to the set of first-order Schiffer variations of ![]() $g$,
$g$, ![]() $X_f$ is isomorphic to
$X_f$ is isomorphic to ![]() $X_g$.
$X_g$.
Proof. The conditions on ![]() $d,\ n$ are used in the following.
$d,\ n$ are used in the following.
Lemma 3.7 For ![]() $f$ generic with
$f$ generic with ![]() $d\geq 4,\ n\geq 2$, if
$d\geq 4,\ n\geq 2$, if ![]() $x\in S^{1}$ is nonzero, then
$x\in S^{1}$ is nonzero, then ![]() $x^{d}\not =0$ in
$x^{d}\not =0$ in ![]() $R^{d}_f$. Furthermore the map
$R^{d}_f$. Furthermore the map ![]() $x\mapsto x^{d}$ induces a (incomplete) Veronese imbedding
$x\mapsto x^{d}$ induces a (incomplete) Veronese imbedding ![]() $v_f: \mathbb {P}(S^{1})\hookrightarrow \mathbb {P}(R_f^{d})$.
$v_f: \mathbb {P}(S^{1})\hookrightarrow \mathbb {P}(R_f^{d})$.
Proof. The statement is equivalent to proving that, if ![]() $f$ is a generic homogeneous polynomial of degree
$f$ is a generic homogeneous polynomial of degree ![]() $d$ in
$d$ in ![]() $n+1$ variables,
$n+1$ variables, ![]() $J_f^{d}\subset S^{d}$ does not contain any power
$J_f^{d}\subset S^{d}$ does not contain any power ![]() $x^{d}$ of a linear form, or any sum
$x^{d}$ of a linear form, or any sum ![]() $x^{d}-y^{d}$ of two such powers. In the first case, we get that
$x^{d}-y^{d}$ of two such powers. In the first case, we get that ![]() $x\cdot x^{d-1}=0$ in
$x\cdot x^{d-1}=0$ in ![]() $R^{d}_f$ and in the second case, we get that
$R^{d}_f$ and in the second case, we get that ![]() $(x-y)(x^{d-1}+x^{d-2}y+\cdots +y^{d-1})=0$ in
$(x-y)(x^{d-1}+x^{d-2}y+\cdots +y^{d-1})=0$ in ![]() $R^{d}_f$. By an easy dimension count, one sees that for generic
$R^{d}_f$. By an easy dimension count, one sees that for generic ![]() $f$, the multiplication map
$f$, the multiplication map ![]() $x:R_f^{d-1}\rightarrow R_f^{d}$ by any nonzero linear form
$x:R_f^{d-1}\rightarrow R_f^{d}$ by any nonzero linear form ![]() $x\in S^{1}$ is injective, so in the first case we conclude that
$x\in S^{1}$ is injective, so in the first case we conclude that ![]() $x^{d-1}=0$ in
$x^{d-1}=0$ in ![]() $R_f^{d-1}$ and in the second case,
$R_f^{d-1}$ and in the second case, ![]() $x^{d-1}+x^{d-2}y+\cdots +y^{d-1}=0$ in
$x^{d-1}+x^{d-2}y+\cdots +y^{d-1}=0$ in ![]() $R_f^{d-1}$, or equivalently
$R_f^{d-1}$, or equivalently
Using the fact that ![]() $n\geq 2$, and choosing a coordinate system such that
$n\geq 2$, and choosing a coordinate system such that ![]() $x=X_0,\,y=X_1$, we can write (40) as
$x=X_0,\,y=X_1$, we can write (40) as
for some nonzero coefficients ![]() $\alpha _i$. We thus get in both cases a nontrivial second-order equation
$\alpha _i$. We thus get in both cases a nontrivial second-order equation
 \[ \sum_i\alpha_i\frac{\partial^{2} f}{\partial X_2 \partial X_i}=0, \]
\[ \sum_i\alpha_i\frac{\partial^{2} f}{\partial X_2 \partial X_i}=0, \]which is excluded by Lemma 3.5.
We now complete the proof. Using the lemma, the projectivized isomorphism ![]() $i$ induces an isomorphism
$i$ induces an isomorphism ![]() $i_1:\mathbb {P}(S^{1})\cong \mathbb {P}(S^{1})$ between the two projected Veronese
$i_1:\mathbb {P}(S^{1})\cong \mathbb {P}(S^{1})$ between the two projected Veronese ![]() $v_f(\mathbb {P}(S^{1})) \subset \mathbb {P}(R^{d}_f)$ and
$v_f(\mathbb {P}(S^{1})) \subset \mathbb {P}(R^{d}_f)$ and ![]() $v_g(\mathbb {P}(S^{1})) \subset \mathbb {P}(R^{d}_g)$, that is,
$v_g(\mathbb {P}(S^{1})) \subset \mathbb {P}(R^{d}_g)$, that is, ![]() $i_1$ satisfies
$i_1$ satisfies ![]() $i\circ v_f=v_g\circ i_1$. The projective isomorphism
$i\circ v_f=v_g\circ i_1$. The projective isomorphism ![]() $i_1$ lifts to a linear isomorphism
$i_1$ lifts to a linear isomorphism ![]() $\tilde {i}_1:S^{1}\cong S^{1}$. The incomplete Veronese embeddings
$\tilde {i}_1:S^{1}\cong S^{1}$. The incomplete Veronese embeddings ![]() $v_f$, respectively
$v_f$, respectively ![]() $v_g$ factor canonically through the complete Veronese embeddings
$v_g$ factor canonically through the complete Veronese embeddings
(respectively ![]() $\mathbb {P}^{n}(S^{1})\stackrel {V_d}{\rightarrow } \mathbb {P}(S^{d})\dashrightarrow \mathbb {P}(R^{d}_f)$,) which implies that the following diagram,
$\mathbb {P}^{n}(S^{1})\stackrel {V_d}{\rightarrow } \mathbb {P}(S^{d})\dashrightarrow \mathbb {P}(R^{d}_f)$,) which implies that the following diagram,

where ![]() $\widetilde {i_d}:S^{d}\cong S^{d}$ is induced by
$\widetilde {i_d}:S^{d}\cong S^{d}$ is induced by ![]() $\widetilde {i_1}$, is commutative up to a scalar.
$\widetilde {i_1}$, is commutative up to a scalar.
The vertical quotient maps have for respective kernels ![]() $J_f^{d}$,
$J_f^{d}$, ![]() $J_g^{d}$. We thus conclude that
$J_g^{d}$. We thus conclude that ![]() ${\widetilde {i_d}(J_f^{d})=J_g^{d}}$, and thus, by Proposition 3.2,
${\widetilde {i_d}(J_f^{d})=J_g^{d}}$, and thus, by Proposition 3.2, ![]() $X_f$ is isomorphic to
$X_f$ is isomorphic to ![]() $X_g$.
$X_g$.
3.1 Formal properties of Schiffer variations
Our strategy for the proof of Theorem 0.7 when ![]() $d$ divides
$d$ divides ![]() $n+1$ consists in finding a characterization of the set of Schiffer variations of a hypersurface
$n+1$ consists in finding a characterization of the set of Schiffer variations of a hypersurface ![]() $X_f$ that can be read from its local variation of Hodge structure. In fact we will need not only the IVHS of
$X_f$ that can be read from its local variation of Hodge structure. In fact we will need not only the IVHS of ![]() $X_f$ but also the ‘deformation of the IVHS’ along the Schiffer variation, which is a higher-order argument. The IVHS itself provides the first-order invariants of the variation of Hodge structure of
$X_f$ but also the ‘deformation of the IVHS’ along the Schiffer variation, which is a higher-order argument. The IVHS itself provides the first-order invariants of the variation of Hodge structure of ![]() $X_f$ at the point
$X_f$ at the point ![]() $[f]$, hence part of the multiplicative structure of the Jacobian ring
$[f]$, hence part of the multiplicative structure of the Jacobian ring ![]() $R_f$, by (6). We wish in this section to analyze the specifics of the first-order Schiffer variations
$R_f$, by (6). We wish in this section to analyze the specifics of the first-order Schiffer variations ![]() $\phi \in R^{d}_f$ as elements of the Jacobian ring
$\phi \in R^{d}_f$ as elements of the Jacobian ring ![]() $R_f^{*}$ and also analyze, using (36), the way the Jacobian ring deforms along them.
$R_f^{*}$ and also analyze, using (36), the way the Jacobian ring deforms along them.
Recall that a first-order Schiffer variation of ![]() $f$ is an element
$f$ is an element ![]() $\phi =x^{d}\in R^{d}_f$, where
$\phi =x^{d}\in R^{d}_f$, where ![]() $x\in S^{1}$. We will consider only the subring
$x\in S^{1}$. We will consider only the subring ![]() $R_f^{d*}$ of
$R_f^{d*}$ of ![]() $R_f^{*}$, because, by Theorem 0.5, this is, when
$R_f^{*}$, because, by Theorem 0.5, this is, when ![]() $d$ divides
$d$ divides ![]() $n+1$, the data that we get from the IVHS of
$n+1$, the data that we get from the IVHS of ![]() $f$. As
$f$. As ![]() $R_f^{d*}$ contains only the graded pieces of degree divisible by
$R_f^{d*}$ contains only the graded pieces of degree divisible by ![]() $d$, it does not contain the linear form
$d$, it does not contain the linear form ![]() $x$ and by Proposition 3.6, recovering the polynomial structure of
$x$ and by Proposition 3.6, recovering the polynomial structure of ![]() $R_f^{d}$ precisely means recognizing the set of powers
$R_f^{d}$ precisely means recognizing the set of powers ![]() $\phi =x^{d}$. However, the ideal of
$\phi =x^{d}$. However, the ideal of ![]() $R_f^{*d}$ generated by such a
$R_f^{*d}$ generated by such a ![]() $\phi \in R_f^{d}$ has some special properties that we can describe using only the multiplication map
$\phi \in R_f^{d}$ has some special properties that we can describe using only the multiplication map ![]() $R^{id}_f\otimes R^{jd}_f\rightarrow R^{(i+j)d}_f$ for
$R^{id}_f\otimes R^{jd}_f\rightarrow R^{(i+j)d}_f$ for ![]() $i+j\leq 3$.
$i+j\leq 3$.
Given ![]() $\phi \in R^{d}_f$ and vector subspaces
$\phi \in R^{d}_f$ and vector subspaces ![]() $I_k^{*d}\subset R^{*d}$ for
$I_k^{*d}\subset R^{*d}$ for ![]() $*=1,2,3$, and
$*=1,2,3$, and ![]() $1\leq k\leq d-1$, consider the following condition
$1\leq k\leq d-1$, consider the following condition ![]() $(*)$:
$(*)$:
Then condition ![]() $(*)$ is satisfied by
$(*)$ is satisfied by ![]() $I_{x,k}^{*d}:=x^{k}R^{*d-k}_f\subset R^{*d}_f$ for
$I_{x,k}^{*d}:=x^{k}R^{*d-k}_f\subset R^{*d}_f$ for ![]() $x\in S^{1}$ generic, with
$x\in S^{1}$ generic, with ![]() $\phi =x^{d}$, at least if
$\phi =x^{d}$, at least if ![]() $d$ is large enough. Indeed, condition (43) follows in that case from the fact that the multiplication by
$d$ is large enough. Indeed, condition (43) follows in that case from the fact that the multiplication by ![]() $x$ is injective in the relevant degrees (see Lemma 1.6), at least if
$x$ is injective in the relevant degrees (see Lemma 1.6), at least if ![]() $d$ or
$d$ or ![]() $n$ are large enough, and the other conditions are obvious.
$n$ are large enough, and the other conditions are obvious.
The second obvious property of a Schiffer variation is described in the following lemma.
Lemma 3.8 Let ![]() $x\in S^{1}$ determine a first-order Schiffer variation
$x\in S^{1}$ determine a first-order Schiffer variation ![]() $f_t=f+tx^{d}$ of
$f_t=f+tx^{d}$ of ![]() $f$ with tangent vector
$f$ with tangent vector ![]() $\phi =x^{d}\in R^{d}_f$, and let
$\phi =x^{d}\in R^{d}_f$, and let ![]() $I_{x,d-1,t}^{*d}:=x^{d-1}R^{*d-d+1}_{f_t}\subset R^{*d}_{f_t}$ be defined as above. Then the quotient ring
$I_{x,d-1,t}^{*d}:=x^{d-1}R^{*d-d+1}_{f_t}\subset R^{*d}_{f_t}$ be defined as above. Then the quotient ring ![]() $R^{*d}_{f_t}/I_{x,d-1,t}^{*d}$ does not deform (as a ring) along the Schiffer variation
$R^{*d}_{f_t}/I_{x,d-1,t}^{*d}$ does not deform (as a ring) along the Schiffer variation ![]() $(f_t)$.
$(f_t)$.
Proof. Indeed, if ![]() $f_t=f+tx^{d}$, then
$f_t=f+tx^{d}$, then ![]() $J_{f_t}=J_{f}$ modulo
$J_{f_t}=J_{f}$ modulo ![]() $x^{d-1}$, and hence the quotient
$x^{d-1}$, and hence the quotient
is constant. A fortiori, its isomorphism class as a graded ring does not depend on ![]() $t$.
$t$.
4. Proof of Theorem 0.7 when  $d$ divides
$d$ divides  $n+1$
$n+1$
4.1 Specialization and Schiffer variations
We will consider in this section singular hypersurfaces ![]() $X_f$ of degree
$X_f$ of degree ![]() $d$ in
$d$ in ![]() $\mathbb {P}^{n}$ defined by a polynomial of the form
$\mathbb {P}^{n}$ defined by a polynomial of the form ![]() $f=\sum _{i=1}^{m}f_ig_i$, with
$f=\sum _{i=1}^{m}f_ig_i$, with ![]() $n-2m\geq 0$. If
$n-2m\geq 0$. If ![]() $d=2d'$ is even, we will choose the
$d=2d'$ is even, we will choose the ![]() $f_i$ and
$f_i$ and ![]() $g_i$ to be of degree
$g_i$ to be of degree ![]() $d'$ and if
$d'$ and if ![]() $d=2d'+1$ we will choose the
$d=2d'+1$ we will choose the ![]() $f_i$ of degree
$f_i$ of degree ![]() $d'$ and the
$d'$ and the ![]() $g_i$ of degree
$g_i$ of degree ![]() $d'+1$. The hypersurface
$d'+1$. The hypersurface ![]() $X_f$ is then singular along the variety
$X_f$ is then singular along the variety ![]() $Z$ defined by the polynomials
$Z$ defined by the polynomials ![]() $f_i$ and
$f_i$ and ![]() $g_i$ which are all of degree
$g_i$ which are all of degree ![]() $\leq {(d+1)}/{2}$, and when they are generically chosen, it is of dimension
$\leq {(d+1)}/{2}$, and when they are generically chosen, it is of dimension ![]() $n-2m$. Let us start with the following result of independent interest, which will be important below and in the next section.
$n-2m$. Let us start with the following result of independent interest, which will be important below and in the next section.
Proposition 4.1 Let ![]() $f$ be a homogeneous polynomial of degree
$f$ be a homogeneous polynomial of degree ![]() $d$ in
$d$ in ![]() $n+1$ variables, defining a hypersurface
$n+1$ variables, defining a hypersurface ![]() $X_f$ singular along a smooth subvariety
$X_f$ singular along a smooth subvariety ![]() $Z$ defined by homogeneous polynomial equations of degree
$Z$ defined by homogeneous polynomial equations of degree ![]() $\leq {(d+1)}/{2}$. Then the dimension of the space
$\leq {(d+1)}/{2}$. Then the dimension of the space ![]() $R^{k}_f$ is equal to the dimension of the space
$R^{k}_f$ is equal to the dimension of the space ![]() $R^{k}_{f_{\rm gen}}$ for a generic polynomial
$R^{k}_{f_{\rm gen}}$ for a generic polynomial ![]() $f_{\rm gen}$, assuming
$f_{\rm gen}$, assuming
Proof Proof of Proposition 4.1
Recall that ![]() $J_f$ is generated by the partial derivatives
$J_f$ is generated by the partial derivatives ![]() ${\partial f}/{\partial X_i}$ for
${\partial f}/{\partial X_i}$ for ![]() $i=0,\ldots, n$. For the generic polynomial
$i=0,\ldots, n$. For the generic polynomial ![]() $f_{\rm gen}$, these partial derivatives form a linear system
$f_{\rm gen}$, these partial derivatives form a linear system ![]() $W$ of degree
$W$ of degree ![]() $d-1$ polynomials with no base-point on
$d-1$ polynomials with no base-point on ![]() $\mathbb {P}^{n}$, and the associated Koszul resolution
$\mathbb {P}^{n}$, and the associated Koszul resolution
twisted by ![]() $\mathcal {O}_{\mathbb {P}^{n}}(k)$, allows us to compute the dimension of
$\mathcal {O}_{\mathbb {P}^{n}}(k)$, allows us to compute the dimension of ![]() $R^{k}_{f_{\rm gen}}$ or, equivalently, of
$R^{k}_{f_{\rm gen}}$ or, equivalently, of ![]() $J^{k}_{f_{\rm gen}}={\rm Im}\,H^{0}(\alpha (k))$, using the fact that this twisted Koszul complex, that we will denote by
$J^{k}_{f_{\rm gen}}={\rm Im}\,H^{0}(\alpha (k))$, using the fact that this twisted Koszul complex, that we will denote by ![]() $\mathcal {K}_{\mathbb {P}^{n},k}^{*}$, remains exact at the level of global sections, at least in strictly negative degrees, where we put the last term
$\mathcal {K}_{\mathbb {P}^{n},k}^{*}$, remains exact at the level of global sections, at least in strictly negative degrees, where we put the last term ![]() $\mathcal {O}_{\mathbb {P}^{n}}(k)$ in degree
$\mathcal {O}_{\mathbb {P}^{n}}(k)$ in degree ![]() $0$, which is what we need to compute
$0$, which is what we need to compute ![]() ${\rm dim}\,J^{k}_{f_{\rm gen}}$. Indeed, we then get an equality
${\rm dim}\,J^{k}_{f_{\rm gen}}$. Indeed, we then get an equality
In our special case, the partial derivatives ![]() ${\partial f}/{\partial X_i}$ form a linear system
${\partial f}/{\partial X_i}$ form a linear system ![]() $W$ of degree
$W$ of degree ![]() $d-1$ polynomials on
$d-1$ polynomials on ![]() $\mathbb {P}^{n}$ with base-locus
$\mathbb {P}^{n}$ with base-locus ![]() $Z$ and we have to understand how this affects the computation. Clearly, the Koszul complex (48) is no more exact. Let
$Z$ and we have to understand how this affects the computation. Clearly, the Koszul complex (48) is no more exact. Let ![]() $\tau :Y\rightarrow \mathbb {P}^{n}$ be the blow-up of
$\tau :Y\rightarrow \mathbb {P}^{n}$ be the blow-up of ![]() $\mathbb {P}^{n}$ along
$\mathbb {P}^{n}$ along ![]() $Z$, and let
$Z$, and let ![]() $E$ be the exceptional divisor of
$E$ be the exceptional divisor of ![]() $\tau$. Then
$\tau$. Then ![]() $W$ provides a base-point free linear system, that we also denote by
$W$ provides a base-point free linear system, that we also denote by ![]() $W$, of sections of the line bundle
$W$, of sections of the line bundle ![]() $L:=\tau ^{*}\mathcal {O}_{\mathbb {P}^{n}}(d-1)(-E)$ on
$L:=\tau ^{*}\mathcal {O}_{\mathbb {P}^{n}}(d-1)(-E)$ on ![]() $Y$. Then we have an exact Koszul complex on
$Y$. Then we have an exact Koszul complex on ![]() $Y$ associated with
$Y$ associated with ![]() $W$, which has the following form:
$W$, which has the following form:
We now twist by ![]() $\tau ^{*}\mathcal {O}_{\mathbb {P}^{n}}(k)$ so that
$\tau ^{*}\mathcal {O}_{\mathbb {P}^{n}}(k)$ so that ![]() ${\rm Im}\,H^{0}(\alpha '(k))= {\rm dim}\,J_f^{k}$. Let
${\rm Im}\,H^{0}(\alpha '(k))= {\rm dim}\,J_f^{k}$. Let ![]() $\mathcal {K}_{Y,k}^{*}$ be this twisted Koszul complex. We observe that, as only nonnegative twists of
$\mathcal {K}_{Y,k}^{*}$ be this twisted Koszul complex. We observe that, as only nonnegative twists of ![]() $E$ appear in
$E$ appear in ![]() $\mathcal {K}_{Y,k}^{*}$, the global sections of
$\mathcal {K}_{Y,k}^{*}$, the global sections of ![]() $\mathcal {K}_{Y,k}^{*}$ are
$\mathcal {K}_{Y,k}^{*}$ are ![]() $\bigwedge ^{i} W\otimes S^{k-i(d-1)}$ in degree
$\bigwedge ^{i} W\otimes S^{k-i(d-1)}$ in degree ![]() $-i$. So our problem is actually to prove that, if the inequality (47) holds, the complex
$-i$. So our problem is actually to prove that, if the inequality (47) holds, the complex ![]() $K_{Y,k}^{*}$ of global sections of
$K_{Y,k}^{*}$ of global sections of ![]() $\mathcal {K}_{Y,k}^{*}$ is as before exact in strictly negative degrees. To prove this, we have to analyze the hypercohomology spectral sequence
$\mathcal {K}_{Y,k}^{*}$ is as before exact in strictly negative degrees. To prove this, we have to analyze the hypercohomology spectral sequence
of ![]() $\mathcal {K}_{Y,k}^{*}$. As
$\mathcal {K}_{Y,k}^{*}$. As ![]() $\mathcal {K}_{Y,k}^{*}$ is exact, one has
$\mathcal {K}_{Y,k}^{*}$ is exact, one has ![]() $\mathbb {H}^{p+q}(Y, \mathcal {K}_{Y,k}^{*})=0$, and hence
$\mathbb {H}^{p+q}(Y, \mathcal {K}_{Y,k}^{*})=0$, and hence
We have
where
We now observe that, when ![]() $-p< n-{\rm dim}\,Z$, we have
$-p< n-{\rm dim}\,Z$, we have ![]() $H^{q}(Y,\mathcal {K}_{Y,k}^{p})=0$ for
$H^{q}(Y,\mathcal {K}_{Y,k}^{p})=0$ for ![]() $q\not = 0,\, n$. This is because one then has
$q\not = 0,\, n$. This is because one then has ![]() $R^{i}\pi _* \mathcal {K}_{Y,k}^{p}=0$ for
$R^{i}\pi _* \mathcal {K}_{Y,k}^{p}=0$ for ![]() $i>0$, and
$i>0$, and
When ![]() $-p\geq n-{\rm dim}\,Z$, we have
$-p\geq n-{\rm dim}\,Z$, we have ![]() $H^{q}(Y,\mathcal {K}_{Y,k}^{p})=0$ for
$H^{q}(Y,\mathcal {K}_{Y,k}^{p})=0$ for ![]() $q< n-{\rm dim}\,Z-1$. Indeed, this follows again from the Leray spectral sequence of
$q< n-{\rm dim}\,Z-1$. Indeed, this follows again from the Leray spectral sequence of ![]() $pL(k)$ with respect to the map
$pL(k)$ with respect to the map ![]() $\tau$ and the fact that
$\tau$ and the fact that ![]() $R^{0}\tau _*(pL(k))$ has nonzero cohomology only in degree
$R^{0}\tau _*(pL(k))$ has nonzero cohomology only in degree ![]() $n$, and the only nonzero other higher direct image is
$n$, and the only nonzero other higher direct image is ![]() $R^{n-{\rm dim}\,Z-1}\tau _*(pL(k))$, which contributes only to cohomology of degree
$R^{n-{\rm dim}\,Z-1}\tau _*(pL(k))$, which contributes only to cohomology of degree ![]() $\geq n-{\rm dim}\,Z-1$.
$\geq n-{\rm dim}\,Z-1$.
A second source of vanishing for the ![]() $E_1^{p,q}$ of this spectral sequence comes from Kodaira vanishing applied to the line bundle
$E_1^{p,q}$ of this spectral sequence comes from Kodaira vanishing applied to the line bundle ![]() $pL(k)$ on
$pL(k)$ on ![]() $Y$. We observe that
$Y$. We observe that ![]() $Z$ is by assumption defined by equations of degree
$Z$ is by assumption defined by equations of degree ![]() $\leq {(d+1)}/{2}$, so that the line bundle
$\leq {(d+1)}/{2}$, so that the line bundle ![]() $\tau ^{*}\mathcal {O}_{\mathbb {P}^{n}}(l)(-mE)$ on
$\tau ^{*}\mathcal {O}_{\mathbb {P}^{n}}(l)(-mE)$ on ![]() $Y$ is nef and big when
$Y$ is nef and big when ![]() $m\geq 0$ and
$m\geq 0$ and ![]() $l>m {(d+1)}/{2}$. Using (53), Kodaira vanishing thus tells us that
$l>m {(d+1)}/{2}$. Using (53), Kodaira vanishing thus tells us that ![]() $H^{q}(Y,\mathcal {K}_{Y,k}^{p})=0$ for
$H^{q}(Y,\mathcal {K}_{Y,k}^{p})=0$ for ![]() $q< n$ if
$q< n$ if ![]() $-p(d-1)-k>-p{(d+1)}/{2}$.
$-p(d-1)-k>-p{(d+1)}/{2}$.
Summarizing, we proved that the spectral sequence (51) has vanishing as follows:
We now complete the proof. The complex ![]() $K_{Y,k}^{*}$ of global sections of the complex
$K_{Y,k}^{*}$ of global sections of the complex ![]() $\mathcal {K}_{Y,k}^{*}$ is the complex
$\mathcal {K}_{Y,k}^{*}$ is the complex ![]() $E_1^{*,0}$ of our spectral sequence, and hence its cohomology is the complex
$E_1^{*,0}$ of our spectral sequence, and hence its cohomology is the complex ![]() $E_2^{*,0}$. Recall that we have to prove the vanishing of the cohomology of
$E_2^{*,0}$. Recall that we have to prove the vanishing of the cohomology of ![]() $K_{Y,k}^{*}$ in strictly negative degrees. Let
$K_{Y,k}^{*}$ in strictly negative degrees. Let ![]() $a<0$ be a fixed negative integer. There is no nonzero differential
$a<0$ be a fixed negative integer. There is no nonzero differential ![]() $d_r$ with
$d_r$ with ![]() $r\geq 2$ starting from
$r\geq 2$ starting from ![]() $E_2^{a,0}$ since
$E_2^{a,0}$ since ![]() $E_r^{p,q}=0$ for
$E_r^{p,q}=0$ for ![]() $q<0$. As
$q<0$. As ![]() $E_\infty ^{a,0}=0$ (see 52), it follows that, if
$E_\infty ^{a,0}=0$ (see 52), it follows that, if ![]() $E_2^{a,0}$ is nonzero, there must be a nonzero differential
$E_2^{a,0}$ is nonzero, there must be a nonzero differential
Let ![]() $p=a-r$. By the vanishing statements (54), (55), we must have
$p=a-r$. By the vanishing statements (54), (55), we must have ![]() $r-1=n$ if
$r-1=n$ if ![]() $-p< n-{\rm dim}\,Z$ and
$-p< n-{\rm dim}\,Z$ and ![]() $r-1\geq n-{\rm dim}\,Z-1$ if
$r-1\geq n-{\rm dim}\,Z-1$ if ![]() $-p\geq n-{\rm dim}\,Z$. If
$-p\geq n-{\rm dim}\,Z$. If ![]() $r-1=n$, then, as
$r-1=n$, then, as ![]() $a<0$,
$a<0$, ![]() ${p=a-r<-n-1}$. The term
${p=a-r<-n-1}$. The term ![]() $\mathcal {K}_{Y,k}^{p}$ is then
$\mathcal {K}_{Y,k}^{p}$ is then ![]() $0$. Hence the only nontrivial differential appears when
$0$. Hence the only nontrivial differential appears when ![]() $r-1\not =n$. But then,
$r-1\not =n$. But then, ![]() $r\geq n-{\rm dim}\,Z$ and thus
$r\geq n-{\rm dim}\,Z$ and thus
Furthermore, using (56), ![]() $-p(d-1)-k\leq -p{(d+1)}/{2}$, that is,
$-p(d-1)-k\leq -p{(d+1)}/{2}$, that is,
Combining (57) and (58), we proved that the existence of a nonzero ![]() $E_2^{a,0}$ for some
$E_2^{a,0}$ for some ![]() $a<0$ implies
$a<0$ implies
which contradicts inequality (47). Proposition 4.1 is thus proved.
Imposing the dimension of ![]() $Z$ to be at most
$Z$ to be at most ![]() $4$ (we will later choose dimension of
$4$ (we will later choose dimension of ![]() $Z$ to be equal to
$Z$ to be equal to ![]() $3$ if
$3$ if ![]() $n$ is even and
$n$ is even and ![]() $4$ if
$4$ if ![]() $n$ is odd), we get the following.
$n$ is odd), we get the following.
Corollary 4.2 For a polynomial ![]() $f$ as in Proposition 4.1 with
$f$ as in Proposition 4.1 with ![]() $d$ dividing
$d$ dividing ![]() $n+1$ and
$n+1$ and ![]() ${\rm dim}\,Z\leq 4$, the dimensions of the spaces
${\rm dim}\,Z\leq 4$, the dimensions of the spaces ![]() $R^{d}_f$,
$R^{d}_f$, ![]() $R^{2d}_f$ and
$R^{2d}_f$ and ![]() $R^{3d}_f$ are respectively equal to the dimensions of the spaces
$R^{3d}_f$ are respectively equal to the dimensions of the spaces ![]() $R^{d}_{f_{\rm gen}}$,
$R^{d}_{f_{\rm gen}}$, ![]() $R^{2d}_{f_{\rm gen}}$ and
$R^{2d}_{f_{\rm gen}}$ and ![]() $R^{3d}_{f_{\rm gen}}$ for generic
$R^{3d}_{f_{\rm gen}}$ for generic ![]() $f_{\rm gen}$, assuming
$f_{\rm gen}$, assuming ![]() $d\geq 13$.
$d\geq 13$.
Proof. Indeed, if ![]() ${\rm dim}\,Z\leq 4$ and
${\rm dim}\,Z\leq 4$ and ![]() $k\leq 3d$, (47) is satisfied if
$k\leq 3d$, (47) is satisfied if
As ![]() $n\geq d-1$ and
$n\geq d-1$ and ![]() $d\geq 3$, (60) is satisfied if
$d\geq 3$, (60) is satisfied if ![]() $3d< (d-4)({(d-3)}/{2})$, hence if
$3d< (d-4)({(d-3)}/{2})$, hence if ![]() $d\geq 13$.
$d\geq 13$.
Remark 4.3 The estimate of Corollary 4.2 is sharp only when ![]() $d=n+1$.
$d=n+1$.
We now assume ![]() $f=\sum _{i=1}^{m}f_ig_i$ with
$f=\sum _{i=1}^{m}f_ig_i$ with ![]() $f_i,\ g_i$ generic and
$f_i,\ g_i$ generic and ![]() $d$,
$d$, ![]() $n$ are such that the conclusion of Corollary 4.2 holds. We observe that, with the same notation as above, as
$n$ are such that the conclusion of Corollary 4.2 holds. We observe that, with the same notation as above, as ![]() $f$ is singular along
$f$ is singular along ![]() $Z$, one has
$Z$, one has ![]() $J_f\subset I_Z$, and hence the Jacobian ring
$J_f\subset I_Z$, and hence the Jacobian ring ![]() $R_f^{d*}$ has
$R_f^{d*}$ has ![]() $H^{0}(Z,\mathcal {O}_Z(d*))$ as a quotient. We will use the notation
$H^{0}(Z,\mathcal {O}_Z(d*))$ as a quotient. We will use the notation ![]() $g_{\mid Z}$ for the image of an element
$g_{\mid Z}$ for the image of an element ![]() $g$ in this quotient. For subspaces
$g$ in this quotient. For subspaces ![]() $I_k^{id}\subset R^{id}_f$, let us denote
$I_k^{id}\subset R^{id}_f$, let us denote ![]() $\bar {I}_k^{id}:=I_{k\mid Z}\subset H^{0}(Z,\mathcal {O}_Z(id))$. Let us prove the following.
$\bar {I}_k^{id}:=I_{k\mid Z}\subset H^{0}(Z,\mathcal {O}_Z(id))$. Let us prove the following.
Lemma 4.4 Let ![]() $\phi \in R_f^{d}$ and
$\phi \in R_f^{d}$ and ![]() $I_k^{*d}\subset R_f^{*d}$ satisfy condition
$I_k^{*d}\subset R_f^{*d}$ satisfy condition ![]() $(*)$ (see (43)–(46)). Then either
$(*)$ (see (43)–(46)). Then either ![]() ${\bar {I}_{d-1}^{d}=0}$ and
${\bar {I}_{d-1}^{d}=0}$ and ![]() $\bar {I}_{d-1}^{2d}=0$ or there exists an element
$\bar {I}_{d-1}^{2d}=0$ or there exists an element ![]() $g$ of
$g$ of ![]() $R^{k}_f$ with
$R^{k}_f$ with ![]() $k\geq d-1$, such that
$k\geq d-1$, such that ![]() $g_{\mid Z}\not =0$ and
$g_{\mid Z}\not =0$ and
Proof. For a nonzero linear system ![]() $W$ on
$W$ on ![]() $Z$, let us denote by
$Z$, let us denote by ![]() ${\rm FL}(W)$ (for the ‘fixed locus’) the divisorial part of the base-locus of
${\rm FL}(W)$ (for the ‘fixed locus’) the divisorial part of the base-locus of ![]() $W$. We now observe that, as
$W$. We now observe that, as ![]() $Z$ is a smooth complete intersection of dimension at least
$Z$ is a smooth complete intersection of dimension at least ![]() $3$, one has
$3$, one has ![]() ${\rm Pic}\,Z=\mathbb {Z}\mathcal {O}_Z(1)$ by the Grothendieck–Lefschetz theorem. In particular, if
${\rm Pic}\,Z=\mathbb {Z}\mathcal {O}_Z(1)$ by the Grothendieck–Lefschetz theorem. In particular, if ![]() $\bar {I}_l^{k}\not =0$, we have
$\bar {I}_l^{k}\not =0$, we have
for some nonnegative integers ![]() $d_{l,k}$.
$d_{l,k}$.
We first make the following claim.
Claim 4.5 For ![]() $d$ large enough, one has
$d$ large enough, one has ![]() $\bar {I}_1^{d}\not =0$, and
$\bar {I}_1^{d}\not =0$, and ![]() $d_{1,d}\leq 1$.
$d_{1,d}\leq 1$.
Proof. This is proved by a dimension argument. Indeed, it suffices to prove that
As ![]() ${\rm dim}\,I_1^{d}={\rm dim}\,R^{d-1}_f$ by (43), one has
${\rm dim}\,I_1^{d}={\rm dim}\,R^{d-1}_f$ by (43), one has ![]() ${\rm dim}\,\bar {I}_1^{d}\geq {\rm dim}\,S^{d-1}-{\rm dim}\,I_Z(d)$ and it thus suffices to prove that
${\rm dim}\,\bar {I}_1^{d}\geq {\rm dim}\,S^{d-1}-{\rm dim}\,I_Z(d)$ and it thus suffices to prove that
Recalling that ![]() $Z$ is a complete intersection of
$Z$ is a complete intersection of ![]() $2m< n$ hypersurfaces defined by equations
$2m< n$ hypersurfaces defined by equations ![]() $f_i$ of degree
$f_i$ of degree ![]() $d'$ and
$d'$ and ![]() $g_i$ of degree
$g_i$ of degree ![]() $d''$, with
$d''$, with ![]() $d''-1\leq d'\leq d''$, and
$d''-1\leq d'\leq d''$, and ![]() $d'+d''=d$, we conclude that
$d'+d''=d$, we conclude that
and that
Inequality (63) will thus be a consequence of
Inequality (64) easily follows (at least for ![]() $d$ large enough) from our conditions
$d$ large enough) from our conditions ![]() $n> 2m$ and
$n> 2m$ and ![]() $d'=d'' =d/2$ if
$d'=d'' =d/2$ if ![]() $d$ is even,
$d$ is even, ![]() $d'=d''_1 =(d-1)/2$ if
$d'=d''_1 =(d-1)/2$ if ![]() $d$ is odd.
$d$ is odd.
We now use the fact that ![]() $\bar {I}_1^{d}\bar {I}_{d-1}^{d}\subset \phi _{\mid Z}\cdot H^{0}(Z,\mathcal {O}_Z(d))$ (see (44)). Combined with Claim 4.5, this implies that, either
$\bar {I}_1^{d}\bar {I}_{d-1}^{d}\subset \phi _{\mid Z}\cdot H^{0}(Z,\mathcal {O}_Z(d))$ (see (44)). Combined with Claim 4.5, this implies that, either ![]() $\bar {I}_{d-1}=0$, or
$\bar {I}_{d-1}=0$, or ![]() $d_{d-1,d}\geq d-1$. Similarly, as
$d_{d-1,d}\geq d-1$. Similarly, as
we conclude that ![]() $d_{d-1,2d}=:k\geq d-1$. Finally we use the fact that
$d_{d-1,2d}=:k\geq d-1$. Finally we use the fact that ![]() $H^{0}(Z,\mathcal {O}_Z(d))\cdot \bar {I}_{d-1}^{d}\subset \bar {I}_{d-1}^{2d}$ (see (45)) to deduce that the same
$H^{0}(Z,\mathcal {O}_Z(d))\cdot \bar {I}_{d-1}^{d}\subset \bar {I}_{d-1}^{2d}$ (see (45)) to deduce that the same ![]() $g$ of degree
$g$ of degree ![]() $k\geq d-1$ works for both
$k\geq d-1$ works for both ![]() $\bar {I}_{d-1}^{d}$ and
$\bar {I}_{d-1}^{d}$ and ![]() $\bar {I}_{d-1}^{2d}$. Lemma 4.4 is now proved.
$\bar {I}_{d-1}^{2d}$. Lemma 4.4 is now proved.
We now want to study, for a generic polynomial ![]() $f$ of the form
$f$ of the form ![]() $\sum _{i=1}^{m}f_ig_i$ as above, the elements
$\sum _{i=1}^{m}f_ig_i$ as above, the elements ![]() $\phi \in R^{d}_f$ which both satisfy condition
$\phi \in R^{d}_f$ which both satisfy condition ![]() $(*)$ and the property described in the assertion of Lemma 3.8. As Lemma 4.1 and Corollary 4.2 hold only for
$(*)$ and the property described in the assertion of Lemma 3.8. As Lemma 4.1 and Corollary 4.2 hold only for ![]() $R^{d}_f$,
$R^{d}_f$, ![]() $R^{2d}_f$ and
$R^{2d}_f$ and ![]() $R^{3d}_f$ and not for the whole
$R^{3d}_f$ and not for the whole ![]() $R^{*d}_f$ when
$R^{*d}_f$ when ![]() $f$ is singular, we are going to use only the data of the multiplication map of
$f$ is singular, we are going to use only the data of the multiplication map of ![]() $R^{*}_f$ in degree
$R^{*}_f$ in degree ![]() $d$, which is described by a triple
$d$, which is described by a triple ![]() $(R^{d}_f,R^{2d}_f,\mu )$ consisting of (isomorphism class of) two vector spaces of dimensions
$(R^{d}_f,R^{2d}_f,\mu )$ consisting of (isomorphism class of) two vector spaces of dimensions ![]() ${\rm dim}\,R^{d}_{f_{\rm gen}}$, respectively
${\rm dim}\,R^{d}_{f_{\rm gen}}$, respectively ![]() ${\rm dim}\,R^{2d}_{f_{\rm gen}}$, and a symmetric linear map
${\rm dim}\,R^{2d}_{f_{\rm gen}}$, and a symmetric linear map
We will also consider similar data ![]() $\bar {\mu }_f: \bar {R}^{d}\otimes \bar {R}^{d}\rightarrow \bar {R}^{2d}$ for quotients of
$\bar {\mu }_f: \bar {R}^{d}\otimes \bar {R}^{d}\rightarrow \bar {R}^{2d}$ for quotients of ![]() $R_f^{d*}$ and
$R_f^{d*}$ and ![]() $\mu :S^{d}\otimes S^{d}\rightarrow S^{2d}$ for the multiplication in the polynomial ring itself. We will call such data a ‘partial ring.’
$\mu :S^{d}\otimes S^{d}\rightarrow S^{2d}$ for the multiplication in the polynomial ring itself. We will call such data a ‘partial ring.’
We now study elements ![]() $\phi \in R^{d}_f$ satisfying the following condition
$\phi \in R^{d}_f$ satisfying the following condition ![]() $(**)$ (satisfied by Schiffer variations, see § 3.1).
$(**)$ (satisfied by Schiffer variations, see § 3.1).
![]() $(**)$ (i) For
$(**)$ (i) For ![]() $1\leq k\leq d-1$, there exist vector subspaces
$1\leq k\leq d-1$, there exist vector subspaces ![]() $I_{k}^d\subset R^d_f$,
$I_{k}^d\subset R^d_f$, ![]() $I_{k}^{2d}\subset R^{2d}_f$,
$I_{k}^{2d}\subset R^{2d}_f$, ![]() $I_{k}^{3d}\subset R^{3d}_f$ satisfying condition
$I_{k}^{3d}\subset R^{3d}_f$ satisfying condition ![]() $(*)$ (see (43)–(46)).
$(*)$ (see (43)–(46)).
(ii) Along a one-parameter family ![]() $f_t$, with
$f_t$, with ![]() $f_0=f$ and
$f_0=f$ and ![]() $({d}/{dt})(f_t)_{|t=0}=\phi$, there exist data
$({d}/{dt})(f_t)_{|t=0}=\phi$, there exist data ![]() $I_{k,t}^{*d}\subset R_{f_t}^{*d}$,
$I_{k,t}^{*d}\subset R_{f_t}^{*d}$, ![]() $*=1,2,3$,
$*=1,2,3$, ![]() $k=1,\ldots, d-1$, associated to
$k=1,\ldots, d-1$, associated to ![]() $\phi _t=({d}/{dt})(f_t)\in R^{d}_{f_t}$, and also satisfying condition
$\phi _t=({d}/{dt})(f_t)\in R^{d}_{f_t}$, and also satisfying condition ![]() $(*)$.
$(*)$.
(iii) The (isomorphism class of the) partial ring ![]() $(R^{d}_{f_t}/I_{d-1,t}^{d}, R^{2d}_{f_t}/I_{d-1,t}^{2d},\bar {\mu })$ does not deform with
$(R^{d}_{f_t}/I_{d-1,t}^{d}, R^{2d}_{f_t}/I_{d-1,t}^{2d},\bar {\mu })$ does not deform with ![]() $t$.
$t$.
Proposition 4.6 For ![]() $d$ sufficiently large and for a generic
$d$ sufficiently large and for a generic ![]() $f=\sum _{i=1}^{m}f_ig_i$ as above, any
$f=\sum _{i=1}^{m}f_ig_i$ as above, any ![]() $\phi \in R^{d}_f$ satisfying
$\phi \in R^{d}_f$ satisfying ![]() $(**)$ is a first-order Schiffer variations of
$(**)$ is a first-order Schiffer variations of ![]() $f$.
$f$.
Remark 4.7 We will also prove later on (see Lemma 4.15) that, in the situation of Proposition 4.6, for a generic first-order Schiffer variation ![]() $\phi =x^{d}$, the only spaces
$\phi =x^{d}$, the only spaces ![]() $I_k^{id}$ satisfying Condition
$I_k^{id}$ satisfying Condition ![]() $(*)$ with the given
$(*)$ with the given ![]() $\phi$ are the spaces
$\phi$ are the spaces ![]() $I_{x,k}^{id}=x^{k}R^{id-k}_f$, and hence are determined by
$I_{x,k}^{id}=x^{k}R^{id-k}_f$, and hence are determined by ![]() $\phi$.
$\phi$.
The proof of Proposition 4.6 will use several preliminary lemmas.
Lemma 4.8 The assumptions being the same as in Proposition 4.6, then we have the following.
(a) If
 $\bar {I}_{d-1}^{2d}=0$,
$\bar {I}_{d-1}^{2d}=0$,  $f_t$ remains singular along
$f_t$ remains singular along  $Z$ (or rather, a subvariety deduced from
$Z$ (or rather, a subvariety deduced from  $Z$ by the action of an automorphism of
$Z$ by the action of an automorphism of  ${\rm PGL}(n+1)$). In particular
${\rm PGL}(n+1)$). In particular  $\phi _{\mid Z}=0$.
$\phi _{\mid Z}=0$.(b) If
 ${\rm FL}(\bar {I}_{d-1}^{2d})$ is defined by
${\rm FL}(\bar {I}_{d-1}^{2d})$ is defined by  $g\in H^{0}(Z,\mathcal {O}_Z(k))$,
$g\in H^{0}(Z,\mathcal {O}_Z(k))$,  $f_t$ remains (modulo the action of
$f_t$ remains (modulo the action of  ${\rm PGL}(n+1)$) singular along the locus
${\rm PGL}(n+1)$) singular along the locus  $Z_g:=\{g=0\}\subset Z$.
$Z_g:=\{g=0\}\subset Z$.(c) If
 $k\geq d$ in (b),
$k\geq d$ in (b),  $f_t$ remains (modulo the action of
$f_t$ remains (modulo the action of  ${\rm PGL}(n+1)$) singular along
${\rm PGL}(n+1)$) singular along  $Z$.
$Z$.
Proof. (a) If ![]() $\bar {I}_{d-1}^{2d}=0$, the partial ring
$\bar {I}_{d-1}^{2d}=0$, the partial ring ![]() $(R^{d}_{f}/I_{d-1}^{d}, R^{2d}_{f}/I_{d-1}^{2d},\bar {\mu }_f)$ admits the partial ring
$(R^{d}_{f}/I_{d-1}^{d}, R^{2d}_{f}/I_{d-1}^{2d},\bar {\mu }_f)$ admits the partial ring ![]() $(H^{0}(Z,\mathcal {O}_Z(d)), H^{0}(Z,\mathcal {O}_Z(2d)),\mu _Z)$ as a quotient. As by assumption, the quotient
$(H^{0}(Z,\mathcal {O}_Z(d)), H^{0}(Z,\mathcal {O}_Z(2d)),\mu _Z)$ as a quotient. As by assumption, the quotient
of ![]() $(R^{d}_{f_t}, R^{2d}_{f_t},{\mu }_{f_t})$ is isomorphic to
$(R^{d}_{f_t}, R^{2d}_{f_t},{\mu }_{f_t})$ is isomorphic to ![]() $(R^{d}_f/I_{d-1}^{d}, R^{2d}_f/I_{d-1}^{2d},\bar {\mu })$, we conclude that the partial ring
$(R^{d}_f/I_{d-1}^{d}, R^{2d}_f/I_{d-1}^{2d},\bar {\mu })$, we conclude that the partial ring ![]() $(R^{d}_{f_t},R^{2d}_{f_t},\mu _{f_t})$ also admits the partial ring
$(R^{d}_{f_t},R^{2d}_{f_t},\mu _{f_t})$ also admits the partial ring ![]() $(H^{0}(Z,\mathcal {O}_Z(d)), H^{0}(Z,\mathcal {O}_Z(2d)),\mu _Z)$ as a quotient. Denoting by
$(H^{0}(Z,\mathcal {O}_Z(d)), H^{0}(Z,\mathcal {O}_Z(2d)),\mu _Z)$ as a quotient. Denoting by ![]() $\alpha _t: S^{*d}\rightarrow H^{0}(Z,\mathcal {O}_Z(*d))$ the quotient map for
$\alpha _t: S^{*d}\rightarrow H^{0}(Z,\mathcal {O}_Z(*d))$ the quotient map for ![]() $*=1,\,2$, this means that we have a commutative diagram,
$*=1,\,2$, this means that we have a commutative diagram,

where ![]() $\alpha _t$ is surjective with kernel containing
$\alpha _t$ is surjective with kernel containing ![]() $J_{f_t}$, since it factors through
$J_{f_t}$, since it factors through ![]() $R_{f_t}$. The map
$R_{f_t}$. The map ![]() $\alpha _t$ gives an embedding
$\alpha _t$ gives an embedding ![]() $j_t$ of
$j_t$ of ![]() $Z$ in
$Z$ in ![]() $\mathbb {P}((S^{d})^{*})$. As the quadrics in
$\mathbb {P}((S^{d})^{*})$. As the quadrics in ![]() ${\rm Ker}\,\mu$ are the defining equations for the
${\rm Ker}\,\mu$ are the defining equations for the ![]() $d$th Veronese embedding
$d$th Veronese embedding ![]() $V_d(\mathbb {P}^{n})$ in
$V_d(\mathbb {P}^{n})$ in ![]() $\mathbb {P}((S^{d})^{*})$, one concludes that
$\mathbb {P}((S^{d})^{*})$, one concludes that ![]() $j_t$ factors through an embedding
$j_t$ factors through an embedding ![]() $j'_t$ of
$j'_t$ of ![]() $Z$ in
$Z$ in ![]() $\mathbb {P}^{n}=\mathbb {P}((S^{1})^{*})$, that is
$\mathbb {P}^{n}=\mathbb {P}((S^{1})^{*})$, that is ![]() $j_t=V_d\circ j'_t$. As
$j_t=V_d\circ j'_t$. As ![]() $Z\stackrel {j'_0}{\hookrightarrow }\mathbb {P}^{n}$ is the natural embedding of a complete intersection in
$Z\stackrel {j'_0}{\hookrightarrow }\mathbb {P}^{n}$ is the natural embedding of a complete intersection in ![]() $\mathbb {P}^{n}$ of dimension
$\mathbb {P}^{n}$ of dimension ![]() $>0$, the small deformations of the morphism
$>0$, the small deformations of the morphism ![]() $j'_0: Z\rightarrow \mathbb {P}^{n}$ are induced by the action of
$j'_0: Z\rightarrow \mathbb {P}^{n}$ are induced by the action of ![]() ${\rm PGL}(n+1)$. Hence for
${\rm PGL}(n+1)$. Hence for ![]() $t$ close to
$t$ close to ![]() $0$,
$0$, ![]() $j'_t$ is, up to the action of
$j'_t$ is, up to the action of ![]() ${\rm PGL}(n+1)$, the original embedding. Finally, as the map
${\rm PGL}(n+1)$, the original embedding. Finally, as the map ![]() $\alpha _t=(j'_t)^{*}$ contains
$\alpha _t=(j'_t)^{*}$ contains ![]() $J_{f_t}$ in its kernel,
$J_{f_t}$ in its kernel, ![]() $J_{f_t}$ vanishes on
$J_{f_t}$ vanishes on ![]() $j'_t(Z)$, which means that
$j'_t(Z)$, which means that ![]() $f_t$ is singular along
$f_t$ is singular along ![]() $j'_t(Z)$.
$j'_t(Z)$.
(b) We know that for ![]() $t=0$, and
$t=0$, and ![]() $*=1,\,2$,
$*=1,\,2$, ![]() $(I_{d-1}^{*d})_{\mid Z}$ is contained in the ideal generated by
$(I_{d-1}^{*d})_{\mid Z}$ is contained in the ideal generated by ![]() $g$. It follows that the partial ring
$g$. It follows that the partial ring ![]() $(R^{d}_{f}/I_{d-1}^{d}, R^{2d}_{f}/I_{d-1}^{2d},\bar {\mu }_f)$ has the partial ring
$(R^{d}_{f}/I_{d-1}^{d}, R^{2d}_{f}/I_{d-1}^{2d},\bar {\mu }_f)$ has the partial ring
as a quotient, where ![]() $Z_g:=\{g=0\}\subset Z$. We can then argue exactly as before, using the fact that
$Z_g:=\{g=0\}\subset Z$. We can then argue exactly as before, using the fact that ![]() $Z_g$ is a complete intersection of strictly positive dimension in
$Z_g$ is a complete intersection of strictly positive dimension in ![]() $\mathbb {P}^{n}$. We then conclude that
$\mathbb {P}^{n}$. We then conclude that ![]() $f_t$ is singular along
$f_t$ is singular along ![]() $j'_t(Z_g)\subset \mathbb {P}^{n}$ and that the embedding
$j'_t(Z_g)\subset \mathbb {P}^{n}$ and that the embedding ![]() $j'_t$ of
$j'_t$ of ![]() $Z_g$ in
$Z_g$ in ![]() $\mathbb {P}^{n}$ is deduced from
$\mathbb {P}^{n}$ is deduced from ![]() $j'_0$ by the action of an element of
$j'_0$ by the action of an element of ![]() ${\rm PGL}(n+1)$.
${\rm PGL}(n+1)$.
(c) By (b), we know that, modulo the action of ![]() ${\rm PGL}(n+1)$,
${\rm PGL}(n+1)$, ![]() $f_t$ remains singular along the hypersurface
$f_t$ remains singular along the hypersurface ![]() $\{g=0\}$ in
$\{g=0\}$ in ![]() $Z$. As the singular locus of
$Z$. As the singular locus of ![]() $f_t$ is defined by the partial derivatives of
$f_t$ is defined by the partial derivatives of ![]() $f_t$ which are degree
$f_t$ which are degree ![]() $d-1$ polynomials, and
$d-1$ polynomials, and ![]() $Z$ is smooth connected, we conclude, when
$Z$ is smooth connected, we conclude, when ![]() ${k={\rm deg}\,g\geq d}$, that the partial derivatives of
${k={\rm deg}\,g\geq d}$, that the partial derivatives of ![]() $f_t$ vanish along
$f_t$ vanish along ![]() $Z$, which proves (c).
$Z$, which proves (c).
We next make the following observation.
Lemma 4.9 Let ![]() $Z$ be a smooth complete intersection of dimension
$Z$ be a smooth complete intersection of dimension ![]() $\geq 3$ of hypersurfaces
$\geq 3$ of hypersurfaces ![]() $X_{h_j}$ of degrees
$X_{h_j}$ of degrees ![]() $d_j\geq 2$ and let
$d_j\geq 2$ and let ![]() $f_t$ be a polynomial of degree
$f_t$ be a polynomial of degree ![]() $d$ such that
$d$ such that ![]() $f_t$ is singular along
$f_t$ is singular along ![]() $Z_g$ for some
$Z_g$ for some ![]() $0\not =g\in H^{0}(\mathcal {O}_Z(k))$ with
$0\not =g\in H^{0}(\mathcal {O}_Z(k))$ with ![]() $k\geq d-1$. Then either
$k\geq d-1$. Then either ![]() $f_t$ is singular along
$f_t$ is singular along ![]() $Z$ or there exists an element
$Z$ or there exists an element ![]() $x\in S^{1}$ such that
$x\in S^{1}$ such that ![]() $g=x^{d-1}_{\mid Z}$ and
$g=x^{d-1}_{\mid Z}$ and ![]() $f_t-\alpha _t x^{d}$ is singular along
$f_t-\alpha _t x^{d}$ is singular along ![]() $Z$ for some scalar
$Z$ for some scalar ![]() $\alpha _t$.
$\alpha _t$.
Proof. We first claim that if ![]() $f_{t\mid Z}=0$, then
$f_{t\mid Z}=0$, then ![]() $f_t$ is singular along
$f_t$ is singular along ![]() $Z$. This is proved as follows. As
$Z$. This is proved as follows. As ![]() $f_{t\mid Z}=0$, we can write
$f_{t\mid Z}=0$, we can write ![]() $f_t=\sum _ja_j h_j$, with
$f_t=\sum _ja_j h_j$, with ![]() ${\rm deg}\,a_j=d-d_j$. As
${\rm deg}\,a_j=d-d_j$. As ![]() $Z$ is smooth, the differential of
$Z$ is smooth, the differential of ![]() $f_t$ vanishes at a point
$f_t$ vanishes at a point ![]() $z\in Z$ if and only if all
$z\in Z$ if and only if all ![]() $a_j$ vanish at
$a_j$ vanish at ![]() $z$. As the
$z$. As the ![]() $a_j$ are of degree
$a_j$ are of degree ![]() $< d-1$ and
$< d-1$ and ![]() ${\rm deg}\,g\geq d-1$, the vanishing of
${\rm deg}\,g\geq d-1$, the vanishing of ![]() $df_t$ along
$df_t$ along ![]() $Z_g$ implies the vanishing of
$Z_g$ implies the vanishing of ![]() $df_t$ along
$df_t$ along ![]() $Z$.
$Z$.
Next, if ![]() $k\geq d$, we conclude that the partial derivatives of
$k\geq d$, we conclude that the partial derivatives of ![]() $f$ vanish identically along
$f$ vanish identically along ![]() $Z$, since they vanish along
$Z$, since they vanish along ![]() $Z_g$, so
$Z_g$, so ![]() $f$ is singular along
$f$ is singular along ![]() $Z$. We can thus assume that
$Z$. We can thus assume that ![]() $f_{\mid Z}\not =0$ and
$f_{\mid Z}\not =0$ and ![]() $k=d-1$.
$k=d-1$.
We then claim that there exists an ![]() $x\in S^{1}$ and a scalar
$x\in S^{1}$ and a scalar ![]() $\alpha _t$ such that
$\alpha _t$ such that ![]() $(f_t-\alpha _tx^{d})_{\mid Z}=0$ and
$(f_t-\alpha _tx^{d})_{\mid Z}=0$ and ![]() $g= x^{d-1}_{\mid Z}$. We use here the fact that
$g= x^{d-1}_{\mid Z}$. We use here the fact that ![]() ${\rm dim}\,Z\geq 3$ so that
${\rm dim}\,Z\geq 3$ so that ![]() ${\rm Pic}\,Z=\mathbb {Z}\mathcal {O}_Z(1)$. We decompose
${\rm Pic}\,Z=\mathbb {Z}\mathcal {O}_Z(1)$. We decompose ![]() $g\in H^{0}(Z,\mathcal {O}_Z(d-1))$ into irreducible factors as
$g\in H^{0}(Z,\mathcal {O}_Z(d-1))$ into irreducible factors as
where ![]() $\gamma _j\in H^{0}(Z,\mathcal {O}_Z(d_j))$ and
$\gamma _j\in H^{0}(Z,\mathcal {O}_Z(d_j))$ and ![]() $\sum _ja_jd_j=d-1$. Now if
$\sum _ja_jd_j=d-1$. Now if ![]() $f_{t\mid Z}$ vanishes to order
$f_{t\mid Z}$ vanishes to order ![]() $b_j$ along
$b_j$ along ![]() $\{\gamma _j=0\}$,
$\{\gamma _j=0\}$, ![]() $df_{t}$ vanishes to order
$df_{t}$ vanishes to order ![]() $\leq b_j-1$ along
$\leq b_j-1$ along ![]() $\{\gamma _j=0\}$. We thus conclude that
$\{\gamma _j=0\}$. We thus conclude that ![]() $b_j\geq a_j+1$. As
$b_j\geq a_j+1$. As ![]() $\sum _jb_j\leq d$ and
$\sum _jb_j\leq d$ and ![]() $\sum _ja_j=d-1$, we conclude that there is a single
$\sum _ja_j=d-1$, we conclude that there is a single ![]() $j$ and the corresponding
$j$ and the corresponding ![]() $a_j$ equals
$a_j$ equals ![]() $d-1$, which proves that
$d-1$, which proves that ![]() $g= x^{d-1}_{\mid Z}$ for some
$g= x^{d-1}_{\mid Z}$ for some ![]() $x\in S^{1}$. It follows that
$x\in S^{1}$. It follows that ![]() $f_{\mid Z}$ vanishes along
$f_{\mid Z}$ vanishes along ![]() $x^{d-1}_{\mid Z}=0$ and the fact that the derivatives of
$x^{d-1}_{\mid Z}=0$ and the fact that the derivatives of ![]() $f$ also vanish along
$f$ also vanish along ![]() $x^{d-1}_{\mid Z}=0$ implies that
$x^{d-1}_{\mid Z}=0$ implies that ![]() $f_{\mid Z}$ is proportional to
$f_{\mid Z}$ is proportional to ![]() $x^{d}_{\mid Z}$, proving the second claim.
$x^{d}_{\mid Z}$, proving the second claim.
The second claim finally implies Lemma 4.9 since ![]() $f_t-\alpha _t x^{d}$ vanishes along
$f_t-\alpha _t x^{d}$ vanishes along ![]() $Z$ and is also singular along
$Z$ and is also singular along ![]() $Z_g$, with
$Z_g$, with ![]() $g=x^{d-1}_{\mid Z}$, so that the first claim applies to show that
$g=x^{d-1}_{\mid Z}$, so that the first claim applies to show that ![]() $f_t-\alpha _tx^{d}$ is singular along
$f_t-\alpha _tx^{d}$ is singular along ![]() $Z$.
$Z$.
Proof Proof of Proposition 4.6
With the notation and assumptions of Proposition 4.6, Lemma 4.8 tells us that, modulo the action of ![]() ${\rm GL}(n+1)$, we can assume
${\rm GL}(n+1)$, we can assume ![]() $f_t$ is singular along
$f_t$ is singular along ![]() $Z$ or
$Z$ or ![]() $f_t$ is singular along
$f_t$ is singular along ![]() $Z_g$. Lemma 4.9 then says that, for some
$Z_g$. Lemma 4.9 then says that, for some ![]() $x\in S^{1}$,
$x\in S^{1}$, ![]() $g=x^{d-1}_{\mid Z}$ and
$g=x^{d-1}_{\mid Z}$ and ![]() $f_t-\alpha _t x^{d}$ is singular along
$f_t-\alpha _t x^{d}$ is singular along ![]() $Z$ for any
$Z$ for any ![]() $t$, and the same is true for
$t$, and the same is true for ![]() $\phi =({\partial f_t}/{\partial t})_{\mid t=0}$. It follows that either (i)
$\phi =({\partial f_t}/{\partial t})_{\mid t=0}$. It follows that either (i) ![]() $\phi \in I_Z^{2}(d)$ or (ii)
$\phi \in I_Z^{2}(d)$ or (ii) ![]() $\phi -x^{d}\in I_Z^{2}(d)$.
$\phi -x^{d}\in I_Z^{2}(d)$.
We use now the fact (this is (44) in condition ![]() $(*)$) that
$(*)$) that
for ![]() $1\leq i\leq d$, with
$1\leq i\leq d$, with ![]() $I_k^{d}\subset R^{d}_f$ of dimension equal to
$I_k^{d}\subset R^{d}_f$ of dimension equal to ![]() ${\rm dim}\,R^{d-k}_f$ (this is (43) in condition
${\rm dim}\,R^{d-k}_f$ (this is (43) in condition ![]() $(*)$). We previously used this condition only for
$(*)$). We previously used this condition only for ![]() $k=1$. We are going to use it for
$k=1$. We are going to use it for ![]() $k=3$ to prove the following claim which excludes case (i).
$k=3$ to prove the following claim which excludes case (i).
Claim 4.10 For ![]() $d$ large enough and
$d$ large enough and ![]() $f,\,Z$ generic, a nonzero element
$f,\,Z$ generic, a nonzero element ![]() $\phi \in R^{d}_f$ satisfying condition
$\phi \in R^{d}_f$ satisfying condition ![]() $(*)$ for adequate spaces
$(*)$ for adequate spaces ![]() $I_k^{*d}\subset R^{*d}_f$ cannot belong to
$I_k^{*d}\subset R^{*d}_f$ cannot belong to ![]() $I_Z^{2}(d)$.
$I_Z^{2}(d)$.
Proof. We argue by contradiction and assume that ![]() $\phi \in I_Z^{2}(d)$ and its image in
$\phi \in I_Z^{2}(d)$ and its image in ![]() $R^{d}_f$ satis- fies condition
$R^{d}_f$ satis- fies condition ![]() $(*)$. First of all, we use the same dimension arguments as in the proof of Claim 4.5 to show that
$(*)$. First of all, we use the same dimension arguments as in the proof of Claim 4.5 to show that ![]() $\bar {I}^{d}_3:=({I}_3^{d})_{\mid Z}\not =0$. More precisely, we can show that it is of dimension
$\bar {I}^{d}_3:=({I}_3^{d})_{\mid Z}\not =0$. More precisely, we can show that it is of dimension ![]() $>h^{0}(Z,\mathcal {O}_Z(d-4))$, at least if
$>h^{0}(Z,\mathcal {O}_Z(d-4))$, at least if ![]() $d$ is large enough. As
$d$ is large enough. As ![]() $\phi \in I_Z^{2}(d)$, we have in particular
$\phi \in I_Z^{2}(d)$, we have in particular ![]() $\phi _{\mid Z}=0$, and thus
$\phi _{\mid Z}=0$, and thus ![]() $I_{d-3}^{d}\subset I_Z(d)$ since
$I_{d-3}^{d}\subset I_Z(d)$ since
On the one hand, as ![]() ${\rm dim}\,I_{d-3}^{d}={\rm dim}\,S^{3}$ for
${\rm dim}\,I_{d-3}^{d}={\rm dim}\,S^{3}$ for ![]() $d>4$, and
$d>4$, and ![]() ${\rm dim}\,I_Z^{2}(d)<{\rm dim}\,S^{3}$,
${\rm dim}\,I_Z^{2}(d)<{\rm dim}\,S^{3}$, ![]() $I_{d-3}^{d}$ is not contained in
$I_{d-3}^{d}$ is not contained in ![]() $I_Z^{2}(d)$. On the other hand, if we look at the image of
$I_Z^{2}(d)$. On the other hand, if we look at the image of ![]() $I_{d-3}^{d}$ in
$I_{d-3}^{d}$ in ![]() $I_Z(d)/(I_Z^{2}(d)+J_f^{d})$, it is annihilated by multiplication by elements of
$I_Z(d)/(I_Z^{2}(d)+J_f^{d})$, it is annihilated by multiplication by elements of ![]() $\bar {I}_3^{d}$ acting by
$\bar {I}_3^{d}$ acting by
This follows indeed from the condition that ![]() $\phi \in I_Z^{2}(d)$ and (67). Now, writing
$\phi \in I_Z^{2}(d)$ and (67). Now, writing ![]() $f=\sum _jf_jg_j$ with
$f=\sum _jf_jg_j$ with ![]() ${\rm deg}\,f_j=d'$ and
${\rm deg}\,f_j=d'$ and ![]() ${\rm deg}\,g_j=d''$ , we have a graded isomorphism (given by differentiation along
${\rm deg}\,g_j=d''$ , we have a graded isomorphism (given by differentiation along ![]() $Z$)
$Z$)
 \[ (I_Z/I_Z^{2})(*)\cong \bigoplus_{j=1}^{m} H^{0}(Z,\mathcal{O}_Z(*-d'))\oplus \bigoplus_{j=1}^{m}H^{0}(Z,\mathcal{O}_Z(*-d'')), \]
\[ (I_Z/I_Z^{2})(*)\cong \bigoplus_{j=1}^{m} H^{0}(Z,\mathcal{O}_Z(*-d'))\oplus \bigoplus_{j=1}^{m}H^{0}(Z,\mathcal{O}_Z(*-d'')), \]
which to ![]() $\sum _ja_jf_j+b_jg_j$ associates
$\sum _ja_jf_j+b_jg_j$ associates ![]() $(a_{j|Z},b_{j|Z})_{j=1,\ldots,m}$. By the Leibniz rule, this isomorphism maps
$(a_{j|Z},b_{j|Z})_{j=1,\ldots,m}$. By the Leibniz rule, this isomorphism maps ![]() ${\partial f}/{\partial X_i}\in J_f$ to the
${\partial f}/{\partial X_i}\in J_f$ to the ![]() $2m$-uple
$2m$-uple ![]() $({\partial g_j}/{\partial X_i},{\partial f_j}/{\partial X_i})_{j=1,\ldots,m}$. In other words, observing that we have a natural isomorphism
$({\partial g_j}/{\partial X_i},{\partial f_j}/{\partial X_i})_{j=1,\ldots,m}$. In other words, observing that we have a natural isomorphism ![]() $N_{Z/\mathbb {P}^{n}}\cong N_{Z/\mathbb {P}^{n}}^{*}(d)$ given by the quadratic form defined as the Hessian of
$N_{Z/\mathbb {P}^{n}}\cong N_{Z/\mathbb {P}^{n}}^{*}(d)$ given by the quadratic form defined as the Hessian of ![]() $f$ along
$f$ along ![]() $Z$, we have on the one hand the composite morphism
$Z$, we have on the one hand the composite morphism ![]() $\mathcal {I}_Z\rightarrow N_Z^{*}\cong N_Z(-d)$ and on the other hand the normal bundle sequence of
$\mathcal {I}_Z\rightarrow N_Z^{*}\cong N_Z(-d)$ and on the other hand the normal bundle sequence of ![]() $Z$
$Z$
Then the computation above shows that
and these isomorphisms are compatible with the multiplication map by ![]() $b\in H^{0}(Z,\mathcal {O}_Z(d))$. Finally, the exact sequence (68) together with the fact that
$b\in H^{0}(Z,\mathcal {O}_Z(d))$. Finally, the exact sequence (68) together with the fact that ![]() ${\rm dim}\,Z\geq 3$ show that the right hand side in (69) is isomorphic to
${\rm dim}\,Z\geq 3$ show that the right hand side in (69) is isomorphic to ![]() $H^{1}(Z,T_Z)$ for
$H^{1}(Z,T_Z)$ for ![]() $*=d$. Let now
$*=d$. Let now ![]() $w\in I_{d-3}^{d}\subset I_Z(d)$ such that
$w\in I_{d-3}^{d}\subset I_Z(d)$ such that ![]() $w\not =0$ in
$w\not =0$ in ![]() $I_Z(d)/(J_f^{d}+I_Z^{2}(d))$. Then
$I_Z(d)/(J_f^{d}+I_Z^{2}(d))$. Then ![]() $w$ has a nonzero image
$w$ has a nonzero image ![]() $\bar {w}\in H^{1}(Z,T_Z)$ and
$\bar {w}\in H^{1}(Z,T_Z)$ and ![]() $\bar {w}$ is annihilated by multiplication by any
$\bar {w}$ is annihilated by multiplication by any ![]() $b\in \bar {I}_3^{d}\subset H^{0}(Z,\mathcal {O}_Z(d))$, that is,
$b\in \bar {I}_3^{d}\subset H^{0}(Z,\mathcal {O}_Z(d))$, that is,
for any ![]() $b\in \bar {I}_3^{d}$. The extension class
$b\in \bar {I}_3^{d}$. The extension class ![]() $\bar {w}\in H^{1}(Z,T_{Z})$ determines a vector bundle
$\bar {w}\in H^{1}(Z,T_{Z})$ determines a vector bundle ![]() $F$ on
$F$ on ![]() $Z$ which fits in an exact sequence
$Z$ which fits in an exact sequence
and the condition (70) says equivalently that ![]() $\bar {I}_3^{d}\subset H^{0}(Z,\mathcal {O}_Z(d))$ lifts to sections of
$\bar {I}_3^{d}\subset H^{0}(Z,\mathcal {O}_Z(d))$ lifts to sections of ![]() $F(d)$. Let
$F(d)$. Let ![]() $\mathcal {G}\subset F(d)$ be the coherent subsheaf generated by the global sections of
$\mathcal {G}\subset F(d)$ be the coherent subsheaf generated by the global sections of ![]() $F(d)$. Observe that
$F(d)$. Observe that ![]() ${\rm det}\,\mathcal {G}=\mathcal {O}_Z(k)$ with
${\rm det}\,\mathcal {G}=\mathcal {O}_Z(k)$ with ![]() $k\geq 0$ since
$k\geq 0$ since ![]() ${\rm Pic}\,Z=\mathbb {Z}\mathcal {O}_Z(1)$ and
${\rm Pic}\,Z=\mathbb {Z}\mathcal {O}_Z(1)$ and ![]() $\mathcal {G}$ is generated by its sections. Assume first that
$\mathcal {G}$ is generated by its sections. Assume first that ![]() $\mathcal {G}$ has rank
$\mathcal {G}$ has rank ![]() $1$. Then we have
$1$. Then we have
and we already noted that the right hand side is ![]() $>h^{0}(Z,\mathcal {O}_Z(d-4))$. It follows that
$>h^{0}(Z,\mathcal {O}_Z(d-4))$. It follows that ![]() $k\geq d-3$, and that for some
$k\geq d-3$, and that for some ![]() $0\not =\sigma \in h^{0}(Z,\mathcal {O}_Z(3))$, one has
$0\not =\sigma \in h^{0}(Z,\mathcal {O}_Z(3))$, one has
Equation (72) says that ![]() $\bar {w}$ is coming from a section of
$\bar {w}$ is coming from a section of ![]() $H^{0}(Z_\sigma,T_{Z\mid Z_\sigma }(3))$, where
$H^{0}(Z_\sigma,T_{Z\mid Z_\sigma }(3))$, where ![]() ${Z_\sigma :=\{\sigma =0\}\subset Z}$. A dimension count shows that for
${Z_\sigma :=\{\sigma =0\}\subset Z}$. A dimension count shows that for ![]() $d$ large enough and
$d$ large enough and ![]() $Z$ generic as above, there does not exist a cubic section
$Z$ generic as above, there does not exist a cubic section ![]() $Z_\sigma$ of
$Z_\sigma$ of ![]() $Z$ and a nonzero section of
$Z$ and a nonzero section of ![]() $T_{Z\mid Z_\sigma }(3)$. This case is thus ruled out. We thus conclude that the rank of
$T_{Z\mid Z_\sigma }(3)$. This case is thus ruled out. We thus conclude that the rank of ![]() $\mathcal {G}$ is at least
$\mathcal {G}$ is at least ![]() $2$. We then get a contradiction as follows. Let now
$2$. We then get a contradiction as follows. Let now ![]() $\mathcal {G}':={\rm Ker}\,\alpha : (\mathcal {G}\rightarrow \mathcal {O}_Z(d))$, where the morphism
$\mathcal {G}':={\rm Ker}\,\alpha : (\mathcal {G}\rightarrow \mathcal {O}_Z(d))$, where the morphism ![]() $\alpha$ is the restriction to
$\alpha$ is the restriction to ![]() $\mathcal {G}$ of the morphism
$\mathcal {G}$ of the morphism ![]() $F(d)\rightarrow \mathcal {O}_Z(d)$ deduced from the exact sequence (71). By this exact sequence,
$F(d)\rightarrow \mathcal {O}_Z(d)$ deduced from the exact sequence (71). By this exact sequence, ![]() $\mathcal {G'}$ is a subsheaf of
$\mathcal {G'}$ is a subsheaf of ![]() $T_Z(d)$ and we have
$T_Z(d)$ and we have ![]() ${\rm det}\,\mathcal {G}'=\mathcal {O}_Z(k')$ with
${\rm det}\,\mathcal {G}'=\mathcal {O}_Z(k')$ with ![]() $k'\geq -d$. Thus the slope of
$k'\geq -d$. Thus the slope of ![]() $\mathcal {G}'$ is at least
$\mathcal {G}'$ is at least ![]() $-d$. Recall that
$-d$. Recall that ![]() $Z$ is a complete intersection of
$Z$ is a complete intersection of ![]() $m$ hypersurfaces of degree
$m$ hypersurfaces of degree ![]() $d'$ and
$d'$ and ![]() $m$ hypersurfaces of degree
$m$ hypersurfaces of degree ![]() $d''$ with
$d''$ with ![]() $d'+d''=d$ and that
$d'+d''=d$ and that ![]() $s:={\rm dim}\,Z$ is equal to
$s:={\rm dim}\,Z$ is equal to ![]() $3$ or
$3$ or ![]() $4$. It follows that
$4$. It follows that ![]() $n=2m+s$ and
$n=2m+s$ and
It follows that ![]() ${\rm det}\,T_Z(d)=\mathcal {O}_Z(-m(d-2)+s+1+sd)$ and for
${\rm det}\,T_Z(d)=\mathcal {O}_Z(-m(d-2)+s+1+sd)$ and for ![]() $-m(d-2)+s+1+sd<0$, the slope of
$-m(d-2)+s+1+sd<0$, the slope of ![]() $T_Z(d)$ is thus at most
$T_Z(d)$ is thus at most ![]() ${(-m(d-2)+s+1+sd)}/{4}\leq {(-m(d-2)+5+4d)}/{4}$. Hence we have
${(-m(d-2)+s+1+sd)}/{4}\leq {(-m(d-2)+5+4d)}/{4}$. Hence we have
which holds if ![]() $m\geq 10,\ d\geq 13$. This gives a contradiction for
$m\geq 10,\ d\geq 13$. This gives a contradiction for ![]() $d$ large enough since
$d$ large enough since ![]() $Z$ is a variety with ample canonical bundle, and hence has stable tangent bundle by [Reference BogomolovBog78], [Reference YauYau78] or [Reference TsujiTsu88]. The claim is thus proved.
$Z$ is a variety with ample canonical bundle, and hence has stable tangent bundle by [Reference BogomolovBog78], [Reference YauYau78] or [Reference TsujiTsu88]. The claim is thus proved.
We are thus in case (ii), that is,
for some ![]() $\alpha \in I_Z^{2}(d)$, and we need to show that, in fact,
$\alpha \in I_Z^{2}(d)$, and we need to show that, in fact, ![]() $\phi = x^{d}$ mod
$\phi = x^{d}$ mod ![]() $J_f^{d}$. We start with the following lemma, where we use again the notation
$J_f^{d}$. We start with the following lemma, where we use again the notation ![]() $\bar {I}_{k}^{d}:=(I_{k}^{d})_{\mid Z}$.
$\bar {I}_{k}^{d}:=(I_{k}^{d})_{\mid Z}$.
Lemma 4.11 One has ![]() $\bar {I}_{1}^{d}\subset xH^{0}(Z,\mathcal {O}_Z(d-1))$.
$\bar {I}_{1}^{d}\subset xH^{0}(Z,\mathcal {O}_Z(d-1))$.
Proof. As ![]() $\phi _{\mid Z}=x^{d}_{\mid Z}$, we have, by (44) and (46) of condition
$\phi _{\mid Z}=x^{d}_{\mid Z}$, we have, by (44) and (46) of condition ![]() $(*)$ followed by restriction to
$(*)$ followed by restriction to ![]() $Z$,
$Z$,
 \begin{equation} \begin{aligned} \bar{I}_{1}^{d}\cdot \bar{I}_{d-1}^{d}\subset x^{d}H^{0}(Z,\mathcal{O}_Z(d)),\\ \bar{I}_{1}^{d}\cdot \bar{I}_{d-1}^{2d}\subset x^{d}H^{0}(Z,\mathcal{O}_Z(2d)). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \bar{I}_{1}^{d}\cdot \bar{I}_{d-1}^{d}\subset x^{d}H^{0}(Z,\mathcal{O}_Z(d)),\\ \bar{I}_{1}^{d}\cdot \bar{I}_{d-1}^{2d}\subset x^{d}H^{0}(Z,\mathcal{O}_Z(2d)). \end{aligned} \end{equation}
If ![]() $\bar {I}_{1}^{d}\not \subset xH^{0}(Z,\mathcal {O}_Z(d-1))$, then (74) imply that
$\bar {I}_{1}^{d}\not \subset xH^{0}(Z,\mathcal {O}_Z(d-1))$, then (74) imply that
By Lemma 4.8(c), this implies that ![]() $f_t$ remains singular along
$f_t$ remains singular along ![]() $Z$. Thus
$Z$. Thus ![]() $f_t\in I_Z^{2}(d)$ and
$f_t\in I_Z^{2}(d)$ and ![]() $\phi \in I_Z^{2}(d)$, contradicting (73).
$\phi \in I_Z^{2}(d)$, contradicting (73).
Corollary 4.12 Let ![]() $I'_1\subset I_1^{d}$ be defined by
$I'_1\subset I_1^{d}$ be defined by ![]() $I'_1=I_1^{d}\cap xR^{d-1}_f$, and let
$I'_1=I_1^{d}\cap xR^{d-1}_f$, and let ![]() $\bar {I}'_1:=(I'_1)_{\mid Z}\subset xH^{0}(Z,\mathcal {O}_Z(d-1))$. Then for
$\bar {I}'_1:=(I'_1)_{\mid Z}\subset xH^{0}(Z,\mathcal {O}_Z(d-1))$. Then for ![]() $d$ (hence also
$d$ (hence also ![]() $n$) large enough
$n$) large enough
Proof. Indeed, as ![]() $\bar {I}^{d}_1\subset xH^{0}(Z,\mathcal {O}_Z(d-1))$, we have
$\bar {I}^{d}_1\subset xH^{0}(Z,\mathcal {O}_Z(d-1))$, we have ![]() $I^{d}_1\subset xR^{d-1}_f+I_Z(d)$, hence
$I^{d}_1\subset xR^{d-1}_f+I_Z(d)$, hence
which implies a fortiori
Using the fact that ![]() ${\rm dim}\,I_1^{d}={\rm dim}\,R^{d-1}_f$ (see (43) in condition
${\rm dim}\,I_1^{d}={\rm dim}\,R^{d-1}_f$ (see (43) in condition ![]() $(*)$), the inequality
$(*)$), the inequality ![]() ${\rm dim}\,\bar {I}'_1>h^{0}(Z,\mathcal {O}_Z(d-2))$ is then proved for
${\rm dim}\,\bar {I}'_1>h^{0}(Z,\mathcal {O}_Z(d-2))$ is then proved for ![]() $d$ large enough in the same way as the inequality (62) proved in Claim 4.5.
$d$ large enough in the same way as the inequality (62) proved in Claim 4.5.
We come back to our ![]() $\phi =x^{d}+\alpha$ satisfying condition
$\phi =x^{d}+\alpha$ satisfying condition ![]() $(**)$, with
$(**)$, with ![]() $0\not =x\in S^{1}$, and
$0\not =x\in S^{1}$, and ![]() $\alpha \in I_Z^{2}(d)$. By (74) and using the fact that
$\alpha \in I_Z^{2}(d)$. By (74) and using the fact that ![]() ${\rm dim}\,\bar {I}_1^{d}> h^{0}(Z,\mathcal {O}_Z(d-2))$, we conclude that
${\rm dim}\,\bar {I}_1^{d}> h^{0}(Z,\mathcal {O}_Z(d-2))$, we conclude that
so that we can write, for any ![]() $w\in I_{d-1}^{d}$,
$w\in I_{d-1}^{d}$, ![]() $w=x^{d-1}y+k_y$, where
$w=x^{d-1}y+k_y$, where ![]() $y\in S^{1}$ and
$y\in S^{1}$ and ![]() $k_y\in I_Z(d)$ mod
$k_y\in I_Z(d)$ mod ![]() $J_f^{d}$. For
$J_f^{d}$. For ![]() $a=xa'\in I_1'\subset I_{1}^{d}\subset R^{d}_f$, and
$a=xa'\in I_1'\subset I_{1}^{d}\subset R^{d}_f$, and ![]() $w\in I_{d-1}^{d}$, we then have by (44) and (46) in condition
$w\in I_{d-1}^{d}$, we then have by (44) and (46) in condition ![]() $(*)$ and recalling that
$(*)$ and recalling that ![]() $\phi =x^{d}+\alpha$,
$\phi =x^{d}+\alpha$,
Restricting to ![]() $Z$, and using the fact that
$Z$, and using the fact that ![]() $k_y\in I_Z(d),\,\alpha \in I_Z^{2}(d)$, we get
$k_y\in I_Z(d),\,\alpha \in I_Z^{2}(d)$, we get ![]() $(\gamma _{a',w})_{\mid Z}=a'_{\mid Z}y_{\mid Z}$, which we write
$(\gamma _{a',w})_{\mid Z}=a'_{\mid Z}y_{\mid Z}$, which we write
for some ![]() $\gamma '_{a',w}\in I_Z(d)$ which depends linearly on
$\gamma '_{a',w}\in I_Z(d)$ which depends linearly on ![]() $a'$, for
$a'$, for ![]() $w$ fixed.
$w$ fixed.
We now use again the observation that ![]() ${\rm dim}\,I_Z(d)$ is (asymptotically) small compared to
${\rm dim}\,I_Z(d)$ is (asymptotically) small compared to ![]() $h^{0}(Z,\mathcal {O}_Z(d-2))$ and conclude that for
$h^{0}(Z,\mathcal {O}_Z(d-2))$ and conclude that for ![]() $a'$ in a subspace
$a'$ in a subspace ![]() $I_1''\subset I'_1$ such that
$I_1''\subset I'_1$ such that ![]() ${\rm dim}(I''_1)_{\mid Z}> h^{0}(Z,\mathcal {O}_Z(d-2))$, one can take
${\rm dim}(I''_1)_{\mid Z}> h^{0}(Z,\mathcal {O}_Z(d-2))$, one can take ![]() $\gamma '_{a',w}=0$ in
$\gamma '_{a',w}=0$ in ![]() $R^{d}_f$, so that (76) becomes
$R^{d}_f$, so that (76) becomes
that is,
The right hand side belongs to ![]() $(I_{Z}^{2}(2d)+J_f^{2d})/J_f^{2d}$. We argue now as in the proof of Claim 4.10 to deduce that
$(I_{Z}^{2}(2d)+J_f^{2d})/J_f^{2d}$. We argue now as in the proof of Claim 4.10 to deduce that ![]() $k_y\in (I_{Z}^{2}(d)+J_f^{d})/J_f^{d}$. Indeed, we consider the image
$k_y\in (I_{Z}^{2}(d)+J_f^{d})/J_f^{d}$. Indeed, we consider the image ![]() $\bar {k}_y$ of
$\bar {k}_y$ of ![]() $k_y$ in
$k_y$ in ![]() $I_Z(d)/(I_Z^{2}+J_f^{d})$ and (77) says that it is annihilated by multiplication by
$I_Z(d)/(I_Z^{2}+J_f^{d})$ and (77) says that it is annihilated by multiplication by ![]() $xa'$ for
$xa'$ for ![]() $xa'\in I_1'$, which is of large dimension. Then we conclude that
$xa'\in I_1'$, which is of large dimension. Then we conclude that ![]() $\bar {k}_y=0$.
$\bar {k}_y=0$.
Equations (77) are thus relations in ![]() $(I_Z^{2}+J_f)/J_f$. We claim that
$(I_Z^{2}+J_f)/J_f$. We claim that
Indeed, recall from the proof of Claim 4.10 that the image of ![]() $J_f^{*}$ in
$J_f^{*}$ in ![]() $I_Z(*)/I_Z^{2}$ identifies naturally with the image of
$I_Z(*)/I_Z^{2}$ identifies naturally with the image of ![]() $H^{0}(\mathbb {P}^{n}, T_{\mathbb {P}^{n}}(*-d+1))$ in
$H^{0}(\mathbb {P}^{n}, T_{\mathbb {P}^{n}}(*-d+1))$ in ![]() $H^{0}(Z,N_Z(*-d+1))$. We have the exact sequence
$H^{0}(Z,N_Z(*-d+1))$. We have the exact sequence
and we observe as in the proof of Claim 4.10 that the stability of the tangent bundle of ![]() $Z$ implies that
$Z$ implies that ![]() $h^{0}(Z,T_Z(d))=0$ for
$h^{0}(Z,T_Z(d))=0$ for ![]() $d$ (hence
$d$ (hence ![]() $n$) large enough. It follows that the map
$n$) large enough. It follows that the map ![]() $H^{0}(Z,T_{\mathbb {P}^{n}\mid Z}(d))\rightarrow H^{0}(Z,N_Z(d))$ is injective, and thus
$H^{0}(Z,T_{\mathbb {P}^{n}\mid Z}(d))\rightarrow H^{0}(Z,N_Z(d))$ is injective, and thus
comes from ![]() $H^{0}(\mathbb {P}^{n},T_{\mathbb {P}^{n}}\otimes \mathcal {I}_{Z}(d))$, which proves (78). We thus conclude that
$H^{0}(\mathbb {P}^{n},T_{\mathbb {P}^{n}}\otimes \mathcal {I}_{Z}(d))$, which proves (78). We thus conclude that
which is, for ![]() $d$ (hence
$d$ (hence ![]() $n$) large enough, much smaller than
$n$) large enough, much smaller than ![]() ${\rm dim}\,I''_1$. It follows that, taking representatives of
${\rm dim}\,I''_1$. It follows that, taking representatives of ![]() $k_y,\,\alpha$ in
$k_y,\,\alpha$ in ![]() $I_Z^{2}(d)$, (77) provides an actual vanishing
$I_Z^{2}(d)$, (77) provides an actual vanishing
for some nonzero ![]() $a''\in S^{d}$, which implies that
$a''\in S^{d}$, which implies that ![]() $xk_y=\alpha y$ in
$xk_y=\alpha y$ in ![]() $I_Z^{2}(d+1)$. Using the fact that the space of
$I_Z^{2}(d+1)$. Using the fact that the space of ![]() $(y,k_y)$ satisfying this property has dimension
$(y,k_y)$ satisfying this property has dimension ![]() $\geq n+1$, we conclude that
$\geq n+1$, we conclude that ![]() $k_y=0$ for generic
$k_y=0$ for generic ![]() $(y,k_y)$ and thus
$(y,k_y)$ and thus ![]() $\alpha =0$. Proposition 4.6 is now proved.
$\alpha =0$. Proposition 4.6 is now proved.
Remark 4.13 Note that, in turn, ![]() $\alpha =0$ and (79) imply that
$\alpha =0$ and (79) imply that ![]() $k_y=0$, so that we also proved that
$k_y=0$, so that we also proved that ![]() $I_{d-1}^{d}=x^{d-1}S^{1}$ mod
$I_{d-1}^{d}=x^{d-1}S^{1}$ mod ![]() $J_f^{d}$. This will be used below.
$J_f^{d}$. This will be used below.
4.2 Proof of Theorem 0.7
We complete in this section the proof of Theorem 0.7. We start by establishing the following.
Proposition 4.14 Let ![]() $f$ be a generic homogeneous polynomial of degree
$f$ be a generic homogeneous polynomial of degree ![]() $d$ in
$d$ in ![]() $n+1$ variables with
$n+1$ variables with ![]() $d$ dividing
$d$ dividing ![]() $n+1$ and
$n+1$ and ![]() $d$ large enough. Let
$d$ large enough. Let ![]() $\phi \in R^{d}_f$,
$\phi \in R^{d}_f$, ![]() $I_k^{*d}\subset R^{*d}_f$, for
$I_k^{*d}\subset R^{*d}_f$, for ![]() $*\leq 3$ and
$*\leq 3$ and ![]() $1\leq k\leq d-1$ satisfy condition
$1\leq k\leq d-1$ satisfy condition ![]() $(**)$ of § 4.1. Then
$(**)$ of § 4.1. Then ![]() $\phi$ is a (first-order) Schiffer variation of
$\phi$ is a (first-order) Schiffer variation of ![]() $f$.
$f$.
Proof. Proposition 4.6 proves Proposition 4.14 when ![]() $f=\sum _{j=1}^{m}f_jg_j$ is the singular polynomial used in previous section. It thus remains to see that this implies the same result for the generic
$f=\sum _{j=1}^{m}f_jg_j$ is the singular polynomial used in previous section. It thus remains to see that this implies the same result for the generic ![]() $f$. This almost follows because the condition
$f$. This almost follows because the condition ![]() $(**)$ is closed on
$(**)$ is closed on ![]() $(f,\,\phi )$ once the dimensions of the spaces
$(f,\,\phi )$ once the dimensions of the spaces ![]() $R^{d}_f$,
$R^{d}_f$, ![]() $R^{2d}_f$,
$R^{2d}_f$, ![]() $R^{3d}_f$ remain respectively equal to the dimensions of the spaces
$R^{3d}_f$ remain respectively equal to the dimensions of the spaces ![]() $R^{d}_{f_{\rm gen}}$,
$R^{d}_{f_{\rm gen}}$, ![]() $R^{2d}_{f_{\rm gen}}$,
$R^{2d}_{f_{\rm gen}}$, ![]() $R^{3d}_{f_{\rm gen}}$ for the generic
$R^{3d}_{f_{\rm gen}}$ for the generic ![]() $f_{\rm gen}$, which is guaranteed for
$f_{\rm gen}$, which is guaranteed for ![]() $d$ large enough by Lemma 4.1. This is not completely true because we did not prove the statement of Proposition 4.6 schematically for the special
$d$ large enough by Lemma 4.1. This is not completely true because we did not prove the statement of Proposition 4.6 schematically for the special ![]() $f$. In fact, what we have to do in order to finish is to prove the following complement to Proposition 4.6.
$f$. In fact, what we have to do in order to finish is to prove the following complement to Proposition 4.6.
Lemma 4.15 Let the notation and assumption on ![]() $f,\,\phi$ be as in Proposition 4.6. Assume moreover that
$f,\,\phi$ be as in Proposition 4.6. Assume moreover that ![]() $\phi =x^{d}$ in
$\phi =x^{d}$ in ![]() $R^{d}_f$, with
$R^{d}_f$, with ![]() $x$ generic in
$x$ generic in ![]() $S^{1}$. Then
$S^{1}$. Then ![]() $I_k^{d}=x^{k}R^{d-k}_f$ for
$I_k^{d}=x^{k}R^{d-k}_f$ for ![]() $1\leq k\leq d-1$.
$1\leq k\leq d-1$.
Furthermore, inside ![]() $\mathbb {P}(R^{d}_f)\times \prod _{k=0}^{d-1}{\rm Grass}(r_k,R^{d}_f)$, where
$\mathbb {P}(R^{d}_f)\times \prod _{k=0}^{d-1}{\rm Grass}(r_k,R^{d}_f)$, where ![]() $r_k:={\rm dim}\,R^{d-k}_f$, the set of points
$r_k:={\rm dim}\,R^{d-k}_f$, the set of points ![]() $(\phi =x^{d},I_{k}^{d}=x^{k}R^{d-k}_f)$, is schematically defined, at least at its generic point, by the condition
$(\phi =x^{d},I_{k}^{d}=x^{k}R^{d-k}_f)$, is schematically defined, at least at its generic point, by the condition ![]() $(*)$.
$(*)$.
Remark 4.16 The spaces ![]() $I_k^{2d},\ I_k^{3d}$ are defined by the spaces
$I_k^{2d},\ I_k^{3d}$ are defined by the spaces ![]() $I_k^{d}$ using (45), so we can consider condition
$I_k^{d}$ using (45), so we can consider condition ![]() $(*)$ as a condition on
$(*)$ as a condition on ![]() $(\phi,\,I_{k}^{d})$ only.
$(\phi,\,I_{k}^{d})$ only.
Remark 4.17 We did not use up to now (46) of Condition ![]() $(*)$. We will need it for the proof of this lemma.
$(*)$. We will need it for the proof of this lemma.
Proof Proof of Lemma 4.15
We already noted in Remark 4.13 that ![]() $I_{d-1}^{d}=x^{d-1}R^{d-1}_f$. We study again the equations
$I_{d-1}^{d}=x^{d-1}R^{d-1}_f$. We study again the equations
for ![]() $a$ in a subspace
$a$ in a subspace ![]() $I_1^{d}\subset R^{d}_f$ of dimension
$I_1^{d}\subset R^{d}_f$ of dimension ![]() ${\rm dim}\,R^{d-1}_f$, and
${\rm dim}\,R^{d-1}_f$, and ![]() $w$ in
$w$ in ![]() $I_{d-1}^{d}=x^{d-1} S^{1}$. We already proved in Lemma 4.11 that
$I_{d-1}^{d}=x^{d-1} S^{1}$. We already proved in Lemma 4.11 that ![]() $\bar {I}_1^{d}=I^{d}_{1\mid Z}\subset xH^{0}(Z,\mathcal {O}_Z(d-1))$. We thus conclude that elements
$\bar {I}_1^{d}=I^{d}_{1\mid Z}\subset xH^{0}(Z,\mathcal {O}_Z(d-1))$. We thus conclude that elements ![]() $a\in I_1^{d}$ can be written as
$a\in I_1^{d}$ can be written as
with ![]() $a'\in S^{d-1},\ k_a\in I_Z(d)$. Restricting (80) to
$a'\in S^{d-1},\ k_a\in I_Z(d)$. Restricting (80) to ![]() $Z$, we also get
$Z$, we also get
for some ![]() $\gamma '\in I_Z(d)$. Equation (80) then becomes
$\gamma '\in I_Z(d)$. Equation (80) then becomes
where ![]() $w'$ is generic in
$w'$ is generic in ![]() $S^{1}$. One then easily concludes that
$S^{1}$. One then easily concludes that ![]() $k_a=0$ mod
$k_a=0$ mod ![]() $\langle xS^{d-1},J_f\rangle$, that is,
$\langle xS^{d-1},J_f\rangle$, that is, ![]() $I_1^{d}\subset xR^{d-1}_f$. Hence we proved (by dimension reasons) that
$I_1^{d}\subset xR^{d-1}_f$. Hence we proved (by dimension reasons) that
We now use (46). We get
which provides, using (82) ![]() $x^{2}R^{2d-2}_f\subset I_2^{2d}$. Using (43), this inclusion gives in turn, by dimension reasons,
$x^{2}R^{2d-2}_f\subset I_2^{2d}$. Using (43), this inclusion gives in turn, by dimension reasons,
Here, in order to apply the dimension argument, we need to know that multiplication by ![]() $x^{2}$ is injective on
$x^{2}$ is injective on ![]() $R^{2d-2}_f$. More generally we will need to know that multiplication by
$R^{2d-2}_f$. More generally we will need to know that multiplication by ![]() $x^{i}$ is injective on
$x^{i}$ is injective on ![]() $R^{d+i}_f$ for
$R^{d+i}_f$ for ![]() $1\leq i\leq d$, which is not hard to prove since
$1\leq i\leq d$, which is not hard to prove since ![]() $x$ is generic. We next use (45)
$x$ is generic. We next use (45)
that is,
and easily conclude that ![]() $I_2^{d}\subset x^{2}R^{d-2}_f$, hence
$I_2^{d}\subset x^{2}R^{d-2}_f$, hence ![]() $I_2^{d}= x^{2}R^{d-2}_f$ by dimension reasons. We continue this way and prove that
$I_2^{d}= x^{2}R^{d-2}_f$ by dimension reasons. We continue this way and prove that ![]() $I_{k}^{d}=x^{k}R^{d-k}_f$ for all
$I_{k}^{d}=x^{k}R^{d-k}_f$ for all ![]() $1\leq k\leq d-1$. Thus the first statement is proved.
$1\leq k\leq d-1$. Thus the first statement is proved.
In order to prove the schematic statement, we consider a first-order variation ![]() $(h,h_1,\ldots,h_{d-1})$ of
$(h,h_1,\ldots,h_{d-1})$ of ![]() $(x^{d},I^{d}_1,\ldots,I^{d}_{d-1})$ satisfying conditions
$(x^{d},I^{d}_1,\ldots,I^{d}_{d-1})$ satisfying conditions ![]() $(*)$ at first order. We thus have a first-order deformation
$(*)$ at first order. We thus have a first-order deformation ![]() $x^{d}+\epsilon h\in R^{d}_f$ of
$x^{d}+\epsilon h\in R^{d}_f$ of ![]() $x^{d}$ and
$x^{d}$ and
satisfying the infinitesimal version of (44)–(46). We have to prove that there is a ![]() $y\in S^{1}/x$ such that
$y\in S^{1}/x$ such that
is given by multiplication by ![]() $lyx^{l-1}$. We first observe that it suffices to prove the result for
$lyx^{l-1}$. We first observe that it suffices to prove the result for ![]() $l=1$, because the reasoning above, which deduces the equality
$l=1$, because the reasoning above, which deduces the equality ![]() $I_{k}^{d}=x^{k}R^{d-k}_f$ for all
$I_{k}^{d}=x^{k}R^{d-k}_f$ for all ![]() $1\leq k\leq d-1$ from the equality (82) using (45) and (46) work as well schematically.
$1\leq k\leq d-1$ from the equality (82) using (45) and (46) work as well schematically.
We thus have a first-order deformation ![]() $x^{d}+\epsilon h\in R^{d}_f$ of
$x^{d}+\epsilon h\in R^{d}_f$ of ![]() $x^{d}$ and
$x^{d}$ and
satisfying the equations
for any ![]() $a=x a'\in xR^{d-1}_f$,
$a=x a'\in xR^{d-1}_f$, ![]() $w=x^{d-1}w'\in x^{d-1}S^{1}$, and for
$w=x^{d-1}w'\in x^{d-1}S^{1}$, and for ![]() $\gamma _\epsilon =\gamma +\epsilon \gamma _1$, where
$\gamma _\epsilon =\gamma +\epsilon \gamma _1$, where ![]() $\gamma$ is as in (80). We want to prove that there exists
$\gamma$ is as in (80). We want to prove that there exists ![]() $y\in S^{1}/\langle x\rangle$, such that for any
$y\in S^{1}/\langle x\rangle$, such that for any ![]() $a=xa'$, the following holds in
$a=xa'$, the following holds in ![]() $R^{d}_f$
$R^{d}_f$
Looking at the previous proof, we deduce from (81) with ![]() $k_a=0$ that
$k_a=0$ that ![]() $\gamma '=0$ (using injectivity of the multiplication by
$\gamma '=0$ (using injectivity of the multiplication by ![]() $x^{d}$), so
$x^{d}$), so ![]() $\gamma =a'w'$ in
$\gamma =a'w'$ in ![]() $R^{d}_f$. We thus have
$R^{d}_f$. We thus have ![]() $\gamma _\epsilon =a'w'+\epsilon \gamma _1$. Equation (84) then gives
$\gamma _\epsilon =a'w'+\epsilon \gamma _1$. Equation (84) then gives
for any ![]() $a=x a'\in xR^{d-1}_f$,
$a=x a'\in xR^{d-1}_f$, ![]() $w=x^{d-1}w'\in x^{d-1}S^{1}$. We claim that
$w=x^{d-1}w'\in x^{d-1}S^{1}$. We claim that
Indeed, (86) first implies that ![]() $h=xh'$ since it becomes divisible by
$h=xh'$ since it becomes divisible by ![]() $x$ after multiplication by any element of
$x$ after multiplication by any element of ![]() $R^{d}_f$, and then, after simplification by
$R^{d}_f$, and then, after simplification by ![]() $x$, that
$x$, that
We rewrite (88) in the form
We now restrict (89) to ![]() $Z$. As
$Z$. As ![]() $x^{d-2}$ and
$x^{d-2}$ and ![]() $a'$ have no common divisor on
$a'$ have no common divisor on ![]() $Z$ for
$Z$ for ![]() $a'$ generic, it follows that
$a'$ generic, it follows that
which proves (87) since ![]() $w'\in S^{1}$ is generic.
$w'\in S^{1}$ is generic.
We can even conclude by similar arguments that
for some ![]() $m_1\in H^{0}(Z,\mathcal {O}_Z(1))$. We can see
$m_1\in H^{0}(Z,\mathcal {O}_Z(1))$. We can see ![]() $m_1$ as an element
$m_1$ as an element ![]() $y\in S^{1}$ because the map of restriction to
$y\in S^{1}$ because the map of restriction to ![]() $Z$ is an isomorphism in degree
$Z$ is an isomorphism in degree ![]() $1$, and we can thus write in
$1$, and we can thus write in ![]() $R_f^{d}$
$R_f^{d}$
where ![]() $k_1(a')\in I_Z(d)$ for any
$k_1(a')\in I_Z(d)$ for any ![]() $a'\in R^{d-1}_f$. Equation (89) then gives
$a'\in R^{d-1}_f$. Equation (89) then gives ![]() $x^{d-2}((y a'+k_1(a'))w'-x\gamma _1)+a'(h_{d-1}(w)-h' w')=0$ in
$x^{d-2}((y a'+k_1(a'))w'-x\gamma _1)+a'(h_{d-1}(w)-h' w')=0$ in ![]() $R^{2d-1}_f$, that is
$R^{2d-1}_f$, that is
The term ![]() $x^{d-2}(k_1(a')w'-x\gamma _1)$ belongs by (91) to
$x^{d-2}(k_1(a')w'-x\gamma _1)$ belongs by (91) to ![]() $x^{d-2}I_Z(d+1)\cap \langle a'\rangle$. For
$x^{d-2}I_Z(d+1)\cap \langle a'\rangle$. For ![]() $a'$ generic, it is easy to show that it implies that it belongs to
$a'$ generic, it is easy to show that it implies that it belongs to ![]() $a'x^{d-2}I_Z(2)=0$. Thus
$a'x^{d-2}I_Z(2)=0$. Thus ![]() $x^{d-2}(k_1(a')w'-x\gamma _1)=0\ {\rm in}\ R^{2d-1}_f$, hence
$x^{d-2}(k_1(a')w'-x\gamma _1)=0\ {\rm in}\ R^{2d-1}_f$, hence ![]() $k_1(a')w'-x\gamma _1=0$, and
$k_1(a')w'-x\gamma _1=0$, and ![]() $k_1(a')=0$ mod
$k_1(a')=0$ mod ![]() $\langle x\rangle$. This is true for
$\langle x\rangle$. This is true for ![]() $a'$ generic in
$a'$ generic in ![]() $R^{d-1}_f$, hence for all
$R^{d-1}_f$, hence for all ![]() $a'$. Thus (85) is proved.
$a'$. Thus (85) is proved.
Lemma 4.15 is a schematic version of Proposition 4.6 that guarantees that the Veronese image ![]() $v_f(\mathbb {P}(S^{1}))\subset \mathbb {P}(R^{d}_f)$ is characterized not only set theoretically but also schematically (at the generic point) by condition
$v_f(\mathbb {P}(S^{1}))\subset \mathbb {P}(R^{d}_f)$ is characterized not only set theoretically but also schematically (at the generic point) by condition ![]() $(**)$ (in fact, we can see from the proof above that condition
$(**)$ (in fact, we can see from the proof above that condition ![]() $(*)$ even suffices for the scheme-theoretic statement, but condition
$(*)$ even suffices for the scheme-theoretic statement, but condition ![]() $(**)$ was needed to prove the set-theoretic statement for the special
$(**)$ was needed to prove the set-theoretic statement for the special ![]() $f$). It follows that for generic
$f$). It follows that for generic ![]() $f_{\rm gen}$, the Veronese image
$f_{\rm gen}$, the Veronese image ![]() $v_f(\mathbb {P}(S^{1}))\subset \mathbb {P}(R^{d}_f)$ is also characterized by condition
$v_f(\mathbb {P}(S^{1}))\subset \mathbb {P}(R^{d}_f)$ is also characterized by condition ![]() $(**)$.
$(**)$.
Proof Proof of Theorem 0.7(1)
Fix integers ![]() $d,\,n$ with
$d,\,n$ with ![]() $d$ dividing
$d$ dividing ![]() $n+1$, and for which the conclusion of Proposition 4.14 holds. We want to show that if
$n+1$, and for which the conclusion of Proposition 4.14 holds. We want to show that if ![]() $X_f$ is a very general hypersurface of degree
$X_f$ is a very general hypersurface of degree ![]() $d$ in
$d$ in ![]() $\mathbb {P}^{n}$, then any smooth hypersurface
$\mathbb {P}^{n}$, then any smooth hypersurface ![]() $X_g$ of degree
$X_g$ of degree ![]() $d$ in
$d$ in ![]() $\mathbb {P}^{n}$ such that there exists an isomorphism
$\mathbb {P}^{n}$ such that there exists an isomorphism
of rational Hodge structures, is isomorphic to ![]() $X_f$.
$X_f$.
We first argue as in § 1.1. Denote by ![]() $U_{d,n}^{0}\subset U_{d,n}$ the Zariski open set parameterizing automorphisms free smooth hypersurfaces. As
$U_{d,n}^{0}\subset U_{d,n}$ the Zariski open set parameterizing automorphisms free smooth hypersurfaces. As ![]() $f$ is very general,
$f$ is very general, ![]() $f\in U_{d,n}^{0}$ and our assumption provides simply connected Euclidean open neighborhoods
$f\in U_{d,n}^{0}$ and our assumption provides simply connected Euclidean open neighborhoods ![]() $U\subset U_{d,n}^{0},\,V\subset U_{d,n}^{0}$ of
$U\subset U_{d,n}^{0},\,V\subset U_{d,n}^{0}$ of ![]() $f$,
$f$, ![]() $g$ respectively, a holomorphic diffeomorphism
$g$ respectively, a holomorphic diffeomorphism ![]() $i:U\cong V$ with
$i:U\cong V$ with ![]() $i(f)=g$, and an isomorphism of complex variations of Hodge structures
$i(f)=g$, and an isomorphism of complex variations of Hodge structures
on ![]() $U$. Here, if
$U$. Here, if ![]() $\pi :\mathcal {X}_{d,n}\rightarrow U_{d,n}^{0}$ is the universal hypersurface,
$\pi :\mathcal {X}_{d,n}\rightarrow U_{d,n}^{0}$ is the universal hypersurface, ![]() $H^{n-1}_\mathbb {C}$ is the local system
$H^{n-1}_\mathbb {C}$ is the local system ![]() $R^{n-1}\pi _*\mathbb {C}_{{\rm prim}}$ on
$R^{n-1}\pi _*\mathbb {C}_{{\rm prim}}$ on ![]() $U_{d,n}^{0}$, and
$U_{d,n}^{0}$, and ![]() $F^{\cdot }\mathcal {H}^{n-1}$ is the Hodge filtration on the associated flat holomorphic vector bundle
$F^{\cdot }\mathcal {H}^{n-1}$ is the Hodge filtration on the associated flat holomorphic vector bundle ![]() $\mathcal {H}^{n-1}=H^{n-1}_\mathbb {C}\otimes \mathcal {O}_{U_{d,n}^{0}}$.
$\mathcal {H}^{n-1}=H^{n-1}_\mathbb {C}\otimes \mathcal {O}_{U_{d,n}^{0}}$.
The differential ![]() $i_*:T_{U,f}\rightarrow T_{V,g}$ is a linear isomorphism
$i_*:T_{U,f}\rightarrow T_{V,g}$ is a linear isomorphism
Claim 4.18 In the situation described above, the differential ![]() $i_*$ sends the set of first-order Schiffer variations of
$i_*$ sends the set of first-order Schiffer variations of ![]() $f$ to the set of first-order Schiffer variations of
$f$ to the set of first-order Schiffer variations of ![]() $g$.
$g$.
Proof. Indeed, the local diffeomorphism ![]() $i$ induces an isomorphism of variations of Hodge structures. It thus sends a one-parameter Schiffer variation
$i$ induces an isomorphism of variations of Hodge structures. It thus sends a one-parameter Schiffer variation ![]() $(f_t)_{t\in \Delta }$ of
$(f_t)_{t\in \Delta }$ of ![]() $f$ to a one-parameter variation
$f$ to a one-parameter variation ![]() $(g_t)_{t\in \Delta }$,
$(g_t)_{t\in \Delta }$, ![]() $g_t:=i(f_t)$, of
$g_t:=i(f_t)$, of ![]() $g$, which satisfies the assumptions of Proposition 4.14. Proposition 4.14 then tells us that
$g$, which satisfies the assumptions of Proposition 4.14. Proposition 4.14 then tells us that ![]() $\psi :=({\partial g_t}/{\partial t})_{\mid t=0}$ is a first-order Schiffer variation of
$\psi :=({\partial g_t}/{\partial t})_{\mid t=0}$ is a first-order Schiffer variation of ![]() $g$. But
$g$. But ![]() $\phi :=({\partial f_t}/{\partial t})_{\mid t=0}$ is an arbitrary first-order Schiffer variation of
$\phi :=({\partial f_t}/{\partial t})_{\mid t=0}$ is an arbitrary first-order Schiffer variation of ![]() $f$ and we have
$f$ and we have ![]() $\psi =i_*(\phi )$.
$\psi =i_*(\phi )$.
Having the claim, the proof of the theorem is finished using Proposition 3.6.
Acknowledgements
I thank Nick Shepherd-Barron for reminding me that the Donagi method a priori works only starting from ![]() $n=3$ and that Theorem 0.2 is actually wrong for
$n=3$ and that Theorem 0.2 is actually wrong for ![]() $(d,n)=(4,2)$. I also thank the referees for their very careful reading and constructive criticism. This work was started at MSRI during the program ‘Birational Geometry and Moduli Spaces’ in the Spring 2019. I thank the organizers for inviting me to stay there and the Clay Institute for its generous support.
$(d,n)=(4,2)$. I also thank the referees for their very careful reading and constructive criticism. This work was started at MSRI during the program ‘Birational Geometry and Moduli Spaces’ in the Spring 2019. I thank the organizers for inviting me to stay there and the Clay Institute for its generous support.