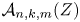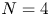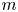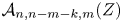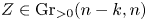1. Introduction
1.1 The amplituhedron and its triangulations
The amplituhedron ![]() $\mathcal {A}_{n,k,m}(Z)$ is a remarkable compact subspace of the real Grassmannian
$\mathcal {A}_{n,k,m}(Z)$ is a remarkable compact subspace of the real Grassmannian ![]() $\operatorname {Gr}(k,k+m)$ that was introduced by Arkani-Hamed and Trnka [Reference Arkani-Hamed and TrnkaAT14] in order to give a geometric basis for computing scattering amplitudes in
$\operatorname {Gr}(k,k+m)$ that was introduced by Arkani-Hamed and Trnka [Reference Arkani-Hamed and TrnkaAT14] in order to give a geometric basis for computing scattering amplitudes in ![]() $N= 4$ super Yang–Mills theory. It is defined to be the image of Postnikov's totally nonnegative Grassmannian
$N= 4$ super Yang–Mills theory. It is defined to be the image of Postnikov's totally nonnegative Grassmannian ![]() $\operatorname {Gr}_{\ge 0}(k,n)$ under the (rational) map
$\operatorname {Gr}_{\ge 0}(k,n)$ under the (rational) map ![]() $Z: \operatorname {Gr}(k,n) \dashrightarrow \operatorname {Gr}(k,k+m)$ induced by a
$Z: \operatorname {Gr}(k,n) \dashrightarrow \operatorname {Gr}(k,k+m)$ induced by a ![]() $(k+m) \times n$ matrix
$(k+m) \times n$ matrix ![]() $Z$ with positive maximal minors. Triangulations of the amplituhedron play a key role in the connection between the geometry of the amplituhedron and the physics of scattering amplitudes.
$Z$ with positive maximal minors. Triangulations of the amplituhedron play a key role in the connection between the geometry of the amplituhedron and the physics of scattering amplitudes.
The totally nonnegative Grassmannian ![]() $\operatorname {Gr}(k,n)_{\geq 0}$ has a stratification by positroid cells denoted
$\operatorname {Gr}(k,n)_{\geq 0}$ has a stratification by positroid cells denoted ![]() $\Pi ^{>0}_{k+f}$, where
$\Pi ^{>0}_{k+f}$, where ![]() $f$ is an affine permutation. We say that a collection of affine permutations
$f$ is an affine permutation. We say that a collection of affine permutations ![]() $f_1,f_2,\ldots ,f_N$ forms a
$f_1,f_2,\ldots ,f_N$ forms a ![]() $Z$-triangulation if the images
$Z$-triangulation if the images ![]() $Z(\Pi ^{>0}_{k+f_i})$ all have the same dimension as
$Z(\Pi ^{>0}_{k+f_i})$ all have the same dimension as ![]() $\mathcal {A}_{n,k,m}(Z)$ and are mutually non-overlapping, the union of the images is dense (in the analytic topology)Footnote 1 in
$\mathcal {A}_{n,k,m}(Z)$ and are mutually non-overlapping, the union of the images is dense (in the analytic topology)Footnote 1 in ![]() $\mathcal {A}_{n,k,m}(Z)$, and the maps
$\mathcal {A}_{n,k,m}(Z)$, and the maps ![]() $Z: \Pi ^{>0}_{k+f_i} \to Z(\Pi ^{>0}_{k+f_i})$ are injective. We say that these affine permutations form an
$Z: \Pi ^{>0}_{k+f_i} \to Z(\Pi ^{>0}_{k+f_i})$ are injective. We say that these affine permutations form an ![]() $(n,k,m)$-triangulation if they form a
$(n,k,m)$-triangulation if they form a ![]() $Z$-triangulation for all
$Z$-triangulation for all ![]() $Z \in \operatorname {Gr}_{>0}(k+m,n)$.
$Z \in \operatorname {Gr}_{>0}(k+m,n)$.
The amplituhedron depends on nonnegative integer parameters ![]() $k, m, n$, where
$k, m, n$, where ![]() $k + m \leq n$. Setting
$k + m \leq n$. Setting ![]() $\ell := n-k-m$, we have
$\ell := n-k-m$, we have ![]() $k+\ell +m = n$. Throughout the paper, we only deal with the case where
$k+\ell +m = n$. Throughout the paper, we only deal with the case where ![]() $m$ is even. Our first main result states that
$m$ is even. Our first main result states that ![]() $(n,k,m)$-triangulations of the amplituhedron are in bijection with
$(n,k,m)$-triangulations of the amplituhedron are in bijection with ![]() $(n,\ell ,m)$-triangulations of the amplituhedron. This bijection is obtained by taking an affine permutation to its inverse. One of the enumerative motivations of our work is a conjectural formula of Karp et al. [Reference Karp, Williams and ZhangKWZ17] for the number of cells in a particular triangulation of the amplituhedron. This formula is invariant under the operation of swapping the parameters
$(n,\ell ,m)$-triangulations of the amplituhedron. This bijection is obtained by taking an affine permutation to its inverse. One of the enumerative motivations of our work is a conjectural formula of Karp et al. [Reference Karp, Williams and ZhangKWZ17] for the number of cells in a particular triangulation of the amplituhedron. This formula is invariant under the operation of swapping the parameters ![]() $k$ and
$k$ and ![]() $\ell$, which is called parity duality in physics.
$\ell$, which is called parity duality in physics.
1.2 The stacked twist map
The twist map is a rational map ![]() $\tau : \operatorname {Mat}(r,n) \dashrightarrow \operatorname {Mat}(r,n)$ on matrices first defined by Marsh and Scott [Reference Marsh and ScottMS16]. It was motivated by the twist map on a unipotent group, due to Berenstein et al. [Reference Berenstein, Fomin and ZelevinskyBFZ96, Reference Berenstein and ZelevinskyBZ97]. Marsh and Scott's work has subsequently been extended by Muller and Speyer [Reference Muller and SpeyerMS17]. The main interest of Marsh and Scott, and Muller and Speyer, is the induced twist map
$\tau : \operatorname {Mat}(r,n) \dashrightarrow \operatorname {Mat}(r,n)$ on matrices first defined by Marsh and Scott [Reference Marsh and ScottMS16]. It was motivated by the twist map on a unipotent group, due to Berenstein et al. [Reference Berenstein, Fomin and ZelevinskyBFZ96, Reference Berenstein and ZelevinskyBZ97]. Marsh and Scott's work has subsequently been extended by Muller and Speyer [Reference Muller and SpeyerMS17]. The main interest of Marsh and Scott, and Muller and Speyer, is the induced twist map ![]() $\operatorname {Gr}(r,n) \dashrightarrow \operatorname {Gr}(r,n)$ on the Grassmannian. Taking
$\operatorname {Gr}(r,n) \dashrightarrow \operatorname {Gr}(r,n)$ on the Grassmannian. Taking ![]() $r := k+\ell$, we study instead the stacked twist map
$r := k+\ell$, we study instead the stacked twist map
At the heart of our approach is the result that the (rational) stacked twist map restricts to a diffeomorphism
on positroid cells indexed by affine permutations related by inversion. (See (4.5) for a definition of ![]() $\operatorname {Gr}_{>0}^\perp (k+m,n)$.) This allows us not only to relate triangulations under parity duality, but to study other geometric questions such as subdivisions and whether images of positroid cells overlap.
$\operatorname {Gr}_{>0}^\perp (k+m,n)$.) This allows us not only to relate triangulations under parity duality, but to study other geometric questions such as subdivisions and whether images of positroid cells overlap.
1.3 The amplituhedron form
The physical motivation for the study of the amplituhedron is an important (but conjectural) top-degree rational differential form ![]() $\omega _{\mathcal {A}_{n,k,m}(Z)}$ on the Grassmannian
$\omega _{\mathcal {A}_{n,k,m}(Z)}$ on the Grassmannian ![]() $\operatorname {Gr}(k,k+m)$ called the amplituhedron form. The case of main interest in physics is the case
$\operatorname {Gr}(k,k+m)$ called the amplituhedron form. The case of main interest in physics is the case ![]() $m = 4$. Roughly speaking, scattering amplitudes in
$m = 4$. Roughly speaking, scattering amplitudes in ![]() $N=4$ super Yang–Mills theory can be computed by formally integrating
$N=4$ super Yang–Mills theory can be computed by formally integrating ![]() $\omega _{\mathcal {A}_{n,k,m}(Z)}$ to obtain a rational function depending on a
$\omega _{\mathcal {A}_{n,k,m}(Z)}$ to obtain a rational function depending on a ![]() $4 \times n$ matrix, thought of as the momentum four-vectors of
$4 \times n$ matrix, thought of as the momentum four-vectors of ![]() $n$ particles. The integral removes the dependence of the form on the Grassmannian
$n$ particles. The integral removes the dependence of the form on the Grassmannian ![]() $\operatorname {Gr}(k,k+4)$, leaving only the dependence on the
$\operatorname {Gr}(k,k+4)$, leaving only the dependence on the ![]() $(k+4) \times n$ matrix
$(k+4) \times n$ matrix ![]() $Z$; furthermore,
$Z$; furthermore, ![]() $k$ of the
$k$ of the ![]() $k+4$ rows of
$k+4$ rows of ![]() $Z$ are taken to be Grassmann or fermionic parameters to account for the supersymmetry of the theory [Reference Arkani-Hamed and TrnkaAT14].
$Z$ are taken to be Grassmann or fermionic parameters to account for the supersymmetry of the theory [Reference Arkani-Hamed and TrnkaAT14].
The amplituhedron form ![]() $\omega _{\mathcal {A}_{n,k,m}(Z)}$ can be obtained from a triangulation of the amplituhedron as follows. Each positroid cell
$\omega _{\mathcal {A}_{n,k,m}(Z)}$ can be obtained from a triangulation of the amplituhedron as follows. Each positroid cell ![]() $\Pi ^{>0}_{k+f}$ has a canonical form
$\Pi ^{>0}_{k+f}$ has a canonical form ![]() $\omega _{k+f}$ of top degree in
$\omega _{k+f}$ of top degree in ![]() $\Pi ^{>0}_{k+f}$. Conjecturally,
$\Pi ^{>0}_{k+f}$. Conjecturally, ![]() $\omega _{\mathcal {A}_{n,k,m}(Z)}$ is obtained by summing the pushforwards
$\omega _{\mathcal {A}_{n,k,m}(Z)}$ is obtained by summing the pushforwards ![]() $Z_* \omega _{k+f}$ over any triangulation of the amplituhedron.
$Z_* \omega _{k+f}$ over any triangulation of the amplituhedron.
The form ![]() $\omega _{\mathcal {A}_{n,k,m}(Z)}$ has degree
$\omega _{\mathcal {A}_{n,k,m}(Z)}$ has degree ![]() $km$ while the form
$km$ while the form ![]() $\omega _{\mathcal {A}_{n,\ell ,m}(Z')}$ has degree
$\omega _{\mathcal {A}_{n,\ell ,m}(Z')}$ has degree ![]() $\ell m$. To relate them, we consider the universal amplituhedron
$\ell m$. To relate them, we consider the universal amplituhedron ![]() $\mathcal {A}_{n,k,m}$, a compact subset of the two-step flag variety
$\mathcal {A}_{n,k,m}$, a compact subset of the two-step flag variety ![]() $\textrm {Fl}(\ell ,k+\ell ;n)$. The fiber of
$\textrm {Fl}(\ell ,k+\ell ;n)$. The fiber of ![]() $\mathcal {A}_{n,k,m}$ over a point
$\mathcal {A}_{n,k,m}$ over a point ![]() $Z^\perp \in \operatorname {Gr}(\ell ,n)$ can be canonically identified with the amplituhedron
$Z^\perp \in \operatorname {Gr}(\ell ,n)$ can be canonically identified with the amplituhedron ![]() $\mathcal {A}_{n,k,m}(Z)$, and hence the terminology is ‘universal’. A related construction in the complex algebraic setting was studied in [Reference LamLam16b]. The dimension of
$\mathcal {A}_{n,k,m}(Z)$, and hence the terminology is ‘universal’. A related construction in the complex algebraic setting was studied in [Reference LamLam16b]. The dimension of ![]() $\mathcal {A}_{n,k,m}$ is equal to
$\mathcal {A}_{n,k,m}$ is equal to ![]() $k \ell + km+\ell m$.
$k \ell + km+\ell m$.
We show that the stacked twist map descends to a homeomorphism ![]() ${\tilde \theta }: \mathcal {A}_{n,k,\ge m} \to \mathcal {A}_{n,\ell ,\ge m}$ between subsets
${\tilde \theta }: \mathcal {A}_{n,k,\ge m} \to \mathcal {A}_{n,\ell ,\ge m}$ between subsets ![]() $\mathcal {A}_{n,k,\ge m} \subset \mathcal {A}_{n,k,m}$ and
$\mathcal {A}_{n,k,\ge m} \subset \mathcal {A}_{n,k,m}$ and ![]() $\mathcal {A}_{n,\ell ,\ge m} \subset \mathcal {A}_{n,\ell ,m}$ that contain the respective interiors. In particular, triangulations of
$\mathcal {A}_{n,\ell ,\ge m} \subset \mathcal {A}_{n,\ell ,m}$ that contain the respective interiors. In particular, triangulations of ![]() $\mathcal {A}_{n,k,m}$ are taken to triangulations of
$\mathcal {A}_{n,k,m}$ are taken to triangulations of ![]() $\mathcal {A}_{n,\ell ,m}$ via the stacked twist map. We introduce the universal amplituhedron form, a top-degree rational differential form
$\mathcal {A}_{n,\ell ,m}$ via the stacked twist map. We introduce the universal amplituhedron form, a top-degree rational differential form ![]() $\omega _{\mathcal {A}_{n,k,\ge m}}$ defined by summing pushforward canonical forms over a triangulation of the universal amplituhedron. Our main result concerning universal amplituhedron forms is that they are related by pullback under the stacked twist map:
$\omega _{\mathcal {A}_{n,k,\ge m}}$ defined by summing pushforward canonical forms over a triangulation of the universal amplituhedron. Our main result concerning universal amplituhedron forms is that they are related by pullback under the stacked twist map: ![]() ${\tilde \theta }^*\omega _{\mathcal {A}_{n,\ell ,\ge m}} = \omega _{\mathcal {A}_{n,k,\ge m}}$.
${\tilde \theta }^*\omega _{\mathcal {A}_{n,\ell ,\ge m}} = \omega _{\mathcal {A}_{n,k,\ge m}}$.
Outline
We recall some preliminaries on the positroid stratification of ![]() $\operatorname {Gr}_{\ge 0}(k,n)$ in § 2. Next, we define triangulations of the amplituhedron in § 3 and state a duality result for them (Theorem 3.5). We then explain the construction and some properties of the stacked twist map
$\operatorname {Gr}_{\ge 0}(k,n)$ in § 2. Next, we define triangulations of the amplituhedron in § 3 and state a duality result for them (Theorem 3.5). We then explain the construction and some properties of the stacked twist map ![]() $\theta$ and use them to give a short proof to Theorem 3.5 in § 4. After that, we discuss canonical forms of positroid cells in § 5 and state that they are preserved by
$\theta$ and use them to give a short proof to Theorem 3.5 in § 4. After that, we discuss canonical forms of positroid cells in § 5 and state that they are preserved by ![]() $\theta$ in Theorems 5.9 and 5.13. In § 6, we give several examples that illustrate our main results. In § 7, we define subdivisions of the amplituhedron, and give an analog of Theorem 3.5 for them (Theorem 7.2). In the same section, we define the universal amplituhedron and its subdivisions. We explain the relationship of our results with physics in § 8, where we define the universal amplituhedron form and show that it is preserved by the stacked twist map (Theorem 8.16). We then proceed to proving the numerous properties of the stacked twist map that we have mentioned in the previous sections. We discuss the topology of the amplituhedron in § 9. In § 10, we prove that
$\theta$ in Theorems 5.9 and 5.13. In § 6, we give several examples that illustrate our main results. In § 7, we define subdivisions of the amplituhedron, and give an analog of Theorem 3.5 for them (Theorem 7.2). In the same section, we define the universal amplituhedron and its subdivisions. We explain the relationship of our results with physics in § 8, where we define the universal amplituhedron form and show that it is preserved by the stacked twist map (Theorem 8.16). We then proceed to proving the numerous properties of the stacked twist map that we have mentioned in the previous sections. We discuss the topology of the amplituhedron in § 9. In § 10, we prove that ![]() $\theta$ takes triangulations to triangulations. In § 11, we prove that
$\theta$ takes triangulations to triangulations. In § 11, we prove that ![]() $\theta$ preserves the canonical form, and in § 12, we show that
$\theta$ preserves the canonical form, and in § 12, we show that ![]() $\theta$ preserves the universal amplituhedron form. Finally, we discuss some open problems in § 13.
$\theta$ preserves the universal amplituhedron form. Finally, we discuss some open problems in § 13.
2. The totally nonnegative Grassmannian
Let ![]() $n \geq 2$ be a positive integer, and denote
$n \geq 2$ be a positive integer, and denote ![]() $[n]:=\{1,2,\dots ,n\}$. Let
$[n]:=\{1,2,\dots ,n\}$. Let ![]() $\tilde {S_n}$ be the affine Coxeter group of type
$\tilde {S_n}$ be the affine Coxeter group of type ![]() $A$: the elements of
$A$: the elements of ![]() $\tilde {S_n}$ are all bijections
$\tilde {S_n}$ are all bijections ![]() $f:\mathbb {Z}\to \mathbb {Z}$ satisfying the following:
$f:\mathbb {Z}\to \mathbb {Z}$ satisfying the following:
(1)
 $f(i+n)=f(i)+n$ for all
$f(i+n)=f(i)+n$ for all  $i\in \mathbb {Z}$;
$i\in \mathbb {Z}$;(2)
 $\sum _{i=1}^{n}(f(i)-i)=0$.
$\sum _{i=1}^{n}(f(i)-i)=0$.
Given any bijection ![]() $f:\mathbb {Z}\to \mathbb {Z}$ satisfying (1), its number of inversions
$f:\mathbb {Z}\to \mathbb {Z}$ satisfying (1), its number of inversions ![]() $\operatorname {inv}(f)$ is the number of pairs
$\operatorname {inv}(f)$ is the number of pairs ![]() $(i,j)$ such that
$(i,j)$ such that ![]() $i \in [n]$,
$i \in [n]$, ![]() $j \in \mathbb {Z}$,
$j \in \mathbb {Z}$, ![]() $i < j$, and
$i < j$, and ![]() $f(i)>f(j)$. We will work with certain finite subsets of
$f(i)>f(j)$. We will work with certain finite subsets of ![]() $\tilde {S_n}$. Namely, for integers
$\tilde {S_n}$. Namely, for integers ![]() $a,b\geq 0$, define
$a,b\geq 0$, define
A ![]() $(k,n)$-bounded affine permutation is a bijection
$(k,n)$-bounded affine permutation is a bijection ![]() $f:\mathbb {Z}\to \mathbb {Z}$ satisfying the following:
$f:\mathbb {Z}\to \mathbb {Z}$ satisfying the following:
•
 $f(i+n)=f(i)+n$ for all
$f(i+n)=f(i)+n$ for all  $i\in \mathbb {Z}$;
$i\in \mathbb {Z}$;•
 $\sum _{i=1}^{n}(f(i)-i)=kn$;
$\sum _{i=1}^{n}(f(i)-i)=kn$;•
 $i\leq f(i)\leq i+n$ for all
$i\leq f(i)\leq i+n$ for all  $i\in \mathbb {Z}$.
$i\in \mathbb {Z}$.
We let ![]() ${\mathcal {B}}(k,n)$ denote the set of
${\mathcal {B}}(k,n)$ denote the set of ![]() $(k,n)$-bounded affine permutations. There is a distinguished element
$(k,n)$-bounded affine permutations. There is a distinguished element ![]() $\operatorname {id}_{k}\in {\mathcal {B}}(k,n)$ defined by
$\operatorname {id}_{k}\in {\mathcal {B}}(k,n)$ defined by ![]() $\operatorname {id}_{k}(i):=i+k$ for all
$\operatorname {id}_{k}(i):=i+k$ for all ![]() $i\in \mathbb {Z}$, and it is clear that we have
$i\in \mathbb {Z}$, and it is clear that we have ![]() $k+f\in {\mathcal {B}}(k,n)$ if and only if
$k+f\in {\mathcal {B}}(k,n)$ if and only if ![]() $f\in \tilde {S_n}(-k,n-k)$. Here
$f\in \tilde {S_n}(-k,n-k)$. Here ![]() $k+f$ is defined by
$k+f$ is defined by ![]() $(k+f)(i):=f(i)+k$ for all
$(k+f)(i):=f(i)+k$ for all ![]() $i\in \mathbb {Z}$. Throughout the text, we will work with
$i\in \mathbb {Z}$. Throughout the text, we will work with ![]() $\tilde {S_n}(-k,n-k)$ rather than with
$\tilde {S_n}(-k,n-k)$ rather than with ![]() ${\mathcal {B}}(k,n)$.
${\mathcal {B}}(k,n)$.
Let ![]() $k \leq n$ and
$k \leq n$ and ![]() $\operatorname {Gr}(k,n)$ denote the Grassmannian of
$\operatorname {Gr}(k,n)$ denote the Grassmannian of ![]() $k$-planes in
$k$-planes in ![]() $\mathbb {R}^n$. We let
$\mathbb {R}^n$. We let ![]() $ (\begin{smallmatrix}[n]\\ k\end{smallmatrix} )$ be the collection of all
$ (\begin{smallmatrix}[n]\\ k\end{smallmatrix} )$ be the collection of all ![]() $k$-element subsets of
$k$-element subsets of ![]() $[n]$. For
$[n]$. For ![]() $I\in (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )$ and
$I\in (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )$ and ![]() $X\in \operatorname {Gr}(k,n)$, we denote by
$X\in \operatorname {Gr}(k,n)$, we denote by ![]() $\Delta _I(X)$ the Plücker coordinate of
$\Delta _I(X)$ the Plücker coordinate of ![]() $X$, i.e. the maximal minor of
$X$, i.e. the maximal minor of ![]() $X$ with column set
$X$ with column set ![]() $I$. The totally nonnegative Grassmannian
$I$. The totally nonnegative Grassmannian ![]() $\operatorname {Gr}_{\ge 0}(k,n)\subset \operatorname {Gr}(k,n)$ consists of all
$\operatorname {Gr}_{\ge 0}(k,n)\subset \operatorname {Gr}(k,n)$ consists of all ![]() $X\in \operatorname {Gr}(k,n)$ such that
$X\in \operatorname {Gr}(k,n)$ such that ![]() $\Delta _I(X)\geq 0$ for all
$\Delta _I(X)\geq 0$ for all ![]() $I \in (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )$. Similarly, the totally positive Grassmannian
$I \in (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )$. Similarly, the totally positive Grassmannian ![]() $\operatorname {Gr}_{>0}(k,n)\subset \operatorname {Gr}_{\ge 0}(k,n)$ is the set of
$\operatorname {Gr}_{>0}(k,n)\subset \operatorname {Gr}_{\ge 0}(k,n)$ is the set of ![]() $X\in \operatorname {Gr}(k,n)$ with all Plücker coordinates strictly positive.
$X\in \operatorname {Gr}(k,n)$ with all Plücker coordinates strictly positive.
The totally nonnegative Grassmannian has a stratification by positroid cells that are indexed by bounded affine permutations, or equivalently by ![]() $\tilde {S_n}(-k,n-k)$. As we will explain in Definition 11.1, each
$\tilde {S_n}(-k,n-k)$. As we will explain in Definition 11.1, each ![]() $f\in \tilde {S_n}(-k,n-k)$ gives rise to a certain collection
$f\in \tilde {S_n}(-k,n-k)$ gives rise to a certain collection ![]() $\mathcal {M}_{k+f}$ of
$\mathcal {M}_{k+f}$ of ![]() $k$-element subsets of
$k$-element subsets of ![]() $[n]$ called a positroid, and then we associate an open positroid cell
$[n]$ called a positroid, and then we associate an open positroid cell ![]() $\Pi ^{>0}_{k+f}\subset \operatorname {Gr}_{\ge 0}(k,n)$ to
$\Pi ^{>0}_{k+f}\subset \operatorname {Gr}_{\ge 0}(k,n)$ to ![]() $f$ by
$f$ by
We similarly define a closed positroid cell ![]() $\Pi ^{\ge 0}_{k+f}$ by requiring
$\Pi ^{\ge 0}_{k+f}$ by requiring ![]() $\Delta _J(X)\geq 0$ for
$\Delta _J(X)\geq 0$ for ![]() $J\in \mathcal {M}_{k+f}$ and
$J\in \mathcal {M}_{k+f}$ and ![]() $\Delta _J(X)=0$ for
$\Delta _J(X)=0$ for ![]() $J\notin \mathcal {M}_{k+f}$. The positroid cell has dimension
$J\notin \mathcal {M}_{k+f}$. The positroid cell has dimension ![]() $\operatorname {dim}(f):=k(n-k)-\operatorname {inv}(f)$, so we say that it has codimension
$\operatorname {dim}(f):=k(n-k)-\operatorname {inv}(f)$, so we say that it has codimension ![]() $\operatorname {inv}(f)$. The unique cell
$\operatorname {inv}(f)$. The unique cell ![]() $\Pi ^{>0}_{\operatorname {id}_{k}}$ of codimension zero coincides with
$\Pi ^{>0}_{\operatorname {id}_{k}}$ of codimension zero coincides with ![]() $\operatorname {Gr}_{>0}(k,n)$. Each element
$\operatorname {Gr}_{>0}(k,n)$. Each element ![]() $X\in \operatorname {Gr}_{\ge 0}(k,n)$ belongs to
$X\in \operatorname {Gr}_{\ge 0}(k,n)$ belongs to ![]() $\Pi ^{>0}_{k+f}$ for a unique
$\Pi ^{>0}_{k+f}$ for a unique ![]() $f\in \tilde {S_n}(-k,n-k)$, and thus the totally nonnegative Grassmannian decomposes as a union of positroid cells:
$f\in \tilde {S_n}(-k,n-k)$, and thus the totally nonnegative Grassmannian decomposes as a union of positroid cells:
See Lemma 10.3 for an alternative definition of ![]() $\Pi ^{>0}_{k+f}$.
$\Pi ^{>0}_{k+f}$.
3. Triangulations of amplituhedra
Fix four nonnegative integers ![]() $k,\ell ,m,n$ such that
$k,\ell ,m,n$ such that ![]() $m$ is even and
$m$ is even and ![]() $k+\ell +m=n$. Let
$k+\ell +m=n$. Let ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$ be a matrix with all maximal minors positive.Footnote 2 We treat
$Z\in \operatorname {Gr}_{>0}(k+m,n)$ be a matrix with all maximal minors positive.Footnote 2 We treat ![]() $Z$ as a map from
$Z$ as a map from ![]() $\operatorname {Gr}_{\ge 0}(k,n)$ to
$\operatorname {Gr}_{\ge 0}(k,n)$ to ![]() $\operatorname {Gr}(k,k+m)$ sending (the row span of) a
$\operatorname {Gr}(k,k+m)$ sending (the row span of) a ![]() $k\times n$ matrix
$k\times n$ matrix ![]() $V$ to (the row span of)
$V$ to (the row span of) ![]() $V\cdot Z^\text {t}$, where
$V\cdot Z^\text {t}$, where ![]() $^\text {t}$ denotes matrix transpose. The (tree) amplituhedron
$^\text {t}$ denotes matrix transpose. The (tree) amplituhedron ![]() $\mathcal {A}_{n,k,m}(Z)$ is defined to be the image of
$\mathcal {A}_{n,k,m}(Z)$ is defined to be the image of ![]() $\operatorname {Gr}_{\ge 0}(k,n)$ under
$\operatorname {Gr}_{\ge 0}(k,n)$ under ![]() $Z$. We note that
$Z$. We note that ![]() $\mathcal {A}_{n,k,m}(Z)\subset \operatorname {Gr}(k,k+m)$ is a
$\mathcal {A}_{n,k,m}(Z)\subset \operatorname {Gr}(k,k+m)$ is a ![]() $km$-dimensional compact subset of
$km$-dimensional compact subset of ![]() $\operatorname {Gr}(k,k+m)$.
$\operatorname {Gr}(k,k+m)$.
Definition 3.1 Let ![]() $f\in \tilde {S_n}(-k,n-k)$ be an affine permutation. We say that
$f\in \tilde {S_n}(-k,n-k)$ be an affine permutation. We say that ![]() $f$ is
$f$ is ![]() $Z$-admissible if the restriction of the map
$Z$-admissible if the restriction of the map ![]() $Z$ to the positroid cell
$Z$ to the positroid cell ![]() $\Pi ^{>0}_{k+f}$ is injective. We say that
$\Pi ^{>0}_{k+f}$ is injective. We say that ![]() $f$ is
$f$ is ![]() $(n,k,m)$-admissible if it is
$(n,k,m)$-admissible if it is ![]() $Z$-admissible for any
$Z$-admissible for any ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$.
$Z\in \operatorname {Gr}_{>0}(k+m,n)$.
Clearly, in order for an affine permutation ![]() $f$ to be
$f$ to be ![]() $Z$-admissible, the dimension of
$Z$-admissible, the dimension of ![]() $\Pi ^{>0}_{k+f}$ must be at most
$\Pi ^{>0}_{k+f}$ must be at most ![]() $km$. Thus the codimension of
$km$. Thus the codimension of ![]() $\Pi ^{>0}_{k+f}$ in
$\Pi ^{>0}_{k+f}$ in ![]() $\operatorname {Gr}(k,n)$ must be at least
$\operatorname {Gr}(k,n)$ must be at least ![]() $k\ell$, equivalently, we must have
$k\ell$, equivalently, we must have ![]() $\operatorname {inv}(f)\geq k\ell$. If
$\operatorname {inv}(f)\geq k\ell$. If ![]() $f$ is
$f$ is ![]() $Z$-admissible, then in order for
$Z$-admissible, then in order for ![]() $Z(\Pi ^{>0}_{k+f})$ to be a full-dimensional subset of
$Z(\Pi ^{>0}_{k+f})$ to be a full-dimensional subset of ![]() $\mathcal {A}_{n,k,m}(Z)$ it is necessary to have
$\mathcal {A}_{n,k,m}(Z)$ it is necessary to have ![]() $\operatorname {inv}(f)=k\ell$. However, it is not sufficient.
$\operatorname {inv}(f)=k\ell$. However, it is not sufficient.
Lemma 3.2 Let ![]() $f\in \tilde {S_n}(-k,n-k)$ be an affine permutation with
$f\in \tilde {S_n}(-k,n-k)$ be an affine permutation with ![]() $\operatorname {inv}(f)=k\ell$ and let
$\operatorname {inv}(f)=k\ell$ and let ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$. If
$Z\in \operatorname {Gr}_{>0}(k+m,n)$. If ![]() $f\notin \tilde {S_n}(-k,\ell )$ then
$f\notin \tilde {S_n}(-k,\ell )$ then ![]() $f$ is not
$f$ is not ![]() $Z$-admissible, the dimension of
$Z$-admissible, the dimension of ![]() $Z(\Pi ^{>0}_{k+f})$ is less than
$Z(\Pi ^{>0}_{k+f})$ is less than ![]() $km$, and
$km$, and ![]() $Z(\Pi ^{>0}_{k+f})$ is a subset of the boundary of
$Z(\Pi ^{>0}_{k+f})$ is a subset of the boundary of ![]() $\mathcal {A}_{n,k,m}(Z)$.
$\mathcal {A}_{n,k,m}(Z)$.
Definition 3.3 Let ![]() $f,g\in \tilde {S_n}(-k,n-k)$ be two affine permutations. We say that
$f,g\in \tilde {S_n}(-k,n-k)$ be two affine permutations. We say that ![]() $f$ and
$f$ and ![]() $g$ are
$g$ are ![]() $Z$-compatible if the images
$Z$-compatible if the images ![]() $Z(\Pi ^{>0}_{k+f})$ and
$Z(\Pi ^{>0}_{k+f})$ and ![]() $Z(\Pi ^{>0}_{k+g})$ do not intersect. We say that
$Z(\Pi ^{>0}_{k+g})$ do not intersect. We say that ![]() $f$ and
$f$ and ![]() $g$ are
$g$ are ![]() $(n,k,m)$-compatible if they are
$(n,k,m)$-compatible if they are ![]() $Z$-compatible for any
$Z$-compatible for any ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$.
$Z\in \operatorname {Gr}_{>0}(k+m,n)$.
Definition 3.4 Let ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ be a collection of
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ be a collection of ![]() $Z$-admissible and pairwise
$Z$-admissible and pairwise ![]() $Z$-compatible affine permutations, and assume that
$Z$-compatible affine permutations, and assume that ![]() $\operatorname {inv}(f_s)=k\ell$ for
$\operatorname {inv}(f_s)=k\ell$ for ![]() $1\leq s\leq N$. We say that
$1\leq s\leq N$. We say that ![]() $f_1,\dots ,f_N$ form a
$f_1,\dots ,f_N$ form a ![]() $Z$-triangulation if the images
$Z$-triangulation if the images ![]() $Z(\Pi ^{>0}_{k+f_1}),\dots ,Z(\Pi ^{>0}_{k+f_N})$ form a dense subset of
$Z(\Pi ^{>0}_{k+f_1}),\dots ,Z(\Pi ^{>0}_{k+f_N})$ form a dense subset of ![]() $\mathcal {A}_{n,k,m}(Z)$. We say that
$\mathcal {A}_{n,k,m}(Z)$. We say that ![]() $f_1,\dots ,f_N$ form an
$f_1,\dots ,f_N$ form an ![]() $(n,k,m)$-triangulation if they form a
$(n,k,m)$-triangulation if they form a ![]() $Z$-triangulation for any
$Z$-triangulation for any ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$.
$Z\in \operatorname {Gr}_{>0}(k+m,n)$.
Thus by Lemma 3.2, if ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ form a
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ form a ![]() $Z$-triangulation for some
$Z$-triangulation for some ![]() $Z$ then they all must belong to
$Z$ then they all must belong to ![]() $\tilde {S_n}(-k,\ell )$. We are now ready to state our first main result.
$\tilde {S_n}(-k,\ell )$. We are now ready to state our first main result.
Theorem 3.5
(1) Let
 $f\in \tilde {S_n}(-k,\ell )$ be an affine permutation. Then
$f\in \tilde {S_n}(-k,\ell )$ be an affine permutation. Then  $f$ is
$f$ is  $(n,k,m)$-admissible if and only if
$(n,k,m)$-admissible if and only if  $f^{-1}\in \tilde {S_n}(-\ell ,k)$ is
$f^{-1}\in \tilde {S_n}(-\ell ,k)$ is  $(n,\ell ,m)$-admissible.
$(n,\ell ,m)$-admissible.(2) Let
 $f,g\in \tilde {S_n}(-k,\ell )$ be two affine permutations. Then
$f,g\in \tilde {S_n}(-k,\ell )$ be two affine permutations. Then  $f$ and
$f$ and  $g$ are
$g$ are  $(n,k,m)$-compatible if and only if
$(n,k,m)$-compatible if and only if  $f^{-1},g^{-1}\in \tilde {S_n}(-\ell ,k)$ are
$f^{-1},g^{-1}\in \tilde {S_n}(-\ell ,k)$ are  $(n,\ell ,m)$-compatible.
$(n,\ell ,m)$-compatible.(3) Let
 $f_1,\dots ,f_N\in \tilde {S_n}(-k,\ell )$ be a collection of affine permutations. Then they form an
$f_1,\dots ,f_N\in \tilde {S_n}(-k,\ell )$ be a collection of affine permutations. Then they form an  $(n,k,m)$-triangulation of the amplituhedron if and only if
$(n,k,m)$-triangulation of the amplituhedron if and only if  $f_1^{-1},\dots ,f_N^{-1}\in \tilde {S_n}(-\ell ,k)$ form an
$f_1^{-1},\dots ,f_N^{-1}\in \tilde {S_n}(-\ell ,k)$ form an  $(n,\ell ,m)$-triangulation of the amplituhedron.
$(n,\ell ,m)$-triangulation of the amplituhedron.
Using the properties of the stacked twist map, we give a simple proof of this theorem in § 4. In § 7, we define a more general notion of ![]() $Z$-subdivisions and give an analog of Theorem 3.5.
$Z$-subdivisions and give an analog of Theorem 3.5.
3.1 Motivation and further remarks
We discuss the relationship of Theorem 3.5 with some results present in the literature on amplituhedra.
Remark 3.6 For ![]() $k=1$, the amplituhedron
$k=1$, the amplituhedron ![]() $\mathcal {A}_{n,k,m}(Z)\subset \operatorname {Gr}(1,m+1)$ is just the cyclic polytope in the
$\mathcal {A}_{n,k,m}(Z)\subset \operatorname {Gr}(1,m+1)$ is just the cyclic polytope in the ![]() $m$-dimensional projective space. The combinatorics of its triangulationsFootnote 3 is well-understood, see e.g. [Reference RambauRam97, Reference Edelman, Rambau and ReinerERR00, Reference ThomasTho02, Reference Oppermann and ThomasOT12]. Therefore, in this case Theorem 3.5 describes explicitly the triangulations of the
$m$-dimensional projective space. The combinatorics of its triangulationsFootnote 3 is well-understood, see e.g. [Reference RambauRam97, Reference Edelman, Rambau and ReinerERR00, Reference ThomasTho02, Reference Oppermann and ThomasOT12]. Therefore, in this case Theorem 3.5 describes explicitly the triangulations of the ![]() $\ell =1$ amplituhedron, which has not yet been studied in the literature. We refer the reader to § 6 for an illustration.
$\ell =1$ amplituhedron, which has not yet been studied in the literature. We refer the reader to § 6 for an illustration.
Remark 3.7 From the point of view of physics, the most interesting case is ![]() $m=4$, which corresponds to computing tree level scattering amplitudes in the planar
$m=4$, which corresponds to computing tree level scattering amplitudes in the planar ![]() $N=4$ supersymmetric Yang–Mills theory. In particular, the terms in the BCFW recurrence introduced in [Reference Britto, Cachazo and FengBCF05, Reference Britto, Cachazo, Feng and WittenBCFW05] for computing these amplitudes correspond to a collection of affine permutations called the BCFW triangulation. (It is a conjecture that these affine permutations indeed form an
$N=4$ supersymmetric Yang–Mills theory. In particular, the terms in the BCFW recurrence introduced in [Reference Britto, Cachazo and FengBCF05, Reference Britto, Cachazo, Feng and WittenBCFW05] for computing these amplitudes correspond to a collection of affine permutations called the BCFW triangulation. (It is a conjecture that these affine permutations indeed form an ![]() $(n,k,m)$-triangulation of the amplituhedron.) We note that in this special
$(n,k,m)$-triangulation of the amplituhedron.) We note that in this special ![]() $m=4$ case, the map
$m=4$ case, the map ![]() $f\mapsto f^{-1}$ sends a BCFW triangulation for
$f\mapsto f^{-1}$ sends a BCFW triangulation for ![]() $(k,\ell )$ to a BCFW triangulation for
$(k,\ell )$ to a BCFW triangulation for ![]() $(\ell ,k)$. It amounts to switching the colors of the vertices in the corresponding plabic graphs in
$(\ell ,k)$. It amounts to switching the colors of the vertices in the corresponding plabic graphs in ![]() $\operatorname {Gr}(k+2,n)$ and
$\operatorname {Gr}(k+2,n)$ and ![]() $\operatorname {Gr}(\ell +2,n)$ (the indices are shifted by
$\operatorname {Gr}(\ell +2,n)$ (the indices are shifted by ![]() $2$ because of a transition from the momentum space to the momentum-twistor space). See [Reference Arkani-Hamed, Thomas and TrnkaATT18, § 11], [Reference Karp, Williams and ZhangKWZ17, Proposition 8.4], or § 13.5 for further discussion.
$2$ because of a transition from the momentum space to the momentum-twistor space). See [Reference Arkani-Hamed, Thomas and TrnkaATT18, § 11], [Reference Karp, Williams and ZhangKWZ17, Proposition 8.4], or § 13.5 for further discussion.
The following conjecture states that the notions of ![]() $Z$-admissibility,
$Z$-admissibility, ![]() $Z$-compatibility, and
$Z$-compatibility, and ![]() $Z$-triangulation do not depend on the choice of
$Z$-triangulation do not depend on the choice of ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$. It is widely believed to be true in the physics literature.
$Z\in \operatorname {Gr}_{>0}(k+m,n)$. It is widely believed to be true in the physics literature.
Conjecture 3.8 Fix some ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$.
$Z\in \operatorname {Gr}_{>0}(k+m,n)$.
(1) Let
 $f\in \tilde {S_n}(-k,n-k)$ be an affine permutation. Then
$f\in \tilde {S_n}(-k,n-k)$ be an affine permutation. Then  $f$ is
$f$ is  $Z$-admissible if and only if
$Z$-admissible if and only if  $f$ is
$f$ is  $(n,k,m)$-admissible.
$(n,k,m)$-admissible.(2) Let
 $f,g\in \tilde {S_n}(-k,n-k)$ be two affine permutations. Then
$f,g\in \tilde {S_n}(-k,n-k)$ be two affine permutations. Then  $f$ and
$f$ and  $g$ are
$g$ are  $Z$-compatible if and only if they are
$Z$-compatible if and only if they are  $(n,k,m)$-compatible.
$(n,k,m)$-compatible.(3) Let
 $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ be a collection of affine permutations. Then they form a
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ be a collection of affine permutations. Then they form a  $Z$-triangulation if and only if they form an
$Z$-triangulation if and only if they form an  $(n,k,m)$-triangulation.
$(n,k,m)$-triangulation.
Therefore, assuming Conjecture 3.8, the notion of, say, ![]() $Z$-compatibility does not depend on
$Z$-compatibility does not depend on ![]() $Z$, and thus gives rise to an interesting binary relation on the set
$Z$, and thus gives rise to an interesting binary relation on the set ![]() $\tilde {S_n}(-k,n-k)$.
$\tilde {S_n}(-k,n-k)$.
Let us now explain some motivation that led to Theorem 3.5. For integers ![]() $a,b,c\geq 1$, define
$a,b,c\geq 1$, define
 \[ M(a,b,c):=\prod_{p=1}^a\prod_{q=1}^b\prod_{r=1}^c \frac{p+q+r-1}{p+q+r-2} \]
\[ M(a,b,c):=\prod_{p=1}^a\prod_{q=1}^b\prod_{r=1}^c \frac{p+q+r-1}{p+q+r-2} \]
to be the number of plane partitions that fit into an ![]() $a\times b\times c$ box [Reference MacMahonMac04]. This expression is symmetric in
$a\times b\times c$ box [Reference MacMahonMac04]. This expression is symmetric in ![]() $a,b,c$. In [Reference Karp, Williams and ZhangKWZ17, Conjecture 8.1], the authors noted that in all cases where a (conjectural) triangulation of
$a,b,c$. In [Reference Karp, Williams and ZhangKWZ17, Conjecture 8.1], the authors noted that in all cases where a (conjectural) triangulation of ![]() $\mathcal {A}_{n,k,m}(Z)$ is known, it has precisely
$\mathcal {A}_{n,k,m}(Z)$ is known, it has precisely ![]() $M(k,\ell ,m/2)$ cells, and they conjectured that for all
$M(k,\ell ,m/2)$ cells, and they conjectured that for all ![]() $n,k,m$, there exists a triangulation of the amplituhedron with
$n,k,m$, there exists a triangulation of the amplituhedron with ![]() $M(k,\ell ,m/2)$ cells. For example, for
$M(k,\ell ,m/2)$ cells. For example, for ![]() $m=4$, the number of terms in the BCFW recurrence, which correspond to the cells in the conjectural BCFW triangulation of
$m=4$, the number of terms in the BCFW recurrence, which correspond to the cells in the conjectural BCFW triangulation of ![]() $\mathcal {A}_{n,k,m}(Z)$, equals
$\mathcal {A}_{n,k,m}(Z)$, equals
(a Narayana number), see [Reference Arkani-Hamed, Bourjaily, Cachazo, Goncharov, Postnikov and TrnkaABC16] [Equation (17.7)]. We generalize [Reference Karp, Williams and ZhangKWZ17, Conjecture 8.1] as follows.
Conjecture 3.9 For every triangulation ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ of
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ of ![]() $\mathcal {A}_{n,k,m}(Z)$ (where
$\mathcal {A}_{n,k,m}(Z)$ (where ![]() $m$ is even), the number
$m$ is even), the number ![]() $N$ of cells equals
$N$ of cells equals ![]() $M(k,\ell ,m/2)$.
$M(k,\ell ,m/2)$.
This conjecture holds for ![]() $k=1$ (see e.g. [Reference RambauRam97]), and therefore by Theorem 3.5 it holds for
$k=1$ (see e.g. [Reference RambauRam97]), and therefore by Theorem 3.5 it holds for ![]() $\ell =1$ as well. Additionally, we have experimentally verified it in the case
$\ell =1$ as well. Additionally, we have experimentally verified it in the case ![]() $k=\ell =m=2$,
$k=\ell =m=2$, ![]() $n=6$, where there are
$n=6$, where there are ![]() $120$ triangulations of the amplituhedron, and each of them has size
$120$ triangulations of the amplituhedron, and each of them has size ![]() $M(2,2,1)=6$. We discuss this example in more detail in § 13.4. See also [Reference Karp, Williams and ZhangKWZ17, § 8] for a list of other cases where Conjecture 3.9 holds in a weaker form.
$M(2,2,1)=6$. We discuss this example in more detail in § 13.4. See also [Reference Karp, Williams and ZhangKWZ17, § 8] for a list of other cases where Conjecture 3.9 holds in a weaker form.
Remark 3.10 In [Reference Karp, Williams and ZhangKWZ17, Remark 8.2], a similar conjecture is given for odd values of ![]() $m$. One could generalize this conjecture as follows: for odd
$m$. One could generalize this conjecture as follows: for odd ![]() $m$, the maximal number of cells in a triangulation of the amplituhedron is equal to
$m$, the maximal number of cells in a triangulation of the amplituhedron is equal to ![]() $M(k,\ell ,({m+1})/2)$. This conjecture remains open, but we note that the result of Theorem 3.5 does not hold for odd
$M(k,\ell ,({m+1})/2)$. This conjecture remains open, but we note that the result of Theorem 3.5 does not hold for odd ![]() $m$, as one can easily observe already in the case
$m$, as one can easily observe already in the case ![]() $k=1$,
$k=1$, ![]() $\ell =2$,
$\ell =2$, ![]() $m=1$,
$m=1$, ![]() $n=4$. In this case, the maximal number of cells in a triangulation is indeed
$n=4$. In this case, the maximal number of cells in a triangulation is indeed ![]() $M(1,2,1)=3$ and is invariant under switching
$M(1,2,1)=3$ and is invariant under switching ![]() $k$ and
$k$ and ![]() $\ell$, however, replacing each affine permutation with its inverse does not take
$\ell$, however, replacing each affine permutation with its inverse does not take ![]() $(n,k,m)$-triangulations to
$(n,k,m)$-triangulations to ![]() $(n,\ell ,m)$-triangulations.
$(n,\ell ,m)$-triangulations.
Remark 3.11 Theorem 3.5 provides partial progress to answering [Reference Karp, Williams and ZhangKWZ17, Question 8.5]: assuming that for each ![]() $n$,
$n$, ![]() $k$, and even
$k$, and even ![]() $m$ there exists an
$m$ there exists an ![]() $(n,k,m)$-triangulation of the amplituhedron, [Reference Karp, Williams and ZhangKWZ17, Question 8.5] has a positive answer.
$(n,k,m)$-triangulation of the amplituhedron, [Reference Karp, Williams and ZhangKWZ17, Question 8.5] has a positive answer.
Remark 3.12 For ![]() $m = 4$, it was already observed in [Reference Golden, Goncharov, Spradlin, Vergu and VolovichGGS+14, Reference Arkani-Hamed, Thomas and TrnkaATT18] that the twist map of
$m = 4$, it was already observed in [Reference Golden, Goncharov, Spradlin, Vergu and VolovichGGS+14, Reference Arkani-Hamed, Thomas and TrnkaATT18] that the twist map of ![]() $\operatorname {Gr}(4,n)$ is related to the parity duality of scattering amplitudes. However, without the stacked twist map, the remarkable combinatorics and geometry of triangulations is hidden.
$\operatorname {Gr}(4,n)$ is related to the parity duality of scattering amplitudes. However, without the stacked twist map, the remarkable combinatorics and geometry of triangulations is hidden.
4. The stacked twist map
In this section, we explain a construction that lies at the core of the proof of Theorem 3.5. It is based on the twist map of Marsh and Scott [Reference Marsh and ScottMS16]. For our purposes, it is more convenient to use the version of the twist map from [Reference Muller and SpeyerMS17], which differs from the one in [Reference Marsh and ScottMS16] by a column rescaling. See [Reference Muller and SpeyerMS17, Remark 6.3] for details.
Let ![]() $k,\ell ,m,n$ be as in the previous section, that is, they are all nonnegative integers such that
$k,\ell ,m,n$ be as in the previous section, that is, they are all nonnegative integers such that ![]() $m$ is even and
$m$ is even and ![]() $n=k+\ell +m$. Let
$n=k+\ell +m$. Let ![]() $V$ be a
$V$ be a ![]() $k\times n$ matrix and
$k\times n$ matrix and ![]() $W$ be an
$W$ be an ![]() $\ell \times n$ matrix. For
$\ell \times n$ matrix. For ![]() $j=1,2,\dots ,n$, define
$j=1,2,\dots ,n$, define ![]() $V(j)\in \mathbb {R}^k$ (respectively,
$V(j)\in \mathbb {R}^k$ (respectively, ![]() $W(j)\in \mathbb {R}^\ell$) to be the
$W(j)\in \mathbb {R}^\ell$) to be the ![]() $j$th column of
$j$th column of ![]() $V$ (respectively,
$V$ (respectively, ![]() $W$). We extend this to any
$W$). We extend this to any ![]() $j\in \mathbb {Z}$ by the condition that
$j\in \mathbb {Z}$ by the condition that ![]() $V(j+n)=(-1)^{k-1}V(j)$ and
$V(j+n)=(-1)^{k-1}V(j)$ and ![]() $W(j+n)=(-1)^{k-1}W(j)$. Define
$W(j+n)=(-1)^{k-1}W(j)$. Define
to be a ![]() $(k+\ell )\times n$ block matrix obtained by stacking
$(k+\ell )\times n$ block matrix obtained by stacking ![]() $V$ on top of
$V$ on top of ![]() $W$. That is, the
$W$. That is, the ![]() $j$th column
$j$th column ![]() $U(j)$ of
$U(j)$ of ![]() $U$ equals
$U$ equals ![]() $(V(j),W(j))\in \mathbb {R}^{k+\ell }$, and thus we also have
$(V(j),W(j))\in \mathbb {R}^{k+\ell }$, and thus we also have ![]() $U(j+n)=(-1)^{k-1}U(j)$ for all
$U(j+n)=(-1)^{k-1}U(j)$ for all ![]() $j\in \mathbb {Z}$.
$j\in \mathbb {Z}$.
Definition 4.1 Given a ![]() $(k+\ell )\times n$ matrix
$(k+\ell )\times n$ matrix ![]() $U$, we write
$U$, we write ![]() $U\in \operatorname {Mat}^\circ (k+\ell ,n)$ if for all
$U\in \operatorname {Mat}^\circ (k+\ell ,n)$ if for all ![]() $j\in \mathbb {Z}$, the vectors
$j\in \mathbb {Z}$, the vectors ![]() $U(j-\ell ),U(j-\ell +1),\dots ,U(j+k-1)$ form a basis of
$U(j-\ell ),U(j-\ell +1),\dots ,U(j+k-1)$ form a basis of ![]() $\mathbb {R}^{k+\ell }$.
$\mathbb {R}^{k+\ell }$.
We now define a map ![]() $\tau :\operatorname {Mat}^\circ (k+\ell ,n)\to \operatorname {Mat}^\circ (k+\ell ,n)$ sending a matrix
$\tau :\operatorname {Mat}^\circ (k+\ell ,n)\to \operatorname {Mat}^\circ (k+\ell ,n)$ sending a matrix ![]() $U$ to a matrix
$U$ to a matrix ![]() ${\tilde {U}}$ with columns
${\tilde {U}}$ with columns ![]() ${\tilde U}(j),j\in \mathbb {Z}$. Up to sign changes and a cyclic shift, this map coincides with the right twist of [Reference Muller and SpeyerMS17], see (10.1). For each
${\tilde U}(j),j\in \mathbb {Z}$. Up to sign changes and a cyclic shift, this map coincides with the right twist of [Reference Muller and SpeyerMS17], see (10.1). For each ![]() $j\in \mathbb {Z}$, define a vector
$j\in \mathbb {Z}$, define a vector ![]() ${\tilde U}(j)\in \mathbb {R}^{k+\ell }$ by the following conditions:
${\tilde U}(j)\in \mathbb {R}^{k+\ell }$ by the following conditions:
where ![]() $\langle \cdot ,\cdot \rangle$ denotes the standard inner product on
$\langle \cdot ,\cdot \rangle$ denotes the standard inner product on ![]() $\mathbb {R}^{k+\ell }$. Since the vectors
$\mathbb {R}^{k+\ell }$. Since the vectors ![]() $U(j-\ell ),U(j-\ell +1),\dots ,U(j+k-1)$ form a basis, the above conditions determine
$U(j-\ell ),U(j-\ell +1),\dots ,U(j+k-1)$ form a basis, the above conditions determine ![]() ${\tilde U}(j)$ uniquely. It is also not hard to see directly that
${\tilde U}(j)$ uniquely. It is also not hard to see directly that ![]() ${\tilde {U}}\in \operatorname {Mat}^\circ (k+\ell ,n)$ (alternatively, see (10.3)). Moreover, we have
${\tilde {U}}\in \operatorname {Mat}^\circ (k+\ell ,n)$ (alternatively, see (10.3)). Moreover, we have ![]() ${\tilde U}(j+n)=(-1)^{n+k-1}{\tilde U}(j)=(-1)^{\ell -1}{\tilde U}(j)$, because
${\tilde U}(j+n)=(-1)^{n+k-1}{\tilde U}(j)=(-1)^{\ell -1}{\tilde U}(j)$, because ![]() $m$ is assumed to be even. This defines
$m$ is assumed to be even. This defines ![]() ${\tilde {U}}=\tau (U)\in \operatorname {Mat}^\circ (k+\ell ,n)$. Muller and Speyer also define a left twist
${\tilde {U}}=\tau (U)\in \operatorname {Mat}^\circ (k+\ell ,n)$. Muller and Speyer also define a left twist ![]() $\stackrel {\leftarrow }{\tau }:\operatorname {Mat}^\circ (k+\ell ,n)\to \operatorname {Mat}^\circ (k+\ell ,n)$. They show the following.
$\stackrel {\leftarrow }{\tau }:\operatorname {Mat}^\circ (k+\ell ,n)\to \operatorname {Mat}^\circ (k+\ell ,n)$. They show the following.
Theorem 4.2 [MS17, Theorem 6.7] The left and right twists are inverse diffeomorphisms of ![]() $\operatorname {Mat}^\circ (k+\ell ,n)$.
$\operatorname {Mat}^\circ (k+\ell ,n)$.
Finally, let ![]() ${\tilde {W}}$ (respectively,
${\tilde {W}}$ (respectively, ![]() ${\tilde V}$) be the
${\tilde V}$) be the ![]() $k\times n$ matrix (respectively, the
$k\times n$ matrix (respectively, the ![]() $\ell \times n$ matrix) such that
$\ell \times n$ matrix) such that ![]() ${\tilde {U}}=\operatorname {stack}({\tilde {W}},{\tilde V})$. In other words, we let the
${\tilde {U}}=\operatorname {stack}({\tilde {W}},{\tilde V})$. In other words, we let the ![]() $j$th column
$j$th column ![]() ${\tilde W}(j)$ of
${\tilde W}(j)$ of ![]() ${\tilde {W}}$ and
${\tilde {W}}$ and ![]() ${\tilde V}(j)$ of
${\tilde V}(j)$ of ![]() ${\tilde V}$ be defined so that
${\tilde V}$ be defined so that ![]() ${\tilde U}(j)=({\tilde W}(j),{\tilde V}(j))$.
${\tilde U}(j)=({\tilde W}(j),{\tilde V}(j))$.
Definition 4.3 Given a ![]() $k\times n$ matrix
$k\times n$ matrix ![]() $V$ and an
$V$ and an ![]() $\ell \times n$ matrix
$\ell \times n$ matrix ![]() $W$ such that
$W$ such that ![]() $\operatorname {stack}(V,W)\in \operatorname {Mat}^\circ (k+\ell ,n)$, we denote
$\operatorname {stack}(V,W)\in \operatorname {Mat}^\circ (k+\ell ,n)$, we denote ![]() $\theta (V,W):=({\tilde {W}},{\tilde V})$, where
$\theta (V,W):=({\tilde {W}},{\tilde V})$, where ![]() ${\tilde {W}}$ and
${\tilde {W}}$ and ![]() ${\tilde V}$ are defined above. The map
${\tilde V}$ are defined above. The map ![]() $\theta$ is called the stacked twist map.
$\theta$ is called the stacked twist map.
The relationship between the maps ![]() $\tau$,
$\tau$, ![]() $\operatorname {stack}$, and
$\operatorname {stack}$, and ![]() $\theta$ is shown in (
$\theta$ is shown in (
). Dashed (respectively, solid) arrows denote rational (respectively, regular) maps.

Our first goal is to view ![]() $\theta$ as a map on pairs of subspaces rather than pairs of matrices. Thus we would like to treat
$\theta$ as a map on pairs of subspaces rather than pairs of matrices. Thus we would like to treat ![]() $V$ and
$V$ and ![]() $W$ not as matrices but as their row spans. The following result will be deduced as a simple consequence of Lemma 10.1.
$W$ not as matrices but as their row spans. The following result will be deduced as a simple consequence of Lemma 10.1.
Lemma 4.4 The map ![]() $\theta$ descends to a rational map
$\theta$ descends to a rational map
It turns out that ![]() $\theta$ has remarkable properties when restricted to the totally nonnegative Grassmannian. For each
$\theta$ has remarkable properties when restricted to the totally nonnegative Grassmannian. For each ![]() $0\leq m\leq n-k$, define a subset
$0\leq m\leq n-k$, define a subset ![]() $\operatorname {Gr}_{\ge m}(k,n)\subset \operatorname {Gr}_{\ge 0}(k,n)$ by
$\operatorname {Gr}_{\ge m}(k,n)\subset \operatorname {Gr}_{\ge 0}(k,n)$ by
Comparing this to (2.1), we see that setting ![]() $m=0$ indeed recovers
$m=0$ indeed recovers ![]() $\operatorname {Gr}_{\ge 0}(k,n)$. More generally, we have
$\operatorname {Gr}_{\ge 0}(k,n)$. More generally, we have
As we will see in Lemma 10.3, the set ![]() $\operatorname {Gr}_{\ge m}(k,n)$ can be alternatively described as follows.
$\operatorname {Gr}_{\ge m}(k,n)$ can be alternatively described as follows.
Proposition 4.5 For ![]() $0\leq m\leq n-k$ and
$0\leq m\leq n-k$ and ![]() $\ell =n-k-m$, we have
$\ell =n-k-m$, we have
Here ![]() $[V(j-\ell )|V(j-\ell +1)|\dots |V(j+k-1)]$ denotes the
$[V(j-\ell )|V(j-\ell +1)|\dots |V(j+k-1)]$ denotes the ![]() $k\times (k+\ell )$ matrix with columns
$k\times (k+\ell )$ matrix with columns ![]() $V(j-\ell ),\dots ,V(j+k-1)$, and
$V(j-\ell ),\dots ,V(j+k-1)$, and ![]() ${\mathrm {rk}}$ denotes its rank. We set
${\mathrm {rk}}$ denotes its rank. We set
Let us also define
Here for ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$ we denote by
$Z\in \operatorname {Gr}_{>0}(k+m,n)$ we denote by ![]() $W:=Z^\perp \in \operatorname {Gr}(\ell ,n)$ the subspace orthogonal to
$W:=Z^\perp \in \operatorname {Gr}(\ell ,n)$ the subspace orthogonal to ![]() $Z$.
$Z$.
Remark 4.6 The sets ![]() $\operatorname {Gr}_{>0}^\perp (k+m,n)$ and
$\operatorname {Gr}_{>0}^\perp (k+m,n)$ and ![]() $\operatorname {Gr}_{>0}(\ell ,n)$ are related as follows. Define a map
$\operatorname {Gr}_{>0}(\ell ,n)$ are related as follows. Define a map ![]() $\operatorname {alt}:\operatorname {Gr}(\ell ,n)\to \operatorname {Gr}(\ell ,n)$ sending a matrix
$\operatorname {alt}:\operatorname {Gr}(\ell ,n)\to \operatorname {Gr}(\ell ,n)$ sending a matrix ![]() $W\in \operatorname {Gr}(\ell ,n)$ with columns
$W\in \operatorname {Gr}(\ell ,n)$ with columns ![]() $W(j), 1\leq j\leq n$ to a matrix
$W(j), 1\leq j\leq n$ to a matrix ![]() $W':=\operatorname {alt}(W)$ with columns
$W':=\operatorname {alt}(W)$ with columns ![]() $W'(j)=(-1)^{j-1}W(j)$. It turns out
$W'(j)=(-1)^{j-1}W(j)$. It turns out ![]() $\operatorname {alt}$ is a diffeomorphism between
$\operatorname {alt}$ is a diffeomorphism between ![]() $\operatorname {Gr}_{>0}(\ell ,n)$ and
$\operatorname {Gr}_{>0}(\ell ,n)$ and ![]() $\operatorname {Gr}_{>0}^\perp (k+m,n)$. In fact, for any set
$\operatorname {Gr}_{>0}^\perp (k+m,n)$. In fact, for any set ![]() $I\subset [n]$ of size
$I\subset [n]$ of size ![]() $\ell$, we have
$\ell$, we have
where ![]() $Z:=W^\perp$. See [Reference Karp and WilliamsKW17, Lemma 3.3] and references therein.
$Z:=W^\perp$. See [Reference Karp and WilliamsKW17, Lemma 3.3] and references therein.
The following result is the main ingredient of the proof of Theorem 3.5.
Theorem 4.7 Let ![]() $V\in \operatorname {Gr}_{\ge m}(k,n)$ and
$V\in \operatorname {Gr}_{\ge m}(k,n)$ and ![]() $W\in \operatorname {Gr}_{>0}^\perp (k+m,n)$.
$W\in \operatorname {Gr}_{>0}^\perp (k+m,n)$.
(i) We have
 $\operatorname {stack}(V,W)\in \operatorname {Mat}^\circ (k+\ell ,n)$, and thus
$\operatorname {stack}(V,W)\in \operatorname {Mat}^\circ (k+\ell ,n)$, and thus  $\theta (V,W)=({\tilde {W}},{\tilde V})$ is well-defined.
$\theta (V,W)=({\tilde {W}},{\tilde V})$ is well-defined.(ii) We have
 ${\tilde {W}}\in \operatorname {Gr}_{>0}^\perp (\ell +m,n)$ and
${\tilde {W}}\in \operatorname {Gr}_{>0}^\perp (\ell +m,n)$ and  ${\tilde V}\in \operatorname {Gr}_{\ge m}(\ell ,n)$.
${\tilde V}\in \operatorname {Gr}_{\ge m}(\ell ,n)$.(iii) Let
 $f\in \tilde {S_n}(-k,\ell )$ be the unique affine permutation such that
$f\in \tilde {S_n}(-k,\ell )$ be the unique affine permutation such that  $V\in \Pi ^{>0}_{k+f}$. Then
$V\in \Pi ^{>0}_{k+f}$. Then  ${\tilde V}\in \Pi ^{>0}_{\ell +f^{-1}}$.
${\tilde V}\in \Pi ^{>0}_{\ell +f^{-1}}$.
By Theorem 4.2, we conclude that ![]() $\theta$ restricts to a homeomorphism
$\theta$ restricts to a homeomorphism
and for each ![]() $f\in \tilde {S_n}(-k,\ell )$,
$f\in \tilde {S_n}(-k,\ell )$, ![]() $\theta$ restricts to a diffeomorphism
$\theta$ restricts to a diffeomorphism
Finally, we note that ![]() $\theta$ ‘preserves the fibers’ of the map
$\theta$ ‘preserves the fibers’ of the map ![]() $Z:\operatorname {Gr}_{\ge m}(k,n)\to \mathcal {A}_{n,k,\ge m}(Z)$. More precisely, given
$Z:\operatorname {Gr}_{\ge m}(k,n)\to \mathcal {A}_{n,k,\ge m}(Z)$. More precisely, given ![]() $V\in \operatorname {Gr}_{\ge m}(k,n)$, let us define a fiber
$V\in \operatorname {Gr}_{\ge m}(k,n)$, let us define a fiber ![]() $\operatorname {F}(V,Z)$ of
$\operatorname {F}(V,Z)$ of ![]() $Z$ by
$Z$ by
As we will see later in Proposition 9.2, for ![]() $V\in \operatorname {Gr}_{\ge m}(k,n)$ we have
$V\in \operatorname {Gr}_{\ge m}(k,n)$ we have ![]() $\operatorname {F}(V,Z)\subset \operatorname {Gr}_{\ge m}(k,n)$.
$\operatorname {F}(V,Z)\subset \operatorname {Gr}_{\ge m}(k,n)$.
Proposition 4.8 Let ![]() $V\in \operatorname {Gr}_{\ge m}(k,n)$,
$V\in \operatorname {Gr}_{\ge m}(k,n)$, ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$,
$Z\in \operatorname {Gr}_{>0}(k+m,n)$, ![]() $W:=Z^\perp \in \operatorname {Gr}_{>0}^\perp (k+m,n)$,
$W:=Z^\perp \in \operatorname {Gr}_{>0}^\perp (k+m,n)$, ![]() $\theta (V,W)=({\tilde {W}},{\tilde V})$, and
$\theta (V,W)=({\tilde {W}},{\tilde V})$, and ![]() ${\tilde Z}:={\tilde {W}}^\perp \in \operatorname {Gr}_{>0}(\ell +m,n)$. Then for any
${\tilde Z}:={\tilde {W}}^\perp \in \operatorname {Gr}_{>0}(\ell +m,n)$. Then for any ![]() $V'\in \operatorname {F}(V,Z)$, we have
$V'\in \operatorname {F}(V,Z)$, we have ![]() $\theta (V',W)=({\tilde {W}},{\tilde V}')$ for some
$\theta (V',W)=({\tilde {W}},{\tilde V}')$ for some ![]() ${\tilde V}'\in \operatorname {F}({\tilde V},{\tilde Z})$. The map
${\tilde V}'\in \operatorname {F}({\tilde V},{\tilde Z})$. The map ![]() $V'\mapsto {\tilde V}'$ is a homeomorphism between
$V'\mapsto {\tilde V}'$ is a homeomorphism between ![]() $\operatorname {F}(V,Z)\subset \operatorname {Gr}_{\ge m}(k,n)$ and
$\operatorname {F}(V,Z)\subset \operatorname {Gr}_{\ge m}(k,n)$ and ![]() $\operatorname {F}({\tilde V},{\tilde Z})\subset \operatorname {Gr}_{\ge m}(\ell ,n)$.
$\operatorname {F}({\tilde V},{\tilde Z})\subset \operatorname {Gr}_{\ge m}(\ell ,n)$.
We postpone the proof of Theorem 4.7 and Proposition 4.8 until § 10. Let us now give a simple proof of Theorem 3.5 using these results.
Proof of Theorem 3.5 Let ![]() $f\in \tilde {S_n}(-k,\ell )$ be an affine permutation. Then
$f\in \tilde {S_n}(-k,\ell )$ be an affine permutation. Then ![]() $f$ is
$f$ is ![]() $(n,k,m)$-admissible if and only if
$(n,k,m)$-admissible if and only if ![]() $\Pi ^{>0}_{k+f}\cap \operatorname {F}(V,Z)$ contains at most one point for each
$\Pi ^{>0}_{k+f}\cap \operatorname {F}(V,Z)$ contains at most one point for each ![]() $V\in \operatorname {Gr}_{\ge m}(k,n)$ and
$V\in \operatorname {Gr}_{\ge m}(k,n)$ and ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$. By Proposition 4.8, this fiber
$Z\in \operatorname {Gr}_{>0}(k+m,n)$. By Proposition 4.8, this fiber ![]() $\operatorname {F}(V,Z)$ maps bijectively to a fiber
$\operatorname {F}(V,Z)$ maps bijectively to a fiber ![]() $\operatorname {F}({\tilde V},{\tilde Z})$ for some
$\operatorname {F}({\tilde V},{\tilde Z})$ for some ![]() ${\tilde Z}\in \operatorname {Gr}_{>0}(\ell +m,n)$ and
${\tilde Z}\in \operatorname {Gr}_{>0}(\ell +m,n)$ and ![]() ${\tilde V}\in \operatorname {Gr}_{\ge m}(\ell ,n)$. Moreover, the points of
${\tilde V}\in \operatorname {Gr}_{\ge m}(\ell ,n)$. Moreover, the points of ![]() $\Pi ^{>0}_{k+f}\cap \operatorname {F}(V,Z)$ map bijectively to the points of
$\Pi ^{>0}_{k+f}\cap \operatorname {F}(V,Z)$ map bijectively to the points of ![]() $\Pi ^{>0}_{\ell +f^{-1}} \cap \operatorname {F}({\tilde V},{\tilde Z})$ by Theorem 4.7, part (iii). This proves Theorem 3.5, part (1).
$\Pi ^{>0}_{\ell +f^{-1}} \cap \operatorname {F}({\tilde V},{\tilde Z})$ by Theorem 4.7, part (iii). This proves Theorem 3.5, part (1).
Similarly, if ![]() $f,g\in \tilde {S_n}(-k,\ell )$ are two affine permutations then they are
$f,g\in \tilde {S_n}(-k,\ell )$ are two affine permutations then they are ![]() $(n,k,m)$-compatible if and only if either one of
$(n,k,m)$-compatible if and only if either one of ![]() $\Pi ^{>0}_{k+f}\cap \operatorname {F}(V,Z)$ or
$\Pi ^{>0}_{k+f}\cap \operatorname {F}(V,Z)$ or ![]() $\Pi ^{>0}_{k+g}\cap \operatorname {F}(V,Z)$ is empty for each
$\Pi ^{>0}_{k+g}\cap \operatorname {F}(V,Z)$ is empty for each ![]() $V\in \operatorname {Gr}_{\ge m}(k,n)$ and
$V\in \operatorname {Gr}_{\ge m}(k,n)$ and ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$. Again by Proposition 4.8 and Theorem 4.7, part (iii), this is equivalent to saying that either one of
$Z\in \operatorname {Gr}_{>0}(k+m,n)$. Again by Proposition 4.8 and Theorem 4.7, part (iii), this is equivalent to saying that either one of ![]() $\Pi ^{>0}_{\ell +f^{-1}}\cap \operatorname {F}({\tilde V},{\tilde Z})$ or
$\Pi ^{>0}_{\ell +f^{-1}}\cap \operatorname {F}({\tilde V},{\tilde Z})$ or ![]() $\Pi ^{>0}_{\ell +g^{-1}}\cap \operatorname {F}({\tilde V},{\tilde Z})$ is empty, showing Theorem 3.5, part (2).
$\Pi ^{>0}_{\ell +g^{-1}}\cap \operatorname {F}({\tilde V},{\tilde Z})$ is empty, showing Theorem 3.5, part (2).
Finally, let ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,\ell )$ be a collection of
$f_1,\dots ,f_N\in \tilde {S_n}(-k,\ell )$ be a collection of ![]() $(n,k,m)$-admissible and pairwise
$(n,k,m)$-admissible and pairwise ![]() $(n,k,m)$-compatible affine permutations. By the previous two parts, we see that
$(n,k,m)$-compatible affine permutations. By the previous two parts, we see that ![]() $f_1^{-1},\dots ,f_N^{-1}\in \tilde {S_n}(-\ell ,k)$ are
$f_1^{-1},\dots ,f_N^{-1}\in \tilde {S_n}(-\ell ,k)$ are ![]() $(n,\ell ,m)$-admissible and pairwise
$(n,\ell ,m)$-admissible and pairwise ![]() $(n,\ell ,m)$-compatible. Suppose now that
$(n,\ell ,m)$-compatible. Suppose now that ![]() $f_1,\dots ,f_N$ form an
$f_1,\dots ,f_N$ form an ![]() $(n,k,m)$-triangulation. This means that the union of the images
$(n,k,m)$-triangulation. This means that the union of the images ![]() $Z(\Pi ^{\ge 0}_{k+f_1})$,
$Z(\Pi ^{\ge 0}_{k+f_1})$, ![]() $\dots$,
$\dots$, ![]() $Z(\Pi ^{\ge 0}_{k+f_N})$ is equal to
$Z(\Pi ^{\ge 0}_{k+f_N})$ is equal to ![]() $\mathcal {A}_{n,k,m}(Z)$ for each
$\mathcal {A}_{n,k,m}(Z)$ for each ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$. In particular, this implies that for all
$Z\in \operatorname {Gr}_{>0}(k+m,n)$. In particular, this implies that for all ![]() $V\in \operatorname {Gr}_{\ge m}(k,n)$ and
$V\in \operatorname {Gr}_{\ge m}(k,n)$ and ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$,
$Z\in \operatorname {Gr}_{>0}(k+m,n)$, ![]() $\operatorname {F}(V,Z)$ contains a point
$\operatorname {F}(V,Z)$ contains a point ![]() $V'$ of
$V'$ of ![]() $\Pi ^{\ge 0}_{k+f_s}$ for some
$\Pi ^{\ge 0}_{k+f_s}$ for some ![]() $1\leq s\leq N$. Since
$1\leq s\leq N$. Since ![]() $V$ belongs to
$V$ belongs to ![]() $\operatorname {Gr}_{\ge m}(k,n)$, there is a unique affine permutation
$\operatorname {Gr}_{\ge m}(k,n)$, there is a unique affine permutation ![]() $f\in \tilde {S_n}(-k,\ell )$ such that
$f\in \tilde {S_n}(-k,\ell )$ such that ![]() $V'\in \Pi ^{>0}_{k+f}\subset \Pi ^{\ge 0}_{k+f_s}$. As we will see in (7.2) below, this implies
$V'\in \Pi ^{>0}_{k+f}\subset \Pi ^{\ge 0}_{k+f_s}$. As we will see in (7.2) below, this implies ![]() $\Pi ^{>0}_{\ell +f^{-1}}\subset \Pi ^{\ge 0}_{\ell +f_s^{-1}}$. Applying Theorem 4.7, part (iii) together with Proposition 4.8, we get that for all
$\Pi ^{>0}_{\ell +f^{-1}}\subset \Pi ^{\ge 0}_{\ell +f_s^{-1}}$. Applying Theorem 4.7, part (iii) together with Proposition 4.8, we get that for all ![]() ${\tilde V}\in \operatorname {Gr}_{\ge m}(\ell ,n)$ and
${\tilde V}\in \operatorname {Gr}_{\ge m}(\ell ,n)$ and ![]() ${\tilde Z}\in \operatorname {Gr}_{>0}(\ell +m,n)$,
${\tilde Z}\in \operatorname {Gr}_{>0}(\ell +m,n)$, ![]() $\operatorname {F}({\tilde V},{\tilde Z})$ contains a point
$\operatorname {F}({\tilde V},{\tilde Z})$ contains a point ![]() ${\tilde V}'\in \Pi ^{>0}_{\ell +f^{-1}}\subset \Pi ^{\ge 0}_{\ell +f_s^{-1}}$ for some
${\tilde V}'\in \Pi ^{>0}_{\ell +f^{-1}}\subset \Pi ^{\ge 0}_{\ell +f_s^{-1}}$ for some ![]() $1\leq s\leq N$. Thus the union of the images
$1\leq s\leq N$. Thus the union of the images ![]() ${\tilde Z}(\Pi ^{\ge 0}_{\ell +f_1^{-1}}),\dots ,{\tilde Z}(\Pi ^{\ge 0}_{\ell +f_N^{-1}})$ contains
${\tilde Z}(\Pi ^{\ge 0}_{\ell +f_1^{-1}}),\dots ,{\tilde Z}(\Pi ^{\ge 0}_{\ell +f_N^{-1}})$ contains ![]() $\mathcal {A}_{n,\ell ,\ge m}({\tilde Z})$. Since this union is closed, it must contain the closure of
$\mathcal {A}_{n,\ell ,\ge m}({\tilde Z})$. Since this union is closed, it must contain the closure of ![]() $\mathcal {A}_{n,\ell ,\ge m}({\tilde Z})$, which is clearly equal to
$\mathcal {A}_{n,\ell ,\ge m}({\tilde Z})$, which is clearly equal to ![]() $\mathcal {A}_{n,\ell ,m}(Z)$ (see also Proposition 9.1), finishing the proof of Theorem 3.5, part (3).
$\mathcal {A}_{n,\ell ,m}(Z)$ (see also Proposition 9.1), finishing the proof of Theorem 3.5, part (3).
5. The canonical form
In this section, we give an accessible introduction to the canonical form on the Grassmannian and explain its relationship with the stacked twist map.
5.1 The canonical form for the top cell
The Grassmannian ![]() $\operatorname {Gr}(k,n)$ is a
$\operatorname {Gr}(k,n)$ is a ![]() $k(n-k)$-dimensional manifold. It can be covered by various coordinate charts. For example, one can represent any generic element
$k(n-k)$-dimensional manifold. It can be covered by various coordinate charts. For example, one can represent any generic element ![]() $X\in \operatorname {Gr}(k,n)$ as the row span of a
$X\in \operatorname {Gr}(k,n)$ as the row span of a ![]() $k\times n$ block matrix
$k\times n$ block matrix ![]() $[\operatorname {Id}_k\mid A]$ for a unique
$[\operatorname {Id}_k\mid A]$ for a unique ![]() $k\times (n-k)$ matrix
$k\times (n-k)$ matrix ![]() $A$. Here
$A$. Here ![]() $\operatorname {Id}_k$ denotes the
$\operatorname {Id}_k$ denotes the ![]() $k\times k$ identity matrix. Alternatively, any generic
$k\times k$ identity matrix. Alternatively, any generic ![]() $X$ is determined by its Plücker coordinates lying in a cluster
$X$ is determined by its Plücker coordinates lying in a cluster ![]() $\{\Delta _J\mid J\in \mathcal {C}\}$ (see [Reference Fomin and ZelevinskyFZ02, Reference ScottSco06] and Definition 11.3), where
$\{\Delta _J\mid J\in \mathcal {C}\}$ (see [Reference Fomin and ZelevinskyFZ02, Reference ScottSco06] and Definition 11.3), where ![]() $\mathcal {C}$ is a collection of
$\mathcal {C}$ is a collection of ![]() $k(n-k)+1$ subsets of
$k(n-k)+1$ subsets of ![]() $[n]$, each of size
$[n]$, each of size ![]() $k$, satisfying certain properties. Here we view
$k$, satisfying certain properties. Here we view ![]() $\{\Delta _J\mid J\in \mathcal {C}\}$ as an element of the
$\{\Delta _J\mid J\in \mathcal {C}\}$ as an element of the ![]() $k(n-k)$-dimensional projective space. There is a (rational) differential
$k(n-k)$-dimensional projective space. There is a (rational) differential ![]() $k(n-k)$-form
$k(n-k)$-form ![]() $\omega _{k,n}$ on
$\omega _{k,n}$ on ![]() $\operatorname {Gr}(k,n)$ with remarkable properties called the canonical form. Before we give its definition, we note that
$\operatorname {Gr}(k,n)$ with remarkable properties called the canonical form. Before we give its definition, we note that ![]() $\omega _{k,n}$ is a rational top form (i.e. an
$\omega _{k,n}$ is a rational top form (i.e. an ![]() $r$-form on an
$r$-form on an ![]() $r$-dimensional manifold), and on the chart
$r$-dimensional manifold), and on the chart ![]() $[\operatorname {Id}_k\mid A]$ it can therefore be written as
$[\operatorname {Id}_k\mid A]$ it can therefore be written as ![]() $f(A)\,d^{k\times (n-k)}(A)$, where
$f(A)\,d^{k\times (n-k)}(A)$, where ![]() $f(A)$ is some rational function of the entries of
$f(A)$ is some rational function of the entries of ![]() $A$, and
$A$, and
Thus defining ![]() $\omega _{k,n}$ amounts to giving a formula for
$\omega _{k,n}$ amounts to giving a formula for ![]() $f(A)$. For
$f(A)$. For ![]() $X\in \operatorname {Gr}(k,n)$, define
$X\in \operatorname {Gr}(k,n)$, define
 \[ \Delta_{k}^{\operatorname{circ}}(X):=\prod_{i=1}^n \Delta_{\{i,i+1,\dots,i+k-1\}}(X) \]
\[ \Delta_{k}^{\operatorname{circ}}(X):=\prod_{i=1}^n \Delta_{\{i,i+1,\dots,i+k-1\}}(X) \]
to be the product of all circular (that is, cyclically consecutive) ![]() $k\times k$ minors of
$k\times k$ minors of ![]() $X$, where the indices are taken modulo
$X$, where the indices are taken modulo ![]() $n$.
$n$.
Definition 5.1 The canonical form ![]() $\omega _{k,n}$ on
$\omega _{k,n}$ on ![]() $\operatorname {Gr}(k,n)$ is defined as follows: if
$\operatorname {Gr}(k,n)$ is defined as follows: if ![]() $X\in \operatorname {Gr}(k,n)$ is the row span of
$X\in \operatorname {Gr}(k,n)$ is the row span of ![]() $[\operatorname {Id}_k\mid A]$ for a
$[\operatorname {Id}_k\mid A]$ for a ![]() $k\times (n-k)$ matrix
$k\times (n-k)$ matrix ![]() $A$ then
$A$ then
Until § 8, we view ![]() $\omega _{k,n}$ as only being defined up to a sign.
$\omega _{k,n}$ as only being defined up to a sign.
Example 5.2 Consider an element ![]() $X\in \operatorname {Gr}(2,4)$ given by the row span of
$X\in \operatorname {Gr}(2,4)$ given by the row span of
Then we have
What makes ![]() $\omega _{k,n}$ special is that it can be alternatively computed using other coordinate charts on
$\omega _{k,n}$ special is that it can be alternatively computed using other coordinate charts on ![]() $\operatorname {Gr}(k,n)$ in a simple way. For the proof of the following result, see [Reference LamLam16b, Proposition 13.3].
$\operatorname {Gr}(k,n)$ in a simple way. For the proof of the following result, see [Reference LamLam16b, Proposition 13.3].
Proposition 5.3 Suppose that the Plücker coordinates ![]() $\{\Delta _J\mid J\in \mathcal {C}\}$ form a cluster for some
$\{\Delta _J\mid J\in \mathcal {C}\}$ form a cluster for some ![]() $\mathcal {C}=\{J_0,J_1,\dots ,J_{k(n-k)}\}$ (see Definition 11.3), and suppose that they are normalized so that
$\mathcal {C}=\{J_0,J_1,\dots ,J_{k(n-k)}\}$ (see Definition 11.3), and suppose that they are normalized so that ![]() $\Delta _{J_0}(X')=1$ for all
$\Delta _{J_0}(X')=1$ for all ![]() $X'$ in the neighborhood of
$X'$ in the neighborhood of ![]() $X\in \operatorname {Gr}(k,n)$. Then
$X\in \operatorname {Gr}(k,n)$. Then
 \begin{equation} \omega_{k,n}(X)={\pm} \frac{d(\Delta_{J_1}(X))\wedge d(\Delta_{J_2}(X))\wedge\dots\wedge d(\Delta_{J_{k(n-k)}}(X))}{\Delta_{J_1}(X) \cdot\Delta_{J_2}(X)\cdots\Delta_{J_{k(n-k)}}(X)}.\end{equation}
\begin{equation} \omega_{k,n}(X)={\pm} \frac{d(\Delta_{J_1}(X))\wedge d(\Delta_{J_2}(X))\wedge\dots\wedge d(\Delta_{J_{k(n-k)}}(X))}{\Delta_{J_1}(X) \cdot\Delta_{J_2}(X)\cdots\Delta_{J_{k(n-k)}}(X)}.\end{equation} The normalization ![]() $\Delta _{J_0}(X')=1$ means that the homogeneous coordinates
$\Delta _{J_0}(X')=1$ means that the homogeneous coordinates ![]() $\Delta _{J_i}(X)$ become rational functions on
$\Delta _{J_i}(X)$ become rational functions on ![]() $\operatorname {Gr}(k,n)$. Instead of normalization, one could also replace
$\operatorname {Gr}(k,n)$. Instead of normalization, one could also replace ![]() $\Delta _{J_i}(X)$ by the rational function
$\Delta _{J_i}(X)$ by the rational function ![]() $\Delta _{J_i}(X)/\Delta _{J_0}(X)$ in (5.3).
$\Delta _{J_i}(X)/\Delta _{J_0}(X)$ in (5.3).
The form ![]() $\omega _{k,n}(X)$ depends neither on the choice of the cluster
$\omega _{k,n}(X)$ depends neither on the choice of the cluster ![]() $\mathcal {C}$ nor on the choice of
$\mathcal {C}$ nor on the choice of ![]() $J_0\in \mathcal {C}$. This result will serve as a definition of the canonical form for any positroid cell in the next section.
$J_0\in \mathcal {C}$. This result will serve as a definition of the canonical form for any positroid cell in the next section.
Example 5.4 There are two clusters in ![]() $\operatorname {Gr}(2,4)$:
$\operatorname {Gr}(2,4)$: ![]() $\mathcal {C}:=\{\{1,2\},\{2,3\},\{3,4\},\{1,4\},\{1,3\}\}$ and
$\mathcal {C}:=\{\{1,2\},\{2,3\},\{3,4\},\{1,4\},\{1,3\}\}$ and ![]() $\mathcal {C}':=\{\{1,2\},\{2,3\},\{3,4\},\{1,4\},\{2,4\}\}$. For
$\mathcal {C}':=\{\{1,2\},\{2,3\},\{3,4\},\{1,4\},\{2,4\}\}$. For ![]() $X$ being the row span of the matrix given in (5.1), we have
$X$ being the row span of the matrix given in (5.1), we have
Letting ![]() $J_0$ be
$J_0$ be ![]() $\{1,2\}$ and applying Proposition 5.3 to
$\{1,2\}$ and applying Proposition 5.3 to ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $\mathcal {C}'$ yields the following two expressions for
$\mathcal {C}'$ yields the following two expressions for ![]() $\omega _{k,n}(X)$:
$\omega _{k,n}(X)$:
One easily checks that each of these expressions is indeed equal up to a sign to the one given in (5.2): we have ![]() $d(ps-rq)=p\,ds+s\,dp-r\,dq-q\,dr$, but only one of these four terms stays non-zero after taking the wedge with
$d(ps-rq)=p\,ds+s\,dp-r\,dq-q\,dr$, but only one of these four terms stays non-zero after taking the wedge with ![]() $dp\wedge ds\wedge dr$ or
$dp\wedge ds\wedge dr$ or ![]() $dp\wedge ds\wedge dq$.
$dp\wedge ds\wedge dq$.
Remark 5.5 Yet another simple alternative way to compute ![]() $\omega _{k,n}$ is to use Postnikov's parametrization [Reference PostnikovPos07] in terms of edge weights of a plabic graph. See [Reference LamLam16b, § 13] for the proof that all three ways of computing
$\omega _{k,n}$ is to use Postnikov's parametrization [Reference PostnikovPos07] in terms of edge weights of a plabic graph. See [Reference LamLam16b, § 13] for the proof that all three ways of computing ![]() $\omega _{k,n}$ produce the same answer.
$\omega _{k,n}$ produce the same answer.
Remark 5.6 The definition of the canonical form given in Proposition 5.3 generalizes to all cluster algebras, see [Reference Arkani-Hamed, Bai and LamABL17, § 5.7].
Before we state the main result of this section, let us give a warm-up result on the relationship between the twist map of [Reference Marsh and ScottMS16] and the canonical form. Recall that ![]() $\tau :\operatorname {Mat}^\circ (k+\ell ,n)\to \operatorname {Mat}^\circ (k+\ell ,n)$ sends a matrix
$\tau :\operatorname {Mat}^\circ (k+\ell ,n)\to \operatorname {Mat}^\circ (k+\ell ,n)$ sends a matrix ![]() $U\in \operatorname {Mat}^\circ (k+\ell ,n)$ to another matrix
$U\in \operatorname {Mat}^\circ (k+\ell ,n)$ to another matrix ![]() ${\tilde {U}}\in \operatorname {Mat}^\circ (k+\ell ,n)$ defined in (4.1). Similarly to Lemma 4.4, one can prove that
${\tilde {U}}\in \operatorname {Mat}^\circ (k+\ell ,n)$ defined in (4.1). Similarly to Lemma 4.4, one can prove that ![]() $\tau$ descends to a rational map
$\tau$ descends to a rational map ![]() $\operatorname {Gr}(k+\ell ,n)\dashrightarrow \operatorname {Gr}(k+\ell ,n)$. Let
$\operatorname {Gr}(k+\ell ,n)\dashrightarrow \operatorname {Gr}(k+\ell ,n)$. Let ![]() $\omega _{k+\ell ,n}$ denote the canonical form on
$\omega _{k+\ell ,n}$ denote the canonical form on ![]() $\operatorname {Gr}(k+\ell ,n)$.
$\operatorname {Gr}(k+\ell ,n)$.
Proposition 5.7 The twist map ![]() $\tau :\operatorname {Gr}(k+\ell ,n)\dashrightarrow \operatorname {Gr}(k+\ell ,n)$ preserves the canonical form
$\tau :\operatorname {Gr}(k+\ell ,n)\dashrightarrow \operatorname {Gr}(k+\ell ,n)$ preserves the canonical form ![]() $\omega _{k+\ell ,n}$ up to a sign. That is,
$\omega _{k+\ell ,n}$ up to a sign. That is, ![]() $\omega _{k+\ell ,n}$ is equal to the pullback
$\omega _{k+\ell ,n}$ is equal to the pullback ![]() $\pm \tau ^\ast \omega _{k+\ell ,n}$ of
$\pm \tau ^\ast \omega _{k+\ell ,n}$ of ![]() $\omega _{k+\ell ,n}$ via
$\omega _{k+\ell ,n}$ via ![]() $\tau$.
$\tau$.
Example 5.8 Let ![]() $k+\ell =2$,
$k+\ell =2$, ![]() $n=4$, and suppose that
$n=4$, and suppose that ![]() $U$ is the row span of (5.1). After possibly switching the signs of some columns,
$U$ is the row span of (5.1). After possibly switching the signs of some columns, ![]() ${\tilde {U}}:=\tau (U)$ is the row span of
${\tilde {U}}:=\tau (U)$ is the row span of
Here ![]() ${ \operatorname {diag}}$ denotes a diagonal matrix, and the matrix on the right-hand side is obtained from the matrix on the left-hand side by multiplying the bottom row by
${ \operatorname {diag}}$ denotes a diagonal matrix, and the matrix on the right-hand side is obtained from the matrix on the left-hand side by multiplying the bottom row by ![]() $-s$ and switching the two rows (these operations preserve its row span). Thus a cluster of Plücker coordinates of
$-s$ and switching the two rows (these operations preserve its row span). Thus a cluster of Plücker coordinates of ![]() ${\tilde {U}}$ is given by
${\tilde {U}}$ is given by
Applying Proposition 5.3, we see that the pullback of ![]() $\omega _{k+\ell ,n}$ under
$\omega _{k+\ell ,n}$ under ![]() $\tau$ is equal to
$\tau$ is equal to
 \begin{equation} {\pm}\frac{ds\wedge d \bigl(\frac{s}{p}\bigr)\wedge d\bigl(\frac{r}{p}\bigr)\wedge d\bigl(\frac{s}{ps-rq}\bigr)}{s\cdot \frac{s}{p}\cdot \frac{r}{p}\cdot \frac{s}{ps-rq}}={\pm}\frac{ds\wedge \frac{s\,dp}{p^2}\wedge \frac{dr}{p}\wedge \frac{sr\,dq}{(ps-rq)^2}}{s\cdot \frac{s}{p}\cdot \frac{r}{p}\cdot \frac{s}{ps-rq}}. \end{equation}
\begin{equation} {\pm}\frac{ds\wedge d \bigl(\frac{s}{p}\bigr)\wedge d\bigl(\frac{r}{p}\bigr)\wedge d\bigl(\frac{s}{ps-rq}\bigr)}{s\cdot \frac{s}{p}\cdot \frac{r}{p}\cdot \frac{s}{ps-rq}}={\pm}\frac{ds\wedge \frac{s\,dp}{p^2}\wedge \frac{dr}{p}\wedge \frac{sr\,dq}{(ps-rq)^2}}{s\cdot \frac{s}{p}\cdot \frac{r}{p}\cdot \frac{s}{ps-rq}}. \end{equation}
Here e.g. ![]() $d(\Delta _{23})=\pm ds$ and
$d(\Delta _{23})=\pm ds$ and ![]() $d(\Delta _{34})=\pm ({ds}/{p}-{s\,dp}/{p^2})$, but because we are already taking the wedge with
$d(\Delta _{34})=\pm ({ds}/{p}-{s\,dp}/{p^2})$, but because we are already taking the wedge with ![]() $ds$, only the
$ds$, only the ![]() ${s\,dp}/{p^2}$ term appears in the numerator of (5.4). We see that after some cancellations, (5.4) indeed yields the same result as (5.2), in agreement with Proposition 5.7.
${s\,dp}/{p^2}$ term appears in the numerator of (5.4). We see that after some cancellations, (5.4) indeed yields the same result as (5.2), in agreement with Proposition 5.7.
Consider the manifold ![]() $\operatorname {Gr}(k,n)\times \operatorname {Gr}(\ell ,n)$ for some
$\operatorname {Gr}(k,n)\times \operatorname {Gr}(\ell ,n)$ for some ![]() $k+\ell +m=n$ as above with
$k+\ell +m=n$ as above with ![]() $m$ even. One can consider a top form
$m$ even. One can consider a top form ![]() $\omega _{k,n}\wedge \omega _{\ell ,n}$ on this manifold. We are now ready to state the main result of this section.
$\omega _{k,n}\wedge \omega _{\ell ,n}$ on this manifold. We are now ready to state the main result of this section.
Theorem 5.9 The stacked twist map ![]() $\theta :\operatorname {Gr}(k,n)\times \operatorname {Gr}(\ell ,n)\dashrightarrow \operatorname {Gr}(k,n)\times \operatorname {Gr}(\ell ,n)$ preserves the form
$\theta :\operatorname {Gr}(k,n)\times \operatorname {Gr}(\ell ,n)\dashrightarrow \operatorname {Gr}(k,n)\times \operatorname {Gr}(\ell ,n)$ preserves the form ![]() $\omega _{k,n}\wedge \omega _{\ell ,n}$ up to a sign.
$\omega _{k,n}\wedge \omega _{\ell ,n}$ up to a sign.
Proposition 5.7 has a short proof using the results of [Reference Marsh and ScottMS16, Reference Muller and SpeyerMS17], see § 11.4. On the other hand, the proof of Theorem 5.9 is quite involved and is given in § 11.5. See § 6.3 for an example.
5.2 The canonical form for lower positroid cells
Given an affine permutation ![]() $f\in \tilde {S_n}(-k,n-k)$, one can consider certain collections
$f\in \tilde {S_n}(-k,n-k)$, one can consider certain collections ![]() $\mathcal {C}\subset { (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )}$ of
$\mathcal {C}\subset { (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )}$ of ![]() $k$-element subsets of
$k$-element subsets of ![]() $[n]$ called clusters, see Definition 11.3. All clusters have the same size, and give a parametrization of
$[n]$ called clusters, see Definition 11.3. All clusters have the same size, and give a parametrization of ![]() $\Pi ^{>0}_{k+f}$.
$\Pi ^{>0}_{k+f}$.
Proposition 5.10 [OPS15] Let ![]() $\mathcal {C}$ be a cluster for
$\mathcal {C}$ be a cluster for ![]() $f\in \tilde {S_n}(-k,n-k)$. Then it has size
$f\in \tilde {S_n}(-k,n-k)$. Then it has size
The map ![]() $\Pi ^{>0}_{k+f} \to {{\mathbb {R}}\mathbb {P}}_{>0}^\mathcal {C}$ given by
$\Pi ^{>0}_{k+f} \to {{\mathbb {R}}\mathbb {P}}_{>0}^\mathcal {C}$ given by ![]() $X\mapsto \{\Delta _J(X)\mid J\in \mathcal {C}\}$ is a diffeomorphism.
$X\mapsto \{\Delta _J(X)\mid J\in \mathcal {C}\}$ is a diffeomorphism.
Here ![]() ${{\mathbb {R}}\mathbb {P}}_{>0}^{\mathcal {C}}$ denotes the subset of the
${{\mathbb {R}}\mathbb {P}}_{>0}^{\mathcal {C}}$ denotes the subset of the ![]() $(|\mathcal {C}|-1)$-dimensional real projective space where all coordinates are positive.
$(|\mathcal {C}|-1)$-dimensional real projective space where all coordinates are positive.
Thus we have various coordinate charts on ![]() $\Pi ^{>0}_{k+f}$, which now allows us to use Proposition 5.3 to define a canonical form on this manifold.
$\Pi ^{>0}_{k+f}$, which now allows us to use Proposition 5.3 to define a canonical form on this manifold.
Definition 5.11 Let ![]() $\mathcal {C}=\{J_0,J_1,\dots ,J_N\}$ be a cluster for
$\mathcal {C}=\{J_0,J_1,\dots ,J_N\}$ be a cluster for ![]() $f\in \tilde {S_n}(-k,n-k)$, where
$f\in \tilde {S_n}(-k,n-k)$, where ![]() $n=k (n-k) -\operatorname {inv}(f)$. Suppose that the values of the Plücker coordinates are rescaled so that
$n=k (n-k) -\operatorname {inv}(f)$. Suppose that the values of the Plücker coordinates are rescaled so that ![]() $\Delta _{J_0}(X')=1$ for
$\Delta _{J_0}(X')=1$ for ![]() $X'$ in the neighborhood of
$X'$ in the neighborhood of ![]() $X\in \Pi ^{>0}_{k+f}$. Then the canonical form
$X\in \Pi ^{>0}_{k+f}$. Then the canonical form ![]() $\omega _{k+f}$ on
$\omega _{k+f}$ on ![]() $\Pi ^{>0}_{k+f}$ is defined by
$\Pi ^{>0}_{k+f}$ is defined by
Proposition 5.12 The form ![]() $\omega _{k+f}$ depends neither on the choice of
$\omega _{k+f}$ depends neither on the choice of ![]() $\mathcal {C}$ nor on the choice of
$\mathcal {C}$ nor on the choice of ![]() $J_0\in \mathcal {C}$.
$J_0\in \mathcal {C}$.
See [Reference LamLam16b, Theorem 13.2] for a proof. In fact, we will see later that the form ![]() $\omega _{k+f}$ can be obtained from the form
$\omega _{k+f}$ can be obtained from the form ![]() $\omega _{k,n}=\omega _{k+\operatorname {id}_{0}}$ by subsequently taking residues (see § 12.1 for a definition). This implies Proposition 5.12, as well as a generalization of Theorem 5.9 to lower cells, which we now explain.
$\omega _{k,n}=\omega _{k+\operatorname {id}_{0}}$ by subsequently taking residues (see § 12.1 for a definition). This implies Proposition 5.12, as well as a generalization of Theorem 5.9 to lower cells, which we now explain.
By (4.6), the set ![]() $\operatorname {Gr}_{>0}^\perp (k+m,n)$ can be identified with
$\operatorname {Gr}_{>0}^\perp (k+m,n)$ can be identified with ![]() $\operatorname {Gr}_{>0}(\ell ,n)$ by changing the sign of every second column, and since the form
$\operatorname {Gr}_{>0}(\ell ,n)$ by changing the sign of every second column, and since the form ![]() $\omega _{\ell ,n}$ is only defined up to a sign, we can view
$\omega _{\ell ,n}$ is only defined up to a sign, we can view ![]() $\omega _{\ell ,n}$ as a top rational form on
$\omega _{\ell ,n}$ as a top rational form on ![]() $\operatorname {Gr}_{>0}^\perp (k+m,n)$ instead. The following is our main result regarding canonical forms.
$\operatorname {Gr}_{>0}^\perp (k+m,n)$ instead. The following is our main result regarding canonical forms.
Theorem 5.13 For ![]() $f\in \tilde {S_n}(-k,\ell )$, under the stacked twist map diffeomorphism
$f\in \tilde {S_n}(-k,\ell )$, under the stacked twist map diffeomorphism
(see (4.7)) we have
We discuss the application of Theorem 5.13 to the amplituhedron form in § 8.
6. Examples
In this section, we illustrate each of our main results by an example.
6.1 Triangulations of a pentagon
As a warm-up, we let ![]() $k=1$,
$k=1$, ![]() $\ell =2$,
$\ell =2$, ![]() $m=2$,
$m=2$, ![]() $n=5$. In this case, the amplituhedron
$n=5$. In this case, the amplituhedron ![]() $\mathcal {A}_{n,k,m}(Z)$ is a pentagon in
$\mathcal {A}_{n,k,m}(Z)$ is a pentagon in ![]() ${{\mathbb {R}}\mathbb {P}}^2$ whose vertices are the five columns of
${{\mathbb {R}}\mathbb {P}}^2$ whose vertices are the five columns of ![]() $Z\in \operatorname {Gr}_{>0}(3,5)$. We write
$Z\in \operatorname {Gr}_{>0}(3,5)$. We write ![]() $f\in \tilde {S_n}$ in window notation, i.e.
$f\in \tilde {S_n}$ in window notation, i.e. ![]() $f=[f(1),f(2),\dots , f(n)]$. Let
$f=[f(1),f(2),\dots , f(n)]$. Let ![]() $P_{n,k,m}\subset \tilde {S_n}(-k,n-k)$ be the set of affine permutations
$P_{n,k,m}\subset \tilde {S_n}(-k,n-k)$ be the set of affine permutations ![]() $f$ with
$f$ with ![]() $\operatorname {inv}(f)=k\ell =2$. We say that
$\operatorname {inv}(f)=k\ell =2$. We say that ![]() $f,g\in \tilde {S_n}$ are the same up to rotation if for some
$f,g\in \tilde {S_n}$ are the same up to rotation if for some ![]() $s\in \mathbb {Z}$ we have
$s\in \mathbb {Z}$ we have ![]() $f(i+s)=g(i)+s$ for all
$f(i+s)=g(i)+s$ for all ![]() $i\in \mathbb {Z}$. There are ten affine permutations in
$i\in \mathbb {Z}$. There are ten affine permutations in ![]() $P_{5,1,2}$, and up to rotation, they form two classes of five affine permutations in each, shown in Figure 1 (bottom). All of these ten affine permutations are
$P_{5,1,2}$, and up to rotation, they form two classes of five affine permutations in each, shown in Figure 1 (bottom). All of these ten affine permutations are ![]() $(n,k,m)$-admissible, and the images of the corresponding positroid cells are the
$(n,k,m)$-admissible, and the images of the corresponding positroid cells are the ![]() $ (\begin {smallmatrix}5\\ 3 \end {smallmatrix} )=10$ triangles in a pentagon. The affine permutation
$ (\begin {smallmatrix}5\\ 3 \end {smallmatrix} )=10$ triangles in a pentagon. The affine permutation ![]() $[2,1,3,5,4]$ in Figure 1 (bottom left) corresponds to the convex hull of the triangle with vertex set
$[2,1,3,5,4]$ in Figure 1 (bottom left) corresponds to the convex hull of the triangle with vertex set ![]() $\{1,3,4\}$ inside a pentagon, while the affine permutation
$\{1,3,4\}$ inside a pentagon, while the affine permutation ![]() $[3,1,2,4,5]$ in Figure 1 (bottom right) corresponds to the convex hull of a triangle with vertex set
$[3,1,2,4,5]$ in Figure 1 (bottom right) corresponds to the convex hull of a triangle with vertex set ![]() $\{1,4,5\}$. These two permutations are therefore
$\{1,4,5\}$. These two permutations are therefore ![]() $(5,1,2)$-compatible and together with the permutation
$(5,1,2)$-compatible and together with the permutation ![]() $[1,2,5,3,4]$ (corresponding to a triangle with vertex set
$[1,2,5,3,4]$ (corresponding to a triangle with vertex set ![]() $\{1,2,3\}$) they form a triangulation of
$\{1,2,3\}$) they form a triangulation of ![]() $\mathcal {A}_{n,k,m}(Z)$.
$\mathcal {A}_{n,k,m}(Z)$.

Figure 1. Up to rotation, there are three affine permutations in ![]() $\tilde {S_n}(-k,n-k)$ for
$\tilde {S_n}(-k,n-k)$ for ![]() $k=2,n=5$ with two inversions (top). There are only two such affine permutations in
$k=2,n=5$ with two inversions (top). There are only two such affine permutations in ![]() $\tilde {S_n}(-k,n-k)$ for
$\tilde {S_n}(-k,n-k)$ for ![]() $k=1,n=5$ (bottom).
$k=1,n=5$ (bottom).
6.2 Triangulations of the  $\ell =1$ amplituhedron
$\ell =1$ amplituhedron
We now study the ‘dual’ case ![]() $k=2$,
$k=2$, ![]() $\ell =1$,
$\ell =1$, ![]() $m=2$,
$m=2$, ![]() $n=5$ in detail. There are 15 affine permutations in
$n=5$ in detail. There are 15 affine permutations in ![]() $P_{5,2,2}$, and they form three classes (up to rotation) of five permutations in each, shown in Figure 1 (top).
$P_{5,2,2}$, and they form three classes (up to rotation) of five permutations in each, shown in Figure 1 (top).
The permutations ![]() $f=[2,1,3,5,4]$ and
$f=[2,1,3,5,4]$ and ![]() $g=[2,3,1,4,5]$ belong to
$g=[2,3,1,4,5]$ belong to ![]() $\tilde {S_n}(-k,\ell )$ while
$\tilde {S_n}(-k,\ell )$ while ![]() $h=[1,4, 2,3,5]$ does not belong to
$h=[1,4, 2,3,5]$ does not belong to ![]() $\tilde {S_n}(-k,\ell )$ because
$\tilde {S_n}(-k,\ell )$ because ![]() $h(2)=4>2+\ell$. Thus by Lemma 3.2,
$h(2)=4>2+\ell$. Thus by Lemma 3.2, ![]() $h$ is not
$h$ is not ![]() $(n,k,m)$-admissible (and it is indeed easy to check directly that
$(n,k,m)$-admissible (and it is indeed easy to check directly that ![]() $h$ is not
$h$ is not ![]() $Z$-admissible for any
$Z$-admissible for any ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$). Note that
$Z\in \operatorname {Gr}_{>0}(k+m,n)$). Note that ![]() $h^{-1}$ does not correspond to any triangle inside a pentagon.
$h^{-1}$ does not correspond to any triangle inside a pentagon.
Let us now fix ![]() $f=[2,1,3,5,4]$ and consider
$f=[2,1,3,5,4]$ and consider ![]() $V\in \Pi ^{>0}_{k+f}$ and
$V\in \Pi ^{>0}_{k+f}$ and ![]() $W\in \operatorname {Gr}_{>0}^\perp (k+m,n)$ given by
$W\in \operatorname {Gr}_{>0}^\perp (k+m,n)$ given by
The fact that ![]() $V\in \Pi ^{>0}_{k+f}$ can be easily checked using (10.4) while the fact that
$V\in \Pi ^{>0}_{k+f}$ can be easily checked using (10.4) while the fact that ![]() $W\in \operatorname {Gr}_{>0}^\perp (k+m,n)$ follows since
$W\in \operatorname {Gr}_{>0}^\perp (k+m,n)$ follows since ![]() $\operatorname {alt}(W)$ is totally positive, see (4.6). We would like to compute
$\operatorname {alt}(W)$ is totally positive, see (4.6). We would like to compute ![]() $({\tilde {W}},{\tilde V})=\theta (V,W)$. To do so, we first need to find the matrix
$({\tilde {W}},{\tilde V})=\theta (V,W)$. To do so, we first need to find the matrix ![]() ${\tilde {U}}=\tau (U)$. Let us introduce a diagonal
${\tilde {U}}=\tau (U)$. Let us introduce a diagonal ![]() $n\times n$ matrix
$n\times n$ matrix ![]() $D={ \operatorname {diag}}(|\Delta _{J_1}(U)|,\dots ,|\Delta _{J_n}(U)|)$, where
$D={ \operatorname {diag}}(|\Delta _{J_1}(U)|,\dots ,|\Delta _{J_n}(U)|)$, where ![]() $J_j=\{j-\ell ,j-\ell +1,\dots ,j+k-1\}$. We will consider the matrix
$J_j=\{j-\ell ,j-\ell +1,\dots ,j+k-1\}$. We will consider the matrix ![]() ${\tilde {U}}\cdot D$ rather than
${\tilde {U}}\cdot D$ rather than ![]() ${\tilde {U}}$ itself in order to clear the denominators (cf. (10.1)). The matrix
${\tilde {U}}$ itself in order to clear the denominators (cf. (10.1)). The matrix ![]() $U$ is given in Figure 2 (top), so
$U$ is given in Figure 2 (top), so
Thus the column ![]() ${\tilde {U}}(j)$ gets rescaled by the absolute value of
${\tilde {U}}(j)$ gets rescaled by the absolute value of ![]() $\Delta _{J_j}(U)$. The matrix
$\Delta _{J_j}(U)$. The matrix ![]() ${\tilde {U}}\cdot D$ is given in Figure 2 (bottom): we encourage the reader to check that the column
${\tilde {U}}\cdot D$ is given in Figure 2 (bottom): we encourage the reader to check that the column ![]() ${\tilde {U}}(j)$ is orthogonal to the columns
${\tilde {U}}(j)$ is orthogonal to the columns ![]() $U(j)$ and
$U(j)$ and ![]() $U(j+1)$, and that
$U(j+1)$, and that ![]() $\langle {\tilde {U}}(j),U(j-1)\rangle =(-1)^j$. (Recall also that
$\langle {\tilde {U}}(j),U(j-1)\rangle =(-1)^j$. (Recall also that ![]() $U(j+n)=(-1)^{k-1}U(j)$ and
$U(j+n)=(-1)^{k-1}U(j)$ and ![]() ${\tilde {U}}(j+n)=(-1)^{\ell -1}{\tilde {U}}(j)$, which is consistent with Figure 2.) Thus the output of the stacked twist map in this case is given by
${\tilde {U}}(j+n)=(-1)^{\ell -1}{\tilde {U}}(j)$, which is consistent with Figure 2.) Thus the output of the stacked twist map in this case is given by

Figure 2. The columns of ![]() $U$ (top) and of
$U$ (top) and of ![]() ${\tilde {U}}\cdot D$ (bottom) for
${\tilde {U}}\cdot D$ (bottom) for ![]() $j=-1,0,\dots ,7$.
$j=-1,0,\dots ,7$.
We observe that ![]() $\operatorname {alt}({\tilde {W}})$ is a totally positive
$\operatorname {alt}({\tilde {W}})$ is a totally positive ![]() $2\times 5$ matrix, and thus
$2\times 5$ matrix, and thus ![]() ${\tilde {W}}\in \operatorname {Gr}_{>0}^\perp (\ell +m,n)$. Similarly,
${\tilde {W}}\in \operatorname {Gr}_{>0}^\perp (\ell +m,n)$. Similarly, ![]() ${\tilde V}$ is a totally nonnegative
${\tilde V}$ is a totally nonnegative ![]() $1\times 5$ matrix. Moreover, we have
$1\times 5$ matrix. Moreover, we have ![]() ${\tilde V}\in \Pi ^{>0}_{\ell +f'}$ for
${\tilde V}\in \Pi ^{>0}_{\ell +f'}$ for ![]() $f'=[2,1,3,5,4]=f^{-1}$, as predicted by Theorem 4.7, part (iii).
$f'=[2,1,3,5,4]=f^{-1}$, as predicted by Theorem 4.7, part (iii).
We now consider the fibers of ![]() $Z$. Let
$Z$. Let ![]() $V,W$ be given by (6.1), and consider a
$V,W$ be given by (6.1), and consider a ![]() $4\times 5$ matrix
$4\times 5$ matrix ![]() $Z:=W^\perp$. Suppose that
$Z:=W^\perp$. Suppose that ![]() $V'\cdot Z^\text {t}=V\cdot Z^\text {t}$ for some
$V'\cdot Z^\text {t}=V\cdot Z^\text {t}$ for some ![]() $V'\in \operatorname {Gr}_{\ge 0}(k,n)$, then we must have
$V'\in \operatorname {Gr}_{\ge 0}(k,n)$, then we must have ![]() $V'=V+A\cdot W$ for some
$V'=V+A\cdot W$ for some ![]() $2\times 1$ matrix
$2\times 1$ matrix ![]() $A= (\begin {smallmatrix} a \\ b \end {smallmatrix} )$ with
$A= (\begin {smallmatrix} a \\ b \end {smallmatrix} )$ with ![]() $a,b\in \mathbb {R}$. The matrix
$a,b\in \mathbb {R}$. The matrix ![]() $U':=\operatorname {stack}(V',W)$ is therefore given by
$U':=\operatorname {stack}(V',W)$ is therefore given by
 \[ U'= \begin{pmatrix} a + 1 & -a & 3 a & -2 a - 2 & a - 1 \\ b & -b + 1 & 3 b + 1 & -2 b + 2 & b \\ 1 & -1 & 3 & -2 & 1 \end{pmatrix}. \]
\[ U'= \begin{pmatrix} a + 1 & -a & 3 a & -2 a - 2 & a - 1 \\ b & -b + 1 & 3 b + 1 & -2 b + 2 & b \\ 1 & -1 & 3 & -2 & 1 \end{pmatrix}. \]
We then find the matrix ![]() ${\tilde {U}}':=\tau (U')$:
${\tilde {U}}':=\tau (U')$:
 \[ {\tilde{U}}'\cdot D= \begin{pmatrix} -1 & 4 & -8 & 2 & 0 \\ 1 & 0 & -6 & 4 & -2 \\ a - b + 1 & -4 a & 8 a + 6 b + 2 & -2 a - 4 b + 2 & 2 b \end{pmatrix}. \]
\[ {\tilde{U}}'\cdot D= \begin{pmatrix} -1 & 4 & -8 & 2 & 0 \\ 1 & 0 & -6 & 4 & -2 \\ a - b + 1 & -4 a & 8 a + 6 b + 2 & -2 a - 4 b + 2 & 2 b \end{pmatrix}. \]
Here ![]() $D={ \operatorname {diag}}(2,4,8,10,4)$ is unchanged since
$D={ \operatorname {diag}}(2,4,8,10,4)$ is unchanged since ![]() $U'$ is obtained from
$U'$ is obtained from ![]() $U$ by row operations. Setting
$U$ by row operations. Setting ![]() $({\tilde {W}}',{\tilde V}'):=\theta (V',W)$, we get
$({\tilde {W}}',{\tilde V}'):=\theta (V',W)$, we get
(Note that by Proposition 4.8, ![]() ${\tilde {W}}'={\tilde {W}}$. As we will later see in Lemma 10.6, we have
${\tilde {W}}'={\tilde {W}}$. As we will later see in Lemma 10.6, we have ![]() ${\tilde V}'={\tilde V}-A^\text {t}\cdot {\tilde {W}}$.) We can now write down the fiber
${\tilde V}'={\tilde V}-A^\text {t}\cdot {\tilde {W}}$.) We can now write down the fiber ![]() $\operatorname {F}(V,Z)$ as the set of pairs
$\operatorname {F}(V,Z)$ as the set of pairs ![]() $(a,b)$ for which
$(a,b)$ for which ![]() $V'=V+A\cdot W$ is totally nonnegative. There are
$V'=V+A\cdot W$ is totally nonnegative. There are ![]() $ (\begin {smallmatrix}5\\ 2\end {smallmatrix} )=10$ minors of
$ (\begin {smallmatrix}5\\ 2\end {smallmatrix} )=10$ minors of ![]() $V'$, and each of them turns out to be a linear polynomial in the variables
$V'$, and each of them turns out to be a linear polynomial in the variables ![]() $a,b$. For example,
$a,b$. For example, ![]() $\Delta _{13}(V')=(a+1)(3b+1)-3ab=a+3b+1.$
$\Delta _{13}(V')=(a+1)(3b+1)-3ab=a+3b+1.$
The ten lines ![]() $\Delta _I(V')=0$ in the
$\Delta _I(V')=0$ in the ![]() $(a,b)$-plane are shown in Figure 3. For example, the line
$(a,b)$-plane are shown in Figure 3. For example, the line ![]() $\Delta _{13}(V')=0$ is the black line passing through the points
$\Delta _{13}(V')=0$ is the black line passing through the points ![]() $(-1,0)$ and
$(-1,0)$ and ![]() $(0,-\frac 13)$. The region where
$(0,-\frac 13)$. The region where ![]() $V'$ is totally nonnegative is the shaded pentagon. The vertices of this pentagon correspond to
$V'$ is totally nonnegative is the shaded pentagon. The vertices of this pentagon correspond to ![]() $V'$ being in
$V'$ being in ![]() $\Pi ^{>0}_{k+f'}$ for
$\Pi ^{>0}_{k+f'}$ for ![]() $f'$ equal to
$f'$ equal to ![]() $f$ up to rotation (in particular, the vertex
$f$ up to rotation (in particular, the vertex ![]() $(0,0)$ corresponds to
$(0,0)$ corresponds to ![]() $f$ itself). Thus
$f$ itself). Thus ![]() $\operatorname {F}(V,Z)$ intersects
$\operatorname {F}(V,Z)$ intersects ![]() $\Pi ^{>0}_{k+f'}$ for all such
$\Pi ^{>0}_{k+f'}$ for all such ![]() $f'$, and hence
$f'$, and hence ![]() $f$ is not
$f$ is not ![]() $(n,k,m)$-compatible with any of its four rotations. Observe that the inverses of these five permutations correspond to the triangles in a pentagon with vertex sets
$(n,k,m)$-compatible with any of its four rotations. Observe that the inverses of these five permutations correspond to the triangles in a pentagon with vertex sets ![]() $\{1,3,4\}$,
$\{1,3,4\}$, ![]() $\{2,4,5\}$,
$\{2,4,5\}$, ![]() $\{1,3,5\}$,
$\{1,3,5\}$, ![]() $\{1,2,4\}$, and
$\{1,2,4\}$, and ![]() $\{2,3,5\}$. No two of these five triangles can appear together in a triangulation of the pentagon, in agreement with part (2) of Theorem 3.5.
$\{2,3,5\}$. No two of these five triangles can appear together in a triangulation of the pentagon, in agreement with part (2) of Theorem 3.5.

Figure 3. Each of the ten lines represents the set of pairs ![]() $(a,b)$ for which one of the minors of
$(a,b)$ for which one of the minors of ![]() $V'$ is zero. We have
$V'$ is zero. We have ![]() $V'\in \operatorname {Gr}_{\ge 0}(k,n)$ precisely when
$V'\in \operatorname {Gr}_{\ge 0}(k,n)$ precisely when ![]() $(a,b)$ belongs to the shaded region.
$(a,b)$ belongs to the shaded region.
On the other hand, ![]() ${\tilde V}'$ is a
${\tilde V}'$ is a ![]() $1\times 5$ matrix and thus has only five minors. However, the
$1\times 5$ matrix and thus has only five minors. However, the ![]() $(a,b)$-region where all of them are nonnegative turns out to be exactly the same as the shaded pentagon in Figure 3. More precisely, for each
$(a,b)$-region where all of them are nonnegative turns out to be exactly the same as the shaded pentagon in Figure 3. More precisely, for each ![]() $j\in \mathbb {Z}$, we have
$j\in \mathbb {Z}$, we have ![]() $\Delta _{\{j\}}({\tilde V}'\cdot D)=\Delta _{\{j,j+1\}}(V')$ (see Lemma 11.5 for a general statement). For example,
$\Delta _{\{j\}}({\tilde V}'\cdot D)=\Delta _{\{j,j+1\}}(V')$ (see Lemma 11.5 for a general statement). For example,
Since the boundary of the shaded region in Figure 3 only involves circular minors of ![]() $V'$ being zero, we see that the fibers
$V'$ being zero, we see that the fibers ![]() $\operatorname {F}(V,Z)$ and
$\operatorname {F}(V,Z)$ and ![]() $\operatorname {F}({\tilde V},{\tilde Z})$ are equal as regions in the
$\operatorname {F}({\tilde V},{\tilde Z})$ are equal as regions in the ![]() $(a,b)$-plane. However, the five vertices of the pentagon
$(a,b)$-plane. However, the five vertices of the pentagon ![]() $\operatorname {F}({\tilde V},{\tilde Z})$ correspond to the five rotations of
$\operatorname {F}({\tilde V},{\tilde Z})$ correspond to the five rotations of ![]() $f^{-1}$. The main idea of our proof in § 10 is based on the observations made in this example.
$f^{-1}$. The main idea of our proof in § 10 is based on the observations made in this example.
6.3 Canonical forms for lower cells
Let ![]() $k=2$,
$k=2$, ![]() $\ell =1$,
$\ell =1$, ![]() $m=2$,
$m=2$, ![]() $n=5$,
$n=5$, ![]() $f=[2,3,1,5,4]$. Consider parametrizations of
$f=[2,3,1,5,4]$. Consider parametrizations of ![]() $\Pi ^{>0}_{k+f}$ and
$\Pi ^{>0}_{k+f}$ and ![]() $\operatorname {Gr}_{>0}^\perp (k+m,n)$ by
$\operatorname {Gr}_{>0}^\perp (k+m,n)$ by
We can take ![]() $\mathcal {C}:=\{\{1,2\},\{2,4\},\{4,5\},\{2,5\}\}$ to be a cluster for
$\mathcal {C}:=\{\{1,2\},\{2,4\},\{4,5\},\{2,5\}\}$ to be a cluster for ![]() $V$:
$V$:
and thus
Since ![]() $\omega _{\ell ,n}=\pm ({dp\wedge dq\wedge dr\wedge ds})/{pqrs}$, the form
$\omega _{\ell ,n}=\pm ({dp\wedge dq\wedge dr\wedge ds})/{pqrs}$, the form ![]() $\omega _{k+f}\wedge \omega _{\ell ,n}$ is given by
$\omega _{k+f}\wedge \omega _{\ell ,n}$ is given by
Let us now see what happens to this form when we apply the stacked twist map. Let ![]() $({\tilde {W}},{\tilde V}):=\theta (V,W)$. We find
$({\tilde {W}},{\tilde V}):=\theta (V,W)$. We find
 \[ {\tilde{W}}:=\begin{pmatrix} -\frac{p}{c p + s} & 1 & -\frac{b}{a} & \frac{s}{c} & 0 \\ \frac{q}{c p + s} & 0 & -1 & \frac{c r + a s}{b c} & -\frac{1}{b} \\ \end{pmatrix},\quad {\tilde V}:=\begin{pmatrix} \frac{1}{c p + s} & 0 & 0 & 1 & 0 \end{pmatrix}. \]
\[ {\tilde{W}}:=\begin{pmatrix} -\frac{p}{c p + s} & 1 & -\frac{b}{a} & \frac{s}{c} & 0 \\ \frac{q}{c p + s} & 0 & -1 & \frac{c r + a s}{b c} & -\frac{1}{b} \\ \end{pmatrix},\quad {\tilde V}:=\begin{pmatrix} \frac{1}{c p + s} & 0 & 0 & 1 & 0 \end{pmatrix}. \]
Note that ![]() $f^{-1}=[3,1,2,5,4]$, and indeed
$f^{-1}=[3,1,2,5,4]$, and indeed ![]() ${\tilde V}\in \Pi ^{>0}_{\ell +f^{-1}}$, while
${\tilde V}\in \Pi ^{>0}_{\ell +f^{-1}}$, while ![]() ${\tilde {W}}\in \operatorname {Gr}_{>0}^\perp (\ell +m,n)$ because
${\tilde {W}}\in \operatorname {Gr}_{>0}^\perp (\ell +m,n)$ because ![]() $\operatorname {alt}({\tilde {W}})\in \operatorname {Gr}_{>0}(k,n)$, see (4.6). Choosing a cluster
$\operatorname {alt}({\tilde {W}})\in \operatorname {Gr}_{>0}(k,n)$, see (4.6). Choosing a cluster ![]() $\mathcal {C}':=\{\{4\},\{1\}\}$ for
$\mathcal {C}':=\{\{4\},\{1\}\}$ for ![]() $\Pi ^{>0}_{\ell +f^{-1}}$, we get that the pullback of
$\Pi ^{>0}_{\ell +f^{-1}}$, we get that the pullback of ![]() $\omega _{\ell +f^{-1}}$ to
$\omega _{\ell +f^{-1}}$ to ![]() $\Pi ^{>0}_{k+f}\times \operatorname {Gr}_{>0}^\perp (k+m,n)$ under
$\Pi ^{>0}_{k+f}\times \operatorname {Gr}_{>0}^\perp (k+m,n)$ under ![]() $\theta$ is
$\theta$ is
Let us now compute the pullback of ![]() $\omega _{k,n}$ to
$\omega _{k,n}$ to ![]() $\Pi ^{>0}_{k+f}\times \operatorname {Gr}_{>0}^\perp (k+m,n)$ under
$\Pi ^{>0}_{k+f}\times \operatorname {Gr}_{>0}^\perp (k+m,n)$ under ![]() $\theta$. Applying row operations to
$\theta$. Applying row operations to ![]() ${\tilde {W}}$, we transform it into
${\tilde {W}}$, we transform it into
 \[ {\tilde{W}}'=\begin{pmatrix} -\frac{a p + b q}{{(c p + s)} a} & 1 & 0 & -\frac{r}{a} & \frac{1}{a} \\ -\frac{q}{c p + s} & 0 & 1 & -\frac{c r + a s}{b c} & \frac{1}{b} \end{pmatrix}. \]
\[ {\tilde{W}}'=\begin{pmatrix} -\frac{a p + b q}{{(c p + s)} a} & 1 & 0 & -\frac{r}{a} & \frac{1}{a} \\ -\frac{q}{c p + s} & 0 & 1 & -\frac{c r + a s}{b c} & \frac{1}{b} \end{pmatrix}. \]
The submatrix of ![]() ${\tilde {W}}'$ with column set
${\tilde {W}}'$ with column set ![]() $\{2,3\}$ is an identity matrix, and thus we can use Definition 5.1 (together with the fact that
$\{2,3\}$ is an identity matrix, and thus we can use Definition 5.1 (together with the fact that ![]() $\omega _{k,n}$ is cyclically invariant) to calculate
$\omega _{k,n}$ is cyclically invariant) to calculate
 \begin{equation} \theta^\ast \omega_{k,n}={\pm}\frac{d^{2\times 3}\begin{pmatrix} -\frac{a p + b q}{{(c p + s)} a} & -\frac{r}{a} & \frac{1}{a} \\ -\frac{q}{c p + s} & -\frac{c r + a s}{b c} & \frac{1}{b} \end{pmatrix}}{\Delta_{k}^{\operatorname{circ}}({\tilde{W}}')}. \end{equation}
\begin{equation} \theta^\ast \omega_{k,n}={\pm}\frac{d^{2\times 3}\begin{pmatrix} -\frac{a p + b q}{{(c p + s)} a} & -\frac{r}{a} & \frac{1}{a} \\ -\frac{q}{c p + s} & -\frac{c r + a s}{b c} & \frac{1}{b} \end{pmatrix}}{\Delta_{k}^{\operatorname{circ}}({\tilde{W}}')}. \end{equation}
Computing the circular minors of ![]() ${\tilde {W}}'$, we get
${\tilde {W}}'$, we get
The denominator in the right-hand side of (6.6) is therefore
A longer computation is needed to find the numerator in the right-hand side of (6.6), which in the end produces the following answer (the symbol ![]() $\wedge$ is omitted):
$\wedge$ is omitted):
The reader is invited to check that the form ![]() $\theta ^\ast (\omega _{k,n}\wedge \omega _{\ell +f^{-1}})=\theta ^\ast \omega _{k,n}\wedge \theta ^\ast \omega _{\ell +f^{-1}}$, obtained by taking the wedge of the right-hand sides of (6.5) and (6.7), is equal to
$\theta ^\ast (\omega _{k,n}\wedge \omega _{\ell +f^{-1}})=\theta ^\ast \omega _{k,n}\wedge \theta ^\ast \omega _{\ell +f^{-1}}$, obtained by taking the wedge of the right-hand sides of (6.5) and (6.7), is equal to ![]() $\pm \omega _{k+f}\wedge \omega _{\ell ,n}$, which is given on the right-hand side of (6.4).
$\pm \omega _{k+f}\wedge \omega _{\ell ,n}$, which is given on the right-hand side of (6.4).
7. Subdivisions and the universal amplituhedron
In this section, we introduce a more general set up. First, similarly to triangulations of ![]() $\mathcal {A}_{n,k,m}(Z)$ defined in § 3 we define its subdivisions. Second, we describe the universal amplituhedron (originally studied in the complex algebraic setting in [Reference LamLam16b, § 18.1]), and define its subdivisions as well. The universal amplituhedron provides a convenient framework to formulate the results of § 4, as well as some other results regarding canonical forms as we do in § 8.
$\mathcal {A}_{n,k,m}(Z)$ defined in § 3 we define its subdivisions. Second, we describe the universal amplituhedron (originally studied in the complex algebraic setting in [Reference LamLam16b, § 18.1]), and define its subdivisions as well. The universal amplituhedron provides a convenient framework to formulate the results of § 4, as well as some other results regarding canonical forms as we do in § 8.
7.1 Subdivisions
Let ![]() $Z \in \operatorname {Gr}_{>0}(k+m,n)$. We denote by
$Z \in \operatorname {Gr}_{>0}(k+m,n)$. We denote by ![]() $\leq$ the Bruhat order on
$\leq$ the Bruhat order on ![]() $\tilde {S_n}$, defined as follows. We say that
$\tilde {S_n}$, defined as follows. We say that ![]() $t\in \tilde {S_n}$ is a transposition if we have
$t\in \tilde {S_n}$ is a transposition if we have ![]() $t(i)\neq i$ for precisely two indices
$t(i)\neq i$ for precisely two indices ![]() $i\in [n]$, and then we define the covering relation
$i\in [n]$, and then we define the covering relation ![]() $\lessdot$ of the Bruhat order by
$\lessdot$ of the Bruhat order by
Here ![]() $\circ$ denotes the composition of bijections
$\circ$ denotes the composition of bijections ![]() $\mathbb {Z}\to \mathbb {Z}$. Given two affine permutations
$\mathbb {Z}\to \mathbb {Z}$. Given two affine permutations ![]() $f,g\in \tilde {S_n}(-k,n-k)$, we have
$f,g\in \tilde {S_n}(-k,n-k)$, we have ![]() $f \leq g$ if and only if
$f \leq g$ if and only if ![]() $\Pi ^{\ge 0}_{k+f} \subseteq \Pi ^{\ge 0}_{k+g}$, see e.g. [Reference LamLam16b, Theorem 8.1]. In particular, this implies the following property that was used in the proof of Theorem 3.5: for
$\Pi ^{\ge 0}_{k+f} \subseteq \Pi ^{\ge 0}_{k+g}$, see e.g. [Reference LamLam16b, Theorem 8.1]. In particular, this implies the following property that was used in the proof of Theorem 3.5: for ![]() $f,g\in \tilde {S_n}(-k,\ell )$, we have
$f,g\in \tilde {S_n}(-k,\ell )$, we have
Definition 7.1 Let ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ be a collection of pairwise
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ be a collection of pairwise ![]() $Z$-compatible affine permutations. We say that
$Z$-compatible affine permutations. We say that ![]() $f_1,\dots ,f_N$ form a
$f_1,\dots ,f_N$ form a ![]() $Z$-subdivision of the amplituhedron if the union of the images
$Z$-subdivision of the amplituhedron if the union of the images ![]() $Z(\Pi ^{>0}_{k+f_1}),\dots ,Z(\Pi ^{>0}_{k+f_N})$ forms a dense subset of
$Z(\Pi ^{>0}_{k+f_1}),\dots ,Z(\Pi ^{>0}_{k+f_N})$ forms a dense subset of ![]() $\mathcal {A}_{n,k,m}(Z)$, and we have
$\mathcal {A}_{n,k,m}(Z)$, and we have ![]() $\operatorname {dim} (Z(\Pi ^{>0}_{k+f_s}))=km$ for each
$\operatorname {dim} (Z(\Pi ^{>0}_{k+f_s}))=km$ for each ![]() $1\leq s\leq N$.
$1\leq s\leq N$.
More generally, suppose that ![]() $g \in \tilde {S_n}(-k,n-k)$ and
$g \in \tilde {S_n}(-k,n-k)$ and ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ is a collection of pairwise
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ is a collection of pairwise ![]() $Z$-compatible affine permutations satisfying
$Z$-compatible affine permutations satisfying ![]() $f_s \leq g$ for all
$f_s \leq g$ for all ![]() $1 \leq s \leq N$. We say that
$1 \leq s \leq N$. We say that ![]() $f_1,\dots ,f_N$ form a
$f_1,\dots ,f_N$ form a ![]() $Z$-subdivision of
$Z$-subdivision of ![]() $Z(\Pi ^{\ge 0}_{k+g})$ if the images
$Z(\Pi ^{\ge 0}_{k+g})$ if the images ![]() $Z(\Pi ^{>0}_{k+f_1}),\dots ,Z(\Pi ^{>0}_{k+f_N})$ form a dense subset of
$Z(\Pi ^{>0}_{k+f_1}),\dots ,Z(\Pi ^{>0}_{k+f_N})$ form a dense subset of ![]() $Z(\Pi ^{\ge 0}_{k+g})$, and we have
$Z(\Pi ^{\ge 0}_{k+g})$, and we have ![]() $\operatorname {dim} (Z(\Pi ^{>0}_{k+f_s}))=\operatorname {dim} (Z(\Pi ^{>0}_{k+g}))$ for each
$\operatorname {dim} (Z(\Pi ^{>0}_{k+f_s}))=\operatorname {dim} (Z(\Pi ^{>0}_{k+g}))$ for each ![]() $1\leq s\leq N$.
$1\leq s\leq N$.
We say that ![]() $f_1,\dots ,f_N$ form an
$f_1,\dots ,f_N$ form an ![]() $(n,k,m)$-subdivision of the amplituhedron (respectively, of
$(n,k,m)$-subdivision of the amplituhedron (respectively, of ![]() $g$) if they form a
$g$) if they form a ![]() $Z$-subdivision of the amplituhedron (respectively, of
$Z$-subdivision of the amplituhedron (respectively, of ![]() $Z(\Pi ^{\ge 0}_{k+g})$) for any
$Z(\Pi ^{\ge 0}_{k+g})$) for any ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$.
$Z\in \operatorname {Gr}_{>0}(k+m,n)$.
It thus follows that a (![]() $Z$- or
$Z$- or ![]() $(n,k,m)$-) triangulation of the amplituhedron is a (
$(n,k,m)$-) triangulation of the amplituhedron is a (![]() $Z$- or
$Z$- or ![]() $(n,k,m)$-) subdivision
$(n,k,m)$-) subdivision ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ of
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ of ![]() $\mathcal {A}_{n,k,m}(Z)$ such that the permutations
$\mathcal {A}_{n,k,m}(Z)$ such that the permutations ![]() $f_1,\dots ,f_N$ are (
$f_1,\dots ,f_N$ are (![]() $Z$- or
$Z$- or ![]() $(n,k,m)$-)admissible.
$(n,k,m)$-)admissible.
The following result gives an analog to part (3) of Theorem 3.5, with the same proof, which we omit.
Theorem 7.2 Let ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,\ell )$ be a collection of affine permutations. Then they form an
$f_1,\dots ,f_N\in \tilde {S_n}(-k,\ell )$ be a collection of affine permutations. Then they form an ![]() $(n,k,m)$-subdivision of the amplituhedron (respectively, of
$(n,k,m)$-subdivision of the amplituhedron (respectively, of ![]() $g \in \tilde {S_n}(-k,\ell )$) if and only if
$g \in \tilde {S_n}(-k,\ell )$) if and only if ![]() $f_1^{-1},\dots ,f_N^{-1}\in \tilde {S_n}(-\ell ,k)$ form an
$f_1^{-1},\dots ,f_N^{-1}\in \tilde {S_n}(-\ell ,k)$ form an ![]() $(n,\ell ,m)$-subdivision of the amplituhedron (respectively, of
$(n,\ell ,m)$-subdivision of the amplituhedron (respectively, of ![]() $g^{-1} \in \tilde {S_n}(-\ell ,k)$).
$g^{-1} \in \tilde {S_n}(-\ell ,k)$).
7.2 The universal amplituhedron
Let ![]() $\textrm {Fl}(\ell ,k+\ell ;n)$ be the two-step flag variety consisting of pairs of subspaces
$\textrm {Fl}(\ell ,k+\ell ;n)$ be the two-step flag variety consisting of pairs of subspaces ![]() $W \subset U \subset \mathbb {R}^n$ such that
$W \subset U \subset \mathbb {R}^n$ such that ![]() $\operatorname {dim}(W) =\ell$ and
$\operatorname {dim}(W) =\ell$ and ![]() $\operatorname {dim}(U) = k+\ell$. Define the universal amplituhedron
$\operatorname {dim}(U) = k+\ell$. Define the universal amplituhedron ![]() $\mathcal {A}_{n,k,m} \subset \textrm {Fl}(\ell ,k+\ell ;n)$ to be the closure (in the analytic topology)
$\mathcal {A}_{n,k,m} \subset \textrm {Fl}(\ell ,k+\ell ;n)$ to be the closure (in the analytic topology)
Let
be the projection ![]() $(W,U)\mapsto W$. Let us fix
$(W,U)\mapsto W$. Let us fix ![]() $Z \in \operatorname {Gr}_{>0}(k+m,n)$ and let
$Z \in \operatorname {Gr}_{>0}(k+m,n)$ and let ![]() $W:=Z^\perp$. The fiber
$W:=Z^\perp$. The fiber ![]() $\pi ^{-1}(W) \cap \mathcal {A}_{n,k,m}$ can be identified with the
$\pi ^{-1}(W) \cap \mathcal {A}_{n,k,m}$ can be identified with the ![]() $Z$-amplituhedron
$Z$-amplituhedron ![]() $\mathcal {A}_{n,k,m}(Z)$ via the map sending
$\mathcal {A}_{n,k,m}(Z)$ via the map sending ![]() $U$ to the row span of the
$U$ to the row span of the ![]() $(k+m)\times (k+m)$ matrix
$(k+m)\times (k+m)$ matrix ![]() $U\cdot Z^\text {t}$ (which has rank
$U\cdot Z^\text {t}$ (which has rank ![]() $k$). Thus we have
$k$). Thus we have
We have a map
given by ![]() $(V,W) \mapsto (W,\operatorname {span}(V,W))$. Since the matrix
$(V,W) \mapsto (W,\operatorname {span}(V,W))$. Since the matrix ![]() $U\cdot Z^\text {t}$ has rank
$U\cdot Z^\text {t}$ has rank ![]() $k$, and the subspace
$k$, and the subspace ![]() $U$ contains the kernel
$U$ contains the kernel ![]() $W$ of
$W$ of ![]() $Z$, it follows that the subspace
$Z$, it follows that the subspace ![]() $\operatorname {span}(V,W)$ always has dimension
$\operatorname {span}(V,W)$ always has dimension ![]() $k+\ell$. For
$k+\ell$. For ![]() $f \in \tilde {S_n}(-k,n-k)$, define
$f \in \tilde {S_n}(-k,n-k)$, define
 \begin{align*} \mathcal{A}^{{>}0}_{k+f} &:= \mathcal{Z}(\Pi^{{>}0}_{k+f} \times \operatorname{Gr}_{{>}0}^\perp(k+m,n)) \subset \mathcal{A}_{n,k,m}, \\ \mathcal{A}^{\ge0}_{k+f} &:= \overline{\mathcal{A}^{{>}0}_{k+f}} \subset \mathcal{A}_{n,k,m}. \end{align*}
\begin{align*} \mathcal{A}^{{>}0}_{k+f} &:= \mathcal{Z}(\Pi^{{>}0}_{k+f} \times \operatorname{Gr}_{{>}0}^\perp(k+m,n)) \subset \mathcal{A}_{n,k,m}, \\ \mathcal{A}^{\ge0}_{k+f} &:= \overline{\mathcal{A}^{{>}0}_{k+f}} \subset \mathcal{A}_{n,k,m}. \end{align*} Define ![]() $\mathcal {A}_{n,k,\ge m} \subset \mathcal {A}_{n,k,m}$ by
$\mathcal {A}_{n,k,\ge m} \subset \mathcal {A}_{n,k,m}$ by
The map ![]() $\mathcal {Z}$ restricts to a map
$\mathcal {Z}$ restricts to a map ![]() $\mathcal {Z}: \operatorname {Gr}_{\ge m}(k,n)\times \operatorname {Gr}_{>0}^\perp (k+m,n)\to \mathcal {A}_{n,k,\ge m}$. Let
$\mathcal {Z}: \operatorname {Gr}_{\ge m}(k,n)\times \operatorname {Gr}_{>0}^\perp (k+m,n)\to \mathcal {A}_{n,k,\ge m}$. Let ![]() $\mathcal {Z}^{\operatorname {op}}:\operatorname {Gr}_{>0}^\perp (\ell +m,n) \times \operatorname {Gr}_{\ge m}(k,n) \to \mathcal {A}_{n,\ell ,\ge m}$ denote the similar map sending
$\mathcal {Z}^{\operatorname {op}}:\operatorname {Gr}_{>0}^\perp (\ell +m,n) \times \operatorname {Gr}_{\ge m}(k,n) \to \mathcal {A}_{n,\ell ,\ge m}$ denote the similar map sending ![]() $({\tilde {W}},{\tilde V})$ to
$({\tilde {W}},{\tilde V})$ to ![]() $({\tilde {W}},\operatorname {span}({\tilde {W}}, {\tilde V}))$.
$({\tilde {W}},\operatorname {span}({\tilde {W}}, {\tilde V}))$.
Theorem 7.3 The stacked twist map
descends to a homeomorphism ![]() ${\tilde \theta }: \mathcal {A}_{n,k,\ge m} \to \mathcal {A}_{n,\ell ,\ge m}$, forming the following commutative diagram.
${\tilde \theta }: \mathcal {A}_{n,k,\ge m} \to \mathcal {A}_{n,\ell ,\ge m}$, forming the following commutative diagram.

The map ![]() ${\tilde \theta }$ restricts to homeomorphisms
${\tilde \theta }$ restricts to homeomorphisms ![]() ${\tilde \theta }:\mathcal {A}^{>0}_{k+f} \to \mathcal {A}^{>0}_{\ell +f^{-1}}$ for each
${\tilde \theta }:\mathcal {A}^{>0}_{k+f} \to \mathcal {A}^{>0}_{\ell +f^{-1}}$ for each ![]() $f\in \tilde {S_n}(-k,\ell )$.
$f\in \tilde {S_n}(-k,\ell )$.
Proof. Suppose ![]() $(W,U) \in \mathcal {A}_{n,k,\ge m}$. Let
$(W,U) \in \mathcal {A}_{n,k,\ge m}$. Let ![]() $V \in \operatorname {Gr}_{\ge m}(k,n)$ be chosen so that
$V \in \operatorname {Gr}_{\ge m}(k,n)$ be chosen so that ![]() $U = \operatorname {span}(V,W)$. Then
$U = \operatorname {span}(V,W)$. Then ![]() ${\tilde \theta }(W,U):=({\tilde {W}},{\tilde {U}})$, where
${\tilde \theta }(W,U):=({\tilde {W}},{\tilde {U}})$, where ![]() $\theta (V,W) = ({\tilde {W}},{\tilde V})$ and
$\theta (V,W) = ({\tilde {W}},{\tilde V})$ and ![]() ${\tilde {U}} = \operatorname {span}({\tilde {W}},{\tilde V})$. It follows from Proposition 4.8 that
${\tilde {U}} = \operatorname {span}({\tilde {W}},{\tilde V})$. It follows from Proposition 4.8 that ![]() $({\tilde {W}},{\tilde {U}})$ does not depend on the choice of
$({\tilde {W}},{\tilde {U}})$ does not depend on the choice of ![]() $V$. Thus
$V$. Thus ![]() ${\tilde \theta }$ is well-defined. (Alternatively, the rational map
${\tilde \theta }$ is well-defined. (Alternatively, the rational map ![]() ${\tilde \theta }: \textrm {Fl}(\ell ,k+\ell ;n) \dashrightarrow \textrm {Fl}(k,k+\ell ;n)$ can be defined directly from Lemma 10.1.) The last statement is immediate from Theorem 4.7.
${\tilde \theta }: \textrm {Fl}(\ell ,k+\ell ;n) \dashrightarrow \textrm {Fl}(k,k+\ell ;n)$ can be defined directly from Lemma 10.1.) The last statement is immediate from Theorem 4.7.
7.3 Subdivisions of the universal amplituhedron
We recast the notions of ![]() $(n,k,m)$-triangulations/subdivisions in the language of the universal amplituhedron.
$(n,k,m)$-triangulations/subdivisions in the language of the universal amplituhedron.
Lemma 7.4
(1) Let
 $f\in \tilde {S_n}(-k,n-k)$ be an affine permutation. Then
$f\in \tilde {S_n}(-k,n-k)$ be an affine permutation. Then  $f$ is
$f$ is  $(n,k,m)$-admissible if and only if
$(n,k,m)$-admissible if and only if  $\pi ^{-1}(W)\cap \mathcal {A}^{>0}_{k+f}$ contains at most
$\pi ^{-1}(W)\cap \mathcal {A}^{>0}_{k+f}$ contains at most  $1$ point for all
$1$ point for all  $W\in \operatorname {Gr}_{>0}^\perp (k+m,n)$.
$W\in \operatorname {Gr}_{>0}^\perp (k+m,n)$.(2) Let
 $f,g\in \tilde {S_n}(-k,n-k)$ be two affine permutations. Then
$f,g\in \tilde {S_n}(-k,n-k)$ be two affine permutations. Then  $f$ and
$f$ and  $g$ are
$g$ are  $(n,k,m)$-compatible if and only if
$(n,k,m)$-compatible if and only if  $\mathcal {A}^{>0}_{k+f}$ and
$\mathcal {A}^{>0}_{k+f}$ and  $\mathcal {A}^{>0}_{k+g}$ do not intersect.
$\mathcal {A}^{>0}_{k+g}$ do not intersect.
The following is an analog of Definition 7.1.
Definition 7.5 Let ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ be a collection of pairwise
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ be a collection of pairwise ![]() $(n,k,m)$-compatible affine permutations. We say that
$(n,k,m)$-compatible affine permutations. We say that ![]() $f_1,\dots ,f_N$ form a subdivision of the universal amplituhedron if the union of
$f_1,\dots ,f_N$ form a subdivision of the universal amplituhedron if the union of ![]() $\mathcal {A}^{>0}_{k+f_1},\dots ,\mathcal {A}^{>0}_{k+f_N}$ is a dense subset of
$\mathcal {A}^{>0}_{k+f_1},\dots ,\mathcal {A}^{>0}_{k+f_N}$ is a dense subset of ![]() $\mathcal {A}_{n,k,m}$, and we have
$\mathcal {A}_{n,k,m}$, and we have ![]() $\operatorname {dim} (\mathcal {A}^{>0}_{k+f_s})=\operatorname {dim}(\mathcal {A}_{n,k,m})$ for each
$\operatorname {dim} (\mathcal {A}^{>0}_{k+f_s})=\operatorname {dim}(\mathcal {A}_{n,k,m})$ for each ![]() $1\leq s\leq N$.
$1\leq s\leq N$.
More generally, suppose that ![]() $g \in \tilde {S_n}(-k,n-k)$ and
$g \in \tilde {S_n}(-k,n-k)$ and ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ is a collection of pairwise
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ is a collection of pairwise ![]() $(n,k,m)$-compatible affine permutations satisfying
$(n,k,m)$-compatible affine permutations satisfying ![]() $f_s \leq g$ for all
$f_s \leq g$ for all ![]() $1 \leq s \leq N$. We say that
$1 \leq s \leq N$. We say that ![]() $f_1,\dots ,f_N$ form a subdivision of
$f_1,\dots ,f_N$ form a subdivision of ![]() $\mathcal {A}^{\ge 0}_{k+g}$ if the union of
$\mathcal {A}^{\ge 0}_{k+g}$ if the union of ![]() $\mathcal {A}^{>0}_{k+f_1},\dots ,\mathcal {A}^{>0}_{k+f_N}$ is a dense subset of
$\mathcal {A}^{>0}_{k+f_1},\dots ,\mathcal {A}^{>0}_{k+f_N}$ is a dense subset of ![]() $\mathcal {A}^{\ge 0}_{k+g}$, and we have
$\mathcal {A}^{\ge 0}_{k+g}$, and we have ![]() $\operatorname {dim} (\mathcal {A}^{>0}_{k+f_s})=\operatorname {dim}(\mathcal {A}^{>0}_{k+g})$ for each
$\operatorname {dim} (\mathcal {A}^{>0}_{k+f_s})=\operatorname {dim}(\mathcal {A}^{>0}_{k+g})$ for each ![]() $1\leq s\leq N$.
$1\leq s\leq N$.
Lemma 7.6
• Let
 $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ be a collection of affine permutations. Then
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ be a collection of affine permutations. Then  $f_1,\dots ,f_N$ form an
$f_1,\dots ,f_N$ form an  $(n,k,m)$-subdivision of the amplituhedron if and only if they form a subdivision of the universal amplituhedron.
$(n,k,m)$-subdivision of the amplituhedron if and only if they form a subdivision of the universal amplituhedron.• Suppose that
 $g \in \tilde {S_n}(-k,n-k)$ and
$g \in \tilde {S_n}(-k,n-k)$ and  $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ is a collection of affine permutations. Then
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ is a collection of affine permutations. Then  $f_1,\dots ,f_N$ form an
$f_1,\dots ,f_N$ form an  $(n,k,m)$-subdivision of
$(n,k,m)$-subdivision of  $g$ if and only if they form a subdivision of
$g$ if and only if they form a subdivision of  $\mathcal {A}^{\ge 0}_{k+g}$.
$\mathcal {A}^{\ge 0}_{k+g}$.
Proof. Let
so that by definition ![]() $\mathcal {A}_{n,k,m}$ is the closure of
$\mathcal {A}_{n,k,m}$ is the closure of ![]() $\mathcal {A}'_{n,k,m}$. Suppose that
$\mathcal {A}'_{n,k,m}$. Suppose that ![]() $f_1,\dots ,f_N$ form an
$f_1,\dots ,f_N$ form an ![]() $(n,k,m)$-subdivision of the amplituhedron. Thus the images
$(n,k,m)$-subdivision of the amplituhedron. Thus the images ![]() $Z(\Pi ^{>0}_{k+f_1}),\dots ,Z(\Pi ^{>0}_{k+f_N})$ form a dense subset of
$Z(\Pi ^{>0}_{k+f_1}),\dots ,Z(\Pi ^{>0}_{k+f_N})$ form a dense subset of ![]() $\mathcal {A}_{n,k,m}(Z)$ for any
$\mathcal {A}_{n,k,m}(Z)$ for any ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$. We claim that
$Z\in \operatorname {Gr}_{>0}(k+m,n)$. We claim that ![]() $\mathcal {A}^{>0}_{k+f_1},\dots ,\mathcal {A}^{>0}_{k+f_N}$ form a dense subset of
$\mathcal {A}^{>0}_{k+f_1},\dots ,\mathcal {A}^{>0}_{k+f_N}$ form a dense subset of ![]() $\mathcal {A}'_{n,k,m}$, from which it follows that their union is dense in
$\mathcal {A}'_{n,k,m}$, from which it follows that their union is dense in ![]() $\mathcal {A}_{n,k,m}$. Indeed, take a pair
$\mathcal {A}_{n,k,m}$. Indeed, take a pair ![]() $(W,U)\in \mathcal {A}'_{n,k,m}$ and let
$(W,U)\in \mathcal {A}'_{n,k,m}$ and let ![]() $Z:=W^\perp \in \operatorname {Gr}_{>0}(k+m,n)$. There exists
$Z:=W^\perp \in \operatorname {Gr}_{>0}(k+m,n)$. There exists ![]() $1\leq s\leq N$ such that
$1\leq s\leq N$ such that ![]() $U\cdot Z^\text {t}$ belongs
$U\cdot Z^\text {t}$ belongs ![]() $Z(\Pi ^{\ge 0}_{k+f_s})$, and thus
$Z(\Pi ^{\ge 0}_{k+f_s})$, and thus ![]() $(W,U)$ belongs to the closure of
$(W,U)$ belongs to the closure of ![]() $\mathcal {A}^{>0}_{k+f_s}$.
$\mathcal {A}^{>0}_{k+f_s}$.
Conversely, suppose that ![]() $\mathcal {A}^{>0}_{k+f_1},\dots ,\mathcal {A}^{>0}_{k+f_N}$ form a dense subset of
$\mathcal {A}^{>0}_{k+f_1},\dots ,\mathcal {A}^{>0}_{k+f_N}$ form a dense subset of ![]() $\mathcal {A}_{n,k,m}$. Fix
$\mathcal {A}_{n,k,m}$. Fix ![]() $Z\in \operatorname {Gr}_{>0} (k+m,n)$, let
$Z\in \operatorname {Gr}_{>0} (k+m,n)$, let ![]() $W:=Z^\perp$,
$W:=Z^\perp$, ![]() $V\in \operatorname {Gr}_{\ge 0}(k,n)$,
$V\in \operatorname {Gr}_{\ge 0}(k,n)$, ![]() $U:=\operatorname {span}(V,W)$, and consider the point
$U:=\operatorname {span}(V,W)$, and consider the point ![]() $Y:=V\cdot Z^\text {t}$ of the amplituhedron
$Y:=V\cdot Z^\text {t}$ of the amplituhedron ![]() $\mathcal {A}_{n,k,m}(Z)$. We want to show that
$\mathcal {A}_{n,k,m}(Z)$. We want to show that ![]() $Y$ belongs to the closure of
$Y$ belongs to the closure of ![]() $Z(\Pi ^{>0}_{k+f_s})$ for some
$Z(\Pi ^{>0}_{k+f_s})$ for some ![]() $1\leq s\leq N$. We know that
$1\leq s\leq N$. We know that ![]() $(W,U)$ belongs to the closure of
$(W,U)$ belongs to the closure of ![]() $\mathcal {A}^{>0}_{k+f_s}$ for some
$\mathcal {A}^{>0}_{k+f_s}$ for some ![]() $1\leq s\leq N$. By assumption, there exists a sequence
$1\leq s\leq N$. By assumption, there exists a sequence ![]() $(W_1,U_1),(W_2,U_2),\dots$ converging to
$(W_1,U_1),(W_2,U_2),\dots$ converging to ![]() $(W,U)$ in
$(W,U)$ in ![]() $\textrm {Fl}(\ell ,k+\ell ;n)$ such that
$\textrm {Fl}(\ell ,k+\ell ;n)$ such that ![]() $(W_i,U_i)\in \mathcal {A}^{>0}_{k+f_s}$ for all
$(W_i,U_i)\in \mathcal {A}^{>0}_{k+f_s}$ for all ![]() $i\geq 1$. By the definition of
$i\geq 1$. By the definition of ![]() $\mathcal {A}^{>0}_{k+f_s}$, for each
$\mathcal {A}^{>0}_{k+f_s}$, for each ![]() $i\geq 1$ there exists
$i\geq 1$ there exists ![]() $V_i\in \Pi ^{>0}_{k+f_s}$ such that
$V_i\in \Pi ^{>0}_{k+f_s}$ such that ![]() $U_i = \operatorname {span}(V_i,W_i)$. Let us now consider the sequence
$U_i = \operatorname {span}(V_i,W_i)$. Let us now consider the sequence ![]() $(W,\operatorname {span}(V_i,W))\in \mathcal {A}^{>0}_{k+f_s}$ for
$(W,\operatorname {span}(V_i,W))\in \mathcal {A}^{>0}_{k+f_s}$ for ![]() $i\geq 1$. We claim that a subsequence of the points
$i\geq 1$. We claim that a subsequence of the points ![]() $\operatorname {span}(V_i,W)$ converges to
$\operatorname {span}(V_i,W)$ converges to ![]() $U$ in
$U$ in ![]() $\operatorname {Gr}(k+\ell ,n)$, and thus
$\operatorname {Gr}(k+\ell ,n)$, and thus ![]() $(W,U)$ belongs to the closure of
$(W,U)$ belongs to the closure of ![]() $\mathcal {A}^{>0}_{k+f_s}$. The points
$\mathcal {A}^{>0}_{k+f_s}$. The points ![]() $V_i$ all belong to the compact set
$V_i$ all belong to the compact set ![]() $\Pi ^{\ge 0}_{k+f_s}$ and therefore a subsequence
$\Pi ^{\ge 0}_{k+f_s}$ and therefore a subsequence ![]() $V_{i_1},V_{i_2},\ldots$ converges to
$V_{i_1},V_{i_2},\ldots$ converges to ![]() $V' \in \Pi ^{\ge 0}_{k+f_s}$. Any subspace
$V' \in \Pi ^{\ge 0}_{k+f_s}$. Any subspace ![]() $V''\in \operatorname {Gr}(k,n)$ in the neighborhood of
$V''\in \operatorname {Gr}(k,n)$ in the neighborhood of ![]() $V'$ satisfies
$V'$ satisfies ![]() $V''\cap W=\{0\}$, and thus the map
$V''\cap W=\{0\}$, and thus the map ![]() $V''\mapsto \operatorname {span}(V'',W)$ is continuous at
$V''\mapsto \operatorname {span}(V'',W)$ is continuous at ![]() $V'$. We get that
$V'$. We get that ![]() $\operatorname {span}(V_{i_1},W) = U_{i_1}, \operatorname {span}(V_{i_2},W) = U_{i_2}, \ldots$ converges to
$\operatorname {span}(V_{i_1},W) = U_{i_1}, \operatorname {span}(V_{i_2},W) = U_{i_2}, \ldots$ converges to ![]() $\operatorname {span}(W,V')$ in
$\operatorname {span}(W,V')$ in ![]() $\operatorname {Gr}(k+\ell ,n)$, and we must also have
$\operatorname {Gr}(k+\ell ,n)$, and we must also have ![]() $\operatorname {span}(W,V') = U$.
$\operatorname {span}(W,V') = U$.
We have shown the first part of the lemma, and the proof of the second part is completely analogous.
Definition 7.7 A triangulation of the universal amplituhedron (respectively, of ![]() $\mathcal {A}^{\ge 0}_{k+g}$) is a subdivision
$\mathcal {A}^{\ge 0}_{k+g}$) is a subdivision ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ of the universal amplituhedron that consists of
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ of the universal amplituhedron that consists of ![]() $(n,k,m)$-admissible affine permutations.
$(n,k,m)$-admissible affine permutations.
The following result follows from Lemmas 7.4 and 7.6 together with Theorem 3.5.
Corollary 7.8 Let ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ be a collection of affine permutations. The following are equivalent:
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ be a collection of affine permutations. The following are equivalent:
•
 $f_1,\dots ,f_N$ form an
$f_1,\dots ,f_N$ form an  $(n,k,m)$-triangulation of the amplituhedron;
$(n,k,m)$-triangulation of the amplituhedron;•
 $f_1,\dots ,f_N$ form a triangulation of the universal amplituhedron
$f_1,\dots ,f_N$ form a triangulation of the universal amplituhedron  $\mathcal {A}_{n,k,m}$;
$\mathcal {A}_{n,k,m}$;•
 $f_1^{-1},\dots ,f_N^{-1}$ form a triangulation of the universal amplituhedron
$f_1^{-1},\dots ,f_N^{-1}$ form a triangulation of the universal amplituhedron  $\mathcal {A}_{n,\ell ,m}$.
$\mathcal {A}_{n,\ell ,m}$.
A similar result applies to triangulations of ![]() $g \in \tilde {S_n}(-k,n-k)$.
$g \in \tilde {S_n}(-k,n-k)$.
8. The amplituhedron form
We review the definition of the amplituhedron form, which is a rational differential form on the Grassmannian. In § 8.5, the constructions are illustrated by computations for ![]() $k=\ell =1$,
$k=\ell =1$, ![]() $m=2$, and
$m=2$, and ![]() $n=4$.
$n=4$.
It is natural to work over the complex numbers, and we denote by ![]() $\operatorname {Gr}_\mathbb {C}(k,n)$ and
$\operatorname {Gr}_\mathbb {C}(k,n)$ and ![]() $\textrm {Fl}_\mathbb {C}(a,b;n)$ the complex Grassmannian and the complex two-step flag variety, respectively. The map
$\textrm {Fl}_\mathbb {C}(a,b;n)$ the complex Grassmannian and the complex two-step flag variety, respectively. The map ![]() $Z$ induces a rational map
$Z$ induces a rational map ![]() $Z: \operatorname {Gr}_\mathbb {C}(k,n) \dashrightarrow \operatorname {Gr}_\mathbb {C}(k,k+m)$, the image of which is equal to
$Z: \operatorname {Gr}_\mathbb {C}(k,n) \dashrightarrow \operatorname {Gr}_\mathbb {C}(k,k+m)$, the image of which is equal to ![]() $\operatorname {Gr}_\mathbb {C}(k, k+m)$. Given an affine permutation
$\operatorname {Gr}_\mathbb {C}(k, k+m)$. Given an affine permutation ![]() $f\in \tilde {S_n}(-k,n-k)$, denote by
$f\in \tilde {S_n}(-k,n-k)$, denote by ![]() $\Pi _{k+f}^\mathbb {C}\subseteq \operatorname {Gr}_\mathbb {C}(k,n)$ the Zariski closure of
$\Pi _{k+f}^\mathbb {C}\subseteq \operatorname {Gr}_\mathbb {C}(k,n)$ the Zariski closure of ![]() $\Pi ^{>0}_{k+f}$ in
$\Pi ^{>0}_{k+f}$ in ![]() $\operatorname {Gr}_\mathbb {C}(k,n)$, called the positroid variety. See Definition 11.1 for an alternative description.
$\operatorname {Gr}_\mathbb {C}(k,n)$, called the positroid variety. See Definition 11.1 for an alternative description.
8.1 Degree  $1$ cells
$1$ cells
Definition 8.1 Let ![]() $Z \in \operatorname {Gr}_\mathbb {C}(k+m,n)$. We say that an affine permutation
$Z \in \operatorname {Gr}_\mathbb {C}(k+m,n)$. We say that an affine permutation ![]() $f\in \tilde {S_n}(-k,n-k)$ has
$f\in \tilde {S_n}(-k,n-k)$ has ![]() $Z$-degree
$Z$-degree ![]() $1$ if
$1$ if ![]() $\operatorname {dim} \Pi _{k+f}^\mathbb {C}=\operatorname {dim} Z(\Pi _{k+f}^\mathbb {C})=km$ and the rational map
$\operatorname {dim} \Pi _{k+f}^\mathbb {C}=\operatorname {dim} Z(\Pi _{k+f}^\mathbb {C})=km$ and the rational map ![]() $Z:\Pi _{k+f}^\mathbb {C} \dashrightarrow \operatorname {Gr}_\mathbb {C}(k, k+m)$ is birational, that is, it restricts to an isomorphism between Zariski open subsets
$Z:\Pi _{k+f}^\mathbb {C} \dashrightarrow \operatorname {Gr}_\mathbb {C}(k, k+m)$ is birational, that is, it restricts to an isomorphism between Zariski open subsets ![]() $A\subset \Pi _{k+f}^\mathbb {C}$ and
$A\subset \Pi _{k+f}^\mathbb {C}$ and ![]() $B\subset \operatorname {Gr}_\mathbb {C}(k,k+m)$.
$B\subset \operatorname {Gr}_\mathbb {C}(k,k+m)$.
We say that an affine permutation ![]() $f\in \tilde {S_n}(-k,n-k)$ has degree
$f\in \tilde {S_n}(-k,n-k)$ has degree ![]() $1$ if it has
$1$ if it has ![]() $Z$-degree
$Z$-degree ![]() $1$ for
$1$ for ![]() $Z$ belonging to a non-empty Zariski open subset of
$Z$ belonging to a non-empty Zariski open subset of ![]() $\operatorname {Gr}_\mathbb {C}(k+m,n)$.
$\operatorname {Gr}_\mathbb {C}(k+m,n)$.
Thus in order for ![]() $f$ to have
$f$ to have ![]() $Z$-degree
$Z$-degree ![]() $1$, we must have
$1$, we must have ![]() $\operatorname {inv}(f)=k\ell$. We note that if
$\operatorname {inv}(f)=k\ell$. We note that if ![]() $f$ satisfies
$f$ satisfies ![]() $\operatorname {dim} \Pi _{k+f}^\mathbb {C}=\operatorname {dim} Z(\Pi _{k+f}^\mathbb {C})=km$ for a generic
$\operatorname {dim} \Pi _{k+f}^\mathbb {C}=\operatorname {dim} Z(\Pi _{k+f}^\mathbb {C})=km$ for a generic ![]() $Z\in \operatorname {Gr}_\mathbb {C}(k,k+m)$ then
$Z\in \operatorname {Gr}_\mathbb {C}(k,k+m)$ then ![]() $f$ is said to have kinematical support, see [Reference Arkani-Hamed, Bourjaily, Cachazo, Goncharov, Postnikov and TrnkaABC16, § 10].
$f$ is said to have kinematical support, see [Reference Arkani-Hamed, Bourjaily, Cachazo, Goncharov, Postnikov and TrnkaABC16, § 10].
Remark 8.2 Suppose that ![]() $f$ has degree
$f$ has degree ![]() $1$. Since
$1$. Since ![]() $\operatorname {Gr}_{>0}(k+m,n)$ is Zariski dense in
$\operatorname {Gr}_{>0}(k+m,n)$ is Zariski dense in ![]() $\operatorname {Gr}_\mathbb {C}(k+m, n)$,
$\operatorname {Gr}_\mathbb {C}(k+m, n)$, ![]() $f$ has
$f$ has ![]() $Z$-degree
$Z$-degree ![]() $1$ for
$1$ for ![]() $Z$ belonging to an open dense subset of
$Z$ belonging to an open dense subset of ![]() $\operatorname {Gr}_{>0}(k+m,n)$ in the analytic topology.
$\operatorname {Gr}_{>0}(k+m,n)$ in the analytic topology.
Remark 8.3 Suppose that ![]() $f$ has
$f$ has ![]() $Z$-degree
$Z$-degree ![]() $1$. Since
$1$. Since ![]() $\Pi ^{>0}_{k+f}$ is Zariski dense in
$\Pi ^{>0}_{k+f}$ is Zariski dense in ![]() $\Pi _{k+f}^\mathbb {C}$, it follows that
$\Pi _{k+f}^\mathbb {C}$, it follows that ![]() $Z$ restricts to a diffeomorphism on an open dense subset of
$Z$ restricts to a diffeomorphism on an open dense subset of ![]() $\Pi ^{>0}_{k+f}$ in the analytic topology.
$\Pi ^{>0}_{k+f}$ in the analytic topology.
Thus if ![]() $f$ has
$f$ has ![]() $Z$-degree
$Z$-degree ![]() $1$ then
$1$ then ![]() $Z$ is injective on an open dense subset of the positroid cell
$Z$ is injective on an open dense subset of the positroid cell ![]() $\Pi ^{>0}_{k+f}$, but not necessarily on the whole positroid cell.
$\Pi ^{>0}_{k+f}$, but not necessarily on the whole positroid cell.
Conjecture 8.4 Let ![]() $f\in \tilde {S_n}(-k,n-k)$ be an affine permutation with
$f\in \tilde {S_n}(-k,n-k)$ be an affine permutation with ![]() $\operatorname {inv}(f)=k\ell$. Then the following are equivalent:
$\operatorname {inv}(f)=k\ell$. Then the following are equivalent:
(a)
 $f$ is
$f$ is  $(n,k,m)$-admissible;
$(n,k,m)$-admissible;(b)
 $f$ has degree
$f$ has degree  $1$;
$1$;(c)
 $f$ has
$f$ has  $Z$-degree
$Z$-degree  $1$ for all
$1$ for all  $Z \in \operatorname {Gr}_{>0}(k+m,n)$.
$Z \in \operatorname {Gr}_{>0}(k+m,n)$.
In each case, ![]() $Z$ is a diffeomorphism
$Z$ is a diffeomorphism ![]() $\Pi ^{>0}_{k+f}\to Z(\Pi ^{>0}_{k+f})$.
$\Pi ^{>0}_{k+f}\to Z(\Pi ^{>0}_{k+f})$.
It is clear that (c) implies (b). In what follows, we restrict ourselves to only ![]() $(n,k,m)$-admissible affine permutations that have degree
$(n,k,m)$-admissible affine permutations that have degree ![]() $1$. It is not difficult to see that Conjecture 8.4 holds for
$1$. It is not difficult to see that Conjecture 8.4 holds for ![]() $k =1$, since in this case every affine permutation
$k =1$, since in this case every affine permutation ![]() $f\in \tilde {S_n}(-k,n-k)$ with
$f\in \tilde {S_n}(-k,n-k)$ with ![]() $\operatorname {inv}(f)=k\ell$ satisfies (a), (b), and (c). Let us now explain why Conjecture 8.4 also holds for
$\operatorname {inv}(f)=k\ell$ satisfies (a), (b), and (c). Let us now explain why Conjecture 8.4 also holds for ![]() $\ell = 1$. Let
$\ell = 1$. Let ![]() $\ell =1$, and consider an affine permutation
$\ell =1$, and consider an affine permutation ![]() $f\in \tilde {S_n}(-k,\ell )$ with
$f\in \tilde {S_n}(-k,\ell )$ with ![]() $\operatorname {inv}(f)=k\ell$. Then
$\operatorname {inv}(f)=k\ell$. Then ![]() $f$ satisfies (a) by Theorem 3.5, part (1). Next,
$f$ satisfies (a) by Theorem 3.5, part (1). Next, ![]() $f$ satisfies (b) by Proposition 8.5 below. Finally, we have already noted above that
$f$ satisfies (b) by Proposition 8.5 below. Finally, we have already noted above that ![]() $f^{-1}$ satisfies (c), i.e. that
$f^{-1}$ satisfies (c), i.e. that ![]() $f^{-1}\in \tilde {S_n}(-\ell ,k)$ has
$f^{-1}\in \tilde {S_n}(-\ell ,k)$ has ![]() ${\tilde Z}$-degree
${\tilde Z}$-degree ![]() $1$ for all
$1$ for all ![]() ${\tilde Z} \in \operatorname {Gr}_{>0}(\ell +m,n)$. In particular, it is easy to see that for any
${\tilde Z} \in \operatorname {Gr}_{>0}(\ell +m,n)$. In particular, it is easy to see that for any ![]() ${\tilde V}\in \operatorname {Gr}_{>0}(\ell ,n)$, there exists a unique
${\tilde V}\in \operatorname {Gr}_{>0}(\ell ,n)$, there exists a unique ![]() ${\tilde V}'\in \Pi _{\ell +f^{-1}}^\mathbb {C}$ such that
${\tilde V}'\in \Pi _{\ell +f^{-1}}^\mathbb {C}$ such that ![]() ${\tilde V}\cdot {\tilde Z}^\text {t}={\tilde V}'\cdot {\tilde Z}^\text {t}$. By Lemma 10.6, it follows that for any
${\tilde V}\cdot {\tilde Z}^\text {t}={\tilde V}'\cdot {\tilde Z}^\text {t}$. By Lemma 10.6, it follows that for any ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$ and
$Z\in \operatorname {Gr}_{>0}(k+m,n)$ and ![]() $V\in \operatorname {Gr}_{>0}(k,n)$, there exists a unique
$V\in \operatorname {Gr}_{>0}(k,n)$, there exists a unique ![]() $V'\in \Pi _{k+f}^\mathbb {C}$ such that
$V'\in \Pi _{k+f}^\mathbb {C}$ such that ![]() $V\cdot Z^\text {t}=V'\cdot Z^\text {t}$. Since this holds for all
$V\cdot Z^\text {t}=V'\cdot Z^\text {t}$. Since this holds for all ![]() $V\in \operatorname {Gr}_{>0}(k,n)$, it must hold for
$V\in \operatorname {Gr}_{>0}(k,n)$, it must hold for ![]() $V$ belonging to a Zariski dense subset of
$V$ belonging to a Zariski dense subset of ![]() $\operatorname {Gr}_\mathbb {C}(k,n)$, and thus
$\operatorname {Gr}_\mathbb {C}(k,n)$, and thus ![]() $f$ indeed has
$f$ indeed has ![]() $Z$-degree
$Z$-degree ![]() $1$ for any
$1$ for any ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$. This shows that Conjecture 8.4 holds for
$Z\in \operatorname {Gr}_{>0}(k+m,n)$. This shows that Conjecture 8.4 holds for ![]() $\ell =1$.
$\ell =1$.
We will see in Lemma 9.3 that if ![]() $f\in \tilde {S_n}(-k,n-k)$ has degree
$f\in \tilde {S_n}(-k,n-k)$ has degree ![]() $1$ then we must have
$1$ then we must have ![]() $f\in \tilde {S_n}(-k,\ell )$. By a result of [Reference LamLam16a],
$f\in \tilde {S_n}(-k,\ell )$. By a result of [Reference LamLam16a], ![]() $f$ has degree
$f$ has degree ![]() $1$ if and only if the coefficient of a certain rectangular Schur function in the corresponding affine Stanley symmetric function is equal to
$1$ if and only if the coefficient of a certain rectangular Schur function in the corresponding affine Stanley symmetric function is equal to ![]() $1$. An important corollary of this is the following result that we prove in § 12.3.
$1$. An important corollary of this is the following result that we prove in § 12.3.
Proposition 8.5 An affine permutation ![]() $f\in \tilde {S_n}(-k,\ell )$ has degree
$f\in \tilde {S_n}(-k,\ell )$ has degree ![]() $1$ if and only if
$1$ if and only if ![]() $f^{-1}\in \tilde {S_n}(-\ell ,k)$ has degree
$f^{-1}\in \tilde {S_n}(-\ell ,k)$ has degree ![]() $1$.
$1$.
Definition 8.6 Given ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$, we say that
$Z\in \operatorname {Gr}_{>0}(k+m,n)$, we say that ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ form a
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ form a ![]() $Z$-triangulation of degree
$Z$-triangulation of degree ![]() $1$ if they form a
$1$ if they form a ![]() $Z$-triangulation and
$Z$-triangulation and ![]() $f_s$ has
$f_s$ has ![]() $Z$-degree
$Z$-degree ![]() $1$ for
$1$ for ![]() $1\leq s\leq N$.
$1\leq s\leq N$.
We say that ![]() $f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ form an
$f_1,\dots ,f_N\in \tilde {S_n}(-k,n-k)$ form an ![]() $(n,k,m)$-triangulation of degree
$(n,k,m)$-triangulation of degree ![]() $1$ if they form an
$1$ if they form an ![]() $(n,k,m)$-triangulation of the amplituhedron and
$(n,k,m)$-triangulation of the amplituhedron and ![]() $f_s$ has degree
$f_s$ has degree ![]() $1$ for
$1$ for ![]() $1\leq s\leq N$.
$1\leq s\leq N$.
Note that (without knowing Conjecture 8.4) it may not be true that an ![]() $(n,k,m)$-triangulation of degree
$(n,k,m)$-triangulation of degree ![]() $1$ is a
$1$ is a ![]() $Z$-triangulation of degree
$Z$-triangulation of degree ![]() $1$ for all
$1$ for all ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$, but only for all
$Z\in \operatorname {Gr}_{>0}(k+m,n)$, but only for all ![]() $Z$ belonging to an open dense subset of
$Z$ belonging to an open dense subset of ![]() $\operatorname {Gr}_{>0}(k+m,n)$.
$\operatorname {Gr}_{>0}(k+m,n)$.
Corollary 8.7 Let ![]() $\mathcal {T}=\{f_1,\dots ,f_N\}\subset \tilde {S_n}(-k,\ell )$ be an
$\mathcal {T}=\{f_1,\dots ,f_N\}\subset \tilde {S_n}(-k,\ell )$ be an ![]() $(n,k,m)$-triangulation of degree
$(n,k,m)$-triangulation of degree ![]() $1$. Define
$1$. Define ![]() $\mathcal {T}':=\{f_1^{-1},\dots ,f_N^{-1}\}\subset \tilde {S_n}(-\ell ,k)$. Then
$\mathcal {T}':=\{f_1^{-1},\dots ,f_N^{-1}\}\subset \tilde {S_n}(-\ell ,k)$. Then ![]() $\mathcal {T}'$ is an
$\mathcal {T}'$ is an ![]() $(n,\ell ,m)$-triangulation of degree
$(n,\ell ,m)$-triangulation of degree ![]() $1$.
$1$.
8.2 The amplituhedron form
For us, the crucial property of a degree ![]() $1$ map is that it allows one to define the pushforward form
$1$ map is that it allows one to define the pushforward form ![]() $\omega _{Z(\Pi _{k+f}^{\mathbb {C}})}$ on
$\omega _{Z(\Pi _{k+f}^{\mathbb {C}})}$ on ![]() $\operatorname {Gr}_\mathbb {C}(k,k+m)$ via a pullback. Suppose that
$\operatorname {Gr}_\mathbb {C}(k,k+m)$ via a pullback. Suppose that ![]() $f\in \tilde {S_n}(-k,n-k)$ has
$f\in \tilde {S_n}(-k,n-k)$ has ![]() $Z$-degree
$Z$-degree ![]() $1$ and
$1$ and ![]() $\operatorname {inv}(f) = k\ell$. Thus
$\operatorname {inv}(f) = k\ell$. Thus ![]() $Z$ restricts to an isomorphism between Zariski open subsets
$Z$ restricts to an isomorphism between Zariski open subsets ![]() $A\subset \Pi _{k+f}^\mathbb {C}$ and
$A\subset \Pi _{k+f}^\mathbb {C}$ and ![]() $B\subset \operatorname {Gr}_\mathbb {C}(k,k+m)$. We define the rational top form
$B\subset \operatorname {Gr}_\mathbb {C}(k,k+m)$. We define the rational top form ![]() $\omega _{Z(\Pi _{k+f}^{\mathbb {C}})}$ on
$\omega _{Z(\Pi _{k+f}^{\mathbb {C}})}$ on ![]() $B$, and by extensionFootnote 4 on
$B$, and by extensionFootnote 4 on ![]() $\operatorname {Gr}_\mathbb {C}(k,k+m)$, as the pullback
$\operatorname {Gr}_\mathbb {C}(k,k+m)$, as the pullback
where ![]() $Z^{-1}:B\to A$ denotes the inverse of the isomorphism
$Z^{-1}:B\to A$ denotes the inverse of the isomorphism ![]() $Z:A\to B$.
$Z:A\to B$.
Recall from § 5.2 that for ![]() $f\in \tilde {S_n}(-k,n-k)$, the canonical form
$f\in \tilde {S_n}(-k,n-k)$, the canonical form ![]() $\omega _{k+f}$ on
$\omega _{k+f}$ on ![]() $\Pi ^{>0}_{k+f}$ is defined up to a sign. For the purposes of the amplituhedron form, we need to add up the forms
$\Pi ^{>0}_{k+f}$ is defined up to a sign. For the purposes of the amplituhedron form, we need to add up the forms ![]() $\omega _{Z(\Pi _{k+f}^{\mathbb {C}})}$ for various
$\omega _{Z(\Pi _{k+f}^{\mathbb {C}})}$ for various ![]() $f$. Thus it is necessary pick a particular sign of
$f$. Thus it is necessary pick a particular sign of ![]() $\omega _{k+f}$ for each
$\omega _{k+f}$ for each ![]() $f\in \tilde {S_n}(-k,n-k)$.
$f\in \tilde {S_n}(-k,n-k)$.
Proposition 8.8 Let ![]() $f\in \tilde {S_n}(-k,n-k)$ be an affine permutation of
$f\in \tilde {S_n}(-k,n-k)$ be an affine permutation of ![]() $Z$-degree
$Z$-degree ![]() $1$. Recall that by Remark 8.3, there exists an open dense subset
$1$. Recall that by Remark 8.3, there exists an open dense subset ![]() $A\subset \Pi ^{>0}_{k+f}$ such that the restriction of
$A\subset \Pi ^{>0}_{k+f}$ such that the restriction of ![]() $Z$ to
$Z$ to ![]() $A$ is a diffeomorphism. If
$A$ is a diffeomorphism. If ![]() $f$ is
$f$ is ![]() $Z$-admissible then the Jacobian of
$Z$-admissible then the Jacobian of ![]() $Z$ on
$Z$ on ![]() $A$ has constant sign.
$A$ has constant sign.
Thus for an ![]() $(n,k,m)$-admissible affine permutation of degree
$(n,k,m)$-admissible affine permutation of degree ![]() $1$, we can distinguish between
$1$, we can distinguish between ![]() $Z$ being orientation reversing or orientation preserving on the real manifold
$Z$ being orientation reversing or orientation preserving on the real manifold ![]() $\Pi ^{>0}_{k+f}$.
$\Pi ^{>0}_{k+f}$.
Let us choose some rational top form ![]() $\omega ^{\operatorname {ref}}_{k,k+m}$ on
$\omega ^{\operatorname {ref}}_{k,k+m}$ on ![]() $\operatorname {Gr}(k,k+m)$ that is non-vanishing on
$\operatorname {Gr}(k,k+m)$ that is non-vanishing on ![]() $\mathcal {A}_{n,k,m}(Z)$. This is always possible since
$\mathcal {A}_{n,k,m}(Z)$. This is always possible since ![]() $\mathcal {A}_{n,k,m}(Z)$ lies completely within some open Schubert cell (diffeomorphic to the orientable manifold
$\mathcal {A}_{n,k,m}(Z)$ lies completely within some open Schubert cell (diffeomorphic to the orientable manifold ![]() $\mathbb {R}^{km})$ of
$\mathbb {R}^{km})$ of ![]() $\operatorname {Gr}(k,k+m)$, see [Reference LamLam16b, Proposition 15.2 and Lemma 15.6]. We call
$\operatorname {Gr}(k,k+m)$, see [Reference LamLam16b, Proposition 15.2 and Lemma 15.6]. We call ![]() $\omega ^{\operatorname {ref}}_{k,k+m}$ the reference form.
$\omega ^{\operatorname {ref}}_{k,k+m}$ the reference form.
Definition 8.9 Suppose that ![]() $f\in \tilde {S_n}(-k,n-k)$ has
$f\in \tilde {S_n}(-k,n-k)$ has ![]() $Z$-degree
$Z$-degree ![]() $1$. We say that the form
$1$. We say that the form ![]() $\omega _{k+f}$ is positive with respect to
$\omega _{k+f}$ is positive with respect to ![]() $\omega ^{\operatorname {ref}}_{k,k+m}$ if the forms
$\omega ^{\operatorname {ref}}_{k,k+m}$ if the forms ![]() $\omega _{Z(\Pi _{k+f}^{\mathbb {C}})}$ and
$\omega _{Z(\Pi _{k+f}^{\mathbb {C}})}$ and ![]() $\omega ^{\operatorname {ref}}_{k,k+m}$ have the same sign when restricted to
$\omega ^{\operatorname {ref}}_{k,k+m}$ have the same sign when restricted to ![]() $Z(\Pi ^{>0}_{k+f})$ (whenever both are non-zero).
$Z(\Pi ^{>0}_{k+f})$ (whenever both are non-zero).
We note that ![]() $\omega _{k+f}$ is non-vanishing on
$\omega _{k+f}$ is non-vanishing on ![]() $\Pi ^{>0}_{k+f}$. By Proposition 8.8, we may and will pick a sign for
$\Pi ^{>0}_{k+f}$. By Proposition 8.8, we may and will pick a sign for ![]() $\omega _{k+f}$ so that the pushforward form
$\omega _{k+f}$ so that the pushforward form ![]() $\omega _{Z(\Pi _{k+f}^{\mathbb {C}})}$ is positive with respect to the fixed reference form
$\omega _{Z(\Pi _{k+f}^{\mathbb {C}})}$ is positive with respect to the fixed reference form ![]() $\omega ^{\operatorname {ref}}_{k,k+m}$ on
$\omega ^{\operatorname {ref}}_{k,k+m}$ on ![]() $\operatorname {Gr}(k,k+m)$.
$\operatorname {Gr}(k,k+m)$.
Definition 8.10 For ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$ and a
$Z\in \operatorname {Gr}_{>0}(k+m,n)$ and a ![]() $Z$-triangulation
$Z$-triangulation ![]() $\mathcal {T}=\{f_1,\dots ,f_N\}$ of degree
$\mathcal {T}=\{f_1,\dots ,f_N\}$ of degree ![]() $1$, define the amplituhedron form
$1$, define the amplituhedron form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ on
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ on ![]() $\operatorname {Gr}_\mathbb {C}(k,k+m)$ by
$\operatorname {Gr}_\mathbb {C}(k,k+m)$ by
 \begin{equation} \omega^{{({\mathcal{T}})}}_{\mathcal{A}_{n,k,m}(Z)}:=\sum_{s=1}^N\omega_{Z(\Pi_{k+f_s}^\mathbb{C})}. \end{equation}
\begin{equation} \omega^{{({\mathcal{T}})}}_{\mathcal{A}_{n,k,m}(Z)}:=\sum_{s=1}^N\omega_{Z(\Pi_{k+f_s}^\mathbb{C})}. \end{equation} We emphasize again that the sign of every summand in the right-hand side of the above equation is chosen so that the signs of ![]() $\omega _{Z(\Pi _{k+f_s}^\mathbb {C})}$ and
$\omega _{Z(\Pi _{k+f_s}^\mathbb {C})}$ and ![]() $\omega ^{\operatorname {ref}}_{k,k+m}$ coincide on
$\omega ^{\operatorname {ref}}_{k,k+m}$ coincide on ![]() $Z(\Pi ^{>0}_{k+f_s})$ for each
$Z(\Pi ^{>0}_{k+f_s})$ for each ![]() $1\leq s\leq N$. The following has been numerically verified in the physics literature in a number of cases when
$1\leq s\leq N$. The following has been numerically verified in the physics literature in a number of cases when ![]() $m = 4$.
$m = 4$.
Conjecture 8.11 The form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ does not depend on the choice of a triangulation
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ does not depend on the choice of a triangulation ![]() $\mathcal {T}$.
$\mathcal {T}$.
When Conjecture 8.11 holds, we denote by ![]() $\omega _{\mathcal {A}_{n,k,m}(Z)}$ the triangulation independent amplituhedron form. This conjectural amplituhedron form is the one presented in the original definition of the amplituhedron [Reference Arkani-Hamed and TrnkaAT14]. A different conjectural characterization of the amplituhedron form via ‘positive geometries’ is given in [Reference Arkani-Hamed, Bai and LamABL17]. It is an important open problem to give a formula for
$\omega _{\mathcal {A}_{n,k,m}(Z)}$ the triangulation independent amplituhedron form. This conjectural amplituhedron form is the one presented in the original definition of the amplituhedron [Reference Arkani-Hamed and TrnkaAT14]. A different conjectural characterization of the amplituhedron form via ‘positive geometries’ is given in [Reference Arkani-Hamed, Bai and LamABL17]. It is an important open problem to give a formula for ![]() $\omega _{\mathcal {A}_{n,k,m}(Z)}$ without referring to triangulations. See Conjecture 13.5 for a related discussion.
$\omega _{\mathcal {A}_{n,k,m}(Z)}$ without referring to triangulations. See Conjecture 13.5 for a related discussion.
8.3 The universal amplituhedron form
The form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ is a top form on
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ is a top form on ![]() $\operatorname {Gr}_\mathbb {C}(k,k+m)$ that depends on
$\operatorname {Gr}_\mathbb {C}(k,k+m)$ that depends on ![]() $Z$. We now let
$Z$. We now let ![]() $Z$ vary over
$Z$ vary over ![]() $\operatorname {Gr}_{>0}(k+m,n)$, and define a closely related top form
$\operatorname {Gr}_{>0}(k+m,n)$, and define a closely related top form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ on
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ on ![]() $\textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n)$.
$\textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n)$.
As in the construction of ![]() $\omega ^{\operatorname {ref}}_{k,k+m}$, each
$\omega ^{\operatorname {ref}}_{k,k+m}$, each ![]() $Z$-amplituhedron
$Z$-amplituhedron ![]() $\mathcal {A}_{n,k,m}(Z)$ is contained in an open Schubert cell
$\mathcal {A}_{n,k,m}(Z)$ is contained in an open Schubert cell ![]() $C(Z)$ of
$C(Z)$ of ![]() $\operatorname {Gr}(k,k+m)$. Thus the interior of the universal amplituhedron is contained in the orientable submanifold of
$\operatorname {Gr}(k,k+m)$. Thus the interior of the universal amplituhedron is contained in the orientable submanifold of ![]() $\textrm {Fl}(\ell ,k+\ell ;n)$, which maps to
$\textrm {Fl}(\ell ,k+\ell ;n)$, which maps to ![]() $\operatorname {Gr}_{>0}(k+m,n)$ with fiber
$\operatorname {Gr}_{>0}(k+m,n)$ with fiber ![]() $C(Z)$ over each
$C(Z)$ over each ![]() $Z \in \operatorname {Gr}_{>0}(k+m,n)$. (Note that
$Z \in \operatorname {Gr}_{>0}(k+m,n)$. (Note that ![]() $\operatorname {Gr}_{>0}(k+m,n)$ is diffeomorphic to an open ball and is in particular orientable and contractible.) We may thus choose a reference top form
$\operatorname {Gr}_{>0}(k+m,n)$ is diffeomorphic to an open ball and is in particular orientable and contractible.) We may thus choose a reference top form ![]() $\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}$ on
$\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}$ on ![]() $\textrm {Fl}(\ell ,k+\ell ;n)$ so that it is non-vanishing on the interior of
$\textrm {Fl}(\ell ,k+\ell ;n)$ so that it is non-vanishing on the interior of ![]() $\mathcal {A}_{n,k,m}$.
$\mathcal {A}_{n,k,m}$.
Proposition 8.12 Suppose that ![]() $f\in \tilde {S_n}(-k,n-k)$ has degree
$f\in \tilde {S_n}(-k,n-k)$ has degree ![]() $1$. Then the rational map
$1$. Then the rational map
sending ![]() $(V,W)$ to
$(V,W)$ to ![]() $(W, \operatorname {span}(V,W))$ is a birational map.
$(W, \operatorname {span}(V,W))$ is a birational map.
Proposition 8.13 Let ![]() $f\in \tilde {S_n}(-k,n-k)$ be an
$f\in \tilde {S_n}(-k,n-k)$ be an ![]() $(n,k,m)$-admissible affine permutation of degree
$(n,k,m)$-admissible affine permutation of degree ![]() $1$. Then there exists an open dense subset
$1$. Then there exists an open dense subset ![]() $A\subset \Pi ^{>0}_{k+f} \times \operatorname {Gr}_{>0}^\perp (k+m,n)$ such that the restriction of
$A\subset \Pi ^{>0}_{k+f} \times \operatorname {Gr}_{>0}^\perp (k+m,n)$ such that the restriction of ![]() $\mathcal {Z}$ to
$\mathcal {Z}$ to ![]() $A$ is a diffeomorphism, and the Jacobian of
$A$ is a diffeomorphism, and the Jacobian of ![]() $\mathcal {Z}$ on
$\mathcal {Z}$ on ![]() $A$ has constant sign.
$A$ has constant sign.
By Proposition 8.12, if ![]() $f$ has degree
$f$ has degree ![]() $1$ then the pushforward form
$1$ then the pushforward form ![]() $\mathcal {Z}_* (\omega _{k+f} \wedge \omega _{\ell ,n})$ on
$\mathcal {Z}_* (\omega _{k+f} \wedge \omega _{\ell ,n})$ on ![]() $\textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n)$ can be defined as the pullback via the inverse of
$\textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n)$ can be defined as the pullback via the inverse of ![]() $\mathcal {Z}$ (see (8.1)). By Proposition 8.13, if
$\mathcal {Z}$ (see (8.1)). By Proposition 8.13, if ![]() $f$ is furthermore
$f$ is furthermore ![]() $(n,k,m)$-admissible we may choose a sign for
$(n,k,m)$-admissible we may choose a sign for ![]() $\omega _{k+f}$ such that the form
$\omega _{k+f}$ such that the form ![]() $\mathcal {Z}_* (\omega _{k+f} \wedge \omega _{\ell ,n})$ has the same sign as
$\mathcal {Z}_* (\omega _{k+f} \wedge \omega _{\ell ,n})$ has the same sign as ![]() $\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}$ when restricted to
$\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}$ when restricted to ![]() $\mathcal {A}^{>0}_{k+f}$.
$\mathcal {A}^{>0}_{k+f}$.
Definition 8.14 Given an ![]() $(n,k,m)$-triangulation
$(n,k,m)$-triangulation ![]() $\mathcal {T}=\{f_1,\dots ,f_N\}\subset \tilde {S_n}(-k,\ell )$ of degree
$\mathcal {T}=\{f_1,\dots ,f_N\}\subset \tilde {S_n}(-k,\ell )$ of degree ![]() $1$, the universal amplituhedron form
$1$, the universal amplituhedron form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ on
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ on ![]() $\textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n)$ is defined by
$\textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n)$ is defined by
 \begin{equation} \omega^{{({\mathcal{T}})}}_{\mathcal{A}_{n,k,\ge m}}=\sum_{s=1}^N \mathcal{Z}_* (\omega_{k+f_s} \wedge \omega_{\ell,n}). \end{equation}
\begin{equation} \omega^{{({\mathcal{T}})}}_{\mathcal{A}_{n,k,\ge m}}=\sum_{s=1}^N \mathcal{Z}_* (\omega_{k+f_s} \wedge \omega_{\ell,n}). \end{equation}Here the signs of the terms in the right-hand side are chosen in the same fashion as in (8.2).
Conjecture 8.15 The form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ does not depend on the choice of a triangulation
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ does not depend on the choice of a triangulation ![]() $\mathcal {T}$.
$\mathcal {T}$.
It follows from Proposition 8.19 below that Conjecture 8.15 is equivalent to Conjecture 8.11 for all ![]() $Z$ such that the triangulations in question have
$Z$ such that the triangulations in question have ![]() $Z$-degree
$Z$-degree ![]() $1$. Also, Conjectures 8.11 and 8.15 are known for
$1$. Also, Conjectures 8.11 and 8.15 are known for ![]() $k = 1$: a triangulation independent construction of the polytope form is given in [Reference Arkani-Hamed, Bai and LamABL17]. It follows from Theorem 8.16 that the two conjectures also hold for
$k = 1$: a triangulation independent construction of the polytope form is given in [Reference Arkani-Hamed, Bai and LamABL17]. It follows from Theorem 8.16 that the two conjectures also hold for ![]() $\ell =1$.
$\ell =1$.
We state our main result on the amplituhedron form.
Theorem 8.16 Suppose that we are given an ![]() $(n,k,m)$-triangulation
$(n,k,m)$-triangulation ![]() $\mathcal {T}=\{f_1,\dots ,f_N\}\subset \tilde {S_n}(-k,\ell )$ of degree
$\mathcal {T}=\{f_1,\dots ,f_N\}\subset \tilde {S_n}(-k,\ell )$ of degree ![]() $1$, and let
$1$, and let ![]() $\mathcal {T}':=\{f_1^{-1},\dots ,f_N^{-1}\}\subset \tilde {S_n}(-\ell ,k)$ be the corresponding
$\mathcal {T}':=\{f_1^{-1},\dots ,f_N^{-1}\}\subset \tilde {S_n}(-\ell ,k)$ be the corresponding ![]() $(n,\ell ,m)$-triangulation of degree
$(n,\ell ,m)$-triangulation of degree ![]() $1$ (cf. Corollary 8.7). Then the stacked twist map preserves the universal amplituhedron form:
$1$ (cf. Corollary 8.7). Then the stacked twist map preserves the universal amplituhedron form:
In (8.4), the map ![]() ${\tilde \theta }$ can be considered either as a diffeomorphism between the interiors of
${\tilde \theta }$ can be considered either as a diffeomorphism between the interiors of ![]() $\mathcal {A}_{n,k,\ge m}$ and
$\mathcal {A}_{n,k,\ge m}$ and ![]() $\mathcal {A}_{n,\ell ,\ge m}$, or as a rational map
$\mathcal {A}_{n,\ell ,\ge m}$, or as a rational map ![]() ${\tilde \theta }: \textrm {Fl}_\mathbb {C}(\ell ,k+\ell ,n) \dashrightarrow \textrm {Fl}_\mathbb {C}(k,k+\ell ;n)$.
${\tilde \theta }: \textrm {Fl}_\mathbb {C}(\ell ,k+\ell ,n) \dashrightarrow \textrm {Fl}_\mathbb {C}(k,k+\ell ;n)$.
Remark 8.17 Definition 8.14 can be extended to forms ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}^{\ge 0}_{k+g}}$ for a triangulation
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}^{\ge 0}_{k+g}}$ for a triangulation ![]() $\mathcal {T}$ of
$\mathcal {T}$ of ![]() $\mathcal {A}^{\ge 0}_{k+g}$. It is straightforward to generalize Theorem 8.16 to
$\mathcal {A}^{\ge 0}_{k+g}$. It is straightforward to generalize Theorem 8.16 to ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}^{\ge 0}_{k+g}}$. We still expect the analog of Conjecture 8.11 to hold in this case. Furthermore, assuming that Conjecture 8.11 holds for all
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}^{\ge 0}_{k+g}}$. We still expect the analog of Conjecture 8.11 to hold in this case. Furthermore, assuming that Conjecture 8.11 holds for all ![]() $\mathcal {A}^{\ge 0}_{k+g}$, the forms are expected to be compatible with subdivisions. Namely, if
$\mathcal {A}^{\ge 0}_{k+g}$, the forms are expected to be compatible with subdivisions. Namely, if ![]() $f_1,f_2,\ldots ,f_N$ form an
$f_1,f_2,\ldots ,f_N$ form an ![]() $(n,k,m)$-subdivision of
$(n,k,m)$-subdivision of ![]() $g$, then we should have
$g$, then we should have ![]() $\omega _{\mathcal {A}^{\ge 0}_{k+g}} = \sum _{i=1}^N \omega _{{\mathcal {A}^{\ge 0}_{k+f_i}}}$.
$\omega _{\mathcal {A}^{\ge 0}_{k+g}} = \sum _{i=1}^N \omega _{{\mathcal {A}^{\ge 0}_{k+f_i}}}$.
Remark 8.18 We expect that ![]() $\mathcal {A}_{n,k,m}$ is a positive geometry in the sense of [Reference Arkani-Hamed, Bai and LamABL17], and that the conjectural universal amplituhedron form
$\mathcal {A}_{n,k,m}$ is a positive geometry in the sense of [Reference Arkani-Hamed, Bai and LamABL17], and that the conjectural universal amplituhedron form ![]() $\omega _{\mathcal {A}_{n,k,\ge m}}$ we have defined is its canonical form.
$\omega _{\mathcal {A}_{n,k,\ge m}}$ we have defined is its canonical form.
8.4 From the universal amplituhedron form back to the amplituhedron form
In this section we explain how the amplituhedron form can be recovered from the universal amplituhedron form.
First suppose that ![]() $f \in \tilde {S_n}(-k,\ell )$ is
$f \in \tilde {S_n}(-k,\ell )$ is ![]() $(n,k,m)$-admissible and has degree
$(n,k,m)$-admissible and has degree ![]() $1$. Then we have
$1$. Then we have
where we assume that ![]() $\mathcal {Z}$ and
$\mathcal {Z}$ and ![]() $\mathcal {Z}^{-1}$ have been restricted to the locus where they are isomorphisms.
$\mathcal {Z}^{-1}$ have been restricted to the locus where they are isomorphisms.
Suppose that ![]() $Z \in \operatorname {Gr}_{>0}(k+m,n)$ and
$Z \in \operatorname {Gr}_{>0}(k+m,n)$ and ![]() $f$ has
$f$ has ![]() $Z$-degree
$Z$-degree ![]() $1$. Let
$1$. Let
be the inclusion of a fiber of ![]() $\pi : \textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n) \to \operatorname {Gr}_\mathbb {C}(\ell ,n)$ over
$\pi : \textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n) \to \operatorname {Gr}_\mathbb {C}(\ell ,n)$ over ![]() $Z^\perp$. We have an isomorphism
$Z^\perp$. We have an isomorphism ![]() $\pi ^{-1}(Z^\perp ) \cong \operatorname {Gr}_\mathbb {C}(k,k+m)$ and
$\pi ^{-1}(Z^\perp ) \cong \operatorname {Gr}_\mathbb {C}(k,k+m)$ and ![]() $\mathcal {Z}$ restricts to a map
$\mathcal {Z}$ restricts to a map ![]() $\mathcal {Z}: \Pi _{k+f}^\mathbb {C} \to \pi ^{-1}(Z^\perp )$ that can be identified with
$\mathcal {Z}: \Pi _{k+f}^\mathbb {C} \to \pi ^{-1}(Z^\perp )$ that can be identified with ![]() $Z:\Pi _{k+f}^\mathbb {C}\to \operatorname {Gr}_\mathbb {C}(k,k+m)$. It follows that
$Z:\Pi _{k+f}^\mathbb {C}\to \operatorname {Gr}_\mathbb {C}(k,k+m)$. It follows that
as forms on ![]() $\pi ^{-1}(Z^\perp ) \cong \operatorname {Gr}_\mathbb {C}(k,k+m)$.
$\pi ^{-1}(Z^\perp ) \cong \operatorname {Gr}_\mathbb {C}(k,k+m)$.
Now suppose that we are given an ![]() $(n,k,m)$-triangulation
$(n,k,m)$-triangulation ![]() $\mathcal {T}=\{f_1,\dots ,f_N\}\subset \tilde {S_n}(-k,\ell )$ of degree
$\mathcal {T}=\{f_1,\dots ,f_N\}\subset \tilde {S_n}(-k,\ell )$ of degree ![]() $1$. Then
$1$. Then
 \begin{equation} \omega^{{({\mathcal{T}})}}_{\mathcal{A}_{n,k,\ge m}}=\sum_{s=1}^N \mathcal{Z}_* (\omega_{k+f_s} \wedge \omega_{\ell,n}) =\bigg(\sum_{s=1}^N \mathcal{Z}_* (\omega_{k+f_s})\bigg)\wedge \pi^\ast(\omega_{\ell,n}) \end{equation}
\begin{equation} \omega^{{({\mathcal{T}})}}_{\mathcal{A}_{n,k,\ge m}}=\sum_{s=1}^N \mathcal{Z}_* (\omega_{k+f_s} \wedge \omega_{\ell,n}) =\bigg(\sum_{s=1}^N \mathcal{Z}_* (\omega_{k+f_s})\bigg)\wedge \pi^\ast(\omega_{\ell,n}) \end{equation}
and thus when ![]() $Z$ belongs to some Zariski open subset of
$Z$ belongs to some Zariski open subset of ![]() $\operatorname {Gr}_{>0}(k+m,n)$,
$\operatorname {Gr}_{>0}(k+m,n)$, ![]() $f_1,f_2,\ldots ,f_N$ all have
$f_1,f_2,\ldots ,f_N$ all have ![]() $Z$-degree
$Z$-degree ![]() $1$, and we obtain
$1$, and we obtain
 \[ j_Z^*\bigg(\sum_{s=1}^N \mathcal{Z}_* (\omega_{k+f_s})\bigg) =\omega^{{({\mathcal{T}})}}_{\mathcal{A}_{n,k,m}(Z)} \]
\[ j_Z^*\bigg(\sum_{s=1}^N \mathcal{Z}_* (\omega_{k+f_s})\bigg) =\omega^{{({\mathcal{T}})}}_{\mathcal{A}_{n,k,m}(Z)} \]
under the isomorphism ![]() $\pi ^{-1}(Z^\perp ) \cong \operatorname {Gr}_\mathbb {C}(k,k+m)$.
$\pi ^{-1}(Z^\perp ) \cong \operatorname {Gr}_\mathbb {C}(k,k+m)$.
Finally, suppose we have the equality ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}} = \eta \wedge \omega _{\ell ,n} = \eta ' \wedge \omega _{\ell ,n}$ for two rational forms
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}} = \eta \wedge \omega _{\ell ,n} = \eta ' \wedge \omega _{\ell ,n}$ for two rational forms ![]() $\eta , \eta '$ of degree
$\eta , \eta '$ of degree ![]() $km$ on
$km$ on ![]() $\textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n)$. Then
$\textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n)$. Then ![]() $(\eta - \eta ') \wedge \omega _{\ell ,n} = 0$. The form
$(\eta - \eta ') \wedge \omega _{\ell ,n} = 0$. The form ![]() $\omega _{\ell ,n}$ contracts to 0 with any vertical tangent vector (i.e. a tangent vector of a fiber
$\omega _{\ell ,n}$ contracts to 0 with any vertical tangent vector (i.e. a tangent vector of a fiber ![]() $\pi ^{-1}(Z^\perp )$). It follows that the top form
$\pi ^{-1}(Z^\perp )$). It follows that the top form ![]() $j_Z^*(\eta -\eta ')$ on
$j_Z^*(\eta -\eta ')$ on ![]() $\pi ^{-1}(Z^\perp )$ is equal to 0. We have thus shown the following.
$\pi ^{-1}(Z^\perp )$ is equal to 0. We have thus shown the following.
Proposition 8.19 Let ![]() $Z \in \operatorname {Gr}_{>0}(k+m,n)$. Suppose that we have an
$Z \in \operatorname {Gr}_{>0}(k+m,n)$. Suppose that we have an ![]() $(n,k,m)$-triangulation
$(n,k,m)$-triangulation ![]() $\mathcal {T}=\{f_1,\dots ,f_N\}\subset \tilde {S_n}(-k,\ell )$ of degree
$\mathcal {T}=\{f_1,\dots ,f_N\}\subset \tilde {S_n}(-k,\ell )$ of degree ![]() $1$ such that
$1$ such that ![]() $f_1,f_2,\ldots ,f_N$ all have
$f_1,f_2,\ldots ,f_N$ all have ![]() $Z$-degree
$Z$-degree ![]() $1$. Then there exists a rational form
$1$. Then there exists a rational form ![]() $\eta$ of degree
$\eta$ of degree ![]() $km$ such that
$km$ such that ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}} = \eta \wedge \omega _{\ell ,n}$. Any such form satisfies
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}} = \eta \wedge \omega _{\ell ,n}$. Any such form satisfies
Thus in order to reconstruct the amplituhedron form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ from the universal amplituhedron form
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ from the universal amplituhedron form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$, one needs to represent
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$, one needs to represent ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ as a wedge of
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ as a wedge of ![]() $\eta$ and
$\eta$ and ![]() $\omega _{\ell ,n}$ for some form
$\omega _{\ell ,n}$ for some form ![]() $\eta$, and then use (8.6). Conversely, if
$\eta$, and then use (8.6). Conversely, if ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ exists for generic
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ exists for generic ![]() $Z \in \operatorname {Gr}_{>0}(k+m,n)$, it will depend continuously on
$Z \in \operatorname {Gr}_{>0}(k+m,n)$, it will depend continuously on ![]() $Z$, and one can find a form
$Z$, and one can find a form ![]() $\eta$ satisfying (8.6) and use it to find
$\eta$ satisfying (8.6) and use it to find ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}=\eta \wedge \omega _{\ell ,n}$. As Proposition 8.19 and the example in the next section show, with the right choice of coordinates (explained in § 11.3 in full generality), the universal amplituhedron form
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}=\eta \wedge \omega _{\ell ,n}$. As Proposition 8.19 and the example in the next section show, with the right choice of coordinates (explained in § 11.3 in full generality), the universal amplituhedron form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ carries essentially the same information and computational complexity as the amplituhedron form
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ carries essentially the same information and computational complexity as the amplituhedron form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$.
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$.
8.5 Example
In this section, we compute the amplituhedron form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ and the universal amplituhedron form
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ and the universal amplituhedron form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$, and explain how the former can be recovered from the latter, in the case
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$, and explain how the former can be recovered from the latter, in the case ![]() $k=\ell =1$,
$k=\ell =1$, ![]() $m=2$,
$m=2$, ![]() $n=4$. In this case, the amplituhedron
$n=4$. In this case, the amplituhedron ![]() $\mathcal {A}_{n,k,m}(Z)$ is a quadrilateral in
$\mathcal {A}_{n,k,m}(Z)$ is a quadrilateral in ![]() ${{\mathbb {R}}\mathbb {P}}^2$ with vertices being given by the four columns of a totally positive
${{\mathbb {R}}\mathbb {P}}^2$ with vertices being given by the four columns of a totally positive ![]() $3\times 4$ matrix
$3\times 4$ matrix ![]() $Z$, which we may assume to be given by
$Z$, which we may assume to be given by
 \[ Z=\begin{pmatrix} 1 & s & 0 & 0\\ 0 & p & 1 & 0\\ 0 & -q & 0 & 1 \end{pmatrix};\quad W:=Z^\perp{=}({-}s\quad 1\quad -p\quad q) \]
\[ Z=\begin{pmatrix} 1 & s & 0 & 0\\ 0 & p & 1 & 0\\ 0 & -q & 0 & 1 \end{pmatrix};\quad W:=Z^\perp{=}({-}s\quad 1\quad -p\quad q) \]
for some ![]() $s,p,q>0$.
$s,p,q>0$.
There are precisely two ![]() $(n,k,m)$-triangulations of the amplituhedron, each of them contains
$(n,k,m)$-triangulations of the amplituhedron, each of them contains ![]() $M(1,1,1)=2$ cells and has degree
$M(1,1,1)=2$ cells and has degree ![]() $1$. We choose the triangulation
$1$. We choose the triangulation ![]() $\mathcal {T}=\{f,g\}$ with
$\mathcal {T}=\{f,g\}$ with ![]() $f=[2,1,3,4]$ and
$f=[2,1,3,4]$ and ![]() $g=[1,2,4,3]$ in window notation. The cells
$g=[1,2,4,3]$ in window notation. The cells ![]() $\Pi ^{>0}_{k+f}$ and
$\Pi ^{>0}_{k+f}$ and ![]() $\Pi ^{>0}_{k+g}$ are parameterized as follows. Each
$\Pi ^{>0}_{k+g}$ are parameterized as follows. Each ![]() $V\in \Pi ^{>0}_{k+f}$ can be represented by a matrix
$V\in \Pi ^{>0}_{k+f}$ can be represented by a matrix ![]() $(1\ 0 \ b \ c)$ while each
$(1\ 0 \ b \ c)$ while each ![]() $V\in \Pi ^{>0}_{k+g}$ can be represented by a matrix
$V\in \Pi ^{>0}_{k+g}$ can be represented by a matrix ![]() $(1 \ a \ b \ 0)$ for some
$(1 \ a \ b \ 0)$ for some ![]() $a,b,c>0$.
$a,b,c>0$.
We would like to find ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ using (8.2), so let us compute
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ using (8.2), so let us compute ![]() $\omega _{Z(\Pi ^{>0}_{k+f})}$ and
$\omega _{Z(\Pi ^{>0}_{k+f})}$ and ![]() $\omega _{Z(\Pi ^{>0}_{k+g})}$ separately and then add them up. Each generic point in
$\omega _{Z(\Pi ^{>0}_{k+g})}$ separately and then add them up. Each generic point in ![]() $\operatorname {Gr}(k,k+m)$ is the row span of a matrix
$\operatorname {Gr}(k,k+m)$ is the row span of a matrix ![]() $(1 \ x \ y)$, so we fix a reference form
$(1 \ x \ y)$, so we fix a reference form ![]() $\omega ^{\operatorname {ref}}_{k,k+m}:=dx\wedge dy$ on
$\omega ^{\operatorname {ref}}_{k,k+m}:=dx\wedge dy$ on ![]() $\operatorname {Gr}(k,k+m)$.
$\operatorname {Gr}(k,k+m)$.
The restriction of ![]() $Z$ to
$Z$ to ![]() $\Pi ^{>0}_{k+f}$ maps
$\Pi ^{>0}_{k+f}$ maps ![]() $(1\ 0\ b\ c)$ to the row span of
$(1\ 0\ b\ c)$ to the row span of ![]() $(1 \ b \ c)$ in
$(1 \ b \ c)$ in ![]() $\operatorname {Gr}(k,k+m)$, and thus we have
$\operatorname {Gr}(k,k+m)$, and thus we have ![]() $x=b$ and
$x=b$ and ![]() $y=c$ on
$y=c$ on ![]() $Z(\Pi ^{>0}_{k+f})$. Therefore, the map
$Z(\Pi ^{>0}_{k+f})$. Therefore, the map ![]() $Z^{-1}$ is given by
$Z^{-1}$ is given by ![]() $b=x$ and
$b=x$ and ![]() $c=y$, and since
$c=y$, and since ![]() $\omega _{k+f}=({db\wedge dc})/({b\cdot c})$, the pullback
$\omega _{k+f}=({db\wedge dc})/({b\cdot c})$, the pullback ![]() $(Z^{-1})^\ast \omega _{k+f}$ equals
$(Z^{-1})^\ast \omega _{k+f}$ equals
Furthermore, since the functions ![]() $x=b$ and
$x=b$ and ![]() $y=c$ are positive on
$y=c$ are positive on ![]() $Z(\Pi ^{>0}_{k+f})$, the form
$Z(\Pi ^{>0}_{k+f})$, the form ![]() $Z_\ast \omega _{k+f}$ is positive with respect to
$Z_\ast \omega _{k+f}$ is positive with respect to ![]() $\omega ^{\operatorname {ref}}_{k,k+m}$ if the sign above is chosen to be
$\omega ^{\operatorname {ref}}_{k,k+m}$ if the sign above is chosen to be ![]() $+$.
$+$.
The computation of ![]() $\omega _{Z(\Pi ^{>0}_{k+g})}$ is more involved. The restriction of
$\omega _{Z(\Pi ^{>0}_{k+g})}$ is more involved. The restriction of ![]() $Z$ to
$Z$ to ![]() $\Pi ^{>0}_{k+g}$ maps
$\Pi ^{>0}_{k+g}$ maps ![]() $(1 \ a \ b\ 0)$ to the row span of
$(1 \ a \ b\ 0)$ to the row span of
in ![]() $\operatorname {Gr}(k,k+m)$. Thus we have
$\operatorname {Gr}(k,k+m)$. Thus we have ![]() $x=({pa+b})/({1+sa})$ and
$x=({pa+b})/({1+sa})$ and ![]() $y={-qa}/({1+sa})$ on
$y={-qa}/({1+sa})$ on ![]() $Z(\Pi ^{>0}_{k+g})$. The fact that
$Z(\Pi ^{>0}_{k+g})$. The fact that ![]() $g$ has degree
$g$ has degree ![]() $1$ means that
$1$ means that ![]() $Z$ is birational when restricted to
$Z$ is birational when restricted to ![]() $\Pi ^{>0}_{k+g}$, equivalently, that we can solve the above equations for
$\Pi ^{>0}_{k+g}$, equivalently, that we can solve the above equations for ![]() $a$ and
$a$ and ![]() $b$ and write them as rational functions of
$b$ and write them as rational functions of ![]() $x$ and
$x$ and ![]() $y$. Indeed, this can be done, and the map
$y$. Indeed, this can be done, and the map ![]() $Z^{-1}:Z(\Pi ^{>0}_{k+g})\dashrightarrow \Pi ^{>0}_{k+g}$ is given by
$Z^{-1}:Z(\Pi ^{>0}_{k+g})\dashrightarrow \Pi ^{>0}_{k+g}$ is given by
We can now find the pullback of the form ![]() $\omega _{k+g}=({da\wedge db})/({a\cdot b})$ under
$\omega _{k+g}=({da\wedge db})/({a\cdot b})$ under ![]() $Z^{-1}$:
$Z^{-1}$:
 \begin{equation} Z_\ast \omega_{k+g}={\pm}\frac{d \left(\frac{-y}{sy+q}\right)\wedge d \left(\frac{qx+py}{sy+q}\right)}{\frac{-y}{sy+q}\cdot \frac{qx+py}{sy+q}}={\pm}\frac{q^2\cdot dx\wedge dy}{(qx+py)(sy+q)y}. \end{equation}
\begin{equation} Z_\ast \omega_{k+g}={\pm}\frac{d \left(\frac{-y}{sy+q}\right)\wedge d \left(\frac{qx+py}{sy+q}\right)}{\frac{-y}{sy+q}\cdot \frac{qx+py}{sy+q}}={\pm}\frac{q^2\cdot dx\wedge dy}{(qx+py)(sy+q)y}. \end{equation}
Here in fact we must choose the ![]() $-$ sign, because the functions
$-$ sign, because the functions ![]() $qx+py$ and
$qx+py$ and ![]() $sy+q$ are positive on
$sy+q$ are positive on ![]() $Z(\Pi ^{>0}_{k+g})$ while the function
$Z(\Pi ^{>0}_{k+g})$ while the function ![]() $y={-qa}/({1+sa})$ is negative. We are finally able to find the amplituhedron form:
$y={-qa}/({1+sa})$ is negative. We are finally able to find the amplituhedron form:
We encourage the reader to check that choosing ![]() $\mathcal {T}$ to be the other triangulation of
$\mathcal {T}$ to be the other triangulation of ![]() $\mathcal {A}_{n,k,m}(Z)$ (consisting of affine permutations
$\mathcal {A}_{n,k,m}(Z)$ (consisting of affine permutations ![]() $f'=[1,3,2,4]$ and
$f'=[1,3,2,4]$ and ![]() $g'=[0,2,3,5]$) yields the same expression for
$g'=[0,2,3,5]$) yields the same expression for ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$. Agreeing with general expectations (see [Reference Arkani-Hamed, Bai and LamABL17]), the form
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$. Agreeing with general expectations (see [Reference Arkani-Hamed, Bai and LamABL17]), the form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ has four poles (along the hypersurfaces
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ has four poles (along the hypersurfaces ![]() $qx+py$,
$qx+py$, ![]() $sy+q$,
$sy+q$, ![]() $x$, and at infinity), which corresponds to the four facets of the quadrilateral
$x$, and at infinity), which corresponds to the four facets of the quadrilateral ![]() $\mathcal {A}_{n,k,m}(Z)$.
$\mathcal {A}_{n,k,m}(Z)$.
We now compute the universal amplituhedron form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ on
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ on ![]() $\textrm {Fl}(\ell ,k+\ell ;n)$. In order for it to be compatible with our previous calculations, we introduce the following coordinates on
$\textrm {Fl}(\ell ,k+\ell ;n)$. In order for it to be compatible with our previous calculations, we introduce the following coordinates on ![]() $\textrm {Fl}(\ell ,k+\ell ;n)$. For each generic pair
$\textrm {Fl}(\ell ,k+\ell ;n)$. For each generic pair ![]() $(W,U)\in \textrm {Fl}(\ell ,k+\ell ;n)$, there are unique numbers
$(W,U)\in \textrm {Fl}(\ell ,k+\ell ;n)$, there are unique numbers ![]() $s,p,q,x,y$ such that
$s,p,q,x,y$ such that ![]() $W$ is the row span of
$W$ is the row span of ![]() $(-s\ 1\ -p\ q)$ while
$(-s\ 1\ -p\ q)$ while ![]() $U$ is the row span of
$U$ is the row span of
Our goal is to find ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ from (8.5). We first compute
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,\ge m}}$ from (8.5). We first compute ![]() $\pi ^\ast (\omega _{\ell ,n})$, which is a
$\pi ^\ast (\omega _{\ell ,n})$, which is a ![]() $(k\ell +\ell m)$-form on
$(k\ell +\ell m)$-form on ![]() $\textrm {Fl}(\ell ,k+\ell ;n)$. In our coordinates, the map
$\textrm {Fl}(\ell ,k+\ell ;n)$. In our coordinates, the map ![]() $\pi :\textrm {Fl}(\ell ,k+\ell ;n)\to \operatorname {Gr}(\ell ,n)$ simply sends the row span of
$\pi :\textrm {Fl}(\ell ,k+\ell ;n)\to \operatorname {Gr}(\ell ,n)$ simply sends the row span of ![]() $U$ given by (8.9) to the row span of
$U$ given by (8.9) to the row span of ![]() $(-s\ 1\ -p \ q)$, and thus we have
$(-s\ 1\ -p \ q)$, and thus we have
We now compute ![]() $\mathcal {Z}_\ast (\omega _{k+f})$. The map
$\mathcal {Z}_\ast (\omega _{k+f})$. The map ![]() $\mathcal {Z}$ sends a pair
$\mathcal {Z}$ sends a pair ![]() $(V,W)$ to
$(V,W)$ to ![]() $(W,\operatorname {span}(V,W))$, and assuming
$(W,\operatorname {span}(V,W))$, and assuming ![]() $V$ is the row span of
$V$ is the row span of ![]() $( 1\ 0\ b\ c)$ for some
$( 1\ 0\ b\ c)$ for some ![]() $b,c>0$, we get that our coordinates (8.9) for the pair
$b,c>0$, we get that our coordinates (8.9) for the pair ![]() $(W,\operatorname {span}(V,W))$ are given by
$(W,\operatorname {span}(V,W))$ are given by ![]() $s=s$,
$s=s$, ![]() $p=p$,
$p=p$, ![]() $q=q$,
$q=q$, ![]() $x=b$, and
$x=b$, and ![]() $y=c$. Thus
$y=c$. Thus ![]() $\mathcal {Z}_\ast (\omega _{k+f})=({dx\wedge dy})/({x\cdot y})$ as a
$\mathcal {Z}_\ast (\omega _{k+f})=({dx\wedge dy})/({x\cdot y})$ as a ![]() $km$-form on
$km$-form on ![]() $\textrm {Fl}(\ell ,k+\ell ;n)$.
$\textrm {Fl}(\ell ,k+\ell ;n)$.
Similarly, we find ![]() $\mathcal {Z}_\ast (\omega _{k+g})$. Assuming
$\mathcal {Z}_\ast (\omega _{k+g})$. Assuming ![]() $V$ is the row span of
$V$ is the row span of ![]() $(1 \ a \ b\ 0)$ for some
$(1 \ a \ b\ 0)$ for some ![]() $a,b>0$, we get that our coordinates (8.9) for the pair
$a,b>0$, we get that our coordinates (8.9) for the pair ![]() $(W,U':=\operatorname {span}(V,W))$ are given by
$(W,U':=\operatorname {span}(V,W))$ are given by ![]() $s=s$,
$s=s$, ![]() $p=p$,
$p=p$, ![]() $q=q$, but in order to find
$q=q$, but in order to find ![]() $x$ and
$x$ and ![]() $y$, we need to transform the matrix
$y$, we need to transform the matrix ![]() $U':= (\begin {smallmatrix} -s & 1 & -p & q\\ 1 & a & b & 0 \end {smallmatrix} )$ into the form (8.9) by row operations, which yields
$U':= (\begin {smallmatrix} -s & 1 & -p & q\\ 1 & a & b & 0 \end {smallmatrix} )$ into the form (8.9) by row operations, which yields
 \[ \begin{pmatrix} -s & 1 & -p & q\\ 1 & 0 & \frac{b+pa}{1+sa} & \frac{-qa}{1+sa} \end{pmatrix}. \]
\[ \begin{pmatrix} -s & 1 & -p & q\\ 1 & 0 & \frac{b+pa}{1+sa} & \frac{-qa}{1+sa} \end{pmatrix}. \]
Thus we have ![]() $x=({b+pa})/({1+sa})$ and
$x=({b+pa})/({1+sa})$ and ![]() $y={-qa}/({1+sa})$, and as we have already computed earlier, solving for
$y={-qa}/({1+sa})$, and as we have already computed earlier, solving for ![]() $a$ and
$a$ and ![]() $b$ yields
$b$ yields ![]() $a={-y}/({sy+q})$,
$a={-y}/({sy+q})$, ![]() $b=({qx+py})/({sy+q})$. The form
$b=({qx+py})/({sy+q})$. The form ![]() $\mathcal {Z}_\ast (\omega _{k+g})$ now however is given by an expression that is slightly different from (8.7):
$\mathcal {Z}_\ast (\omega _{k+g})$ now however is given by an expression that is slightly different from (8.7):
where ![]() $\alpha$ denotes a sum of terms containing either one of
$\alpha$ denotes a sum of terms containing either one of ![]() $ds$,
$ds$, ![]() $dp$, or
$dp$, or ![]() $dq$. All those terms vanish after we take the wedge with
$dq$. All those terms vanish after we take the wedge with ![]() $\pi ^\ast (\omega _{\ell ,n})$, so we use (8.5) to find the universal amplituhedron form:
$\pi ^\ast (\omega _{\ell ,n})$, so we use (8.5) to find the universal amplituhedron form:
This is a top form on ![]() $\textrm {Fl}(\ell ,k+\ell ;n)$, and we can choose the form
$\textrm {Fl}(\ell ,k+\ell ;n)$, and we can choose the form ![]() $\eta$ from Proposition 8.19 to be
$\eta$ from Proposition 8.19 to be
where ![]() $\beta$ is an arbitrary sum of terms containing either one of
$\beta$ is an arbitrary sum of terms containing either one of ![]() $ds$,
$ds$, ![]() $dp$, or
$dp$, or ![]() $dq$. Comparing (8.8), (8.10), and (8.11), the similarities between the forms in Proposition 8.19 become apparent. We are done with the computation, and will continue the discussion of this example in § 13.2.
$dq$. Comparing (8.8), (8.10), and (8.11), the similarities between the forms in Proposition 8.19 become apparent. We are done with the computation, and will continue the discussion of this example in § 13.2.
9. The interior of the amplituhedron
In this section, we discuss some topological properties of ![]() $\mathcal {A}_{n,k,m}(Z)$. In particular, we explain why it is sufficient for our purposes to concentrate on
$\mathcal {A}_{n,k,m}(Z)$. In particular, we explain why it is sufficient for our purposes to concentrate on ![]() $\operatorname {Gr}_{\ge m}(k,n)$ rather than
$\operatorname {Gr}_{\ge m}(k,n)$ rather than ![]() $\operatorname {Gr}_{\ge 0}(k,n)$.
$\operatorname {Gr}_{\ge 0}(k,n)$.
Recall that ![]() $\mathcal {A}_{n,k,\ge m}(Z)$ was defined in (4.4) to be the image of
$\mathcal {A}_{n,k,\ge m}(Z)$ was defined in (4.4) to be the image of ![]() $\operatorname {Gr}_{\ge m}(k,n)$ under
$\operatorname {Gr}_{\ge m}(k,n)$ under ![]() $Z$. Let us also denote by
$Z$. Let us also denote by ![]() $\mathcal {A}^{\circ }_{n,k,m}(Z)$ the interior of the amplituhedron. The following result implies Lemma 3.2.
$\mathcal {A}^{\circ }_{n,k,m}(Z)$ the interior of the amplituhedron. The following result implies Lemma 3.2.
Proposition 9.1 We have inclusions
Note that this proposition implies in particular that the amplituhedron is equal to the closure of its interior (see Lemma 9.4 below), because ![]() $\mathcal {A}_{n,k,m}(Z)$ is equal to the closure of
$\mathcal {A}_{n,k,m}(Z)$ is equal to the closure of ![]() $Z(\operatorname {Gr}_{>0}(k,n))$. We expect that the first inclusion
$Z(\operatorname {Gr}_{>0}(k,n))$. We expect that the first inclusion ![]() $Z(\operatorname {Gr}_{>0}(k,n))\subset \mathcal {A}^{\circ }_{n,k,m}(Z)$ is actually an equality. Showing this remains an open problem.
$Z(\operatorname {Gr}_{>0}(k,n))\subset \mathcal {A}^{\circ }_{n,k,m}(Z)$ is actually an equality. Showing this remains an open problem.
Suppose that ![]() $V\in \operatorname {Gr}_{\ge 0}(k,n)$,
$V\in \operatorname {Gr}_{\ge 0}(k,n)$, ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$, and let
$Z\in \operatorname {Gr}_{>0}(k+m,n)$, and let ![]() $W:=Z^\perp$. Then by Lemma 10.5, having
$W:=Z^\perp$. Then by Lemma 10.5, having ![]() $V\in \operatorname {Gr}_{\ge m}(k,n)$ is equivalent to saying that the circular
$V\in \operatorname {Gr}_{\ge m}(k,n)$ is equivalent to saying that the circular ![]() $(k+\ell )$-minors of
$(k+\ell )$-minors of ![]() $U:=\operatorname {stack}(V,W)$ are all non-zero. For
$U:=\operatorname {stack}(V,W)$ are all non-zero. For ![]() $V'\in \operatorname {F}(V,Z)$, it follows from (10.7) that the matrix
$V'\in \operatorname {F}(V,Z)$, it follows from (10.7) that the matrix ![]() $\operatorname {stack}(V',W)$ has the same maximal minors. Therefore, for all
$\operatorname {stack}(V',W)$ has the same maximal minors. Therefore, for all ![]() $V'\in \operatorname {F}(V,Z)$ we have
$V'\in \operatorname {F}(V,Z)$ we have ![]() $V'\in \operatorname {Gr}_{\ge m}(k,n)$. We have shown the following result.
$V'\in \operatorname {Gr}_{\ge m}(k,n)$. We have shown the following result.
Proposition 9.2 For each point ![]() $Y\in \mathcal {A}_{n,k,m}(Z)$, exactly one of the following holds:
$Y\in \mathcal {A}_{n,k,m}(Z)$, exactly one of the following holds:
• for all
 $V\in \operatorname {Gr}_{\ge 0}(k,n)$ such that
$V\in \operatorname {Gr}_{\ge 0}(k,n)$ such that  $V\cdot Z^\text {t}=Y$, we have
$V\cdot Z^\text {t}=Y$, we have  $V\in \operatorname {Gr}_{\ge m}(k,n)$; or
$V\in \operatorname {Gr}_{\ge m}(k,n)$; or• for all
 $V\in \operatorname {Gr}_{\ge 0}(k,n)$ such that
$V\in \operatorname {Gr}_{\ge 0}(k,n)$ such that  $V\cdot Z^\text {t}=Y$, we have
$V\cdot Z^\text {t}=Y$, we have  $V\notin \operatorname {Gr}_{\ge m}(k,n)$.
$V\notin \operatorname {Gr}_{\ge m}(k,n)$.
Note also that the first condition holds if and only if ![]() $Y\in \mathcal {A}_{n,k,\ge m}(Z)$. The next lemma characterizes
$Y\in \mathcal {A}_{n,k,\ge m}(Z)$. The next lemma characterizes ![]() $\mathcal {A}_{n,k,\ge m}(Z)$ as a subset of
$\mathcal {A}_{n,k,\ge m}(Z)$ as a subset of ![]() $\mathcal {A}_{n,k,m}(Z)$ satisfying certain boundary inequalities and implies Lemma 3.2. Recall that the columns of
$\mathcal {A}_{n,k,m}(Z)$ satisfying certain boundary inequalities and implies Lemma 3.2. Recall that the columns of ![]() $Z$ satisfy
$Z$ satisfy ![]() $Z(j+n)=(-1)^{k-1}Z(j)$.
$Z(j+n)=(-1)^{k-1}Z(j)$.
Lemma 9.3 Let ![]() $Y\in \mathcal {A}_{n,k,m}(Z)$ be represented by a
$Y\in \mathcal {A}_{n,k,m}(Z)$ be represented by a ![]() $k\times (k+m)$ matrix, and denote by
$k\times (k+m)$ matrix, and denote by ![]() $y_1,\dots ,y_{k}\in \mathbb {R}^{k+m}$ the row vectors of
$y_1,\dots ,y_{k}\in \mathbb {R}^{k+m}$ the row vectors of ![]() $Y$. Then for each
$Y$. Then for each ![]() $j\in \mathbb {Z}$, the function
$j\in \mathbb {Z}$, the function
takes a fixed sign on ![]() $\mathcal {A}_{n,k,m}(Z)$ and we have
$\mathcal {A}_{n,k,m}(Z)$ and we have ![]() $Y\in \mathcal {A}_{n,k,\ge m}(Z)$ if and only if
$Y\in \mathcal {A}_{n,k,\ge m}(Z)$ if and only if ![]() $\alpha (Y,Z,j)\neq 0$ for all
$\alpha (Y,Z,j)\neq 0$ for all ![]() $j\in \mathbb {Z}$.
$j\in \mathbb {Z}$.
Proof. By [Reference LamLam16b, Proposition 20.3], ![]() $\alpha (Y,Z,j)$ takes a fixed sign on
$\alpha (Y,Z,j)$ takes a fixed sign on ![]() $\mathcal {A}_{n,k,m}(Z)$. It remains to show that
$\mathcal {A}_{n,k,m}(Z)$. It remains to show that ![]() $Y\in \mathcal {A}_{n,k,\ge m}(Z)$ if and only if
$Y\in \mathcal {A}_{n,k,\ge m}(Z)$ if and only if ![]() $\alpha (Y,Z,j)\neq 0$. Let
$\alpha (Y,Z,j)\neq 0$. Let ![]() $W:=Z^\perp$ and
$W:=Z^\perp$ and ![]() $V\in \operatorname {Gr}_{\ge 0}(k,n)$ be such that
$V\in \operatorname {Gr}_{\ge 0}(k,n)$ be such that ![]() $V\cdot Z^\text {t}=Y$. Define
$V\cdot Z^\text {t}=Y$. Define ![]() $X:=(\operatorname {span}(V,W))^\perp$. Thus
$X:=(\operatorname {span}(V,W))^\perp$. Thus ![]() $X$ is an
$X$ is an ![]() $m$-dimensional subspace inside the row span of
$m$-dimensional subspace inside the row span of ![]() $Z$. By [Reference Karp and WilliamsKW17, Lemma 3.10], we have
$Z$. By [Reference Karp and WilliamsKW17, Lemma 3.10], we have ![]() $\Delta _{\{j,j+1,\dots ,j+m-1\}}(X)=\alpha (Y,Z,j)$. Let
$\Delta _{\{j,j+1,\dots ,j+m-1\}}(X)=\alpha (Y,Z,j)$. Let ![]() $J\subset [n]$ denote the complement of the set
$J\subset [n]$ denote the complement of the set ![]() $\{j,j+1,\dots ,j+m-1\}$ (viewed modulo
$\{j,j+1,\dots ,j+m-1\}$ (viewed modulo ![]() $n$) inside
$n$) inside ![]() $[n]$. By (4.6),
$[n]$. By (4.6), ![]() $\Delta _J(\operatorname {stack}(V,W))=\Delta _{\{j,j+1,\dots ,j+m-1\}}(X)$, and thus
$\Delta _J(\operatorname {stack}(V,W))=\Delta _{\{j,j+1,\dots ,j+m-1\}}(X)$, and thus ![]() $\alpha (Y,Z,j)\neq 0$ for all
$\alpha (Y,Z,j)\neq 0$ for all ![]() $j\in \mathbb {Z}$ if and only if all circular minors of
$j\in \mathbb {Z}$ if and only if all circular minors of ![]() $U:=\operatorname {stack}(V,W)$ are non-zero. This happens precisely when
$U:=\operatorname {stack}(V,W)$ are non-zero. This happens precisely when ![]() $U\in \operatorname {Mat}^\circ (k+\ell ,n)$, and the result now follows from Proposition 9.2.
$U\in \operatorname {Mat}^\circ (k+\ell ,n)$, and the result now follows from Proposition 9.2.
Proof Proof of Proposition 9.1 Lemma 9.3 proves the second inclusion ![]() $\mathcal {A}^{\circ }_{n,k,m}(Z) \subset \mathcal {A}_{n,k,\ge m}(Z)$ in (9.1). The third inclusion
$\mathcal {A}^{\circ }_{n,k,m}(Z) \subset \mathcal {A}_{n,k,\ge m}(Z)$ in (9.1). The third inclusion ![]() $\mathcal {A}_{n,k,\ge m}(Z)\subset \mathcal {A}_{n,k,m}(Z)$ is obvious, and the first inclusion is the content of Lemma 9.4 below.
$\mathcal {A}_{n,k,\ge m}(Z)\subset \mathcal {A}_{n,k,m}(Z)$ is obvious, and the first inclusion is the content of Lemma 9.4 below.
Lemma 9.4 The closure of the interior of ![]() $\mathcal {A}_{n,k,m}(Z)$ equals
$\mathcal {A}_{n,k,m}(Z)$ equals ![]() $\mathcal {A}_{n,k,m}(Z)$, and we have
$\mathcal {A}_{n,k,m}(Z)$, and we have
Proof. Let ![]() $V\in \operatorname {Gr}_{>0}(k,n)$ and
$V\in \operatorname {Gr}_{>0}(k,n)$ and ![]() $Y:=V\cdot Z^\text {t}$. We would like to show that
$Y:=V\cdot Z^\text {t}$. We would like to show that ![]() $Y$ belongs to the interior of
$Y$ belongs to the interior of ![]() $\mathcal {A}_{n,k,m}(Z)$. Note that
$\mathcal {A}_{n,k,m}(Z)$. Note that ![]() $\operatorname {GL}_{k+m}(\mathbb {R})$ acts transitively on
$\operatorname {GL}_{k+m}(\mathbb {R})$ acts transitively on ![]() $\operatorname {Gr}(k,k+m)$, so let
$\operatorname {Gr}(k,k+m)$, so let ![]() $A(\mathcal {E})=\operatorname {Id}_{k+m}+\mathcal {E}\in \operatorname {GL}_{k+m}(\mathbb {R})$ belong to the neighborhood of the identity for each sufficiently small
$A(\mathcal {E})=\operatorname {Id}_{k+m}+\mathcal {E}\in \operatorname {GL}_{k+m}(\mathbb {R})$ belong to the neighborhood of the identity for each sufficiently small ![]() $(k+m)\times (k+m)$ matrix
$(k+m)\times (k+m)$ matrix ![]() $\mathcal {E}$. We need to show that
$\mathcal {E}$. We need to show that ![]() $Y\cdot A(\mathcal {E})$ belongs to the image of
$Y\cdot A(\mathcal {E})$ belongs to the image of ![]() $\operatorname {Gr}_{>0}(k,n)$, equivalently, that there exists
$\operatorname {Gr}_{>0}(k,n)$, equivalently, that there exists ![]() $V'(\mathcal {E})\in \operatorname {Gr}_{>0}(k,n)$ such that
$V'(\mathcal {E})\in \operatorname {Gr}_{>0}(k,n)$ such that ![]() $V'(\mathcal {E})\cdot Z^\text {t}=Y\cdot A(\mathcal {E})$, for all small
$V'(\mathcal {E})\cdot Z^\text {t}=Y\cdot A(\mathcal {E})$, for all small ![]() $\mathcal {E}$. Let us construct this
$\mathcal {E}$. Let us construct this ![]() $V'(\mathcal {E})$ explicitly. Assume without loss of generality that
$V'(\mathcal {E})$ explicitly. Assume without loss of generality that ![]() $Z=[\operatorname {Id}_{k+m}\mid S^\text {t}]$ for an
$Z=[\operatorname {Id}_{k+m}\mid S^\text {t}]$ for an ![]() $\ell \times (k+m)$ matrix
$\ell \times (k+m)$ matrix ![]() $S$, where
$S$, where ![]() $\operatorname {Id}_{k+m}$ is the
$\operatorname {Id}_{k+m}$ is the ![]() $(k+m)\times (k+m)$ identity matrix. Then set
$(k+m)\times (k+m)$ identity matrix. Then set
Clearly for small ![]() $\mathcal {E}$ this matrix is close to
$\mathcal {E}$ this matrix is close to ![]() $V$ and thus totally positive. Let us calculate the image of
$V$ and thus totally positive. Let us calculate the image of ![]() $V'(\mathcal {E})$ under
$V'(\mathcal {E})$ under ![]() $Z$:
$Z$:
10. The stacked twist map: proofs
In this section, we examine the stacked twist map from § 4. We adopt the setting and all notation from that section. Our ultimate goal is to prove Theorem 4.7 and Proposition 4.8.
We first discuss the relationship between the stacked twist map and the twist map of [Reference Marsh and ScottMS16]. We remark that in [Reference Muller and SpeyerMS17], the twist map of [Reference Marsh and ScottMS16] was extended to ![]() $U$ not necessarily belonging to
$U$ not necessarily belonging to ![]() $\operatorname {Mat}^\circ (k+\ell ,n)$. However, we only focus on
$\operatorname {Mat}^\circ (k+\ell ,n)$. However, we only focus on ![]() $U\in \operatorname {Mat}^\circ (k+\ell ,n)$, and mostly use the results of [Reference Marsh and ScottMS16].
$U\in \operatorname {Mat}^\circ (k+\ell ,n)$, and mostly use the results of [Reference Marsh and ScottMS16].
For two integers ![]() $a < b$, we denote
$a < b$, we denote ![]() $[a,b):=\{a,a+1,\dots ,b-1\}\subset \mathbb {Z}$. Let
$[a,b):=\{a,a+1,\dots ,b-1\}\subset \mathbb {Z}$. Let ![]() $j\in \mathbb {Z}$,
$j\in \mathbb {Z}$, ![]() $J:=[j-\ell, j+k)$,
$J:=[j-\ell, j+k)$, ![]() $U\in \operatorname {Mat}^\circ (k+\ell ,n)$, and let
$U\in \operatorname {Mat}^\circ (k+\ell ,n)$, and let ![]() ${\tilde {U}}:=\tau (U)$ be defined by (4.1). Denote by
${\tilde {U}}:=\tau (U)$ be defined by (4.1). Denote by ![]() ${\tilde {U}}'$ the result of applying the twist map of [Reference Marsh and ScottMS16] to
${\tilde {U}}'$ the result of applying the twist map of [Reference Marsh and ScottMS16] to ![]() $U$, and let
$U$, and let ![]() ${\tilde {U}}''$ be the result of applying the right twist map of [Reference Muller and SpeyerMS17]. Then we haveFootnote 5
${\tilde {U}}''$ be the result of applying the right twist map of [Reference Muller and SpeyerMS17]. Then we haveFootnote 5
Here ![]() $\Delta _J(U):={ \operatorname {det}}(U(J))$, where
$\Delta _J(U):={ \operatorname {det}}(U(J))$, where ![]() $U(J)$ denotes the submatrix
$U(J)$ denotes the submatrix ![]() $[{\tilde U}(j-\ell )|\dots |{\tilde U}(j+k-1)]$ of
$[{\tilde U}(j-\ell )|\dots |{\tilde U}(j+k-1)]$ of ![]() $U$ with column set
$U$ with column set ![]() $J$. Thus for example the definition of
$J$. Thus for example the definition of ![]() $\tau$ given in (4.1) can be restated as follows:
$\tau$ given in (4.1) can be restated as follows:
We now use (10.1) to apply some results of [Reference Marsh and ScottMS16] to our setting.
Lemma 10.1 Let ![]() $g\in \operatorname {GL}_{k+\ell }(\mathbb {R})$ be an invertible
$g\in \operatorname {GL}_{k+\ell }(\mathbb {R})$ be an invertible ![]() $(k+\ell )\times (k+\ell )$ matrix and
$(k+\ell )\times (k+\ell )$ matrix and ![]() $U\in \operatorname {Mat}^\circ (k+\ell ,n)$. Then
$U\in \operatorname {Mat}^\circ (k+\ell ,n)$. Then
Proof. This follows from (10.1) combined with the proof of [Reference Marsh and ScottMS16, Lemma 2.3].
Proof of Lemma 4.4. Proof of Lemma 4.4 For ![]() $g_1\in \operatorname {GL}_k(\mathbb {R}), g_2\in \operatorname {GL}_\ell (\mathbb {R})$, we can take
$g_1\in \operatorname {GL}_k(\mathbb {R}), g_2\in \operatorname {GL}_\ell (\mathbb {R})$, we can take ![]() $g:= (\begin {smallmatrix} g_1 & 0\\ 0 & g_2 \end {smallmatrix} )$ to be a block matrix, and thus for
$g:= (\begin {smallmatrix} g_1 & 0\\ 0 & g_2 \end {smallmatrix} )$ to be a block matrix, and thus for ![]() $\theta (V,W)=({\tilde {W}},{\tilde V})$ we have
$\theta (V,W)=({\tilde {W}},{\tilde V})$ we have
Lemma 10.2 Let ![]() $j\in \mathbb {Z}$,
$j\in \mathbb {Z}$, ![]() $J:=[j-\ell ,j+k)$, and
$J:=[j-\ell ,j+k)$, and ![]() $K:=[j,j+k+\ell )$. Then for every
$K:=[j,j+k+\ell )$. Then for every ![]() $U\in \operatorname {Mat}^\circ (k+\ell ,n)$ and
$U\in \operatorname {Mat}^\circ (k+\ell ,n)$ and ![]() ${\tilde {U}}:=\tau (U)$, we have
${\tilde {U}}:=\tau (U)$, we have
Proof. This follows from [Reference Marsh and ScottMS16, Remark 3.7], but we deduce this as a simple consequence of Lemma 10.1. Namely, if the submatrix ![]() $U(J)$ of
$U(J)$ of ![]() $U$ is the identity matrix then the submatrix
$U$ is the identity matrix then the submatrix ![]() ${\tilde {U}}(K)$ is upper triangular with diagonal entries
${\tilde {U}}(K)$ is upper triangular with diagonal entries ![]() $(-1)^{j},\dots ,(-1)^{j+k+\ell -1}$, so in this case (10.3) is obvious. We can write any matrix
$(-1)^{j},\dots ,(-1)^{j+k+\ell -1}$, so in this case (10.3) is obvious. We can write any matrix ![]() $U$ as
$U$ as ![]() $U(J)\cdot U'$ where
$U(J)\cdot U'$ where ![]() $U'(J)$ is the identity matrix, and thus by Lemma 10.1,
$U'(J)$ is the identity matrix, and thus by Lemma 10.1, ![]() ${\tilde {U}}=(U(J)^{-1})^\text {t}\cdot \tau (U'(J))$, which proves (10.3) in general.
${\tilde {U}}=(U(J)^{-1})^\text {t}\cdot \tau (U'(J))$, which proves (10.3) in general.
For a subspace ![]() $V\in \operatorname {Gr}(k,n)$ and integers
$V\in \operatorname {Gr}(k,n)$ and integers ![]() $a< b\in \mathbb {Z}$, define
$a< b\in \mathbb {Z}$, define
The positroid cell ![]() $\Pi ^{>0}_{k+f}$ is defined in Definition 11.1, however, we will work with a more convenient alternative characterization.
$\Pi ^{>0}_{k+f}$ is defined in Definition 11.1, however, we will work with a more convenient alternative characterization.
Lemma 10.3 Let ![]() $V\in \operatorname {Gr}_{\ge 0}(k,n)$. Then the unique affine permutation
$V\in \operatorname {Gr}_{\ge 0}(k,n)$. Then the unique affine permutation ![]() $f\in \tilde {S_n}(-k,n-k)$ such that
$f\in \tilde {S_n}(-k,n-k)$ such that ![]() $V\in \Pi ^{>0}_{k+f}$ is characterized by the property that for each
$V\in \Pi ^{>0}_{k+f}$ is characterized by the property that for each ![]() $a< b\in \mathbb {Z}$,
$a< b\in \mathbb {Z}$,
Proof. This is well-known, see e.g. [Reference Knutson, Lam and SpeyerKLS13, § 5.2].
Thus Proposition 4.5 follows from Lemma 10.3 as a simple corollary. We can now describe the relationship between ![]() $\Pi ^{>0}_{k+f}$ and
$\Pi ^{>0}_{k+f}$ and ![]() $\Pi ^{>0}_{\ell +f^{-1}}$ for
$\Pi ^{>0}_{\ell +f^{-1}}$ for ![]() $f\in \tilde {S_n}(-k,\ell )$. Note that by Proposition 4.5, we have
$f\in \tilde {S_n}(-k,\ell )$. Note that by Proposition 4.5, we have ![]() ${\mathrm {rk}}(V;a,b)=k$ for
${\mathrm {rk}}(V;a,b)=k$ for ![]() $V\in \operatorname {Gr}_{\ge m}(k,n)$ when
$V\in \operatorname {Gr}_{\ge m}(k,n)$ when ![]() $b-a\geq k+\ell$.
$b-a\geq k+\ell$.
Lemma 10.4 Let ![]() $f\in \tilde {S_n}(-k,\ell ),g\in \tilde {S_n}(-\ell ,k)$, and consider subspaces
$f\in \tilde {S_n}(-k,\ell ),g\in \tilde {S_n}(-\ell ,k)$, and consider subspaces ![]() $V\in \Pi ^{>0}_{k+f}$,
$V\in \Pi ^{>0}_{k+f}$, ![]() ${\tilde V}\in \Pi ^{>0}_{\ell +g}$. Then we have
${\tilde V}\in \Pi ^{>0}_{\ell +g}$. Then we have ![]() $g=f^{-1}$ if and only if for every
$g=f^{-1}$ if and only if for every ![]() $a< b\in \mathbb {Z}$ satisfying
$a< b\in \mathbb {Z}$ satisfying ![]() $b-a < k+\ell$,
$b-a < k+\ell$,
Proof. By Lemma 10.3,
 \begin{gather*} {\mathrm{rk}}(V;a,b)=\#\{i < a\mid a\leq f(i)+k < b\},\\ {\mathrm{rk}}({\tilde V};b-k,a+\ell)=\#\{j < b-k\mid b-k\leq g(j)+\ell < a+\ell\}. \end{gather*}
\begin{gather*} {\mathrm{rk}}(V;a,b)=\#\{i < a\mid a\leq f(i)+k < b\},\\ {\mathrm{rk}}({\tilde V};b-k,a+\ell)=\#\{j < b-k\mid b-k\leq g(j)+\ell < a+\ell\}. \end{gather*}
Since ![]() $\#\{i < a\mid a\leq f(i)+k\}=k$, we get that
$\#\{i < a\mid a\leq f(i)+k\}=k$, we get that ![]() $\#\{i < a\mid b\leq f(i)+k\}=k-{\mathrm {rk}}(V;a,b)$. Now, using the fact that
$\#\{i < a\mid b\leq f(i)+k\}=k-{\mathrm {rk}}(V;a,b)$. Now, using the fact that ![]() $i-k\leq f(i)\leq i+\ell$, we find that
$i-k\leq f(i)\leq i+\ell$, we find that
On the other hand, since ![]() $\#\{j\in \mathbb {Z}\mid b-k\leq g(j)+\ell < a+\ell \}=\ell +k+a-b$, we get that
$\#\{j\in \mathbb {Z}\mid b-k\leq g(j)+\ell < a+\ell \}=\ell +k+a-b$, we get that ![]() $\#\{b-k\leq j\mid b-k\leq g(j)+\ell < a+\ell \}=\ell +k+a-b-{\mathrm {rk}}({\tilde V};b-k,a+\ell )$. Using the fact that
$\#\{b-k\leq j\mid b-k\leq g(j)+\ell < a+\ell \}=\ell +k+a-b-{\mathrm {rk}}({\tilde V};b-k,a+\ell )$. Using the fact that ![]() $j-\ell \leq g(j)\leq j+k$, we find
$j-\ell \leq g(j)\leq j+k$, we find
We arrive at
Rearranging the terms in the right-hand side of (10.6), we get
Thus if ![]() $f=g^{-1}$ then
$f=g^{-1}$ then ![]() $i=g(j)\mapsto j=f(i)$ is a bijection between the sets in the left-hand sides of the two equations above, so we get
$i=g(j)\mapsto j=f(i)$ is a bijection between the sets in the left-hand sides of the two equations above, so we get ![]() $\ell +k+a-b-{\mathrm {rk}}({\tilde V};b-k,a+\ell )=k-{\mathrm {rk}}(V;a,b)$, which is equivalent to (10.5). This proves one direction of the lemma.
$\ell +k+a-b-{\mathrm {rk}}({\tilde V};b-k,a+\ell )=k-{\mathrm {rk}}(V;a,b)$, which is equivalent to (10.5). This proves one direction of the lemma.
Conversely, if (10.5) holds, then ![]() $f$ and
$f$ and ![]() $g^{-1}$ must define two positroid cells such that the ranks of columns
$g^{-1}$ must define two positroid cells such that the ranks of columns ![]() $a,a+1,\dots , b-1$ are the same for all
$a,a+1,\dots , b-1$ are the same for all ![]() $a < b$. By Lemma 10.3, the two cells must therefore be the same and we conclude that
$a < b$. By Lemma 10.3, the two cells must therefore be the same and we conclude that ![]() $f=g^{-1}$.
$f=g^{-1}$.
The next lemma proves part (i) of Theorem 4.7.
Lemma 10.5 Let ![]() $V\in \operatorname {Gr}_{\ge 0}(k,n)$,
$V\in \operatorname {Gr}_{\ge 0}(k,n)$, ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$,
$Z\in \operatorname {Gr}_{>0}(k+m,n)$, ![]() $W:=Z^\perp$, and
$W:=Z^\perp$, and ![]() $U:=\operatorname {stack}(V,W)$. Let
$U:=\operatorname {stack}(V,W)$. Let ![]() $f\in \tilde {S_n}(-k,n-k)$ be such that
$f\in \tilde {S_n}(-k,n-k)$ be such that ![]() $V\in \Pi ^{>0}_{k+f}$. Then
$V\in \Pi ^{>0}_{k+f}$. Then ![]() $f\in \tilde {S_n}(-k,\ell )$ if and only if
$f\in \tilde {S_n}(-k,\ell )$ if and only if ![]() $U\in \operatorname {Mat}^\circ (k+\ell ,n)$.
$U\in \operatorname {Mat}^\circ (k+\ell ,n)$.
Proof. This is essentially [Reference LamLam16b, Proposition 20.3], but we include the proof for completeness. Let ![]() $J:=[j-\ell ,j+k)$. The minor
$J:=[j-\ell ,j+k)$. The minor ![]() $\Delta _J(U)$ can be written as a sum
$\Delta _J(U)$ can be written as a sum
 \[ \Delta_J(U)=\sum_{I\in{J\choose k}} ({-}1)^{\operatorname{inv}(I,J\setminus I)}\Delta_I(V)\Delta_{J\setminus I}(W), \]
\[ \Delta_J(U)=\sum_{I\in{J\choose k}} ({-}1)^{\operatorname{inv}(I,J\setminus I)}\Delta_I(V)\Delta_{J\setminus I}(W), \]
where ![]() $\operatorname {inv}(I,J\setminus I)=\#\{i\in I,i'\in J\setminus I: i' < i\}$. Moreover,
$\operatorname {inv}(I,J\setminus I)=\#\{i\in I,i'\in J\setminus I: i' < i\}$. Moreover, ![]() $\Delta _I(V)$ is nonnegative and the sign of
$\Delta _I(V)$ is nonnegative and the sign of ![]() $\Delta _{J\setminus I}(W)$ depends only on the parity of
$\Delta _{J\setminus I}(W)$ depends only on the parity of ![]() $\sum _{i'\in J\setminus I} i'$, because
$\sum _{i'\in J\setminus I} i'$, because ![]() $\operatorname {alt}(W)\in \operatorname {Gr}_{>0}(\ell ,n)$ by (4.6). It follows that all the terms in the above sum have the same sign, because the terms corresponding to
$\operatorname {alt}(W)\in \operatorname {Gr}_{>0}(\ell ,n)$ by (4.6). It follows that all the terms in the above sum have the same sign, because the terms corresponding to ![]() $I$ and
$I$ and ![]() $I\setminus \{i\}\cup \{i+1\}$ have the same sign for each
$I\setminus \{i\}\cup \{i+1\}$ have the same sign for each ![]() $i\in I$ such that
$i\in I$ such that ![]() $i+1\in J\setminus I$. Moreover,
$i+1\in J\setminus I$. Moreover, ![]() $\Delta _{J\setminus I}(W)$ is always non-zero, and thus
$\Delta _{J\setminus I}(W)$ is always non-zero, and thus ![]() $\Delta _J(U)$ is non-zero if and only if
$\Delta _J(U)$ is non-zero if and only if ![]() $\Delta _I(V)$ is non-zero for some
$\Delta _I(V)$ is non-zero for some ![]() $I\subset J$. This is exactly equivalent to saying that the rank of
$I\subset J$. This is exactly equivalent to saying that the rank of ![]() $[V(j-\ell )|V(j-\ell +1)|\dots |V(j+ k-1)]$ is equal to
$[V(j-\ell )|V(j-\ell +1)|\dots |V(j+ k-1)]$ is equal to ![]() $k$, so the result follows by Proposition 4.5.
$k$, so the result follows by Proposition 4.5.
Let ![]() $\operatorname {Mat}_\mathbb {C}^\circ (k+\ell ,n)$ denote the set of complex
$\operatorname {Mat}_\mathbb {C}^\circ (k+\ell ,n)$ denote the set of complex ![]() $(k+\ell )\times n$ matrices with non-zero circular minors. We give a simple result relating the fibers
$(k+\ell )\times n$ matrices with non-zero circular minors. We give a simple result relating the fibers ![]() $\operatorname {F}(V,Z)$ with their images under
$\operatorname {F}(V,Z)$ with their images under ![]() $\theta$.
$\theta$.
Lemma 10.6 Let ![]() $V\in \operatorname {Gr}_\mathbb {C}(k,n)$,
$V\in \operatorname {Gr}_\mathbb {C}(k,n)$, ![]() $W\in \operatorname {Gr}_\mathbb {C}(\ell ,n)$ be such that
$W\in \operatorname {Gr}_\mathbb {C}(\ell ,n)$ be such that ![]() $\operatorname {stack}(V,W)\in \operatorname {Mat}_\mathbb {C}^\circ (k+\ell ,n)$. Denote
$\operatorname {stack}(V,W)\in \operatorname {Mat}_\mathbb {C}^\circ (k+\ell ,n)$. Denote ![]() $Z:=W^\perp$, and let
$Z:=W^\perp$, and let ![]() $V'\in \operatorname {Gr}_\mathbb {C}(k,n)$ be such that
$V'\in \operatorname {Gr}_\mathbb {C}(k,n)$ be such that ![]() $V'\cdot Z^\text {t}=V\cdot Z^\text {t}$. Let
$V'\cdot Z^\text {t}=V\cdot Z^\text {t}$. Let ![]() $(\tilde {W},{\tilde V}):=\theta (V,W)$ and
$(\tilde {W},{\tilde V}):=\theta (V,W)$ and ![]() $(\tilde {W}',{\tilde V}'):=\theta (V',W)$. Then we have
$(\tilde {W}',{\tilde V}'):=\theta (V',W)$. Then we have ![]() $\tilde {W}'=\tilde {W}$ and there exists a
$\tilde {W}'=\tilde {W}$ and there exists a ![]() $k\times \ell$ matrix
$k\times \ell$ matrix ![]() $A$ such that the following hold:
$A$ such that the following hold:
•
 $V'=V+A\cdot W$; and
$V'=V+A\cdot W$; and•
 ${\tilde V}'={\tilde V}-A^\text {t}\cdot \tilde {W}$.
${\tilde V}'={\tilde V}-A^\text {t}\cdot \tilde {W}$.
Proof. It is clear that ![]() $V\cdot Z^\text {t}=V'\cdot Z^\text {t}$ is equivalent to saying that
$V\cdot Z^\text {t}=V'\cdot Z^\text {t}$ is equivalent to saying that ![]() $V'=V+A\cdot W$ for some
$V'=V+A\cdot W$ for some ![]() $k\times \ell$ matrix
$k\times \ell$ matrix ![]() $A$. But then
$A$. But then ![]() $U':=\operatorname {stack}(V',W)$ is obtained from
$U':=\operatorname {stack}(V',W)$ is obtained from ![]() $U:=\operatorname {stack}(V,W)$ by
$U:=\operatorname {stack}(V,W)$ by
By Lemma 10.1, the matrix ![]() $\tilde {U}'=\operatorname {stack}(\tilde {W},{\tilde V}')$ is obtained from
$\tilde {U}'=\operatorname {stack}(\tilde {W},{\tilde V}')$ is obtained from ![]() $\tilde {U}$ by
$\tilde {U}$ by
which finishes the proof.
Lemma 10.7 Let ![]() $V\in \operatorname {Gr}_{\ge m}(k,n)$,
$V\in \operatorname {Gr}_{\ge m}(k,n)$, ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$,
$Z\in \operatorname {Gr}_{>0}(k+m,n)$, ![]() $W:=Z^\perp$, and
$W:=Z^\perp$, and ![]() $({\tilde {W}},{\tilde V}):=\theta (V,W)$. Then for every
$({\tilde {W}},{\tilde V}):=\theta (V,W)$. Then for every ![]() $a < b\in \mathbb {Z}$, we have the following:
$a < b\in \mathbb {Z}$, we have the following:
(a) if
 $b-a=k$ then the vectors
$b-a=k$ then the vectors  $\tilde {W}(a),\dots ,\tilde {W}(b-1)$ form a basis of
$\tilde {W}(a),\dots ,\tilde {W}(b-1)$ form a basis of  $\mathbb {R}^k$;
$\mathbb {R}^k$;(b) if
 $b-a\geq k+\ell$ then
$b-a\geq k+\ell$ then  ${\mathrm {rk}}(V;a,b)=k$ and
${\mathrm {rk}}(V;a,b)=k$ and  ${\mathrm {rk}}({\tilde V};a,b)=\ell$;
${\mathrm {rk}}({\tilde V};a,b)=\ell$;(c) if
 $b-a < k+\ell$ then
$b-a < k+\ell$ then  ${\mathrm {rk}}({\tilde V};b-k,a+\ell )+b-a=\ell +{\mathrm {rk}}(V;a,b).$
${\mathrm {rk}}({\tilde V};b-k,a+\ell )+b-a=\ell +{\mathrm {rk}}(V;a,b).$
Proof. Part (b) follows from Lemmas 10.2 and 10.5. We now prove part (a), so let ![]() $b:=a+k$. Denote
$b:=a+k$. Denote ![]() $r:={\mathrm {rk}}(\tilde {W};a,b)$, and consider the
$r:={\mathrm {rk}}(\tilde {W};a,b)$, and consider the ![]() $(k-r)$-dimensional space
$(k-r)$-dimensional space
Recall that the matrix ![]() $\tilde {U}$ has columns
$\tilde {U}$ has columns ![]() $\tilde {U}(j)=(\tilde {W}(j),{\tilde V}(j))$, and by (10.3), the column vectors
$\tilde {U}(j)=(\tilde {W}(j),{\tilde V}(j))$, and by (10.3), the column vectors ![]() $\tilde {U}(a),\dots ,\tilde {U}(b-1)$ are linearly independent. Therefore, we get an injective linear map
$\tilde {U}(a),\dots ,\tilde {U}(b-1)$ are linearly independent. Therefore, we get an injective linear map ![]() $\lambda :Q\to \mathbb {R}^{\ell }$ defined by
$\lambda :Q\to \mathbb {R}^{\ell }$ defined by ![]() $\lambda (q)=q_a{\tilde V}(a)+\dots +q_{b-1}{\tilde V}(b-1)$, so that
$\lambda (q)=q_a{\tilde V}(a)+\dots +q_{b-1}{\tilde V}(b-1)$, so that ![]() $q_a \tilde {U}(a)+\dots +q_{b-1}\tilde {U}(b-1)=(\mathbf {0}_k,\lambda (q))\in \mathbb {R}^{k+\ell }$. Here
$q_a \tilde {U}(a)+\dots +q_{b-1}\tilde {U}(b-1)=(\mathbf {0}_k,\lambda (q))\in \mathbb {R}^{k+\ell }$. Here ![]() $\mathbf {0}_k\in \mathbb {R}^k$ denotes the zero vector.
$\mathbf {0}_k\in \mathbb {R}^k$ denotes the zero vector.
Recall that we have ![]() $a+k=b$. By (4.1), each of the columns
$a+k=b$. By (4.1), each of the columns ![]() $\tilde {U}(a),\dots ,\tilde {U}(b-1)=\tilde {U}(a+k-1)$ is orthogonal to each of the columns
$\tilde {U}(a),\dots ,\tilde {U}(b-1)=\tilde {U}(a+k-1)$ is orthogonal to each of the columns ![]() $U(b-\ell )=U(a+k-\ell ),\dots ,U(a+k-1)$, where
$U(b-\ell )=U(a+k-\ell ),\dots ,U(a+k-1)$, where ![]() $U(j)=(V(j),W(j))$. Thus
$U(j)=(V(j),W(j))$. Thus ![]() $\lambda (q)$ is orthogonal to
$\lambda (q)$ is orthogonal to ![]() $W(a+k-\ell ),\dots ,W(a+k-1)$. Since these vectors are the columns of
$W(a+k-\ell ),\dots ,W(a+k-1)$. Since these vectors are the columns of ![]() $W$, they must form a basis of
$W$, they must form a basis of ![]() $\mathbb {R}^\ell$, which implies that
$\mathbb {R}^\ell$, which implies that ![]() $Q$ must be a zero-dimensional space, and thus
$Q$ must be a zero-dimensional space, and thus ![]() $k-r=0$. This finishes the proof of (a).
$k-r=0$. This finishes the proof of (a).
The proof of (c) will be completely similar. Denote ![]() $r:={\mathrm {rk}}(V;a,b)$, and consider the
$r:={\mathrm {rk}}(V;a,b)$, and consider the ![]() $(b-a-r)$-dimensional space
$(b-a-r)$-dimensional space
By Lemma 10.5, we get an injective map ![]() $\lambda :Q\to \mathbb {R}^\ell$ defined by
$\lambda :Q\to \mathbb {R}^\ell$ defined by ![]() $\lambda (q)=q_aW(a)+\dots +q_{b-1}W(b-1)$, so that
$\lambda (q)=q_aW(a)+\dots +q_{b-1}W(b-1)$, so that ![]() $q_aU(a)+\dots +q_{b-1}U(b-1)=(\mathbf {0}_k,\lambda (q))$. By (4.1), each of the vectors
$q_aU(a)+\dots +q_{b-1}U(b-1)=(\mathbf {0}_k,\lambda (q))$. By (4.1), each of the vectors ![]() $U(a),\dots ,U(b-1)$ is orthogonal to each of the vectors
$U(a),\dots ,U(b-1)$ is orthogonal to each of the vectors ![]() $\tilde {U}(b-k),\dots ,\tilde {U}(a+\ell -1)$, so
$\tilde {U}(b-k),\dots ,\tilde {U}(a+\ell -1)$, so ![]() $\lambda (q)$ is orthogonal to
$\lambda (q)$ is orthogonal to ![]() ${\tilde V}(b-k),\dots ,{\tilde V}(a+\ell -1)$. This implies that
${\tilde V}(b-k),\dots ,{\tilde V}(a+\ell -1)$. This implies that ![]() ${\mathrm {rk}}({\tilde V};b-k,a+\ell )\leq \ell -\operatorname {dim}(Q)=\ell -b+a+{\mathrm {rk}}(V;a,b)$. This inequality is in fact an equality, since for any vector
${\mathrm {rk}}({\tilde V};b-k,a+\ell )\leq \ell -\operatorname {dim}(Q)=\ell -b+a+{\mathrm {rk}}(V;a,b)$. This inequality is in fact an equality, since for any vector ![]() $h\in \mathbb {R}^\ell$ that is orthogonal to
$h\in \mathbb {R}^\ell$ that is orthogonal to ![]() ${\tilde V}(b-k),\dots ,{\tilde V}(a+\ell -1)$, the vector
${\tilde V}(b-k),\dots ,{\tilde V}(a+\ell -1)$, the vector ![]() $(\mathbf {0}_k,h)$ is orthogonal to
$(\mathbf {0}_k,h)$ is orthogonal to ![]() $\tilde {U}(b-k),\dots ,\tilde {U}(a+\ell -1)$, The latter vectors are linearly independent and span the orthogonal complement of the span of
$\tilde {U}(b-k),\dots ,\tilde {U}(a+\ell -1)$, The latter vectors are linearly independent and span the orthogonal complement of the span of ![]() $U(a),\dots ,U(b-1)$ in
$U(a),\dots ,U(b-1)$ in ![]() $\mathbb {R}^{k+\ell }$. Thus there are coefficients
$\mathbb {R}^{k+\ell }$. Thus there are coefficients ![]() $(q_a,\dots ,q_{b-1})\in \mathbb {R}^{b-a}$ such that
$(q_a,\dots ,q_{b-1})\in \mathbb {R}^{b-a}$ such that ![]() $(\mathbf {0}_k,h)=q_aU(a)+\dots +q_{b-1}U(b-1)$. It follows that
$(\mathbf {0}_k,h)=q_aU(a)+\dots +q_{b-1}U(b-1)$. It follows that ![]() $h$ belongs to the image of
$h$ belongs to the image of ![]() $\lambda$, which finishes the proof of (c).
$\lambda$, which finishes the proof of (c).
An important special case of part (c) of Lemma 10.7 is ![]() $b=a+k$, where we get
$b=a+k$, where we get ![]() ${\mathrm {rk}}({\tilde V};a,a+\ell )+k=\ell +{\mathrm {rk}}(V;a,a+k)$. Thus we have
${\mathrm {rk}}({\tilde V};a,a+\ell )+k=\ell +{\mathrm {rk}}(V;a,a+k)$. Thus we have ![]() ${\mathrm {rk}}(V;a,a+k)=k$ if and only if
${\mathrm {rk}}(V;a,a+k)=k$ if and only if ![]() ${\mathrm {rk}}({\tilde V};a,a+\ell )=\ell$.
${\mathrm {rk}}({\tilde V};a,a+\ell )=\ell$.
Proof of Theorem 4.7 The only ingredient missing to show Theorem 4.7 is to prove that ![]() ${\tilde V}\in \operatorname {Gr}_{\ge 0}(\ell ,n)$ and
${\tilde V}\in \operatorname {Gr}_{\ge 0}(\ell ,n)$ and ![]() ${\tilde {W}}\in \operatorname {Gr}_{>0}^\perp (\ell +m,n)$. This would imply part (ii) of the theorem, and then part (iii) will follow from Lemma 10.7 combined with (10.5). Note that as long as
${\tilde {W}}\in \operatorname {Gr}_{>0}^\perp (\ell +m,n)$. This would imply part (ii) of the theorem, and then part (iii) will follow from Lemma 10.7 combined with (10.5). Note that as long as ![]() $V\in \operatorname {Gr}_{>0}(k,n)$, Lemma 10.7 implies that
$V\in \operatorname {Gr}_{>0}(k,n)$, Lemma 10.7 implies that ![]() ${\mathrm {rk}}({\tilde V};a,a+\ell )=\ell$ for all
${\mathrm {rk}}({\tilde V};a,a+\ell )=\ell$ for all ![]() $a\in \mathbb {Z}$. It suffices to find one pair
$a\in \mathbb {Z}$. It suffices to find one pair ![]() $(V_0,W_0)\in \operatorname {Gr}_{>0}(k,n)\times \operatorname {Gr}_{>0}^\perp (k+m,n)$ for which the image
$(V_0,W_0)\in \operatorname {Gr}_{>0}(k,n)\times \operatorname {Gr}_{>0}^\perp (k+m,n)$ for which the image ![]() $\theta (V_0,W_0)=({\tilde {W}}_0,{\tilde V}_0)$ belongs to
$\theta (V_0,W_0)=({\tilde {W}}_0,{\tilde V}_0)$ belongs to ![]() $\operatorname {Gr}_{>0}^\perp (\ell +m,n)\times \operatorname {Gr}_{>0}(\ell ,n)$. Indeed, then for any other pair
$\operatorname {Gr}_{>0}^\perp (\ell +m,n)\times \operatorname {Gr}_{>0}(\ell ,n)$. Indeed, then for any other pair ![]() $(V,W)\in \operatorname {Gr}_{\ge m}(k,n)\times \operatorname {Gr}_{>0}^\perp (k+m,n)$, one can construct a path
$(V,W)\in \operatorname {Gr}_{\ge m}(k,n)\times \operatorname {Gr}_{>0}^\perp (k+m,n)$, one can construct a path ![]() $(V_t,W_t)$,
$(V_t,W_t)$, ![]() $0\leq t\leq 1$ such that
$0\leq t\leq 1$ such that ![]() $(V_0,W_0)$ is as above,
$(V_0,W_0)$ is as above, ![]() $(V_1,W_1)=(V,W)$, and for
$(V_1,W_1)=(V,W)$, and for ![]() $0\leq t<1$,
$0\leq t<1$, ![]() $(V_t,W_t)$ belongs to
$(V_t,W_t)$ belongs to ![]() $\operatorname {Gr}_{>0}(k,n)\times \operatorname {Gr}_{>0}^\perp (k+m,n)$. In this case, the image
$\operatorname {Gr}_{>0}(k,n)\times \operatorname {Gr}_{>0}^\perp (k+m,n)$. In this case, the image ![]() $({\tilde {W}}_t,{\tilde V}_t)=\theta (V_t,W_t)$ will belong to
$({\tilde {W}}_t,{\tilde V}_t)=\theta (V_t,W_t)$ will belong to ![]() $\operatorname {Gr}_{>0}^\perp (\ell +m,n)\times \operatorname {Gr}_{>0}(\ell ,n)$, because in order to exit this space, one of the circular minors of either
$\operatorname {Gr}_{>0}^\perp (\ell +m,n)\times \operatorname {Gr}_{>0}(\ell ,n)$, because in order to exit this space, one of the circular minors of either ![]() ${\tilde V}_t$ or
${\tilde V}_t$ or ![]() ${\tilde {W}}_t$ must vanish. It follows by continuity that
${\tilde {W}}_t$ must vanish. It follows by continuity that ![]() $({\tilde {W}},{\tilde V})\in \operatorname {Gr}_{\ge 0}(\ell +m,n)\times \operatorname {Gr}_{\ge 0}(\ell ,n)$, and by Lemma 10.7,
$({\tilde {W}},{\tilde V})\in \operatorname {Gr}_{\ge 0}(\ell +m,n)\times \operatorname {Gr}_{\ge 0}(\ell ,n)$, and by Lemma 10.7, ![]() $({\tilde {W}},{\tilde V})$ actually must belong to
$({\tilde {W}},{\tilde V})$ actually must belong to ![]() $\operatorname {Gr}_{>0}(\ell +m,n)\times \operatorname {Gr}_{\ge m}(\ell ,n)$.
$\operatorname {Gr}_{>0}(\ell +m,n)\times \operatorname {Gr}_{\ge m}(\ell ,n)$.
In order to construct this pair ![]() $(V_0,W_0)$, we make use of the cyclically symmetric amplituhedron introduced in [Reference Galashin, Karp and LamGKL17, § 5]. In fact, the computation we need is almost literally the same as the one outlined in [Reference ScottSco79], see [Reference KarpKar19] or [Reference Galashin, Karp and LamGKL17, Lemma 3.1] for details.
$(V_0,W_0)$, we make use of the cyclically symmetric amplituhedron introduced in [Reference Galashin, Karp and LamGKL17, § 5]. In fact, the computation we need is almost literally the same as the one outlined in [Reference ScottSco79], see [Reference KarpKar19] or [Reference Galashin, Karp and LamGKL17, Lemma 3.1] for details.
Consider the set of ![]() $n$th roots of
$n$th roots of ![]() $(-1)^{k-1}$, and let
$(-1)^{k-1}$, and let ![]() $z_1,\dots ,z_k$ be those
$z_1,\dots ,z_k$ be those ![]() $k$ of them with the largest real part and let
$k$ of them with the largest real part and let ![]() $z_{k+1},\dots ,z_{k+\ell }$ be those
$z_{k+1},\dots ,z_{k+\ell }$ be those ![]() $\ell$ of them with the smallest real part. Let
$\ell$ of them with the smallest real part. Let ![]() $V_0$ be (the real
$V_0$ be (the real ![]() $k$-dimensional subspace of) the linear
$k$-dimensional subspace of) the linear ![]() $\mathbb {C}$-span of the vectors
$\mathbb {C}$-span of the vectors ![]() $(1,z_i,\dots ,z_i^{n-1})$, for
$(1,z_i,\dots ,z_i^{n-1})$, for ![]() $1\leq i\leq k$, and let
$1\leq i\leq k$, and let ![]() $W_0$ be (the real
$W_0$ be (the real ![]() $\ell$-dimensional subspace of) the linear
$\ell$-dimensional subspace of) the linear ![]() $\mathbb {C}$-span of the vectors
$\mathbb {C}$-span of the vectors ![]() $(1,z_i,\dots ,z_i^{n-1})$, for
$(1,z_i,\dots ,z_i^{n-1})$, for ![]() $k+1\leq i\leq k+\ell$. Then we have
$k+1\leq i\leq k+\ell$. Then we have ![]() $V_0\in \operatorname {Gr}_{>0}(k,n)$ and
$V_0\in \operatorname {Gr}_{>0}(k,n)$ and ![]() $W_0\in \operatorname {Gr}_{>0}^\perp (k+m,n)$, see [Reference Galashin, Karp and LamGKL17, Lemma 3.1].
$W_0\in \operatorname {Gr}_{>0}^\perp (k+m,n)$, see [Reference Galashin, Karp and LamGKL17, Lemma 3.1].
Proposition 10.8 Let ![]() $\theta (V_0,W_0)=({\tilde {W}}_0,{\tilde V}_0)$. Then
$\theta (V_0,W_0)=({\tilde {W}}_0,{\tilde V}_0)$. Then ![]() ${\tilde V}_0\in \operatorname {Gr}_{>0}(\ell ,n)$ and
${\tilde V}_0\in \operatorname {Gr}_{>0}(\ell ,n)$ and ![]() ${\tilde {W}}_0\in \operatorname {Gr}_{>0}^\perp (\ell +m,n)$. Moreover, we have
${\tilde {W}}_0\in \operatorname {Gr}_{>0}^\perp (\ell +m,n)$. Moreover, we have ![]() ${\tilde V}_0=\operatorname {alt}(W_0)$ and
${\tilde V}_0=\operatorname {alt}(W_0)$ and ![]() ${\tilde {W}}_0=\operatorname {alt}(V_0)$.
${\tilde {W}}_0=\operatorname {alt}(V_0)$.
Proof. Recall from § 4 that the columns of ![]() $U:=\operatorname {stack}(V_0,W_0)$ satisfy
$U:=\operatorname {stack}(V_0,W_0)$ satisfy ![]() $U(j+n)=(-1)^{k-1}U(j)$ for all
$U(j+n)=(-1)^{k-1}U(j)$ for all ![]() $j\in \mathbb {Z}$. We see that
$j\in \mathbb {Z}$. We see that ![]() $U$ is just the Vandermonde matrix with entries
$U$ is just the Vandermonde matrix with entries ![]() $(z_i^{j-1})_{1\leq i\leq k+\ell ,1\leq j\leq n}$. Thus by (10.2), the vector
$(z_i^{j-1})_{1\leq i\leq k+\ell ,1\leq j\leq n}$. Thus by (10.2), the vector ![]() $\tilde {U}(j)$ has coordinates given by ratios of Vandermonde determinants. More precisely, its
$\tilde {U}(j)$ has coordinates given by ratios of Vandermonde determinants. More precisely, its ![]() $i$th coordinate equals
$i$th coordinate equals
 \[ {\tilde{U}}_{ij}=\dfrac{\displaystyle({-}1)^{i+j-1}{ \operatorname{det}}(z_p^{s-1})_{\substack{1\leq p\leq k+\ell:\,p\neq i;\\ j-\ell < s < j+k}}}{\displaystyle{ \operatorname{det}}(z_p^{s-1})_{\substack{1\leq p\leq k+\ell;\\ j-\ell\leq s < j+k}}} = ({-}1)^{j}z_i^{-(j-\ell-1)} \cdot h(i), \]
\[ {\tilde{U}}_{ij}=\dfrac{\displaystyle({-}1)^{i+j-1}{ \operatorname{det}}(z_p^{s-1})_{\substack{1\leq p\leq k+\ell:\,p\neq i;\\ j-\ell < s < j+k}}}{\displaystyle{ \operatorname{det}}(z_p^{s-1})_{\substack{1\leq p\leq k+\ell;\\ j-\ell\leq s < j+k}}} = ({-}1)^{j}z_i^{-(j-\ell-1)} \cdot h(i), \]where
 \[ h(i):=({-}1)^{i-1} \dfrac{(z_1\cdots z_{k+\ell})^{j-\ell-1}\displaystyle\prod_{\substack{1\leq s < t\leq k+\ell:\\ s,t\neq i}}(z_t-z_s)}{(z_1\cdots z_{k+\ell})^{j-\ell}\displaystyle\prod_{1\leq s < t\leq k+\ell}(z_t-z_s)}. \]
\[ h(i):=({-}1)^{i-1} \dfrac{(z_1\cdots z_{k+\ell})^{j-\ell-1}\displaystyle\prod_{\substack{1\leq s < t\leq k+\ell:\\ s,t\neq i}}(z_t-z_s)}{(z_1\cdots z_{k+\ell})^{j-\ell}\displaystyle\prod_{1\leq s < t\leq k+\ell}(z_t-z_s)}. \]
After dividing row ![]() $i$ of
$i$ of ![]() $\tilde {U}$ by
$\tilde {U}$ by ![]() $h(i)$ for each
$h(i)$ for each ![]() $i$ (which does not affect total positivity of either
$i$ (which does not affect total positivity of either ![]() ${\tilde V}_0$ or
${\tilde V}_0$ or ![]() $\tilde {W}_0$), the
$\tilde {W}_0$), the ![]() $(i,j)$th entry of
$(i,j)$th entry of ![]() $\tilde {U}$ becomes
$\tilde {U}$ becomes ![]() $(-1)^{j}z_i^{-(j-\ell -1)}$. We can now divide row
$(-1)^{j}z_i^{-(j-\ell -1)}$. We can now divide row ![]() $i$ of
$i$ of ![]() $\tilde {U}$ by
$\tilde {U}$ by ![]() $z_i^{\ell +1}$, and after that the
$z_i^{\ell +1}$, and after that the ![]() $i$th entry becomes just
$i$th entry becomes just ![]() $(-1)^jz_i^{-j}$. This matrix is obtained from
$(-1)^jz_i^{-j}$. This matrix is obtained from ![]() $\operatorname {alt}(U)$ by switching the rows that correspond to pairs of inverse
$\operatorname {alt}(U)$ by switching the rows that correspond to pairs of inverse ![]() $z_i$. It is clear that each of the sets
$z_i$. It is clear that each of the sets ![]() $\{z_1,\dots ,z_k\}$ and
$\{z_1,\dots ,z_k\}$ and ![]() $\{z_{k+1},\dots ,z_{k+\ell }\}$ is closed under taking the inverse, and thus these row operations belong to
$\{z_{k+1},\dots ,z_{k+\ell }\}$ is closed under taking the inverse, and thus these row operations belong to ![]() $\operatorname {GL}_k(\mathbb {C})\times \operatorname {GL}_\ell (\mathbb {C})\subset \operatorname {GL}_{k+\ell }(\mathbb {C})$. Therefore, we indeed get that the span
$\operatorname {GL}_k(\mathbb {C})\times \operatorname {GL}_\ell (\mathbb {C})\subset \operatorname {GL}_{k+\ell }(\mathbb {C})$. Therefore, we indeed get that the span ![]() ${\tilde V}_0$ of the last
${\tilde V}_0$ of the last ![]() $\ell$ rows of
$\ell$ rows of ![]() $\tilde {U}$ is totally positive and equal to
$\tilde {U}$ is totally positive and equal to ![]() $\operatorname {alt}(W_0)$, while the span
$\operatorname {alt}(W_0)$, while the span ![]() $\tilde {W}_0$ of the first
$\tilde {W}_0$ of the first ![]() $k$ rows of
$k$ rows of ![]() $\tilde {U}$ is equal to
$\tilde {U}$ is equal to ![]() $\operatorname {alt}(V_0)$ and thus belongs to
$\operatorname {alt}(V_0)$ and thus belongs to ![]() $\operatorname {Gr}_{>0}^\perp (\ell +m,n)$ by (4.6). We are done with the proof.
$\operatorname {Gr}_{>0}^\perp (\ell +m,n)$ by (4.6). We are done with the proof.
As we have explained earlier, Proposition 10.8 finishes the proof of Theorem 4.7.□
It remains to note that Proposition 4.8 now follows from Lemma 10.6.
11. The canonical form: proofs
In this section, we prove Theorem 5.9, and then deduce its generalization, Theorem 5.13, as a corollary. We start by recalling some notions related to the combinatorics of clusters of Plücker coordinates.
11.1 Clusters
Let ![]() $f\in \tilde {S_n}(-k,n-k)$ be an affine permutation. The Grassmann necklace associated with
$f\in \tilde {S_n}(-k,n-k)$ be an affine permutation. The Grassmann necklace associated with ![]() $f$ is a sequence
$f$ is a sequence ![]() $\mathcal {I}_{k+f}=(I_1,I_2,\dots ,I_n)$ of
$\mathcal {I}_{k+f}=(I_1,I_2,\dots ,I_n)$ of ![]() $k$-element subsets of
$k$-element subsets of ![]() $[n]$ defined for
$[n]$ defined for ![]() $i\in [n]$ by
$i\in [n]$ by
For each ![]() $i\in [n]$, define a total order
$i\in [n]$, define a total order ![]() $\preceq _i$ on
$\preceq _i$ on ![]() $[n]$ by
$[n]$ by
where the indices again are taken modulo ![]() $n$. For two sets
$n$. For two sets ![]() $S,T\in (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )$, we write
$S,T\in (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )$, we write ![]() $S\preceq _i T$ if
$S\preceq _i T$ if ![]() $S=\{s_1\prec _i\dots \prec _i s_k\}$,
$S=\{s_1\prec _i\dots \prec _i s_k\}$, ![]() $T=\{t_1\prec _i\dots \prec _i t_k\}$ with
$T=\{t_1\prec _i\dots \prec _i t_k\}$ with ![]() $s_j\preceq _i t_j$ for
$s_j\preceq _i t_j$ for ![]() $j\in [k]$. The positroid
$j\in [k]$. The positroid ![]() $\mathcal {M}_{k+f}\subset { (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )}$ of
$\mathcal {M}_{k+f}\subset { (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )}$ of ![]() $f$ is a collection of subsets of
$f$ is a collection of subsets of ![]() $[n]$ given by
$[n]$ given by
where ![]() $\mathcal {I}_{k+f}=(I_1,\dots ,I_n)$ is the Grassmann necklace associated with
$\mathcal {I}_{k+f}=(I_1,\dots ,I_n)$ is the Grassmann necklace associated with ![]() $f$.
$f$.
Definition 11.1 The sets ![]() $\Pi ^{>0}_{k+f}\subset \Pi ^{\ge 0}_{k+f} \subset \operatorname {Gr}(k,n)$ and
$\Pi ^{>0}_{k+f}\subset \Pi ^{\ge 0}_{k+f} \subset \operatorname {Gr}(k,n)$ and ![]() $\Pi _{k+f}^\mathbb {C}\subset \operatorname {Gr}_\mathbb {C}(k,n)$, are defined by
$\Pi _{k+f}^\mathbb {C}\subset \operatorname {Gr}_\mathbb {C}(k,n)$, are defined by
 \begin{align*} \Pi^{{>}0}_{k+f}&:=\{X\in\operatorname{Gr}_{\ge 0}(k,n)\mid \Delta_J(X)>0 \hbox{ for } J\in\mathcal{M}_{k+f} \hbox{ and } \Delta_J(X)=0 \hbox{ for } J\notin\mathcal{M}_{k+f}\},\\ \Pi^{\ge0}_{k+f}&:=\{X\in\operatorname{Gr}_{\ge 0}(k,n)\mid \Delta_J(X)\geq0 \hbox{ for } J\in\mathcal{M}_{k+f} \hbox{ and } \Delta_J(X)=0 \hbox{ for } J\notin\mathcal{M}_{k+f}\},\\ \Pi_{k+f}^\mathbb{C}&:=\{X\in\operatorname{Gr}_\mathbb{C}(k,n)\mid \Delta_J(X)=0 \hbox{ for } J\notin\mathcal{M}_{k+f}\}. \end{align*}
\begin{align*} \Pi^{{>}0}_{k+f}&:=\{X\in\operatorname{Gr}_{\ge 0}(k,n)\mid \Delta_J(X)>0 \hbox{ for } J\in\mathcal{M}_{k+f} \hbox{ and } \Delta_J(X)=0 \hbox{ for } J\notin\mathcal{M}_{k+f}\},\\ \Pi^{\ge0}_{k+f}&:=\{X\in\operatorname{Gr}_{\ge 0}(k,n)\mid \Delta_J(X)\geq0 \hbox{ for } J\in\mathcal{M}_{k+f} \hbox{ and } \Delta_J(X)=0 \hbox{ for } J\notin\mathcal{M}_{k+f}\},\\ \Pi_{k+f}^\mathbb{C}&:=\{X\in\operatorname{Gr}_\mathbb{C}(k,n)\mid \Delta_J(X)=0 \hbox{ for } J\notin\mathcal{M}_{k+f}\}. \end{align*} The variety ![]() $\Pi _{k+f}^\mathbb {C}$ can alternatively be defined either as the Zariski closure of
$\Pi _{k+f}^\mathbb {C}$ can alternatively be defined either as the Zariski closure of ![]() $\Pi ^{>0}_{k+f}$ in
$\Pi ^{>0}_{k+f}$ in ![]() $\operatorname {Gr}_\mathbb {C}(k,n)$ or as the set of all
$\operatorname {Gr}_\mathbb {C}(k,n)$ or as the set of all ![]() $V\in \operatorname {Gr}_\mathbb {C}(k,n)$ satisfying
$V\in \operatorname {Gr}_\mathbb {C}(k,n)$ satisfying
for all integers ![]() $a < b$. See [Reference Knutson, Lam and SpeyerKLS13].
$a < b$. See [Reference Knutson, Lam and SpeyerKLS13].
For instance, when ![]() $f=\operatorname {id}_{0}:\mathbb {Z}\to \mathbb {Z}$ is the identity map, we have
$f=\operatorname {id}_{0}:\mathbb {Z}\to \mathbb {Z}$ is the identity map, we have ![]() $I_i=\{i,i+1,\dots ,i+k-1\}$ (modulo
$I_i=\{i,i+1,\dots ,i+k-1\}$ (modulo ![]() $n$) for all
$n$) for all ![]() $i\in [n]$,
$i\in [n]$, ![]() $\mathcal {M}_{k+f}={ (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )}$,
$\mathcal {M}_{k+f}={ (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )}$, ![]() $\Pi ^{>0}_{k+f}=\operatorname {Gr}_{>0}(k,n)$,
$\Pi ^{>0}_{k+f}=\operatorname {Gr}_{>0}(k,n)$, ![]() $\Pi ^{\ge 0}_{k+f}=\operatorname {Gr}_{\ge 0}(k,n)$, and
$\Pi ^{\ge 0}_{k+f}=\operatorname {Gr}_{\ge 0}(k,n)$, and ![]() $\Pi _{k+f}^\mathbb {C} = \operatorname {Gr}_\mathbb {C}(k,n)$.
$\Pi _{k+f}^\mathbb {C} = \operatorname {Gr}_\mathbb {C}(k,n)$.
By Definition 11.1, an element ![]() $X\in \Pi ^{>0}_{k+f}$ can be described by a collection
$X\in \Pi ^{>0}_{k+f}$ can be described by a collection ![]() $\{\Delta _J(X)\mid J\in \mathcal {M}_{k+f}\}\in {{\mathbb {R}}\mathbb {P}}_{>0}^{\mathcal {M}_{k+f}}$ of positive real numbers, however, this data is highly redundant.
$\{\Delta _J(X)\mid J\in \mathcal {M}_{k+f}\}\in {{\mathbb {R}}\mathbb {P}}_{>0}^{\mathcal {M}_{k+f}}$ of positive real numbers, however, this data is highly redundant.
Definition 11.2 [LZ98] We say that two sets ![]() $S,T\in { (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )}$ are weakly separated if there do not exist
$S,T\in { (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )}$ are weakly separated if there do not exist ![]() $1\leq a < b < c < d\leq n$ such that
$1\leq a < b < c < d\leq n$ such that ![]() $a,c\in S\setminus T$ and
$a,c\in S\setminus T$ and ![]() $b,d\in T\setminus S$, or vice versa.
$b,d\in T\setminus S$, or vice versa.
We say that a collection ![]() $\mathcal {C}\subset { (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )}$ is weakly separated if any two of its elements are weakly separated. For example, it is not hard to check that
$\mathcal {C}\subset { (\begin {smallmatrix}[n]\\ k\end {smallmatrix} )}$ is weakly separated if any two of its elements are weakly separated. For example, it is not hard to check that ![]() $\mathcal {I}_{k+f}$ is a weakly separated collection for any
$\mathcal {I}_{k+f}$ is a weakly separated collection for any ![]() $f\in \tilde {S_n}(-k,n-k)$, see [Reference Oh, Postnikov and SpeyerOPS15, Lemma 4.5].
$f\in \tilde {S_n}(-k,n-k)$, see [Reference Oh, Postnikov and SpeyerOPS15, Lemma 4.5].
Definition 11.3 Given an affine permutation ![]() $f\in \tilde {S_n}(-k,n-k)$, a weakly separated collection
$f\in \tilde {S_n}(-k,n-k)$, a weakly separated collection ![]() $\mathcal {C}\subset \mathcal {M}_{k+f}$ is called a cluster if it contains
$\mathcal {C}\subset \mathcal {M}_{k+f}$ is called a cluster if it contains ![]() $\mathcal {I}_{k+f}$ and is not contained inside any other weakly separated collection
$\mathcal {I}_{k+f}$ and is not contained inside any other weakly separated collection ![]() $\mathcal {C}'\subset \mathcal {M}_{k+f}$.
$\mathcal {C}'\subset \mathcal {M}_{k+f}$.
Recall from Proposition 5.10 that if ![]() $\mathcal {C}$ is a cluster for
$\mathcal {C}$ is a cluster for ![]() $f$ then the size of
$f$ then the size of ![]() $\mathcal {C}$ is given by (5.5), and the map
$\mathcal {C}$ is given by (5.5), and the map ![]() $X\mapsto \{\Delta _J(X)\mid J\in \mathcal {C}\}$, is a diffeomorphism between
$X\mapsto \{\Delta _J(X)\mid J\in \mathcal {C}\}$, is a diffeomorphism between ![]() $\Pi ^{>0}_{k+f}$ and the positive part
$\Pi ^{>0}_{k+f}$ and the positive part ![]() ${{\mathbb {R}}\mathbb {P}}_{>0}^{\mathcal {C}}$ of the
${{\mathbb {R}}\mathbb {P}}_{>0}^{\mathcal {C}}$ of the ![]() $(k(n-k)-\operatorname {inv}(f))$-dimensional projective space.
$(k(n-k)-\operatorname {inv}(f))$-dimensional projective space.
11.2 Circular minors
We state an identity from [Reference Marsh and ScottMS16] relating certain minors of ![]() ${\tilde {U}}$ to those of
${\tilde {U}}$ to those of ![]() $U$.
$U$.
Lemma 11.4 Fix ![]() $k,\ell ,m,n$, and let
$k,\ell ,m,n$, and let ![]() $U\in \operatorname {Mat}^\circ (k+\ell ,n)$ and
$U\in \operatorname {Mat}^\circ (k+\ell ,n)$ and ![]() ${\tilde {U}}:=\tau (U)$. Let
${\tilde {U}}:=\tau (U)$. Let ![]() $p,q\geq 0$ be integers such that
$p,q\geq 0$ be integers such that ![]() $p+q=k+\ell$, and choose some
$p+q=k+\ell$, and choose some ![]() $a,b\in [n]$ so that the following two sets (viewed modulo
$a,b\in [n]$ so that the following two sets (viewed modulo ![]() $n$) have size
$n$) have size ![]() $k+\ell$:
$k+\ell$:
Then
Proof. Follows from (10.1) together with [Reference Marsh and ScottMS16, Proposition 3.5].
Using Lemma 11.4, we give a formula for circular minors of ![]() ${\tilde {W}}$ and
${\tilde {W}}$ and ![]() ${\tilde V}$.
${\tilde V}$.
Lemma 11.5 Let ![]() $({\tilde {W}},{\tilde V}):=\theta (V,W)$ and
$({\tilde {W}},{\tilde V}):=\theta (V,W)$ and ![]() $U:=\operatorname {stack}(V,W)$. Then for
$U:=\operatorname {stack}(V,W)$. Then for ![]() $j\in \mathbb {Z}$, we have
$j\in \mathbb {Z}$, we have
Proof. The proof is similar to that of Lemma 10.2. Let us denote ![]() $K:=[k+\ell ]$,
$K:=[k+\ell ]$, ![]() ${\tilde {U}}:=\tau (U)=\operatorname {stack}({\tilde {W}},{\tilde V})$,
${\tilde {U}}:=\tau (U)=\operatorname {stack}({\tilde {W}},{\tilde V})$, ![]() $U':=(U(K))^{-1}\cdot U$, and
$U':=(U(K))^{-1}\cdot U$, and ![]() ${\tilde {U}}':=\tau (U')$, which by Lemma 10.1 equals
${\tilde {U}}':=\tau (U')$, which by Lemma 10.1 equals ![]() $(U(K))^\text {t}\cdot {\tilde {U}}$. Let
$(U(K))^\text {t}\cdot {\tilde {U}}$. Let ![]() $V',W',{\tilde V}',{\tilde {W}}'$ be such that
$V',W',{\tilde V}',{\tilde {W}}'$ be such that ![]() $U'=\operatorname {stack}(V',W')$ and
$U'=\operatorname {stack}(V',W')$ and ![]() ${\tilde {U}}'=\operatorname {stack}({\tilde {W}}',{\tilde V}')$. Note that the submatrix of
${\tilde {U}}'=\operatorname {stack}({\tilde {W}}',{\tilde V}')$. Note that the submatrix of ![]() ${\tilde {U}}'$ with column set
${\tilde {U}}'$ with column set ![]() $[\ell +1,2\ell +k+1)$ is upper triangular with
$[\ell +1,2\ell +k+1)$ is upper triangular with ![]() $\pm 1$ on the diagonal. Applying Lemma 11.4 to
$\pm 1$ on the diagonal. Applying Lemma 11.4 to ![]() $U'$ and
$U'$ and ![]() ${\tilde {U}}'$ with
${\tilde {U}}'$ with ![]() $a=\ell -k+1$,
$a=\ell -k+1$, ![]() $b=j$,
$b=j$, ![]() $p=k$,
$p=k$, ![]() $q=\ell$ yields
$q=\ell$ yields
Let ![]() $r:={ \operatorname {det}}(U(K))$. Applying the same lemma to
$r:={ \operatorname {det}}(U(K))$. Applying the same lemma to ![]() $U$ and
$U$ and ![]() ${\tilde {U}}$, we get
${\tilde {U}}$, we get
This proves (11.4). The proof of (11.3) is completely similar, except that we need to set ![]() $U':=w_0\cdot (U(K))^{-1}\cdot U$, where
$U':=w_0\cdot (U(K))^{-1}\cdot U$, where ![]() $w_0$ is the
$w_0$ is the ![]() $(k+\ell )\times (k+\ell )$ permutation matrix having
$(k+\ell )\times (k+\ell )$ permutation matrix having ![]() $(i,j)$th entry equal to
$(i,j)$th entry equal to ![]() $1$ if
$1$ if ![]() $i+j=k+\ell +1$ and to
$i+j=k+\ell +1$ and to ![]() $0$ otherwise.
$0$ otherwise.
Example 11.6 Let ![]() $k=2$,
$k=2$, ![]() $\ell =1$,
$\ell =1$, ![]() $n=5$, and
$n=5$, and ![]() $U$ and
$U$ and ![]() ${\tilde {U}}\cdot D$ be given in Figure 2, with the matrix
${\tilde {U}}\cdot D$ be given in Figure 2, with the matrix ![]() $D={ \operatorname {diag}}(2,4,8,10,4)$ given in (6.2). Furthermore, let
$D={ \operatorname {diag}}(2,4,8,10,4)$ given in (6.2). Furthermore, let ![]() $p=1$,
$p=1$, ![]() $q=2$,
$q=2$, ![]() $a=1$,
$a=1$, ![]() $b=3$, so (11.1) yields
$b=3$, so (11.1) yields ![]() $J=\{1,3,4\}$ and
$J=\{1,3,4\}$ and ![]() $I=\{1,2,4\}$. By (11.2), we have
$I=\{1,2,4\}$. By (11.2), we have
We note that ![]() $\Delta _{134}({\tilde {U}}\cdot D)=20$, so the left-hand side of (11.5) is
$\Delta _{134}({\tilde {U}}\cdot D)=20$, so the left-hand side of (11.5) is ![]() $\Delta _{134}({\tilde {U}})=\frac {20}{2\times 8\times 10}=\frac 18$. On the other hand, we have
$\Delta _{134}({\tilde {U}})=\frac {20}{2\times 8\times 10}=\frac 18$. On the other hand, we have
so the right-hand side of (11.5) is ![]() ${\pm }\frac 18$, in agreement with Lemma 11.4.
${\pm }\frac 18$, in agreement with Lemma 11.4.
Let us now set ![]() $j:=3$, and verify (11.3) and (11.4). We have
$j:=3$, and verify (11.3) and (11.4). We have
and thus the left-hand side of (11.3) is ![]() $\frac {-4}{2\times 4}=-\frac {1}{2}$. The right-hand side of (11.3) is given by
$\frac {-4}{2\times 4}=-\frac {1}{2}$. The right-hand side of (11.3) is given by ![]() ${\pm }{\Delta _{2}(W)}/{\Delta _{125}(U)}={\pm }\frac {1}{2}$.
${\pm }{\Delta _{2}(W)}/{\Delta _{125}(U)}={\pm }\frac {1}{2}$.
Similarly, the left-hand side of (11.4) is ![]() $\Delta _{3}({\tilde V})=\frac 28=\frac 14$, because
$\Delta _{3}({\tilde V})=\frac 28=\frac 14$, because ![]() $\Delta _3({\tilde V}\cdot D)=2$. The right-hand side of (11.4) is
$\Delta _3({\tilde V}\cdot D)=2$. The right-hand side of (11.4) is ![]() ${\pm }{\Delta _{34}(V)}/{\Delta _{234}(U)}=\pm \frac 28=\pm \frac 14$.
${\pm }{\Delta _{34}(V)}/{\Delta _{234}(U)}=\pm \frac 28=\pm \frac 14$.
11.3 Coordinates on  $\operatorname {Gr}(k,n)\times \operatorname {Gr}(\ell ,n)$
$\operatorname {Gr}(k,n)\times \operatorname {Gr}(\ell ,n)$
For a ![]() $k\times \ell$ matrix
$k\times \ell$ matrix ![]() $T$ and an
$T$ and an ![]() $\ell \times k$ matrix
$\ell \times k$ matrix ![]() $S$, define
$S$, define
Remark 11.7 By the well-known formula for the determinant of a block matrix, we have
For ![]() $U,U'\in \operatorname {Mat}^\circ (k+\ell ,n)$, we write
$U,U'\in \operatorname {Mat}^\circ (k+\ell ,n)$, we write ![]() $U\simeq _{k,\ell } U'$ if
$U\simeq _{k,\ell } U'$ if ![]() $U=g\cdot U'$ for some
$U=g\cdot U'$ for some ![]() $g\in \operatorname {GL}_k(\mathbb {R})\times \operatorname {GL}_\ell (\mathbb {R})$.
$g\in \operatorname {GL}_k(\mathbb {R})\times \operatorname {GL}_\ell (\mathbb {R})$.
Lemma 11.8 For ![]() $M(T,S)\in \operatorname {GL}_{k+\ell }(\mathbb {R})$ and
$M(T,S)\in \operatorname {GL}_{k+\ell }(\mathbb {R})$ and ![]() $U\in \operatorname {Mat}^\circ (k+\ell ,n)$, we have
$U\in \operatorname {Mat}^\circ (k+\ell ,n)$, we have
Proof. First, note that the matrix ![]() $M(-T,-S)$ must also be invertible because it has the same determinant as
$M(-T,-S)$ must also be invertible because it has the same determinant as ![]() $M(T,S)$ by (11.6). Multiplying them together, we get
$M(T,S)$ by (11.6). Multiplying them together, we get
In particular, the matrix on the right-hand side (which we denote by ![]() $g$) must be invertible:
$g$) must be invertible: ![]() $g\in \operatorname {GL}_k(\mathbb {R})\times \operatorname {GL}_\ell (\mathbb {R})$. Thus
$g\in \operatorname {GL}_k(\mathbb {R})\times \operatorname {GL}_\ell (\mathbb {R})$. Thus ![]() $g^{-1}\cdot M(-T,-S)=M(T,S)^{-1}$, i.e.
$g^{-1}\cdot M(-T,-S)=M(T,S)^{-1}$, i.e. ![]() $M(-T,-S)\simeq _{k,l}M(T,S)^{-1}$. Lemma 11.8 now follows from Lemma 10.1.
$M(-T,-S)\simeq _{k,l}M(T,S)^{-1}$. Lemma 11.8 now follows from Lemma 10.1.
We introduce a convenient coordinate chart on ![]() $\operatorname {Gr}(k,n)\times \operatorname {Gr}(\ell ,n)$. Let
$\operatorname {Gr}(k,n)\times \operatorname {Gr}(\ell ,n)$. Let ![]() $T,S,A,B$ be
$T,S,A,B$ be ![]() $k\times \ell, \ell \times k, k\times m,$ and
$k\times \ell, \ell \times k, k\times m,$ and ![]() $\ell \times m$ matrices, respectively. Denote
$\ell \times m$ matrices, respectively. Denote
Take a generic pair ![]() $(V,W)\in \operatorname {Gr}(k,n)\times \operatorname {Gr}(\ell ,n)$, and let
$(V,W)\in \operatorname {Gr}(k,n)\times \operatorname {Gr}(\ell ,n)$, and let ![]() $\operatorname {span}(V,W) \in \operatorname {Gr}(k+\ell ,n)$ be the row span of
$\operatorname {span}(V,W) \in \operatorname {Gr}(k+\ell ,n)$ be the row span of ![]() $U:=\operatorname {stack}(V,W)$. Since the pair
$U:=\operatorname {stack}(V,W)$. Since the pair ![]() $(V,W)$ is generic, there exists a unique pair
$(V,W)$ is generic, there exists a unique pair ![]() $T,S$ such that
$T,S$ such that ![]() $U([k+\ell ])\simeq _{k,l}M(T,S)$, and thus we can write
$U([k+\ell ])\simeq _{k,l}M(T,S)$, and thus we can write
Here ![]() $V\in \operatorname {Gr}(k,n)$ is the row span of
$V\in \operatorname {Gr}(k,n)$ is the row span of ![]() $[\operatorname {Id}_k|T|A+TB]$, and
$[\operatorname {Id}_k|T|A+TB]$, and ![]() $W\in \operatorname {Gr}(\ell ,n)$ is the row span of
$W\in \operatorname {Gr}(\ell ,n)$ is the row span of ![]() $[S|\operatorname {Id}_\ell |B+SA]$.
$[S|\operatorname {Id}_\ell |B+SA]$.
Recall from Definition 5.1 that the canonical forms on ![]() $\operatorname {Gr}(k,n)$,
$\operatorname {Gr}(k,n)$, ![]() $\operatorname {Gr}(\ell ,n)$, and
$\operatorname {Gr}(\ell ,n)$, and ![]() $\operatorname {Gr}(k+\ell ,n)$ are given in these coordinates by
$\operatorname {Gr}(k+\ell ,n)$ are given in these coordinates by
 \begin{gather*} \omega_{k,n}(V)={\pm}\frac{d^{k\times\ell}(T)\wedge d^{k\times m }(A+TB)}{\Delta_{k}^{\operatorname{circ}}(V)},\quad \omega_{\ell,n}(W)={\pm}\frac{d^{\ell\times k}(S)\wedge d^{\ell\times m}(B+SA)}{\Delta_{\ell}^{\operatorname{circ}}(W)},\\ \omega_{k+\ell,n}(U):={\pm}\frac{d^{k\times m}(A)\wedge d^{\ell\times m}(B)}{\Delta_{k+\ell}^{\operatorname{circ}}(N(0,0,A,B))}. \end{gather*}
\begin{gather*} \omega_{k,n}(V)={\pm}\frac{d^{k\times\ell}(T)\wedge d^{k\times m }(A+TB)}{\Delta_{k}^{\operatorname{circ}}(V)},\quad \omega_{\ell,n}(W)={\pm}\frac{d^{\ell\times k}(S)\wedge d^{\ell\times m}(B+SA)}{\Delta_{\ell}^{\operatorname{circ}}(W)},\\ \omega_{k+\ell,n}(U):={\pm}\frac{d^{k\times m}(A)\wedge d^{\ell\times m}(B)}{\Delta_{k+\ell}^{\operatorname{circ}}(N(0,0,A,B))}. \end{gather*}Lemma 11.9 In the above notation, we have
Proof. We need to show that after taking the wedge with ![]() $d^{k\times \ell }(T)\wedge d^{\ell \times k}(S)$ (i.e. treating the entries of
$d^{k\times \ell }(T)\wedge d^{\ell \times k}(S)$ (i.e. treating the entries of ![]() $T$ and
$T$ and ![]() $S$ as constants), we have
$S$ as constants), we have
Consider a linear operator on the ![]() $(k+\ell )$-dimensional vector space
$(k+\ell )$-dimensional vector space ![]() $\mathbb {R}^{k+\ell }$ given by the matrix
$\mathbb {R}^{k+\ell }$ given by the matrix ![]() $M(T,S)$. For vectors
$M(T,S)$. For vectors ![]() $v\in \mathbb {R}^k$ and
$v\in \mathbb {R}^k$ and ![]() $w\in \mathbb {R}^\ell$, this operator sends
$w\in \mathbb {R}^\ell$, this operator sends ![]() $(v,w)\in \mathbb {R}^{k+\ell }$ to
$(v,w)\in \mathbb {R}^{k+\ell }$ to ![]() $(v+Tw,w+Sv)$. Therefore, it sends the form
$(v+Tw,w+Sv)$. Therefore, it sends the form ![]() $\omega (v,w):=dv_1\wedge \dots \wedge dv_k\wedge dw_1\wedge \dots \wedge dw_\ell$ to
$\omega (v,w):=dv_1\wedge \dots \wedge dv_k\wedge dw_1\wedge \dots \wedge dw_\ell$ to ![]() ${ \operatorname {det}}(M(T,S))\cdot \omega (v,w)$. Letting
${ \operatorname {det}}(M(T,S))\cdot \omega (v,w)$. Letting ![]() $v:=A(j)$ and
$v:=A(j)$ and ![]() $w:=B(j)$ for
$w:=B(j)$ for ![]() $j\in [n]$, we get that
$j\in [n]$, we get that ![]() $(A+TB)(j)=v+Tw$ and
$(A+TB)(j)=v+Tw$ and ![]() $(B+SA)(j)=w+Sv$, and thus
$(B+SA)(j)=w+Sv$, and thus
The result follows by applying this to ![]() $j=1,2,\dots ,m$.
$j=1,2,\dots ,m$.
Lemma 11.9 implies that ![]() $\omega _{k,n}\wedge \omega _{\ell ,n}=\pm \omega _{k+\ell ,n}\wedge \omega _{ \operatorname {Ker}}$, where
$\omega _{k,n}\wedge \omega _{\ell ,n}=\pm \omega _{k+\ell ,n}\wedge \omega _{ \operatorname {Ker}}$, where
We first prove Proposition 5.7, which states that ![]() $\omega _{k+\ell ,n}$ is preserved by
$\omega _{k+\ell ,n}$ is preserved by ![]() $\tau$, and then we will concentrate on showing that
$\tau$, and then we will concentrate on showing that ![]() $\omega _{k+\ell ,n}\wedge \omega _{ \operatorname {Ker}}$ is preserved by
$\omega _{k+\ell ,n}\wedge \omega _{ \operatorname {Ker}}$ is preserved by ![]() $\theta$.
$\theta$.
11.4 Proof of Proposition 5.7
We start by constructing two collections ![]() $\mathcal {C},\mathcal {C}^{\operatorname {op}}$ of
$\mathcal {C},\mathcal {C}^{\operatorname {op}}$ of ![]() $(k+\ell )$-element subsets of
$(k+\ell )$-element subsets of ![]() $[n]$ such that they both form clusters for
$[n]$ such that they both form clusters for ![]() $\operatorname {Gr}(k+\ell ,n)$, and whenever
$\operatorname {Gr}(k+\ell ,n)$, and whenever ![]() $I$ and
$I$ and ![]() $J$ are related by (11.1), we have
$J$ are related by (11.1), we have ![]() $I\in \mathcal {C}$ if and only if
$I\in \mathcal {C}$ if and only if ![]() $J\in \mathcal {C}^{\operatorname {op}}$. Explicitly,
$J\in \mathcal {C}^{\operatorname {op}}$. Explicitly, ![]() $\mathcal {C}$ is the set of all
$\mathcal {C}$ is the set of all ![]() $I\in { (\begin {smallmatrix}[n]\\ k+\ell \end {smallmatrix} )}$ that are unions of two cyclic intervals, one of which is of the form
$I\in { (\begin {smallmatrix}[n]\\ k+\ell \end {smallmatrix} )}$ that are unions of two cyclic intervals, one of which is of the form ![]() $[c,1+k)$ for
$[c,1+k)$ for ![]() $c\in [n]$ (if
$c\in [n]$ (if ![]() $c>1+k$ then we view this interval modulo
$c>1+k$ then we view this interval modulo ![]() $n$). Either of the two cyclic intervals is allowed to be empty. Similarly,
$n$). Either of the two cyclic intervals is allowed to be empty. Similarly, ![]() $\mathcal {C}^{\operatorname {op}}$ is the set of all
$\mathcal {C}^{\operatorname {op}}$ is the set of all ![]() $J\in { (\begin {smallmatrix}[n]\\ k+\ell \end {smallmatrix} )}$ that are unions of two cyclic intervals, one of which is of the form
$J\in { (\begin {smallmatrix}[n]\\ k+\ell \end {smallmatrix} )}$ that are unions of two cyclic intervals, one of which is of the form ![]() $[1,1+p)$ for some
$[1,1+p)$ for some ![]() $p\geq 0$. It is easy to checkFootnote 6 that both
$p\geq 0$. It is easy to checkFootnote 6 that both ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $\mathcal {C}^{\operatorname {op}}$ are maximal weakly separated collections of size
$\mathcal {C}^{\operatorname {op}}$ are maximal weakly separated collections of size ![]() $(k+\ell )m+1$, which is one more than the dimension of
$(k+\ell )m+1$, which is one more than the dimension of ![]() $\operatorname {Gr}(k+\ell ,n)$.
$\operatorname {Gr}(k+\ell ,n)$.
Let us index the elements of ![]() $\mathcal {C}$ by
$\mathcal {C}$ by ![]() $\mathcal {C}:=\{I_0,I_1,\dots ,I_{(k+\ell )m}\}$ and consider the coordinate chart on
$\mathcal {C}:=\{I_0,I_1,\dots ,I_{(k+\ell )m}\}$ and consider the coordinate chart on ![]() $\operatorname {Gr}(k+\ell ,n)$ given by
$\operatorname {Gr}(k+\ell ,n)$ given by ![]() $\{\Delta _I\mid I\in \mathcal {C}\}$, rescaled so that
$\{\Delta _I\mid I\in \mathcal {C}\}$, rescaled so that ![]() $\Delta _{I_0}=1$ for
$\Delta _{I_0}=1$ for ![]() $I_0:=[\ell +1,2\ell +k+1)$ modulo
$I_0:=[\ell +1,2\ell +k+1)$ modulo ![]() $n$. Then by Proposition 5.3, we have
$n$. Then by Proposition 5.3, we have
 \[ \omega_{k+\ell,n}(U)={\pm}\frac{d\Delta_{I_1}(U)}{\Delta_{I_1}(U)}\wedge\dots\wedge\frac{d\Delta_{I_{(k+\ell)m}}(U)}{\Delta_{I_{(k+\ell)m}}(U)}. \]
\[ \omega_{k+\ell,n}(U)={\pm}\frac{d\Delta_{I_1}(U)}{\Delta_{I_1}(U)}\wedge\dots\wedge\frac{d\Delta_{I_{(k+\ell)m}}(U)}{\Delta_{I_{(k+\ell)m}}(U)}. \]
Similarly, letting ![]() $\mathcal {C}^{\operatorname {op}}:=\{J_0,J_1,\dots ,J_{(k+\ell )m}\}$ so that
$\mathcal {C}^{\operatorname {op}}:=\{J_0,J_1,\dots ,J_{(k+\ell )m}\}$ so that ![]() $J_0=[k+\ell ]$, we have
$J_0=[k+\ell ]$, we have
 \[ \omega_{k+\ell,n}({\tilde{U}})={\pm}\frac{d\Delta_{J_1}({\tilde{U}})}{\Delta_{J_1}({\tilde{U}})}\wedge\dots\wedge\frac{d\Delta_{J_{(k+\ell)m}}({\tilde{U}})}{\Delta_{J_{(k+\ell)m}}({\tilde{U}})}. \]
\[ \omega_{k+\ell,n}({\tilde{U}})={\pm}\frac{d\Delta_{J_1}({\tilde{U}})}{\Delta_{J_1}({\tilde{U}})}\wedge\dots\wedge\frac{d\Delta_{J_{(k+\ell)m}}({\tilde{U}})}{\Delta_{J_{(k+\ell)m}}({\tilde{U}})}. \]
If ![]() $I\in \mathcal {C}$ is a cyclic interval (there are
$I\in \mathcal {C}$ is a cyclic interval (there are ![]() $n$ such intervals in both
$n$ such intervals in both ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $\mathcal {C}^{\operatorname {op}}$), then Lemma 10.2 provides a cyclic interval
$\mathcal {C}^{\operatorname {op}}$), then Lemma 10.2 provides a cyclic interval ![]() $J\in \mathcal {C}^{\operatorname {op}}$ such that
$J\in \mathcal {C}^{\operatorname {op}}$ such that
Differentiating both sides, we get that
 \[ \frac{d\Delta_J({\tilde{U}})}{\Delta_J({\tilde{U}})}={\pm}\frac{d\Delta_I(U)}{\Delta_I(U)}. \]
\[ \frac{d\Delta_J({\tilde{U}})}{\Delta_J({\tilde{U}})}={\pm}\frac{d\Delta_I(U)}{\Delta_I(U)}. \]
Thus the expression for ![]() $\omega _{k+\ell ,n}({\tilde {U}})$ contains
$\omega _{k+\ell ,n}({\tilde {U}})$ contains ![]() $d\Delta _K(U)$ for all cyclic intervals
$d\Delta _K(U)$ for all cyclic intervals ![]() $K$ of
$K$ of ![]() $[n]$ of size
$[n]$ of size ![]() $k+\ell$. Therefore, we may treat them as constants while computing
$k+\ell$. Therefore, we may treat them as constants while computing ![]() $d\Delta _J({\tilde {U}})$ for other
$d\Delta _J({\tilde {U}})$ for other ![]() $J\in \mathcal {C}^{\operatorname {op}}$. For each
$J\in \mathcal {C}^{\operatorname {op}}$. For each ![]() $J\in \mathcal {C}^{\operatorname {op}}$, Lemma 11.4 provides a set
$J\in \mathcal {C}^{\operatorname {op}}$, Lemma 11.4 provides a set ![]() $I\in \mathcal {C}$ and cyclic intervals
$I\in \mathcal {C}$ and cyclic intervals ![]() $K,L\subset [n]$ such that
$K,L\subset [n]$ such that
Differentiating both sides and ignoring the terms with ![]() $d\Delta _K(U)$ and
$d\Delta _K(U)$ and ![]() $d\Delta _L(U)$, we get
$d\Delta _L(U)$, we get
 \[ \frac{d\Delta_J({\tilde{U}})}{\Delta_J({\tilde{U}})}={\pm}\frac{d\Delta_I(U)}{\Delta_I(U)}. \]
\[ \frac{d\Delta_J({\tilde{U}})}{\Delta_J({\tilde{U}})}={\pm}\frac{d\Delta_I(U)}{\Delta_I(U)}. \]
Applying this to all ![]() $J\in \mathcal {C}^{\operatorname {op}}$ finishes the proof.
$J\in \mathcal {C}^{\operatorname {op}}$ finishes the proof.
11.5 Proof of Theorem 5.9
Consider the cyclic shift map ![]() $\sigma :\operatorname {Mat}^\circ (k+\ell ,n)\to \operatorname {Mat}^\circ (k+\ell ,n)$ sending a matrix
$\sigma :\operatorname {Mat}^\circ (k+\ell ,n)\to \operatorname {Mat}^\circ (k+\ell ,n)$ sending a matrix ![]() $U$ with columns
$U$ with columns ![]() $U(j), j\in \mathbb {Z}$ such that
$U(j), j\in \mathbb {Z}$ such that ![]() $U(j+n)=(-1)^{k-1}U(j)$ to a matrix
$U(j+n)=(-1)^{k-1}U(j)$ to a matrix ![]() $\sigma U$ defined by
$\sigma U$ defined by ![]() $(\sigma U)(j):=U(j-1)$. This operator acts on
$(\sigma U)(j):=U(j-1)$. This operator acts on ![]() $V$ and
$V$ and ![]() $W$ similarly. Rather than working with the maps
$W$ similarly. Rather than working with the maps ![]() $\theta$ and
$\theta$ and ![]() $\tau$, we will work with their cyclically shifted versions:
$\tau$, we will work with their cyclically shifted versions:
By (10.1), the map ![]() $\tau '$ coincides (up to sign) with the right twist map of [Reference Muller and SpeyerMS17]. Since the map
$\tau '$ coincides (up to sign) with the right twist map of [Reference Muller and SpeyerMS17]. Since the map ![]() $\theta '$ differs from the map
$\theta '$ differs from the map ![]() $\theta$ by a cyclic shift, and the forms
$\theta$ by a cyclic shift, and the forms ![]() $\omega _{k,n}$,
$\omega _{k,n}$, ![]() $\omega _{\ell ,n}$, and
$\omega _{\ell ,n}$, and ![]() $\omega _{k+\ell ,n}$ are preserved by
$\omega _{k+\ell ,n}$ are preserved by ![]() $\sigma$, it suffices to prove the version of Theorem 5.9 with
$\sigma$, it suffices to prove the version of Theorem 5.9 with ![]() $\theta$ replaced with
$\theta$ replaced with ![]() $\theta '$.
$\theta '$.
Proof of Theorem 5.9 We have shown above that ![]() $\omega _{k+\ell ,n}$ is preserved by
$\omega _{k+\ell ,n}$ is preserved by ![]() $\theta$, and therefore by
$\theta$, and therefore by ![]() $\theta '$. What we need to show in order to complete the proof of Theorem 5.9 is that
$\theta '$. What we need to show in order to complete the proof of Theorem 5.9 is that ![]() $\omega _{ \operatorname {Ker}}\wedge \omega _{k+\ell ,n}$ is preserved by
$\omega _{ \operatorname {Ker}}\wedge \omega _{k+\ell ,n}$ is preserved by ![]() $\theta '$ up to a sign. Let us split
$\theta '$ up to a sign. Let us split ![]() $\omega _{ \operatorname {Ker}}$ into a product of two terms
$\omega _{ \operatorname {Ker}}$ into a product of two terms
Here we are using the fact that ![]() $\Delta _{k+\ell }^{\operatorname {circ}}(U)=({ \operatorname {det}}(M(T,S)))^{n} \cdot \Delta _{k+\ell }^{\operatorname {circ}}(N(0,0,A,B))$.
$\Delta _{k+\ell }^{\operatorname {circ}}(U)=({ \operatorname {det}}(M(T,S)))^{n} \cdot \Delta _{k+\ell }^{\operatorname {circ}}(N(0,0,A,B))$.
By Lemma 10.5, we have ![]() $\Delta _{k+\ell }^{\operatorname {circ}}(U)\cdot \Delta _{k+\ell }^{\operatorname {circ}}(\tilde {U})=\pm 1$, and then Lemma 11.5 implies
$\Delta _{k+\ell }^{\operatorname {circ}}(U)\cdot \Delta _{k+\ell }^{\operatorname {circ}}(\tilde {U})=\pm 1$, and then Lemma 11.5 implies
 \begin{equation} \frac{\Delta_{k+\ell}^{\operatorname{circ}}(U)}{\Delta_{k}^{\operatorname{circ}}(V)\cdot \Delta_{\ell}^{\operatorname{circ}}(W)} ={\pm}\frac{\Delta_{k+\ell}^{\operatorname{circ}}({\tilde{U}})}{\Delta_{k}^{\operatorname{circ}}({\tilde{W}})\cdot \Delta_{\ell}^{\operatorname{circ}}({\tilde V})}. \end{equation}
\begin{equation} \frac{\Delta_{k+\ell}^{\operatorname{circ}}(U)}{\Delta_{k}^{\operatorname{circ}}(V)\cdot \Delta_{\ell}^{\operatorname{circ}}(W)} ={\pm}\frac{\Delta_{k+\ell}^{\operatorname{circ}}({\tilde{U}})}{\Delta_{k}^{\operatorname{circ}}({\tilde{W}})\cdot \Delta_{\ell}^{\operatorname{circ}}({\tilde V})}. \end{equation} Note that ![]() $\omega _{ \operatorname {Ker}}$ itself may not be preserved by
$\omega _{ \operatorname {Ker}}$ itself may not be preserved by ![]() $\theta '$. Indeed, let
$\theta '$. Indeed, let ![]() ${\tilde {T}},{\tilde {S}},{\tilde {A}},{\tilde {B}}$ be the unique matrices such that
${\tilde {T}},{\tilde {S}},{\tilde {A}},{\tilde {B}}$ be the unique matrices such that
Let us write down ![]() ${\tilde {T}},{\tilde {S}},{\tilde {A}},{\tilde {B}}$ more explicitly. Recall that
${\tilde {T}},{\tilde {S}},{\tilde {A}},{\tilde {B}}$ more explicitly. Recall that ![]() $N(T,S,A+TB,B+SA)=M(T,S)\cdot N(0,0,A,B)$. Thus by Lemma 11.8, we have
$N(T,S,A+TB,B+SA)=M(T,S)\cdot N(0,0,A,B)$. Thus by Lemma 11.8, we have
where ![]() $H:=\tau '(N(0,0,A,B))$,
$H:=\tau '(N(0,0,A,B))$, ![]() $H([k+\ell ])$ is the square submatrix of
$H([k+\ell ])$ is the square submatrix of ![]() $H$ spanned by the first
$H$ spanned by the first ![]() $k+\ell$ columns, and
$k+\ell$ columns, and ![]() $H':=(H([k+\ell ]))^{-1}\cdot H$. We see that the first
$H':=(H([k+\ell ]))^{-1}\cdot H$. We see that the first ![]() $k+\ell$ columns of
$k+\ell$ columns of ![]() $H'$ form an identity matrix, and therefore we can write
$H'$ form an identity matrix, and therefore we can write ![]() $H'=N(0,0,{\tilde {A}},{\tilde {B}})$ for some
$H'=N(0,0,{\tilde {A}},{\tilde {B}})$ for some ![]() ${\tilde {A}},{\tilde {B}}$. Thus
${\tilde {A}},{\tilde {B}}$. Thus ![]() ${\tilde {T}},{\tilde {S}}$ are the unique matrices such that
${\tilde {T}},{\tilde {S}}$ are the unique matrices such that
(We will later show that such matrices exist, i.e. that the upper left ![]() $k\times k$ and the lower right
$k\times k$ and the lower right ![]() $\ell \times \ell$ submatrices of the matrix on the right-hand side are invertible.) We see that the entries of
$\ell \times \ell$ submatrices of the matrix on the right-hand side are invertible.) We see that the entries of ![]() $H$, and therefore of
$H$, and therefore of ![]() ${\tilde {A}}$ and
${\tilde {A}}$ and ![]() ${\tilde {B}}$, depend on the entries of
${\tilde {B}}$, depend on the entries of ![]() $A$ and
$A$ and ![]() $B$ but not on the entries of
$B$ but not on the entries of ![]() $T$ and
$T$ and ![]() $S$. However, the entries of
$S$. However, the entries of ![]() ${\tilde {T}}$ and
${\tilde {T}}$ and ![]() ${\tilde {S}}$ depend on the entries of all four matrices
${\tilde {S}}$ depend on the entries of all four matrices ![]() $T,S,A,B$. By definition,
$T,S,A,B$. By definition, ![]() $\omega _{ \operatorname {Ker}}$ is proportional to
$\omega _{ \operatorname {Ker}}$ is proportional to ![]() $d^{k\times \ell }(T)\wedge d^{\ell \times k}(S)$, so the pullback of
$d^{k\times \ell }(T)\wedge d^{\ell \times k}(S)$, so the pullback of ![]() $\omega _{ \operatorname {Ker}}$ under
$\omega _{ \operatorname {Ker}}$ under ![]() $\theta '$ will be proportional to
$\theta '$ will be proportional to ![]() $d^{k\times \ell }(\tilde {T})\wedge d^{\ell \times k}(\tilde {S})$, and therefore will contain
$d^{k\times \ell }(\tilde {T})\wedge d^{\ell \times k}(\tilde {S})$, and therefore will contain ![]() $da_{ij}$ and
$da_{ij}$ and ![]() $db_{ij}$ as well as quantities of
$db_{ij}$ as well as quantities of ![]() $dt_{ij}$ and
$dt_{ij}$ and ![]() $ds_{ij}$. This shows that
$ds_{ij}$. This shows that ![]() $\omega _{ \operatorname {Ker}}$ is not in general preserved by
$\omega _{ \operatorname {Ker}}$ is not in general preserved by ![]() $\theta '$.
$\theta '$.
On the other hand, since ![]() $\omega _{k+\ell ,n}$ is preserved by
$\omega _{k+\ell ,n}$ is preserved by ![]() $\theta '$ and is proportional to
$\theta '$ and is proportional to ![]() $d^{k\times m}(A)\wedge d^{\ell \times m}(B)$, we only need to show that
$d^{k\times m}(A)\wedge d^{\ell \times m}(B)$, we only need to show that ![]() $\omega _{ \operatorname {Ker}}$ is preserved by
$\omega _{ \operatorname {Ker}}$ is preserved by ![]() $\theta '$ when we treat
$\theta '$ when we treat ![]() $A$ and
$A$ and ![]() $B$ as constants. We now investigate how exactly the matrices
$B$ as constants. We now investigate how exactly the matrices ![]() ${\tilde {T}}$ and
${\tilde {T}}$ and ![]() ${\tilde {S}}$ depend on
${\tilde {S}}$ depend on ![]() $T,S,A,B$.
$T,S,A,B$.
Lemma 11.10 The matrix ![]() $H([k+\ell ])$ from (11.9) is an upper triangular
$H([k+\ell ])$ from (11.9) is an upper triangular ![]() $(k+\ell )\times (k+\ell )$ matrix with
$(k+\ell )\times (k+\ell )$ matrix with ![]() $\pm 1$ on the diagonal.
$\pm 1$ on the diagonal.
Proof. This is clear from the definition of the map ![]() $\tau '$: for
$\tau '$: for ![]() $j\leq k+\ell$, the
$j\leq k+\ell$, the ![]() $j$th column of
$j$th column of ![]() $H$ is orthogonal to columns
$H$ is orthogonal to columns ![]() $j+1,j+2,\dots ,k+\ell$ of
$j+1,j+2,\dots ,k+\ell$ of ![]() $N(0,0,A,B)$, and its scalar product with the
$N(0,0,A,B)$, and its scalar product with the ![]() $j$th column of
$j$th column of ![]() $N(0,0,A,B)$ is equal to
$N(0,0,A,B)$ is equal to ![]() $\pm 1$. Since the first
$\pm 1$. Since the first ![]() $k+\ell$ columns of
$k+\ell$ columns of ![]() $N(0,0,A,B)$ form an identity matrix, the result follows.
$N(0,0,A,B)$ form an identity matrix, the result follows.
In particular, it follows from Lemma 11.10 that the upper left ![]() $k\times k$ and lower right
$k\times k$ and lower right ![]() $\ell \times \ell$ submatrices of
$\ell \times \ell$ submatrices of ![]() $M(-S^\text {t},-T^\text {t})\cdot H([k+\ell ])$ are invertible, which proves the existence of
$M(-S^\text {t},-T^\text {t})\cdot H([k+\ell ])$ are invertible, which proves the existence of ![]() ${\tilde {T}},{\tilde {S}}$ satisfying (11.9). Recall that the entries of
${\tilde {T}},{\tilde {S}}$ satisfying (11.9). Recall that the entries of ![]() $H([k+\ell ])$ depend only on the entries of
$H([k+\ell ])$ depend only on the entries of ![]() $A$ and
$A$ and ![]() $B$, which we treat as constants since we are taking the wedge with
$B$, which we treat as constants since we are taking the wedge with ![]() $d^{k\times m}(A)\wedge d^{\ell \times m}(B)$. Our next result is illustrated in Example 11.12.
$d^{k\times m}(A)\wedge d^{\ell \times m}(B)$. Our next result is illustrated in Example 11.12.
Lemma 11.11 Suppose that for some constant upper triangular ![]() $(k+\ell )\times (k+\ell )$ matrix
$(k+\ell )\times (k+\ell )$ matrix ![]() $E$ with
$E$ with ![]() $\pm 1$ on the diagonal, we have
$\pm 1$ on the diagonal, we have
Then
 \begin{equation} \frac{d^{k\times\ell}(\tilde{T})\wedge d^{\ell\times k}(\tilde{S})}{({ \operatorname{det}}(M({\tilde{T}},{\tilde{S}})))^{k+\ell}}={\pm}\frac{d^{k\times \ell}(T)\wedge d^{\ell\times k}(S)}{({ \operatorname{det}}(M(T,S)))^{k+\ell}}. \end{equation}
\begin{equation} \frac{d^{k\times\ell}(\tilde{T})\wedge d^{\ell\times k}(\tilde{S})}{({ \operatorname{det}}(M({\tilde{T}},{\tilde{S}})))^{k+\ell}}={\pm}\frac{d^{k\times \ell}(T)\wedge d^{\ell\times k}(S)}{({ \operatorname{det}}(M(T,S)))^{k+\ell}}. \end{equation}Proof. We can write ![]() $E$ as a block matrix
$E$ as a block matrix
where ![]() $P$ (respectively,
$P$ (respectively, ![]() $R$) is an upper triangular matrix of size
$R$) is an upper triangular matrix of size ![]() $k\times k$ (respectively,
$k\times k$ (respectively, ![]() $\ell \times \ell$) with
$\ell \times \ell$) with ![]() $\pm 1$ on the diagonal. In this notation,
$\pm 1$ on the diagonal. In this notation,
If ![]() $Q=0$ then we clearly have
$Q=0$ then we clearly have
and by (11.6), ![]() ${ \operatorname {det}}(M({\tilde {T}},{\tilde {S}}))={ \operatorname {det}}(M(T,S))$, which shows (11.10) in this case. Note that if
${ \operatorname {det}}(M({\tilde {T}},{\tilde {S}}))={ \operatorname {det}}(M(T,S))$, which shows (11.10) in this case. Note that if ![]() $E=E^{({1})}\cdot E^{({2})}\cdots E^{({N})}$ is a product of upper triangular matrices with
$E=E^{({1})}\cdot E^{({2})}\cdots E^{({N})}$ is a product of upper triangular matrices with ![]() $\pm 1$ on diagonals, then it suffices to prove the lemma for
$\pm 1$ on diagonals, then it suffices to prove the lemma for ![]() $E^{({i})}$ for each
$E^{({i})}$ for each ![]() $1\leq i\leq N$, because then the result will follow by induction. The case when
$1\leq i\leq N$, because then the result will follow by induction. The case when ![]() $E$ is a diagonal matrix has already been shown above, and we may thus assume that
$E$ is a diagonal matrix has already been shown above, and we may thus assume that ![]() $E$ is a Chevalley generator, i.e. a unit upper triangular matrix with a single non-zero off-diagonal entry in position
$E$ is a Chevalley generator, i.e. a unit upper triangular matrix with a single non-zero off-diagonal entry in position ![]() $(i,i+1)$ for some
$(i,i+1)$ for some ![]() $1\leq i < k+\ell$. If
$1\leq i < k+\ell$. If ![]() $i\neq k$ then
$i\neq k$ then ![]() $Q=0$ so we are done. Now suppose that
$Q=0$ so we are done. Now suppose that ![]() $i=k$ and thus
$i=k$ and thus ![]() $Q$ has a single non-zero entry
$Q$ has a single non-zero entry ![]() $Q_{k1}=q$ for some constant
$Q_{k1}=q$ for some constant ![]() $q$. We are going to verify (11.10) in this case by a direct computation, see also Example 11.12 below.
$q$. We are going to verify (11.10) in this case by a direct computation, see also Example 11.12 below.
We have ![]() ${\tilde {T}}=Q+T$ and thus
${\tilde {T}}=Q+T$ and thus ![]() $d^{k\times \ell }(\tilde {T})=d^{k\times \ell }(T)$. Now, we have
$d^{k\times \ell }(\tilde {T})=d^{k\times \ell }(T)$. Now, we have ![]() ${\tilde {S}}=(\operatorname {Id}_\ell +SQ)^{-1}S$. Denote
${\tilde {S}}=(\operatorname {Id}_\ell +SQ)^{-1}S$. Denote ![]() $S=(s_{ij})$. Let us first compute the matrix
$S=(s_{ij})$. Let us first compute the matrix ![]() $\operatorname {Id}_\ell +SQ$ and its inverse:
$\operatorname {Id}_\ell +SQ$ and its inverse:
 \[ \operatorname{Id}_\ell+SQ=\begin{pmatrix} 1+qs_{1k} & 0 & \dots & 0\\ qs_{2k} & 1 & \dots & 0\\ \vdots & 0 & \ddots & 0\\ qs_{\ell k} & 0 & \dots & 1 \end{pmatrix};\quad (\operatorname{Id}_\ell+SQ)^{{-}1}=\begin{pmatrix} \frac1{1+qs_{1k}} & 0 & \dots & 0\\ -\frac{qs_{2k}}{1+qs_{1k}} & 1 & \dots & 0\\ \vdots & 0 & \ddots & 0\\ -\frac{qs_{\ell k}}{1+qs_{1k}} & 0 & \dots & 1 \end{pmatrix}. \]
\[ \operatorname{Id}_\ell+SQ=\begin{pmatrix} 1+qs_{1k} & 0 & \dots & 0\\ qs_{2k} & 1 & \dots & 0\\ \vdots & 0 & \ddots & 0\\ qs_{\ell k} & 0 & \dots & 1 \end{pmatrix};\quad (\operatorname{Id}_\ell+SQ)^{{-}1}=\begin{pmatrix} \frac1{1+qs_{1k}} & 0 & \dots & 0\\ -\frac{qs_{2k}}{1+qs_{1k}} & 1 & \dots & 0\\ \vdots & 0 & \ddots & 0\\ -\frac{qs_{\ell k}}{1+qs_{1k}} & 0 & \dots & 1 \end{pmatrix}. \]
Thus ![]() ${ \operatorname {det}}((\operatorname {Id}_\ell +SQ)^{-1})=1/({1+qs_{1k}})$. Note that
${ \operatorname {det}}((\operatorname {Id}_\ell +SQ)^{-1})=1/({1+qs_{1k}})$. Note that
and therefore
It remains to compute ![]() $d^{\ell \times k}(\tilde {S})$, so denote
$d^{\ell \times k}(\tilde {S})$, so denote ![]() ${\tilde {S}}=({\tilde {s}}_{ij})$. We have
${\tilde {S}}=({\tilde {s}}_{ij})$. We have
 \begin{align*} {\tilde{s}}_{1k}&=\frac{s_{1k}}{1+qs_{1k}},\quad d{\tilde{s}}_{1k}=\frac{ds_{1k}}{(1+qs_{1k})^2};\\ {\tilde{s}}_{1j}&=\frac{s_{1j}}{1+qs_{1k}},\quad d{\tilde{s}}_{1j}=\frac{ds_{1j}}{1+qs_{1k}}+\alpha\quad (1\leq j < k);\\ {\tilde{s}}_{ik}&=\frac{-qs_{ik}s_{1k}}{1+qs_{1k}}+s_{ik}=\frac{s_{ik}}{1+qs_{1k}},\quad d{\tilde{s}}_{ik}=\frac{ds_{ik}}{1+qs_{1k}}+\beta \quad (1 < i\leq \ell);\\ {\tilde{s}}_{ij}&=\frac{-qs_{ik}s_{1j}}{1+qs_{1k}}+s_{ij},\quad d{\tilde{s}}_{ij}=ds_{ij}+\gamma \quad (1\leq j < k, 1 < i\leq \ell). \end{align*}
\begin{align*} {\tilde{s}}_{1k}&=\frac{s_{1k}}{1+qs_{1k}},\quad d{\tilde{s}}_{1k}=\frac{ds_{1k}}{(1+qs_{1k})^2};\\ {\tilde{s}}_{1j}&=\frac{s_{1j}}{1+qs_{1k}},\quad d{\tilde{s}}_{1j}=\frac{ds_{1j}}{1+qs_{1k}}+\alpha\quad (1\leq j < k);\\ {\tilde{s}}_{ik}&=\frac{-qs_{ik}s_{1k}}{1+qs_{1k}}+s_{ik}=\frac{s_{ik}}{1+qs_{1k}},\quad d{\tilde{s}}_{ik}=\frac{ds_{ik}}{1+qs_{1k}}+\beta \quad (1 < i\leq \ell);\\ {\tilde{s}}_{ij}&=\frac{-qs_{ik}s_{1j}}{1+qs_{1k}}+s_{ij},\quad d{\tilde{s}}_{ij}=ds_{ij}+\gamma \quad (1\leq j < k, 1 < i\leq \ell). \end{align*}
Here ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ denote sums of terms involving
$\beta$ denote sums of terms involving ![]() $ds_{1k}$, while
$ds_{1k}$, while ![]() $\gamma$ denotes a sum of terms involving
$\gamma$ denotes a sum of terms involving ![]() $ds_{1k}$,
$ds_{1k}$, ![]() $ds_{1j}$, and
$ds_{1j}$, and ![]() $ds_{ik}$. Thus each of those terms vanishes when we take the wedge of all the
$ds_{ik}$. Thus each of those terms vanishes when we take the wedge of all the ![]() ${\tilde {s}}_{ij}$. We have shown that
${\tilde {s}}_{ij}$. We have shown that
and combining this with (11.11), we get
 \[ \frac{d^{k\times\ell}(\tilde{T})\wedge d^{\ell\times k}(\tilde{S})}{({ \operatorname{det}}(M({\tilde{T}},{\tilde{S}})))^{k+\ell}}=\frac{d^{k\times \ell}(T)\wedge d^{\ell\times k}(S)}{(1+qs_{1k})^{k+\ell}({ \operatorname{det}}(M({\tilde{T}},{\tilde{S}})))^{k+\ell}}=\frac{d^{k\times \ell}(T)\wedge d^{\ell\times k}(S)}{({ \operatorname{det}}(M(T,S)))^{k+\ell}}, \]
\[ \frac{d^{k\times\ell}(\tilde{T})\wedge d^{\ell\times k}(\tilde{S})}{({ \operatorname{det}}(M({\tilde{T}},{\tilde{S}})))^{k+\ell}}=\frac{d^{k\times \ell}(T)\wedge d^{\ell\times k}(S)}{(1+qs_{1k})^{k+\ell}({ \operatorname{det}}(M({\tilde{T}},{\tilde{S}})))^{k+\ell}}=\frac{d^{k\times \ell}(T)\wedge d^{\ell\times k}(S)}{({ \operatorname{det}}(M(T,S)))^{k+\ell}}, \]finishing the proof of Lemma 11.11.
Theorem 5.9 follows from Lemmas 11.10 and 11.11, combined with (11.8) and (11.9).□
Example 11.12 Let us illustrate Lemma 11.11 in the case ![]() $k=\ell =1$. We have
$k=\ell =1$. We have ![]() $M(T,S)= (\begin {smallmatrix} 1 & t\\ s & 1 \end {smallmatrix} )$, so the right-hand side of (11.10) is
$M(T,S)= (\begin {smallmatrix} 1 & t\\ s & 1 \end {smallmatrix} )$, so the right-hand side of (11.10) is ![]() $({dt\wedge ds})/{(1-st)^2}$. Suppose that
$({dt\wedge ds})/{(1-st)^2}$. Suppose that ![]() $E= (\begin {smallmatrix} 1 & q\\ 0 & 1 \end {smallmatrix} )$ for some constant
$E= (\begin {smallmatrix} 1 & q\\ 0 & 1 \end {smallmatrix} )$ for some constant ![]() $q$. Thus
$q$. Thus
So ![]() ${\tilde {t}}=q+t$ and
${\tilde {t}}=q+t$ and ![]() ${\tilde {s}}={s}/({1+qs})$. We have
${\tilde {s}}={s}/({1+qs})$. We have
and therefore the left-hand side of (11.10) equals
Proof of Theorem 5.13 We deduce the result as a simple corollary of Theorem 5.9. For an affine permutation ![]() $f\in \tilde {S_n}(-k,\ell )$, we need to show that
$f\in \tilde {S_n}(-k,\ell )$, we need to show that ![]() $\theta$ sends
$\theta$ sends ![]() $\omega _{k+f}\wedge \omega _{\ell ,n}$ to
$\omega _{k+f}\wedge \omega _{\ell ,n}$ to ![]() $\pm \omega _{k,n}\wedge \omega _{\ell +f^{-1}}$. We proceed by induction on
$\pm \omega _{k,n}\wedge \omega _{\ell +f^{-1}}$. We proceed by induction on ![]() $\operatorname {inv}(f)$, the base case
$\operatorname {inv}(f)$, the base case ![]() $\operatorname {inv}(f)=0$ being precisely the content of Theorem 5.9. Suppose that
$\operatorname {inv}(f)=0$ being precisely the content of Theorem 5.9. Suppose that ![]() $g\lessdot f$ in the affine Bruhat order for some
$g\lessdot f$ in the affine Bruhat order for some ![]() $f,g\in \tilde {S_n}(-k,\ell )$, and that the result has already been shown for
$f,g\in \tilde {S_n}(-k,\ell )$, and that the result has already been shown for ![]() $f$. By Proposition 12.1 below, the form
$f$. By Proposition 12.1 below, the form ![]() $\omega _{k+g}$ is obtained from
$\omega _{k+g}$ is obtained from ![]() $\omega _{k+f}$ by taking a residue, and the same is true for
$\omega _{k+f}$ by taking a residue, and the same is true for ![]() $f^{-1}$ and
$f^{-1}$ and ![]() $g^{-1}$:
$g^{-1}$:
Let ![]() $A \subset \Pi _{k+f}^\mathbb {C} \times \operatorname {Gr}_\mathbb {C}(\ell ,n)$ be the Zariski open subset such that the following are true:
$A \subset \Pi _{k+f}^\mathbb {C} \times \operatorname {Gr}_\mathbb {C}(\ell ,n)$ be the Zariski open subset such that the following are true:
(1)
 $\operatorname {stack}(V,W) \in \operatorname {Mat}^\circ (k+\ell ,n)$ whenever
$\operatorname {stack}(V,W) \in \operatorname {Mat}^\circ (k+\ell ,n)$ whenever  $(V,W) \in A$;
$(V,W) \in A$;(2)
 $\theta$ extends to an isomorphism
$\theta$ extends to an isomorphism  $\theta : A \to B$, where
$\theta : A \to B$, where  $B \subset \operatorname {Gr}_\mathbb {C}(k,n) \times \Pi _{\ell +f^{-1}}^\mathbb {C}$;
$B \subset \operatorname {Gr}_\mathbb {C}(k,n) \times \Pi _{\ell +f^{-1}}^\mathbb {C}$;(3)
 $\theta$ sends
$\theta$ sends  $A \cap (\Pi _{k+g}^\mathbb {C} \times \operatorname {Gr}_\mathbb {C}(\ell ,n))$ isomorphically to
$A \cap (\Pi _{k+g}^\mathbb {C} \times \operatorname {Gr}_\mathbb {C}(\ell ,n))$ isomorphically to  $B \cap (\operatorname {Gr}_\mathbb {C}(\ell ,n) \times \Pi _{\ell +g^{-1}}^\mathbb {C})$.
$B \cap (\operatorname {Gr}_\mathbb {C}(\ell ,n) \times \Pi _{\ell +g^{-1}}^\mathbb {C})$.
Both ![]() $A \subset \Pi _{k+f}^\mathbb {C} \times \operatorname {Gr}_\mathbb {C}(\ell ,n)$ and
$A \subset \Pi _{k+f}^\mathbb {C} \times \operatorname {Gr}_\mathbb {C}(\ell ,n)$ and ![]() $A \cap (\Pi _{k+g}^\mathbb {C} \times \operatorname {Gr}_\mathbb {C}(\ell ,n)) \subset \Pi _{k+g}^\mathbb {C} \times \operatorname {Gr}_\mathbb {C}(\ell ,n)$ will be non-empty Zariski open subsets, since by Theorem 4.7 the corresponding positive points will be contained in this locus. Taking residues commutes with isomorphisms, so by induction we compute
$A \cap (\Pi _{k+g}^\mathbb {C} \times \operatorname {Gr}_\mathbb {C}(\ell ,n)) \subset \Pi _{k+g}^\mathbb {C} \times \operatorname {Gr}_\mathbb {C}(\ell ,n)$ will be non-empty Zariski open subsets, since by Theorem 4.7 the corresponding positive points will be contained in this locus. Taking residues commutes with isomorphisms, so by induction we compute
 \begin{align*} \theta^*(\omega_{k,n} \wedge\omega_{\ell+g^{{-}1}}) & = \theta^*(\operatorname{Res}_{B \cap (\operatorname{Gr}_\mathbb{C}(\ell,n) \times \Pi_{\ell+g^{{-}1}}^\mathbb{C})} \omega_{k,n} \wedge\omega_{\ell+f^{{-}1}})\\ &= \operatorname{Res}_{A \cap (\Pi_{k+g}^\mathbb{C} \times \operatorname{Gr}_\mathbb{C}(\ell,n))} \theta^*(\omega_{k,n} \wedge\omega_{\ell+f^{{-}1}}) \\ &={\pm} \operatorname{Res}_{A \cap (\Pi_{k+g}^\mathbb{C} \times \operatorname{Gr}_\mathbb{C}(\ell,n))} (\omega_{k+f} \wedge \omega_{\ell,n})\\ &={\pm} \omega_{k+g} \wedge \omega_{\ell,n}. \end{align*}
\begin{align*} \theta^*(\omega_{k,n} \wedge\omega_{\ell+g^{{-}1}}) & = \theta^*(\operatorname{Res}_{B \cap (\operatorname{Gr}_\mathbb{C}(\ell,n) \times \Pi_{\ell+g^{{-}1}}^\mathbb{C})} \omega_{k,n} \wedge\omega_{\ell+f^{{-}1}})\\ &= \operatorname{Res}_{A \cap (\Pi_{k+g}^\mathbb{C} \times \operatorname{Gr}_\mathbb{C}(\ell,n))} \theta^*(\omega_{k,n} \wedge\omega_{\ell+f^{{-}1}}) \\ &={\pm} \operatorname{Res}_{A \cap (\Pi_{k+g}^\mathbb{C} \times \operatorname{Gr}_\mathbb{C}(\ell,n))} (\omega_{k+f} \wedge \omega_{\ell,n})\\ &={\pm} \omega_{k+g} \wedge \omega_{\ell,n}. \end{align*}12. The amplituhedron form: proofs
In this section, we prove Theorem 8.16, as well as several other statements given in § 8. Before we proceed, we recall some further background that was omitted from that section.
12.1 Residues
We start with the definition of the residue operator ![]() $\operatorname {Res}$. Suppose we are given a rational form
$\operatorname {Res}$. Suppose we are given a rational form ![]() $\omega$ on a complex variety
$\omega$ on a complex variety ![]() $X$. Let
$X$. Let ![]() $C\subset X$ be an irreducible subvariety of codimension one. Consider some smooth Zariski open subset
$C\subset X$ be an irreducible subvariety of codimension one. Consider some smooth Zariski open subset ![]() $U\subset X$ such that
$U\subset X$ such that ![]() $U \cap C$ is Zariski open in
$U \cap C$ is Zariski open in ![]() $C$. Suppose that
$C$. Suppose that ![]() $z:U\to \mathbb {C}$ is a regular map such that
$z:U\to \mathbb {C}$ is a regular map such that ![]() $C \cap U$ is the set of solutions to
$C \cap U$ is the set of solutions to ![]() $z=0$. Denote the remaining coordinates on
$z=0$. Denote the remaining coordinates on ![]() $U$ by
$U$ by ![]() $u$, so that every point in
$u$, so that every point in ![]() $U$ is written as
$U$ is written as ![]() $(z,u)$ in this coordinate chart. We say that
$(z,u)$ in this coordinate chart. We say that ![]() $\omega$ has a simple pole at
$\omega$ has a simple pole at ![]() $C$ if inside
$C$ if inside ![]() $U$ we have
$U$ we have
where ![]() $\omega ''(z,u)$ and
$\omega ''(z,u)$ and ![]() $\omega '(u)$ are rational forms on
$\omega '(u)$ are rational forms on ![]() $U$, and
$U$, and ![]() $\omega '(u)$ is non-zero. When
$\omega '(u)$ is non-zero. When ![]() $\omega$ has a simple pole at
$\omega$ has a simple pole at ![]() $C$, we define the residue by
$C$, we define the residue by
This defines ![]() $\operatorname {Res}_C\omega$ as a rational form on
$\operatorname {Res}_C\omega$ as a rational form on ![]() $U\cap C$, and thus on
$U\cap C$, and thus on ![]() $C$.
$C$.
Proposition 12.1 [Lam16b, Theorem 13.2] For affine permutations ![]() $f,g\in \tilde {S_n}(-k,n-k)$ such that
$f,g\in \tilde {S_n}(-k,n-k)$ such that ![]() $g\lessdot f$ in the affine Bruhat order, we have
$g\lessdot f$ in the affine Bruhat order, we have
12.2 Degree of a map
Let ![]() $\alpha : X \to Y$ be a morphism between irreducible complex varieties of the same dimension. If
$\alpha : X \to Y$ be a morphism between irreducible complex varieties of the same dimension. If ![]() $\operatorname {dim}(\alpha (X)) = \operatorname {dim}(X) (=\operatorname {dim}(Y))$, then there exists a non-empty Zariski open subset
$\operatorname {dim}(\alpha (X)) = \operatorname {dim}(X) (=\operatorname {dim}(Y))$, then there exists a non-empty Zariski open subset ![]() $B \subseteq Y$ such that
$B \subseteq Y$ such that ![]() $\alpha$ restricts to a
$\alpha$ restricts to a ![]() $d$-fold covering map from
$d$-fold covering map from ![]() $\alpha ^{-1}(B)$ to
$\alpha ^{-1}(B)$ to ![]() $B$. In other words,
$B$. In other words, ![]() $\alpha$ is locally a diffeomorphism on
$\alpha$ is locally a diffeomorphism on ![]() $\alpha ^{-1}(B)$, and for
$\alpha ^{-1}(B)$, and for ![]() $y \in B$ we have
$y \in B$ we have ![]() $|\alpha ^{-1}(y)| = d$. We say that
$|\alpha ^{-1}(y)| = d$. We say that ![]() $\alpha$ has degree
$\alpha$ has degree ![]() $\deg (\alpha ) = d$. If
$\deg (\alpha ) = d$. If ![]() $\operatorname {dim}(\alpha (X)) < \operatorname {dim}(X)$, we define
$\operatorname {dim}(\alpha (X)) < \operatorname {dim}(X)$, we define ![]() $\deg (\alpha ) = \infty$. If
$\deg (\alpha ) = \infty$. If ![]() $\alpha : X\dashrightarrow Y$ is instead a rational map, then we have
$\alpha : X\dashrightarrow Y$ is instead a rational map, then we have ![]() $\deg (\alpha ) = \deg (\alpha |_A)$ where
$\deg (\alpha ) = \deg (\alpha |_A)$ where ![]() $A \subseteq X$ is the locus where
$A \subseteq X$ is the locus where ![]() $\alpha$ is defined. If
$\alpha$ is defined. If ![]() $\alpha$ has degree
$\alpha$ has degree ![]() $\deg (\alpha ) = 1$, then it is birational: it restricts to an isomorphism between dense Zariski open subsets of
$\deg (\alpha ) = 1$, then it is birational: it restricts to an isomorphism between dense Zariski open subsets of ![]() $X$ and
$X$ and ![]() $Y$.
$Y$.
In [Reference LamLam16a], an integer ![]() $d_f \in \{1,2,\ldots ,\infty \}$ is assigned to each
$d_f \in \{1,2,\ldots ,\infty \}$ is assigned to each ![]() $f \in \tilde {S_n}(-k,n-k)$ so that for a dense Zariski open subset
$f \in \tilde {S_n}(-k,n-k)$ so that for a dense Zariski open subset ![]() $A \subset \operatorname {Gr}_\mathbb {C}(k+m,n)$, the rational map
$A \subset \operatorname {Gr}_\mathbb {C}(k+m,n)$, the rational map ![]() $Z: \operatorname {Gr}_\mathbb {C}(k,n) \dashrightarrow \operatorname {Gr}_\mathbb {C}(k,k+m)$ has degree
$Z: \operatorname {Gr}_\mathbb {C}(k,n) \dashrightarrow \operatorname {Gr}_\mathbb {C}(k,k+m)$ has degree ![]() $d_f$ whenever
$d_f$ whenever ![]() $Z \in A$. Since
$Z \in A$. Since ![]() $\operatorname {Gr}_{>0}(k+m,n)$ is Zariski dense in
$\operatorname {Gr}_{>0}(k+m,n)$ is Zariski dense in ![]() $\operatorname {Gr}_\mathbb {C}(k+m,n)$, this statement also holds for
$\operatorname {Gr}_\mathbb {C}(k+m,n)$, this statement also holds for ![]() $Z$ in an open dense subset of
$Z$ in an open dense subset of ![]() $\operatorname {Gr}_{>0}(k+m,n)$. An affine permutation
$\operatorname {Gr}_{>0}(k+m,n)$. An affine permutation ![]() $f\in \tilde {S_n}(-k,n-k)$ such that
$f\in \tilde {S_n}(-k,n-k)$ such that ![]() $\operatorname {inv}(f)=km$ has degree
$\operatorname {inv}(f)=km$ has degree ![]() $1$ in the sense of Definition 8.1 if and only if
$1$ in the sense of Definition 8.1 if and only if ![]() $d_f = 1$.
$d_f = 1$.
Proof Proof of Proposition 8.12 Suppose that ![]() $d_f = 1$. Let
$d_f = 1$. Let ![]() $A \subset \operatorname {Gr}_\mathbb {C}(k+m,n)$ be the Zariski open dense subset such that
$A \subset \operatorname {Gr}_\mathbb {C}(k+m,n)$ be the Zariski open dense subset such that ![]() $Z:\operatorname {Gr}(k,n) \dashrightarrow \operatorname {Gr}(k,k+m)$ has degree
$Z:\operatorname {Gr}(k,n) \dashrightarrow \operatorname {Gr}(k,k+m)$ has degree ![]() $1$ for
$1$ for ![]() $Z\in A$. For
$Z\in A$. For ![]() $Z \in A$, let
$Z \in A$, let ![]() $B_Z \subset \operatorname {Gr}_\mathbb {C}(k,k+m)$ be the dense Zariski open subset such that
$B_Z \subset \operatorname {Gr}_\mathbb {C}(k,k+m)$ be the dense Zariski open subset such that ![]() $Z: Z^{-1}(B_Z) \to B_Z$ is an isomorphism. Consider the Zariski open subset
$Z: Z^{-1}(B_Z) \to B_Z$ is an isomorphism. Consider the Zariski open subset ![]() $C \subset \textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n)$ defined by
$C \subset \textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n)$ defined by
Then ![]() $\mathcal {Z}: \mathcal {Z}^{-1}(C) \to C$ is an isomorphism, and thus
$\mathcal {Z}: \mathcal {Z}^{-1}(C) \to C$ is an isomorphism, and thus ![]() $\mathcal {Z}: \Pi _{k+f}^\mathbb {C} \times \operatorname {Gr}_\mathbb {C}(\ell ,n) \dashrightarrow \textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n)$ has degree 1.
$\mathcal {Z}: \Pi _{k+f}^\mathbb {C} \times \operatorname {Gr}_\mathbb {C}(\ell ,n) \dashrightarrow \textrm {Fl}_\mathbb {C}(\ell ,k+\ell ;n)$ has degree 1.
Proof Proof of Proposition 8.8 Note that ![]() $\Pi ^{>0}_{k+f}$ is homeomorphic to an open ball. Since
$\Pi ^{>0}_{k+f}$ is homeomorphic to an open ball. Since ![]() $f$ is
$f$ is ![]() $(n,k,m)$-admissible, the restriction of
$(n,k,m)$-admissible, the restriction of ![]() $Z$ to
$Z$ to ![]() $\Pi ^{>0}_{k+f}$ is injective. By Brouwer's invariance of domain theorem [Reference BrouwerBro12], we get that it is a homeomorphism onto its image, because the dimension of
$\Pi ^{>0}_{k+f}$ is injective. By Brouwer's invariance of domain theorem [Reference BrouwerBro12], we get that it is a homeomorphism onto its image, because the dimension of ![]() $\Pi ^{>0}_{k+f}$ equals
$\Pi ^{>0}_{k+f}$ equals ![]() $km$. Therefore, the restriction of
$km$. Therefore, the restriction of ![]() $Z$ to
$Z$ to ![]() $\Pi ^{>0}_{k+f}$ either preserves or reverses its topological orientation (see [Reference Greenberg and HarperGH81, § 22] for background on topological orientation). For smooth manifolds, it is well known that the notions of topological and smooth orientation agree with each other. Thus whenever the Jacobian of
$\Pi ^{>0}_{k+f}$ either preserves or reverses its topological orientation (see [Reference Greenberg and HarperGH81, § 22] for background on topological orientation). For smooth manifolds, it is well known that the notions of topological and smooth orientation agree with each other. Thus whenever the Jacobian of ![]() $Z$ is non-zero on
$Z$ is non-zero on ![]() $\Pi ^{>0}_{k+f}$, its sign is the same.
$\Pi ^{>0}_{k+f}$, its sign is the same.
Proof Proof of Proposition 8.13 The product ![]() $\Pi ^{>0}_{k+f} \times \operatorname {Gr}_{>0}^\perp (k+m,n)$ is homeomorphic to an open ball. When
$\Pi ^{>0}_{k+f} \times \operatorname {Gr}_{>0}^\perp (k+m,n)$ is homeomorphic to an open ball. When ![]() $f$ is
$f$ is ![]() $(n,k,m)$-admissible, the restriction of
$(n,k,m)$-admissible, the restriction of ![]() $\mathcal {Z}$ to
$\mathcal {Z}$ to ![]() $\Pi ^{>0}_{k+f} \times \operatorname {Gr}_{>0}^\perp (k+m,n)$ is injective. The rest of the proof is identical to that of Proposition 8.8.
$\Pi ^{>0}_{k+f} \times \operatorname {Gr}_{>0}^\perp (k+m,n)$ is injective. The rest of the proof is identical to that of Proposition 8.8.
Remark 12.2 Even when ![]() $d_f > 1$, we can still define the pushforward
$d_f > 1$, we can still define the pushforward ![]() $Z_* \omega _{k+f}$ of the canonical form, but the definition is more complicated. See [Reference LamLam16b] for details.
$Z_* \omega _{k+f}$ of the canonical form, but the definition is more complicated. See [Reference LamLam16b] for details.
12.3 Affine Stanley symmetric functions
We review the results of the second author [Reference LamLam06, Reference LamLam16a] that allow one to give a purely combinatorial characterization of a degree ![]() $1$ positroid cell. We refer the reader to [Reference StanleySta99] for background on symmetric functions.
$1$ positroid cell. We refer the reader to [Reference StanleySta99] for background on symmetric functions.
Definition 12.3 An element ![]() $v\in \tilde {S_n}$ is called cyclically decreasing if it has a reduced word
$v\in \tilde {S_n}$ is called cyclically decreasing if it has a reduced word ![]() $v=s_{j_1}s_{j_2}\dots s_{j_N}$ such that the indices
$v=s_{j_1}s_{j_2}\dots s_{j_N}$ such that the indices ![]() $j_1,j_2,\dots ,j_N$ are pairwise distinct modulo
$j_1,j_2,\dots ,j_N$ are pairwise distinct modulo ![]() $n$, and if
$n$, and if ![]() $j_a=i+1$ and
$j_a=i+1$ and ![]() $j_b=i$ modulo
$j_b=i$ modulo ![]() $n$ for some
$n$ for some ![]() $a,b\leq N$ then we have
$a,b\leq N$ then we have ![]() $a < b$.
$a < b$.
Given an element ![]() $f\in \tilde {S_n}$, define the affine Stanley symmetric function
$f\in \tilde {S_n}$, define the affine Stanley symmetric function
where the sum is over all factorizations ![]() $f=f_1f_2\dots f_r$ such that
$f=f_1f_2\dots f_r$ such that ![]() $f_1,\dots ,f_r\in \tilde {S_n}$ are cyclically decreasing. We list some properties of
$f_1,\dots ,f_r\in \tilde {S_n}$ are cyclically decreasing. We list some properties of ![]() ${\tilde F}_f$ together with the references to the places where they have been proven in the literature.
${\tilde F}_f$ together with the references to the places where they have been proven in the literature.
Proposition 12.4
(1) For each
 $f\in \tilde {S_n}$,
$f\in \tilde {S_n}$,  ${\tilde F}_f$ is a symmetric function [Reference LamLam06, Theorem 6].
${\tilde F}_f$ is a symmetric function [Reference LamLam06, Theorem 6].(2) For each
 $f\in \tilde {S_n}$, we have
$f\in \tilde {S_n}$, we have  $\omega ^+ {\tilde F}_f={\tilde F}_{f^{-1}}$ [Reference LamLam06, Theorem 15].
$\omega ^+ {\tilde F}_f={\tilde F}_{f^{-1}}$ [Reference LamLam06, Theorem 15].(3) If
 $\operatorname {inv}(f)=k\ell$ for some
$\operatorname {inv}(f)=k\ell$ for some  $f\in \tilde {S_n}(-k,n-k)$ then
$f\in \tilde {S_n}(-k,n-k)$ then  $f$ has degree
$f$ has degree  $1$ if and only if the coefficient of
$1$ if and only if the coefficient of  $s_{\ell ^k}$ in
$s_{\ell ^k}$ in  ${\tilde F}_f$ is equal to
${\tilde F}_f$ is equal to  $1$ [Reference LamLam16a, Proposition 4.8].
$1$ [Reference LamLam16a, Proposition 4.8].
Here ![]() $\omega ^+$ denotes a certain involution on a subset
$\omega ^+$ denotes a certain involution on a subset ![]() $\Lambda ^{({n})}$ of the algebra
$\Lambda ^{({n})}$ of the algebra ![]() $\Lambda$ of symmetric functions, and
$\Lambda$ of symmetric functions, and ![]() $s_{\ell ^k}\in \Lambda ^{({n})}$ denotes the Schur function indexed by a rectangular partition
$s_{\ell ^k}\in \Lambda ^{({n})}$ denotes the Schur function indexed by a rectangular partition ![]() $\ell ^k:=(\underbrace {\ell ,\ell ,\dots ,\ell }_{k \times})$. Since
$\ell ^k:=(\underbrace {\ell ,\ell ,\dots ,\ell }_{k \times})$. Since ![]() $\omega ^+ s_{\ell ^k}=s_{k^\ell }$, Proposition 12.4 implies Proposition 8.5.
$\omega ^+ s_{\ell ^k}=s_{k^\ell }$, Proposition 12.4 implies Proposition 8.5.
12.4 Proof of Theorem 8.16
The proof of Theorem 5.13 shows that for the rational map
we have ![]() $\theta ^*(\omega _{k,n}\wedge \omega _{\ell +{f^{-1}}}) = \pm \omega _{k+f}\wedge \omega _{\ell ,n}$ for each
$\theta ^*(\omega _{k,n}\wedge \omega _{\ell +{f^{-1}}}) = \pm \omega _{k+f}\wedge \omega _{\ell ,n}$ for each ![]() $f\in \tilde {S_n}(-k,\ell )$. By Theorem 3.5 together with Corollary 8.7, the only thing left to show is that the sign is ‘
$f\in \tilde {S_n}(-k,\ell )$. By Theorem 3.5 together with Corollary 8.7, the only thing left to show is that the sign is ‘![]() $+$’ when both forms are chosen to be positive as in Definition 8.9. We choose some reference form
$+$’ when both forms are chosen to be positive as in Definition 8.9. We choose some reference form ![]() $\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}$ on
$\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}$ on ![]() $\textrm {Fl}(\ell ,k+\ell ;n)$ and some reference form
$\textrm {Fl}(\ell ,k+\ell ;n)$ and some reference form ![]() $\omega ^{\operatorname {ref}}_{\textrm {Fl}(k,k+\ell ;n)}$ on
$\omega ^{\operatorname {ref}}_{\textrm {Fl}(k,k+\ell ;n)}$ on ![]() $\textrm {Fl}(k,k+\ell ;n)$ so that
$\textrm {Fl}(k,k+\ell ;n)$ so that ![]() $\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}={\tilde \theta }^\ast \omega ^{\operatorname {ref}}_{\textrm {Fl}(k,k+\ell ;n)}$. The sign of
$\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}={\tilde \theta }^\ast \omega ^{\operatorname {ref}}_{\textrm {Fl}(k,k+\ell ;n)}$. The sign of ![]() $\omega _{k+f}$ is chosen in such a way that the forms
$\omega _{k+f}$ is chosen in such a way that the forms ![]() $\mathcal {Z}_*(\omega _{k+f}\wedge \omega _{\ell ,n})$ and
$\mathcal {Z}_*(\omega _{k+f}\wedge \omega _{\ell ,n})$ and ![]() $\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}$ have the same sign on
$\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}$ have the same sign on ![]() $\mathcal {A}^{>0}_{k+f}$. The sign of
$\mathcal {A}^{>0}_{k+f}$. The sign of ![]() $\omega _{\ell +{f^{-1}}}$ is chosen in such a way that the forms
$\omega _{\ell +{f^{-1}}}$ is chosen in such a way that the forms ![]() $\mathcal {Z}_*(\omega _{k,n}\wedge \omega _{\ell +{f^{-1}}})$ and
$\mathcal {Z}_*(\omega _{k,n}\wedge \omega _{\ell +{f^{-1}}})$ and ![]() $\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}$ have the same sign on
$\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}$ have the same sign on ![]() $\mathcal {A}^{>0}_{\ell +f^{-1}}$. Note that
$\mathcal {A}^{>0}_{\ell +f^{-1}}$. Note that ![]() ${\tilde \theta }$ sends
${\tilde \theta }$ sends ![]() $\mathcal {A}^{>0}_{k+f}$ to
$\mathcal {A}^{>0}_{k+f}$ to ![]() $\mathcal {A}^{>0}_{\ell +f^{-1}}$ and pulls
$\mathcal {A}^{>0}_{\ell +f^{-1}}$ and pulls ![]() $\omega ^{\operatorname {ref}}_{\textrm {Fl}(k,k+\ell ;n)}$ back to
$\omega ^{\operatorname {ref}}_{\textrm {Fl}(k,k+\ell ;n)}$ back to ![]() $\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}$. Since the diagram (7.3) is commutative, we conclude that
$\omega ^{\operatorname {ref}}_{\textrm {Fl}(\ell ,k+\ell ;n)}$. Since the diagram (7.3) is commutative, we conclude that ![]() $\theta ^*(\omega _{k,n}\wedge \omega _{\ell +{f^{-1}}}) = \omega _{k+f}\wedge \omega _{\ell ,n}$ with the above choice of signs, finishing the proof of Theorem 8.16.
$\theta ^*(\omega _{k,n}\wedge \omega _{\ell +{f^{-1}}}) = \omega _{k+f}\wedge \omega _{\ell ,n}$ with the above choice of signs, finishing the proof of Theorem 8.16.
13. Open questions and future directions
In addition to the multiple conjectures already mentioned in the text (Conjectures 3.8, 3.9, 8.4, 8.11, 8.15), we list several other exciting questions.
13.1 Positive Laurent formulas for the twisted Plücker coordinates
Let ![]() $\theta (V,W)=({\tilde {W}},{\tilde V})$. Theorem 4.7(ii) asserts that if the Plücker coordinates of
$\theta (V,W)=({\tilde {W}},{\tilde V})$. Theorem 4.7(ii) asserts that if the Plücker coordinates of ![]() $V$ and
$V$ and ![]() $Z:=W^\perp$ are nonnegative then so are the Plücker coordinates of
$Z:=W^\perp$ are nonnegative then so are the Plücker coordinates of ![]() ${\tilde Z}:={\tilde {W}}^\perp$ and
${\tilde Z}:={\tilde {W}}^\perp$ and ![]() ${\tilde V}$. In fact, we believe that an even stronger property holds.
${\tilde V}$. In fact, we believe that an even stronger property holds.
Conjecture 13.1 Let ![]() $U:=\operatorname {stack}(V,W)\in \operatorname {Mat}^\circ (k+\ell ,n)$,
$U:=\operatorname {stack}(V,W)\in \operatorname {Mat}^\circ (k+\ell ,n)$, ![]() $\theta (V,W)=({\tilde {W}},{\tilde V})$,
$\theta (V,W)=({\tilde {W}},{\tilde V})$, ![]() ${\tilde {U}}:=\tau (U)=\operatorname {stack}({\tilde {W}},{\tilde V})$,
${\tilde {U}}:=\tau (U)=\operatorname {stack}({\tilde {W}},{\tilde V})$, ![]() $Z:=W^\perp$, and
$Z:=W^\perp$, and ![]() ${\tilde Z}:={\tilde {W}}^\perp$. Then there exist some polynomials
${\tilde Z}:={\tilde {W}}^\perp$. Then there exist some polynomials ![]() $H$ and
$H$ and ![]() $H'$ in the maximal minors of
$H'$ in the maximal minors of ![]() $V$ and
$V$ and ![]() $Z$ with nonnegative integer coefficients such that
$Z$ with nonnegative integer coefficients such that
(1) the maximal minor
 $\Delta _I({\tilde Z})$ for
$\Delta _I({\tilde Z})$ for  $I\in { (\begin {smallmatrix}[n]\\ \ell +m \end {smallmatrix} )}$ is equal to
$I\in { (\begin {smallmatrix}[n]\\ \ell +m \end {smallmatrix} )}$ is equal to
 \[ \frac{H}{\pm \prod_{j\in I}\Delta_{[j-\ell,j+k)}(U)}; \]
\[ \frac{H}{\pm \prod_{j\in I}\Delta_{[j-\ell,j+k)}(U)}; \](2) the maximal minor
 $\Delta _I({\tilde V})$ for
$\Delta _I({\tilde V})$ for  $I\in { (\begin {smallmatrix}[n]\\ \ell \end {smallmatrix} )}$ is equal to
$I\in { (\begin {smallmatrix}[n]\\ \ell \end {smallmatrix} )}$ is equal to
 \[ \frac{H'}{\pm \prod_{j\in I}\Delta_{[j-\ell,j+k)}(U)}. \]
\[ \frac{H'}{\pm \prod_{j\in I}\Delta_{[j-\ell,j+k)}(U)}. \]
Here the sign ![]() $\pm$ in the denominator is chosen so that it is positive. (Recall that the sign of
$\pm$ in the denominator is chosen so that it is positive. (Recall that the sign of ![]() $\Delta _{[j-\ell ,j+k)}(U)$ is predicted by Lemma 10.5.)
$\Delta _{[j-\ell ,j+k)}(U)$ is predicted by Lemma 10.5.)
Note that the case of this conjecture where ![]() $I$ is a circular interval of
$I$ is a circular interval of ![]() $[n]$ follows from Lemma 11.5.
$[n]$ follows from Lemma 11.5.
Example 13.2 For the case ![]() $k=2$,
$k=2$, ![]() $\ell =1$,
$\ell =1$, ![]() $m=2$,
$m=2$, ![]() $n=5$, let us suppose that
$n=5$, let us suppose that ![]() $W$ is the row span of the
$W$ is the row span of the ![]() $1\times 5$ matrix
$1\times 5$ matrix ![]() $(p,-q,r,-s,t)$, so that the maximal minors of
$(p,-q,r,-s,t)$, so that the maximal minors of ![]() $Z$ are precisely
$Z$ are precisely ![]() $p,q,r,s,t\geq 0$. Then we have
$p,q,r,s,t\geq 0$. Then we have
Specifically, for the matrices ![]() $V$ and
$V$ and ![]() $W$ considered in (6.1), we have
$W$ considered in (6.1), we have
thus the formula above yields
which is indeed the case as we see by computing ![]() $\Delta _{13}(\operatorname {alt}({\tilde {W}}))$ directly from (6.3).
$\Delta _{13}(\operatorname {alt}({\tilde {W}}))$ directly from (6.3).
Remark 13.3 There is a formal similarity between our stacked twist map and the geometric ![]() $R$-matrix of Frieden [Reference FriedenFri17], which is essentially also a birational map
$R$-matrix of Frieden [Reference FriedenFri17], which is essentially also a birational map ![]() $R: \operatorname {Gr}(k,n) \times \operatorname {Gr}(\ell ,n) \dashrightarrow \operatorname {Gr}(\ell ,n) \times \operatorname {Gr}(k,n)$. Furthermore, the geometric
$R: \operatorname {Gr}(k,n) \times \operatorname {Gr}(\ell ,n) \dashrightarrow \operatorname {Gr}(\ell ,n) \times \operatorname {Gr}(k,n)$. Furthermore, the geometric ![]() $R$-matrix can be written in terms of subtraction-free rational formulae, and tropicalizes to the combinatorial
$R$-matrix can be written in terms of subtraction-free rational formulae, and tropicalizes to the combinatorial ![]() $R$-matrix. We do not know of a direct relation between the stacked twist map and the geometric
$R$-matrix. We do not know of a direct relation between the stacked twist map and the geometric ![]() $R$-matrix.
$R$-matrix.
The twist map ![]() $\tau :\operatorname {Mat}^\circ (k+\ell ,n)\to \operatorname {Mat}^\circ (k+\ell ,n)$ satisfies Lemma 10.1. Given any subgroup
$\tau :\operatorname {Mat}^\circ (k+\ell ,n)\to \operatorname {Mat}^\circ (k+\ell ,n)$ satisfies Lemma 10.1. Given any subgroup ![]() $G\subset \operatorname {GL}_{k+\ell }(\mathbb {R})$, one can consider the subgroup
$G\subset \operatorname {GL}_{k+\ell }(\mathbb {R})$, one can consider the subgroup ![]() $G^\text {t}:=\{g^\text {t}\mid g\in G\}$. By Lemma 10.1, if we have
$G^\text {t}:=\{g^\text {t}\mid g\in G\}$. By Lemma 10.1, if we have ![]() $U'=g\cdot U$ for
$U'=g\cdot U$ for ![]() $U,U'\in \operatorname {Mat}^\circ (k+\ell ,n)$ and
$U,U'\in \operatorname {Mat}^\circ (k+\ell ,n)$ and ![]() $g\in G$ then the matrices
$g\in G$ then the matrices ![]() ${\tilde {U}}:=\tau (U)$ and
${\tilde {U}}:=\tau (U)$ and ![]() ${\tilde {U}}':=\tau (U')$ are related by
${\tilde {U}}':=\tau (U')$ are related by ![]() ${\tilde {U}}'=(g^{-1})^\text {t}\cdot {\tilde {U}}$. Therefore,
${\tilde {U}}'=(g^{-1})^\text {t}\cdot {\tilde {U}}$. Therefore, ![]() $\tau$ reduces to a map
$\tau$ reduces to a map ![]() $\operatorname {Mat}^\circ (k+\ell ,n)/G\to \operatorname {Mat}^\circ (k+\ell ,n)/G^\text {t}$, where we are taking the quotients modulo the left action of
$\operatorname {Mat}^\circ (k+\ell ,n)/G\to \operatorname {Mat}^\circ (k+\ell ,n)/G^\text {t}$, where we are taking the quotients modulo the left action of ![]() $G$ (respectively,
$G$ (respectively, ![]() $G^\text {t}$). There are several interesting choices for
$G^\text {t}$). There are several interesting choices for ![]() $G$.
$G$.
![]() $\bullet$ Taking
$\bullet$ Taking ![]() $G:=\operatorname {GL}_k(\mathbb {R})\times \operatorname {GL}_\ell (\mathbb {R})$ recovers the stacked twist map.
$G:=\operatorname {GL}_k(\mathbb {R})\times \operatorname {GL}_\ell (\mathbb {R})$ recovers the stacked twist map.
![]() $\bullet$ Taking
$\bullet$ Taking ![]() $G$ to be a maximal parabolic subgroup consisting of block matrices
$G$ to be a maximal parabolic subgroup consisting of block matrices ![]() $ (\begin {smallmatrix} A & B\\ 0 & C \end {smallmatrix} )$, where
$ (\begin {smallmatrix} A & B\\ 0 & C \end {smallmatrix} )$, where ![]() $A$ is
$A$ is ![]() $k\times k$,
$k\times k$, ![]() $B$ is
$B$ is ![]() $k\times \ell$, and
$k\times \ell$, and ![]() $C$ is
$C$ is ![]() $\ell \times \ell$, yields a map on two-step flag varieties:
$\ell \times \ell$, yields a map on two-step flag varieties: ![]() $\tau :\textrm {Fl}^\circ (\ell ,k+\ell ;n)\to \textrm {Fl}^\circ (k,k+\ell ;n)$ sending
$\tau :\textrm {Fl}^\circ (\ell ,k+\ell ;n)\to \textrm {Fl}^\circ (k,k+\ell ;n)$ sending ![]() $(W,U)$ to
$(W,U)$ to ![]() $({\tilde {W}},{\tilde {U}})$. Conjecturally, the maximal minors of
$({\tilde {W}},{\tilde {U}})$. Conjecturally, the maximal minors of ![]() ${\tilde {W}}$ can be written as rational functions in terms of the maximal minors of
${\tilde {W}}$ can be written as rational functions in terms of the maximal minors of ![]() $W$ and
$W$ and ![]() $U$. For instance, in the setting of Example 13.2, we could also write
$U$. For instance, in the setting of Example 13.2, we could also write
which for ![]() $W$ and
$W$ and ![]() $U$ given in (6.1) yields
$U$ given in (6.1) yields ![]() $\frac {1\times (-8)+1\times (-6)}{2\times (-8)}=\frac {7}{8}$. However, the total positivity of
$\frac {1\times (-8)+1\times (-6)}{2\times (-8)}=\frac {7}{8}$. However, the total positivity of ![]() $\operatorname {alt}({\tilde {W}})$ is obscure in this expression, because
$\operatorname {alt}({\tilde {W}})$ is obscure in this expression, because ![]() $\Delta _{134}(U)$ can be both negative and positive when
$\Delta _{134}(U)$ can be both negative and positive when ![]() $V\in \operatorname {Gr}_{>0}(k,n)$ and
$V\in \operatorname {Gr}_{>0}(k,n)$ and ![]() ${\tilde {W}}\in \operatorname {Gr}_{>0}^\perp (k+m,n)$.
${\tilde {W}}\in \operatorname {Gr}_{>0}^\perp (k+m,n)$.
![]() $\bullet$ Finally, taking
$\bullet$ Finally, taking ![]() $G$ to be the subgroup of lower-triangular matrices and letting
$G$ to be the subgroup of lower-triangular matrices and letting ![]() $r:=k+\ell$ yields a map
$r:=k+\ell$ yields a map ![]() $\tau :\textrm {Fl}^\circ (1,2,\dots ,r;n)\to \textrm {Fl}^\circ (1,2,\dots ,r;n)$ that takes a partial flag
$\tau :\textrm {Fl}^\circ (1,2,\dots ,r;n)\to \textrm {Fl}^\circ (1,2,\dots ,r;n)$ that takes a partial flag ![]() $V_\bullet :=V_1\subset V_2\subset \dots \subset V_r$ (where
$V_\bullet :=V_1\subset V_2\subset \dots \subset V_r$ (where ![]() $V_i$ is the span of the first
$V_i$ is the span of the first ![]() $i$ rows of
$i$ rows of ![]() $U$) to a partial flag
$U$) to a partial flag ![]() ${\tilde V}_\bullet :={\tilde V}_1\subset {\tilde V}_2\subset \dots \subset {\tilde V}_r$ (where
${\tilde V}_\bullet :={\tilde V}_1\subset {\tilde V}_2\subset \dots \subset {\tilde V}_r$ (where ![]() ${\tilde V}_i$ is the span of the last
${\tilde V}_i$ is the span of the last ![]() $i$ rows of
$i$ rows of ![]() ${\tilde {U}}$). The partial flag
${\tilde {U}}$). The partial flag ![]() $V_\bullet$ is determined by the flag minors of
$V_\bullet$ is determined by the flag minors of ![]() $U$, where a flag minor is a minor of
$U$, where a flag minor is a minor of ![]() $U$ with row set
$U$ with row set ![]() $[i]$ and column set
$[i]$ and column set ![]() $J\in { (\begin {smallmatrix}[n]\\ i\end {smallmatrix} )}$ for
$J\in { (\begin {smallmatrix}[n]\\ i\end {smallmatrix} )}$ for ![]() $1\leq i\leq r$. Similarly, the partial flag
$1\leq i\leq r$. Similarly, the partial flag ![]() ${\tilde V}_\bullet$ is determined by the opposite flag minors of
${\tilde V}_\bullet$ is determined by the opposite flag minors of ![]() $U$, i.e. minors of
$U$, i.e. minors of ![]() $U$ with row set
$U$ with row set ![]() $\{n-i+1,\dots ,n\}$ and column set
$\{n-i+1,\dots ,n\}$ and column set ![]() $J\in { (\begin {smallmatrix}[n]\\ i\end {smallmatrix} )}$ for
$J\in { (\begin {smallmatrix}[n]\\ i\end {smallmatrix} )}$ for ![]() $1\leq i\leq r$. In fact, an explicit combinatorial formula in terms of matchings in a plabic graph [Reference PostnikovPos07] for the opposite flag minors of
$1\leq i\leq r$. In fact, an explicit combinatorial formula in terms of matchings in a plabic graph [Reference PostnikovPos07] for the opposite flag minors of ![]() ${\tilde {U}}$ in terms of flag minors of
${\tilde {U}}$ in terms of flag minors of ![]() $U$ can be proven in a straightforward but tedious fashion. To do so, one needs to combine the technique used in the proof of Lemma 11.5 with [Reference Marsh and ScottMS16, Theorem 1.1]. As a consequence of their formula, we get the following result.
$U$ can be proven in a straightforward but tedious fashion. To do so, one needs to combine the technique used in the proof of Lemma 11.5 with [Reference Marsh and ScottMS16, Theorem 1.1]. As a consequence of their formula, we get the following result.
Proposition 13.4 If ![]() ${\tilde {U}}=\tau (U)$ for some
${\tilde {U}}=\tau (U)$ for some ![]() $U\in \operatorname {Mat}^\circ (k+\ell ,n)$ then the opposite flag minors of
$U\in \operatorname {Mat}^\circ (k+\ell ,n)$ then the opposite flag minors of ![]() ${\tilde {U}}$ are positive Laurent polynomials in the flag minors of
${\tilde {U}}$ are positive Laurent polynomials in the flag minors of ![]() $U$.
$U$.
13.2 A polynomial expression for the amplituhedron form
Recall that in our example in § 6.3, we have computed the amplituhedron form ![]() $\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ for
$\omega ^{{({\mathcal {T}})}}_{\mathcal {A}_{n,k,m}(Z)}$ for ![]() $k=\ell =1$,
$k=\ell =1$, ![]() $m=2$,
$m=2$, ![]() $n=4$, see (8.8). We observe that this expression equals
$n=4$, see (8.8). We observe that this expression equals
where ![]() $U$ is given by (8.5) and
$U$ is given by (8.5) and ![]() $H(s,p,q,x,y)=qsx+psy+pq$. Let us generalize this observation to other values of
$H(s,p,q,x,y)=qsx+psy+pq$. Let us generalize this observation to other values of ![]() $k,\ell ,m,n$ using our coordinates from § 11.3.
$k,\ell ,m,n$ using our coordinates from § 11.3.
Similarly to (8.9), the coordinates that we assign to a pair ![]() $(W,U)\in \textrm {Fl}(\ell ,k+\ell ;n)$ are going to be matrices
$(W,U)\in \textrm {Fl}(\ell ,k+\ell ;n)$ are going to be matrices ![]() $S,A,B$ of respective sizes
$S,A,B$ of respective sizes ![]() $\ell \times k$,
$\ell \times k$, ![]() $k\times m$, and
$k\times m$, and ![]() $\ell \times m$ so that
$\ell \times m$ so that ![]() $W$ is the row span of
$W$ is the row span of ![]() $[S|\operatorname {Id}_\ell |B]$ while
$[S|\operatorname {Id}_\ell |B]$ while ![]() $U$ is the row span of
$U$ is the row span of
Taking
we get ![]() $Z^\perp =W$.
$Z^\perp =W$.
Conjecture 13.5 There exists a polynomial ![]() $H(S,A,B)$ in the entries of the matrices
$H(S,A,B)$ in the entries of the matrices ![]() $S,A,B$ such that
$S,A,B$ such that
where ![]() $U$ is given by (13.1) and
$U$ is given by (13.1) and ![]() $Z$ is given by (13.2). The universal amplituhedron form can be written in the coordinates (13.1) as
$Z$ is given by (13.2). The universal amplituhedron form can be written in the coordinates (13.1) as
where ![]() $W=Z^\perp$ is the row span of
$W=Z^\perp$ is the row span of ![]() $[S|\operatorname {Id}_\ell |B]$.
$[S|\operatorname {Id}_\ell |B]$.
The polynomial ![]() $H(S,A,B)$ from the above conjecture should take positive values whenever there exists
$H(S,A,B)$ from the above conjecture should take positive values whenever there exists ![]() $V\in \operatorname {Gr}_{>0}(k,n)$ such that
$V\in \operatorname {Gr}_{>0}(k,n)$ such that ![]() $\operatorname {span}(V,W)=U$ for
$\operatorname {span}(V,W)=U$ for ![]() $U$ being given by (13.1) and
$U$ being given by (13.1) and ![]() $W\in \operatorname {Gr}_{>0}^\perp (k+m,n)$ being the row span of
$W\in \operatorname {Gr}_{>0}^\perp (k+m,n)$ being the row span of ![]() $[S|\operatorname {Id}_\ell |B]$.
$[S|\operatorname {Id}_\ell |B]$.
13.3 Stackable cells
Even though for the amplituhedron we naturally have ![]() $W\in \operatorname {Gr}_{>0}^\perp (k+m,n)$, the stacked twist map construction suggests that there should be symmetry between
$W\in \operatorname {Gr}_{>0}^\perp (k+m,n)$, the stacked twist map construction suggests that there should be symmetry between ![]() $V$ and
$V$ and ![]() $W$. In this section, we generalize our previous results to the case when both
$W$. In this section, we generalize our previous results to the case when both ![]() $V$ and
$V$ and ![]() $Z:=W^\perp$ belong to lower positroid cells. Let us define
$Z:=W^\perp$ belong to lower positroid cells. Let us define
Definition 13.6 For two affine permutations ![]() $f\in \tilde {S_n}(-k,n-k)$ and
$f\in \tilde {S_n}(-k,n-k)$ and ![]() $g\in \tilde {S_n}(-\ell ,n-\ell )$, we say that
$g\in \tilde {S_n}(-\ell ,n-\ell )$, we say that ![]() $f$ and
$f$ and ![]() $g$ are stackable if for all
$g$ are stackable if for all ![]() $V\in \Pi ^{>0}_{k+f}$ and
$V\in \Pi ^{>0}_{k+f}$ and ![]() $W\in \operatorname {alt} (\Pi ^{>0}_{\ell +g} )$, we have
$W\in \operatorname {alt} (\Pi ^{>0}_{\ell +g} )$, we have ![]() $\operatorname {stack}(V,W)\in \operatorname {Mat}^\circ (k+\ell ,n)$.
$\operatorname {stack}(V,W)\in \operatorname {Mat}^\circ (k+\ell ,n)$.
As we saw in the proof of Lemma 10.5, ![]() $f$ and
$f$ and ![]() $g$ are stackable if and only if for every
$g$ are stackable if and only if for every ![]() $j\in \mathbb {Z}$, there exists
$j\in \mathbb {Z}$, there exists ![]() $I\in \mathcal {M}_{k+f}$ and
$I\in \mathcal {M}_{k+f}$ and ![]() $J\in \mathcal {M}_{\ell +g}$ such that
$J\in \mathcal {M}_{\ell +g}$ such that ![]() $I\cup J=\{j-\ell ,j-\ell +1,\dots ,j+k-1\}$ modulo
$I\cup J=\{j-\ell ,j-\ell +1,\dots ,j+k-1\}$ modulo ![]() $n$. This operation corresponds to taking the union of matroids, more precisely,
$n$. This operation corresponds to taking the union of matroids, more precisely, ![]() $f$ and
$f$ and ![]() $g$ are stackable if the positroid envelope (in the sense of [Reference Knutson, Lam and SpeyerKLS13]) of the matroid union
$g$ are stackable if the positroid envelope (in the sense of [Reference Knutson, Lam and SpeyerKLS13]) of the matroid union ![]() $\mathcal {M}_{k+f}\vee \mathcal {M}_{\ell +g}$ is the uniform matroid of rank
$\mathcal {M}_{k+f}\vee \mathcal {M}_{\ell +g}$ is the uniform matroid of rank ![]() $k+\ell$ on
$k+\ell$ on ![]() $n$ elements.
$n$ elements.
Of course one can check whether ![]() $f$ and
$f$ and ![]() $g$ are stackable by going through all
$g$ are stackable by going through all ![]() $j\in [n]$ and all pairs of
$j\in [n]$ and all pairs of ![]() $I\in \mathcal {M}_{k+f}$ and
$I\in \mathcal {M}_{k+f}$ and ![]() $J\in \mathcal {M}_{\ell +g}$, and this algorithm works in general for unions of matroids. We ask whether the fact that the matroids
$J\in \mathcal {M}_{\ell +g}$, and this algorithm works in general for unions of matroids. We ask whether the fact that the matroids ![]() $\mathcal {M}_{k+f}$ and
$\mathcal {M}_{k+f}$ and ![]() $\mathcal {M}_{\ell +g}$ are positroids makes this easier to check.
$\mathcal {M}_{\ell +g}$ are positroids makes this easier to check.
Problem 13.7 Find a simple necessary and sufficient condition for ![]() $f$ and
$f$ and ![]() $g$ to be stackable.
$g$ to be stackable.
The following result extends Theorems 3.5 and 5.13, and has a similar proof.
Theorem 13.8 If ![]() $f\in \tilde {S_n}(-k,\ell )$ and
$f\in \tilde {S_n}(-k,\ell )$ and ![]() $g\in \tilde {S_n}(-\ell ,k)$ are stackable cells then the stacked twist map descends to a diffeomorphism
$g\in \tilde {S_n}(-\ell ,k)$ are stackable cells then the stacked twist map descends to a diffeomorphism
satisfying
We note that however in the original description of the problem coming from physics, the matrices ![]() $Z$ and
$Z$ and ![]() $V$ play asymmetric roles. Namely,
$V$ play asymmetric roles. Namely, ![]() $Z$ encodes external data, i.e. the momenta of the particles in the experiment, while the matrix
$Z$ encodes external data, i.e. the momenta of the particles in the experiment, while the matrix ![]() $V$ are hidden variables or degrees of freedom that are integrated out in the final scattering amplitude [Reference Arkani-Hamed and TrnkaAT14].
$V$ are hidden variables or degrees of freedom that are integrated out in the final scattering amplitude [Reference Arkani-Hamed and TrnkaAT14].
Problem 13.9 Explain the symmetry between ![]() $V$ and
$V$ and ![]() $W=Z^\perp$ from the point of view of scattering amplitudes.
$W=Z^\perp$ from the point of view of scattering amplitudes.
13.4 Bistellar flips and the generalized Baues problem
Recall that for ![]() $k=1$, the amplituhedron
$k=1$, the amplituhedron ![]() $\mathcal {A}_{n,k,m}(Z)$ is just a cyclic polytope
$\mathcal {A}_{n,k,m}(Z)$ is just a cyclic polytope ![]() $C(n,m)$ in the
$C(n,m)$ in the ![]() $m$-dimensional projective space [Reference SturmfelsStu88]. Thus the amplituhedron is a direct generalization of a cyclic polytope, and in this section we list some properties of cyclic polytopes that we expect to generalize to amplituhedra. One of such properties is already stated as Conjecture 3.9.
$m$-dimensional projective space [Reference SturmfelsStu88]. Thus the amplituhedron is a direct generalization of a cyclic polytope, and in this section we list some properties of cyclic polytopes that we expect to generalize to amplituhedra. One of such properties is already stated as Conjecture 3.9.
Recall that for any ![]() $g\in \tilde {S_n}(-k,\ell )$, we have defined triangulations of
$g\in \tilde {S_n}(-k,\ell )$, we have defined triangulations of ![]() $Z(\Pi ^{>0}_{k+g})$ in § 7. For example if
$Z(\Pi ^{>0}_{k+g})$ in § 7. For example if ![]() $g\in \tilde {S_n}(-k,\ell )$ satisfies
$g\in \tilde {S_n}(-k,\ell )$ satisfies ![]() $\operatorname {inv}(g)=k\ell$ and is
$\operatorname {inv}(g)=k\ell$ and is ![]() $(n,k,m)$-admissible then
$(n,k,m)$-admissible then ![]() $Z(\Pi ^{>0}_{k+g})$ has only one triangulation
$Z(\Pi ^{>0}_{k+g})$ has only one triangulation ![]() $\{g\}$. Let us say that
$\{g\}$. Let us say that ![]() $g\in \tilde {S_n}(-k,n-k)$ is nearly
$g\in \tilde {S_n}(-k,n-k)$ is nearly ![]() $(n,k,m)$-admissible if
$(n,k,m)$-admissible if ![]() $\operatorname {inv}(g)=k\ell -1$,
$\operatorname {inv}(g)=k\ell -1$, ![]() $\operatorname {dim}(Z(\Pi ^{>0}_{k+g}))=km$ for all
$\operatorname {dim}(Z(\Pi ^{>0}_{k+g}))=km$ for all ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$, and for any
$Z\in \operatorname {Gr}_{>0}(k+m,n)$, and for any ![]() $h\lessdot g$, we have either
$h\lessdot g$, we have either ![]() $\deg h=1$ for all
$\deg h=1$ for all ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$ or
$Z\in \operatorname {Gr}_{>0}(k+m,n)$ or ![]() $\deg h=\infty$ for all
$\deg h=\infty$ for all ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$.
$Z\in \operatorname {Gr}_{>0}(k+m,n)$.
Conjecture 13.10 Let ![]() $g\in \tilde {S_n}(-k,n-k)$ be a nearly
$g\in \tilde {S_n}(-k,n-k)$ be a nearly ![]() $(n,k,m)$-admissible affine permutation. Then there exist two disjoint sets
$(n,k,m)$-admissible affine permutation. Then there exist two disjoint sets ![]() $\mathcal {T}_g=\{h_1,\dots ,h_N\}\subset \tilde {S_n}(-k,\ell )$ and
$\mathcal {T}_g=\{h_1,\dots ,h_N\}\subset \tilde {S_n}(-k,\ell )$ and ![]() $\mathcal {T}_g'=\{h'_1,\dots ,h'_{N}\}\subset \tilde {S_n}(-k,\ell )$ of affine permutations of the same size such that for each
$\mathcal {T}_g'=\{h'_1,\dots ,h'_{N}\}\subset \tilde {S_n}(-k,\ell )$ of affine permutations of the same size such that for each ![]() $Z\in \operatorname {Gr}_{>0}(k+m,n)$,
$Z\in \operatorname {Gr}_{>0}(k+m,n)$, ![]() $\mathcal {T}_g$ and
$\mathcal {T}_g$ and ![]() $\mathcal {T}_g'$ are the only two triangulations of
$\mathcal {T}_g'$ are the only two triangulations of ![]() $Z(\Pi ^{>0}_{k+g})$. The union
$Z(\Pi ^{>0}_{k+g})$. The union ![]() $\mathcal {T}_g\cup \mathcal {T}_g'$ consists of all affine permutations
$\mathcal {T}_g\cup \mathcal {T}_g'$ consists of all affine permutations ![]() $h\lessdot g$ such that
$h\lessdot g$ such that ![]() $\deg h=1$.
$\deg h=1$.
Assuming that the above conjecture is true, we say that two ![]() $(n,k,m)$-triangulations
$(n,k,m)$-triangulations ![]() $\mathcal {T},\mathcal {T}'\subset \tilde {S_n}(-k,n-k)$ of the amplituhedron differ by a flip if there exists a nearly
$\mathcal {T},\mathcal {T}'\subset \tilde {S_n}(-k,n-k)$ of the amplituhedron differ by a flip if there exists a nearly ![]() $(n,k,m)$-admissible affine permutation
$(n,k,m)$-admissible affine permutation ![]() $g\in \tilde {S_n}(-k,n-k)$ such that
$g\in \tilde {S_n}(-k,n-k)$ such that ![]() $\mathcal {T}_g\subset \mathcal {T}$,
$\mathcal {T}_g\subset \mathcal {T}$, ![]() $\mathcal {T}_g'\subset \mathcal {T}'$, and
$\mathcal {T}_g'\subset \mathcal {T}'$, and
This is a direct generalization of bistellar flips of triangulations of polytopes. In particular, it was shown in [Reference RambauRam97, Theorem 1.1] that any two triangulations of a cyclic polytope ![]() $C(n,m)$ are connected by a sequence of flips.
$C(n,m)$ are connected by a sequence of flips.
Conjecture 13.11 Any two triangulations of the amplituhedron are connected by a sequence of flips.
We note that Conjectures 13.10 and 13.11 together imply that all triangulations of the amplituhedron have the same cardinality. This is a major step towards Conjecture 3.9, but the latter additionally gives a simple formula for the size of any such triangulation.
Example 13.12 Let ![]() $k=2$,
$k=2$, ![]() $\ell =2$,
$\ell =2$, ![]() $m=4$,
$m=4$, ![]() $n=8$, and consider an affine permutation
$n=8$, and consider an affine permutation ![]() $h\in \tilde {S_n}(-k,\ell )$ given by
$h\in \tilde {S_n}(-k,\ell )$ given by ![]() $h=[2,1,4,3,6,5,8,7]$ in window notation. The corresponding positroid cell
$h=[2,1,4,3,6,5,8,7]$ in window notation. The corresponding positroid cell ![]() $\Pi ^{>0}_{k+h}$, known as the four-mass box [Reference Arkani-Hamed, Bourjaily, Cachazo, Goncharov, Postnikov and TrnkaABC16, § 11], satisfies
$\Pi ^{>0}_{k+h}$, known as the four-mass box [Reference Arkani-Hamed, Bourjaily, Cachazo, Goncharov, Postnikov and TrnkaABC16, § 11], satisfies ![]() $\deg h=2$. Let us now take
$\deg h=2$. Let us now take ![]() $g:=[1,2,4,3,6,5,8,7]$, so that
$g:=[1,2,4,3,6,5,8,7]$, so that ![]() $h\lessdot g$ in the affine Bruhat order. Thus
$h\lessdot g$ in the affine Bruhat order. Thus ![]() $g$ is not nearly
$g$ is not nearly ![]() $(n,k,m)$-admissible. It is not clear to us whether
$(n,k,m)$-admissible. It is not clear to us whether ![]() $g$ has any proper subdivisions, and whether there exists a subdivision of the amplituhedron, which involves
$g$ has any proper subdivisions, and whether there exists a subdivision of the amplituhedron, which involves ![]() $g$ as one of the cells. If such a subdivision exists and
$g$ as one of the cells. If such a subdivision exists and ![]() $g$ has no triangulations then it is not the case that every subdivision of the amplituhedron can be further refined to a triangulation.
$g$ has no triangulations then it is not the case that every subdivision of the amplituhedron can be further refined to a triangulation.
Additionally, we note that apart from ![]() $h$ there are eight affine permutations
$h$ there are eight affine permutations ![]() $h'\lessdot g$ satisfying
$h'\lessdot g$ satisfying ![]() $\deg h'\neq \infty$, and all of them actually have degree
$\deg h'\neq \infty$, and all of them actually have degree ![]() $1$. Together with
$1$. Together with ![]() $h$, these nine affine permutations give rise to an identity involving pushforwards of canonical forms, as explained in [Reference Arkani-Hamed, Bourjaily, Cachazo, Goncharov, Postnikov and TrnkaABC16, § 11]. Moreover, there exists an expression for
$h$, these nine affine permutations give rise to an identity involving pushforwards of canonical forms, as explained in [Reference Arkani-Hamed, Bourjaily, Cachazo, Goncharov, Postnikov and TrnkaABC16, § 11]. Moreover, there exists an expression for ![]() $\omega _{\mathcal {A}_{n,k,m}(Z)}$ of the form (8.2) with
$\omega _{\mathcal {A}_{n,k,m}(Z)}$ of the form (8.2) with ![]() $M(2,2,2)=20$ terms in the right-hand side, one of which is
$M(2,2,2)=20$ terms in the right-hand side, one of which is ![]() $\omega _{Z(\Pi ^{>0}_{k+h})}$. Even though by Conjectures 3.9 and 8.11, each
$\omega _{Z(\Pi ^{>0}_{k+h})}$. Even though by Conjectures 3.9 and 8.11, each ![]() $(n,k,m)$-triangulation of the amplituhedron has
$(n,k,m)$-triangulation of the amplituhedron has ![]() $20$ cells and yields an expression for
$20$ cells and yields an expression for ![]() $\omega _{\mathcal {A}_{n,k,m}(Z)}$ with
$\omega _{\mathcal {A}_{n,k,m}(Z)}$ with ![]() $20$ terms, the corresponding
$20$ terms, the corresponding ![]() $20$ affine permutations mentioned above do not form an
$20$ affine permutations mentioned above do not form an ![]() $(n,k,m)$-triangulation since
$(n,k,m)$-triangulation since ![]() $h$ is not
$h$ is not ![]() $(n,k,m)$-admissible, and some other permutations in this collection are not
$(n,k,m)$-admissible, and some other permutations in this collection are not ![]() $(n,k,m)$-compatible with each other. We thank Jake Bourjaily for sharing the details of this example with us.
$(n,k,m)$-compatible with each other. We thank Jake Bourjaily for sharing the details of this example with us.
Consider a simple graph ![]() $G$ whose vertices are triangulations of the amplituhedron, and two triangulations are connected by an edge if they differ by a flip. Thus Conjecture 13.11 states that this graph is connected. One can continue this process by ‘gluing’ a higher-dimensional cell to this graph corresponding to each coarser subdivision of the amplituhedron. In the case of polytopes, the homotopy type of the resulting CW complex is the subject of the generalized Baues problem of [Reference Billera, Kapranov and SturmfelsBKS94], see [Reference ReinerRei99] for a survey. Formally, define the Baues poset
$G$ whose vertices are triangulations of the amplituhedron, and two triangulations are connected by an edge if they differ by a flip. Thus Conjecture 13.11 states that this graph is connected. One can continue this process by ‘gluing’ a higher-dimensional cell to this graph corresponding to each coarser subdivision of the amplituhedron. In the case of polytopes, the homotopy type of the resulting CW complex is the subject of the generalized Baues problem of [Reference Billera, Kapranov and SturmfelsBKS94], see [Reference ReinerRei99] for a survey. Formally, define the Baues poset ![]() $\omega (\mathcal {A}_{n,k,m}(Z))$ to be the partially ordered set consisting of all properFootnote 7
$\omega (\mathcal {A}_{n,k,m}(Z))$ to be the partially ordered set consisting of all properFootnote 7 ![]() $(n,k,m)$-subdivisions of the amplituhedron, ordered by refinement.
$(n,k,m)$-subdivisions of the amplituhedron, ordered by refinement.
Problem 13.13 Is it true that the Baues poset ![]() $\omega (\mathcal {A}_{n,k,m}(Z))$ is homotopy equivalent to a
$\omega (\mathcal {A}_{n,k,m}(Z))$ is homotopy equivalent to a ![]() $(k\ell -1)$-dimensional sphere?
$(k\ell -1)$-dimensional sphere?
For the case ![]() $k=1$, the statement of Problem 13.13 was shown in [Reference Rambau and SantosRS00]. We note that Theorem 7.2 shows that the Baues poset of the
$k=1$, the statement of Problem 13.13 was shown in [Reference Rambau and SantosRS00]. We note that Theorem 7.2 shows that the Baues poset of the ![]() $(n,k,m)$-amplituhedron is isomorphic to that of the
$(n,k,m)$-amplituhedron is isomorphic to that of the ![]() $(n,\ell ,m)$-amplituhedron, and thus Problem 13.13 has a positive answer also in the case
$(n,\ell ,m)$-amplituhedron, and thus Problem 13.13 has a positive answer also in the case ![]() $\ell =1$. We do not know whether Example 13.12 provides any obstructions for the statement of Problem 13.13 to be true.
$\ell =1$. We do not know whether Example 13.12 provides any obstructions for the statement of Problem 13.13 to be true.
For polytopes, the generalized Baues problem is closely related to regular triangulations and secondary polytopes of [Reference Gelfand, Kapranov and ZelevinskyGKZ08].
Problem 13.14 Generalize the notion of a regular triangulation to the amplituhedron case.
Example 13.15 We have verified our conjectures computationally in the case ![]() $k=\ell =m=2$ and
$k=\ell =m=2$ and ![]() $n=6$. There are
$n=6$. There are ![]() $48$
$48$ ![]() $(n,k,m)$-admissible affine permutations
$(n,k,m)$-admissible affine permutations ![]() $f\in \tilde {S_n}(-k,n-k)$ such that
$f\in \tilde {S_n}(-k,n-k)$ such that ![]() $\operatorname {inv}(f)=k\ell$, and they are precisely all affine permutations that have degree
$\operatorname {inv}(f)=k\ell$, and they are precisely all affine permutations that have degree ![]() $1$ (see Conjecture 8.4). They form
$1$ (see Conjecture 8.4). They form ![]() $120$ triangulations, and each of those consists of
$120$ triangulations, and each of those consists of ![]() $M(2,2,1)=6$ cells (see Conjecture 3.9). The flip graph
$M(2,2,1)=6$ cells (see Conjecture 3.9). The flip graph ![]() $G$ in this case has
$G$ in this case has ![]() $120$ vertices and
$120$ vertices and ![]() $278$ edges, and is connected (see Conjecture 13.11). Finally, there are
$278$ edges, and is connected (see Conjecture 13.11). Finally, there are ![]() $696$ proper subdivisions of the amplituhedron, and the corresponding Baues poset has homology groups equal to that of a three-dimensional sphere, showing some substantial evidence towards the positive answer to Problem 13.13.
$696$ proper subdivisions of the amplituhedron, and the corresponding Baues poset has homology groups equal to that of a three-dimensional sphere, showing some substantial evidence towards the positive answer to Problem 13.13.
13.5 BCFW cells
For ![]() $m=4$, there is a certain interesting collection
$m=4$, there is a certain interesting collection ![]() $\mathcal {T}_{k,\ell }=\{f_1,\dots ,f_N\}\subset \tilde {S_n}(-k,\ell )$ of positroid cells for each
$\mathcal {T}_{k,\ell }=\{f_1,\dots ,f_N\}\subset \tilde {S_n}(-k,\ell )$ of positroid cells for each ![]() $k$ and
$k$ and ![]() $\ell$, see [Reference Britto, Cachazo, Feng and WittenBCFW05, Reference Arkani-Hamed, Bourjaily, Cachazo, Goncharov, Postnikov and TrnkaABC16, Reference Arkani-Hamed and TrnkaAT14]. Up to a cyclic shift, we get
$\ell$, see [Reference Britto, Cachazo, Feng and WittenBCFW05, Reference Arkani-Hamed, Bourjaily, Cachazo, Goncharov, Postnikov and TrnkaABC16, Reference Arkani-Hamed and TrnkaAT14]. Up to a cyclic shift, we get ![]() $\mathcal {T}_{\ell ,k}=\{f_1^{-1},\dots ,f_N^{-1}\}$, as we have noted in Remark 3.7. This collection of cells, known as the BCFW triangulation, is believed to have all the nice properties that we have considered in this paper, in particular, it can be used (and in fact is widely used) to compute the amplituhedron form.
$\mathcal {T}_{\ell ,k}=\{f_1^{-1},\dots ,f_N^{-1}\}$, as we have noted in Remark 3.7. This collection of cells, known as the BCFW triangulation, is believed to have all the nice properties that we have considered in this paper, in particular, it can be used (and in fact is widely used) to compute the amplituhedron form.
Conjecture 13.16 The BCFW triangulation ![]() $\mathcal {T}_{k,\ell }$ is an
$\mathcal {T}_{k,\ell }$ is an ![]() $(n,k,m)$-triangulation of degree
$(n,k,m)$-triangulation of degree ![]() $1$ for each
$1$ for each ![]() $k$ and
$k$ and ![]() $\ell$ (and
$\ell$ (and ![]() $m=4$).
$m=4$).
This conjecture holds in the case ![]() $k=1$ of cyclic polytopes (and therefore it holds for
$k=1$ of cyclic polytopes (and therefore it holds for ![]() $\ell =1$ as well by Corollary 8.7). A part of Conjecture 13.16 (that the elements of
$\ell =1$ as well by Corollary 8.7). A part of Conjecture 13.16 (that the elements of ![]() $\mathcal {T}_{k,\ell }$ are pairwise
$\mathcal {T}_{k,\ell }$ are pairwise ![]() $(n,k,m)$-compatible) has been proven for
$(n,k,m)$-compatible) has been proven for ![]() $k=2$ in [Reference Karp, Williams and ZhangKWZ17]. As before, our results imply that the elements of
$k=2$ in [Reference Karp, Williams and ZhangKWZ17]. As before, our results imply that the elements of ![]() $\mathcal {T}_{\ell ,k}$ are pairwise
$\mathcal {T}_{\ell ,k}$ are pairwise ![]() $(n,\ell ,m)$-compatible for
$(n,\ell ,m)$-compatible for ![]() $k=2$.
$k=2$.
13.6 Cohomology classes
Let ![]() $X$ be a smooth projective complex algebraic variety and
$X$ be a smooth projective complex algebraic variety and ![]() $Y \subset X$ a subvariety. Let
$Y \subset X$ a subvariety. Let ![]() $[Y] \in H^\ast (X,\mathbb {Z})$ denote the cohomology class of
$[Y] \in H^\ast (X,\mathbb {Z})$ denote the cohomology class of ![]() $Y$. The cohomology classes
$Y$. The cohomology classes ![]() $[Z(\Pi _{k+f}^\mathbb {C})] \in H^\ast (\operatorname {Gr}_\mathbb {C}(k,k+m),\mathbb {Z})$ for generic
$[Z(\Pi _{k+f}^\mathbb {C})] \in H^\ast (\operatorname {Gr}_\mathbb {C}(k,k+m),\mathbb {Z})$ for generic ![]() $Z \in \operatorname {Gr}_\mathbb {C}(k+m,n)$ (or, equivalently, for
$Z \in \operatorname {Gr}_\mathbb {C}(k+m,n)$ (or, equivalently, for ![]() $Z$ belonging to a dense subset of
$Z$ belonging to a dense subset of ![]() $\operatorname {Gr}_{>0}(k+m,n)$) were determined in [Reference LamLam16a]. Recall that in § 12.3, we have defined the affine Stanley symmetric function
$\operatorname {Gr}_{>0}(k+m,n)$) were determined in [Reference LamLam16a]. Recall that in § 12.3, we have defined the affine Stanley symmetric function ![]() ${\tilde F}_f$. In [Reference LamLam16a], it is shown that the cohomology class
${\tilde F}_f$. In [Reference LamLam16a], it is shown that the cohomology class ![]() $[Z(\Pi _{k+f}^\mathbb {C})]$ is represented by the symmetric function
$[Z(\Pi _{k+f}^\mathbb {C})]$ is represented by the symmetric function ![]() $\tau _{k+m}({\tilde F}_f)$, defined by
$\tau _{k+m}({\tilde F}_f)$, defined by
Here ![]() $\mu ^{+\ell }$ is the partition obtained from
$\mu ^{+\ell }$ is the partition obtained from ![]() $\mu$ by adding
$\mu$ by adding ![]() $\ell$ columns of height
$\ell$ columns of height ![]() $k$ to the left of
$k$ to the left of ![]() $\mu$ (in English notation). The term is omitted if this is not a partition.
$\mu$ (in English notation). The term is omitted if this is not a partition.
It is an open problem to understand the cohomology classes ![]() $[Z(\Pi _{k+f}^\mathbb {C})]$ when
$[Z(\Pi _{k+f}^\mathbb {C})]$ when ![]() $Z$ is not generic. Note that in the
$Z$ is not generic. Note that in the ![]() $k = 1$ polytope case,
$k = 1$ polytope case, ![]() $Z(\Pi _{k+f}^\mathbb {C})$ is always a linear hypersubspace of projective space, so the cohomology class
$Z(\Pi _{k+f}^\mathbb {C})$ is always a linear hypersubspace of projective space, so the cohomology class ![]() $[Z(\Pi _{k+f}^\mathbb {C})] \in H^\ast (\operatorname {Gr}_\mathbb {C}(k,k+m),\mathbb {Z})$ is simply the effective generator of
$[Z(\Pi _{k+f}^\mathbb {C})] \in H^\ast (\operatorname {Gr}_\mathbb {C}(k,k+m),\mathbb {Z})$ is simply the effective generator of ![]() $H^d(\operatorname {Gr}_\mathbb {C}(k,k+m),\mathbb {Z})$ where
$H^d(\operatorname {Gr}_\mathbb {C}(k,k+m),\mathbb {Z})$ where ![]() $d$ is the codimension of
$d$ is the codimension of ![]() $Z(\Pi _{k+f}^\mathbb {C})$.
$Z(\Pi _{k+f}^\mathbb {C})$.
It would be interesting to extend the calculation of [Reference LamLam16a] to the universal setting.
Problem 13.17 What is the cohomology class ![]() $[\mathcal {A}^{\mathbb {C}}_{k+f}]$ in
$[\mathcal {A}^{\mathbb {C}}_{k+f}]$ in ![]() $H^\ast (\textrm {Fl}_\mathbb {C}(k,k+\ell ;n),\mathbb {Z})$ and how is it related to
$H^\ast (\textrm {Fl}_\mathbb {C}(k,k+\ell ;n),\mathbb {Z})$ and how is it related to ![]() $[\mathcal {A}^{\mathbb {C}}_{\ell +f^{-1}}]$?
$[\mathcal {A}^{\mathbb {C}}_{\ell +f^{-1}}]$?
Acknowledgements
We are grateful to Steven Karp for numerous conversations on topics related to this work, and for helpful comments and suggestions at various stages of this project. We thank Nima Arkani-Hamed, Jake Bourjaily, and Alex Postnikov for inspiring conversations. We also thank the anonymous referee for their valuable comments on the first version of this manuscript.