Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-11T13:34:51.379Z Has data issue: false hasContentIssue false
  • English
  • Français

Log-isocristaux surconvergents et holonomie

Part of: (Co)homology theory

Published online by Cambridge University Press:  24 September 2009

Daniel Caro
Daniel Caro*
Affiliation:
Laboratoire de Mathématiques Nicolas Oresme, Université de Caen, Campus 2, 14032 Caen Cedex, France (email: daniel.caro@math.unicaen.fr)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

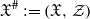Let đ’± be a complete discrete valuation ring of unequal characteristic with perfect residue field. Let be a separated smooth formal đ’±-scheme, đ’” be a normal crossing divisor of , be the induced formal log-scheme over đ’± and be the canonical morphism. Let X and Z be the special fibers of and đ’”, T be a divisor of X and ℰ be a log-isocrystal on overconvergent along T, that is, a coherent left 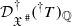-module, locally projective of finite type over 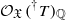. We check the relative duality isomorphism: . We prove the isomorphism , which implies their holonomicity as -modules. We obtain the canonical morphism ρℰ : uT,+(ℰ)→ℰ(†Z). When ℰ is moreover an isocrystal on overconvergent along T, we prove that ρℰ is an isomorphism.

Keywords

arithmetical 𝒟-moduleslog-isocrystalsholonomicity

MSC classification

Secondary: 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials 14F30: $p$-adic cohomology, crystalline cohomology
Type
Research Article
Information
Compositio Mathematica , Volume 145 , Issue 6 , November 2009 , pp. 1465 - 1503
Copyright
Copyright © Foundation Compositio Mathematica 2009

References

[1]Berthelot, P., Cohomologie rigide et thĂ©orie des 𝒟-modules, in p-adic analysis (Trento, 1989) (Springer, Berlin, 1990), 80–124.CrossRefGoogle Scholar
[2]Berthelot, P., CohĂ©rence diffĂ©rentielle des algĂšbres de fonctions surconvergentes, C. R. Acad. Sci. Paris SĂ©r. I Math. 323 (1996), 35–40.Google Scholar
[3]Berthelot, P., 𝒟-modules arithmĂ©tiques. I. OpĂ©rateurs diffĂ©rentiels de niveau fini, Ann. Sci. École Norm. Sup. (4) 29 (1996), 185–272.CrossRefGoogle Scholar
[4]Berthelot, P., 𝒟-modules arithmĂ©tiques. II. Descente par Frobenius, MĂ©m. Soc. Math. Fr. (N.S.) (81) (2000), vi+136.Google Scholar
[5]Berthelot, P., 𝒟-modules arithmĂ©tiques. IV. VariĂ©tĂ© caractĂ©ristique, en prĂ©paration.Google Scholar
[6]Calderón-Moreno, F. J., Logarithmic differential operators and logarithmic de Rham complexes relative to a free divisor, Ann. Sci. École Norm. Sup. (4) 32 (1999), 701–714.CrossRefGoogle Scholar
[7]CalderĂłn Moreno, F. J. and NarvĂĄez Macarro, L., DualitĂ© et comparaison sur les complexes de de Rham logarithmiques par rapport aux diviseurs libres, Ann. Inst. Fourier (Grenoble) 55 (2005), 47–75.CrossRefGoogle Scholar
[8]Caro, D., CohĂ©rence diffĂ©rentielle des F-isocristaux unitĂ©s, C. R. Math. Acad. Sci. Paris 338 (2004), 145–150.Google Scholar
[9]Caro, D., Comparaison des foncteurs duaux des isocristaux surconvergents, Rend. Sem. Mat. Univ. Padova 114 (2005), 131–211.Google Scholar
[10]Caro, D., DĂ©vissages des F-complexes de 𝒟-modules arithmĂ©tiques en F-isocristaux surconvergents, Invent. Math. 166 (2006), 397–456.CrossRefGoogle Scholar
[11]Caro, D., Fonctions L associĂ©es aux 𝒟-modules arithmĂ©tiques. Cas des courbes, Compositio Math. 142 (2006), 169–206.CrossRefGoogle Scholar
[12]Caro, D., Overconvergent F-isocrystals and differential overcoherence, Invent. Math. 170 (2007), 507–539.CrossRefGoogle Scholar
[13]Caro, D., 𝒟-modules arithmĂ©tiques surholonomes, Ann. Sci. École Norm. Sup. (4) 42 (2009), 141–192.CrossRefGoogle Scholar
[14]Caro, D. and Tsuzuki, N., Overholonomicity of overconvergent F-isocrystals over smooth varieties, ArXiv Mathematics e-prints (2008).Google Scholar
[15]de Jong, A. J., Smoothness, semi-stability and alterations, Publ. Math. Inst. Hautes Études Sci. 83 (1996), 51–93.CrossRefGoogle Scholar
[16]Grothendieck, A., ÉlĂ©ments de gĂ©omĂ©trie algĂ©brique. I. Le langage des schĂ©mas, Publ. Math. Inst. Hautes Études Sci. (4) (1960), 228.Google Scholar
[17]Kashiwara, M., Algebraic study of systems of partial differential equations, MĂ©m. Soc. Math. France (N.S.) (63) (1995), xiv+72.CrossRefGoogle Scholar
[18]Kedlaya, K. S., Semistable reduction for overconvergent F-isocrystals on a curve, Math. Res. Lett. 10 (2003), 151–159.CrossRefGoogle Scholar
[19]Kedlaya, K. S., Semistable reduction for overconvergent F-isocrystals, IV: Local semistable reduction at nonmonomial valuations, ArXiv Mathematics e-print (2007).CrossRefGoogle Scholar
[20]Kedlaya, K. S., Semistable reduction for overconvergent F-isocrystals. I. Unipotence and logarithmic extensions, Compositio Math. 143 (2007), 1164–1212.CrossRefGoogle Scholar
[21]Kedlaya, K. S., Semistable reduction for overconvergent F-isocrystals. II. A valuation-theoretic approach, Compositio Math. 144 (2008), 657–672.CrossRefGoogle Scholar
[22]Kedlaya, K. S., Semistable reduction for overconvergent F-isocrystals, III: Local semistable reduction at monomial valuations, Compositio Math. 145 (2009), 143–172.CrossRefGoogle Scholar
[23]Montagnon, C., GĂ©nĂ©ralisation de la thĂ©orie arithmĂ©tique des 𝒟-modules Ă  la gĂ©omĂ©trie logarithmique, ThĂšse, UniversitĂ© de Rennes I, 2002.Google Scholar
[24]Noot-Huyghe, C., Finitude de la dimension homologique d’algĂšbres d’opĂ©rateurs diffĂ©rentiels faiblement complĂštes et Ă  coefficients surconvergents, J. Algebra 307 (2007), 499–540.CrossRefGoogle Scholar
[25]Nakkajima, Y. and Shiho, A., Weight filtrations on log crystalline cohomologies of families of open smooth varieties, Lecture Notes in Mathematics, vol. 1959 (Springer, Berlin, 2008).CrossRefGoogle Scholar
[26]Berthelot, P., Grothendieck, A. and Illusie, L., ThĂ©orie des intersections et thĂ©orĂšme de Riemann–Roch, in SĂ©minaire de GĂ©omĂ©trie AlgĂ©grique du Bois-Marie 1966–1967 (SGA 6), Avec la collaboration de D. Ferrand, J. P. Jouanolou, O. Jussila, S. Kleiman, M. Raynaud et J. P. Serre, Lecture Notes in Mathematics, vol. 225 (Springer, Berlin, 1971).Google Scholar
[27]Shiho, A., Crystalline fundamental groups. II. Log convergent cohomology and rigid cohomology, J. Math. Sci. Univ. Tokyo 9 (2002), 1–163.Google Scholar
[28]Tsuzuki, N., Morphisms of F-isocrystals and the finite monodromy theorem for unit-rootF-isocrystals, Duke Math. J. 111 (2002), 385–418.CrossRefGoogle Scholar
[29]Virrion, A., DualitĂ© locale et holonomie pour les 𝒟-modules arithmĂ©tiques, Bull. Soc. Math. France 128 (2000), 1–68.CrossRefGoogle Scholar