Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T15:10:20.188Z Has data issue: false hasContentIssue false
  • English
  • Français

A local-global question in automorphic forms

Part of: Lie groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  26 April 2013

U. K. Anandavardhanan  and
Dipendra Prasad
U. K. Anandavardhanan
Affiliation:
Department of Mathematics, Indian Institute of Technology Bombay, Mumbai - 400 076, India email anand@math.iitb.ac.in
Dipendra Prasad
Affiliation:
Tata Institute of Fundamental Research, Homi Bhabha Road, Mumbai - 400 005, India email dprasad@math.tifr.res.in
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider the 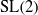$\mathrm{SL} (2)$ analogue of two well-known theorems about period integrals of automorphic forms on 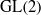$\mathrm{GL} (2)$: one due to Harder–Langlands–Rapoport about non-vanishing of period integrals on 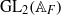${\mathrm{GL} }_{2} ({ \mathbb{A} }_{F} )$ of cuspidal automorphic representations on 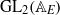${\mathrm{GL} }_{2} ({ \mathbb{A} }_{E} )$ where 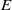$E$ is a quadratic extension of a number field 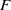$F$, and the other due to Waldspurger involving toric periods of automorphic forms on 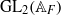${\mathrm{GL} }_{2} ({ \mathbb{A} }_{F} )$. In both these cases, now involving 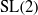$\mathrm{SL} (2)$, we analyze period integrals on global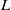$L$-packets; we prove that under certain conditions, a global automorphic $L$-packet which at each place of a number field has a distinguished representation, contains globally distinguished representations, and further, an automorphic representation which is locally distinguished is globally distinguished.

Keywords

period integralslocally distinguished representationsglobally distinguished representationsbase changeAsai liftAsai L-functioncentral L-valuesepsilon factorsfibers of functorial liftssimultaneous non-vanishing of L-functions

MSC classification

Secondary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields 22E55: Representations of Lie and linear algebraic groups over global fields and adèle rings
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 6 , June 2013 , pp. 959 - 995
Copyright
© The Author(s) 2013 

References

Anandavardhanan, U. K., Kable, A. C. and Tandon, R., Distinguished representations and poles of twisted tensor $L$-functions, Proc. Amer. Math. Soc. 132 (2004), 2875–2883; MR 2063106 (2005g:11080).Google Scholar
Anandavardhanan, U. K. and Prasad, D., Distinguished representations for $\mathrm{SL} (2)$, Math. Res. Lett. 10 (2003), 867–878; MR 2025061 (2004j:22018).Google Scholar
Anandavardhanan, U. K. and Prasad, D., On the $\mathrm{SL} (2)$ period integral, Amer. J. Math. 128 (2006), 1429–1453; MR 2275907 (2008b:22014).Google Scholar
Blasius, D., On multiplicities for $\mathrm{SL} (n)$, Israel J. Math. 88 (1994), 237–251; MR 1303497 (95i:11049).Google Scholar
Flicker, Y. Z., Twisted tensors and Euler products, Bull. Soc. Math. France 116 (1988), 295–313; MR 984899 (89m:11049).Google Scholar
Flicker, Y. Z., On distinguished representations, J. Reine Angew. Math. 418 (1991), 139–172; MR 1111204 (92i:22019).Google Scholar
Flicker, Y. Z. and Hakim, J. L., Quaternionic distinguished representations, Amer. J. Math. 116 (1994), 683–736; MR 1277452 (95i:22028).Google Scholar
Friedberg, S. and Hoffstein, J., Nonvanishing theorems for automorphic $L$-functions on $\mathrm{GL} (2)$, Ann. of Math. (2) 142 (1995), 385–423; MR 1343325 (96e:11072).Google Scholar
Fröhlich, A. and Queyrut, J., On the functional equation of the Artin $L$-function for characters of real representations, Invent. Math. 20 (1973), 125–138; MR 0321888 (48 #253).Google Scholar
Gan, W. T., Gross, B. H. and Prasad, D., Symplectic local root numbers, central critical l-values, and restriction problems in the representation theory of classical groups, Astérisque 346 (2012), 1–109.Google Scholar
Gross, B. H. and Prasad, D., On the decomposition of a representation of ${\mathrm{SO} }_{n} $ when restricted to ${\mathrm{SO} }_{n- 1} $, Canad. J. Math. 44 (1992), 974–1002; MR 1186476 (93j:22031).Google Scholar
Hakim, J., Distinguished $p$-adic representations, Duke Math. J. 62 (1991), 1–22; MR 1104321 (92c:22037).Google Scholar
Harder, G., Langlands, R. P. and Rapoport, M., Algebraische Zyklen auf Hilbert–Blumenthal–Flächen, J. Reine Angew. Math. 366 (1986), 53–120; MR 833013 (87k:11066).Google Scholar
Jacquet, H., On the nonvanishing of some $L$-functions, Proc. Indian Acad. Sci. Math. Sci. 97 (1987), 117–155; MR 983610 (90e:11079).Google Scholar
Jacquet, H. and Lai, K. F., A relative trace formula, Compositio Math. 54 (1985), 243–310; MR 783512 (86j:11059).Google Scholar
Kable, A. C., Asai $L$-functions and Jacquet’s conjecture, Amer. J. Math. 126 (2004), 789–820; MR 2075482 (2005g:11083).CrossRefGoogle Scholar
Krishnamurthy, M., The Asai transfer to ${\mathrm{GL} }_{4} $ via the Langlands–Shahidi method, Int. Math. Res. Not. 41 (2003), 2221–2254; MR 2000968 (2004i:11050).Google Scholar
Krishnamurthy, M., Determination of cusp forms on $GL(2)$ by coefficients restricted to quadratic subfields, J. Number Theory 132 (2012), 1359–1384; with an appendix by Dipendra Prasad and Dinakar Remakrishnan; MR 2899809.Google Scholar
Larsen, M., On the conjugacy of element-conjugate homomorphisms, Israel J. Math. 88 (1994), 253–277; MR 1303498 (95k:20073).Google Scholar
Labesse, J.-P. and Langlands, R. P., $L$-indistinguishability for $\mathrm{SL} (2)$, Canad. J. Math. 31 (1979), 726–785; MR 540902 (81b:22017).Google Scholar
Murty, V. K. and Prasad, D., Tate cycles on a product of two Hilbert modular surfaces, J. Number Theory 80 (2000), 25–43; MR 1735646 (2000m:14028).Google Scholar
Prasad, D., Invariant forms for representations of ${\mathrm{GL} }_{2} $ over a local field, Amer. J. Math. 114 (1992), 1317–1363; MR 1198305 (93m:22011).Google Scholar
Prasad, D., On an extension of a theorem of Tunnell, Compositio Math. 94 (1994), 19–28; MR 1302309 (95k:22023).Google Scholar
Prasad, D., A relative local langlands conjecture.Google Scholar
Ramakrishnan, D., Modularity of the Rankin–Selberg $L$-series, and multiplicity one for $\mathrm{SL} (2)$, Ann. of Math. (2) 152 (2000), 45–111; MR 1792292 (2001g:11077).Google Scholar
Saito, H., On Tunnell’s formula for characters of $\mathrm{GL} (2)$, Compositio Math. 85 (1993), 99–108; MR 1199206 (93m:22021).Google Scholar
Sakellaridis, Y. and Venkatesh, A., Periods and harmonic analysis on spherical varieties.Google Scholar
Serre, J.-P., Galois cohomology, Springer Monographs in Mathematics, English edition (Springer, Berlin, 2002), translated from the French by Patrick Ion and revised by the author; MR 1867431 (2002i:12004.Google Scholar
Tunnell, J. B., Local $\epsilon $-factors and characters of $\mathrm{GL} (2)$, Amer. J. Math. 105 (1983), 1277–1307; MR 721997 (86a:22018).Google Scholar
Waldspurger, J.-L., Sur les valeurs de certaines fonctions $L$ automorphes en leur centre de symétrie, Compositio Math. 54 (1985), 173–242; MR 783511 (87g:11061b).Google Scholar
Waldspurger, J.-L., Correspondances de Shimura et quaternions, Forum Math. 3 (1991), 219–307; MR 1103429 (92g:11054).Google Scholar