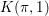Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-06T02:53:59.077Z Has data issue: false hasContentIssue false
  • English
  • Français

$K({\it\pi},1)$-neighborhoods and comparison theorems

Part of: (Co)homology theory

Published online by Cambridge University Press:  05 June 2015

Piotr Achinger
Piotr Achinger*
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720, USA email achinger@math.berkeley.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A technical ingredient in Faltings’ original approach to $p$-adic comparison theorems involves the construction of 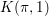$K({\it\pi},1)$-neighborhoods for a smooth scheme 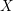$X$ over a mixed characteristic discrete valuation ring with a perfect residue field: every point 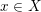$x\in X$ has an open neighborhood 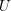$U$ whose generic fiber is a 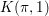$K({\it\pi},1)$ scheme (a notion analogous to having a contractible universal cover). We show how to extend this result to the logarithmically smooth case, which might help to simplify some proofs in 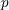$p$-adic Hodge theory. The main ingredient of the proof is a variant of a trick of Nagata used in his proof of the Noether normalization lemma.

Keywords

Faltings’ toposétale cohomologylogarithmic geometrysemistable reductionp-adic Hodge theoryK (𝜋, 1) schemes

MSC classification

Primary: 14F20: Étale and other Grothendieck topologies and (co)homologies
Secondary: 14F30: $p$-adic cohomology, crystalline cohomology
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 10 , October 2015 , pp. 1945 - 1964
Copyright
© The Author 2015 

References

Abramovich, D., Chen, Q., Gillam, D., Huang, Y., Olsson, M., Satriano, M. and Sun, S., Logarithmic geometry and moduli, in Handbook of moduli. Vol. I, Advanced Lectures in Mathematics (ALM), vol. 24 (International Press, Somerville, MA, 2013), 1–61; MR 3184161.Google Scholar
Abbes, A. and Gros, M., Topos co-évanescents et généralisations, Ann. of Math. Stud., to appear, arXiv:1107.2380v3 [math.AG].Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. III. Étude cohomologique des faisceaux cohérents. I, Publ. Math. Inst. Hautes Études Sci. 11 (1961), 167; MR 0217085 (36 #177c).Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV, Publ. Math. Inst. Hautes Études Sci. 32 (1967), 361; MR 0238860 (39 #220).Google Scholar
Faltings, G., p-adic Hodge theory, J. Amer. Math. Soc. 1 (1988), 255–299; MR 924705 (89g:14008).Google Scholar
Faltings, G., Almost étale extensions, in Cohomologies p-adiques et applications arithmétiques, II, Astérisque, vol. 279 (Société Mathématique de France, 2002), 185–270; MR 1922831 (2003m:14031).Google Scholar
Fontaine, J.-M., Sur certains types de représentations p-adiques du groupe de Galois d’un corps local; construction d’un anneau de Barsotti-Tate, Ann. of Math. (2) 115 (1982), 529–577; MR 657238 (84d:14010).CrossRefGoogle Scholar
Gabber, O. and Ramero, L., Foundations for almost ring theory – Release 6.8, Preprint (2014),arXiv:math/0409584v9 [math.AG].Google Scholar
Gross, M. and Siebert, B., Mirror symmetry via logarithmic degeneration data. I, J. Differential Geom. 72 (2006), 169–338; MR 2213573 (2007b:14087).CrossRefGoogle Scholar
Gross, M. and Siebert, B., Mirror symmetry via logarithmic degeneration data, II, J. Algebraic Geom. 19 (2010), 679–780; MR 2669728 (2011m:14066).CrossRefGoogle Scholar
Gross, M. and Siebert, B., From real affine geometry to complex geometry, Ann. of Math. (2) 174 (2011), 1301–1428; MR 2846484.CrossRefGoogle Scholar
Kato, K., Logarithmic structures of Fontaine-Illusie, in Algebraic analysis, geometry, and number theory (Baltimore, MD, 1988) (Johns Hopkins University Press, Baltimore, MD, 1989), 191–224; MR 1463703 (99b:14020).Google Scholar
Kato, K., Toric singularities, Amer. J. Math. 116 (1994), 1073–1099; MR 1296725 (95g:14056).CrossRefGoogle Scholar
Milnor, J., Singular points of complex hypersurfaces, Annals of Mathematics Studies, No. 61 (Princeton University Press, Princeton, N.J., 1968); MR 0239612 (39 #969).Google Scholar
Mumford, D., The red book of varieties and schemes, Lecture Notes in Mathematics, vol. 1358, expanded edition (Springer, Berlin, 1999); MR 1748380 (2001b:14001).CrossRefGoogle Scholar
Nakayama, C., Nearby cycles for log smooth families, Compositio Math. 112 (1998), 45–75; MR 1622751 (99g:14044).CrossRefGoogle Scholar
Nakayama, C. and Ogus, A., Relative rounding in toric and logarithmic geometry, Geom. Topol. 14 (2010), 2189–2241; MR 2740645 (2012e:14104).CrossRefGoogle Scholar
Ogus, A., Relatively coherent log structures, Preprint (2009).Google Scholar
Olsson, M. C., On Faltings’ method of almost étale extensions, in Algebraic geometry—Seattle 2005. Part 2, Proceedings of Symposia in Pure Mathematics, vol. 80 (American Mathematical Society, Providence, RI, 2009), 811–936; MR 2483956 (2010b:14034).Google Scholar
Grothendieck, A., Revêtements étales et groupe fondamental (SGA1), Documents Mathématiques, vol. 3 (Société Mathématique de France, Paris, 2003); MR 2017446 (2004g:14017).Google Scholar
Artin, M., Grothendieck, A. and Verdier, J.-L., Séminaire de géométrie algébrique du Bois-Marie 1963–1964, Théorie des topos et cohomologie étale des schémas (SGA4), Vol. 3, Lecture Notes in Mathematics, vol. 305 (Springer, 1973); MR 0354654 (50 #7132).Google Scholar
Deligne, P., Séminaire de géométrie algébrique du Bois-Marie – Cohomologie étale – $(\mathit{SGA}4\frac{1}{2})$, Lecture Notes in Mathematics, vol. 569 (Springer, Berlin–New York, 1977); MR 0463174 (57 #3132).CrossRefGoogle Scholar
Deligne, P. and Katz, N., Séminaire de Géométrie Algébrique du Bois-Marie 1967–1969, Groupes de monodromie en géométrie algébrique (SGA7), Vol. II, Lecture Notes in Mathematics, vol. 340 (Springer, 1973); MR 0354657 (50 #7135).Google Scholar
Stacks Project Authors, Stacks project, 2014, http://stacks.math.columbia.edu.Google Scholar