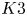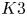Introduction
In [Reference YoshikawaYos04], a holomorphic torsion invariant of ![]() $K3$ surfaces with involution was introduced by the second-named author. The purpose of the present paper is to completely determine the structure of this invariant as a function on the moduli space of such
$K3$ surfaces with involution was introduced by the second-named author. The purpose of the present paper is to completely determine the structure of this invariant as a function on the moduli space of such ![]() $K3$ surfaces. We will express it using Borcherds products and Siegel modular forms. Let us explain our result in detail.
$K3$ surfaces. We will express it using Borcherds products and Siegel modular forms. Let us explain our result in detail.
A pair consisting of a ![]() $K3$ surface and an anti-symplectic involution is called a
$K3$ surface and an anti-symplectic involution is called a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface. By Nikulin [Reference NikulinNik83], the deformation type of a
$K3$ surface. By Nikulin [Reference NikulinNik83], the deformation type of a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface is determined by the isometry class of the invariant lattice of the induced involution on the second integral cohomology. There exist
$K3$ surface is determined by the isometry class of the invariant lattice of the induced involution on the second integral cohomology. There exist ![]() $75$ deformation types, labeled by primitive
$75$ deformation types, labeled by primitive ![]() $2$-elementary Lorentzian sublattices of the
$2$-elementary Lorentzian sublattices of the ![]() $K3$ lattice
$K3$ lattice ![]() ${\Bbb L}_{K3}$. Let
${\Bbb L}_{K3}$. Let ![]() $M\subset {\Bbb L}_{K3}$ be one such sublattice of rank
$M\subset {\Bbb L}_{K3}$ be one such sublattice of rank ![]() $r$. Its orthogonal complement
$r$. Its orthogonal complement ![]() $\Lambda = M^{\perp }\cap {\Bbb L}_{K3}$ is a
$\Lambda = M^{\perp }\cap {\Bbb L}_{K3}$ is a ![]() $2$-elementary lattice of signature
$2$-elementary lattice of signature ![]() $(2,20-r)$. Let
$(2,20-r)$. Let ![]() $\Omega _{\Lambda }^{+}$ be the Hermitian domain of type IV of dimension
$\Omega _{\Lambda }^{+}$ be the Hermitian domain of type IV of dimension ![]() $20-r$ associated to
$20-r$ associated to ![]() $\Lambda$ and let
$\Lambda$ and let ![]() $O^{+}(\Lambda )$ be the index
$O^{+}(\Lambda )$ be the index ![]() $2$ subgroup of the orthogonal group of
$2$ subgroup of the orthogonal group of ![]() $\Lambda$ preserving
$\Lambda$ preserving ![]() $\Omega _{\Lambda }^{+}$. Via the period map, the moduli space of
$\Omega _{\Lambda }^{+}$. Via the period map, the moduli space of ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces of type
$K3$ surfaces of type ![]() $M$ is isomorphic to the quotient
$M$ is isomorphic to the quotient
where ![]() ${\mathcal {D}}_{\Lambda }$ is the discriminant divisor. Hence
${\mathcal {D}}_{\Lambda }$ is the discriminant divisor. Hence ![]() ${\mathcal {M}}_{\Lambda }^{0}$ is a Zariski open subset of a modular variety of orthogonal type of dimension
${\mathcal {M}}_{\Lambda }^{0}$ is a Zariski open subset of a modular variety of orthogonal type of dimension ![]() $20-r$.
$20-r$.
In [Reference YoshikawaYos04], a holomorphic torsion invariant of ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces was defined as follows. Let
$K3$ surfaces was defined as follows. Let ![]() $(X,\iota )$ be a
$(X,\iota )$ be a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface of type
$K3$ surface of type ![]() $M$. Write
$M$. Write ![]() $X^{\iota }$ for the set of fixed points of
$X^{\iota }$ for the set of fixed points of ![]() $\iota$. Depending on
$\iota$. Depending on ![]() $M$,
$M$, ![]() $X^{\iota }$ is either empty or the disjoint union of smooth curves of total genus
$X^{\iota }$ is either empty or the disjoint union of smooth curves of total genus ![]() $g=g(M)$. (See § 3.2 for a formula for
$g=g(M)$. (See § 3.2 for a formula for ![]() $g$.) When
$g$.) When ![]() $X^{\iota }$ is empty, the corresponding type is unique and is called exceptional, in which case
$X^{\iota }$ is empty, the corresponding type is unique and is called exceptional, in which case ![]() $(X,\iota )$ is the universal covering of an Enriques surface endowed with the non-trivial covering transformation. Take an
$(X,\iota )$ is the universal covering of an Enriques surface endowed with the non-trivial covering transformation. Take an ![]() $\iota$-invariant Ricci-flat Kähler form
$\iota$-invariant Ricci-flat Kähler form ![]() $\gamma$ on
$\gamma$ on ![]() $X$ (cf. [Reference YauYau78]) and a holomorphic
$X$ (cf. [Reference YauYau78]) and a holomorphic ![]() $2$-form
$2$-form ![]() $\eta \not =0$ on
$\eta \not =0$ on ![]() $X$. Let
$X$. Let ![]() $\tau _{\textbf {Z}_{2}}(X,\gamma )(\iota )$ be the equivariant analytic torsion of
$\tau _{\textbf {Z}_{2}}(X,\gamma )(\iota )$ be the equivariant analytic torsion of ![]() $(X,\gamma )$ with respect to the
$(X,\gamma )$ with respect to the ![]() $\iota$-action and let
$\iota$-action and let ![]() $\tau (X^{\iota },\gamma |_{X^{\iota }})$ be the analytic torsion of
$\tau (X^{\iota },\gamma |_{X^{\iota }})$ be the analytic torsion of ![]() $(X^{\iota },\gamma |_{X^{\iota }})$ (cf. [Reference Ray and SingerRS73, Reference BismutBis95]). Then the real number
$(X^{\iota },\gamma |_{X^{\iota }})$ (cf. [Reference Ray and SingerRS73, Reference BismutBis95]). Then the real number
depends only on the isomorphism class of ![]() $(X,\iota )$, so that it gives rise to a function
$(X,\iota )$, so that it gives rise to a function ![]() $\tau _{M}$ on
$\tau _{M}$ on ![]() ${\mathcal {M}}_{\Lambda }^{0}$. The goal of this paper is to give an explicit expression for
${\mathcal {M}}_{\Lambda }^{0}$. The goal of this paper is to give an explicit expression for ![]() $\tau _M$ in terms of modular forms. It turns out that
$\tau _M$ in terms of modular forms. It turns out that ![]() $\tau _{M}$ is expressed by two types of modular forms: Borcherds products and Siegel modular forms. Let us explain these modular forms.
$\tau _{M}$ is expressed by two types of modular forms: Borcherds products and Siegel modular forms. Let us explain these modular forms.
Let ![]() $\rho _{\Lambda }\colon {\rm Mp}_{2}(\textbf {Z})\to {\rm GL}(\textbf {C}[A_{\Lambda }])$ be the Weil representation attached to the discriminant group
$\rho _{\Lambda }\colon {\rm Mp}_{2}(\textbf {Z})\to {\rm GL}(\textbf {C}[A_{\Lambda }])$ be the Weil representation attached to the discriminant group ![]() $A_{\Lambda }$ of
$A_{\Lambda }$ of ![]() $\Lambda$, where
$\Lambda$, where ![]() $\textbf {C}[A_{\Lambda }]$ is the group ring of
$\textbf {C}[A_{\Lambda }]$ is the group ring of ![]() $A_{\Lambda }$. By Borcherds [Reference BorcherdsBor98], given an
$A_{\Lambda }$. By Borcherds [Reference BorcherdsBor98], given an ![]() $O^{+}(\Lambda )$-invariant elliptic modular form
$O^{+}(\Lambda )$-invariant elliptic modular form ![]() $f$ of type
$f$ of type ![]() $\rho _{\Lambda }$ and of weight
$\rho _{\Lambda }$ and of weight ![]() $1-(20-r)/2$ with integral Fourier expansion, we can take its Borcherds lift
$1-(20-r)/2$ with integral Fourier expansion, we can take its Borcherds lift ![]() $\Psi _{\Lambda }(\cdot ,f)$. This is a (possibly meromorphic) automorphic form for
$\Psi _{\Lambda }(\cdot ,f)$. This is a (possibly meromorphic) automorphic form for ![]() $O^{+}(\Lambda )$ with infinite product expansion, and its Petersson norm
$O^{+}(\Lambda )$ with infinite product expansion, and its Petersson norm ![]() $\|\Psi _{\Lambda }(\cdot ,f)\|$ descends to a function on
$\|\Psi _{\Lambda }(\cdot ,f)\|$ descends to a function on ![]() ${\mathcal {M}}_{\Lambda }^{0}$. To express
${\mathcal {M}}_{\Lambda }^{0}$. To express ![]() $\tau _{M}$, the Borcherds lift of the following elliptic modular form will be used. Let
$\tau _{M}$, the Borcherds lift of the following elliptic modular form will be used. Let ![]() $\eta (\tau )$ be the Dedekind
$\eta (\tau )$ be the Dedekind ![]() $\eta$-function and let
$\eta$-function and let ![]() $\theta _{{\Bbb A}_{1}^{+}}(\tau )$ be the theta series of the
$\theta _{{\Bbb A}_{1}^{+}}(\tau )$ be the theta series of the ![]() $A_{1}$-lattice. We put
$A_{1}$-lattice. We put
This induces the following modular form of type ![]() $\rho _{\Lambda }$ (cf. [Reference BorcherdsBor00, Reference ScheithauerSch06, Reference YoshikawaYos13]):
$\rho _{\Lambda }$ (cf. [Reference BorcherdsBor00, Reference ScheithauerSch06, Reference YoshikawaYos13]):
where ![]() $|_{\gamma }$ is the Petersson slash operator and
$|_{\gamma }$ is the Petersson slash operator and ![]() $\textbf {e}_{0}\in \textbf {C}[A_{\Lambda }]$ is the vector corresponding to
$\textbf {e}_{0}\in \textbf {C}[A_{\Lambda }]$ is the vector corresponding to ![]() $0\in A_{\Lambda }$. Except for two types, the Borcherds lift of
$0\in A_{\Lambda }$. Except for two types, the Borcherds lift of ![]() $(2^{g-1}+\delta _{r,10})F_{\Lambda }$ will be used in the expression for
$(2^{g-1}+\delta _{r,10})F_{\Lambda }$ will be used in the expression for ![]() $\tau _{M}$, where
$\tau _{M}$, where ![]() $\delta _{i,j}$ denotes the Kronecker delta.
$\delta _{i,j}$ denotes the Kronecker delta.
On the other hand, Siegel modular forms also yield functions on ![]() ${\mathcal {M}}_{\Lambda }^{0}$. The period map for the fixed curves of
${\mathcal {M}}_{\Lambda }^{0}$. The period map for the fixed curves of ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces induces a holomorphic map
$K3$ surfaces induces a holomorphic map
where ![]() ${\mathcal {A}}_{g}$ is the Siegel modular variety of degree
${\mathcal {A}}_{g}$ is the Siegel modular variety of degree ![]() $g$. Then the pullback of the Petersson norm of a Siegel modular form by
$g$. Then the pullback of the Petersson norm of a Siegel modular form by ![]() $J_{M}$ is a function on
$J_{M}$ is a function on ![]() ${\mathcal {M}}_{\Lambda }^{0}$. The following Siegel modular forms of weights
${\mathcal {M}}_{\Lambda }^{0}$. The following Siegel modular forms of weights ![]() $2^{g+1}(2^{g}+1)$ and
$2^{g+1}(2^{g}+1)$ and ![]() $2(2^{g}-1)(2^{g}+2)$ will be used to express
$2(2^{g}-1)(2^{g}+2)$ will be used to express ![]() $\tau _{M}$:
$\tau _{M}$:
where ![]() $\theta _{a,b}$ is the Riemann theta constant with even characteristic
$\theta _{a,b}$ is the Riemann theta constant with even characteristic ![]() $(a, b)$. Let
$(a, b)$. Let ![]() $\|\chi _{g}\|^{2}$ and
$\|\chi _{g}\|^{2}$ and ![]() $\|\Upsilon _{g}\|^{2}$ be their Petersson norms. Hence
$\|\Upsilon _{g}\|^{2}$ be their Petersson norms. Hence ![]() $J_{M}^{*}\|\chi _{g}^{8}\|$ and
$J_{M}^{*}\|\chi _{g}^{8}\|$ and ![]() $J_{M}^{*}\|\Upsilon _{g}\|$ are functions on
$J_{M}^{*}\|\Upsilon _{g}\|$ are functions on ![]() ${\mathcal {M}}_{\Lambda }^{0}$. For convenience, if
${\mathcal {M}}_{\Lambda }^{0}$. For convenience, if ![]() $M$ is exceptional, we set
$M$ is exceptional, we set ![]() $g=1$ and
$g=1$ and ![]() $J_{M}^{*}\|\Upsilon _{g}\|=1$.
$J_{M}^{*}\|\Upsilon _{g}\|=1$.
The main result of this paper is the following (Theorems 8.6, 9.2, 9.4, 9.5, 9.10).
Theorem 0.1 Let ![]() $M\subset {\Bbb L}_{K3}$ be a primitive
$M\subset {\Bbb L}_{K3}$ be a primitive ![]() $2$-elementary Lorentzian sublattice of rank
$2$-elementary Lorentzian sublattice of rank ![]() $r$ with orthogonal complement
$r$ with orthogonal complement ![]() $\Lambda$ and let
$\Lambda$ and let ![]() $\delta \in \{0,1\}$ be the parity of its discriminant form. Then there exists a constant
$\delta \in \{0,1\}$ be the parity of its discriminant form. Then there exists a constant ![]() $C_{M}>0$ depending only on
$C_{M}>0$ depending only on ![]() $M$ such that the following equality of functions on
$M$ such that the following equality of functions on ![]() ${\mathcal {M}}_{\Lambda }^{0}$ holds:
${\mathcal {M}}_{\Lambda }^{0}$ holds:
(1) if
 $(r,\delta )\not =(2,0),(10,0)$, then
$(r,\delta )\not =(2,0),(10,0)$, then
 \[ \tau_{M}^{-2^{g}(2^{g}+1)} = C_{M} \| \Psi_{\Lambda}(\cdot,2^{g-1}F_{\Lambda}+f_{\Lambda}) \| \cdot J_{M}^{*} \| \chi_{g}^{8} \|; \]
\[ \tau_{M}^{-2^{g}(2^{g}+1)} = C_{M} \| \Psi_{\Lambda}(\cdot,2^{g-1}F_{\Lambda}+f_{\Lambda}) \| \cdot J_{M}^{*} \| \chi_{g}^{8} \|; \](2) if
 $(r,\delta )=(2,0)$ or
$(r,\delta )=(2,0)$ or  $(10,0)$, then
$(10,0)$, then
 \[ \tau_{M}^{-(2^{g}-1)(2^{g}+2)} = C_{M} \| \Psi_{\Lambda}(\cdot,2^{g-1}F_{\Lambda}+f_{\Lambda}) \| \cdot J_{M}^{*} \| \Upsilon_{g} \|. \]
\[ \tau_{M}^{-(2^{g}-1)(2^{g}+2)} = C_{M} \| \Psi_{\Lambda}(\cdot,2^{g-1}F_{\Lambda}+f_{\Lambda}) \| \cdot J_{M}^{*} \| \Upsilon_{g} \|. \]
Here ![]() $f_{\Lambda }$ is the elliptic modular form of type
$f_{\Lambda }$ is the elliptic modular form of type ![]() $\rho _{\Lambda }$ given by
$\rho _{\Lambda }$ given by ![]() $f_{\Lambda }=\delta _{r,10} F_{\Lambda }$ for
$f_{\Lambda }=\delta _{r,10} F_{\Lambda }$ for ![]() $r\not =2$ and by (9.5), (9.19) below for
$r\not =2$ and by (9.5), (9.19) below for ![]() $r=2$.
$r=2$.
Case (1) covers the majority of types (![]() $67$), while case (2) covers a further
$67$), while case (2) covers a further ![]() $8$ types. The formula for (1) does not hold in case (2) because
$8$ types. The formula for (1) does not hold in case (2) because ![]() $J_{M}^{*}\chi _{g}$ vanishes identically there. In [Reference YoshikawaYos04, Reference YoshikawaYos12], the automorphy of
$J_{M}^{*}\chi _{g}$ vanishes identically there. In [Reference YoshikawaYos04, Reference YoshikawaYos12], the automorphy of ![]() $\tau _{M}$ was proved (cf. (0.2) below), but the corresponding modular form was given explicitly only for the exceptional
$\tau _{M}$ was proved (cf. (0.2) below), but the corresponding modular form was given explicitly only for the exceptional ![]() $M$. In [Reference YoshikawaYos13], the elliptic modular form
$M$. In [Reference YoshikawaYos13], the elliptic modular form ![]() $F_{\Lambda }$ was introduced and (1) was proved for
$F_{\Lambda }$ was introduced and (1) was proved for ![]() $r\geq 10$. Theorem 0.1 completes this series of work. As a by-product of Theorem 0.1, we prove the quasi-affinity of
$r\geq 10$. Theorem 0.1 completes this series of work. As a by-product of Theorem 0.1, we prove the quasi-affinity of ![]() ${\mathcal {M}}_{\Lambda }^{0}$ when
${\mathcal {M}}_{\Lambda }^{0}$ when ![]() $r>6$ (Theorem 9.16).
$r>6$ (Theorem 9.16).
The invariant ![]() $\tau _{M}$ is closely related to the BCOV invariant
$\tau _{M}$ is closely related to the BCOV invariant ![]() $\tau _{\rm BCOV}$ of Calabi–Yau
$\tau _{\rm BCOV}$ of Calabi–Yau ![]() $3$-folds, which was introduced in [Reference Fang, Lu and YoshikawaFLY08] after the prediction of Bershadsky, Cecotti, Ooguri and Vafa [Reference Bershadsky, Cecotti, Ooguri and VafaBCOV94] on the mirror symmetry at genus
$3$-folds, which was introduced in [Reference Fang, Lu and YoshikawaFLY08] after the prediction of Bershadsky, Cecotti, Ooguri and Vafa [Reference Bershadsky, Cecotti, Ooguri and VafaBCOV94] on the mirror symmetry at genus ![]() $1$. On the moduli space of Calabi–Yau
$1$. On the moduli space of Calabi–Yau ![]() $3$-folds of Borcea and Voisin associated to
$3$-folds of Borcea and Voisin associated to ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces of type
$K3$ surfaces of type ![]() $M$ and elliptic curves, one has the following equality of functions (cf. [Reference Yoshikawa, Bost, Hofer, Labourie, Le Jan, Ma and ZhangYos17]):
$M$ and elliptic curves, one has the following equality of functions (cf. [Reference Yoshikawa, Bost, Hofer, Labourie, Le Jan, Ma and ZhangYos17]):
where ![]() ${\mathcal {C}}_{M}$ is a constant depending only on
${\mathcal {C}}_{M}$ is a constant depending only on ![]() $M$. By Theorem 0.1 and (0.1),
$M$. By Theorem 0.1 and (0.1), ![]() $\tau _{\rm BCOV}$ for Borcea–Voisin
$\tau _{\rm BCOV}$ for Borcea–Voisin ![]() $3$-folds of type
$3$-folds of type ![]() $M$ is given by the product of the Petersson norms of the modular forms
$M$ is given by the product of the Petersson norms of the modular forms ![]() $\Psi _{\Lambda }(\cdot ,F_{\Lambda })$,
$\Psi _{\Lambda }(\cdot ,F_{\Lambda })$, ![]() $\chi _{g}^{8}$ (or
$\chi _{g}^{8}$ (or ![]() $\Upsilon _{g}$) and
$\Upsilon _{g}$) and ![]() $\eta$. Since
$\eta$. Since
is the genus ![]() $1$ string amplitude
$1$ string amplitude ![]() $F_{1}$ in the B-model (cf. [Reference Bershadsky, Cecotti, Ooguri and VafaBCOV94, Reference Fang, Lu and YoshikawaFLY08]), Theorem 0.1 gives an exact result of
$F_{1}$ in the B-model (cf. [Reference Bershadsky, Cecotti, Ooguri and VafaBCOV94, Reference Fang, Lu and YoshikawaFLY08]), Theorem 0.1 gives an exact result of ![]() $F_{1}$ in the B-model for all Borcea–Voisin
$F_{1}$ in the B-model for all Borcea–Voisin ![]() $3$-folds.
$3$-folds.
In Theorem 0.1 the automorphic form corresponding to ![]() $\tau _{M}$ splits into two factors. It is natural to ask if this factorization is realized at the level of holomorphic torsion invariants of
$\tau _{M}$ splits into two factors. It is natural to ask if this factorization is realized at the level of holomorphic torsion invariants of ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces. Thanks to the spin-
$K3$ surfaces. Thanks to the spin-![]() $1/2$ bosonization formula [Reference Alvarez-Gaumé, Moore and VafaAMV86, Reference Bost and NelsonBN86, Reference FayFay92], we have an affirmative answer to this question. Let us introduce the following twisted version of
$1/2$ bosonization formula [Reference Alvarez-Gaumé, Moore and VafaAMV86, Reference Bost and NelsonBN86, Reference FayFay92], we have an affirmative answer to this question. Let us introduce the following twisted version of ![]() $\tau _{M}$.
$\tau _{M}$.
where ![]() $\Sigma$ runs over all ineffective theta characteristics on
$\Sigma$ runs over all ineffective theta characteristics on ![]() $X^{\iota }$ and
$X^{\iota }$ and ![]() $\tau (X^{\iota },\Sigma ;\gamma |_{X^{\iota }})$ is the analytic torsion of
$\tau (X^{\iota },\Sigma ;\gamma |_{X^{\iota }})$ is the analytic torsion of ![]() $\Sigma$ with respect to
$\Sigma$ with respect to ![]() $\gamma |_{X^{\iota }}$. It turns out that
$\gamma |_{X^{\iota }}$. It turns out that ![]() $\tau _{M}^{{\rm spin}}(X,\iota )$ is independent of the choice of an
$\tau _{M}^{{\rm spin}}(X,\iota )$ is independent of the choice of an ![]() $\iota$-invariant Ricci-flat Kähler form
$\iota$-invariant Ricci-flat Kähler form ![]() $\gamma$ and gives rise to a function
$\gamma$ and gives rise to a function ![]() $\tau _{M}^{{\rm spin}}$ on
$\tau _{M}^{{\rm spin}}$ on ![]() ${\mathcal {M}}_{\Lambda }^{0}$. Our second result is stated as follows (cf. Theorem 10.2):
${\mathcal {M}}_{\Lambda }^{0}$. Our second result is stated as follows (cf. Theorem 10.2):
Theorem 0.2 Let ![]() ${\mathcal {H}}_{\Lambda }\subset {\mathcal {M}}_{\Lambda }$ be the characteristic Heegner divisor (cf. § 2). Then there exists a constant
${\mathcal {H}}_{\Lambda }\subset {\mathcal {M}}_{\Lambda }$ be the characteristic Heegner divisor (cf. § 2). Then there exists a constant ![]() $C'_{M}>0$ depending only on
$C'_{M}>0$ depending only on ![]() $M$ such that the following equality of functions on
$M$ such that the following equality of functions on ![]() ${\mathcal {M}}_{\Lambda }^{0}\setminus {\mathcal {H}}_{\Lambda }$ holds:
${\mathcal {M}}_{\Lambda }^{0}\setminus {\mathcal {H}}_{\Lambda }$ holds:
We remark that if ![]() ${\mathcal {H}}_{\Lambda }\not =\emptyset$, then
${\mathcal {H}}_{\Lambda }\not =\emptyset$, then ![]() $\tau _{M}^{{\rm spin}}$ jumps along
$\tau _{M}^{{\rm spin}}$ jumps along ![]() ${\mathcal {H}}_{\Lambda }$ and thus
${\mathcal {H}}_{\Lambda }$ and thus ![]() $\tau _{M}^{{\rm spin}}$ is a discontinuous function on
$\tau _{M}^{{\rm spin}}$ is a discontinuous function on ![]() ${\mathcal {M}}_{\Lambda }^{0}$. For an explicit relation between the constants in Theorems 0.1 and 0.2, see § 10.2 below. After Theorem 0.2, it is very likely that
${\mathcal {M}}_{\Lambda }^{0}$. For an explicit relation between the constants in Theorems 0.1 and 0.2, see § 10.2 below. After Theorem 0.2, it is very likely that ![]() $C'_{M}$ can be determined up to an algebraic number by an Arakelov geometric study of
$C'_{M}$ can be determined up to an algebraic number by an Arakelov geometric study of ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces with maximal Picard number. This subject will be discussed elsewhere. Theorem 0.2 can be interpreted as a formula for the equivariant determinant of Laplacian (with a certain correction term) on the space of invariant Ricci-flat metrics on a
$K3$ surfaces with maximal Picard number. This subject will be discussed elsewhere. Theorem 0.2 can be interpreted as a formula for the equivariant determinant of Laplacian (with a certain correction term) on the space of invariant Ricci-flat metrics on a ![]() $K3$ surface with involution. In § 11 we use this interpretation to study an equivariant analogue of Borcherds’ conjecture [Reference BorcherdsBor98].
$K3$ surface with involution. In § 11 we use this interpretation to study an equivariant analogue of Borcherds’ conjecture [Reference BorcherdsBor98].
According to Theorem 0.2, the invariant ![]() $\tau _{M}^{{\rm spin}}$ is elliptic modular in the sense that it is the Borcherds lift of an elliptic modular form. When
$\tau _{M}^{{\rm spin}}$ is elliptic modular in the sense that it is the Borcherds lift of an elliptic modular form. When ![]() ${\mathcal {D}}_{\Lambda }\not =\emptyset$, the corresponding modular form is determined by
${\mathcal {D}}_{\Lambda }\not =\emptyset$, the corresponding modular form is determined by ![]() $\tau _{M}^{{\rm spin}}$ in a canonical manner (cf. Theorem 10.5). In this way, there is a natural one-to-one correspondence between the holomorphic torsion invariants
$\tau _{M}^{{\rm spin}}$ in a canonical manner (cf. Theorem 10.5). In this way, there is a natural one-to-one correspondence between the holomorphic torsion invariants ![]() $\tau _{M}^{{\rm spin}}$ and the elliptic modular forms
$\tau _{M}^{{\rm spin}}$ and the elliptic modular forms ![]() $2^{g-1}F_{\Lambda }+f_{\Lambda }$. A conceptual account of this unexpected elliptic modularity as well as the geometric meaning of the corresponding modular forms is strongly desired.
$2^{g-1}F_{\Lambda }+f_{\Lambda }$. A conceptual account of this unexpected elliptic modularity as well as the geometric meaning of the corresponding modular forms is strongly desired.
Let us explain the outline of the proof of Theorem 0.1. For the sake of simplicity, we explain only the major case ![]() $\delta =1$. Since
$\delta =1$. Since ![]() $\tau _{M}$ was determined in [Reference YoshikawaYos13] when
$\tau _{M}$ was determined in [Reference YoshikawaYos13] when ![]() $g\leq 2$, we assume
$g\leq 2$, we assume ![]() $3\leq g\leq 10$. The strategy is summarized as follows.
$3\leq g\leq 10$. The strategy is summarized as follows.
(a) Reduce Theorem 0.1 to determining the divisor of
 $J_{M}^{*}\chi _{g}^{8}$.
$J_{M}^{*}\chi _{g}^{8}$.(b) Determine the support of the divisor of
 $J_{M}^{*}\chi _{g}^{8}$ for certain key lattices
$J_{M}^{*}\chi _{g}^{8}$ for certain key lattices  $M_{g,0}$.
$M_{g,0}$.(c) Determine inductively from (b) the support of the divisor of
 $J_{M}^{*}\chi _{g}^{8}$ for all
$J_{M}^{*}\chi _{g}^{8}$ for all  $M$ and prove sharp estimates for its coefficients.
$M$ and prove sharp estimates for its coefficients.(d) Deduce Theorem 0.1 from the estimates in step (c).
Let us see each step in more detail.
(a) From the theory of Quillen metrics [Reference Bismut, Gillet and SouléBGS88, Reference BismutBis95, Reference MaMa00], the automorphy of ![]() $\tau _{M}$ follows [Reference YoshikawaYos04, Reference YoshikawaYos12]. There exist
$\tau _{M}$ follows [Reference YoshikawaYos04, Reference YoshikawaYos12]. There exist ![]() $\ell \in \textbf {Z}_{>0}$ and an automorphic form
$\ell \in \textbf {Z}_{>0}$ and an automorphic form ![]() $\Phi _{M}$ on
$\Phi _{M}$ on ![]() $\Omega _{\Lambda }^{+}$ with
$\Omega _{\Lambda }^{+}$ with
(We will eventually see that ![]() $\ell$ can be taken to be
$\ell$ can be taken to be ![]() $2^{g-1}(2^{g}+1)$.) By construction, the automorphic form
$2^{g-1}(2^{g}+1)$.) By construction, the automorphic form ![]() $\Psi _{\Lambda }(\cdot ,2^{g-1} F_{\Lambda })^{\ell }\otimes J_{M}^{*}\chi _{g}^{8\ell }$ has the same weight as
$\Psi _{\Lambda }(\cdot ,2^{g-1} F_{\Lambda })^{\ell }\otimes J_{M}^{*}\chi _{g}^{8\ell }$ has the same weight as ![]() $\Phi _{M}^{2^{g-1}(2^{g}+1)}$. Hence by the Koecher principle, it is sufficient to show that
$\Phi _{M}^{2^{g-1}(2^{g}+1)}$. Hence by the Koecher principle, it is sufficient to show that
The divisor of ![]() $\Psi _{\Lambda }(\cdot ,2^{g-1} F_{\Lambda })$ is calculated by the theory of Borcherds products [Reference BorcherdsBor98], so the problem is reduced to calculating the divisor of
$\Psi _{\Lambda }(\cdot ,2^{g-1} F_{\Lambda })$ is calculated by the theory of Borcherds products [Reference BorcherdsBor98], so the problem is reduced to calculating the divisor of ![]() $J_{M}^{*}\chi _{g}^{8}$.
$J_{M}^{*}\chi _{g}^{8}$.
Since ![]() $\delta =1$, the isometry class of
$\delta =1$, the isometry class of ![]() $M$ is determined by
$M$ is determined by ![]() $g$ and the number
$g$ and the number ![]() $k+1$ of components of the fixed curve. (See § 3.2 for the formula for the invariants
$k+1$ of components of the fixed curve. (See § 3.2 for the formula for the invariants ![]() $g=g(M)$ and
$g=g(M)$ and ![]() $k=k(M)$.) Write
$k=k(M)$.) Write ![]() $M_{g,k}$ for the lattice with these invariants and set
$M_{g,k}$ for the lattice with these invariants and set ![]() $\Lambda _{g,k}=M_{g,k}^{\perp }$. Let
$\Lambda _{g,k}=M_{g,k}^{\perp }$. Let ![]() ${\mathcal {D}}_{\Lambda _{g,k}}={\mathcal {D}}_{\Lambda _{g,k}}^{+}+{\mathcal {D}}_{\Lambda _{g,k}}^{-}$ be the decomposition according to the type of
${\mathcal {D}}_{\Lambda _{g,k}}={\mathcal {D}}_{\Lambda _{g,k}}^{+}+{\mathcal {D}}_{\Lambda _{g,k}}^{-}$ be the decomposition according to the type of ![]() $(-2)$-vectors of
$(-2)$-vectors of ![]() $\Lambda _{g,k}$, and let
$\Lambda _{g,k}$, and let ![]() ${\mathcal {H}}_{\Lambda _{g,k}}$ be the characteristic Heegner divisor (cf. § 2). We will proceed inductively on
${\mathcal {H}}_{\Lambda _{g,k}}$ be the characteristic Heegner divisor (cf. § 2). We will proceed inductively on ![]() $k$.
$k$.
(b) We first study the series ![]() $k=0$ by a geometric approach (§ 6). Curves with vanishing theta constants are characterized by the existence of certain half-canonical bundle. By analyzing bi-anticanonical sections of Del Pezzo surfaces with such property, we prove that the support of
$k=0$ by a geometric approach (§ 6). Curves with vanishing theta constants are characterized by the existence of certain half-canonical bundle. By analyzing bi-anticanonical sections of Del Pezzo surfaces with such property, we prove that the support of ![]() ${\rm div}(J_{M_{g,0}}^{*}\chi _{g}^{8})$ on
${\rm div}(J_{M_{g,0}}^{*}\chi _{g}^{8})$ on ![]() ${\mathcal {M}}_{\Lambda _{g,0}}^{0}$ coincides with
${\mathcal {M}}_{\Lambda _{g,0}}^{0}$ coincides with ![]() ${\mathcal {H}}_{\Lambda _{g,0}}$. Hence there exist integers
${\mathcal {H}}_{\Lambda _{g,0}}$. Hence there exist integers ![]() $a_{g}, b_{g}, c_{g}\geq 0$ such that
$a_{g}, b_{g}, c_{g}\geq 0$ such that
(c) We have a natural inclusion of lattices ![]() $\Lambda _{g,k+1}\subset \Lambda _{g,k}$, which induces an inclusion of domains
$\Lambda _{g,k+1}\subset \Lambda _{g,k}$, which induces an inclusion of domains ![]() $i\colon \Omega _{\Lambda _{g,k+1}}\hookrightarrow \Omega _{\Lambda _{g,k}}$. Then we show that
$i\colon \Omega _{\Lambda _{g,k+1}}\hookrightarrow \Omega _{\Lambda _{g,k}}$. Then we show that ![]() $J_{M_{g,k}}\circ i=J_{M_{g,k+1}}$ outside a locus of codimension
$J_{M_{g,k}}\circ i=J_{M_{g,k+1}}$ outside a locus of codimension ![]() $2$, that
$2$, that ![]() $i^{*}{\mathcal {H}}_{\Lambda _{g,k}}=2{\mathcal {H}}_{\Lambda _{g,k+1}}$ and that a similar relation holds between
$i^{*}{\mathcal {H}}_{\Lambda _{g,k}}=2{\mathcal {H}}_{\Lambda _{g,k+1}}$ and that a similar relation holds between ![]() ${\mathcal {D}}_{\Lambda _{g,k}}^{\pm }$ and
${\mathcal {D}}_{\Lambda _{g,k}}^{\pm }$ and ![]() ${\mathcal {D}}_{\Lambda _{g,k+1}}^{\pm }$ (cf. §§ 2 and 3). This enables us to inductively extend (0.4) to the case
${\mathcal {D}}_{\Lambda _{g,k+1}}^{\pm }$ (cf. §§ 2 and 3). This enables us to inductively extend (0.4) to the case ![]() $k\geq 1$ (§ 8):
$k\geq 1$ (§ 8):
where ![]() $a_{g,k}, b_{g,k}, c_{g,k}$ are integers satisfying
$a_{g,k}, b_{g,k}, c_{g,k}$ are integers satisfying
By using a formula in [Reference YoshikawaYos13] and the formula [Reference Teixidor i BigasTei88] for the theta-null divisor on the moduli space of curves, we also prove the estimates ![]() $a_{g}\geq 2^{2g-1}$ and
$a_{g}\geq 2^{2g-1}$ and ![]() $b_{g}\geq 2^{4}$.
$b_{g}\geq 2^{4}$.
(d) Substituting these relations and estimates in the left-hand side of (0.3), we obtain the desired inequality when ![]() $g<10$. In the case of
$g<10$. In the case of ![]() $g=10$, an extra argument is required; see § 8. Note that
$g=10$, an extra argument is required; see § 8. Note that ![]() ${\mathcal {H}}_{\Lambda }$ vanishes if
${\mathcal {H}}_{\Lambda }$ vanishes if ![]() $r\geq 10$, which explains why the proof of Theorem 0.1 is much simpler in the range
$r\geq 10$, which explains why the proof of Theorem 0.1 is much simpler in the range ![]() $r\geq 10$,
$r\geq 10$, ![]() $(r,\delta )\not =(10,0)$ (cf. [Reference YoshikawaYos13]). As a by-product of the proof, we determine an explicit formula for the divisor of
$(r,\delta )\not =(10,0)$ (cf. [Reference YoshikawaYos13]). As a by-product of the proof, we determine an explicit formula for the divisor of ![]() $J_{M}^{*}\chi _{g}^{8}$ as a Heegner divisor on
$J_{M}^{*}\chi _{g}^{8}$ as a Heegner divisor on ![]() $\Omega _{\Lambda }^{+}$ for all
$\Omega _{\Lambda }^{+}$ for all ![]() $M$, which is a result of independent interest. See Theorem 9.13 for the details.
$M$, which is a result of independent interest. See Theorem 9.13 for the details.
This paper is organized as follows. Sections 1–5 are mainly preliminaries. In § 6 (respectively, § 7) we study the even theta characteristics of the fixed curve for ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces with
$K3$ surfaces with ![]() $\delta =1$ (respectively,
$\delta =1$ (respectively, ![]() $\delta =0$). In § 8 (respectively, § 9) we prove Theorem 0.1 when
$\delta =0$). In § 8 (respectively, § 9) we prove Theorem 0.1 when ![]() $\delta =1$ (respectively,
$\delta =1$ (respectively, ![]() $\delta =0$). In § 10 we introduce the twisted holomorphic torsion invariant
$\delta =0$). In § 10 we introduce the twisted holomorphic torsion invariant ![]() $\tau _{M}^{{\rm spin}}$ and prove Theorem 0.2. In § 11 we study an equivariant analogue of Borcherds’ conjecture.
$\tau _{M}^{{\rm spin}}$ and prove Theorem 0.2. In § 11 we study an equivariant analogue of Borcherds’ conjecture.
1. Lattices
A free ![]() $\textbf {Z}$-module of finite rank endowed with a non-degenerate, integral, symmetric bilinear form is called a lattice. The rank and signature of a lattice
$\textbf {Z}$-module of finite rank endowed with a non-degenerate, integral, symmetric bilinear form is called a lattice. The rank and signature of a lattice ![]() $L$ are denoted by
$L$ are denoted by ![]() $r(L)$ and
$r(L)$ and ![]() ${\rm sign}(L)=(b^{+}(L),b^{-}(L))$, respectively. For a lattice
${\rm sign}(L)=(b^{+}(L),b^{-}(L))$, respectively. For a lattice ![]() $L=(\textbf {Z}^{r},\langle \cdot ,\cdot \rangle )$ and an integer
$L=(\textbf {Z}^{r},\langle \cdot ,\cdot \rangle )$ and an integer ![]() $k\in \textbf {Z}\setminus \{0\}$, we define
$k\in \textbf {Z}\setminus \{0\}$, we define ![]() $L(k):=(\textbf {Z}^{r},k\langle \cdot ,\cdot \rangle )$. The group of isometries of
$L(k):=(\textbf {Z}^{r},k\langle \cdot ,\cdot \rangle )$. The group of isometries of ![]() $L$ is denoted by
$L$ is denoted by ![]() $O(L)$. The set of roots of
$O(L)$. The set of roots of ![]() $L$ is defined as
$L$ is defined as ![]() $\Delta _{L}:=\{d\in L; \langle d,d\rangle =-2\}$. For the root systems
$\Delta _{L}:=\{d\in L; \langle d,d\rangle =-2\}$. For the root systems ![]() $A_{k}$,
$A_{k}$, ![]() $D_{k}$,
$D_{k}$, ![]() $E_{k}$, the corresponding negative-definite root lattices are denoted by
$E_{k}$, the corresponding negative-definite root lattices are denoted by ![]() ${\Bbb A}_{k}$,
${\Bbb A}_{k}$, ![]() ${\Bbb D}_{k}$,
${\Bbb D}_{k}$, ![]() ${\Bbb E}_{k}$, respectively. We set
${\Bbb E}_{k}$, respectively. We set ![]() ${\Bbb A}_{1}^{+}:={\Bbb A}_{1}(-1)$, etc. The hyperbolic plane
${\Bbb A}_{1}^{+}:={\Bbb A}_{1}(-1)$, etc. The hyperbolic plane ![]() ${\Bbb U}$ is the even unimodular lattice of signature
${\Bbb U}$ is the even unimodular lattice of signature ![]() $(1,1)$.
$(1,1)$.
For an even lattice ![]() $L$, its dual lattice is denoted by
$L$, its dual lattice is denoted by ![]() $L^{\lor }$. The finite abelian group
$L^{\lor }$. The finite abelian group ![]() $A_{L}:=L^{\lor }/L$ is called the discriminant group of
$A_{L}:=L^{\lor }/L$ is called the discriminant group of ![]() $L$, which is equipped with the
$L$, which is equipped with the ![]() $\textbf {Q}/2\textbf {Z}$-valued quadratic form
$\textbf {Q}/2\textbf {Z}$-valued quadratic form ![]() $q_{L}$ called the discriminant form and the
$q_{L}$ called the discriminant form and the ![]() $\textbf {Q}/\textbf {Z}$-valued bilinear form
$\textbf {Q}/\textbf {Z}$-valued bilinear form ![]() $b_{L}$ called the discriminant bilinear form. The automorphism group of
$b_{L}$ called the discriminant bilinear form. The automorphism group of ![]() $(A_{L},q_{L})$ is denoted by
$(A_{L},q_{L})$ is denoted by ![]() $O(q_{L})$.
$O(q_{L})$.
A lattice ![]() $L$ is
$L$ is ![]() $2$-elementary if there exists
$2$-elementary if there exists ![]() $l\in \textbf {Z}_{\geq 0}$ with
$l\in \textbf {Z}_{\geq 0}$ with ![]() $A_{L}\cong (\textbf {Z}/2\textbf {Z})^{\oplus l}$. For a
$A_{L}\cong (\textbf {Z}/2\textbf {Z})^{\oplus l}$. For a ![]() $2$-elementary lattice
$2$-elementary lattice ![]() $L$, we set
$L$, we set ![]() $l(L):=\dim _{\mathbf{F}_{2}}A_{L}$. When
$l(L):=\dim _{\mathbf{F}_{2}}A_{L}$. When ![]() $L$ is an even
$L$ is an even ![]() $2$-elementary lattice, the parity of
$2$-elementary lattice, the parity of ![]() $q_{L}$ is denoted by
$q_{L}$ is denoted by ![]() $\delta (L)\in \{0,1\}$. By Nikulin [Reference NikulinNik80, Theorem 3.6.2], the isometry class of an indefinite even
$\delta (L)\in \{0,1\}$. By Nikulin [Reference NikulinNik80, Theorem 3.6.2], the isometry class of an indefinite even ![]() $2$-elementary lattice
$2$-elementary lattice ![]() $L$ is determined by the triplet
$L$ is determined by the triplet ![]() $({\rm sign}(L),l(L),\delta (L))$. For an even
$({\rm sign}(L),l(L),\delta (L))$. For an even ![]() $2$-elementary lattice
$2$-elementary lattice ![]() $L$, there is a unique element
$L$, there is a unique element ![]() $\textbf {1}_{L}\in A_{L}$, called the characteristic element, such that
$\textbf {1}_{L}\in A_{L}$, called the characteristic element, such that ![]() $b_{L}(\gamma ,\textbf {1}_{L})=q_{L}(\gamma )\mod \textbf {Z}$ for all
$b_{L}(\gamma ,\textbf {1}_{L})=q_{L}(\gamma )\mod \textbf {Z}$ for all ![]() $\gamma \in A_{L}$. Then
$\gamma \in A_{L}$. Then ![]() $g(\textbf {1}_{L})=\textbf {1}_{L}$ for all
$g(\textbf {1}_{L})=\textbf {1}_{L}$ for all ![]() $g\in O(q_{L})$. By definition,
$g\in O(q_{L})$. By definition, ![]() $\textbf {1}_{L}=0$ if and only if
$\textbf {1}_{L}=0$ if and only if ![]() $\delta (L)=0$.
$\delta (L)=0$.
The ![]() $K3$ lattice is defined as the even unimodular lattice of signature
$K3$ lattice is defined as the even unimodular lattice of signature ![]() $(3,19)$:
$(3,19)$:
It is classical that ![]() ${\Bbb L}_{K3}$ is isometric to the second integral cohomology lattice of a
${\Bbb L}_{K3}$ is isometric to the second integral cohomology lattice of a ![]() $K3$ surface. For a sublattice
$K3$ surface. For a sublattice ![]() $\Lambda \subset {\Bbb L}_{K3}$, we define
$\Lambda \subset {\Bbb L}_{K3}$, we define ![]() $\Lambda ^{\perp }:=\{l\in {\Bbb L}_{K3};\,\langle l,\Lambda \rangle =0\}$.
$\Lambda ^{\perp }:=\{l\in {\Bbb L}_{K3};\,\langle l,\Lambda \rangle =0\}$.
A primitive ![]() $2$-elementary Lorentzian sublattice of
$2$-elementary Lorentzian sublattice of ![]() ${\Bbb L}_{K3}$ isometric to
${\Bbb L}_{K3}$ isometric to ![]() ${\Bbb U}(2)\oplus {\Bbb E}_{8}(2)$ is said to be exceptional. (For the reason why this is exceptional, see § 3.2 below.) Its orthogonal complement in
${\Bbb U}(2)\oplus {\Bbb E}_{8}(2)$ is said to be exceptional. (For the reason why this is exceptional, see § 3.2 below.) Its orthogonal complement in ![]() ${\Bbb L}_{K3}$, namely
${\Bbb L}_{K3}$, namely ![]() ${\Bbb U}\oplus {\Bbb U}(2)\oplus {\Bbb E}_{8}(2)$, is also said to be exceptional.
${\Bbb U}\oplus {\Bbb U}(2)\oplus {\Bbb E}_{8}(2)$, is also said to be exceptional.
Proposition 1.1 The isometry classes of primitive ![]() $2$-elementary sublattices
$2$-elementary sublattices ![]() $\Lambda$ of
$\Lambda$ of ![]() ${\Bbb L}_{K3}$ with signature
${\Bbb L}_{K3}$ with signature ![]() $(2,r(\Lambda )-2)$ consist of the
$(2,r(\Lambda )-2)$ consist of the ![]() $75$ classes in Table 1, where
$75$ classes in Table 1, where
Table 1. Primitive ![]() $2$-elementary sublattices of
$2$-elementary sublattices of ![]() ${\Bbb L}_{K3}$ with
${\Bbb L}_{K3}$ with ![]() $b^{+}=2$.
$b^{+}=2$.

Proof. See, for example, [Reference Finashin and KharlamovFK08, Tables 2 and 3, pp. 705–706]. Notice that the representative of each isometry class is not necessarily identical to the one in [Reference Finashin and KharlamovFK08, Tables 2 and 3, pp. 705–706].
For a primitive ![]() $2$-elementary Lorentzian sublattice
$2$-elementary Lorentzian sublattice ![]() $M\subset {\Bbb L}_{K3}$ and a root
$M\subset {\Bbb L}_{K3}$ and a root ![]() $d\in \Delta _{M^{\perp }}$, the smallest sublattice of
$d\in \Delta _{M^{\perp }}$, the smallest sublattice of ![]() ${\Bbb L}_{K3}$ containing
${\Bbb L}_{K3}$ containing ![]() $M$ and
$M$ and ![]() $d$ is given by
$d$ is given by
Then ![]() $[M\perp d]$ is again a primitive
$[M\perp d]$ is again a primitive ![]() $2$-elementary Lorentzian sublattice of
$2$-elementary Lorentzian sublattice of ![]() ${\Bbb L}_{K3}$ with
${\Bbb L}_{K3}$ with ![]() $[M\perp d]^{\perp }=M^{\perp }\cap d^{\perp }$.
$[M\perp d]^{\perp }=M^{\perp }\cap d^{\perp }$.
2. Domains of type IV and modular varieties of orthogonal type
In this section ![]() $\Lambda$ is assumed to be an even
$\Lambda$ is assumed to be an even ![]() $2$-elementary lattice with
$2$-elementary lattice with ![]() ${\rm sign}(\Lambda )=(2,r(\Lambda )-2)$. We define the complex manifold
${\rm sign}(\Lambda )=(2,r(\Lambda )-2)$. We define the complex manifold ![]() $\Omega _{\Lambda }$ with projective
$\Omega _{\Lambda }$ with projective ![]() $O(\Lambda )$-action by
$O(\Lambda )$-action by
Then ![]() $\Omega _{\Lambda }$ has two connected components
$\Omega _{\Lambda }$ has two connected components ![]() $\Omega _{\Lambda }^{\pm }$, each of which is isomorphic to a bounded symmetric domain of type IV of dimension
$\Omega _{\Lambda }^{\pm }$, each of which is isomorphic to a bounded symmetric domain of type IV of dimension ![]() $r(\Lambda )-2$. The orthogonal modular variety
$r(\Lambda )-2$. The orthogonal modular variety ![]() ${\mathcal {M}}_{\Lambda }$ associated to
${\mathcal {M}}_{\Lambda }$ associated to ![]() $\Lambda$ is defined as the analytic space
$\Lambda$ is defined as the analytic space
where
We denote by ![]() ${\mathcal {M}}_{\Lambda }^{*}$ the Baily–Borel–Satake compactification of
${\mathcal {M}}_{\Lambda }^{*}$ the Baily–Borel–Satake compactification of ![]() ${\mathcal {M}}_{\Lambda }$, which is an irreducible normal projective variety of dimension
${\mathcal {M}}_{\Lambda }$, which is an irreducible normal projective variety of dimension ![]() $r(\Lambda )-2$ with
$r(\Lambda )-2$ with ![]() $\dim ({\mathcal {M}}_{\Lambda }^{*}\setminus {\mathcal {M}}_{\Lambda })\leq 1$.
$\dim ({\mathcal {M}}_{\Lambda }^{*}\setminus {\mathcal {M}}_{\Lambda })\leq 1$.
2.1 Discriminant locus
For ![]() $\lambda \in \Lambda$ with
$\lambda \in \Lambda$ with ![]() $\langle \lambda ,\lambda \rangle <0$, we define
$\langle \lambda ,\lambda \rangle <0$, we define
Then ![]() $H_{\lambda }$ is a non-zero divisor on
$H_{\lambda }$ is a non-zero divisor on ![]() $\Omega _{\Lambda }$. For any root
$\Omega _{\Lambda }$. For any root ![]() $d\in \Delta _{\Lambda }$, we have the relation
$d\in \Delta _{\Lambda }$, we have the relation
The discriminant locus of ![]() $\Omega _{\Lambda }$ is the reduced divisor of
$\Omega _{\Lambda }$ is the reduced divisor of ![]() $\Omega _{\Lambda }$ defined by
$\Omega _{\Lambda }$ defined by
We define the ![]() $O(\Lambda )$-invariant Zariski open subset
$O(\Lambda )$-invariant Zariski open subset ![]() $\Omega _{\Lambda }^{0}$ of
$\Omega _{\Lambda }^{0}$ of ![]() $\Omega _{\Lambda }$ by
$\Omega _{\Lambda }$ by
We set
2.2 Some subloci of  ${\mathcal {D}}_{\Lambda }$
${\mathcal {D}}_{\Lambda }$
We define the decomposition ![]() $\Delta _{\Lambda }=\Delta ^{+}_{\Lambda }\amalg \Delta ^{-}_{\Lambda }$ by
$\Delta _{\Lambda }=\Delta ^{+}_{\Lambda }\amalg \Delta ^{-}_{\Lambda }$ by
Then ![]() $\Delta ^{\pm }_{\Lambda }$ are
$\Delta ^{\pm }_{\Lambda }$ are ![]() $O(\Lambda )$-invariant. We define the
$O(\Lambda )$-invariant. We define the ![]() $O(\Lambda )$-invariant reduced divisors
$O(\Lambda )$-invariant reduced divisors ![]() ${\mathcal {D}}^{\pm }_{\Lambda }$ on
${\mathcal {D}}^{\pm }_{\Lambda }$ on ![]() $\Omega _{\Lambda }$ and the corresponding divisors
$\Omega _{\Lambda }$ and the corresponding divisors ![]() $\bar {\mathcal {D}}^{\pm }_{\Lambda }$ on
$\bar {\mathcal {D}}^{\pm }_{\Lambda }$ on ![]() ${\mathcal {M}}_{\Lambda }$ by
${\mathcal {M}}_{\Lambda }$ by
Proposition 2.1 Let ![]() $d\in \Delta _{\Lambda }^{+}$. Let
$d\in \Delta _{\Lambda }^{+}$. Let ![]() $i\colon \Omega _{\Lambda \cap d^{\perp }}=H_{d}\hookrightarrow \Omega _{\Lambda }$ be the inclusion. Then the following equalities of divisors on
$i\colon \Omega _{\Lambda \cap d^{\perp }}=H_{d}\hookrightarrow \Omega _{\Lambda }$ be the inclusion. Then the following equalities of divisors on ![]() $\Omega _{\Lambda \cap d^{\perp }}$ hold:
$\Omega _{\Lambda \cap d^{\perp }}$ hold:
Proof. Let ![]() $\delta \in \Delta _{\Lambda }\setminus \{\pm d\}$. Then
$\delta \in \Delta _{\Lambda }\setminus \{\pm d\}$. Then ![]() $H_{d}\cap H_{\delta }\not =\emptyset$ if and only if
$H_{d}\cap H_{\delta }\not =\emptyset$ if and only if ![]() $L:=\textbf {Z}d+\textbf {Z}\delta$ is negative-definite. Since the Gram matrix of
$L:=\textbf {Z}d+\textbf {Z}\delta$ is negative-definite. Since the Gram matrix of ![]() $L$ with respect to the basis
$L$ with respect to the basis ![]() $\{d,\delta \}$ is given by
$\{d,\delta \}$ is given by ![]() $-2\binom {1\,a}{a\,1}$ where
$-2\binom {1\,a}{a\,1}$ where ![]() $a=-\langle \delta ,d/2\rangle \in \textbf {Z}$, we conclude that
$a=-\langle \delta ,d/2\rangle \in \textbf {Z}$, we conclude that ![]() $H_{d}\cap H_{\delta }\not =\emptyset$ if and only if
$H_{d}\cap H_{\delta }\not =\emptyset$ if and only if ![]() $a=0$, that is,
$a=0$, that is, ![]() $\delta \in \Delta _{\Lambda }\cap d^{\perp }=\Delta _{\Lambda \cap d^{\perp }}$. Since
$\delta \in \Delta _{\Lambda }\cap d^{\perp }=\Delta _{\Lambda \cap d^{\perp }}$. Since ![]() $\Delta _{\Lambda }^{\pm }\cap d^{\perp }=\Delta _{\Lambda \cap d^{\perp }}^{\pm }$, we get
$\Delta _{\Lambda }^{\pm }\cap d^{\perp }=\Delta _{\Lambda \cap d^{\perp }}^{\pm }$, we get
 \begin{gather*} i^{*}({\mathcal{D}}_{\Lambda}^{+}-H_{d}) = \sum_{\delta\in(\Delta_{\Lambda}^{+}\setminus\{\pm d\})/\pm1}i^{*}H_{\delta} = \sum_{\delta\in\Delta_{\Lambda}^{+}\cap d^{\perp}/\pm1}i^{*}H_{\delta} = \sum_{\delta\in\Delta_{\Lambda\cap d^{\perp}}^{+}/\pm1}H_{\delta} = {\mathcal{D}}_{\Lambda\cap d^{\perp}}^{+},\\ i^{*}{\mathcal{D}}_{\Lambda}^{-} = \sum_{\delta\in\Delta_{\Lambda}^{-}/\pm1}i^{*}H_{\delta} = \sum_{\delta\in\Delta_{\Lambda}^{-}\cap d^{\perp}/\pm1}i^{*}H_{\delta} = \sum_{\delta\in\Delta_{\Lambda\cap d^{\perp}}^{-}/\pm1}H_{\delta} = {\mathcal{D}}_{\Lambda\cap d^{\perp}}^{-}. \end{gather*}
\begin{gather*} i^{*}({\mathcal{D}}_{\Lambda}^{+}-H_{d}) = \sum_{\delta\in(\Delta_{\Lambda}^{+}\setminus\{\pm d\})/\pm1}i^{*}H_{\delta} = \sum_{\delta\in\Delta_{\Lambda}^{+}\cap d^{\perp}/\pm1}i^{*}H_{\delta} = \sum_{\delta\in\Delta_{\Lambda\cap d^{\perp}}^{+}/\pm1}H_{\delta} = {\mathcal{D}}_{\Lambda\cap d^{\perp}}^{+},\\ i^{*}{\mathcal{D}}_{\Lambda}^{-} = \sum_{\delta\in\Delta_{\Lambda}^{-}/\pm1}i^{*}H_{\delta} = \sum_{\delta\in\Delta_{\Lambda}^{-}\cap d^{\perp}/\pm1}i^{*}H_{\delta} = \sum_{\delta\in\Delta_{\Lambda\cap d^{\perp}}^{-}/\pm1}H_{\delta} = {\mathcal{D}}_{\Lambda\cap d^{\perp}}^{-}. \end{gather*}This proves the result.
For ![]() $d\in \Delta _{\Lambda }$, we define a non-empty Zariski open subset
$d\in \Delta _{\Lambda }$, we define a non-empty Zariski open subset ![]() $H^{0}_{d}\subset H_{d}$ by
$H^{0}_{d}\subset H_{d}$ by
 \[ H_{d}^{0}:=H_{d}\left\backslash \bigcup_{\delta\in\Delta_{\Lambda}\setminus\{\pm d\}}H_{\delta}.\right. \]
\[ H_{d}^{0}:=H_{d}\left\backslash \bigcup_{\delta\in\Delta_{\Lambda}\setminus\{\pm d\}}H_{\delta}.\right. \]We set
Then ![]() $\Omega _{\Lambda }^{0}\amalg {\mathcal {D}}_{\Lambda }^{0}$ is a Zariski open subset of
$\Omega _{\Lambda }^{0}\amalg {\mathcal {D}}_{\Lambda }^{0}$ is a Zariski open subset of ![]() $\Omega _{\Lambda }$, whose complement has codimension at least
$\Omega _{\Lambda }$, whose complement has codimension at least ![]() $2$ when
$2$ when ![]() $r(\Lambda )\geq 4$ and is empty when
$r(\Lambda )\geq 4$ and is empty when ![]() $r(\Lambda )\leq 3$.
$r(\Lambda )\leq 3$.
2.3 Characteristic Heegner divisor
Set
We define the characteristic Heegner divisor of ![]() $\Omega _{\Lambda }$ as the reduced divisor
$\Omega _{\Lambda }$ as the reduced divisor
where ![]() $[\lambda ]:=\lambda +\Lambda \in A_{\Lambda }$. Since
$[\lambda ]:=\lambda +\Lambda \in A_{\Lambda }$. Since ![]() $\textbf {1}_{\Lambda }$ is
$\textbf {1}_{\Lambda }$ is ![]() $O(q_{\Lambda })$-invariant,
$O(q_{\Lambda })$-invariant, ![]() ${\mathcal {H}}_{\Lambda }$ is
${\mathcal {H}}_{\Lambda }$ is ![]() $O(\Lambda )$-invariant. Since
$O(\Lambda )$-invariant. Since ![]() $\varepsilon _{\Lambda }\geq 0$ when
$\varepsilon _{\Lambda }\geq 0$ when ![]() $r(\Lambda )\leq 12$, we get
$r(\Lambda )\leq 12$, we get ![]() ${\mathcal {H}}_{\Lambda }=0$ if
${\mathcal {H}}_{\Lambda }=0$ if ![]() $r(\Lambda )\leq 12$.
$r(\Lambda )\leq 12$.
Proposition 2.2 Let ![]() $d\in \Delta _{\Lambda }^{+}$. Let
$d\in \Delta _{\Lambda }^{+}$. Let ![]() $i\colon \Omega _{\Lambda \cap d^{\perp }}=H_{d}\hookrightarrow \Omega _{\Lambda }$ be the inclusion. Then the following equality of divisors on
$i\colon \Omega _{\Lambda \cap d^{\perp }}=H_{d}\hookrightarrow \Omega _{\Lambda }$ be the inclusion. Then the following equality of divisors on ![]() $\Omega _{\Lambda \cap d^{\perp }}$ holds:
$\Omega _{\Lambda \cap d^{\perp }}$ holds:
Proof. Since ![]() $r(\Lambda )\leq 21$, we get
$r(\Lambda )\leq 21$, we get ![]() $\varepsilon _{\Lambda }\geq -\frac {9}{2}$. Set
$\varepsilon _{\Lambda }\geq -\frac {9}{2}$. Set ![]() $\Lambda ':=\Lambda \cap d^{\perp }$. Since
$\Lambda ':=\Lambda \cap d^{\perp }$. Since ![]() $d\in \Delta _{\Lambda }^{+}$, we deduce from [Reference Finashin and KharlamovFK08, Proposition 3.1] that
$d\in \Delta _{\Lambda }^{+}$, we deduce from [Reference Finashin and KharlamovFK08, Proposition 3.1] that ![]() $\Lambda$ and
$\Lambda$ and ![]() $\Lambda '\oplus \textbf {Z}d$ have the same invariants
$\Lambda '\oplus \textbf {Z}d$ have the same invariants ![]() $(r,l,\delta )$. Hence we get the orthogonal decomposition
$(r,l,\delta )$. Hence we get the orthogonal decomposition ![]() $\Lambda =\Lambda '\oplus \textbf {Z}d$. Let
$\Lambda =\Lambda '\oplus \textbf {Z}d$. Let ![]() $\lambda \in \Lambda ^{\lor }$ be such that
$\lambda \in \Lambda ^{\lor }$ be such that ![]() $\lambda ^{2}=\varepsilon _{\Lambda }$ and
$\lambda ^{2}=\varepsilon _{\Lambda }$ and ![]() $[\lambda ]=\textbf {1}_{\Lambda }$. Then we can write
$[\lambda ]=\textbf {1}_{\Lambda }$. Then we can write ![]() $\lambda =\lambda '+a(d/2)$, where
$\lambda =\lambda '+a(d/2)$, where ![]() $\lambda '\in (\Lambda ')^{\lor }$ and
$\lambda '\in (\Lambda ')^{\lor }$ and ![]() $a=-\langle \lambda ,d\rangle \in \textbf {Z}$. Since
$a=-\langle \lambda ,d\rangle \in \textbf {Z}$. Since ![]() $[\lambda ]=\textbf {1}_{\Lambda }$, we get
$[\lambda ]=\textbf {1}_{\Lambda }$, we get ![]() $a\equiv 1\bmod 2$. Hence
$a\equiv 1\bmod 2$. Hence ![]() $a=2k+1$ for some
$a=2k+1$ for some ![]() $k\in \textbf {Z}$ and
$k\in \textbf {Z}$ and ![]() $\lambda '\in \textbf {1}_{\Lambda '}$. Since
$\lambda '\in \textbf {1}_{\Lambda '}$. Since ![]() $H_{\lambda '}\not =\emptyset$ if and only if
$H_{\lambda '}\not =\emptyset$ if and only if ![]() $(\lambda ')^{2}<0$, we get
$(\lambda ')^{2}<0$, we get ![]() $i^{*}H_{\lambda }=H_{\lambda '}\not =\emptyset$ if and only if
$i^{*}H_{\lambda }=H_{\lambda '}\not =\emptyset$ if and only if ![]() $0>(\lambda ')^{2}=\lambda ^{2}+a^{2}/2=(\varepsilon _{\Lambda }+\frac {1}{2})+2k(k+1)$. Since
$0>(\lambda ')^{2}=\lambda ^{2}+a^{2}/2=(\varepsilon _{\Lambda }+\frac {1}{2})+2k(k+1)$. Since ![]() $\varepsilon _{\Lambda }\geq -\frac {9}{2}$ and hence
$\varepsilon _{\Lambda }\geq -\frac {9}{2}$ and hence ![]() $-2\leq ({-1-\sqrt {-2\varepsilon _{\Lambda }}})/{2}< ({-1+\sqrt {-2\varepsilon _{\Lambda }}})/{2}\leq 1$, we see that
$-2\leq ({-1-\sqrt {-2\varepsilon _{\Lambda }}})/{2}< ({-1+\sqrt {-2\varepsilon _{\Lambda }}})/{2}\leq 1$, we see that ![]() $(\varepsilon _{\Lambda }+\frac {1}{2})+2k(k+1)<0$ if and only if
$(\varepsilon _{\Lambda }+\frac {1}{2})+2k(k+1)<0$ if and only if ![]() $k=0,-1$. This proves that
$k=0,-1$. This proves that
When ![]() $\lambda =\lambda '\pm (d/2)$, we get
$\lambda =\lambda '\pm (d/2)$, we get ![]() $(\lambda ')^{2}=\varepsilon _{\Lambda }+\frac {1}{2}=\varepsilon _{\Lambda '}$. This, together with (2.2), yields that
$(\lambda ')^{2}=\varepsilon _{\Lambda }+\frac {1}{2}=\varepsilon _{\Lambda '}$. This, together with (2.2), yields that
 \begin{align*} i^{*}{\mathcal{H}}_{\Lambda} &= \sum_{\lambda\in\Lambda^{\lor}/\pm1, \lambda^{2}=\varepsilon_{\Lambda}, [\lambda]=\textbf{1}_{\Lambda}}i^{*}H_{\lambda} = \sum_{\lambda'\in(\Lambda')^{\lor}/\pm1, (\lambda')^{2}=\varepsilon_{\Lambda'}, [\lambda']=\textbf{1}_{\Lambda'}}i^{*}H_{\lambda'\pm(d/2)}\\ &= 2\sum_{\lambda'\in(\Lambda')^{\lor}/\pm1, (\lambda')^{2}=\varepsilon_{\Lambda'}, [\lambda']=\textbf{1}_{\Lambda'}}H_{\lambda'} = 2 {\mathcal{H}}_{\Lambda'}. \end{align*}
\begin{align*} i^{*}{\mathcal{H}}_{\Lambda} &= \sum_{\lambda\in\Lambda^{\lor}/\pm1, \lambda^{2}=\varepsilon_{\Lambda}, [\lambda]=\textbf{1}_{\Lambda}}i^{*}H_{\lambda} = \sum_{\lambda'\in(\Lambda')^{\lor}/\pm1, (\lambda')^{2}=\varepsilon_{\Lambda'}, [\lambda']=\textbf{1}_{\Lambda'}}i^{*}H_{\lambda'\pm(d/2)}\\ &= 2\sum_{\lambda'\in(\Lambda')^{\lor}/\pm1, (\lambda')^{2}=\varepsilon_{\Lambda'}, [\lambda']=\textbf{1}_{\Lambda'}}H_{\lambda'} = 2 {\mathcal{H}}_{\Lambda'}. \end{align*}This proves the proposition.
3.  $2$-elementary
$2$-elementary  $K3$ surfaces and the Torelli map
$K3$ surfaces and the Torelli map
3.1  $2$-elementary
$2$-elementary  $K3$ surfaces
$K3$ surfaces
A ![]() $K3$ surface
$K3$ surface ![]() $X$ equipped with a holomorphic involution
$X$ equipped with a holomorphic involution ![]() $\iota \colon X\to X$ is called a
$\iota \colon X\to X$ is called a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface if
$K3$ surface if ![]() $\iota$ is anti-symplectic:
$\iota$ is anti-symplectic:
The possible deformation types of ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces were determined by Nikulin (see [Reference Alexeev and NikulinAN06, § 2.3] and the references therein). Let
$K3$ surfaces were determined by Nikulin (see [Reference Alexeev and NikulinAN06, § 2.3] and the references therein). Let ![]() $\alpha \colon H^{2}(X,\textbf {Z})\cong {\Bbb L}_{K3}$ be an isometry of lattices. Set
$\alpha \colon H^{2}(X,\textbf {Z})\cong {\Bbb L}_{K3}$ be an isometry of lattices. Set ![]() $H^{2}(X,\textbf {Z})_{\pm }:=\{l\in H^{2}(X,\textbf {Z});\,\iota ^{*}l=\pm l\}$ and
$H^{2}(X,\textbf {Z})_{\pm }:=\{l\in H^{2}(X,\textbf {Z});\,\iota ^{*}l=\pm l\}$ and
Then ![]() $M\subset {\Bbb L}_{K3}$ must be a primitive
$M\subset {\Bbb L}_{K3}$ must be a primitive ![]() $2$-elementary Lorentzian sublattice. Conversely, for any primitive
$2$-elementary Lorentzian sublattice. Conversely, for any primitive ![]() $2$-elementary Lorentzian sublattice
$2$-elementary Lorentzian sublattice ![]() $M\subset {\Bbb L}_{K3}$, there exists a
$M\subset {\Bbb L}_{K3}$, there exists a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface with (3.2). For a
$K3$ surface with (3.2). For a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface
$K3$ surface ![]() $(X,\iota )$, the isometry class of
$(X,\iota )$, the isometry class of ![]() $H^{2}(X,\textbf {Z})_{+}$ is called the type of
$H^{2}(X,\textbf {Z})_{+}$ is called the type of ![]() $(X,\iota )$. By an abuse of notation, the sublattice itself
$(X,\iota )$. By an abuse of notation, the sublattice itself ![]() $\alpha (H^{2}(X,\textbf {Z})_{+})\subset {\Bbb L}_{K3}$ is also called the type of
$\alpha (H^{2}(X,\textbf {Z})_{+})\subset {\Bbb L}_{K3}$ is also called the type of ![]() $(X,\iota )$. Then there is a one-to-one correspondence between the deformation types of
$(X,\iota )$. Then there is a one-to-one correspondence between the deformation types of ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces and the triplets
$K3$ surfaces and the triplets ![]() $(r,l,\delta )$. Since the latter consists of
$(r,l,\delta )$. Since the latter consists of ![]() $75$ points, there exist
$75$ points, there exist ![]() $75$ mutually distinct deformation types of
$75$ mutually distinct deformation types of ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces. For a given primitive
$K3$ surfaces. For a given primitive ![]() $2$-elementary Lorentzian sublattice
$2$-elementary Lorentzian sublattice ![]() $M\subset {\Bbb L}_{K3}$, the moduli space of
$M\subset {\Bbb L}_{K3}$, the moduli space of ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces of type
$K3$ surfaces of type ![]() $M$ is given as follows.
$M$ is given as follows.
Let ![]() $(X,\iota )$ be a
$(X,\iota )$ be a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface of type
$K3$ surface of type ![]() $M$ and let
$M$ and let ![]() $\alpha \colon H^{2}(X,\textbf {Z})\cong {\Bbb L}_{K3}$ be an isometry satisfying (3.2). Since
$\alpha \colon H^{2}(X,\textbf {Z})\cong {\Bbb L}_{K3}$ be an isometry satisfying (3.2). Since ![]() $H^{2,0}(X,\textbf {C})\subset H^{2}(X,\textbf {Z})_{-}\otimes \textbf {C}$ by (3.1), we get
$H^{2,0}(X,\textbf {C})\subset H^{2}(X,\textbf {Z})_{-}\otimes \textbf {C}$ by (3.1), we get
Its ![]() $O(\Lambda )$-orbit is called the Griffiths period of
$O(\Lambda )$-orbit is called the Griffiths period of ![]() $(X,\iota )$ and is denoted by
$(X,\iota )$ and is denoted by
By [Reference YoshikawaYos04, Theorem 1.8] and [Reference YoshikawaYos13, Proposition 11.2], the coarse moduli space of ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces of type
$K3$ surfaces of type ![]() $M$ is isomorphic to
$M$ is isomorphic to ![]() ${\mathcal {M}}_{\Lambda }^{0}$ via the period map
${\mathcal {M}}_{\Lambda }^{0}$ via the period map ![]() $\bar {\pi }_{M}$. In the rest of this paper we identify the point
$\bar {\pi }_{M}$. In the rest of this paper we identify the point ![]() $\bar {\pi }_{M}(X,\iota )\in {\mathcal {M}}_{\Lambda }^{0}$ with the isomorphism class of
$\bar {\pi }_{M}(X,\iota )\in {\mathcal {M}}_{\Lambda }^{0}$ with the isomorphism class of ![]() $(X,\iota )$.
$(X,\iota )$.
3.2 The Torelli map for  $2$-elementary
$2$-elementary  $K3$ surfaces
$K3$ surfaces
3.2.1 The set of fixed points
For a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface
$K3$ surface ![]() $(X,\iota )$ of type
$(X,\iota )$ of type ![]() $M$, set
$M$, set
Then ![]() $X^{\iota }=\emptyset$ if and only if
$X^{\iota }=\emptyset$ if and only if ![]() $M$ is exceptional, that is,
$M$ is exceptional, that is, ![]() $M\cong {\Bbb U}(2)\oplus {\Bbb E}_{8}(2)$. In this case, the quotient
$M\cong {\Bbb U}(2)\oplus {\Bbb E}_{8}(2)$. In this case, the quotient ![]() $X/\iota$ is an Enriques surface and
$X/\iota$ is an Enriques surface and ![]() $(X,\iota )$ is the universal covering of an Enriques surface endowed with the non-trivial covering transformation. When
$(X,\iota )$ is the universal covering of an Enriques surface endowed with the non-trivial covering transformation. When ![]() $M$ is non-exceptional, by Nikulin [Reference NikulinNik83, Theorem 4.2.2], we have
$M$ is non-exceptional, by Nikulin [Reference NikulinNik83, Theorem 4.2.2], we have
for ![]() $M\not \cong {\Bbb U}(N)\oplus {\Bbb E}_{8}(2)$
$M\not \cong {\Bbb U}(N)\oplus {\Bbb E}_{8}(2)$ ![]() $(N=1,2)$ and we have
$(N=1,2)$ and we have ![]() $X^{\iota }=C_{1}^{(1)}\amalg C_{2}^{(1)}$ for
$X^{\iota }=C_{1}^{(1)}\amalg C_{2}^{(1)}$ for ![]() $M\cong {\Bbb U}\oplus {\Bbb E}_{8}(2)$, where
$M\cong {\Bbb U}\oplus {\Bbb E}_{8}(2)$, where ![]() $C^{(g)}$ is a projective curve of genus
$C^{(g)}$ is a projective curve of genus ![]() $g$ and
$g$ and ![]() $E_{i}\cong \mathbf{P}^{1}$ and
$E_{i}\cong \mathbf{P}^{1}$ and
Since ![]() $r(\Lambda )=22-r(M)$ and
$r(\Lambda )=22-r(M)$ and ![]() $l(\Lambda )=l(M)$, we have the relations
$l(\Lambda )=l(M)$, we have the relations
As we defined ![]() $g(\Lambda )=(r(\Lambda )-l(\Lambda ))/2$ in Proposition 1.1, we have
$g(\Lambda )=(r(\Lambda )-l(\Lambda ))/2$ in Proposition 1.1, we have ![]() $g(M)=g(\Lambda )$. Notice that, when
$g(M)=g(\Lambda )$. Notice that, when ![]() $M\cong {\Bbb U}(2)\oplus {\Bbb E}_{8}(2)$ and hence
$M\cong {\Bbb U}(2)\oplus {\Bbb E}_{8}(2)$ and hence ![]() $X^{\iota }$ is empty,
$X^{\iota }$ is empty, ![]() $g(M)=g(\Lambda )=1$ has no geometric meaning.
$g(M)=g(\Lambda )=1$ has no geometric meaning.
3.2.2 The Torelli map
For ![]() $g\geq 0$, let
$g\geq 0$, let ![]() ${\frak S}_{g}$ be the Siegel upper half-space of degree
${\frak S}_{g}$ be the Siegel upper half-space of degree ![]() $g$ and let
$g$ and let ![]() ${\rm Sp}_{2g}(\textbf {Z})$ be the symplectic group of degree
${\rm Sp}_{2g}(\textbf {Z})$ be the symplectic group of degree ![]() $2g$ over
$2g$ over ![]() $\textbf {Z}$. We define
$\textbf {Z}$. We define
The Satake compactification of ![]() ${\mathcal {A}}_{g}$ is denoted by
${\mathcal {A}}_{g}$ is denoted by ![]() ${\mathcal {A}}_{g}^{*}$.
${\mathcal {A}}_{g}^{*}$.
For a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface
$K3$ surface ![]() $(X,\iota )$ of type
$(X,\iota )$ of type ![]() $M$, the period of
$M$, the period of ![]() $X^{\iota }$ is denoted by
$X^{\iota }$ is denoted by ![]() $\Omega (X^{\iota })\in {\mathcal {A}}_{g(M)}$. We define a map
$\Omega (X^{\iota })\in {\mathcal {A}}_{g(M)}$. We define a map ![]() $\bar {J}_{M}^{0}\colon {\mathcal {M}}_{\Lambda }^{0}\to {\mathcal {A}}_{g(M)}$ by
$\bar {J}_{M}^{0}\colon {\mathcal {M}}_{\Lambda }^{0}\to {\mathcal {A}}_{g(M)}$ by
Let ![]() $\Pi _{\Lambda }\colon \Omega _{\Lambda }\to {\mathcal {M}}_{\Lambda }$ be the projection. The Torelli map is the
$\Pi _{\Lambda }\colon \Omega _{\Lambda }\to {\mathcal {M}}_{\Lambda }$ be the projection. The Torelli map is the ![]() $O(\Lambda )$-equivariant holomorphic map
$O(\Lambda )$-equivariant holomorphic map ![]() $J_{M}^{0}\colon \Omega _{\Lambda }^{0}\to {\mathcal {A}}_{g(M)}$ defined by
$J_{M}^{0}\colon \Omega _{\Lambda }^{0}\to {\mathcal {A}}_{g(M)}$ defined by
In Theorem 3.3 below, we will extend ![]() $J_{M}^{0}$ to a certain Zariski open subset of
$J_{M}^{0}$ to a certain Zariski open subset of ![]() $\Omega _{\Lambda }$ containing
$\Omega _{\Lambda }$ containing ![]() $\Omega _{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{0}$ and prove its compatibility with respect to the inclusion
$\Omega _{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{0}$ and prove its compatibility with respect to the inclusion ![]() $\Omega _{\Lambda \cap d^{\perp }}=H_{d}\hookrightarrow \Omega _{\Lambda }$ for
$\Omega _{\Lambda \cap d^{\perp }}=H_{d}\hookrightarrow \Omega _{\Lambda }$ for ![]() $d\in \Delta _{\Lambda }$. For this, we introduce a stratification of
$d\in \Delta _{\Lambda }$. For this, we introduce a stratification of ![]() $\Omega _{\Lambda }$.
$\Omega _{\Lambda }$.
3.2.3 A stratification of  $\Omega _{\Lambda }$
$\Omega _{\Lambda }$
For a primitive sublattice ![]() $L\subset \Lambda$ generated by
$L\subset \Lambda$ generated by ![]() $\Delta _{L}$, we define
$\Delta _{L}$, we define
 \[ H_{L}:=\bigcap_{d\in\Delta_{L}}H_{d}, \quad H_{L}^{0}:=H_{L}\left\backslash\bigcup_{\delta\in\Delta_{\Lambda}\setminus\Delta_{L}}H_{\delta}.\right. \]
\[ H_{L}:=\bigcap_{d\in\Delta_{L}}H_{d}, \quad H_{L}^{0}:=H_{L}\left\backslash\bigcup_{\delta\in\Delta_{\Lambda}\setminus\Delta_{L}}H_{\delta}.\right. \]
Then ![]() $H_{L}\not =\emptyset$ if and only if
$H_{L}\not =\emptyset$ if and only if ![]() $L$ is negative-definite, that is,
$L$ is negative-definite, that is, ![]() $L$ is a root lattice. If
$L$ is a root lattice. If ![]() $H_{L}\not =\emptyset$, then
$H_{L}\not =\emptyset$, then ![]() $H_{L}^{0}$ is a non-empty dense Zariski open subset of
$H_{L}^{0}$ is a non-empty dense Zariski open subset of ![]() $H_{L}$. By definition, it is obvious that if
$H_{L}$. By definition, it is obvious that if ![]() $r(L)=r(L')$ and
$r(L)=r(L')$ and ![]() $L\not =L'$, then
$L\not =L'$, then ![]() $H_{L}^{0}\cap H_{L'}^{0}=\emptyset$. Set
$H_{L}^{0}\cap H_{L'}^{0}=\emptyset$. Set
where ![]() $L$ runs over the set of all primitive root sublattices of
$L$ runs over the set of all primitive root sublattices of ![]() $\Lambda$ of rank
$\Lambda$ of rank ![]() $k$. Then
$k$. Then ![]() $\Omega _{\Lambda }^{\geq k}$ is a Zariski closed subset of
$\Omega _{\Lambda }^{\geq k}$ is a Zariski closed subset of ![]() $\Omega _{\Lambda }$ of pure codimension
$\Omega _{\Lambda }$ of pure codimension ![]() $k$, and
$k$, and ![]() $\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq k+1}$ is a dense Zariski open subset of
$\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq k+1}$ is a dense Zariski open subset of ![]() $\Omega _{\Lambda }$, whose complement has codimension
$\Omega _{\Lambda }$, whose complement has codimension ![]() $k+1$. We have
$k+1$. We have
For a root lattice ![]() ${\Bbb K}$, let
${\Bbb K}$, let ![]() ${\Bbb K}(\Lambda )$ be the set of primitive sublattices of
${\Bbb K}(\Lambda )$ be the set of primitive sublattices of ![]() $\Lambda$ isometric to
$\Lambda$ isometric to ![]() ${\Bbb K}$. Since a root lattice of rank
${\Bbb K}$. Since a root lattice of rank ![]() $2$ is either
$2$ is either ![]() ${\Bbb A}_{1}^{\oplus 2}$ or
${\Bbb A}_{1}^{\oplus 2}$ or ![]() ${\Bbb A}_{2}$, we have
${\Bbb A}_{2}$, we have
 \[ \Omega_{\Lambda}^{\geq2}=\Bigg(\bigcup_{L\in{\Bbb A}_{1}^{\oplus2}(\Lambda)}H_{L}\Bigg)\cup\Bigg(\bigcup_{L\in{\Bbb A}_{2}(\Lambda)}H_{L}\Bigg). \]
\[ \Omega_{\Lambda}^{\geq2}=\Bigg(\bigcup_{L\in{\Bbb A}_{1}^{\oplus2}(\Lambda)}H_{L}\Bigg)\cup\Bigg(\bigcup_{L\in{\Bbb A}_{2}(\Lambda)}H_{L}\Bigg). \]We set
Then ![]() ${\mathcal {D}}_{\Lambda }^{1,+}\amalg {\mathcal {D}}_{\Lambda }^{1,-}=\Omega _{\Lambda }^{2}$ and we have the stratification
${\mathcal {D}}_{\Lambda }^{1,+}\amalg {\mathcal {D}}_{\Lambda }^{1,-}=\Omega _{\Lambda }^{2}$ and we have the stratification
such that ![]() ${\mathcal {D}}_{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}={\mathcal {D}}_{\Lambda }^{0}\amalg {\mathcal {D}}_{\Lambda }^{1,+}\amalg {\mathcal {D}}_{\Lambda }^{1,-}$ is a divisor of
${\mathcal {D}}_{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}={\mathcal {D}}_{\Lambda }^{0}\amalg {\mathcal {D}}_{\Lambda }^{1,+}\amalg {\mathcal {D}}_{\Lambda }^{1,-}$ is a divisor of ![]() $\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}$.
$\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}$.
Lemma 3.1 If ![]() $d\in \Delta _{\Lambda }^{+}$, then
$d\in \Delta _{\Lambda }^{+}$, then ![]() $H_{d}\setminus \Omega _{\Lambda }^{\geq 3}=\Omega _{\Lambda \cap d^{\perp }}^{0}\amalg {\mathcal {D}}_{\Lambda \cap d^{\perp }}^{0}$.
$H_{d}\setminus \Omega _{\Lambda }^{\geq 3}=\Omega _{\Lambda \cap d^{\perp }}^{0}\amalg {\mathcal {D}}_{\Lambda \cap d^{\perp }}^{0}$.
Proof. The proof consists of four steps.
Step 1. By the definition of ![]() ${\mathcal {D}}_{\Lambda }^{0}$, we have
${\mathcal {D}}_{\Lambda }^{0}$, we have ![]() $H_{d}^{0}=H_{d}\cap {\mathcal {D}}_{\Lambda }^{0}$. Since
$H_{d}^{0}=H_{d}\cap {\mathcal {D}}_{\Lambda }^{0}$. Since ![]() $d\in \Delta _{\Lambda }^{+}$, we have
$d\in \Delta _{\Lambda }^{+}$, we have ![]() $H_{d}\cap H_{\delta }\not =\emptyset$ for
$H_{d}\cap H_{\delta }\not =\emptyset$ for ![]() $\delta \in \Delta _{\Lambda }\setminus \{\pm d\}$ if and only if
$\delta \in \Delta _{\Lambda }\setminus \{\pm d\}$ if and only if ![]() $\delta \in \Delta _{\Lambda \cap d^{\perp }}$. Hence
$\delta \in \Delta _{\Lambda \cap d^{\perp }}$. Hence ![]() $H_{d}\cap {\mathcal {D}}_{\Lambda }^{0}=H_{d}^{0}=H_{d}\setminus \bigcup _{\delta \in \Delta _{\Lambda }\setminus \{\pm d\}}H_{\delta } =H_{d}\setminus \bigcup _{\delta \in \Delta _{\Lambda \cap d^{\perp }}}H_{\delta }=\Omega _{\Lambda \cap d^{\perp }}^{0}$.
$H_{d}\cap {\mathcal {D}}_{\Lambda }^{0}=H_{d}^{0}=H_{d}\setminus \bigcup _{\delta \in \Delta _{\Lambda }\setminus \{\pm d\}}H_{\delta } =H_{d}\setminus \bigcup _{\delta \in \Delta _{\Lambda \cap d^{\perp }}}H_{\delta }=\Omega _{\Lambda \cap d^{\perp }}^{0}$.
Step 2. Assume ![]() $H_{d}\cap {\mathcal {D}}_{\Lambda }^{1,-}\not =\emptyset$. Then there exist
$H_{d}\cap {\mathcal {D}}_{\Lambda }^{1,-}\not =\emptyset$. Then there exist ![]() $L\in {\Bbb A}_{2}(\Lambda )$ and
$L\in {\Bbb A}_{2}(\Lambda )$ and ![]() $[\eta ]\in H_{d}\cap H_{L}^{0}$. By the definition of
$[\eta ]\in H_{d}\cap H_{L}^{0}$. By the definition of ![]() $H_{L}^{0}$, we have
$H_{L}^{0}$, we have ![]() $d\in \Delta _{L}$. Since
$d\in \Delta _{L}$. Since ![]() $L\cong {\Bbb A}_{2}$, there exists
$L\cong {\Bbb A}_{2}$, there exists ![]() $\delta \in \Delta _{L}$ with
$\delta \in \Delta _{L}$ with ![]() $\langle d,\delta \rangle =1$. Since
$\langle d,\delta \rangle =1$. Since ![]() $d\in \Delta _{\Lambda }^{+}$, this yields the contradiction
$d\in \Delta _{\Lambda }^{+}$, this yields the contradiction ![]() $\langle d,\delta \rangle =2\langle (d/2),\delta \rangle \in 2\textbf {Z}$. This proves
$\langle d,\delta \rangle =2\langle (d/2),\delta \rangle \in 2\textbf {Z}$. This proves ![]() $H_{d}\cap {\mathcal {D}}_{\Lambda }^{1,-}=\emptyset$.
$H_{d}\cap {\mathcal {D}}_{\Lambda }^{1,-}=\emptyset$.
Step 3. Assume ![]() $H_{d}\cap {\mathcal {D}}_{\Lambda }^{1,+}\not =\emptyset$. Then there exists
$H_{d}\cap {\mathcal {D}}_{\Lambda }^{1,+}\not =\emptyset$. Then there exists ![]() $L\in {\Bbb A}_{1}^{\oplus 2}(\Lambda )$ with
$L\in {\Bbb A}_{1}^{\oplus 2}(\Lambda )$ with ![]() $[\eta ]\in H_{d}\cap H_{L}^{0}$. By the definition of
$[\eta ]\in H_{d}\cap H_{L}^{0}$. By the definition of ![]() $H_{L}^{0}$, we get
$H_{L}^{0}$, we get ![]() $d\in \Delta _{L}$. Hence
$d\in \Delta _{L}$. Hence ![]() $\Delta _{L}=\{\pm d,\pm \delta \}$ for some
$\Delta _{L}=\{\pm d,\pm \delta \}$ for some ![]() $\delta \in \Delta _{\Lambda \cap d^{\perp }}$. Thus
$\delta \in \Delta _{\Lambda \cap d^{\perp }}$. Thus
 \begin{align*} H_{d}\cap{\mathcal{D}}_{\Lambda}^{1,+} &= \bigcup_{L\in{\Bbb A}_{1}^{\oplus2}(\Lambda), d\in L}H_{d}\cap H_{L}^{0} = \bigcup_{\delta\in\Delta_{\Lambda\cap d^{\perp}}} \biggl\{ (H_{d}\cap H_{\delta})\Big\backslash \bigcup_{\epsilon\in\Delta_{\Lambda} \setminus\{\pm d,\pm\delta\}}H_{\epsilon}\biggr\}\\ &=\bigcup_{\delta\in\Delta_{\Lambda\cap d^{\perp}}} \biggl\{ (H_{d}\cap H_{\delta})\Big\backslash \bigcup_{\epsilon\in\Delta_{\Lambda\cap d^{\perp}}\setminus\{\pm\delta\}}H_{\epsilon} \biggr\} = {\mathcal{D}}_{\Lambda\cap d^{\perp}}^{0}. \end{align*}
\begin{align*} H_{d}\cap{\mathcal{D}}_{\Lambda}^{1,+} &= \bigcup_{L\in{\Bbb A}_{1}^{\oplus2}(\Lambda), d\in L}H_{d}\cap H_{L}^{0} = \bigcup_{\delta\in\Delta_{\Lambda\cap d^{\perp}}} \biggl\{ (H_{d}\cap H_{\delta})\Big\backslash \bigcup_{\epsilon\in\Delta_{\Lambda} \setminus\{\pm d,\pm\delta\}}H_{\epsilon}\biggr\}\\ &=\bigcup_{\delta\in\Delta_{\Lambda\cap d^{\perp}}} \biggl\{ (H_{d}\cap H_{\delta})\Big\backslash \bigcup_{\epsilon\in\Delta_{\Lambda\cap d^{\perp}}\setminus\{\pm\delta\}}H_{\epsilon} \biggr\} = {\mathcal{D}}_{\Lambda\cap d^{\perp}}^{0}. \end{align*}
Since ![]() $d\in \Delta _{\Lambda }^{+}$, the third equality follows from the fact that
$d\in \Delta _{\Lambda }^{+}$, the third equality follows from the fact that ![]() $H_{d}\cap H_{\epsilon }\not =\emptyset$ for
$H_{d}\cap H_{\epsilon }\not =\emptyset$ for ![]() $\epsilon \in \Delta _{\Lambda }\setminus \{\pm d\}$ if and only if
$\epsilon \in \Delta _{\Lambda }\setminus \{\pm d\}$ if and only if ![]() $\epsilon \in \Delta _{\Lambda \cap d^{\perp }}$. This proves
$\epsilon \in \Delta _{\Lambda \cap d^{\perp }}$. This proves ![]() $H_{d}\cap {\mathcal {D}}_{\Lambda }^{1,+}={\mathcal {D}}_{\Lambda \cap d^{\perp }}^{0}$.
$H_{d}\cap {\mathcal {D}}_{\Lambda }^{1,+}={\mathcal {D}}_{\Lambda \cap d^{\perp }}^{0}$.
Step 4. Since ![]() $H_{d}\cap \Omega _{\Lambda }^{0}=\emptyset$, the result follows from steps 1–3 and (3.4).
$H_{d}\cap \Omega _{\Lambda }^{0}=\emptyset$, the result follows from steps 1–3 and (3.4).
3.2.4 The local structure of  $\Omega _{\Lambda }^{0}$ near
$\Omega _{\Lambda }^{0}$ near  ${\mathcal {D}}_{\Lambda }^{1}$
${\mathcal {D}}_{\Lambda }^{1}$
Let ![]() $\Delta \subset \textbf {C}$ be the unit disc and set
$\Delta \subset \textbf {C}$ be the unit disc and set ![]() $\Delta ^{*}:=\Delta \setminus \{0\}$. Let
$\Delta ^{*}:=\Delta \setminus \{0\}$. Let ![]() $L_{0}\subset \Delta ^{2}$ be the diagonal locus and set
$L_{0}\subset \Delta ^{2}$ be the diagonal locus and set ![]() $L_{1}:=\{0\}\times \Delta$ and
$L_{1}:=\{0\}\times \Delta$ and ![]() $L_{2}:=\Delta \times \{0\}$. Then
$L_{2}:=\Delta \times \{0\}$. Then ![]() $L_{0}$,
$L_{0}$, ![]() $L_{1}$,
$L_{1}$, ![]() $L_{2}$ are lines with
$L_{2}$ are lines with ![]() $L_{i}\cap L_{j}=\{0\}$ for any
$L_{i}\cap L_{j}=\{0\}$ for any ![]() $i\not =j$. We have
$i\not =j$. We have ![]() $(\Delta ^{*})^{2}=\Delta ^{2}\setminus (L_{1}\cup L_{2})$. Set
$(\Delta ^{*})^{2}=\Delta ^{2}\setminus (L_{1}\cup L_{2})$. Set ![]() $L_{i}^{*}:=L_{i}\setminus \{(0,0)\}$.
$L_{i}^{*}:=L_{i}\setminus \{(0,0)\}$.
Lemma 3.2 Let ![]() $[\eta ]\in {\mathcal {D}}_{\Lambda }^{1,+}\amalg {\mathcal {D}}_{\Lambda }^{1,-}$ and set
$[\eta ]\in {\mathcal {D}}_{\Lambda }^{1,+}\amalg {\mathcal {D}}_{\Lambda }^{1,-}$ and set ![]() $n:=\dim \Omega _{\Lambda }$. Then the following statements hold.
$n:=\dim \Omega _{\Lambda }$. Then the following statements hold.
(1) If
 $[\eta ]\in {\mathcal {D}}_{\Lambda }^{1,+}$, then there is a neighborhood
$[\eta ]\in {\mathcal {D}}_{\Lambda }^{1,+}$, then there is a neighborhood  $U$ of
$U$ of  $[\eta ]$ in
$[\eta ]$ in  $\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}$ such that
$\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}$ such that
 \[ U\cap\Omega_{\Lambda}^{0}\cong(\Delta^{*})^{2}\times\Delta^{n-2}, \quad U\cap{\mathcal{D}}_{\Lambda}^{0}\cong(L_{1}^{*}\amalg L_{2}^{*})\times\Delta^{n-2}, \quad U\cap{\mathcal{D}}_{\Lambda}^{1,+}\cong\{(0,0)\}\times\Delta^{n-2}. \]
\[ U\cap\Omega_{\Lambda}^{0}\cong(\Delta^{*})^{2}\times\Delta^{n-2}, \quad U\cap{\mathcal{D}}_{\Lambda}^{0}\cong(L_{1}^{*}\amalg L_{2}^{*})\times\Delta^{n-2}, \quad U\cap{\mathcal{D}}_{\Lambda}^{1,+}\cong\{(0,0)\}\times\Delta^{n-2}. \](2) If
 $[\eta ]\in {\mathcal {D}}_{\Lambda }^{1,-}$, then there is a neighborhood
$[\eta ]\in {\mathcal {D}}_{\Lambda }^{1,-}$, then there is a neighborhood  $U$ of
$U$ of  $[\eta ]$ in
$[\eta ]$ in  $\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}$ such that
$\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}$ such that  $U\setminus {\mathcal {D}}_{\Lambda }\cong (\Delta ^{2}\setminus L_{0}\cup L_{1}\cup L_{2})\times \Delta ^{n-2}$.
$U\setminus {\mathcal {D}}_{\Lambda }\cong (\Delta ^{2}\setminus L_{0}\cup L_{1}\cup L_{2})\times \Delta ^{n-2}$.
Proof. Since ![]() $[\eta ]\in {\mathcal {D}}_{\Lambda }^{1,+}\amalg {\mathcal {D}}_{\Lambda }^{1,-}$, there exist
$[\eta ]\in {\mathcal {D}}_{\Lambda }^{1,+}\amalg {\mathcal {D}}_{\Lambda }^{1,-}$, there exist ![]() $L\in {\Bbb A}_{1}^{\oplus 2}(\Lambda )\amalg {\Bbb A}_{2}(\Lambda )$ and a neighborhood
$L\in {\Bbb A}_{1}^{\oplus 2}(\Lambda )\amalg {\Bbb A}_{2}(\Lambda )$ and a neighborhood ![]() $U$ of
$U$ of ![]() $[\eta ]$ in
$[\eta ]$ in ![]() $\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}$ such that
$\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}$ such that ![]() $U\cap {\mathcal {D}}_{\Lambda }=U\cap \bigcup _{d\in \Delta _{L}}H_{d}$.
$U\cap {\mathcal {D}}_{\Lambda }=U\cap \bigcup _{d\in \Delta _{L}}H_{d}$.
(1) Assume ![]() $[\eta ]\in {\mathcal {D}}_{\Lambda }^{1,+}$. Then
$[\eta ]\in {\mathcal {D}}_{\Lambda }^{1,+}$. Then ![]() $L\in {\Bbb A}_{1}^{\oplus 2}(\Lambda )$. There exist
$L\in {\Bbb A}_{1}^{\oplus 2}(\Lambda )$. There exist ![]() $d_{1},d_{2}\in \Delta _{L}$ with
$d_{1},d_{2}\in \Delta _{L}$ with ![]() $\langle d_{1},d_{2}\rangle =0$ such that
$\langle d_{1},d_{2}\rangle =0$ such that ![]() $U\cap {\mathcal {D}}_{\Lambda }=U\cap (H_{d_{1}}\cup H_{d_{2}})$. Replacing
$U\cap {\mathcal {D}}_{\Lambda }=U\cap (H_{d_{1}}\cup H_{d_{2}})$. Replacing ![]() $U$ by a smaller neighborhood if necessary, there exist a system of coordinates
$U$ by a smaller neighborhood if necessary, there exist a system of coordinates ![]() $(z_{1},z_{2},w)$,
$(z_{1},z_{2},w)$, ![]() $w=(w_{1},\ldots ,w_{n-2})$, on
$w=(w_{1},\ldots ,w_{n-2})$, on ![]() $U$ such that
$U$ such that ![]() $H_{d_{1}}={\rm div}(z_{1})$,
$H_{d_{1}}={\rm div}(z_{1})$, ![]() $H_{d_{2}}={\rm div}(z_{2})$. The isomorphism
$H_{d_{2}}={\rm div}(z_{2})$. The isomorphism ![]() $\psi \colon (U,[\eta ])\cong (\Delta ^{n},0)$ induced by
$\psi \colon (U,[\eta ])\cong (\Delta ^{n},0)$ induced by ![]() $(z_{1},z_{2},w)$ has the desired property.
$(z_{1},z_{2},w)$ has the desired property.
(2) Assume ![]() $[\eta ]\in {\mathcal {D}}_{\Lambda }^{1,-}$. Since
$[\eta ]\in {\mathcal {D}}_{\Lambda }^{1,-}$. Since ![]() $L\in {\Bbb A}_{2}(\Lambda )$, there exist
$L\in {\Bbb A}_{2}(\Lambda )$, there exist ![]() $d_{0},d_{1},d_{2}\in \Delta _{L}$ with
$d_{0},d_{1},d_{2}\in \Delta _{L}$ with ![]() $d_{0}=d_{1}+d_{2}$ and
$d_{0}=d_{1}+d_{2}$ and ![]() $\langle d_{1},d_{2}\rangle =1$ such that
$\langle d_{1},d_{2}\rangle =1$ such that ![]() $U\cap {\mathcal {D}}_{\Lambda }=U\cap (H_{d_{0}}\cup H_{d_{1}}\cup H_{d_{2}})$. Replacing
$U\cap {\mathcal {D}}_{\Lambda }=U\cap (H_{d_{0}}\cup H_{d_{1}}\cup H_{d_{2}})$. Replacing ![]() $U$ by a smaller neighborhood if necessary, there exist a system of coordinates
$U$ by a smaller neighborhood if necessary, there exist a system of coordinates ![]() $(z_{1},z_{2},w)$ on
$(z_{1},z_{2},w)$ on ![]() $U$ such that
$U$ such that ![]() $H_{d_{1}}={\rm div}(z_{1})$,
$H_{d_{1}}={\rm div}(z_{1})$, ![]() $H_{d_{2}}={\rm div}(z_{2})$,
$H_{d_{2}}={\rm div}(z_{2})$, ![]() $H_{d_{0}}={\rm div}(z_{1}+z_{2})$. The isomorphism
$H_{d_{0}}={\rm div}(z_{1}+z_{2})$. The isomorphism ![]() $\psi \colon (U,[\eta ])\cong (\Delta ^{n},0)$ induced by
$\psi \colon (U,[\eta ])\cong (\Delta ^{n},0)$ induced by ![]() $(z_{1},z_{2},w)$ has the desired property.
$(z_{1},z_{2},w)$ has the desired property.
3.2.5 Inclusion of lattices and the Torelli map
Recall that for ![]() $d\in \Delta _{\Lambda }^{+}$, the equality of sets
$d\in \Delta _{\Lambda }^{+}$, the equality of sets ![]() $H_{d}\setminus \Omega _{\Lambda }^{\geq 3}=\Omega _{\Lambda \cap d^{\perp }}^{0}\cup {\mathcal {D}}_{\Lambda \cap d^{\perp }}^{0}$ follows from Lemma 3.1. By Lemma 3.2 (1),
$H_{d}\setminus \Omega _{\Lambda }^{\geq 3}=\Omega _{\Lambda \cap d^{\perp }}^{0}\cup {\mathcal {D}}_{\Lambda \cap d^{\perp }}^{0}$ follows from Lemma 3.1. By Lemma 3.2 (1), ![]() $\Omega _{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{1,+}$ is a Zariski open subset of
$\Omega _{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{1,+}$ is a Zariski open subset of ![]() $\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}$.
$\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}$.
Theorem 3.3 ![]() $J_{M}^{0}$ extends to a holomorphic map from
$J_{M}^{0}$ extends to a holomorphic map from ![]() $\Omega _{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{1,+}$ to
$\Omega _{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{1,+}$ to ![]() ${\mathcal {A}}_{g}^{*}$.
${\mathcal {A}}_{g}^{*}$.
Proof. Set ![]() $n:=\dim \Omega _{\Lambda }$. Let
$n:=\dim \Omega _{\Lambda }$. Let ![]() $[\eta ]\in {\mathcal {D}}_{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{1,+}$. By Lemma 3.2 (1), there is a neighborhood
$[\eta ]\in {\mathcal {D}}_{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{1,+}$. By Lemma 3.2 (1), there is a neighborhood ![]() $U$ of
$U$ of ![]() $[\eta ]$ in
$[\eta ]$ in ![]() $\Omega _{\Lambda }$ such that either
$\Omega _{\Lambda }$ such that either ![]() $U\setminus ({\mathcal {D}}_{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{1,+})\cong \Delta ^{*}\times \Delta ^{n-1}$ or
$U\setminus ({\mathcal {D}}_{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{1,+})\cong \Delta ^{*}\times \Delta ^{n-1}$ or ![]() $U\setminus ({\mathcal {D}}_{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{1,+})\cong (\Delta ^{*})^{2}\times \Delta ^{n-2}$. By Borel [Reference BorelBor72],
$U\setminus ({\mathcal {D}}_{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{1,+})\cong (\Delta ^{*})^{2}\times \Delta ^{n-2}$. By Borel [Reference BorelBor72], ![]() $J_{M}^{0}$ extends to a holomorphic map from
$J_{M}^{0}$ extends to a holomorphic map from ![]() $U$ to
$U$ to ![]() ${\mathcal {A}}_{g}^{*}$. Since
${\mathcal {A}}_{g}^{*}$. Since ![]() $[\eta ]\in {\mathcal {D}}_{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{1,+}$ is an arbitrary point, we get the result.
$[\eta ]\in {\mathcal {D}}_{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{1,+}$ is an arbitrary point, we get the result.
Remark 3.4 By Lemma 3.2 (2), Borel's extension theorem does not apply to ![]() $J_{M}^{0}$ near
$J_{M}^{0}$ near ![]() ${\mathcal {D}}_{\Lambda }^{1,-}$. This explains why
${\mathcal {D}}_{\Lambda }^{1,-}$. This explains why ![]() $J_{M}$ does not extend to
$J_{M}$ does not extend to ![]() $\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}$ in general.
$\Omega _{\Lambda }\setminus \Omega _{\Lambda }^{\geq 3}$ in general.
Denote the extension of ![]() $J_{M}^{0}$ by
$J_{M}^{0}$ by
and call it again the Torelli map. By [Reference YoshikawaYos13, Theorem 2.5], the equality
holds for all ![]() $d\in \Delta _{\Lambda }$. The following refinement is crucial for the proof Theorem 0.1.
$d\in \Delta _{\Lambda }$. The following refinement is crucial for the proof Theorem 0.1.
Theorem 3.5 If ![]() $d\in \Delta _{\Lambda }^{+}$, then
$d\in \Delta _{\Lambda }^{+}$, then
Proof. Since both ![]() $J_{M}|_{H_{d}\setminus \Omega _{\Lambda }^{\geq 3}}$ and
$J_{M}|_{H_{d}\setminus \Omega _{\Lambda }^{\geq 3}}$ and ![]() $J_{[M\perp d]}|_{\Omega _{\Lambda \cap d^{\perp }}^{0}\cup {\mathcal {D}}_{\Lambda \cap d^{\perp }}^{0}}$ are holomorphic maps from
$J_{[M\perp d]}|_{\Omega _{\Lambda \cap d^{\perp }}^{0}\cup {\mathcal {D}}_{\Lambda \cap d^{\perp }}^{0}}$ are holomorphic maps from ![]() $\Omega _{\Lambda \cap d^{\perp }}^{0}\cup {\mathcal {D}}_{\Lambda \cap d^{\perp }}^{0}$ to
$\Omega _{\Lambda \cap d^{\perp }}^{0}\cup {\mathcal {D}}_{\Lambda \cap d^{\perp }}^{0}$ to ![]() ${\mathcal {A}}_{g}^{*}$ by Lemma 3.1 and Theorem 3.3, it suffices to prove the equality on
${\mathcal {A}}_{g}^{*}$ by Lemma 3.1 and Theorem 3.3, it suffices to prove the equality on ![]() $\Omega _{\Lambda \cap d^{\perp }}^{0}$. Since this was proved in [Reference YoshikawaYos13, Theorem 2.5], we get the result.
$\Omega _{\Lambda \cap d^{\perp }}^{0}$. Since this was proved in [Reference YoshikawaYos13, Theorem 2.5], we get the result.
3.3 Hyperelliptic linear system
This subsection is the technical basis for §§ 6 and 7. We advise the reader to skip it for the moment and return when necessary. We prepare some tools to realize a given 2-elementary ![]() $K3$ surface as a double cover of
$K3$ surface as a double cover of ![]() $\mathbf{P}^2$ or a Hirzebruch surface.
$\mathbf{P}^2$ or a Hirzebruch surface.
We will use the following notation. For ![]() $n\geq 0$ let
$n\geq 0$ let
be the ![]() $n$th Hirzebruch surface, equipped with the natural projection
$n$th Hirzebruch surface, equipped with the natural projection ![]() $\pi :\mathbf{F}_{n}\to \mathbf{P}^1$. When
$\pi :\mathbf{F}_{n}\to \mathbf{P}^1$. When ![]() $n>0$, denote by
$n>0$, denote by ![]() $\Sigma \subset \mathbf{F}_{n}$ its unique
$\Sigma \subset \mathbf{F}_{n}$ its unique ![]() $(-n)$-section. We write
$(-n)$-section. We write ![]() $L_{a,b}$ for the line bundle on
$L_{a,b}$ for the line bundle on ![]() $\mathbf{F}_{n}$ of
$\mathbf{F}_{n}$ of ![]() $\pi$-degree
$\pi$-degree ![]() $a$ with
$a$ with ![]() $(L_{a,b}, \Sigma )=b$. In particular, we have
$(L_{a,b}, \Sigma )=b$. In particular, we have ![]() $\pi ^{\ast }\mathcal {O}_{\mathbf{P}^1}(1)\simeq L_{0,1}$,
$\pi ^{\ast }\mathcal {O}_{\mathbf{P}^1}(1)\simeq L_{0,1}$, ![]() $\mathcal {O}_{\mathbf{F}_{n}}(\Sigma )\simeq L_{1,-n}$ and
$\mathcal {O}_{\mathbf{F}_{n}}(\Sigma )\simeq L_{1,-n}$ and ![]() $K_{\mathbf{F}_{n}}\simeq L_{-2,-2+n}$.
$K_{\mathbf{F}_{n}}\simeq L_{-2,-2+n}$.
Let ![]() $(X, \iota )$ be a 2-elementary
$(X, \iota )$ be a 2-elementary ![]() $K3$ surface. A line bundle
$K3$ surface. A line bundle ![]() $L$ on
$L$ on ![]() $X$ with
$X$ with ![]() $(L, L)=2d>0$ is called hyperelliptic [Reference Saint-DonatSai74] if the linear system
$(L, L)=2d>0$ is called hyperelliptic [Reference Saint-DonatSai74] if the linear system ![]() $|L|$ contains a smooth hyperelliptic member. In that case,
$|L|$ contains a smooth hyperelliptic member. In that case, ![]() $L$ is base point free and every smooth member of
$L$ is base point free and every smooth member of ![]() $|L|$ is hyperelliptic of genus
$|L|$ is hyperelliptic of genus ![]() $d+1$. The associated morphism
$d+1$. The associated morphism
is generically two-to-one onto its image, mapping a smooth member of ![]() $|L|$ to a rational normal curve in a hyperplane of
$|L|$ to a rational normal curve in a hyperplane of ![]() $|L|^{\vee }$. According to Saint-Donat [Reference Saint-DonatSai74, § 5], we have the following possibilities for the image surface
$|L|^{\vee }$. According to Saint-Donat [Reference Saint-DonatSai74, § 5], we have the following possibilities for the image surface ![]() $\phi _L(X)$.
$\phi _L(X)$.
(I)
 $\phi _L(X)$ coincides with
$\phi _L(X)$ coincides with  $|L|^{\vee }\simeq \mathbf{P}^2$: this is the case
$|L|^{\vee }\simeq \mathbf{P}^2$: this is the case  $d=1$.
$d=1$.(II)
 $\phi _L(X)$ is a Veronese surface in
$\phi _L(X)$ is a Veronese surface in  $|L|^{\vee }\simeq \mathbf{P}^5$: this happens when
$|L|^{\vee }\simeq \mathbf{P}^5$: this happens when  $L=2L'$ for
$L=2L'$ for  $L'\in {\rm Pic}(X)$ with
$L'\in {\rm Pic}(X)$ with  $(L', L')=2$.
$(L', L')=2$.(III)
 $\phi _L(X)$ is a rational normal scroll, that is, the embedding image of
$\phi _L(X)$ is a rational normal scroll, that is, the embedding image of  $\mathbf{F}_n$ by a line bundle
$\mathbf{F}_n$ by a line bundle  $L_{1,m}$ with
$L_{1,m}$ with  $m>0$ and
$m>0$ and  $n+2m=d$.
$n+2m=d$.(IV)
 $\phi _L(X)$ is a cone over a rational normal curve, that is, the image of
$\phi _L(X)$ is a cone over a rational normal curve, that is, the image of  $\mathbf{F}_d$ by the bundle
$\mathbf{F}_d$ by the bundle  $L_{1,0}$. In this case
$L_{1,0}$. In this case  $\phi _L$ lifts to a morphism
$\phi _L$ lifts to a morphism  $X\to \mathbf{F}_d$, and we must have
$X\to \mathbf{F}_d$, and we must have  $2\leq d\leq 4$.
$2\leq d\leq 4$.
We now assume that the hyperelliptic bundle ![]() $L$ is
$L$ is ![]() $\iota$-invariant, in the sense that there exists an isomorphism
$\iota$-invariant, in the sense that there exists an isomorphism
Although ![]() $\iota$ may not necessarily act on
$\iota$ may not necessarily act on ![]() $L$ equivariantly, it does so on the morphism (3.6). We then obtain an
$L$ equivariantly, it does so on the morphism (3.6). We then obtain an ![]() $\iota$-equivariant morphism
$\iota$-equivariant morphism
with ![]() $Y=\mathbf{P}^2$ in cases (I) and (II), and
$Y=\mathbf{P}^2$ in cases (I) and (II), and ![]() $Y=\mathbf{F}_n$,
$Y=\mathbf{F}_n$, ![]() $\mathbf{F}_d$ in cases (III) and (IV).
$\mathbf{F}_d$ in cases (III) and (IV).
It will be useful to have a purely lattice-theoretic method for finding an ![]() $\iota$-invariant hyperelliptic bundle. This is based on the following lemmas. Denote by
$\iota$-invariant hyperelliptic bundle. This is based on the following lemmas. Denote by ![]() $H_+=H^2(X, \textbf {Z})_+$ the invariant lattice of
$H_+=H^2(X, \textbf {Z})_+$ the invariant lattice of ![]() $(X, \iota )$.
$(X, \iota )$.
Lemma 3.6 Let ![]() $L\in H_+$ be nef with
$L\in H_+$ be nef with ![]() $(L, L)=2d>0$. Assume that:
$(L, L)=2d>0$. Assume that:
(a) there exists
 $E\in {\rm Pic}(X)$ with
$E\in {\rm Pic}(X)$ with  $(E, E)\geq 0$ and
$(E, E)\geq 0$ and  $(E, L)=2$; and
$(E, L)=2$; and(b) there is no
 $F\in H_+$ with
$F\in H_+$ with  $(F, F)=0$ and
$(F, F)=0$ and  $(F, L)=1$.
$(F, L)=1$.
Then ![]() $L$ is hyperelliptic.
$L$ is hyperelliptic.
Proof. We first show that ![]() $L$ is base point free. Otherwise, by [Reference MayerMay72, Proposition 5] the linear system
$L$ is base point free. Otherwise, by [Reference MayerMay72, Proposition 5] the linear system ![]() $|L|$ would be of the form
$|L|$ would be of the form ![]() $|(d+1)F|+\Gamma$ where
$|(d+1)F|+\Gamma$ where ![]() $F$ is a smooth elliptic curve and
$F$ is a smooth elliptic curve and ![]() $\Gamma$ is a
$\Gamma$ is a ![]() $(-2)$-curve with
$(-2)$-curve with ![]() $(F, \Gamma )=1$. Since
$(F, \Gamma )=1$. Since ![]() $\iota$ acts on
$\iota$ acts on ![]() $|L|$, the class of
$|L|$, the class of ![]() $F$ is
$F$ is ![]() $\iota$-invariant and then would violate assumption
$\iota$-invariant and then would violate assumption ![]() $({\rm b})$. Hence
$({\rm b})$. Hence ![]() $L$ is free, and a general member
$L$ is free, and a general member ![]() $C\in |L|$ is smooth and irreducible of genus
$C\in |L|$ is smooth and irreducible of genus ![]() $d+1$. We show that
$d+1$. We show that ![]() $C$ is hyperelliptic. Since
$C$ is hyperelliptic. Since ![]() $g(C)=2$ when
$g(C)=2$ when ![]() $d=1$, we may assume
$d=1$, we may assume ![]() $d>1$. Let
$d>1$. Let ![]() $E$ be a divisor as in assumption
$E$ be a divisor as in assumption ![]() $({\rm a})$. Since
$({\rm a})$. Since ![]() $h^0(-E)=0$, we have
$h^0(-E)=0$, we have ![]() $h^0(E)\geq 2$ by the Riemann–Roch inequality. Consider the exact sequence
$h^0(E)\geq 2$ by the Riemann–Roch inequality. Consider the exact sequence
Since ![]() $(E-L, L)<0$, we have
$(E-L, L)<0$, we have ![]() $h^0(E-L)=0$ by the nefness of
$h^0(E-L)=0$ by the nefness of ![]() $L$. Hence
$L$. Hence ![]() $h^0(E|_C)\geq h^{0}(E)\geq 2$ and
$h^0(E|_C)\geq h^{0}(E)\geq 2$ and ![]() $E|_C$ gives a
$E|_C$ gives a ![]() $g^1_2$ on
$g^1_2$ on ![]() $C$.
$C$.
Conditions (a) and (b) are purely arithmetic. It is always possible to meet the nefness condition by the following lemma.
Lemma 3.7 Let ![]() $W(X)$ be the Weyl group of
$W(X)$ be the Weyl group of ![]() ${\rm Pic}(X)$ generated by the reflections with respect to
${\rm Pic}(X)$ generated by the reflections with respect to ![]() $(-2)$-vectors in
$(-2)$-vectors in ![]() ${\rm Pic}(X)$. Let
${\rm Pic}(X)$. Let ![]() $L\in H_+$ be a line bundle with
$L\in H_+$ be a line bundle with ![]() $(L, L)\geq 0$ and
$(L, L)\geq 0$ and ![]() $(L, L_0)>0$ for some ample class
$(L, L_0)>0$ for some ample class ![]() $L_0$. Then there exists
$L_0$. Then there exists ![]() $w\in W(X)$ such that
$w\in W(X)$ such that ![]() $w\circ \iota =\iota \circ w$ and
$w\circ \iota =\iota \circ w$ and ![]() $w(L)$ is nef.
$w(L)$ is nef.
Proof. The same argument as in [Reference Barth, Hulek, Peters and Van de VenBHPV04, Proposition 21.1] applies with a few minor modifications. We leave this to the reader.
Thus we can obtain an ![]() $\iota$-equivariant morphism (3.7) by just finding a vector in
$\iota$-equivariant morphism (3.7) by just finding a vector in ![]() $H_+$ with the arithmetic conditions (a) and (b). The
$H_+$ with the arithmetic conditions (a) and (b). The ![]() $\iota$-equivariant Weyl group action as in Lemma 3.7 would then carry this vector to a class of hyperelliptic bundles.
$\iota$-equivariant Weyl group action as in Lemma 3.7 would then carry this vector to a class of hyperelliptic bundles.
We are interested in when ![]() $\iota$ acts by the covering transformation of
$\iota$ acts by the covering transformation of ![]() $\phi :X\to Y$, in which case
$\phi :X\to Y$, in which case ![]() $(X, \iota )$ may be recovered from
$(X, \iota )$ may be recovered from ![]() $Y$ and the branch curve of
$Y$ and the branch curve of ![]() $\phi$. Let
$\phi$. Let ![]() $g$ denote the genus of the main component of the fixed curve
$g$ denote the genus of the main component of the fixed curve ![]() $X^{\iota }$.
$X^{\iota }$.
Lemma 3.8 The involution ![]() $\iota$ acts trivially on
$\iota$ acts trivially on ![]() $Y$ when:
$Y$ when:
(1)
 $g\geq 3$ in the case of
$g\geq 3$ in the case of  $Y=\mathbf{P}^2$;
$Y=\mathbf{P}^2$;(2)
 $g\geq 4$ in the case of
$g\geq 4$ in the case of  $Y=\mathbf{P}^1\times \mathbf{P}^1$; and
$Y=\mathbf{P}^1\times \mathbf{P}^1$; and(3)
 $g\geq n+2$ in the case of
$g\geq n+2$ in the case of  $Y=\mathbf{F}_n$ with
$Y=\mathbf{F}_n$ with  $n>0$.
$n>0$.
Proof. We may assume that ![]() $g>0$. Let
$g>0$. Let ![]() $B\subset Y$ be the branch curve of
$B\subset Y$ be the branch curve of ![]() $\phi$, which belongs to
$\phi$, which belongs to ![]() $|{-}2K_Y|$. Suppose that
$|{-}2K_Y|$. Suppose that ![]() $\iota$ acts non-trivially on
$\iota$ acts non-trivially on ![]() $Y$; then the genus
$Y$; then the genus ![]() $g$ component of
$g$ component of ![]() $X^{\iota }$ is the normalization of the double cover of a curve component
$X^{\iota }$ is the normalization of the double cover of a curve component ![]() $D$ of
$D$ of ![]() $Y^{\iota }$ branched over
$Y^{\iota }$ branched over ![]() $B|_D$. When
$B|_D$. When ![]() $Y=\mathbf{P}^2$,
$Y=\mathbf{P}^2$, ![]() $D$ must be a line and so intersects with
$D$ must be a line and so intersects with ![]() $B$ at six points. When
$B$ at six points. When ![]() $Y=\mathbf{P}^1\times \mathbf{P}^1$,
$Y=\mathbf{P}^1\times \mathbf{P}^1$, ![]() $D$ is either a ruling fiber or a smooth bidegree
$D$ is either a ruling fiber or a smooth bidegree ![]() $(1, 1)$ curve, which satisfies
$(1, 1)$ curve, which satisfies ![]() $(D, B)\leq 8$. Finally, let
$(D, B)\leq 8$. Finally, let ![]() $Y=\mathbf{F}_n$ with
$Y=\mathbf{F}_n$ with ![]() $n>0$. If
$n>0$. If ![]() $\iota$ acts non-trivially on the
$\iota$ acts non-trivially on the ![]() $(-n)$-section
$(-n)$-section ![]() $\Sigma$, then
$\Sigma$, then ![]() $D$ is a ruling fiber so that
$D$ is a ruling fiber so that ![]() $(D, -2K_Y)=4$. If
$(D, -2K_Y)=4$. If ![]() $\iota$ acts trivially on
$\iota$ acts trivially on ![]() $\Sigma$, we have
$\Sigma$, we have ![]() $Y^{\iota }=H+\Sigma$ for a smooth
$Y^{\iota }=H+\Sigma$ for a smooth ![]() $H\in |L_{1,0}|$ because
$H\in |L_{1,0}|$ because ![]() $\iota$ must preserve every fiber of
$\iota$ must preserve every fiber of ![]() $\mathbf{F}_n$ and hence induces a non-trivial involution on every fiber. Then
$\mathbf{F}_n$ and hence induces a non-trivial involution on every fiber. Then ![]() $(\Sigma ,B)=(\Sigma , -2K_Y)\leq 2$ and
$(\Sigma ,B)=(\Sigma , -2K_Y)\leq 2$ and ![]() $(H,B)=(H, -2K_Y)=2n+4$. This gives us the estimate
$(H,B)=(H, -2K_Y)=2n+4$. This gives us the estimate ![]() $2g+2\leq (D, B)\leq 2n+4$.
$2g+2\leq (D, B)\leq 2n+4$.
This criterion is coarse, but will suffice for our purpose.
4. Automorphic forms on the period domain
4.1 Siegel modular forms
Recall that the line bundle on ![]() ${\mathcal {A}}_{g}$ associated with the automorphic factor
${\mathcal {A}}_{g}$ associated with the automorphic factor ![]() ${\rm Sp}_{2g}(\textbf {Z})\ni \binom {A\,B}{C\,D}\mapsto \det (C\Omega +D)\in {\mathcal {O}}({\frak S}_{g})$,
${\rm Sp}_{2g}(\textbf {Z})\ni \binom {A\,B}{C\,D}\mapsto \det (C\Omega +D)\in {\mathcal {O}}({\frak S}_{g})$, ![]() $\Omega \in {\frak S}_{g}$, is called the Hodge line bundle on
$\Omega \in {\frak S}_{g}$, is called the Hodge line bundle on ![]() ${\mathcal {A}}_{g}$ and is denoted by
${\mathcal {A}}_{g}$ and is denoted by ![]() ${\mathcal {F}}_{g}$ in this paper. A holomorphic section of
${\mathcal {F}}_{g}$ in this paper. A holomorphic section of ![]() ${\mathcal {F}}_{g}^{\otimes q}$ is identified with a Siegel modular form of weight
${\mathcal {F}}_{g}^{\otimes q}$ is identified with a Siegel modular form of weight ![]() $q$, and
$q$, and ![]() ${\mathcal {F}}_{g}^{\otimes q}$ is equipped with the Hermitian metric
${\mathcal {F}}_{g}^{\otimes q}$ is equipped with the Hermitian metric ![]() $\|\cdot \|_{{\mathcal {F}}_{g}^{\otimes q}}$ called the Petersson norm: for any Siegel modular form
$\|\cdot \|_{{\mathcal {F}}_{g}^{\otimes q}}$ called the Petersson norm: for any Siegel modular form ![]() $S$ of weight
$S$ of weight ![]() $q$, we define
$q$, we define ![]() $\|S(\Omega )\|_{{\mathcal {F}}_{g}^{\otimes q}}^{2}:=(\det \Im \,\Omega )^{q}|S(\Omega )|^{2}$.
$\|S(\Omega )\|_{{\mathcal {F}}_{g}^{\otimes q}}^{2}:=(\det \Im \,\Omega )^{q}|S(\Omega )|^{2}$.
In this paper, the following Siegel modular forms on ![]() ${\frak S}_{g}$ play crucial roles:
${\frak S}_{g}$ play crucial roles:
 \begin{gather*} \chi_{g}(\Omega)^{8}:=\prod_{(a,b)\,{\rm even}}\theta_{a,b}(\Omega)^{8},\\ \Upsilon_{g}(\Omega):=\chi_{g}(\Omega)^{8}\sum_{(a,b)\,{\rm even}}\theta_{a,b}(\Omega)^{-8}. \end{gather*}
\begin{gather*} \chi_{g}(\Omega)^{8}:=\prod_{(a,b)\,{\rm even}}\theta_{a,b}(\Omega)^{8},\\ \Upsilon_{g}(\Omega):=\chi_{g}(\Omega)^{8}\sum_{(a,b)\,{\rm even}}\theta_{a,b}(\Omega)^{-8}. \end{gather*}Here
is the theta constant with even characteristic ![]() $(a,b)$, where
$(a,b)$, where ![]() $a,b\in \{0,1/2\}^{g}$ and
$a,b\in \{0,1/2\}^{g}$ and ![]() $4{}^{t}ab\equiv 0\bmod 2$. For
$4{}^{t}ab\equiv 0\bmod 2$. For ![]() $g=0$, we set
$g=0$, we set ![]() $\chi _{0}=\Upsilon _{0}=1$. Note that
$\chi _{0}=\Upsilon _{0}=1$. Note that ![]() $\Upsilon _{g}(\Omega )$ is the elementary symmetric polynomial of degree
$\Upsilon _{g}(\Omega )$ is the elementary symmetric polynomial of degree ![]() $2^{g-1}(2^{g}+1)-1=(2^{g-1}+1)(2^{g}-1)$ in the even theta constants
$2^{g-1}(2^{g}+1)-1=(2^{g-1}+1)(2^{g}-1)$ in the even theta constants ![]() $\theta _{a,b}(\Omega )^{8}$. By [Reference IgusaIgu72, Corollary, p. 176, and Theorem 3, p. 182],
$\theta _{a,b}(\Omega )^{8}$. By [Reference IgusaIgu72, Corollary, p. 176, and Theorem 3, p. 182], ![]() $\chi _{g}^{8}$ (respectively,
$\chi _{g}^{8}$ (respectively, ![]() $\Upsilon _{g}$) is a Siegel modular form of weight
$\Upsilon _{g}$) is a Siegel modular form of weight ![]() $2^{g+1}(2^{g}+1)$ (respectively,
$2^{g+1}(2^{g}+1)$ (respectively, ![]() $2(2^{g}-1)(2^{g}+2)$). The locus of vanishing theta-null
$2(2^{g}-1)(2^{g}+2)$). The locus of vanishing theta-null ![]() $\theta _{{\rm null},g}$ is the reduced divisor on
$\theta _{{\rm null},g}$ is the reduced divisor on ![]() ${\mathcal {A}}_{g}$ defined by
${\mathcal {A}}_{g}$ defined by ![]() $\chi _{g}$
$\chi _{g}$
Lemma 4.1 There exist at least two distinct vanishing even theta constants at ![]() $\Omega \in {\frak S}_{g}$ if and only if
$\Omega \in {\frak S}_{g}$ if and only if ![]() $\chi _{g}(\Omega )=\Upsilon _{g}(\Omega )=0$. In particular, a smooth projective curve
$\chi _{g}(\Omega )=\Upsilon _{g}(\Omega )=0$. In particular, a smooth projective curve ![]() $C$ of genus
$C$ of genus ![]() $g$ has at least two effective even theta characteristics if and only if
$g$ has at least two effective even theta characteristics if and only if ![]() $\chi _{g}(\Omega (C))=\Upsilon _{g}(\Omega (C))=0$.
$\chi _{g}(\Omega (C))=\Upsilon _{g}(\Omega (C))=0$.
Proof. Assume ![]() $\chi _{g}(\Omega )=\Upsilon _{g}(\Omega )=0$. Since
$\chi _{g}(\Omega )=\Upsilon _{g}(\Omega )=0$. Since ![]() $\chi _{g}(\Omega )=0$, there is an even pair
$\chi _{g}(\Omega )=0$, there is an even pair ![]() $(a,b)$ with
$(a,b)$ with ![]() $\theta _{a,b}(\Omega )=0$. Then
$\theta _{a,b}(\Omega )=0$. Then ![]() $\Upsilon _{g}(\Omega )=\prod _{(c,d)\not =(a,b)}\theta _{c,d}(\Omega )^{8}$, where
$\Upsilon _{g}(\Omega )=\prod _{(c,d)\not =(a,b)}\theta _{c,d}(\Omega )^{8}$, where ![]() $(c,d)\in \{0,1/2\}^{2g}$ runs over all even pairs distinct from
$(c,d)\in \{0,1/2\}^{2g}$ runs over all even pairs distinct from ![]() $(a,b)$. Since
$(a,b)$. Since ![]() $\Upsilon _{g}(\Omega )=0$, we get
$\Upsilon _{g}(\Omega )=0$, we get ![]() $\theta _{c,d}(\Omega )=0$ for some even pair
$\theta _{c,d}(\Omega )=0$ for some even pair ![]() $(c,d)\not =(a,b)$. Thus
$(c,d)\not =(a,b)$. Thus ![]() $\theta _{a,b}(\Omega )=\theta _{c,d}(\Omega )=0$. The converse is trivial. The second assertion follows from the Riemann singularity theorem [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, p. 226].
$\theta _{a,b}(\Omega )=\theta _{c,d}(\Omega )=0$. The converse is trivial. The second assertion follows from the Riemann singularity theorem [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, p. 226].
For the proof of Theorem 0.1(1) and (2), we need an estimate for the vanishing order of ![]() $\Upsilon _{g}$ for certain ordinary singular families of curves.
$\Upsilon _{g}$ for certain ordinary singular families of curves.
Lemma 4.2 Let ![]() $p\colon {\mathcal {C}}\to \Delta$ be an ordinary singular family of curves of genus
$p\colon {\mathcal {C}}\to \Delta$ be an ordinary singular family of curves of genus ![]() $g>0$ with irreducible
$g>0$ with irreducible ![]() $C_{0}:=p^{-1}(0)$. Namely,
$C_{0}:=p^{-1}(0)$. Namely, ![]() $p\colon {\mathcal {C}}\to \Delta$ is a proper surjective holomorphic function from a complex surface
$p\colon {\mathcal {C}}\to \Delta$ is a proper surjective holomorphic function from a complex surface ![]() ${\mathcal {C}}$ to the unit disc
${\mathcal {C}}$ to the unit disc ![]() $\Delta$ without critical points on
$\Delta$ without critical points on ![]() ${\mathcal {C}}\setminus C_{0}$ and with a unique, non-degenerate critical point on
${\mathcal {C}}\setminus C_{0}$ and with a unique, non-degenerate critical point on ![]() $C_{0}$. Assume that
$C_{0}$. Assume that ![]() $\chi _{g}(\Omega (C_{t}))=0$ and
$\chi _{g}(\Omega (C_{t}))=0$ and ![]() $\Upsilon _{g}(\Omega (C_{t}))\not =0$ for all
$\Upsilon _{g}(\Omega (C_{t}))\not =0$ for all ![]() $t\in \Delta ^{*}$ and that
$t\in \Delta ^{*}$ and that ![]() $\chi _{g-1}(\Omega (\hat {C}_{0}))\not =0$, where
$\chi _{g-1}(\Omega (\hat {C}_{0}))\not =0$, where ![]() $\hat {C}_{0}$ is the normalization of
$\hat {C}_{0}$ is the normalization of ![]() $C_{0}$. Then there exists
$C_{0}$. Then there exists ![]() $h(t)\in {\mathcal {O}}(\Delta )$ such that
$h(t)\in {\mathcal {O}}(\Delta )$ such that
Proof. We follow [Reference YoshikawaYos13, Proof of Lemma 4.1]. For ![]() $\Omega \in {\frak S}_{g}$, write
$\Omega \in {\frak S}_{g}$, write ![]() $\Omega =\binom {z\,{}^{t}\omega }{\omega \,Z}$, where
$\Omega =\binom {z\,{}^{t}\omega }{\omega \,Z}$, where ![]() $z\in {\frak H}$,
$z\in {\frak H}$, ![]() $\omega \in \textbf {C}^{g-1}$,
$\omega \in \textbf {C}^{g-1}$, ![]() $Z\in {\frak S}_{g-1}$. For
$Z\in {\frak S}_{g-1}$. For ![]() $t\in \Delta ^{*}$, we can express
$t\in \Delta ^{*}$, we can express
where ![]() $\psi (t)$ is a holomorphic function on
$\psi (t)$ is a holomorphic function on ![]() $\Delta$ with values in complex symmetric
$\Delta$ with values in complex symmetric ![]() $g\times g$ matrices such that
$g\times g$ matrices such that ![]() $\psi (0)=\binom {\psi _{0}\,{}^{t}\omega _{0}}{\omega _{0}\, Z_{0}}$,
$\psi (0)=\binom {\psi _{0}\,{}^{t}\omega _{0}}{\omega _{0}\, Z_{0}}$, ![]() $Z_{0}\in {\frak S}_{g-1}$,
$Z_{0}\in {\frak S}_{g-1}$, ![]() $\Omega (\hat {C}_{0})=[Z_{0}]\in {\mathcal {A}}_{g-1}$.
$\Omega (\hat {C}_{0})=[Z_{0}]\in {\mathcal {A}}_{g-1}$.
By the assumption ![]() $\chi _{g}(\Omega (C_{t}))=0$,
$\chi _{g}(\Omega (C_{t}))=0$, ![]() $\Upsilon _{g}(\Omega (C_{t}))\not =0$ for all
$\Upsilon _{g}(\Omega (C_{t}))\not =0$ for all ![]() $t\in \Delta ^{*}$ and Lemma 4.1,
$t\in \Delta ^{*}$ and Lemma 4.1, ![]() $C_{t}$ has a unique effective even theta characteristic for
$C_{t}$ has a unique effective even theta characteristic for ![]() $t\in \Delta ^{*}$. By fixing a marking of a reference curve, there is a unique even pair
$t\in \Delta ^{*}$. By fixing a marking of a reference curve, there is a unique even pair ![]() $(a,b)$,
$(a,b)$, ![]() $a,b\in \{0,1/2\}^{g}$, such that
$a,b\in \{0,1/2\}^{g}$, such that ![]() $\theta _{a,b}(\Omega (C_{t}))=0$ on
$\theta _{a,b}(\Omega (C_{t}))=0$ on ![]() $\Delta$ and
$\Delta$ and ![]() $\theta _{c,d}(\Omega (C_{t}))\not =0$ on
$\theta _{c,d}(\Omega (C_{t}))\not =0$ on ![]() $\Delta ^{*}$ for all even
$\Delta ^{*}$ for all even ![]() $(c,d)\not =(a,b)$. Write
$(c,d)\not =(a,b)$. Write ![]() $a=(a_{1},a')$ and
$a=(a_{1},a')$ and ![]() $b=(b_{1},b')$. If
$b=(b_{1},b')$. If ![]() $a_{1}=0$, then we get
$a_{1}=0$, then we get ![]() $\theta _{a',b'}(Z_{0})=0$ for the even pair
$\theta _{a',b'}(Z_{0})=0$ for the even pair ![]() $(a',b')$,
$(a',b')$, ![]() $a',b'\in \{0,1/2\}^{g-1}$, by Yoshikawa [Reference YoshikawaYos13, (4.4)], which contradicts the assumption
$a',b'\in \{0,1/2\}^{g-1}$, by Yoshikawa [Reference YoshikawaYos13, (4.4)], which contradicts the assumption ![]() $\chi _{g-1}(Z_{0})=\chi _{g-1}(\Omega (\hat {C}_{0}))\not =0$. Thus
$\chi _{g-1}(Z_{0})=\chi _{g-1}(\Omega (\hat {C}_{0}))\not =0$. Thus ![]() $a_{1}=1/2$.
$a_{1}=1/2$.
By [Reference YoshikawaYos13, (4.3), (4.4)], there is a holomorphic function ![]() $F_{a,b}(\zeta ,\omega ,Z)$ such that
$F_{a,b}(\zeta ,\omega ,Z)$ such that
Hence there is a holomorphic function ![]() $\phi (\zeta ,\omega ,Z)$ such that
$\phi (\zeta ,\omega ,Z)$ such that
Since ![]() $\Upsilon _{g}(\Omega )$ is a Siegel modular form and hence
$\Upsilon _{g}(\Omega )$ is a Siegel modular form and hence ![]() $\Upsilon _{g}(\Omega +A)=\Upsilon _{g}(\Omega )$,
$\Upsilon _{g}(\Omega +A)=\Upsilon _{g}(\Omega )$, ![]() $\phi (\zeta ,\omega ,Z)$ is an even function in
$\phi (\zeta ,\omega ,Z)$ is an even function in ![]() $\zeta$. There exists a holomorphic function
$\zeta$. There exists a holomorphic function ![]() $h(t)\in {\mathcal {O}}(\Delta )$ such that
$h(t)\in {\mathcal {O}}(\Delta )$ such that
This, together with [Reference YoshikawaYos13, (4.7)], implies the result.
As a consequence of Lemma 4.2, we get the following result.
Lemma 4.3 Let ![]() $M\subset {\Bbb L}_{K3}$ be a primitive
$M\subset {\Bbb L}_{K3}$ be a primitive ![]() $2$-elementary Lorentzian sublattice and set
$2$-elementary Lorentzian sublattice and set ![]() $\Lambda =M^{\perp }$. Let
$\Lambda =M^{\perp }$. Let ![]() $\gamma \colon \Delta \to {\mathcal {M}}_{\Lambda }$ be a holomorphic curve with
$\gamma \colon \Delta \to {\mathcal {M}}_{\Lambda }$ be a holomorphic curve with ![]() $\gamma (\Delta ^{*})\subset {\mathcal {M}}_{\Lambda }^{0}$ intersecting
$\gamma (\Delta ^{*})\subset {\mathcal {M}}_{\Lambda }^{0}$ intersecting ![]() $\bar {\mathcal {D}}_{\Lambda }^{0}$ transversally at
$\bar {\mathcal {D}}_{\Lambda }^{0}$ transversally at ![]() $\gamma (0)\in \bar {\mathcal {D}}_{\Lambda }^{0}$. Let
$\gamma (0)\in \bar {\mathcal {D}}_{\Lambda }^{0}$. Let ![]() $\tilde {\gamma }\colon \Delta \to \Omega _{\Lambda }$ be its lift with
$\tilde {\gamma }\colon \Delta \to \Omega _{\Lambda }$ be its lift with ![]() $\gamma (t^{2})=\Pi _{\Lambda }\circ \tilde {\gamma }(t)$ and let
$\gamma (t^{2})=\Pi _{\Lambda }\circ \tilde {\gamma }(t)$ and let ![]() $d\in \Delta _{\Lambda }^{-}$ be such that
$d\in \Delta _{\Lambda }^{-}$ be such that ![]() $\tilde {\gamma }(0)\in H_{d}$. If
$\tilde {\gamma }(0)\in H_{d}$. If ![]() $\chi _{g}({J}_{M}(\tilde {\gamma }(t)))=0$ and
$\chi _{g}({J}_{M}(\tilde {\gamma }(t)))=0$ and ![]() $\Upsilon _{g}({J}_{M}(\tilde {\gamma }(t)))\not =0$ for all
$\Upsilon _{g}({J}_{M}(\tilde {\gamma }(t)))\not =0$ for all ![]() $t\in \Delta ^{*}$ and if
$t\in \Delta ^{*}$ and if ![]() $\chi _{g-1}(J_{[M\perp d]}(\tilde {\gamma }(0)))\not =0$, then
$\chi _{g-1}(J_{[M\perp d]}(\tilde {\gamma }(0)))\not =0$, then
Proof. Let ![]() $\bar {J}_{M}\colon {\mathcal {M}}_{\Lambda }^{0}\cup \bar {\mathcal {D}}_{\Lambda }^{0}\to {\mathcal {A}}_{g}^{*}$ be the extension of
$\bar {J}_{M}\colon {\mathcal {M}}_{\Lambda }^{0}\cup \bar {\mathcal {D}}_{\Lambda }^{0}\to {\mathcal {A}}_{g}^{*}$ be the extension of ![]() $\bar {J}_{M}^{0}\colon {\mathcal {M}}_{\Lambda }^{0}\to {\mathcal {A}}_{g}$. By [Reference YoshikawaYos13, Theorem 2.3(1) and (2)], there is an ordinary singular family of curves
$\bar {J}_{M}^{0}\colon {\mathcal {M}}_{\Lambda }^{0}\to {\mathcal {A}}_{g}$. By [Reference YoshikawaYos13, Theorem 2.3(1) and (2)], there is an ordinary singular family of curves ![]() $p\colon {\mathcal {C}}\to \Delta$ of genus
$p\colon {\mathcal {C}}\to \Delta$ of genus ![]() $g$ with irreducible
$g$ with irreducible ![]() $C_{0}$ and with period map
$C_{0}$ and with period map ![]() $\bar {J}_{M}\circ \gamma$. By Lemma 4.2, we get
$\bar {J}_{M}\circ \gamma$. By Lemma 4.2, we get
which, together with ![]() $J_{M}(\gamma (t^{2}))=\bar {J}_{M}(\tilde {\gamma }(t))$, yields the result.
$J_{M}(\gamma (t^{2}))=\bar {J}_{M}(\tilde {\gamma }(t))$, yields the result.
4.2 Automorphic forms on  $\Omega _{\Lambda }$
$\Omega _{\Lambda }$
Let ![]() $M\subset {\Bbb L}_{K3}$ be a primitive
$M\subset {\Bbb L}_{K3}$ be a primitive ![]() $2$-elementary Lorentzian sublattice and set
$2$-elementary Lorentzian sublattice and set ![]() $\Lambda =M^{\perp }$ as before. Let
$\Lambda =M^{\perp }$ as before. Let ![]() $q\in \textbf {Z}_{>0}$ be such that
$q\in \textbf {Z}_{>0}$ be such that ![]() ${\mathcal {F}}_{g}^{\otimes q}$ extends to a very ample line bundle on
${\mathcal {F}}_{g}^{\otimes q}$ extends to a very ample line bundle on ![]() ${\mathcal {A}}_{g}^{*}$. Let
${\mathcal {A}}_{g}^{*}$. Let ![]() $i\colon \Omega _{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{0}\hookrightarrow \Omega _{\Lambda }$ be the inclusion and define
$i\colon \Omega _{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{0}\hookrightarrow \Omega _{\Lambda }$ be the inclusion and define ![]() $\lambda _{M}^{q}$ as the trivial extension of
$\lambda _{M}^{q}$ as the trivial extension of ![]() $J_{M}^{*}{\mathcal {F}}_{g(M)}^{\otimes q}$ from
$J_{M}^{*}{\mathcal {F}}_{g(M)}^{\otimes q}$ from ![]() $\Omega _{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{0}$ to
$\Omega _{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{0}$ to ![]() $\Omega _{\Lambda }$, that is,
$\Omega _{\Lambda }$, that is,
Since ![]() $\Omega _{\Lambda }\setminus (\Omega _{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{0})$ has codimension
$\Omega _{\Lambda }\setminus (\Omega _{\Lambda }^{0}\cup {\mathcal {D}}_{\Lambda }^{0})$ has codimension ![]() $2$ in
$2$ in ![]() $\Omega _{\Lambda }$,
$\Omega _{\Lambda }$, ![]() $\lambda _{M}^{q}$ is an
$\lambda _{M}^{q}$ is an ![]() $O(\Lambda )$-equivariant invertible sheaf on
$O(\Lambda )$-equivariant invertible sheaf on ![]() $\Omega _{\Lambda }$. On
$\Omega _{\Lambda }$. On ![]() $\Omega _{\Lambda }^{0}$,
$\Omega _{\Lambda }^{0}$, ![]() $\lambda _{M}^{q}$ is equipped with the Hermitian metric
$\lambda _{M}^{q}$ is equipped with the Hermitian metric
Fix ![]() $l_{\Lambda }\in \Lambda \otimes \textbf {R}$ with
$l_{\Lambda }\in \Lambda \otimes \textbf {R}$ with ![]() $\langle l_{\Lambda },l_{\Lambda }\rangle \geq 0$. Define
$\langle l_{\Lambda },l_{\Lambda }\rangle \geq 0$. Define ![]() $j_{\Lambda }(\gamma ,\cdot )\in {\mathcal {O}}^{*}_{\Omega _{\Lambda }}$,
$j_{\Lambda }(\gamma ,\cdot )\in {\mathcal {O}}^{*}_{\Omega _{\Lambda }}$, ![]() $\gamma \in O(\Lambda )$ and
$\gamma \in O(\Lambda )$ and ![]() $K_{\Lambda }(\cdot )\in C^{\infty }(\Omega _{\Lambda })$ by
$K_{\Lambda }(\cdot )\in C^{\infty }(\Omega _{\Lambda })$ by
Let ![]() $p,q\in \textbf {Z}$. Then
$p,q\in \textbf {Z}$. Then ![]() $F\in H^{0}(\Omega _{\Lambda },\lambda _{M}^{q})$ is called an automorphic form on
$F\in H^{0}(\Omega _{\Lambda },\lambda _{M}^{q})$ is called an automorphic form on ![]() $\Omega _{\Lambda }$ for
$\Omega _{\Lambda }$ for ![]() $O(\Lambda )$ of weight
$O(\Lambda )$ of weight ![]() $(p,q)$ if it satisfies the following functional equation on
$(p,q)$ if it satisfies the following functional equation on ![]() $\Omega _{\Lambda }$:
$\Omega _{\Lambda }$:
The notion of automorphic forms on ![]() $\Omega _{\Lambda }^{+}$ for
$\Omega _{\Lambda }^{+}$ for ![]() $O^{+}(\Lambda )$ of weight
$O^{+}(\Lambda )$ of weight ![]() $(p,q)$ is defined in the same way. In the rest of this paper the vector space of automorphic forms on
$(p,q)$ is defined in the same way. In the rest of this paper the vector space of automorphic forms on ![]() $\Omega _{\Lambda }$ for
$\Omega _{\Lambda }$ for ![]() $O(\Lambda )$ of weight
$O(\Lambda )$ of weight ![]() $(p,q)$ is identified with the vector space of automorphic forms on
$(p,q)$ is identified with the vector space of automorphic forms on ![]() $\Omega _{\Lambda }^{+}$ for
$\Omega _{\Lambda }^{+}$ for ![]() $O^{+}(\Lambda )$ of weight
$O^{+}(\Lambda )$ of weight ![]() $(p,q)$ via the restriction map
$(p,q)$ via the restriction map
We define the Petersson norm of an automorphic form ![]() $F$ on
$F$ on ![]() $\Omega _{\Lambda }$ for
$\Omega _{\Lambda }$ for ![]() $O(\Lambda )$ of weight
$O(\Lambda )$ of weight ![]() $(p,q)$ as the
$(p,q)$ as the ![]() $O(\Lambda )$-invariant
$O(\Lambda )$-invariant ![]() $C^{\infty }$ function on
$C^{\infty }$ function on ![]() $\Omega _{\Lambda }^{0}$ defined as
$\Omega _{\Lambda }^{0}$ defined as
5. The invariant  $\tau _{M}$ and its automorphic property
$\tau _{M}$ and its automorphic property
Let ![]() $(X,\iota )$ be a
$(X,\iota )$ be a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface of type
$K3$ surface of type ![]() $M$. Let
$M$. Let ![]() $\gamma$ be an
$\gamma$ be an ![]() $\iota$-invariant Kähler form on
$\iota$-invariant Kähler form on ![]() $X$. The Laplacian acting on
$X$. The Laplacian acting on ![]() $(0,q)$-forms on
$(0,q)$-forms on ![]() $X$ is denoted by
$X$ is denoted by ![]() $\square _{0.q}$. Write
$\square _{0.q}$. Write ![]() $\sigma (\square _{0,q})$ for the spectrum of
$\sigma (\square _{0,q})$ for the spectrum of ![]() $\square _{0,q}$ and
$\square _{0,q}$ and ![]() $E_{0,q}(\lambda )$ for eigenspace of
$E_{0,q}(\lambda )$ for eigenspace of ![]() $\square _{0,q}$ corresponding to
$\square _{0,q}$ corresponding to ![]() $\lambda \in \sigma (\square _{0,q})$. Since
$\lambda \in \sigma (\square _{0,q})$. Since ![]() $\iota$ preserves
$\iota$ preserves ![]() $\gamma$,
$\gamma$, ![]() $\iota$ acts on
$\iota$ acts on ![]() $E_{0,q}(\lambda )$. The equivariant zeta function of
$E_{0,q}(\lambda )$. The equivariant zeta function of ![]() $\square _{0,q}$ is defined as the following convergent series for
$\square _{0,q}$ is defined as the following convergent series for ![]() $s\in \textbf {C}$ with
$s\in \textbf {C}$ with ![]() $\Re s\gg 0$:
$\Re s\gg 0$:
Then ![]() $\zeta _{0,q}(\iota )(s)$ extends meromorphically to
$\zeta _{0,q}(\iota )(s)$ extends meromorphically to ![]() $\textbf {C}$ and is holomorphic at
$\textbf {C}$ and is holomorphic at ![]() $s=0$. We define the equivariant analytic torsion [Reference BismutBis95] of
$s=0$. We define the equivariant analytic torsion [Reference BismutBis95] of ![]() $(X,\gamma )$ as
$(X,\gamma )$ as
 \[ \tau_{\textbf{Z}_{2}}(X,\gamma)(\iota) := \exp\biggl[ -\sum_{q\geq0}(-1)^{q}q\,\zeta'_{0,q}(\iota)(0)\biggr]. \]
\[ \tau_{\textbf{Z}_{2}}(X,\gamma)(\iota) := \exp\biggl[ -\sum_{q\geq0}(-1)^{q}q\,\zeta'_{0,q}(\iota)(0)\biggr]. \]
Let ![]() $\eta \in H^{0}(X,K_{X})\setminus \{0\}$ and set
$\eta \in H^{0}(X,K_{X})\setminus \{0\}$ and set ![]() $\|\eta \|_{L^{2}}^{2}:=(2\pi )^{-2}\int _{X}\eta \wedge \bar {\eta }$. For a compact Kähler manifold
$\|\eta \|_{L^{2}}^{2}:=(2\pi )^{-2}\int _{X}\eta \wedge \bar {\eta }$. For a compact Kähler manifold ![]() $(V,\omega )$, define
$(V,\omega )$, define ![]() ${\rm Vol}(V,\omega ):=(2\pi )^{-\dim V}\int _{V}\omega ^{\dim V}/(\dim V)!$.
${\rm Vol}(V,\omega ):=(2\pi )^{-\dim V}\int _{V}\omega ^{\dim V}/(\dim V)!$.
When ![]() $X^{\iota }\not =\emptyset$, write
$X^{\iota }\not =\emptyset$, write ![]() $X^{\iota }=\amalg _{i}C_{i}$ for the decomposition into the connected components. Let
$X^{\iota }=\amalg _{i}C_{i}$ for the decomposition into the connected components. Let ![]() $\tau (C_{i},\gamma |_{C_{i}})$ be the analytic torsion [Reference Ray and SingerRS73] of
$\tau (C_{i},\gamma |_{C_{i}})$ be the analytic torsion [Reference Ray and SingerRS73] of ![]() $(C_{i},\gamma |_{C_{i}})$. We define
$(C_{i},\gamma |_{C_{i}})$. We define
When ![]() $X^{\iota }=\emptyset$, we set
$X^{\iota }=\emptyset$, we set ![]() $\tau (X^{\iota },\gamma |_{X^{\iota }})={\rm Vol}(X^{\iota },\gamma |_{X^{\iota }})=1$. Let
$\tau (X^{\iota },\gamma |_{X^{\iota }})={\rm Vol}(X^{\iota },\gamma |_{X^{\iota }})=1$. Let ![]() $c_{1}(X^{\iota },\gamma |_{X^{\iota }})$ be the first Chern form of
$c_{1}(X^{\iota },\gamma |_{X^{\iota }})$ be the first Chern form of ![]() $(X^{\iota },\gamma |_{X^{\iota }})$. By [Reference YoshikawaYos04, Theorem 5.7], the real number
$(X^{\iota },\gamma |_{X^{\iota }})$. By [Reference YoshikawaYos04, Theorem 5.7], the real number
 \begin{align*} \tau_{M}(X,\iota) &:= {\rm Vol}(X,\gamma)^{({14-r(M)})/{4}} \tau_{\textbf{Z}_{2}}(X,\gamma)(\iota)\, {\rm Vol}(X^{\iota},\gamma|_{X^{\iota}}) \tau(X^{\iota},\gamma|_{X^{\iota}})\\ &\quad \times \exp\biggl[\frac{1}{8}\int_{X^{\iota}} \log\left.\biggl(\frac{\eta\wedge\bar{\eta}} {\gamma^{2}/2!}\cdot \frac{{\rm Vol}(X,\gamma)}{\|\eta\|_{L^{2}}^{2}} \biggl)\right|_{X^{\iota}} c_{1}(X^{\iota},\gamma|_{X^{\iota}}) \biggl] \end{align*}
\begin{align*} \tau_{M}(X,\iota) &:= {\rm Vol}(X,\gamma)^{({14-r(M)})/{4}} \tau_{\textbf{Z}_{2}}(X,\gamma)(\iota)\, {\rm Vol}(X^{\iota},\gamma|_{X^{\iota}}) \tau(X^{\iota},\gamma|_{X^{\iota}})\\ &\quad \times \exp\biggl[\frac{1}{8}\int_{X^{\iota}} \log\left.\biggl(\frac{\eta\wedge\bar{\eta}} {\gamma^{2}/2!}\cdot \frac{{\rm Vol}(X,\gamma)}{\|\eta\|_{L^{2}}^{2}} \biggl)\right|_{X^{\iota}} c_{1}(X^{\iota},\gamma|_{X^{\iota}}) \biggl] \end{align*}
is determined by the isomorphism class of ![]() $(X,\iota )$ and hence the period
$(X,\iota )$ and hence the period ![]() $\bar {\pi }_{M}(X,\iota )$. For the arithmetic counterpart of the invariant
$\bar {\pi }_{M}(X,\iota )$. For the arithmetic counterpart of the invariant ![]() $\tau _{M}(X,\iota )$, we refer to [Reference Maillot and RösslerMR09].
$\tau _{M}(X,\iota )$, we refer to [Reference Maillot and RösslerMR09].
We set ![]() $\Lambda =M^{\perp }$ and we regard
$\Lambda =M^{\perp }$ and we regard ![]() $\tau _{M}$ as the
$\tau _{M}$ as the ![]() $O(\Lambda )$-invariant function on
$O(\Lambda )$-invariant function on ![]() $\Omega _{\Lambda }^{0}$ or equivalently the function on
$\Omega _{\Lambda }^{0}$ or equivalently the function on ![]() ${\mathcal {M}}_{\Lambda }^{0}$ defined by
${\mathcal {M}}_{\Lambda }^{0}$ defined by
As an application of the theory of (equivariant) Quillen metrics [Reference Bismut, Gillet and SouléBGS88, Reference BismutBis95, Reference MaMa00], the automorphy of ![]() $\tau _{M}$ has been established.
$\tau _{M}$ has been established.
Theorem 5.1 [Yos04, Yos13, Yos12] There exist ![]() $\ell \in \textbf {Z}_{>0}$ and an automorphic form
$\ell \in \textbf {Z}_{>0}$ and an automorphic form ![]() $\Phi _{M}$ on
$\Phi _{M}$ on ![]() $\Omega _{\Lambda }$ for
$\Omega _{\Lambda }$ for ![]() $O(\Lambda )$ of weight
$O(\Lambda )$ of weight ![]() $(\ell (r(M)-6),4\ell )$ with
$(\ell (r(M)-6),4\ell )$ with
In the rest of this paper we determine ![]() $\Phi _{M}$ for all
$\Phi _{M}$ for all ![]() $M$. Since this was done for exceptional
$M$. Since this was done for exceptional ![]() $M$ in [Reference YoshikawaYos04],
$M$ in [Reference YoshikawaYos04], ![]() $M$ is assumed to be non-exceptional in what follows.
$M$ is assumed to be non-exceptional in what follows.
6. The locus of vanishing theta-null: the case  $\delta =1$
$\delta =1$
In the rest of this paper, for a primitive ![]() $2$-elementary Lorentzian sublattice
$2$-elementary Lorentzian sublattice ![]() $M\subset {\Bbb L}_{K3}$, we write
$M\subset {\Bbb L}_{K3}$, we write ![]() $r$,
$r$, ![]() $l$,
$l$, ![]() $\delta$,
$\delta$, ![]() $g$,
$g$, ![]() $k$ for
$k$ for ![]() $r(M)$,
$r(M)$, ![]() $l(M)$,
$l(M)$, ![]() $\delta (M)$,
$\delta (M)$, ![]() $g(M)$,
$g(M)$, ![]() $k(M)$, respectively, when there is no possibility of confusion. Recall that these invariants are introduced in §§ 1 and 3.2.1. We write
$k(M)$, respectively, when there is no possibility of confusion. Recall that these invariants are introduced in §§ 1 and 3.2.1. We write
Let ![]() ${\frak M}_{g}$ be the moduli space of smooth curves of genus
${\frak M}_{g}$ be the moduli space of smooth curves of genus ![]() $g\geq 1$. In this section and the next we study the Torelli map
$g\geq 1$. In this section and the next we study the Torelli map ![]() $J_M: \Omega _{\Lambda }^0\to \mathcal {A}_g$ from the geometric point of view. We here view the Torelli map rather as a morphism
$J_M: \Omega _{\Lambda }^0\to \mathcal {A}_g$ from the geometric point of view. We here view the Torelli map rather as a morphism
from the moduli space of 2-elementary ![]() $K3$ surfaces to that of curves, which associates to
$K3$ surfaces to that of curves, which associates to ![]() $(X, \iota )$ the genus
$(X, \iota )$ the genus ![]() $g$ component of
$g$ component of ![]() $X^{\iota }$. Our main purpose here is to describe the inverse image of a certain geometric locus in
$X^{\iota }$. Our main purpose here is to describe the inverse image of a certain geometric locus in ![]() $\frak {M}_g$ as a Heegner divisor of
$\frak {M}_g$ as a Heegner divisor of ![]() $\mathcal {M}_{\Lambda }^{0}$ in a few cases. This will be the first and necessary step toward a more complete description, Theorem 9.13, which will be obtained in the final part of the paper.
$\mathcal {M}_{\Lambda }^{0}$ in a few cases. This will be the first and necessary step toward a more complete description, Theorem 9.13, which will be obtained in the final part of the paper.
Recall that the characteristic Heegner divisor ![]() $\mathcal {H}_{\Lambda }$ of
$\mathcal {H}_{\Lambda }$ of ![]() $\Omega _{\Lambda }$ was defined in § 2.3, and that the theta-null divisor
$\Omega _{\Lambda }$ was defined in § 2.3, and that the theta-null divisor ![]() $\theta _{{\rm null},g}$ of
$\theta _{{\rm null},g}$ of ![]() ${\mathcal {A}}_{g}$ was defined in § 4.1. We denote by
${\mathcal {A}}_{g}$ was defined in § 4.1. We denote by
the reduced algebraic divisor corresponding to ![]() $\mathcal {H}_{\Lambda }$, and by
$\mathcal {H}_{\Lambda }$, and by
the reduced theta-null divisor in ![]() ${\frak M}_{g}$. It is well known that
${\frak M}_{g}$. It is well known that ![]() ${\frak M}_{g}'\subset {\frak M}_{g}$ is the locus of curves
${\frak M}_{g}'\subset {\frak M}_{g}$ is the locus of curves ![]() $C$ having an effective even theta characteristic, namely an effective line bundle
$C$ having an effective even theta characteristic, namely an effective line bundle ![]() $L$ with
$L$ with ![]() $L^{\otimes 2}\simeq K_C$ and
$L^{\otimes 2}\simeq K_C$ and ![]() $h^0(L)$ even.
$h^0(L)$ even.
In the present section we treat the moduli spaces in the following two series:
•
 $k=0$,
$k=0$,  $\delta =1$,
$\delta =1$,  $3\leq g\leq 10$;
$3\leq g\leq 10$;•
 $k=1$,
$k=1$,  $6\leq g\leq 9$.
$6\leq g\leq 9$.
Notice that in the second series we have ![]() $\delta =0$ only when
$\delta =0$ only when ![]() $g=6$. We will prove the following theorem.
$g=6$. We will prove the following theorem.
Theorem 6.1 If ![]() $3\leq g\leq 10$ and
$3\leq g\leq 10$ and ![]() $(k,\delta )=(0,1)$, the Heegner divisor
$(k,\delta )=(0,1)$, the Heegner divisor ![]() $\bar {\mathcal {H}}_{\Lambda }$ is irreducible and the following set-theoretic equality of (reduced) divisors of
$\bar {\mathcal {H}}_{\Lambda }$ is irreducible and the following set-theoretic equality of (reduced) divisors of ![]() $\mathcal {M}_{\Lambda }^0$ holds:
$\mathcal {M}_{\Lambda }^0$ holds:
The same assertion also holds for the second series when ![]() $\delta =1$, but the following weaker version will suffice for the rest of the paper.
$\delta =1$, but the following weaker version will suffice for the rest of the paper.
Proposition 6.2 If ![]() $6\leq g\leq 9$ and
$6\leq g\leq 9$ and ![]() $k=1$,
$k=1$, ![]() $\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^0)$ is not contained in
$\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^0)$ is not contained in ![]() ${\frak M}_{g}'$.
${\frak M}_{g}'$.
These results will be used in § 8. Theorem 6.1 will be proved in §§ 6.1–6.3, and Proposition 6.2 in § 6.5.
6.1 Proof of Theorem 6.1: the strategy
Let us first explain the outline of the proof of Theorem 6.1, reducing it to the construction of certain elliptic curves.
As the first step we see the irreducibility of ![]() $\bar {\mathcal {H}}_{\Lambda }$, which holds in a wider range.
$\bar {\mathcal {H}}_{\Lambda }$, which holds in a wider range.
Lemma 6.3 When ![]() $\delta =1$ and
$\delta =1$ and ![]() $r\leq 9$,
$r\leq 9$, ![]() $\bar {\mathcal {H}}_{\Lambda }$ is an irreducible divisor of
$\bar {\mathcal {H}}_{\Lambda }$ is an irreducible divisor of ![]() $\mathcal {M}_{\Lambda }$.
$\mathcal {M}_{\Lambda }$.
Proof. This is restated as the property that vectors ![]() $l\in \Lambda ^{\vee }$ with
$l\in \Lambda ^{\vee }$ with ![]() $(l, l)=\varepsilon _{\Lambda }$ and
$(l, l)=\varepsilon _{\Lambda }$ and ![]() $[l]= {\boldsymbol 1}_{\Lambda }$ are all equivalent under
$[l]= {\boldsymbol 1}_{\Lambda }$ are all equivalent under ![]() $O^+(\Lambda )$. Consider the vector
$O^+(\Lambda )$. Consider the vector ![]() $l'=2l$ in
$l'=2l$ in ![]() $\Lambda$. Since
$\Lambda$. Since ![]() $ {\boldsymbol 1}_{\Lambda }$ is of order
$ {\boldsymbol 1}_{\Lambda }$ is of order ![]() $2$,
$2$, ![]() $l'$ is primitive in
$l'$ is primitive in ![]() $\Lambda$ and satisfies
$\Lambda$ and satisfies
When ![]() $(r, l)\ne (9, 9)$, the lattice
$(r, l)\ne (9, 9)$, the lattice ![]() $\Lambda$ contains
$\Lambda$ contains ![]() $\mathbb {U}\oplus \mathbb {U}$, and then we can resort to the Eichler criterion (cf. [Reference ScattoneSca87]) which says that the
$\mathbb {U}\oplus \mathbb {U}$, and then we can resort to the Eichler criterion (cf. [Reference ScattoneSca87]) which says that the ![]() $O^+_0(\Lambda )$-equivalence class of a primitive vector
$O^+_0(\Lambda )$-equivalence class of a primitive vector ![]() $l'\in \Lambda$ depends only on the norm
$l'\in \Lambda$ depends only on the norm ![]() $(l', l')$ and the element
$(l', l')$ and the element ![]() $[l'/{\rm div}(l')]\in A_{\Lambda }$. Hence the above vectors
$[l'/{\rm div}(l')]\in A_{\Lambda }$. Hence the above vectors ![]() $l'=2l$ are all
$l'=2l$ are all ![]() $O^+_0(\Lambda )$-equivalent. When
$O^+_0(\Lambda )$-equivalent. When ![]() $(r, l)=(9, 9)$,
$(r, l)=(9, 9)$, ![]() $\bar {\mathcal {H}}_{\Lambda }$ is defined by
$\bar {\mathcal {H}}_{\Lambda }$ is defined by ![]() $(-2)$-vectors
$(-2)$-vectors ![]() $l'\in \Lambda$ with
$l'\in \Lambda$ with ![]() $\Lambda =\textbf {Z}l'\oplus (l')^{\perp }$. The isometry class of
$\Lambda =\textbf {Z}l'\oplus (l')^{\perp }$. The isometry class of ![]() $(l')^{\perp }$ is uniquely determined by [Reference NikulinNik80], namely
$(l')^{\perp }$ is uniquely determined by [Reference NikulinNik80], namely ![]() $(l')^{\perp }\simeq {\Bbb U}^{\oplus 2}\oplus {\Bbb E}_{8}(2)$, so that these
$(l')^{\perp }\simeq {\Bbb U}^{\oplus 2}\oplus {\Bbb E}_{8}(2)$, so that these ![]() $(-2)$-vectors
$(-2)$-vectors ![]() $l'$ are all
$l'$ are all ![]() ${\rm O}^{+}(\Lambda )$-equivalent.
${\rm O}^{+}(\Lambda )$-equivalent.
With the irreducibility of ![]() $\bar {\mathcal {H}}_{\Lambda }$ verified, the proof of Theorem 6.1 is reduced to showing the non-emptiness of
$\bar {\mathcal {H}}_{\Lambda }$ verified, the proof of Theorem 6.1 is reduced to showing the non-emptiness of ![]() $\bar {\mu }_{\Lambda }^{-1}({\frak M}_{g}')$ and the inclusion
$\bar {\mu }_{\Lambda }^{-1}({\frak M}_{g}')$ and the inclusion
We only need to verify (6.1) outside a locus of codimension at least ![]() $2$ of
$2$ of ![]() $\mathcal {M}_{\Lambda }^{0}$. Our approach will be based on the following geometric observation.
$\mathcal {M}_{\Lambda }^{0}$. Our approach will be based on the following geometric observation.
Proposition 6.4 Let ![]() $(X,\iota )$ be a
$(X,\iota )$ be a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface. If
$K3$ surface. If ![]() $X$ has a smooth elliptic curve
$X$ has a smooth elliptic curve ![]() $E$ with
$E$ with ![]() $E+\iota (E) \sim X^{\iota }$, then the period of
$E+\iota (E) \sim X^{\iota }$, then the period of ![]() $(X, \iota )$ is contained in the Heegner divisor
$(X, \iota )$ is contained in the Heegner divisor ![]() $\bar {\mathcal {H}}_{\Lambda }$.
$\bar {\mathcal {H}}_{\Lambda }$.
Proof. Let ![]() $H_{\pm }$ denote the
$H_{\pm }$ denote the ![]() $\iota$-(anti-)invariant lattices of
$\iota$-(anti-)invariant lattices of ![]() $(X, \iota )$. The cycle
$(X, \iota )$. The cycle ![]() $D_{\pm }:=E\pm \iota (E)$ is contained in
$D_{\pm }:=E\pm \iota (E)$ is contained in ![]() $H_{\pm }$, respectively. We will show that
$H_{\pm }$, respectively. We will show that ![]() $D_{-}$ satisfies
$D_{-}$ satisfies
The presence of such an anti-invariant cycle in the Picard lattice means that the period of ![]() $(X, \iota )$ lies in
$(X, \iota )$ lies in ![]() $\bar {\mathcal {H}}_{\Lambda }$.
$\bar {\mathcal {H}}_{\Lambda }$.
Since ![]() $E$ is an elliptic curve and hence its class in
$E$ is an elliptic curve and hence its class in ![]() $H^{2}(X,\textbf {Z})$ is isotropic, the first equality of (6.2) follows from
$H^{2}(X,\textbf {Z})$ is isotropic, the first equality of (6.2) follows from
The second property in (6.2) holds because
To see the last equality of (6.2), we note that the anti-isometry ![]() $\lambda :A_{H_+}\to A_{H_-}$ induced from the relation
$\lambda :A_{H_+}\to A_{H_-}$ induced from the relation ![]() $H_+=(H_-)^{\perp }\cap H^2(X,\textbf {Z})$ maps
$H_+=(H_-)^{\perp }\cap H^2(X,\textbf {Z})$ maps ![]() $[D_+/2]$ to
$[D_+/2]$ to ![]() $[D_-/2]$ because
$[D_-/2]$ because ![]() $D_+/2+D_-/2=E$ is contained in
$D_+/2+D_-/2=E$ is contained in ![]() $H^2(X,\textbf {Z})$. Since
$H^2(X,\textbf {Z})$. Since ![]() $[D_+/2]$ is the characteristic element of
$[D_+/2]$ is the characteristic element of ![]() $A_{H_+}$ by Lemma 6.5 below, so is
$A_{H_+}$ by Lemma 6.5 below, so is ![]() $[D_-/2]$ in
$[D_-/2]$ in ![]() $A_{H_-}$.
$A_{H_-}$.
Lemma 6.5 For any 2-elementary ![]() $K3$ surface
$K3$ surface ![]() $(X, \iota )$ the element
$(X, \iota )$ the element ![]() $[X^{\iota }/2]\in A_{H_+}$ is the characteristic element.
$[X^{\iota }/2]\in A_{H_+}$ is the characteristic element.
Proof. Let ![]() $f\colon X\to Y$ be the quotient map by
$f\colon X\to Y$ be the quotient map by ![]() $\iota$, and let
$\iota$, and let ![]() $B\subset Y$ be the branch curve. Every element of the dual lattice
$B\subset Y$ be the branch curve. Every element of the dual lattice ![]() $H_+^{\vee }$ can be written as
$H_+^{\vee }$ can be written as ![]() $f^{\ast }L/2$ for some
$f^{\ast }L/2$ for some ![]() $L\in {\rm Pic}(Y)$. Then
$L\in {\rm Pic}(Y)$. Then
We can see that ![]() $(L+K_Y, L)\in 2\textbf {Z}$ from the Riemann–Roch formula. Therefore
$(L+K_Y, L)\in 2\textbf {Z}$ from the Riemann–Roch formula. Therefore
which means that ![]() $X^{\iota }/2 \in H_+^{\vee }$ and that
$X^{\iota }/2 \in H_+^{\vee }$ and that ![]() $[X^{\iota }/2]$ is characteristic.
$[X^{\iota }/2]$ is characteristic.
In §§ 6.2 and 6.3, we will construct an elliptic curve ![]() $E$ as in Proposition 6.4. The non-emptiness of
$E$ as in Proposition 6.4. The non-emptiness of ![]() $\bar {\mu }_{\Lambda }^{-1}({\frak M}_{g}')$ will be seen in the course of proof.
$\bar {\mu }_{\Lambda }^{-1}({\frak M}_{g}')$ will be seen in the course of proof.
6.2 Proof of Theorem 6.1: the case  $g=3$
$g=3$
We begin with the case ![]() $g=3$. Recall that a smooth curve of genus
$g=3$. Recall that a smooth curve of genus ![]() $3$ has an effective even theta characteristic precisely when it is hyperelliptic. So let
$3$ has an effective even theta characteristic precisely when it is hyperelliptic. So let ![]() $(X, \iota )$ be a 2-elementary
$(X, \iota )$ be a 2-elementary ![]() $K3$ surface with
$K3$ surface with ![]() $(g, k)=(3, 0)$ such that
$(g, k)=(3, 0)$ such that ![]() $X^{\iota }$ is hyperelliptic. Consider the degree
$X^{\iota }$ is hyperelliptic. Consider the degree ![]() $4$ line bundle
$4$ line bundle ![]() $L=\mathcal {O}_{X}(X^{\iota })$, which is hyperelliptic in the sense of § 3.3. By Saint-Donat's classification,
$L=\mathcal {O}_{X}(X^{\iota })$, which is hyperelliptic in the sense of § 3.3. By Saint-Donat's classification, ![]() $L$ defines a degree
$L$ defines a degree ![]() $2$ morphism
$2$ morphism
onto a quadric ![]() $Q\subset \mathbf{P}^3$. We may assume that
$Q\subset \mathbf{P}^3$. We may assume that ![]() $L$ is ample, because the locus where
$L$ is ample, because the locus where ![]() $X^{\iota }$ is hyperelliptic and
$X^{\iota }$ is hyperelliptic and ![]() $\mathcal {O}_{X}(X^{\iota })$ is non-ample has codimension at least
$\mathcal {O}_{X}(X^{\iota })$ is non-ample has codimension at least ![]() $2$ in
$2$ in ![]() $\mathcal {M}_{\Lambda }^0$. In that case
$\mathcal {M}_{\Lambda }^0$. In that case ![]() $Q$ is smooth.
$Q$ is smooth.
Claim 6.6 ![]() $\iota$ acts on
$\iota$ acts on ![]() $Q$ by switching the two rulings on it.
$Q$ by switching the two rulings on it.
Proof. First note that ![]() $\iota$ acts on
$\iota$ acts on ![]() $Q$ non-trivially, for the branch curve of
$Q$ non-trivially, for the branch curve of ![]() $\phi$ is a member of
$\phi$ is a member of ![]() $|{-}2K_{Q}|$ and hence has genus
$|{-}2K_{Q}|$ and hence has genus ![]() $9$. Then
$9$. Then ![]() $\iota$ fixes the curve
$\iota$ fixes the curve ![]() $\phi (X^{\iota })$, which by the definition of
$\phi (X^{\iota })$, which by the definition of ![]() $\phi$ has bidegree
$\phi$ has bidegree ![]() $(1, 1)$. It is easily verified that any non-trivial involution of
$(1, 1)$. It is easily verified that any non-trivial involution of ![]() $Q$ fixing a smooth bidegree
$Q$ fixing a smooth bidegree ![]() $(1, 1)$ curve must switch the two rulings.
$(1, 1)$ curve must switch the two rulings.
We choose a ruling line ![]() $l$ on
$l$ on ![]() $Q$ and put
$Q$ and put ![]() $E = \phi ^{\ast }l$. Then
$E = \phi ^{\ast }l$. Then ![]() $E$ is a smooth elliptic curve on
$E$ is a smooth elliptic curve on ![]() $X$ for a general choice of
$X$ for a general choice of ![]() $l$ and satisfies the linear equivalence
$l$ and satisfies the linear equivalence
By Proposition 6.4, we get the inclusion (6.1).
The non-emptiness of ![]() $\bar {\mu }_{\Lambda }^{-1}({\frak M}_{3}')$ can be seen by reversing this construction: choose a bidegree
$\bar {\mu }_{\Lambda }^{-1}({\frak M}_{3}')$ can be seen by reversing this construction: choose a bidegree ![]() $(4, 4)$ curve
$(4, 4)$ curve ![]() $B\subset \mathbf{P}^1\times \mathbf{P}^1$ preserved by the switch involution of
$B\subset \mathbf{P}^1\times \mathbf{P}^1$ preserved by the switch involution of ![]() $\mathbf{P}^1\times \mathbf{P}^1$ and take the double cover
$\mathbf{P}^1\times \mathbf{P}^1$ and take the double cover ![]() $X\to \mathbf{P}^1\times \mathbf{P}^1$ branched over
$X\to \mathbf{P}^1\times \mathbf{P}^1$ branched over ![]() $B$. The switch involution can be lifted to
$B$. The switch involution can be lifted to ![]() $X$ so that its fixed curve is the preimage of the diagonal of
$X$ so that its fixed curve is the preimage of the diagonal of ![]() $\mathbf{P}^1\times \mathbf{P}^1$, which is hyperelliptic of genus
$\mathbf{P}^1\times \mathbf{P}^1$, which is hyperelliptic of genus ![]() $3$. Thus Theorem 6.1 is proved in the case
$3$. Thus Theorem 6.1 is proved in the case ![]() $g=3$.
$g=3$.
6.3 Proof of Theorem 6.1: the case  $4\leq g\leq 10$
$4\leq g\leq 10$
We next treat the case ![]() $4\leq g\leq 10$ in Theorem 6.1. Let
$4\leq g\leq 10$ in Theorem 6.1. Let ![]() $(X, \iota )$ be a 2-elementary
$(X, \iota )$ be a 2-elementary ![]() $K3$ surface with
$K3$ surface with ![]() $4\leq g\leq 10$,
$4\leq g\leq 10$, ![]() $k=0$ and
$k=0$ and ![]() $\delta =1$. Let
$\delta =1$. Let ![]() $Y=X/\iota$ be the quotient surface and
$Y=X/\iota$ be the quotient surface and ![]() $C\subset Y$ be the branch (
$C\subset Y$ be the branch (![]() $-2K_Y$)-curve. The quotient map
$-2K_Y$)-curve. The quotient map ![]() $X\to Y$ gives the canonical identification
$X\to Y$ gives the canonical identification
The anti-canonical model ![]() $\bar {Y}\subset \mathbf{P}^{g-1}$ of
$\bar {Y}\subset \mathbf{P}^{g-1}$ of ![]() $Y$ is a Gorenstein del Pezzo surface of degree
$Y$ is a Gorenstein del Pezzo surface of degree ![]() $g-1$, and
$g-1$, and ![]() $Y$ is its minimal resolution. Note that if
$Y$ is its minimal resolution. Note that if ![]() $X\to \bar {X}$ is the contraction of
$X\to \bar {X}$ is the contraction of ![]() $(-2)$-curves disjoint from
$(-2)$-curves disjoint from ![]() $X^{\iota }$, we naturally have
$X^{\iota }$, we naturally have ![]() $\bar {Y}\simeq \bar {X}/\iota$. We may view
$\bar {Y}\simeq \bar {X}/\iota$. We may view ![]() $C$ also as lying on the smooth locus of
$C$ also as lying on the smooth locus of ![]() $\bar {Y}$. By the adjunction formula we have
$\bar {Y}$. By the adjunction formula we have ![]() $-K_Y|_C\simeq K_C$, and the restriction map
$-K_Y|_C\simeq K_C$, and the restriction map ![]() $|{-}K_{Y}|\to |K_{C}|$ is isomorphic because
$|{-}K_{Y}|\to |K_{C}|$ is isomorphic because ![]() $h^{0}(K_{Y})=h^{1}(K_{Y})=0$. Therefore the composition of inclusions
$h^{0}(K_{Y})=h^{1}(K_{Y})=0$. Therefore the composition of inclusions
gives the canonical embedding of ![]() $C$, and we can identify
$C$, and we can identify ![]() $\mathbf{P}^{g-1}$ with
$\mathbf{P}^{g-1}$ with ![]() $|K_C|^{\vee }$. This also shows that
$|K_C|^{\vee }$. This also shows that ![]() $C$ is non-hyperelliptic.
$C$ is non-hyperelliptic.
Lemma 6.7 If ![]() $C$ has an effective even theta characteristic
$C$ has an effective even theta characteristic ![]() $L$, then
$L$, then ![]() $h^0(L)=2$.
$h^0(L)=2$.
Proof. If ![]() $h^0(L)\ne 2$, then
$h^0(L)\ne 2$, then ![]() $h^0(L)\geq 4$. By Clifford's theorem we have
$h^0(L)\geq 4$. By Clifford's theorem we have
This holds only when ![]() $g\geq 8$ and
$g\geq 8$ and ![]() $h^0(L)=4$. Actually the case
$h^0(L)=4$. Actually the case ![]() $g=8$ can be excluded because a blow-down of
$g=8$ can be excluded because a blow-down of ![]() $Y$ presents
$Y$ presents ![]() $C$ as a plane sextic with two double points and hence
$C$ as a plane sextic with two double points and hence ![]() $C$ has Clifford index
$C$ has Clifford index ![]() $2$. The case
$2$. The case ![]() $g=10$, where
$g=10$, where ![]() $C$ is a smooth plane sextic, is treated in [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, Exercise VI. B-3]. In the case
$C$ is a smooth plane sextic, is treated in [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, Exercise VI. B-3]. In the case ![]() $g=9$, presenting
$g=9$, presenting ![]() $C$ as plane sextic with a node or cusp, we can argue similarly.
$C$ as plane sextic with a node or cusp, we can argue similarly.
Proposition 6.8 There exists a locus ![]() ${\mathcal {Z}}\subset \mathcal {M}_{\Lambda }^{0}$ of codimension at least
${\mathcal {Z}}\subset \mathcal {M}_{\Lambda }^{0}$ of codimension at least ![]() $2$ with the following property. When
$2$ with the following property. When ![]() $(X, \iota )$ lies outside
$(X, \iota )$ lies outside ![]() ${\mathcal {Z}}$, the curve
${\mathcal {Z}}$, the curve ![]() $C$ has a theta characteristic
$C$ has a theta characteristic ![]() $L$ with
$L$ with ![]() $h^0(L)=2$ if and only if
$h^0(L)=2$ if and only if ![]() $C$ can be cut out from
$C$ can be cut out from ![]() $\bar {Y}$ by a quadric
$\bar {Y}$ by a quadric ![]() $Q\subset \mathbf{P}^{g-1}$ of rank
$Q\subset \mathbf{P}^{g-1}$ of rank ![]() $3$. In this case,
$3$. In this case, ![]() $L$ is base point free.
$L$ is base point free.
Proof. The proof consists of five steps.
Step 1. Assume that ![]() $C\subset \bar {Y}$ is cut out by a quadric
$C\subset \bar {Y}$ is cut out by a quadric ![]() $Q$ of rank
$Q$ of rank ![]() $3$. The vertex of
$3$. The vertex of ![]() $Q$, a
$Q$, a ![]() $(g-4)$-plane, is disjoint from
$(g-4)$-plane, is disjoint from ![]() $\bar {Y}$; otherwise
$\bar {Y}$; otherwise ![]() $C$ would be singular. The pencil of
$C$ would be singular. The pencil of ![]() $(g-3)$-planes in
$(g-3)$-planes in ![]() $Q$ gives
$Q$ gives ![]() $C$ a theta characteristic
$C$ a theta characteristic ![]() $L$ with
$L$ with ![]() $h^0(L)\geq 2$, which is free because
$h^0(L)\geq 2$, which is free because ![]() $C$ is disjoint from the vertex. We have
$C$ is disjoint from the vertex. We have ![]() $h^0(L)=2$, for
$h^0(L)=2$, for ![]() $|L|=|K_C-L|$ is identified with the linear system of hyperplanes of
$|L|=|K_C-L|$ is identified with the linear system of hyperplanes of ![]() $\mathbf{P}^{g-1}$ containing a
$\mathbf{P}^{g-1}$ containing a ![]() $(g-3)$-plane, which is a pencil.
$(g-3)$-plane, which is a pencil.
Step 2. Conversely, suppose that ![]() $C$ has a complete half-canonical pencil
$C$ has a complete half-canonical pencil ![]() $|L|$. Choose a basis
$|L|$. Choose a basis ![]() $\alpha , \beta$ of
$\alpha , \beta$ of ![]() $H^{0}(L)$ and write
$H^{0}(L)$ and write ![]() $|L|=|L_0|+D_0$ with
$|L|=|L_0|+D_0$ with ![]() $|L_0|$ the free part and
$|L_0|$ the free part and ![]() $D_0$ the fixed part. The divisor
$D_0$ the fixed part. The divisor ![]() $D_0$ is defined by
$D_0$ is defined by ![]() $\alpha =\beta =0$. If we set
$\alpha =\beta =0$. If we set
then ![]() $C$ is contained in the rank
$C$ is contained in the rank ![]() $3$ quadric
$3$ quadric ![]() $Q\subset \mathbf{P}^{g-1}$ defined by
$Q\subset \mathbf{P}^{g-1}$ defined by ![]() $u_1u_2=u_3^2$. The vertex of
$u_1u_2=u_3^2$. The vertex of ![]() $Q$ is the
$Q$ is the ![]() $(g-4)$-plane
$(g-4)$-plane ![]() $V$ defined (set-theoretically) by
$V$ defined (set-theoretically) by ![]() $(u_1=u_2=0)\cap Q$. The free part
$(u_1=u_2=0)\cap Q$. The free part ![]() $|L_0|$ is given by the pencil of
$|L_0|$ is given by the pencil of ![]() $(g-3)$-planes in
$(g-3)$-planes in ![]() $Q$ through
$Q$ through ![]() $V$, and the fixed part
$V$, and the fixed part ![]() $D_0$ is defined by
$D_0$ is defined by
In order to show that this quadric ![]() $Q$ cuts out
$Q$ cuts out ![]() $C$ from
$C$ from ![]() $\bar {Y}$, it suffices to prove
$\bar {Y}$, it suffices to prove ![]() $\bar {Y}\not \subset Q$, for then
$\bar {Y}\not \subset Q$, for then ![]() $C$ and
$C$ and ![]() $Q|_{\bar {Y}}$ are both (
$Q|_{\bar {Y}}$ are both (![]() $-2K_{\bar {Y}}$)-curves on
$-2K_{\bar {Y}}$)-curves on ![]() $\bar {Y}$.
$\bar {Y}$.
Step 3. Suppose the contrary: ![]() $\bar {Y}\subset Q$. We then have three linearly independent sections
$\bar {Y}\subset Q$. We then have three linearly independent sections ![]() $\tilde {u}_1, \tilde {u}_2, \tilde {u}_3\in H^0(-K_Y)$ on
$\tilde {u}_1, \tilde {u}_2, \tilde {u}_3\in H^0(-K_Y)$ on ![]() $Y$ with
$Y$ with ![]() $\tilde {u}_1\tilde {u}_2=\tilde {u}_3^2$ and
$\tilde {u}_1\tilde {u}_2=\tilde {u}_3^2$ and ![]() $u_i=\tilde {u}_i|_{C}$. Choose a blow-down
$u_i=\tilde {u}_i|_{C}$. Choose a blow-down ![]() $\pi :Y\to \mathbf{P}^2$ and let
$\pi :Y\to \mathbf{P}^2$ and let ![]() $Z\subset \mathbf{P}^{2}$ be the blown-up points (which possibly contain infinitely near ones). We have
$Z\subset \mathbf{P}^{2}$ be the blown-up points (which possibly contain infinitely near ones). We have ![]() $\# Z = 10-g$. The image
$\# Z = 10-g$. The image ![]() $\pi (C)$ of
$\pi (C)$ of ![]() $C$ is a plane sextic having double points at
$C$ is a plane sextic having double points at ![]() $Z$ and no other singularities. Via the mapping
$Z$ and no other singularities. Via the mapping
we can identify ![]() $|{-}K_Y|$ with the linear system of plane cubics through
$|{-}K_Y|$ with the linear system of plane cubics through ![]() $Z$, and
$Z$, and ![]() $D$ is recovered from
$D$ is recovered from ![]() $\Gamma =\pi (D)$ by
$\Gamma =\pi (D)$ by ![]() $D=\pi ^{\ast }\Gamma -\pi ^{-1}(Z)$. Now by our assumption
$D=\pi ^{\ast }\Gamma -\pi ^{-1}(Z)$. Now by our assumption ![]() $\tilde {u}_1\tilde {u}_2=\tilde {u}_3^{2}$, the divisors of
$\tilde {u}_1\tilde {u}_2=\tilde {u}_3^{2}$, the divisors of ![]() $\tilde {u}_1$,
$\tilde {u}_1$, ![]() $\tilde {u}_2$,
$\tilde {u}_2$, ![]() $\tilde {u}_3$ correspond to three linearly independent cubics
$\tilde {u}_3$ correspond to three linearly independent cubics ![]() $\Gamma _1$,
$\Gamma _1$, ![]() $\Gamma _2$,
$\Gamma _2$, ![]() $\Gamma _3$ with
$\Gamma _3$ with ![]() $\Gamma _1+\Gamma _2=2\Gamma _3$. This equality can hold only when
$\Gamma _1+\Gamma _2=2\Gamma _3$. This equality can hold only when
for some distinct lines ![]() $l_1, l_2, l$. Let
$l_1, l_2, l$. Let ![]() $p=l_1\cap l_2$. The net spanned by
$p=l_1\cap l_2$. The net spanned by ![]() $\Gamma _1, \Gamma _2, \Gamma _3$ consists of splitting cubics
$\Gamma _1, \Gamma _2, \Gamma _3$ consists of splitting cubics ![]() $l+l'+l''$ where
$l+l'+l''$ where ![]() $l', l''$ are lines through
$l', l''$ are lines through ![]() $p$. In particular, its base locus is
$p$. In particular, its base locus is ![]() $p\cup l$. Recall that the restriction of this net to
$p\cup l$. Recall that the restriction of this net to ![]() $C$, after the transformation (6.5), is equal to
$C$, after the transformation (6.5), is equal to ![]() $\mathbf{P}\langle u_1, u_2, u_3\rangle = \mathbf{P}{\rm Sym}^2H^0(L)$.
$\mathbf{P}\langle u_1, u_2, u_3\rangle = \mathbf{P}{\rm Sym}^2H^0(L)$.
Step 4. For a plane curve ![]() $\Gamma$ we write
$\Gamma$ we write ![]() $\hat {\Gamma }$ for its strict transform in
$\hat {\Gamma }$ for its strict transform in ![]() $Y$. We also denote
$Y$. We also denote ![]() $E=\pi ^{-1}(p)$. We observe the following:
$E=\pi ^{-1}(p)$. We observe the following:
(1)
 $Z$ lies on
$Z$ lies on  $p\cup l$;
$p\cup l$;(2)
 $p\in Z$ and
$p\in Z$ and  $p\notin l$;
$p\notin l$;(3) the free part
 $|L_0|$ is given by the projection from
$|L_0|$ is given by the projection from  $p$;
$p$;(4) the fixed part
 $D_0$ is given by
(6.6)
$D_0$ is given by
(6.6) \begin{equation} 2D_0 = (\hat{l}+E)|_{C}. \end{equation}
\begin{equation} 2D_0 = (\hat{l}+E)|_{C}. \end{equation}
Statement (1) is obvious. We can see (3) by noticing that ![]() $\phi _{L_0}:C\to \mathbf{P}^1$ coincides with the projection from
$\phi _{L_0}:C\to \mathbf{P}^1$ coincides with the projection from ![]() $p$ after composing them with the conic embedding
$p$ after composing them with the conic embedding ![]() $\mathbf{P}^1\hookrightarrow \mathbf{P}^2$, the composition being the resolution of the rational map defined by
$\mathbf{P}^1\hookrightarrow \mathbf{P}^2$, the composition being the resolution of the rational map defined by ![]() ${\rm Sym}^2H^0(L)$. Under (2), we have
${\rm Sym}^2H^0(L)$. Under (2), we have ![]() ${\rm div}(\tilde {u}_i)=2\hat {l}_i+E+\hat {l}$ for
${\rm div}(\tilde {u}_i)=2\hat {l}_i+E+\hat {l}$ for ![]() $i=1, 2$, so that (4) follows from (6.4). It remains to see (2). Firstly, if
$i=1, 2$, so that (4) follows from (6.4). It remains to see (2). Firstly, if ![]() $p\notin \pi (C)$, then
$p\notin \pi (C)$, then ![]() $L_0\sim \pi ^{*}\mathcal {O}_{\mathbf{P}^2}(1)|_{C}$ which is absurd. If
$L_0\sim \pi ^{*}\mathcal {O}_{\mathbf{P}^2}(1)|_{C}$ which is absurd. If ![]() $p\in \pi (C)$ but
$p\in \pi (C)$ but ![]() $p\notin Z={\rm Sing}(\pi (C))$, then
$p\notin Z={\rm Sing}(\pi (C))$, then ![]() $L_0\sim \pi ^{*}\mathcal {O}_{\mathbf{P}^2}(1)|_{C} - \pi ^{-1}(p)$ by (3) and
$L_0\sim \pi ^{*}\mathcal {O}_{\mathbf{P}^2}(1)|_{C} - \pi ^{-1}(p)$ by (3) and ![]() $D_0\ni \pi ^{-1}(p)$ by (6.4). It follows that
$D_0\ni \pi ^{-1}(p)$ by (6.4). It follows that ![]() $L\geq \pi ^{*}{\mathcal {O}}_{\mathbf{P}^{2}}(1)|_{C}$, and hence
$L\geq \pi ^{*}{\mathcal {O}}_{\mathbf{P}^{2}}(1)|_{C}$, and hence ![]() ${\dim } |L| \geq 2$, a contradiction. Therefore
${\dim } |L| \geq 2$, a contradiction. Therefore ![]() $p\in Z$. Next assume
$p\in Z$. Next assume ![]() $p\in l\cap Z$. Then both
$p\in l\cap Z$. Then both ![]() $\Gamma _1$ and
$\Gamma _1$ and ![]() $\Gamma _2$ have multiplicity
$\Gamma _2$ have multiplicity ![]() $3$ at
$3$ at ![]() $p$, so that
$p$, so that ![]() ${\rm div}(\tilde {u}_i)=2\hat {l}_i+2E+\hat {l}$ for
${\rm div}(\tilde {u}_i)=2\hat {l}_i+2E+\hat {l}$ for ![]() $i=1, 2$. Then
$i=1, 2$. Then ![]() $2D_{0}=(2E+\hat {l})|_{C}$ by (6.4). Since
$2D_{0}=(2E+\hat {l})|_{C}$ by (6.4). Since ![]() $L_{0}\sim \pi ^{*}\mathcal {O}_{\mathbf{P}^2}(1)|_{C}-E|_{C}$ by (3), we have
$L_{0}\sim \pi ^{*}\mathcal {O}_{\mathbf{P}^2}(1)|_{C}-E|_{C}$ by (3), we have ![]() $L\geq \pi ^{*}{\mathcal {O}}_{\mathbf{P}^{2}}(1)|_{C}$, the same contradiction as before. This verifies (2).
$L\geq \pi ^{*}{\mathcal {O}}_{\mathbf{P}^{2}}(1)|_{C}$, the same contradiction as before. This verifies (2).
Step 5. Now since the ![]() $9-g$ points
$9-g$ points ![]() $Z\backslash p$ lie on
$Z\backslash p$ lie on ![]() $l$ and since no four points of
$l$ and since no four points of ![]() $Z$ can be collinear by the nefness of
$Z$ can be collinear by the nefness of ![]() $-K_{Y}$, we must have
$-K_{Y}$, we must have ![]() $|Z\setminus p|\leq 3$ and thus
$|Z\setminus p|\leq 3$ and thus ![]() $6 \leq g\leq 9$. The right-hand side of (6.6) is divisible by
$6 \leq g\leq 9$. The right-hand side of (6.6) is divisible by ![]() $2$ only if
$2$ only if ![]() $\pi (C)$ is totally tangent to
$\pi (C)$ is totally tangent to ![]() $l$ outside
$l$ outside ![]() $Z={\rm Sing}(\pi (C))$ and
$Z={\rm Sing}(\pi (C))$ and ![]() $\pi (C)$ has a cusp at
$\pi (C)$ has a cusp at ![]() $p$. The cusp condition defines a divisor in the moduli space; when
$p$. The cusp condition defines a divisor in the moduli space; when ![]() $7\leq g \leq 9$ (respectively,
$7\leq g \leq 9$ (respectively, ![]() $g=6$), the tangency condition (respectively, the collinear condition on the three points
$g=6$), the tangency condition (respectively, the collinear condition on the three points ![]() $Z\setminus p$) defines another divisor. These two divisors, both Heegner and irreducible, define a codimension
$Z\setminus p$) defines another divisor. These two divisors, both Heegner and irreducible, define a codimension ![]() $2$ locus
$2$ locus ![]() ${\mathcal {Z}}$ in the moduli space. If
${\mathcal {Z}}$ in the moduli space. If ![]() $(X,\iota )\not \in {\mathcal {Z}}$, then (6.6) cannot hold and thus
$(X,\iota )\not \in {\mathcal {Z}}$, then (6.6) cannot hold and thus ![]() $\bar {Y}\not \subset Q$. By step 2, this implies that
$\bar {Y}\not \subset Q$. By step 2, this implies that ![]() $C$ is cut out from
$C$ is cut out from ![]() $\bar {Y}$ by
$\bar {Y}$ by ![]() $Q$ when
$Q$ when ![]() $(X,\iota )\not \in {\mathcal {Z}}$.
$(X,\iota )\not \in {\mathcal {Z}}$.
Since the intersection of a general Del Pezzo surface ![]() $Y\subset \mathbf{P}^{g-1}$ and a quadric
$Y\subset \mathbf{P}^{g-1}$ and a quadric ![]() $Q\subset \mathbf{P}^{g-1}$ of rank
$Q\subset \mathbf{P}^{g-1}$ of rank ![]() $3$ is a smooth curve, we see the non-emptiness of
$3$ is a smooth curve, we see the non-emptiness of ![]() $\bar {\mu }_{\Lambda }^{-1}({\frak M}_{g}')$.
$\bar {\mu }_{\Lambda }^{-1}({\frak M}_{g}')$.
Now let ![]() $C\subset \bar {Y}$ be cut out by a quadric
$C\subset \bar {Y}$ be cut out by a quadric ![]() $Q$ of rank
$Q$ of rank ![]() $3$. We take the double cover
$3$. We take the double cover
branched over ![]() $Q$. The (contracted) quotient map
$Q$. The (contracted) quotient map ![]() $\bar {X}\to \bar {Y}$ by
$\bar {X}\to \bar {Y}$ by ![]() $\iota$ can be identified with the restriction
$\iota$ can be identified with the restriction ![]() $\pi ^{-1}(\bar {Y})\to \bar {Y}$ of
$\pi ^{-1}(\bar {Y})\to \bar {Y}$ of ![]() $\pi$. We again denote by
$\pi$. We again denote by ![]() $\iota$ the covering transformation of
$\iota$ the covering transformation of ![]() $\pi : \tilde {Q} \to \mathbf{P}^{g-1}$. We also view
$\pi : \tilde {Q} \to \mathbf{P}^{g-1}$. We also view ![]() $\bar {X}\subset \mathbf{P}^{g}$ naturally. Note that
$\bar {X}\subset \mathbf{P}^{g}$ naturally. Note that ![]() $\tilde {Q}$ is a quadric of rank
$\tilde {Q}$ is a quadric of rank ![]() $4$ in
$4$ in ![]() $\mathbf{P}^g$ and hence is the cone over a smooth quadric surface
$\mathbf{P}^g$ and hence is the cone over a smooth quadric surface ![]() $Q_0\simeq \mathbf{P}^1\times \mathbf{P}^1$ with vertex
$Q_0\simeq \mathbf{P}^1\times \mathbf{P}^1$ with vertex ![]() $\mathbf{P}^{g-4}$. Let
$\mathbf{P}^{g-4}$. Let ![]() $f\colon \tilde {Q}\dashrightarrow Q_0$ be the projection from the vertex. Then the pencils
$f\colon \tilde {Q}\dashrightarrow Q_0$ be the projection from the vertex. Then the pencils ![]() $f^{\ast }|\mathcal {O}_{Q_0}(1, 0)|$ and
$f^{\ast }|\mathcal {O}_{Q_0}(1, 0)|$ and ![]() $f^{\ast }|\mathcal {O}_{Q_0}(0, 1)|$ are
$f^{\ast }|\mathcal {O}_{Q_0}(0, 1)|$ are ![]() $\mathbf{P}^1$-families of
$\mathbf{P}^1$-families of ![]() $(g-2)$-planes that sweep out
$(g-2)$-planes that sweep out ![]() $\tilde {Q}$. As is easily verified,
$\tilde {Q}$. As is easily verified, ![]() $\iota$ switches these two rulings. Restricted to
$\iota$ switches these two rulings. Restricted to ![]() $\bar {X}=\pi ^{-1}(\bar {Y})$, the pencil
$\bar {X}=\pi ^{-1}(\bar {Y})$, the pencil ![]() $f^{\ast }|\mathcal {O}_{Q_0}(1, 0)|$ induces an elliptic fibration on
$f^{\ast }|\mathcal {O}_{Q_0}(1, 0)|$ induces an elliptic fibration on ![]() $X$, say
$X$, say ![]() $|E|$. The cycle
$|E|$. The cycle ![]() $E+\iota (E)$ is a hyperplane section of
$E+\iota (E)$ is a hyperplane section of ![]() $\bar {X}\subset \mathbf{P}^{g}$. On the other hand,
$\bar {X}\subset \mathbf{P}^{g}$. On the other hand, ![]() $X^{\iota }\subset \bar {X}$ is the ramification divisor of
$X^{\iota }\subset \bar {X}$ is the ramification divisor of ![]() $\bar {X}\to \bar {Y}$ and hence also cut out by a hyperplane of
$\bar {X}\to \bar {Y}$ and hence also cut out by a hyperplane of ![]() $\mathbf{P}^g$. Therefore
$\mathbf{P}^g$. Therefore ![]() $E+\iota (E)$ is linearly equivalent to
$E+\iota (E)$ is linearly equivalent to ![]() $X^{\iota }$ on
$X^{\iota }$ on ![]() $X$. By Proposition 6.4, Theorem 6.1 is proved in the case
$X$. By Proposition 6.4, Theorem 6.1 is proved in the case ![]() $4\leq g\leq 10$.
$4\leq g\leq 10$.
Remark 6.9 In the above construction, the given half-canonical pencil on ![]() $C\simeq X^{\iota }$ coincides with the restriction of the elliptic fibration
$C\simeq X^{\iota }$ coincides with the restriction of the elliptic fibration ![]() $|E|$: this follows because
$|E|$: this follows because ![]() $|E|$ is the restriction of a
$|E|$ is the restriction of a ![]() $\mathbf{P}^{g-2}$-ruling on
$\mathbf{P}^{g-2}$-ruling on ![]() $\tilde {Q}$, which in turn is a component in the pullback of the family of hyperplanes in
$\tilde {Q}$, which in turn is a component in the pullback of the family of hyperplanes in ![]() $\mathbf{P}^{g-1}$ that cut out doubly from
$\mathbf{P}^{g-1}$ that cut out doubly from ![]() $Q$ the
$Q$ the ![]() $\mathbf{P}^{g-3}$-ruling.
$\mathbf{P}^{g-3}$-ruling.
Remark 6.10 A general member of ![]() $\bar {\mu }_{\Lambda }^{-1}({\frak M}_{g}')$ has a unique effective even theta characteristic, because the period of those
$\bar {\mu }_{\Lambda }^{-1}({\frak M}_{g}')$ has a unique effective even theta characteristic, because the period of those ![]() $(X, \iota )$ having several elliptic curve classes
$(X, \iota )$ having several elliptic curve classes ![]() $[E]$ with
$[E]$ with ![]() $E+\iota (E)\sim X^{\iota }$ lies in (the image of) the intersection of at least two components of
$E+\iota (E)\sim X^{\iota }$ lies in (the image of) the intersection of at least two components of ![]() $\mathcal {H}_{\Lambda }$.
$\mathcal {H}_{\Lambda }$.
6.4 Trigonal curves
This subsection is a prerequisite for the subsequent §§ 6.5 and 7. A smooth projective curve ![]() $C$ of genus
$C$ of genus ![]() $g\geq 5$ is said to be trigonal if it has a degree
$g\geq 5$ is said to be trigonal if it has a degree ![]() $3$ morphism to
$3$ morphism to ![]() $\mathbf{P}^1$. Such a morphism, if it exists, is unique up to
$\mathbf{P}^1$. Such a morphism, if it exists, is unique up to ![]() ${\rm Aut}(\mathbf{P}^1)$. Let us summarize some properties of trigonal curves (cf. [Reference Martens and SchreyerMS86]).
${\rm Aut}(\mathbf{P}^1)$. Let us summarize some properties of trigonal curves (cf. [Reference Martens and SchreyerMS86]).
It is classically known that a trigonal curve ![]() $C$ can be canonically embedded in a Hirzebruch surface. This is due to the fact that the canonical model of
$C$ can be canonically embedded in a Hirzebruch surface. This is due to the fact that the canonical model of ![]() $C$ is contained in a unique rational normal scroll, namely the image of a Hirzebruch surface
$C$ is contained in a unique rational normal scroll, namely the image of a Hirzebruch surface ![]() $\mathbf{F}_n$ by a bundle
$\mathbf{F}_n$ by a bundle ![]() $L_{1,m}$ with
$L_{1,m}$ with ![]() $m>0$ (see § 3.3 for the notation). The integer
$m>0$ (see § 3.3 for the notation). The integer ![]() $n$ is called the scroll invariant, and
$n$ is called the scroll invariant, and ![]() $m$ the Maroni invariant of
$m$ the Maroni invariant of ![]() $C$. As a curve on
$C$. As a curve on ![]() $\mathbf{F}_n$,
$\mathbf{F}_n$, ![]() $C$ belongs to the linear system
$C$ belongs to the linear system ![]() $|L_{3,b}|$ with
$|L_{3,b}|$ with ![]() $b=m-n+2$ by the adjunction formula. The trigonal map of
$b=m-n+2$ by the adjunction formula. The trigonal map of ![]() $C$ is given by the restriction of the projection
$C$ is given by the restriction of the projection ![]() $\mathbf{F}_n\to \mathbf{P}^1$. We have the genus formula
$\mathbf{F}_n\to \mathbf{P}^1$. We have the genus formula ![]() $g=3n+2b-2$, which gives the relation of
$g=3n+2b-2$, which gives the relation of ![]() $n$ and
$n$ and ![]() $m$. These (equivalent) invariants give a stratification of the moduli space of trigonal curves. By the canonicity of the embedding
$m$. These (equivalent) invariants give a stratification of the moduli space of trigonal curves. By the canonicity of the embedding ![]() $C\subset \mathbf{F}_n$, the isomorphism classes of trigonal curves of genus
$C\subset \mathbf{F}_n$, the isomorphism classes of trigonal curves of genus ![]() $g$ and Maroni invariant
$g$ and Maroni invariant ![]() $m$ correspond to the
$m$ correspond to the ![]() ${\rm Aut}(\mathbf{F}_n)$-orbits in the locus of smooth curves in
${\rm Aut}(\mathbf{F}_n)$-orbits in the locus of smooth curves in ![]() $|L_{3,b}|$.
$|L_{3,b}|$.
Maroni described the variety ![]() $W_d^r(C)\subset {\rm Pic}^d(C)$ of line bundles
$W_d^r(C)\subset {\rm Pic}^d(C)$ of line bundles ![]() $L$ of degree
$L$ of degree ![]() $d$ and
$d$ and ![]() $h^0(L)\geq r+1$ (see [Reference Martens and SchreyerMS86, Proposition 1]). We need his description in the case
$h^0(L)\geq r+1$ (see [Reference Martens and SchreyerMS86, Proposition 1]). We need his description in the case ![]() $d=g-1$.
$d=g-1$.
Proposition 6.11 (Maroni) Let ![]() $T=L_{0,1}|_C$ be the trigonal bundle and write
$T=L_{0,1}|_C$ be the trigonal bundle and write ![]() $W_+=rT+W_{g-1-3r}(C)$, where
$W_+=rT+W_{g-1-3r}(C)$, where ![]() $W_{g-1-3r}(C):=W_{g-1-3r}^{0}(C)$. Then
$W_{g-1-3r}(C):=W_{g-1-3r}^{0}(C)$. Then
Using this description, we can give a geometric characterization of trigonal curves having effective theta characteristics.
Lemma 6.12 A trigonal curve ![]() $C$ of scroll invariant
$C$ of scroll invariant ![]() $n$ and Maroni invariant
$n$ and Maroni invariant ![]() $m$ has a theta characteristic
$m$ has a theta characteristic ![]() $L$ with
$L$ with ![]() $h^0(L)\geq r+1$ if and only if there exists a curve
$h^0(L)\geq r+1$ if and only if there exists a curve ![]() $H\in |L_{1,m-2r}|$ on
$H\in |L_{1,m-2r}|$ on ![]() $\mathbf {F}_n$ such that
$\mathbf {F}_n$ such that ![]() $H|_C=2D$ for a divisor
$H|_C=2D$ for a divisor ![]() $D$ of degree
$D$ of degree ![]() $g-1-3r$ on
$g-1-3r$ on ![]() $C$. In that case, the divisor
$C$. In that case, the divisor ![]() $rT+D$ gives such a theta characteristic.
$rT+D$ gives such a theta characteristic.
Proof. A line bundle ![]() $L$ is a theta characteristic with
$L$ is a theta characteristic with ![]() $h^0(L)\geq r+1$ if and only if it is a fixed point of the residual involution on
$h^0(L)\geq r+1$ if and only if it is a fixed point of the residual involution on ![]() $W_{g-1}^r(C)$. Such
$W_{g-1}^r(C)$. Such ![]() $L$ should be contained in
$L$ should be contained in ![]() $W_+ \cap (K_C-W_+)$ by Proposition 6.11, so we can write
$W_+ \cap (K_C-W_+)$ by Proposition 6.11, so we can write ![]() $L=rT+D$ for some
$L=rT+D$ for some ![]() $D\in W_{g-1-3r}(C)$. Since
$D\in W_{g-1-3r}(C)$. Since ![]() $L\sim K_{C}-L$, we have
$L\sim K_{C}-L$, we have ![]() $2D\sim K_C-2rT$. The restriction map
$2D\sim K_C-2rT$. The restriction map ![]() $|L_{1,m-2r}|\to |K_C-2rT|$ is isomorphic because
$|L_{1,m-2r}|\to |K_C-2rT|$ is isomorphic because ![]() $h^i(K_{\mathbf{F}_n}-L_{0,2r})=0$ for
$h^i(K_{\mathbf{F}_n}-L_{0,2r})=0$ for ![]() $i=0, 1$. Thus there exists
$i=0, 1$. Thus there exists ![]() $H\in |L_{1,m-2r}|$ with
$H\in |L_{1,m-2r}|$ with ![]() $H|_C=2D$. Conversely, if we have such
$H|_C=2D$. Conversely, if we have such ![]() $H$ and
$H$ and ![]() $D$, then
$D$, then ![]() $L=rT+D$ is a theta characteristic with
$L=rT+D$ is a theta characteristic with ![]() $h^{0}(L)\geq r+1$ by Proposition 6.11.
$h^{0}(L)\geq r+1$ by Proposition 6.11.
6.5 Proof of Proposition 6.2
We will show that a general member ![]() $C$ of
$C$ of ![]() $\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})$ has no effective even theta characteristic when
$\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})$ has no effective even theta characteristic when ![]() $k=1$ and
$k=1$ and ![]() $6\leq g\leq 9$, using the description of
$6\leq g\leq 9$, using the description of ![]() $C$ given in [Reference MaMa15].
$C$ given in [Reference MaMa15].
We first consider the case ![]() $\delta =1$, where
$\delta =1$, where ![]() $6\leq g \leq 9$. In this case
$6\leq g \leq 9$. In this case ![]() $C$ is a general trigonal curve of genus
$C$ is a general trigonal curve of genus ![]() $g$ with Maroni invariant
$g$ with Maroni invariant ![]() $2$, which can be realized as a general member of the linear system
$2$, which can be realized as a general member of the linear system ![]() $|L_{3,10-g}|$ on
$|L_{3,10-g}|$ on ![]() $\mathbf{F}_{g-6}$ [Reference MaMa15, Corollaries 6.2 and 7.6]. By Lemma 6.12,
$\mathbf{F}_{g-6}$ [Reference MaMa15, Corollaries 6.2 and 7.6]. By Lemma 6.12, ![]() $C$ has a theta characteristic
$C$ has a theta characteristic ![]() $L$ with
$L$ with ![]() $h^0(L)\geq 2$ if and only if there exists a curve
$h^0(L)\geq 2$ if and only if there exists a curve ![]() $H\in |L_{1,0}|$ totally bitangent to
$H\in |L_{1,0}|$ totally bitangent to ![]() $C$. However, it is readily seen that a general member of
$C$. However, it is readily seen that a general member of ![]() $|L_{3,10-g}|$ has no such tangent curve.
$|L_{3,10-g}|$ has no such tangent curve.
When ![]() $\delta =0$, we have
$\delta =0$, we have ![]() $g=6$. In this case
$g=6$. In this case ![]() $C$ is a plane quintic [Reference MaMa15, Corollary 7.3]. Then our assertion follows from the classical fact that any smooth plane quintic has no effective even theta characteristic: indeed, according to [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, p. 211], we have
$C$ is a plane quintic [Reference MaMa15, Corollary 7.3]. Then our assertion follows from the classical fact that any smooth plane quintic has no effective even theta characteristic: indeed, according to [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, p. 211], we have
The residual involution acts on this ![]() $W_5^1(C)$ by switching
$W_5^1(C)$ by switching ![]() $p$ and
$p$ and ![]() $q$. It has no fixed point other than
$q$. It has no fixed point other than ![]() $\mathcal {O}_{\mathbf{P}^2}(1)|_C$, which is an odd theta characteristic. Thus Proposition 6.2 is proved.
$\mathcal {O}_{\mathbf{P}^2}(1)|_C$, which is an odd theta characteristic. Thus Proposition 6.2 is proved.
7. The locus of vanishing theta-null: the case  $\delta =0$
$\delta =0$
We continue the geometric study of the Torelli map, still viewed as a morphism ![]() $\bar {\mu }_{\Lambda }\colon \mathcal {M}_{\Lambda }^{0}\to \frak {M}_{g}$ between the moduli spaces. In this section we treat the following two series:
$\bar {\mu }_{\Lambda }\colon \mathcal {M}_{\Lambda }^{0}\to \frak {M}_{g}$ between the moduli spaces. In this section we treat the following two series:
•
 $r=2, \ \delta =0 \ (g=9, 10)$;
$r=2, \ \delta =0 \ (g=9, 10)$;•
 $r=10, \ \delta =0, \ 4\leq g \leq 6$.
$r=10, \ \delta =0, \ 4\leq g \leq 6$.
In these cases, ![]() $\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})$ is contained in
$\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})$ is contained in ![]() $\frak {M}_{g}'$ because a general member of
$\frak {M}_{g}'$ because a general member of ![]() $\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})$ possesses a rather apparent effective even theta characteristic.
$\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})$ possesses a rather apparent effective even theta characteristic.
For the first series, we will show that an analogue of Theorem 6.1 holds by replacing ![]() $\frak {M}_{g}'$ with the (reduced) divisor
$\frak {M}_{g}'$ with the (reduced) divisor
of ![]() $\frak {M}_{g}'$, where
$\frak {M}_{g}'$, where ![]() $\Upsilon _{g}$ is the Siegel modular form introduced in § 4.1. Geometrically this locus parametrizes curves having at least two effective even theta characteristics (see Lemma 4.1).
$\Upsilon _{g}$ is the Siegel modular form introduced in § 4.1. Geometrically this locus parametrizes curves having at least two effective even theta characteristics (see Lemma 4.1).
Proposition 7.1 When ![]() $(r, \delta )=(2, 0)$ and
$(r, \delta )=(2, 0)$ and ![]() $g=10$, the Heegner divisor
$g=10$, the Heegner divisor ![]() $\bar {\mathcal {H}}_{\Lambda }$ is irreducible and equal to
$\bar {\mathcal {H}}_{\Lambda }$ is irreducible and equal to ![]() $\bar {\mu }_{\Lambda }^{-1}(\frak {M}_{10}'')$. In particular, the genus
$\bar {\mu }_{\Lambda }^{-1}(\frak {M}_{10}'')$. In particular, the genus ![]() $10$ component of
$10$ component of ![]() $X^{\iota }$ has a unique effective even theta characteristic if the period of
$X^{\iota }$ has a unique effective even theta characteristic if the period of ![]() $(X,\iota )$ lies outside
$(X,\iota )$ lies outside ![]() $\bar {\mathcal {H}}_{\Lambda }$.
$\bar {\mathcal {H}}_{\Lambda }$.
In the case ![]() $(r, l, \delta )=(2, 2, 0)$, the Heegner divisor
$(r, l, \delta )=(2, 2, 0)$, the Heegner divisor ![]() $\bar {\mathcal {H}}_{\Lambda }$ is reducible, reflecting the fact that norm
$\bar {\mathcal {H}}_{\Lambda }$ is reducible, reflecting the fact that norm ![]() $-4$ vectors
$-4$ vectors ![]() $l\in \Lambda$ are divided into two classes according to whether
$l\in \Lambda$ are divided into two classes according to whether ![]() ${\rm div}(l)=1$ or
${\rm div}(l)=1$ or ![]() $2$. We accordingly write
$2$. We accordingly write ![]() $\bar {\mathcal {H}}_{\Lambda } = \bar {\mathcal {H}}_1 + \bar {\mathcal {H}}_2$.
$\bar {\mathcal {H}}_{\Lambda } = \bar {\mathcal {H}}_1 + \bar {\mathcal {H}}_2$.
Proposition 7.2 When ![]() $(r, \delta )=(2, 0)$ and
$(r, \delta )=(2, 0)$ and ![]() $g=9$, the component
$g=9$, the component ![]() $\bar {\mathcal {H}}_1$ is irreducible and equal to
$\bar {\mathcal {H}}_1$ is irreducible and equal to ![]() $\bar {\mu }_{\Lambda }^{-1}(\frak {M}_{9}'')$. In particular,
$\bar {\mu }_{\Lambda }^{-1}(\frak {M}_{9}'')$. In particular, ![]() $X^{\iota }$ has a unique effective even theta characteristic if the period of
$X^{\iota }$ has a unique effective even theta characteristic if the period of ![]() $(X,\iota )$ lies outside
$(X,\iota )$ lies outside ![]() $\bar {\mathcal {H}}_{\Lambda }$.
$\bar {\mathcal {H}}_{\Lambda }$.
For the second series, we will prove the following lemmas.
Lemma 7.3 If ![]() $(r, \delta )=(10, 0)$ and
$(r, \delta )=(10, 0)$ and ![]() $g=4, 5$, then
$g=4, 5$, then ![]() $\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^0)$ is not contained in the hyperelliptic locus.
$\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^0)$ is not contained in the hyperelliptic locus.
Lemma 7.4 If ![]() $(r, \delta )=(10, 0)$ and
$(r, \delta )=(10, 0)$ and ![]() $g=6$, then a general member of
$g=6$, then a general member of ![]() $\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^0)$ has exactly one effective even theta characteristic.
$\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^0)$ has exactly one effective even theta characteristic.
In § 9 these results will be used to prove Theorem 0.1 (2), (3). Lemmas 7.3 and 7.4 will be strengthened in Corollary 9.14 by an argument of modular form (a geometric proof is also possible).
7.1 Proof of Proposition 7.1
Proposition 7.1 is proved along similar lines to Theorem 6.1 (as is Proposition 7.2). We begin by checking the irreducibility of the Heegner divisor ![]() $\bar {\mathcal {H}}_{\Lambda }$, which is defined by norm
$\bar {\mathcal {H}}_{\Lambda }$, which is defined by norm ![]() $-4$ vectors in
$-4$ vectors in ![]() $\Lambda$.
$\Lambda$.
Lemma 7.5 When ![]() $(r, l, \delta )=(2, 0, 0)$,
$(r, l, \delta )=(2, 0, 0)$, ![]() $\bar {\mathcal {H}}_{\Lambda }$ is irreducible.
$\bar {\mathcal {H}}_{\Lambda }$ is irreducible.
Proof. Since ![]() $\Lambda \simeq \mathbb {U}^{\oplus 2}\oplus \mathbb {E}_8^{\oplus 2}$ is unimodular, by the Eichler criterion the
$\Lambda \simeq \mathbb {U}^{\oplus 2}\oplus \mathbb {E}_8^{\oplus 2}$ is unimodular, by the Eichler criterion the ![]() $O^{+}(\Lambda )$-equivalence class of a primitive vector of
$O^{+}(\Lambda )$-equivalence class of a primitive vector of ![]() $\Lambda$ is determined by its norm.
$\Lambda$ is determined by its norm.
We describe the members of ![]() $\mathcal {M}_{\Lambda }^{0}$ following the construction in [Reference MaMa15, § 6.1]. We consider curves on the Hirzebruch surface
$\mathcal {M}_{\Lambda }^{0}$ following the construction in [Reference MaMa15, § 6.1]. We consider curves on the Hirzebruch surface ![]() $\mathbf{F}_4$. Let
$\mathbf{F}_4$. Let ![]() $U\subset |L_{3,0}|$ be the open locus of smooth curves. We have a morphism
$U\subset |L_{3,0}|$ be the open locus of smooth curves. We have a morphism ![]() $p\colon U \to \mathcal {M}_{\Lambda }^{0}$ by associating to
$p\colon U \to \mathcal {M}_{\Lambda }^{0}$ by associating to ![]() $C\in U$ the double cover of
$C\in U$ the double cover of ![]() $\mathbf{F}_4$ branched over
$\mathbf{F}_4$ branched over ![]() $C+\Sigma$.
$C+\Sigma$.
Lemma 7.6 There exists a geometric quotient ![]() $U/{\rm Aut}(\mathbf{F}_4)$ and the period map
$U/{\rm Aut}(\mathbf{F}_4)$ and the period map ![]() $p$ descends to a biregular isomorphism
$p$ descends to a biregular isomorphism ![]() $\mathcal {P}\colon U/{\rm Aut}(\mathbf{F}_4) \to \mathcal {M}_{\Lambda }^{0}$. In particular, the Torelli map
$\mathcal {P}\colon U/{\rm Aut}(\mathbf{F}_4) \to \mathcal {M}_{\Lambda }^{0}$. In particular, the Torelli map ![]() $\mathcal {M}_{\Lambda }^{0}\to \frak {M}_{g}$ is given by
$\mathcal {M}_{\Lambda }^{0}\to \frak {M}_{g}$ is given by ![]() $\mathcal {P}^{-1}$ and is injective, with image the trigonal locus of Maroni invariant
$\mathcal {P}^{-1}$ and is injective, with image the trigonal locus of Maroni invariant ![]() $2$.
$2$.
Proof. The ![]() $p$-fibers are the
$p$-fibers are the ![]() ${\rm Aut}(\mathbf{F}_4)$-orbits because the
${\rm Aut}(\mathbf{F}_4)$-orbits because the ![]() ${\rm Aut}(\mathbf{F}_4)$-orbits correspond to the isomorphism classes of trigonal curves of Maroni invariant
${\rm Aut}(\mathbf{F}_4)$-orbits correspond to the isomorphism classes of trigonal curves of Maroni invariant ![]() $2$, and the Torelli map recovers these isomorphism classes. Since
$2$, and the Torelli map recovers these isomorphism classes. Since ![]() $\mathcal {M}_{\Lambda }^{0}$ is normal, [Reference Mumford, Fogarty and KirwanMFK94, Proposition 0.2] tells us that the image of
$\mathcal {M}_{\Lambda }^{0}$ is normal, [Reference Mumford, Fogarty and KirwanMFK94, Proposition 0.2] tells us that the image of ![]() $p$ is identified with the geometric quotient of
$p$ is identified with the geometric quotient of ![]() $U$ by
$U$ by ![]() ${\rm Aut}(\mathbf{F}_4)$. It remains to show the surjectivity of
${\rm Aut}(\mathbf{F}_4)$. It remains to show the surjectivity of ![]() $p$.
$p$.
Let ![]() $(X, \iota )$ be an arbitrary member of
$(X, \iota )$ be an arbitrary member of ![]() $\mathcal {M}_{\Lambda }^{0}$, and let
$\mathcal {M}_{\Lambda }^{0}$, and let ![]() $\{{\frak e},{\frak f}\}$ be the natural hyperbolic basis of its invariant lattice
$\{{\frak e},{\frak f}\}$ be the natural hyperbolic basis of its invariant lattice ![]() $H_+\simeq \mathbb {U}$. The vector
$H_+\simeq \mathbb {U}$. The vector ![]() $2({\frak e}+{\frak f})$ satisfies the arithmetic conditions in Lemma 3.6 and hence gives an
$2({\frak e}+{\frak f})$ satisfies the arithmetic conditions in Lemma 3.6 and hence gives an ![]() $\iota$-invariant hyperelliptic bundle of degree
$\iota$-invariant hyperelliptic bundle of degree ![]() $8$. This defines a generically two-to-one morphism
$8$. This defines a generically two-to-one morphism ![]() $X\to Y$ where
$X\to Y$ where ![]() $Y=\mathbf{P}^{2}$ or
$Y=\mathbf{P}^{2}$ or ![]() $\mathbf{F}_{2n}$ with
$\mathbf{F}_{2n}$ with ![]() $n\leq 2$, on which
$n\leq 2$, on which ![]() $\iota$ acts by the covering transformation by Lemma 3.8. Among these possibilities of
$\iota$ acts by the covering transformation by Lemma 3.8. Among these possibilities of ![]() $Y$, the branch (
$Y$, the branch (![]() $-2K_{Y}$)-curve can contain a component of genus
$-2K_{Y}$)-curve can contain a component of genus ![]() $10$ only when
$10$ only when ![]() $Y=\mathbf{P}^{2}$ or
$Y=\mathbf{P}^{2}$ or ![]() $\mathbf{F}_{4}$. The case
$\mathbf{F}_{4}$. The case ![]() $Y=\mathbf{P}^{2}$ cannot happen because it would be
$Y=\mathbf{P}^{2}$ cannot happen because it would be ![]() $(r, l, \delta )=(1, 1, 1)$ in that case. Hence
$(r, l, \delta )=(1, 1, 1)$ in that case. Hence ![]() $Y=\mathbf{F}_{4}$. Since
$Y=\mathbf{F}_{4}$. Since ![]() $|{-}2K_{\mathbf{F}_{4}}|=\Sigma +|L_{3,0}|$ and since
$|{-}2K_{\mathbf{F}_{4}}|=\Sigma +|L_{3,0}|$ and since ![]() $L_{3,0}$ has arithmetic genus
$L_{3,0}$ has arithmetic genus ![]() $10$, the branch curve should be of the form
$10$, the branch curve should be of the form ![]() $\Sigma +C$ with smooth
$\Sigma +C$ with smooth ![]() $C\in |L_{3,0}|$. Thus
$C\in |L_{3,0}|$. Thus ![]() $(X, \iota )=p(C)$.
$(X, \iota )=p(C)$.
Let ![]() $C$ be a member of
$C$ be a member of ![]() $U$. Since
$U$. Since ![]() $C$ is disjoint from
$C$ is disjoint from ![]() $\Sigma$, the bundle
$\Sigma$, the bundle ![]() $L_{1,-4}|_{C}$ is trivial so that
$L_{1,-4}|_{C}$ is trivial so that ![]() $K_C\simeq L_{1,2}|_C\simeq L_{0,6}|_C$. Hence
$K_C\simeq L_{1,2}|_C\simeq L_{0,6}|_C$. Hence ![]() $L_{0,3}|_C$ is a theta characteristic with
$L_{0,3}|_C$ is a theta characteristic with ![]() $h^{0}(L_{0,3}|_C)=4$. This shows that
$h^{0}(L_{0,3}|_C)=4$. This shows that ![]() $\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})\subset \frak {M}_{10}'$. We are interested in the locus
$\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})\subset \frak {M}_{10}'$. We are interested in the locus ![]() $\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})\cap \frak {M}_{10}''$ where
$\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})\cap \frak {M}_{10}''$ where ![]() $C$ has another effective even theta characteristic.
$C$ has another effective even theta characteristic.
Lemma 7.7 The curve ![]() $C$ has an effective even theta characteristic different from
$C$ has an effective even theta characteristic different from ![]() $L_{0,3}|_C$ if and only if there exists a smooth member
$L_{0,3}|_C$ if and only if there exists a smooth member ![]() $H$ of
$H$ of ![]() $|L_{1,0}|$ such that
$|L_{1,0}|$ such that ![]() $H|_C=2D$ for some divisor
$H|_C=2D$ for some divisor ![]() $D$ of degree
$D$ of degree ![]() $6$ on
$6$ on ![]() $C$.
$C$.
Proof. By Lemma 6.12, ![]() $C$ has a theta characteristic
$C$ has a theta characteristic ![]() $L$ with
$L$ with ![]() $h^0(L)\geq 2$ if and only if there exists
$h^0(L)\geq 2$ if and only if there exists ![]() $H\in |L_{1,0}|$ with
$H\in |L_{1,0}|$ with ![]() $H|_C$ divisible by
$H|_C$ divisible by ![]() $2$, in which case
$2$, in which case ![]() $L$ is given by
$L$ is given by ![]() $(H|_C)/2+L_{0,1}|_C$. If
$(H|_C)/2+L_{0,1}|_C$. If ![]() $H$ is singular, it contains
$H$ is singular, it contains ![]() $\Sigma$ as a component and hence can be written as
$\Sigma$ as a component and hence can be written as ![]() $H=\Sigma +\sum _{i=1}^{4}F_i$ for some
$H=\Sigma +\sum _{i=1}^{4}F_i$ for some ![]() $L_{0,1}$-fibers
$L_{0,1}$-fibers ![]() $F_1, \ldots , F_4$. Since
$F_1, \ldots , F_4$. Since ![]() $H|_C=\sum _{i=1}^{4}F_i|_C$, after renumbering we must have
$H|_C=\sum _{i=1}^{4}F_i|_C$, after renumbering we must have ![]() $F_1=F_2$ and
$F_1=F_2$ and ![]() $F_3=F_4$. Thus
$F_3=F_4$. Thus ![]() $L=L_{0,3}|_C$ in this case.
$L=L_{0,3}|_C$ in this case.
We can now complete the proof of Proposition 7.1. Since ![]() $\bar {\mu }_{\Lambda }({\mathcal {M}}_{\Lambda }^{0})\subset {\frak M}'_{10}$, the inverse image
$\bar {\mu }_{\Lambda }({\mathcal {M}}_{\Lambda }^{0})\subset {\frak M}'_{10}$, the inverse image ![]() $\bar {\mu }_{\Lambda }^{-1}({\frak M}''_{10})$ is a divisor in
$\bar {\mu }_{\Lambda }^{-1}({\frak M}''_{10})$ is a divisor in ![]() ${\mathcal {M}}_{\Lambda }^{0}$. It can be easily checked with Lemma 7.7 that
${\mathcal {M}}_{\Lambda }^{0}$. It can be easily checked with Lemma 7.7 that ![]() $\bar {\mu }_{\Lambda }({\mathcal {M}}_{\Lambda }^{0})\cap {\frak M}''_{10}$ is non-empty. Hence it remains to prove the inclusion
$\bar {\mu }_{\Lambda }({\mathcal {M}}_{\Lambda }^{0})\cap {\frak M}''_{10}$ is non-empty. Hence it remains to prove the inclusion ![]() $\bar {\mu }_{\Lambda }^{-1}({\frak M}''_{10})\subset \bar {\mathcal {H}}_{\Lambda }$. Let
$\bar {\mu }_{\Lambda }^{-1}({\frak M}''_{10})\subset \bar {\mathcal {H}}_{\Lambda }$. Let ![]() $(X,\iota )$ be a
$(X,\iota )$ be a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface with
$K3$ surface with ![]() $(g, k)=(10, 1)$ such that
$(g, k)=(10, 1)$ such that ![]() $\bar {\mu }_{\Lambda }(X,\iota )\in {\frak M}''_{10}$. By Lemmas 7.6 and 7.7, we have
$\bar {\mu }_{\Lambda }(X,\iota )\in {\frak M}''_{10}$. By Lemmas 7.6 and 7.7, we have ![]() $(X, \iota )=p(C)$ for a curve
$(X, \iota )=p(C)$ for a curve ![]() $C$ as in Lemma 7.7. Let
$C$ as in Lemma 7.7. Let ![]() $H$ be a smooth
$H$ be a smooth ![]() $L_{1,0}$-curve with
$L_{1,0}$-curve with ![]() $H|_C$ divisible by
$H|_C$ divisible by ![]() $2$. The pullback of
$2$. The pullback of ![]() $H$ by the covering map
$H$ by the covering map ![]() $\pi : X\to \mathbf{F}_4$ splits into two
$\pi : X\to \mathbf{F}_4$ splits into two ![]() $(-2)$-curves:
$(-2)$-curves: ![]() $\pi ^{\ast }H=E+\iota (E)$. Therefore
$\pi ^{\ast }H=E+\iota (E)$. Therefore ![]() $X$ has the
$X$ has the ![]() $\iota$-anti-invariant cycle
$\iota$-anti-invariant cycle
of norm ![]() $-16$. Let
$-16$. Let ![]() $H_-\subset H^{2}(X,\textbf {Z})$ be the anti-invariant lattice of
$H_-\subset H^{2}(X,\textbf {Z})$ be the anti-invariant lattice of ![]() $(X, \iota )$. Since
$(X, \iota )$. Since
and since ![]() $H_{-}$ is unimodular,
$H_{-}$ is unimodular, ![]() $D_{-}$ is divisible by
$D_{-}$ is divisible by ![]() $2$ in
$2$ in ![]() $H_-$. Therefore
$H_-$. Therefore ![]() ${\rm Pic}(X)$ contains the anti-invariant cycle
${\rm Pic}(X)$ contains the anti-invariant cycle ![]() $D_{-}/2$ of norm
$D_{-}/2$ of norm ![]() $-4$, which implies that the period of
$-4$, which implies that the period of ![]() $(X, \iota )$ lies in
$(X, \iota )$ lies in ![]() $\bar {{\mathcal {H}}}_{\Lambda }$. This proves Proposition 7.1.
$\bar {{\mathcal {H}}}_{\Lambda }$. This proves Proposition 7.1.
7.2 Proof of Proposition 7.2
In this subsection we prove Proposition 7.2. We first explain the decomposition of the Heegner divisor ![]() $\bar {\mathcal {H}}_{\Lambda }$. Recall that
$\bar {\mathcal {H}}_{\Lambda }$. Recall that ![]() $\bar {\mathcal {H}}_{\Lambda }$ is defined by norm
$\bar {\mathcal {H}}_{\Lambda }$ is defined by norm ![]() $-4$ vectors
$-4$ vectors ![]() $l$ in
$l$ in ![]() $\Lambda \simeq \mathbb {U}\oplus \mathbb {U}(2)\oplus \mathbb {E}_8^{\oplus 2}$. Since
$\Lambda \simeq \mathbb {U}\oplus \mathbb {U}(2)\oplus \mathbb {E}_8^{\oplus 2}$. Since ![]() $\Lambda$ cannot contain
$\Lambda$ cannot contain ![]() $\langle -4 \rangle$ as an orthogonal direct summand, we have either
$\langle -4 \rangle$ as an orthogonal direct summand, we have either ![]() ${\rm div}(l)=1$ or
${\rm div}(l)=1$ or ![]() $2$. By the Eichler criterion, each type of norm
$2$. By the Eichler criterion, each type of norm ![]() $-4$ vectors consists of a single
$-4$ vectors consists of a single ![]() $O^{+}_{0}(\Lambda )$-orbit (in the case
$O^{+}_{0}(\Lambda )$-orbit (in the case ![]() ${\rm div}(l)=2$,
${\rm div}(l)=2$, ![]() $[l/2]\in A_{\Lambda }$ is the unique element of norm
$[l/2]\in A_{\Lambda }$ is the unique element of norm ![]() $\equiv 1$ mod
$\equiv 1$ mod ![]() $2\textbf {Z}$). We accordingly obtain the decomposition
$2\textbf {Z}$). We accordingly obtain the decomposition
where ![]() $\bar {\mathcal {H}}_{i}$ is defined by those
$\bar {\mathcal {H}}_{i}$ is defined by those ![]() $l$ with
$l$ with ![]() ${\rm div}(l)=i$, and each
${\rm div}(l)=i$, and each ![]() $\bar {\mathcal {H}}_i$ is irreducible.
$\bar {\mathcal {H}}_i$ is irreducible.
We next recall a (well-known) construction of members of ![]() $\mathcal {M}_{\Lambda }^0$. Let
$\mathcal {M}_{\Lambda }^0$. Let ![]() $\tilde {U}$ be the parameter space of smooth
$\tilde {U}$ be the parameter space of smooth ![]() $(2, 4)$ complete intersections in
$(2, 4)$ complete intersections in ![]() $\mathbf{P}^3$. For each
$\mathbf{P}^3$. For each ![]() $C\in \tilde {U}$ the quadric containing it is unique;
$C\in \tilde {U}$ the quadric containing it is unique; ![]() $\tilde {U}$ is thus stratified according to whether the quadric is smooth or a quadratic cone. In the first case
$\tilde {U}$ is thus stratified according to whether the quadric is smooth or a quadratic cone. In the first case ![]() $C$ is a smooth bidegree
$C$ is a smooth bidegree ![]() $(4, 4)$ curve on
$(4, 4)$ curve on ![]() $Y=\mathbf{P}^1 \times \mathbf{P}^1$, and in the second case
$Y=\mathbf{P}^1 \times \mathbf{P}^1$, and in the second case ![]() $C$ is a smooth
$C$ is a smooth ![]() $L_{4,0}$-curve on
$L_{4,0}$-curve on ![]() $Y=\mathbf{F}_2$. We have a period map
$Y=\mathbf{F}_2$. We have a period map ![]() $p:\tilde {U}\to \mathcal {M}_{\Lambda }^0$ by associating to
$p:\tilde {U}\to \mathcal {M}_{\Lambda }^0$ by associating to ![]() $C$ the double cover of
$C$ the double cover of ![]() $Y$ branched over
$Y$ branched over ![]() $C$.
$C$.
Lemma 7.8 The period map ![]() $p$ descends to a biregular isomorphism
$p$ descends to a biregular isomorphism ![]() $\tilde {U}/{\rm PGL}_4 \to \mathcal {M}_{\Lambda }^0$ from the geometric quotient
$\tilde {U}/{\rm PGL}_4 \to \mathcal {M}_{\Lambda }^0$ from the geometric quotient ![]() $\tilde {U}/{\rm PGL}_4$.
$\tilde {U}/{\rm PGL}_4$.
Proof. This is similar to Lemma 7.6, so we only indicate minimal ingredients of the argument: (1) using the natural norm ![]() $4$ vector in the invariant lattice
$4$ vector in the invariant lattice ![]() $\mathbb {U}(2)$, we can realize a given
$\mathbb {U}(2)$, we can realize a given ![]() $(X, \iota )$ as a double cover of a quadric so that
$(X, \iota )$ as a double cover of a quadric so that ![]() $p$ is surjective; (2) the
$p$ is surjective; (2) the ![]() $p$-fibers are
$p$-fibers are ![]() ${\rm PGL}_4$-orbits either by an argument modeled in § 4.3 of [Reference MaMa15] or by observing that the
${\rm PGL}_4$-orbits either by an argument modeled in § 4.3 of [Reference MaMa15] or by observing that the ![]() ${\rm PGL}_4$-orbits correspond to the isomorphism classes of curves (cf. [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, Exercise IV. F-2]).
${\rm PGL}_4$-orbits correspond to the isomorphism classes of curves (cf. [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, Exercise IV. F-2]).
In the proof of Proposition 7.2 we restrict ourselves to the generic case, namely the smooth quadric case. The quadratic cone case can be dealt with similarly. So let ![]() $Y=\mathbf{P}^1 \times \mathbf{P}^1$ and consider the open locus
$Y=\mathbf{P}^1 \times \mathbf{P}^1$ and consider the open locus ![]() $U\subset |\mathcal {O}_{Y}(4, 4)|$ of smooth bidegree
$U\subset |\mathcal {O}_{Y}(4, 4)|$ of smooth bidegree ![]() $(4, 4)$ curves. If
$(4, 4)$ curves. If ![]() $C\in U$, then
$C\in U$, then ![]() $K_C\simeq \mathcal {O}_{Y}(2, 2)|_C$ and the restriction map
$K_C\simeq \mathcal {O}_{Y}(2, 2)|_C$ and the restriction map ![]() $|\mathcal {O}_{Y}(2, 2)| \to |K_C|$ is isomorphic. In particular, an effective divisor
$|\mathcal {O}_{Y}(2, 2)| \to |K_C|$ is isomorphic. In particular, an effective divisor ![]() $D$ of degree
$D$ of degree ![]() $8$ on
$8$ on ![]() $C$ satisfies
$C$ satisfies ![]() $2D \sim K_C$ if and only if there exists a bidegree
$2D \sim K_C$ if and only if there exists a bidegree ![]() $(2, 2)$ curve
$(2, 2)$ curve ![]() $H$ on
$H$ on ![]() $Y$ with
$Y$ with ![]() $H|_C=2D$. We have one apparent theta characteristic,
$H|_C=2D$. We have one apparent theta characteristic, ![]() $\mathcal {O}_{Y}(1, 1)|_C$, which has
$\mathcal {O}_{Y}(1, 1)|_C$, which has ![]() $h^{0}=4$. This is the case where
$h^{0}=4$. This is the case where ![]() $H$ is a double bidegree
$H$ is a double bidegree ![]() $(1, 1)$ curve. By [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, Exercise IV. F-2], any other effective even theta characteristic of
$(1, 1)$ curve. By [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, Exercise IV. F-2], any other effective even theta characteristic of ![]() $C$, if it exists, must satisfy
$C$, if it exists, must satisfy ![]() $h^{0}=2$.
$h^{0}=2$.
Now let ![]() $V\subset U$ be the locus where
$V\subset U$ be the locus where ![]() $C$ has a theta characteristic with
$C$ has a theta characteristic with ![]() $h^0=2$. By the same argument as in § 7.1, the proof of Proposition 7.2 is reduced to showing the inclusion
$h^0=2$. By the same argument as in § 7.1, the proof of Proposition 7.2 is reduced to showing the inclusion ![]() $p(V)\subset \bar {\mathcal {H}}_1$. So let
$p(V)\subset \bar {\mathcal {H}}_1$. So let ![]() $C\in V$ and
$C\in V$ and ![]() $(X, \iota )=p(C)$. We write
$(X, \iota )=p(C)$. We write ![]() $\pi \colon X\to Y$ for the covering map. The curve
$\pi \colon X\to Y$ for the covering map. The curve ![]() $C$ admits a one-dimensional family
$C$ admits a one-dimensional family ![]() $\{ H_{t} \}_{t\in \mathbf{P}^1}$ of ‘totally tangent’ curves of bidegree
$\{ H_{t} \}_{t\in \mathbf{P}^1}$ of ‘totally tangent’ curves of bidegree ![]() $(2, 2)$, that is,
$(2, 2)$, that is, ![]() $H_t|_C=2D_t$ for some divisors
$H_t|_C=2D_t$ for some divisors ![]() $D_t$ of degree
$D_t$ of degree ![]() $8$ on
$8$ on ![]() $C$, which are not double bidegree
$C$, which are not double bidegree ![]() $(1, 1)$ curves. Then
$(1, 1)$ curves. Then ![]() $\{ D_{t} \}_{t\in \mathbf{P}^1}$ is a (complete) half-canonical pencil of
$\{ D_{t} \}_{t\in \mathbf{P}^1}$ is a (complete) half-canonical pencil of ![]() $C$. Note that this pencil can also be obtained by picking up
$C$. Note that this pencil can also be obtained by picking up ![]() $t=0$ and considering the linear system of bidegree
$t=0$ and considering the linear system of bidegree ![]() $(2, 2)$ curves passing through
$(2, 2)$ curves passing through ![]() $D_0$, which intersect
$D_0$, which intersect ![]() $C$ at
$C$ at ![]() $D_0+D_t$.
$D_0+D_t$.
Claim 7.9 A general member of ![]() $\{ H_{t} \}_{t\in \mathbf{P}^1}$ is smooth.
$\{ H_{t} \}_{t\in \mathbf{P}^1}$ is smooth.
Proof. If ![]() $H_t$ is reducible, its irreducible components are smooth rational curves intersecting
$H_t$ is reducible, its irreducible components are smooth rational curves intersecting ![]() $C$ transversely at at most two points and tangent to
$C$ transversely at at most two points and tangent to ![]() $C$ elsewhere. Their pullback to
$C$ elsewhere. Their pullback to ![]() $X$ splits into two
$X$ splits into two ![]() $(-2)$-curves. So if a general member is reducible, then the
$(-2)$-curves. So if a general member is reducible, then the ![]() $K3$ surface
$K3$ surface ![]() $X$ would be covered by rational curves, which is absurd. By the same reason, a general (irreducible) member cannot be singular.
$X$ would be covered by rational curves, which is absurd. By the same reason, a general (irreducible) member cannot be singular.
Let ![]() $H$ be a general member of
$H$ be a general member of ![]() $\{ H_{t} \}_{t\in \mathbf{P}^1}$. Since
$\{ H_{t} \}_{t\in \mathbf{P}^1}$. Since ![]() $H$ is totally tangent to
$H$ is totally tangent to ![]() $C$ at eight points, its pullback to
$C$ at eight points, its pullback to ![]() $X$ splits into two smooth elliptic curves:
$X$ splits into two smooth elliptic curves: ![]() $\pi ^{\ast } H = E + \iota (E)$. Hence
$\pi ^{\ast } H = E + \iota (E)$. Hence ![]() $(X, \iota )$ possesses the
$(X, \iota )$ possesses the ![]() $\iota$-anti-invariant cycle of norm
$\iota$-anti-invariant cycle of norm ![]() $-16$:
$-16$:
Claim 7.10 ![]() $D_{-}$ is divisible by
$D_{-}$ is divisible by ![]() $2$ in the anti-invariant lattice
$2$ in the anti-invariant lattice ![]() $H_-$ and satisfies
$H_-$ and satisfies ![]() $(D_{-}/2, H_-)=\textbf {Z}$.
$(D_{-}/2, H_-)=\textbf {Z}$.
Proof. Since ![]() $D_{-}/2 = E - \pi ^{\ast }\mathcal {O}_Y(1, 1)$ is contained in
$D_{-}/2 = E - \pi ^{\ast }\mathcal {O}_Y(1, 1)$ is contained in ![]() $H^{2}(X, \textbf {Z})$, we have
$H^{2}(X, \textbf {Z})$, we have ![]() $D_{-}/2\in H_{-}$. If
$D_{-}/2\in H_{-}$. If ![]() $(D_{-}/2, H_-)\ne \textbf {Z}$, then
$(D_{-}/2, H_-)\ne \textbf {Z}$, then ![]() $(D_{-}/2, H_-)\subset 2\textbf {Z}$ so that
$(D_{-}/2, H_-)\subset 2\textbf {Z}$ so that ![]() $D_{-}/4$ would be contained in the dual lattice
$D_{-}/4$ would be contained in the dual lattice ![]() $H_{-}^{\vee }$. Recall that the discriminant forms
$H_{-}^{\vee }$. Recall that the discriminant forms ![]() $A_{H_{+}}$,
$A_{H_{+}}$, ![]() $A_{H_{-}}$ are isometric to
$A_{H_{-}}$ are isometric to ![]() $A_{\mathbb {U}(2)}$. As elements of
$A_{\mathbb {U}(2)}$. As elements of ![]() $A_{H_-}$ and
$A_{H_-}$ and ![]() $A_{H_+}$,
$A_{H_+}$, ![]() $[D_{-}/4]$ and
$[D_{-}/4]$ and ![]() $[\pi ^{\ast }\mathcal {O}_Y(1, 1)/2]$ are respectively the unique elements of norm
$[\pi ^{\ast }\mathcal {O}_Y(1, 1)/2]$ are respectively the unique elements of norm ![]() $\equiv 1$ mod
$\equiv 1$ mod ![]() $2\textbf {Z}$. By Nikulin [Reference NikulinNik80], then
$2\textbf {Z}$. By Nikulin [Reference NikulinNik80], then ![]() $E/2 = D_{-}/4 + \pi ^{\ast }\mathcal {O}_Y(1, 1)/2$ would be contained in
$E/2 = D_{-}/4 + \pi ^{\ast }\mathcal {O}_Y(1, 1)/2$ would be contained in ![]() $H^{2}(X, \textbf {Z})$. This contradicts the well-known fact that the class of a smooth elliptic curve is primitive in
$H^{2}(X, \textbf {Z})$. This contradicts the well-known fact that the class of a smooth elliptic curve is primitive in ![]() ${\rm Pic}(X)$.
${\rm Pic}(X)$.
To sum up, if a smooth bidegree ![]() $(4, 4)$ curve
$(4, 4)$ curve ![]() $C\subset Y$ has a theta characteristic with
$C\subset Y$ has a theta characteristic with ![]() $h^{0}=2$, then the associated 2-elementary
$h^{0}=2$, then the associated 2-elementary ![]() $K3$ surface
$K3$ surface ![]() $(X, \iota )$ has an anti-invariant cycle
$(X, \iota )$ has an anti-invariant cycle ![]() $D_{-}/2$ of norm
$D_{-}/2$ of norm ![]() $-4$ and with
$-4$ and with ![]() $(D_{-}/2, H_{-})=\textbf {Z}$ in its Picard lattice. Hence the period of
$(D_{-}/2, H_{-})=\textbf {Z}$ in its Picard lattice. Hence the period of ![]() $(X, \iota )$ lies in the component
$(X, \iota )$ lies in the component ![]() $\bar {\mathcal {H}}_1$ of
$\bar {\mathcal {H}}_1$ of ![]() $\bar {\mathcal {H}}_{\Lambda }$. This finishes the proof of Proposition 7.2.
$\bar {\mathcal {H}}_{\Lambda }$. This finishes the proof of Proposition 7.2.
7.3 Proof of Lemmas 7.3 and 7.4
Lemma 7.3 is an immediate consequence of the following known description of general members of ![]() $\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})$. When
$\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})$. When ![]() $g=4$, they are general curves in
$g=4$, they are general curves in ![]() ${\frak M}'_{4}$ by Ma [Reference MaMa15, Corollary 9.10]; when
${\frak M}'_{4}$ by Ma [Reference MaMa15, Corollary 9.10]; when ![]() $g=5$, they are general trigonal curves with vanishing theta-null by Kondō [Reference KondōKon94]. Since these curves are not hyperelliptic, Lemma 7.3 follows.
$g=5$, they are general trigonal curves with vanishing theta-null by Kondō [Reference KondōKon94]. Since these curves are not hyperelliptic, Lemma 7.3 follows.
For the proof of Lemma 7.4 we use the generic description given in [Reference MaMa15, Corollary 7.11]. Let ![]() $C$ be a smooth curve on
$C$ be a smooth curve on ![]() $\mathbf{F}_{2}$ belonging to the linear system
$\mathbf{F}_{2}$ belonging to the linear system ![]() $|L_{3,1}|$ such that the
$|L_{3,1}|$ such that the ![]() $L_{0,1}$-fiber
$L_{0,1}$-fiber ![]() $F$ through the point
$F$ through the point ![]() $C\cap \Sigma$ intersects
$C\cap \Sigma$ intersects ![]() $C$ with multiplicity
$C$ with multiplicity ![]() $3$ there. By taking the resolution of the double cover of
$3$ there. By taking the resolution of the double cover of ![]() $\mathbf{F}_2$ branched over
$\mathbf{F}_2$ branched over ![]() $C+F+\Sigma$, we obtain a 2-elementary
$C+F+\Sigma$, we obtain a 2-elementary ![]() $K3$ surface with
$K3$ surface with ![]() $(r, l, \delta )=(10, 0, 0)$. This construction covers general members of
$(r, l, \delta )=(10, 0, 0)$. This construction covers general members of ![]() $\mathcal {M}_{\Lambda }^{0}$, so a general member of
$\mathcal {M}_{\Lambda }^{0}$, so a general member of ![]() $\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})$ is a curve
$\bar {\mu }_{\Lambda }(\mathcal {M}_{\Lambda }^{0})$ is a curve ![]() $C$ as above.
$C$ as above.
Denote ![]() $p:=C\cap \Sigma$ and
$p:=C\cap \Sigma$ and ![]() $T:=L_{0,1}|_C$. Since
$T:=L_{0,1}|_C$. Since
the divisor ![]() $T+2p$ gives a theta characteristic of
$T+2p$ gives a theta characteristic of ![]() $C$ with
$C$ with ![]() $h^0(T+2p)\geq 2$. By Lemma 6.12, we have
$h^0(T+2p)\geq 2$. By Lemma 6.12, we have ![]() $h^0(T+2p)=2$. Conversely, suppose we have a theta characteristic
$h^0(T+2p)=2$. Conversely, suppose we have a theta characteristic ![]() $L$ on
$L$ on ![]() $C$ with
$C$ with ![]() $h^0(L)\geq 2$. By Lemma 6.12 we can find a curve
$h^0(L)\geq 2$. By Lemma 6.12 we can find a curve ![]() $H\in |L_{1,-1}|$ with
$H\in |L_{1,-1}|$ with ![]() $H|_C=2D$ for some divisor
$H|_C=2D$ for some divisor ![]() $D$ satisfying
$D$ satisfying ![]() $L\sim T+D$. Since
$L\sim T+D$. Since ![]() $|L_{1,-1}|=\Sigma +|L_{0,1}|$,
$|L_{1,-1}|=\Sigma +|L_{0,1}|$, ![]() $H$ is of the form
$H$ is of the form ![]() $H=\Sigma +F'$ for some
$H=\Sigma +F'$ for some ![]() $F'\in |L_{0,1}|$. The condition
$F'\in |L_{0,1}|$. The condition ![]() $(\Sigma +F')|_C=2D$ forces
$(\Sigma +F')|_C=2D$ forces ![]() $F'$ to pass through
$F'$ to pass through ![]() $p=\Sigma \cap C$. Therefore
$p=\Sigma \cap C$. Therefore ![]() $F=F'$ and
$F=F'$ and ![]() $2D=4p$. Thus
$2D=4p$. Thus ![]() $L$ is uniquely determined as
$L$ is uniquely determined as ![]() $L\sim T+2p$. This proves Lemma 7.4.
$L\sim T+2p$. This proves Lemma 7.4.
8. The structure of  $\tau _{M}$: the case
$\tau _{M}$: the case  $\delta =1$
$\delta =1$
In this section we determine the structure of ![]() $\Phi _{M}$ when
$\Phi _{M}$ when ![]() $\delta =1$.
$\delta =1$.
8.1 Borcherds products for  $2$-elementary lattices
$2$-elementary lattices
Recall that the Dedekind ![]() $\eta$-function and the Jacobi theta series
$\eta$-function and the Jacobi theta series ![]() $\theta _{{\Bbb A}_{1}^{+}+\epsilon /2}(\tau )$,
$\theta _{{\Bbb A}_{1}^{+}+\epsilon /2}(\tau )$, ![]() $(\epsilon =0,1)$ are the holomorphic functions on the complex upper half-plane
$(\epsilon =0,1)$ are the holomorphic functions on the complex upper half-plane ![]() ${\frak H}$:
${\frak H}$:
 \[ \eta(\tau):=q^{1/24}\prod_{n=1}^{\infty}(1-q^{n}), \quad \theta_{{\Bbb A}_{1}^{+}+\epsilon/2}(\tau):=\sum_{m\in\textbf{Z}+\epsilon/2}q^{m^{2}}, \quad q:=e^{2\pi i\tau}. \]
\[ \eta(\tau):=q^{1/24}\prod_{n=1}^{\infty}(1-q^{n}), \quad \theta_{{\Bbb A}_{1}^{+}+\epsilon/2}(\tau):=\sum_{m\in\textbf{Z}+\epsilon/2}q^{m^{2}}, \quad q:=e^{2\pi i\tau}. \] Let ![]() $\Lambda \subset {\Bbb L}_{K3}$ be a primitive
$\Lambda \subset {\Bbb L}_{K3}$ be a primitive ![]() $2$-elementary sublattice of signature
$2$-elementary sublattice of signature ![]() $(2,r(\Lambda )-2)$. We set
$(2,r(\Lambda )-2)$. We set
 \begin{gather*} \phi_{\Lambda}(\tau):=\eta(\tau)^{-8}\eta(2\tau)^{8}\eta(4\tau)^{-8}\,\theta_{{\Bbb A}_{1}^{+}}(\tau)^{12-r(\Lambda)},\\ \psi_{\Lambda}(\tau):=-16\eta(2\tau)^{-16}\eta(4\tau)^{8}\theta_{{\Bbb A}_{1}^{+}+\frac{1}{2}}(\tau)^{12-r(\Lambda)}. \end{gather*}
\begin{gather*} \phi_{\Lambda}(\tau):=\eta(\tau)^{-8}\eta(2\tau)^{8}\eta(4\tau)^{-8}\,\theta_{{\Bbb A}_{1}^{+}}(\tau)^{12-r(\Lambda)},\\ \psi_{\Lambda}(\tau):=-16\eta(2\tau)^{-16}\eta(4\tau)^{8}\theta_{{\Bbb A}_{1}^{+}+\frac{1}{2}}(\tau)^{12-r(\Lambda)}. \end{gather*}
Let ![]() $\{\textbf {e}_{\gamma }\}_{\gamma \in A_{\Lambda }}$ be the standard basis of the group ring
$\{\textbf {e}_{\gamma }\}_{\gamma \in A_{\Lambda }}$ be the standard basis of the group ring ![]() $\textbf {C}[A_{\Lambda }]$. For
$\textbf {C}[A_{\Lambda }]$. For ![]() $0\leq j\leq 3$, set
$0\leq j\leq 3$, set ![]() $\textbf {v}_{j}:=\sum _{\gamma \in A_{\Lambda }, q_{\Lambda }(\gamma )\equiv j/2}\textbf {e}_{\gamma }$. By [Reference YoshikawaYos13, Definition 7.6, Theorem 7.7], the
$\textbf {v}_{j}:=\sum _{\gamma \in A_{\Lambda }, q_{\Lambda }(\gamma )\equiv j/2}\textbf {e}_{\gamma }$. By [Reference YoshikawaYos13, Definition 7.6, Theorem 7.7], the ![]() $\textbf {C}[A_{\Lambda }]$-valued function
$\textbf {C}[A_{\Lambda }]$-valued function
 \[ F_{\Lambda}(\tau) := \phi_{\Lambda}(\tau)\,\textbf{e}_{0} + 2^{g(\Lambda)-2}\sum_{j=0}^{3}\sum_{k=0}^{3}\phi_{\Lambda}\left(\frac{\tau+k}{4}\right)i^{-jk}\,\textbf{v}_{j} + \psi_{\Lambda}(\tau)\,\textbf{e}_{\textbf{1}_{\Lambda}} \]
\[ F_{\Lambda}(\tau) := \phi_{\Lambda}(\tau)\,\textbf{e}_{0} + 2^{g(\Lambda)-2}\sum_{j=0}^{3}\sum_{k=0}^{3}\phi_{\Lambda}\left(\frac{\tau+k}{4}\right)i^{-jk}\,\textbf{v}_{j} + \psi_{\Lambda}(\tau)\,\textbf{e}_{\textbf{1}_{\Lambda}} \]
is a modular form for ![]() ${\rm Mp}_{2}(\textbf {Z})$ of weight
${\rm Mp}_{2}(\textbf {Z})$ of weight ![]() $1-b^{-}(\Lambda )/2$ with respect to the Weil representation
$1-b^{-}(\Lambda )/2$ with respect to the Weil representation ![]() $\rho _{\Lambda }\colon {\rm Mp}_{2}(\textbf {Z})\to {\rm GL}(\textbf {C}[A_{\Lambda }])$ attached to
$\rho _{\Lambda }\colon {\rm Mp}_{2}(\textbf {Z})\to {\rm GL}(\textbf {C}[A_{\Lambda }])$ attached to ![]() $\Lambda$ [Reference BorcherdsBor98], where
$\Lambda$ [Reference BorcherdsBor98], where ![]() ${\rm Mp}_{2}(\textbf {Z})$ is the metaplectic cover of
${\rm Mp}_{2}(\textbf {Z})$ is the metaplectic cover of ![]() ${\rm SL}_{2}(\textbf {Z})$. By [Reference YoshikawaYos13, (7.9)], the principal part of
${\rm SL}_{2}(\textbf {Z})$. By [Reference YoshikawaYos13, (7.9)], the principal part of ![]() $F_{\Lambda }$ is given by
$F_{\Lambda }$ is given by
 \begin{align} {\mathcal{P}}_{\leq0}[F_{\Lambda}]&:= \{q^{-1}+2(16-r(\Lambda))\}\,\textbf{e}_{0} + 2^{g(\Lambda)+1}\{16-r(\Lambda)\}\,\textbf{v}_{0}\nonumber\\ &\quad +2^{g(\Lambda)}q^{-{1}/{4}}\textbf{v}_{3} - 2^{16-r(\Lambda)}q^{({12-r(\Lambda)})/{4}}\{1+(28-r(\Lambda))q^{2}\}\,\textbf{e}_{\textbf{1}_{\Lambda}}. \end{align}
\begin{align} {\mathcal{P}}_{\leq0}[F_{\Lambda}]&:= \{q^{-1}+2(16-r(\Lambda))\}\,\textbf{e}_{0} + 2^{g(\Lambda)+1}\{16-r(\Lambda)\}\,\textbf{v}_{0}\nonumber\\ &\quad +2^{g(\Lambda)}q^{-{1}/{4}}\textbf{v}_{3} - 2^{16-r(\Lambda)}q^{({12-r(\Lambda)})/{4}}\{1+(28-r(\Lambda))q^{2}\}\,\textbf{e}_{\textbf{1}_{\Lambda}}. \end{align}
By (8.1), we easily see that ![]() ${\mathcal {P}}_{\leq 0}[F_{\Lambda }]=0$ if and only if
${\mathcal {P}}_{\leq 0}[F_{\Lambda }]=0$ if and only if ![]() $(r(\Lambda ),\delta (\Lambda ))=(16,0)$.
$(r(\Lambda ),\delta (\Lambda ))=(16,0)$.
Let ![]() $\ell \in \textbf {Z}_{>0}$ be such that
$\ell \in \textbf {Z}_{>0}$ be such that ![]() $2^{r(\Lambda )-16}|\ell$ for all
$2^{r(\Lambda )-16}|\ell$ for all ![]() $\Lambda$. Then
$\Lambda$. Then ![]() $\ell F_{\Lambda }(\tau )$ has integral Fourier expansion at
$\ell F_{\Lambda }(\tau )$ has integral Fourier expansion at ![]() $+i\infty$. Define
$+i\infty$. Define ![]() $\Psi _{\Lambda }^{\ell }$ as the Borcherds lift of
$\Psi _{\Lambda }^{\ell }$ as the Borcherds lift of ![]() $\ell F_{\Lambda }(\tau )$ (cf. [Reference BorcherdsBor98, Theorem 13.3]):
$\ell F_{\Lambda }(\tau )$ (cf. [Reference BorcherdsBor98, Theorem 13.3]):
If ![]() $r(\Lambda )\leq 16$, then
$r(\Lambda )\leq 16$, then ![]() $\Psi _{\Lambda }(\cdot ,F_{\Lambda })$ is well defined and
$\Psi _{\Lambda }(\cdot ,F_{\Lambda })$ is well defined and ![]() $\Psi _{\Lambda }^{\ell }=\Psi _{\Lambda }(\cdot ,\ell F_{\Lambda })=\Psi _{\Lambda }(\cdot ,F_{\Lambda })^{\ell }$ in the ordinary sense. Since
$\Psi _{\Lambda }^{\ell }=\Psi _{\Lambda }(\cdot ,\ell F_{\Lambda })=\Psi _{\Lambda }(\cdot ,F_{\Lambda })^{\ell }$ in the ordinary sense. Since ![]() $O(\Lambda )$ (equivalently,
$O(\Lambda )$ (equivalently, ![]() $O(q_{\Lambda })$) acts trivially on
$O(q_{\Lambda })$) acts trivially on ![]() $\ell F_{\Lambda }$ by [Reference YoshikawaYos13, Theorem 7.7, (2)],
$\ell F_{\Lambda }$ by [Reference YoshikawaYos13, Theorem 7.7, (2)], ![]() $\Psi _{\Lambda }^{\ell }$ is an automorphic form on
$\Psi _{\Lambda }^{\ell }$ is an automorphic form on ![]() $\Omega _{\Lambda }$ for
$\Omega _{\Lambda }$ for ![]() $O^{+}(\Lambda )$ by [Reference BorcherdsBor98, Theorem 13.3]. Recall that the divisors
$O^{+}(\Lambda )$ by [Reference BorcherdsBor98, Theorem 13.3]. Recall that the divisors ![]() ${\mathcal {D}}_{\Lambda }^{+}$,
${\mathcal {D}}_{\Lambda }^{+}$, ![]() ${\mathcal {D}}_{\Lambda }^{-}$ and
${\mathcal {D}}_{\Lambda }^{-}$ and ![]() ${\mathcal {H}}_{\Lambda }$ were introduced in §§ 2.2 and 2.3.
${\mathcal {H}}_{\Lambda }$ were introduced in §§ 2.2 and 2.3.
Theorem 8.1 The weight and the divisor of ![]() $\Psi _{\Lambda }^{\ell }$ are given as follows.
$\Psi _{\Lambda }^{\ell }$ are given as follows.
(1) If
 $r(\Lambda )\leq 20$, then
$r(\Lambda )\leq 20$, then
 \begin{gather*} {\rm wt}(\Psi_{\Lambda}^{\ell}) = \begin{cases} \begin{array}{@{}ll} (16-r(\Lambda))(2^{g(\Lambda)}+1)\ell & (r(\Lambda)\not=12,20), \\ (16-r(\Lambda))(2^{g(\Lambda)}+1)\ell-8(1-\delta(\Lambda))\ell & (r(\Lambda)=12), \\ (16-r(\Lambda))(2^{g(\Lambda)}+1)\ell-(28-r(\Lambda))2^{15-r(\Lambda)}(1-\delta(\Lambda))\ell & (r(\Lambda)=20), \end{array} \end{cases}\\ {\rm div}(\Psi_{\Lambda}^{\ell}) = \ell\, \{ {\mathcal{D}}_{\Lambda}^{-} + (2^{g(\Lambda)}+1) {\mathcal{D}}_{\Lambda}^{+} - 2^{16-r(\Lambda)} {\mathcal{H}}_{\Lambda}\}. \end{gather*}
\begin{gather*} {\rm wt}(\Psi_{\Lambda}^{\ell}) = \begin{cases} \begin{array}{@{}ll} (16-r(\Lambda))(2^{g(\Lambda)}+1)\ell & (r(\Lambda)\not=12,20), \\ (16-r(\Lambda))(2^{g(\Lambda)}+1)\ell-8(1-\delta(\Lambda))\ell & (r(\Lambda)=12), \\ (16-r(\Lambda))(2^{g(\Lambda)}+1)\ell-(28-r(\Lambda))2^{15-r(\Lambda)}(1-\delta(\Lambda))\ell & (r(\Lambda)=20), \end{array} \end{cases}\\ {\rm div}(\Psi_{\Lambda}^{\ell}) = \ell\, \{ {\mathcal{D}}_{\Lambda}^{-} + (2^{g(\Lambda)}+1) {\mathcal{D}}_{\Lambda}^{+} - 2^{16-r(\Lambda)} {\mathcal{H}}_{\Lambda}\}. \end{gather*}(2) If
 $r(\Lambda )=21$, then
$r(\Lambda )=21$, then
 \[ \begin{array}{c} {\rm wt}(\Psi_{\Lambda}^{\ell}) = (16-r(\Lambda))(2^{g(\Lambda)}+1)\ell = -5^{3}\cdot 41\ell,\\ \begin{aligned} {\rm div}(\Psi_{\Lambda}^{\ell}) & = \ell [ {\mathcal{D}}_{\Lambda}^{-} + (2^{g(\Lambda)}+1) {\mathcal{D}}_{\Lambda}^{+} - 2^{16-r(\Lambda)}\{ {\mathcal{H}}_{\Lambda} + (28-r(\Lambda)) {\mathcal{D}}_{\Lambda}^{+}\} ]\\ & = 2^{-5}\ell\cdot \{ 32{\mathcal{D}}_{\Lambda}^{-} + 3\cdot17\cdot643\cdot{\mathcal{D}}_{\Lambda}^{+} - {\mathcal{H}}_{\Lambda} \}. \end{aligned} \end{array} \]
\[ \begin{array}{c} {\rm wt}(\Psi_{\Lambda}^{\ell}) = (16-r(\Lambda))(2^{g(\Lambda)}+1)\ell = -5^{3}\cdot 41\ell,\\ \begin{aligned} {\rm div}(\Psi_{\Lambda}^{\ell}) & = \ell [ {\mathcal{D}}_{\Lambda}^{-} + (2^{g(\Lambda)}+1) {\mathcal{D}}_{\Lambda}^{+} - 2^{16-r(\Lambda)}\{ {\mathcal{H}}_{\Lambda} + (28-r(\Lambda)) {\mathcal{D}}_{\Lambda}^{+}\} ]\\ & = 2^{-5}\ell\cdot \{ 32{\mathcal{D}}_{\Lambda}^{-} + 3\cdot17\cdot643\cdot{\mathcal{D}}_{\Lambda}^{+} - {\mathcal{H}}_{\Lambda} \}. \end{aligned} \end{array} \]
Proof. By using (8.1), the result follows from [Reference BorcherdsBor98, Theorem 13.3].
The Petersson norm ![]() $\|\Psi _{\Lambda }^{\ell }\|=\|\Psi _{\Lambda }(\cdot ,\ell F_{\Lambda })\|$ is an
$\|\Psi _{\Lambda }^{\ell }\|=\|\Psi _{\Lambda }(\cdot ,\ell F_{\Lambda })\|$ is an ![]() $O(\Lambda )$-invariant function on
$O(\Lambda )$-invariant function on ![]() $\Omega _{\Lambda }$. We identify
$\Omega _{\Lambda }$. We identify ![]() $\|\Psi _{\Lambda }^{\ell }\|$ with the corresponding function on
$\|\Psi _{\Lambda }^{\ell }\|$ with the corresponding function on ![]() ${\mathcal {M}}_{\Lambda }$ and set
${\mathcal {M}}_{\Lambda }$ and set
Then ![]() $\|\Psi _{\Lambda }(\cdot ,F_{\Lambda })\|$ is independent of the choice of
$\|\Psi _{\Lambda }(\cdot ,F_{\Lambda })\|$ is independent of the choice of ![]() $\ell \in \textbf {Z}_{>0}$ with
$\ell \in \textbf {Z}_{>0}$ with ![]() $2^{r(\Lambda )-16}|\ell$. If
$2^{r(\Lambda )-16}|\ell$. If ![]() $r(\Lambda )\leq 16$, then
$r(\Lambda )\leq 16$, then ![]() $\|\Psi _{\Lambda }(\cdot ,F_{\Lambda })\|$ is the ordinary Petersson norm of
$\|\Psi _{\Lambda }(\cdot ,F_{\Lambda })\|$ is the ordinary Petersson norm of ![]() $\Psi _{\Lambda }(\cdot ,F_{\Lambda })$.
$\Psi _{\Lambda }(\cdot ,F_{\Lambda })$.
8.2 The structure of  $\Phi _{M}$: the case
$\Phi _{M}$: the case  $\delta =1$
$\delta =1$
Write ![]() $M_{g,k}$ for a primitive
$M_{g,k}$ for a primitive ![]() $2$-elementary Lorentzian sublattice of
$2$-elementary Lorentzian sublattice of ![]() ${\Bbb L}_{K3}$ such that
${\Bbb L}_{K3}$ such that
Then ![]() $M_{g,0}\cong {\Bbb A}_{1}^{+}\oplus {\Bbb A}_{1}^{\oplus 10-g}$ and
$M_{g,0}\cong {\Bbb A}_{1}^{+}\oplus {\Bbb A}_{1}^{\oplus 10-g}$ and ![]() $(r,l,\delta )=(11-g,11-g,1)$ for
$(r,l,\delta )=(11-g,11-g,1)$ for ![]() $M_{g,0}$. Set
$M_{g,0}$. Set
Lemma 8.2 There exist mutually perpendicular roots ![]() $d_{1},\ldots ,d_{k}\in \Delta _{\Lambda _{g,0}}^{+}$ with
$d_{1},\ldots ,d_{k}\in \Delta _{\Lambda _{g,0}}^{+}$ with
In particular, if ![]() $M_{g,k}$ exists, one has
$M_{g,k}$ exists, one has ![]() $\Omega _{\Lambda _{g,k}}=\Omega _{\Lambda _{g,k-1}}\cap H_{d_{k}}$.
$\Omega _{\Lambda _{g,k}}=\Omega _{\Lambda _{g,k-1}}\cap H_{d_{k}}$.
By Theorem 6.1, there exist integers ![]() $a_{g},b_{g},c_{g}\in \textbf {Z}_{\geq 0}$ for
$a_{g},b_{g},c_{g}\in \textbf {Z}_{\geq 0}$ for ![]() $3\leq g\leq 10$ with
$3\leq g\leq 10$ with
Lemma 8.3 The following inequalities and equality hold:
Proof. We get ![]() $a_{g}>0$ by [Reference YoshikawaYos13, Proposition 4.2 (2)] and
$a_{g}>0$ by [Reference YoshikawaYos13, Proposition 4.2 (2)] and ![]() $b_{g}>0$ by Theorem 6.1. Let
$b_{g}>0$ by Theorem 6.1. Let ![]() $6\leq g\leq 9$. Recall that the Zariski open subset
$6\leq g\leq 9$. Recall that the Zariski open subset ![]() ${\mathcal {D}}_{\Lambda }^{0,+}$ (respectively,
${\mathcal {D}}_{\Lambda }^{0,+}$ (respectively, ![]() ${\mathcal {D}}_{\Lambda }^{0,-}$) of
${\mathcal {D}}_{\Lambda }^{0,-}$) of ![]() ${\mathcal {D}}_{\Lambda }^{+}$ (respectively,
${\mathcal {D}}_{\Lambda }^{+}$ (respectively, ![]() ${\mathcal {D}}_{\Lambda }^{-}$) was defined in § 2.2. By (3.5) and Proposition 6.2, we get
${\mathcal {D}}_{\Lambda }^{-}$) was defined in § 2.2. By (3.5) and Proposition 6.2, we get ![]() $J_{M_{g,0}}({\mathcal {D}}_{\Lambda _{g,0}}^{0,+})=J_{M_{g,1}}(\Omega _{\Lambda _{g,1}}^{0})\not \subset \theta _{{\rm null},g}$, which implies
$J_{M_{g,0}}({\mathcal {D}}_{\Lambda _{g,0}}^{0,+})=J_{M_{g,1}}(\Omega _{\Lambda _{g,1}}^{0})\not \subset \theta _{{\rm null},g}$, which implies ![]() $c_{g}=0$ for
$c_{g}=0$ for ![]() $6\leq g\leq 9$. Let
$6\leq g\leq 9$. Let ![]() $1\leq g\leq 5$. By [Reference YoshikawaYos13, Proposition 4.2 (1)],
$1\leq g\leq 5$. By [Reference YoshikawaYos13, Proposition 4.2 (1)], ![]() $J_{M_{g,g}}(\Omega _{\Lambda _{g,g}}^{0})\not \subset \theta _{{\rm null},g}$. Since
$J_{M_{g,g}}(\Omega _{\Lambda _{g,g}}^{0})\not \subset \theta _{{\rm null},g}$. Since ![]() $J_{M_{g,g-1}}({\mathcal {D}}_{\Lambda _{g,g-1}}^{0,+})=J_{M_{g,g}}(\Omega _{\Lambda _{g,g}}^{0})$ by (3.5) and Lemma 8.2, we get
$J_{M_{g,g-1}}({\mathcal {D}}_{\Lambda _{g,g-1}}^{0,+})=J_{M_{g,g}}(\Omega _{\Lambda _{g,g}}^{0})$ by (3.5) and Lemma 8.2, we get ![]() $J_{M_{g,g-1}}(\Omega _{\Lambda _{g,g-1}}^{0})\not \subset \theta _{{\rm null},g}$ because
$J_{M_{g,g-1}}(\Omega _{\Lambda _{g,g-1}}^{0})\not \subset \theta _{{\rm null},g}$ because ![]() ${\mathcal {D}}_{\Lambda _{g,g-1}}^{0,+}\subset \Omega _{\Lambda _{g,g-1}}$. By (3.5) and Lemma 8.2 again, we get
${\mathcal {D}}_{\Lambda _{g,g-1}}^{0,+}\subset \Omega _{\Lambda _{g,g-1}}$. By (3.5) and Lemma 8.2 again, we get ![]() $J_{M_{g,g-2}}({\mathcal {D}}_{\Lambda _{g,g-2}}^{0,+})=J_{M_{g,g-1}}(\Omega _{\Lambda _{g,g-1}}^{0})\not \subset \theta _{{\rm null},g}$. In the same way, we get inductively
$J_{M_{g,g-2}}({\mathcal {D}}_{\Lambda _{g,g-2}}^{0,+})=J_{M_{g,g-1}}(\Omega _{\Lambda _{g,g-1}}^{0})\not \subset \theta _{{\rm null},g}$. In the same way, we get inductively ![]() $J_{M_{g,k}}({\mathcal {D}}_{\Lambda _{g,k}}^{0,+})\not \subset \theta _{{\rm null},g}$ for
$J_{M_{g,k}}({\mathcal {D}}_{\Lambda _{g,k}}^{0,+})\not \subset \theta _{{\rm null},g}$ for ![]() $k\leq g-1$. This proves
$k\leq g-1$. This proves ![]() $c_{g}=0$ for
$c_{g}=0$ for ![]() $3\leq g\leq 5$.
$3\leq g\leq 5$.
Proposition 8.4 If ![]() $3\leq g\leq 10$, the following equality of divisors on
$3\leq g\leq 10$, the following equality of divisors on ![]() $\Omega _{\Lambda _{g,k}}$ holds:
$\Omega _{\Lambda _{g,k}}$ holds:
Proof. When ![]() $g=10$,
$g=10$, ![]() $M_{g,k}$ makes sense only for
$M_{g,k}$ makes sense only for ![]() $k=0$ by Proposition 1.1 . Hence the assertion is obvious by (8.2) when
$k=0$ by Proposition 1.1 . Hence the assertion is obvious by (8.2) when ![]() $g=10$. We must prove (8.3) when
$g=10$. We must prove (8.3) when ![]() $g\leq 9$. We will prove by induction the existence of integers
$g\leq 9$. We will prove by induction the existence of integers ![]() $a_{g,k},b_{g,k}\in \textbf {Z}$ with
$a_{g,k},b_{g,k}\in \textbf {Z}$ with
When ![]() $k=0$, the assertion follows from (8.2) and Lemma 8.3. We assume (8.4) for
$k=0$, the assertion follows from (8.2) and Lemma 8.3. We assume (8.4) for ![]() $M_{g,k}$. By Lemma 8.2, there exists
$M_{g,k}$. By Lemma 8.2, there exists ![]() $d\in \Delta ^{+}_{\Lambda _{g,k}}$ such that
$d\in \Delta ^{+}_{\Lambda _{g,k}}$ such that ![]() $\Lambda _{g,k}=\Lambda _{g,k+1}\oplus \textbf {Z}d$. Then
$\Lambda _{g,k}=\Lambda _{g,k+1}\oplus \textbf {Z}d$. Then ![]() $\Omega _{\Lambda _{g,k+1}}=H_{d}\cap \Omega _{\Lambda _{g,k}}$. Let
$\Omega _{\Lambda _{g,k+1}}=H_{d}\cap \Omega _{\Lambda _{g,k}}$. Let ![]() $i\colon \Omega _{\Lambda _{g,k+1}}=H_{d}\cap \Omega _{\Lambda _{g,k}}\hookrightarrow \Omega _{\Lambda _{g,k}}$ be the inclusion. By the compatibility of Torelli maps (3.5), we get the equality of holomorphic maps
$i\colon \Omega _{\Lambda _{g,k+1}}=H_{d}\cap \Omega _{\Lambda _{g,k}}\hookrightarrow \Omega _{\Lambda _{g,k}}$ be the inclusion. By the compatibility of Torelli maps (3.5), we get the equality of holomorphic maps
Hence we get the equality of holomorphic sections on ![]() $\Omega _{\Lambda _{g,k+1}}^{0}\cup {\mathcal {D}}_{\Lambda _{g,k+1}}^{0}$:
$\Omega _{\Lambda _{g,k+1}}^{0}\cup {\mathcal {D}}_{\Lambda _{g,k+1}}^{0}$:
Since ![]() $\Omega _{\Lambda _{g,k+1}}\setminus (\Omega _{\Lambda _{g,k+1}}^{0}\cup {\mathcal {D}}_{\Lambda _{g,k+1}}^{0})$ has codimension at least
$\Omega _{\Lambda _{g,k+1}}\setminus (\Omega _{\Lambda _{g,k+1}}^{0}\cup {\mathcal {D}}_{\Lambda _{g,k+1}}^{0})$ has codimension at least ![]() $2$ in
$2$ in ![]() $\Omega _{\Lambda _{g,k+1}}$, we deduce from (8.4) and (8.6) the equality of divisors on
$\Omega _{\Lambda _{g,k+1}}$, we deduce from (8.4) and (8.6) the equality of divisors on ![]() $\Omega _{\Lambda _{g,k+1}}$:
$\Omega _{\Lambda _{g,k+1}}$:
 \begin{align} {\rm div}(J_{M_{g,k+1}}^{*}\chi_{g}^{8}) &= {\rm div}(i^{*}J_{M_{g,k}}^{*}\chi_{g}^{8}) = i^{*}{\rm div}(J_{M_{g,k}}^{*}\chi_{g}^{8}) = i^{*}( a_{g,k}{\mathcal{D}}_{\Lambda_{g,k}}^{-} + b_{g,k}{\mathcal{H}}_{\Lambda_{g,k}})\nonumber\\ &= a_{g,k}{\mathcal{D}}_{\Lambda_{g,k+1}}^{-} + 2b_{g,k}{\mathcal{H}}_{\Lambda_{g,k+1}}. \end{align}
\begin{align} {\rm div}(J_{M_{g,k+1}}^{*}\chi_{g}^{8}) &= {\rm div}(i^{*}J_{M_{g,k}}^{*}\chi_{g}^{8}) = i^{*}{\rm div}(J_{M_{g,k}}^{*}\chi_{g}^{8}) = i^{*}( a_{g,k}{\mathcal{D}}_{\Lambda_{g,k}}^{-} + b_{g,k}{\mathcal{H}}_{\Lambda_{g,k}})\nonumber\\ &= a_{g,k}{\mathcal{D}}_{\Lambda_{g,k+1}}^{-} + 2b_{g,k}{\mathcal{H}}_{\Lambda_{g,k+1}}. \end{align}
Here the last equality follows from Propositions 2.1 and 2.2. This proves (8.4) for ![]() $M_{g,k+1}$. By induction, (8.4) holds for all
$M_{g,k+1}$. By induction, (8.4) holds for all ![]() $M_{g,k}$.
$M_{g,k}$.
Since ![]() $a_{g,k+1}=a_{g,k}$ and
$a_{g,k+1}=a_{g,k}$ and ![]() $b_{g,k+1}=2b_{g,k}$ for
$b_{g,k+1}=2b_{g,k}$ for ![]() $k\geq 0$ by (8.4), (8.7), we get
$k\geq 0$ by (8.4), (8.7), we get
for ![]() $g\leq 9$ and
$g\leq 9$ and ![]() $k\geq 0$. This proves the result.
$k\geq 0$. This proves the result.
Proposition 8.5 If ![]() $3\leq g\leq 10$, then the following inequalities hold:
$3\leq g\leq 10$, then the following inequalities hold:
Proof. The inequality ![]() $a_{g}\geq 2^{2g-1}$ follows from [Reference YoshikawaYos13, Proposition 4.2 (2)]. (To confirm
$a_{g}\geq 2^{2g-1}$ follows from [Reference YoshikawaYos13, Proposition 4.2 (2)]. (To confirm ![]() $J_{M}(\Omega _{\Lambda }^{0})\not \subset \theta _{{\rm null},g}$, it is assumed there that either
$J_{M}(\Omega _{\Lambda }^{0})\not \subset \theta _{{\rm null},g}$, it is assumed there that either ![]() $r>10$ or
$r>10$ or ![]() $(r,\delta )=(10,1)$. Since the same proof of [Reference YoshikawaYos13, Proposition 4.2 (2)] works under the same assumption
$(r,\delta )=(10,1)$. Since the same proof of [Reference YoshikawaYos13, Proposition 4.2 (2)] works under the same assumption ![]() $J_{M}(\Omega _{\Lambda }^{0})\not \subset \theta _{{\rm null},g}$ and since
$J_{M}(\Omega _{\Lambda }^{0})\not \subset \theta _{{\rm null},g}$ and since ![]() $J_{M_{g,0}}(\Omega _{\Lambda _{g,0}}^{0})\not \subset \theta _{{\rm null},g}$ for
$J_{M_{g,0}}(\Omega _{\Lambda _{g,0}}^{0})\not \subset \theta _{{\rm null},g}$ for ![]() $3\leq g\leq 10$ by Theorem 6.1, the same conclusion as in [Reference YoshikawaYos13, Proposition 4.2 (2)] still holds for
$3\leq g\leq 10$ by Theorem 6.1, the same conclusion as in [Reference YoshikawaYos13, Proposition 4.2 (2)] still holds for ![]() $M_{g,0}$.) Let us prove the second inequality.
$M_{g,0}$.) Let us prove the second inequality.
Let ![]() $j\colon {\frak M}_{g}\ni C\to {\rm Jac}(C)\in {\mathcal {A}}_{g}$ be the Torelli map. By [Reference Teixidor i BigasTei88, Proposition 3.1] or [Reference TsuyumineTsu91, Proof of Theorem 1, p. 542], we get the equality of divisors on
$j\colon {\frak M}_{g}\ni C\to {\rm Jac}(C)\in {\mathcal {A}}_{g}$ be the Torelli map. By [Reference Teixidor i BigasTei88, Proposition 3.1] or [Reference TsuyumineTsu91, Proof of Theorem 1, p. 542], we get the equality of divisors on ![]() ${\frak M}_{g}$:
${\frak M}_{g}$:
Set ![]() $\Lambda :=\Lambda _{g,0}$ and
$\Lambda :=\Lambda _{g,0}$ and ![]() ${\mu }_{\Lambda }^{0}:=\bar {\mu }_{\Lambda }\circ \Pi _{\Lambda }|_{\Omega _{\Lambda }^{0}}$, where
${\mu }_{\Lambda }^{0}:=\bar {\mu }_{\Lambda }\circ \Pi _{\Lambda }|_{\Omega _{\Lambda }^{0}}$, where ![]() $\Pi _{\Lambda }\colon \Omega _{\Lambda }\to {\mathcal {M}}_{\Lambda }$ is the projection. Since
$\Pi _{\Lambda }\colon \Omega _{\Lambda }\to {\mathcal {M}}_{\Lambda }$ is the projection. Since ![]() $J_{M_{g,0}}|_{\Omega _{\Lambda }^{0}}=j\circ {\mu }_{\Lambda }^{0}$, we get by (8.9) the following equality of divisors on
$J_{M_{g,0}}|_{\Omega _{\Lambda }^{0}}=j\circ {\mu }_{\Lambda }^{0}$, we get by (8.9) the following equality of divisors on ![]() $\Omega _{\Lambda }^{0}$:
$\Omega _{\Lambda }^{0}$:
Since ![]() ${\rm Supp}(({\mu }_{\Lambda }^{0})^{*}{\frak M}'_{g})\subset {\mathcal {H}}_{\Lambda }\cap \Omega _{\Lambda }^{0}$ and since
${\rm Supp}(({\mu }_{\Lambda }^{0})^{*}{\frak M}'_{g})\subset {\mathcal {H}}_{\Lambda }\cap \Omega _{\Lambda }^{0}$ and since ![]() $\bar {\mathcal {H}}_{\Lambda }$ is irreducible by Theorem 6.1, there exists
$\bar {\mathcal {H}}_{\Lambda }$ is irreducible by Theorem 6.1, there exists ![]() $\beta _{g}\in \textbf {Z}_{>0}$ such that the following equality of divisors on
$\beta _{g}\in \textbf {Z}_{>0}$ such that the following equality of divisors on ![]() $\Omega _{\Lambda }^{0}$ holds:
$\Omega _{\Lambda }^{0}$ holds:
By (8.10), (8.11), we get the equality of divisors on ![]() $\Omega _{\Lambda }^{0}$:
$\Omega _{\Lambda }^{0}$:
Comparing (8.2) with (8.12), we get ![]() $b_{g}=2^{4}\beta _{g}\geq 2^{4}$. This completes the proof.
$b_{g}=2^{4}\beta _{g}\geq 2^{4}$. This completes the proof.
Theorem 8.6 There exists a constant ![]() $C_{g,k,\ell }$ depending only on
$C_{g,k,\ell }$ depending only on ![]() $g$,
$g$, ![]() $k$,
$k$, ![]() $\ell$ such that the following equality of automorphic forms on
$\ell$ such that the following equality of automorphic forms on ![]() $\Omega _{\Lambda _{g,k}}$ holds:
$\Omega _{\Lambda _{g,k}}$ holds:
In particular, there exists a constant ![]() $C_{g,k}$ depending only on
$C_{g,k}$ depending only on ![]() $g$,
$g$, ![]() $k$ such that
$k$ such that
Proof. Since the result was proved in [Reference YoshikawaYos13, Theorem 9.1] in the case ![]() $g\leq 2$, we assume
$g\leq 2$, we assume ![]() $g\geq 3$ in what follows. Set
$g\geq 3$ in what follows. Set ![]() $M:=M_{g,k}$ and
$M:=M_{g,k}$ and ![]() $\Lambda :=\Lambda _{g,k}$. Then
$\Lambda :=\Lambda _{g,k}$. Then ![]() $r(\Lambda )\geq 5$ and hence
$r(\Lambda )\geq 5$ and hence ![]() ${\mathcal {M}}_{\Lambda }^{*}\setminus {\mathcal {M}}_{\Lambda }$ has codimension at least
${\mathcal {M}}_{\Lambda }^{*}\setminus {\mathcal {M}}_{\Lambda }$ has codimension at least ![]() $2$ in
$2$ in ![]() ${\mathcal {M}}^{*}$. By definition,
${\mathcal {M}}^{*}$. By definition, ![]() $M=M_{g,k}$ has invariants
$M=M_{g,k}$ has invariants ![]() $r(M)=11+k-g$ and
$r(M)=11+k-g$ and ![]() $l(M)=11-k-g$, so that
$l(M)=11-k-g$, so that ![]() $r(\Lambda )=11-k+g$ and
$r(\Lambda )=11-k+g$ and ![]() $l(\Lambda )=11-k-g$.
$l(\Lambda )=11-k-g$.
Since ![]() ${\rm wt}(\chi _{g})=2^{g-2}(2^{g}+1)$ and
${\rm wt}(\chi _{g})=2^{g-2}(2^{g}+1)$ and ![]() ${\rm wt}(\Psi _{\Lambda }^{\ell })=\{16-r(\Lambda )\}(2^{g}+1)\ell$ by Theorem 8.1, we get
${\rm wt}(\Psi _{\Lambda }^{\ell })=\{16-r(\Lambda )\}(2^{g}+1)\ell$ by Theorem 8.1, we get
Since ![]() ${\rm wt}(\Phi _{\Lambda })=\ell (16-r(\Lambda ),4)$ by Theorem 5.1, we get by (8.13) that
${\rm wt}(\Phi _{\Lambda })=\ell (16-r(\Lambda ),4)$ by Theorem 5.1, we get by (8.13) that
By (8.14),
descends to a meromorphic function on ![]() ${\mathcal {M}}_{\Lambda }$. Since
${\mathcal {M}}_{\Lambda }$. Since ![]() ${\mathcal {M}}_{\Lambda }^{*}$ is normal and since
${\mathcal {M}}_{\Lambda }^{*}$ is normal and since ![]() $\dim {\mathcal {M}}_{\Lambda }^{*}\setminus {\mathcal {M}}_{\Lambda }\leq \dim {\mathcal {M}}_{\Lambda }^{*}-2$,
$\dim {\mathcal {M}}_{\Lambda }^{*}\setminus {\mathcal {M}}_{\Lambda }\leq \dim {\mathcal {M}}_{\Lambda }^{*}-2$, ![]() $\varphi _{\Lambda }$ extends to a meromorphic function on
$\varphi _{\Lambda }$ extends to a meromorphic function on ![]() ${\mathcal {M}}_{\Lambda }^{*}$.
${\mathcal {M}}_{\Lambda }^{*}$.
(1) Let ![]() $r(M)\geq 2$. Hence
$r(M)\geq 2$. Hence ![]() $r(\Lambda )\leq 20$. By Theorem 8.1 and Proposition 8.4,
$r(\Lambda )\leq 20$. By Theorem 8.1 and Proposition 8.4,
 \begin{align} {\rm div}( \Psi_{\Lambda}^{2^{g-1}} \otimes J_{M}^{*}\chi_{g}^{8} ) &= 2^{g-1} \{ {\mathcal{D}}_{\Lambda}^{-} + (2^{g}+1){\mathcal{D}}_{\Lambda}^{+} - 2^{16-r(\Lambda)}{\mathcal{H}}_{\Lambda} \} + a_{g}{\mathcal{D}}_{\Lambda}^{-} + 2^{k}b_{g}{\mathcal{H}}_{\Lambda}\nonumber\\ &= (2^{g-1}+a_{g}){\mathcal{D}}_{\Lambda}^{-} + 2^{g-1}(2^{g}+1){\mathcal{D}}_{\Lambda}^{+} + 2^{k}(b_{g}-2^{4}){\mathcal{H}}_{\Lambda}. \end{align}
\begin{align} {\rm div}( \Psi_{\Lambda}^{2^{g-1}} \otimes J_{M}^{*}\chi_{g}^{8} ) &= 2^{g-1} \{ {\mathcal{D}}_{\Lambda}^{-} + (2^{g}+1){\mathcal{D}}_{\Lambda}^{+} - 2^{16-r(\Lambda)}{\mathcal{H}}_{\Lambda} \} + a_{g}{\mathcal{D}}_{\Lambda}^{-} + 2^{k}b_{g}{\mathcal{H}}_{\Lambda}\nonumber\\ &= (2^{g-1}+a_{g}){\mathcal{D}}_{\Lambda}^{-} + 2^{g-1}(2^{g}+1){\mathcal{D}}_{\Lambda}^{+} + 2^{k}(b_{g}-2^{4}){\mathcal{H}}_{\Lambda}. \end{align}
Since ![]() ${\rm div}(\Phi _{\Lambda })=\ell {\mathcal {D}}_{\Lambda }$, we deduce from (8.15) that
${\rm div}(\Phi _{\Lambda })=\ell {\mathcal {D}}_{\Lambda }$, we deduce from (8.15) that
Since ![]() $a_{g}\geq 2^{2g-1}$ and
$a_{g}\geq 2^{2g-1}$ and ![]() $b_{g}\geq 2^{4}$ by Proposition 8.5, the divisor of
$b_{g}\geq 2^{4}$ by Proposition 8.5, the divisor of ![]() $\varphi _{\Lambda }$ is effective by (8.16). Since
$\varphi _{\Lambda }$ is effective by (8.16). Since ![]() $\varphi _{\Lambda }$ is a holomorphic function on
$\varphi _{\Lambda }$ is a holomorphic function on ![]() ${\mathcal {M}}_{\Lambda }^{*}$,
${\mathcal {M}}_{\Lambda }^{*}$, ![]() $\varphi _{\Lambda }$ must be a constant function on
$\varphi _{\Lambda }$ must be a constant function on ![]() ${\mathcal {M}}_{\Lambda }^{*}$, which implies that
${\mathcal {M}}_{\Lambda }^{*}$, which implies that
This completes the proof when ![]() $r(M)\geq 2$.
$r(M)\geq 2$.
(2) Assume ![]() $r(M)=1$. Then
$r(M)=1$. Then ![]() $M={\Bbb A}_{1}^{+}$ and
$M={\Bbb A}_{1}^{+}$ and ![]() $r(\Lambda )=21$,
$r(\Lambda )=21$, ![]() $g=10$,
$g=10$, ![]() $k=0$,
$k=0$, ![]() $\delta =1$. By Theorem 8.1 (2), Proposition 8.4 and the equality
$\delta =1$. By Theorem 8.1 (2), Proposition 8.4 and the equality ![]() $(g-1)+16-r(\Lambda )=4$, we get
$(g-1)+16-r(\Lambda )=4$, we get
 \begin{align} {\rm div} ( \Psi_{\Lambda}^{2^{g-1}\ell} \otimes J_{M}^{*}\chi_{g}^{8\ell} ) &= 2^{g-1}\ell \{ {\mathcal{D}}_{\Lambda}^{-} + (2^{g}+1) {\mathcal{D}}_{\Lambda}^{+} - 2^{16-r(\Lambda)} {\mathcal{H}}_{\Lambda} - 2^{16-r(\Lambda)}(28-r(\Lambda)) {\mathcal{D}}_{\Lambda}^{+} \}\nonumber\\ &\quad + \ell\, \{ a_{g} {\mathcal{D}}_{\Lambda}^{-} + b_{g} {\mathcal{H}}_{\Lambda} + c_{g} {\mathcal{D}}_{\Lambda}^{+} \}\nonumber\\ &= \ell \{(2^{g-1}+a_{g}) {\mathcal{D}}_{\Lambda}^{-} + (b_{g}-2^{4}){\mathcal{H}}_{\Lambda} \} + \ell \{(2^{2g-1}+2^{g-1}+c_{g})-2^{4}\cdot7)\}{\mathcal{D}}_{\Lambda}^{+}. \end{align}
\begin{align} {\rm div} ( \Psi_{\Lambda}^{2^{g-1}\ell} \otimes J_{M}^{*}\chi_{g}^{8\ell} ) &= 2^{g-1}\ell \{ {\mathcal{D}}_{\Lambda}^{-} + (2^{g}+1) {\mathcal{D}}_{\Lambda}^{+} - 2^{16-r(\Lambda)} {\mathcal{H}}_{\Lambda} - 2^{16-r(\Lambda)}(28-r(\Lambda)) {\mathcal{D}}_{\Lambda}^{+} \}\nonumber\\ &\quad + \ell\, \{ a_{g} {\mathcal{D}}_{\Lambda}^{-} + b_{g} {\mathcal{H}}_{\Lambda} + c_{g} {\mathcal{D}}_{\Lambda}^{+} \}\nonumber\\ &= \ell \{(2^{g-1}+a_{g}) {\mathcal{D}}_{\Lambda}^{-} + (b_{g}-2^{4}){\mathcal{H}}_{\Lambda} \} + \ell \{(2^{2g-1}+2^{g-1}+c_{g})-2^{4}\cdot7)\}{\mathcal{D}}_{\Lambda}^{+}. \end{align}
Since ![]() ${\rm div}(\Phi _{\Lambda })=\ell {\mathcal {D}}_{\Lambda }$, we get by (8.18) that
${\rm div}(\Phi _{\Lambda })=\ell {\mathcal {D}}_{\Lambda }$, we get by (8.18) that
Since ![]() $a_{g}\geq 2^{2g-1}$ and
$a_{g}\geq 2^{2g-1}$ and ![]() $b_{g}\geq 2^{4}$ by Proposition 8.5, it follows from (8.19) that
$b_{g}\geq 2^{4}$ by Proposition 8.5, it follows from (8.19) that ![]() $\varphi _{\Lambda }$ is a non-zero holomorphic function on
$\varphi _{\Lambda }$ is a non-zero holomorphic function on ![]() ${\mathcal {M}}_{\Lambda }\setminus \bar {\mathcal {D}}_{\Lambda }^{+}$. By Lemma 8.7 below,
${\mathcal {M}}_{\Lambda }\setminus \bar {\mathcal {D}}_{\Lambda }^{+}$. By Lemma 8.7 below, ![]() $\varphi _{\Lambda }$ is a non-zero constant. This completes the proof of Theorem 8.6.
$\varphi _{\Lambda }$ is a non-zero constant. This completes the proof of Theorem 8.6.
Lemma 8.7 When ![]() $M\simeq {\Bbb A}_{1}^{+}$, any holomorphic function on
$M\simeq {\Bbb A}_{1}^{+}$, any holomorphic function on ![]() ${\mathcal {M}}_{\Lambda }\setminus \bar {\mathcal {D}}_{\Lambda }^{+}$ is a constant.
${\mathcal {M}}_{\Lambda }\setminus \bar {\mathcal {D}}_{\Lambda }^{+}$ is a constant.
Proof. Let ![]() $U\subset |\mathcal {O}_{\mathbf{P}^2}(6)|$ be the space of smooth plane sextics, and let
$U\subset |\mathcal {O}_{\mathbf{P}^2}(6)|$ be the space of smooth plane sextics, and let ![]() $V\subset |\mathcal {O}_{\mathbf{P}^2}(6)|$ be that of sextics with at most one node. By the stability criterion for plane sextics [Reference ShahSha80], we have a geometric quotient
$V\subset |\mathcal {O}_{\mathbf{P}^2}(6)|$ be that of sextics with at most one node. By the stability criterion for plane sextics [Reference ShahSha80], we have a geometric quotient ![]() $V/{\rm PGL}_3$ of
$V/{\rm PGL}_3$ of ![]() $V$ by
$V$ by ![]() ${\rm PGL}_3$, which contains
${\rm PGL}_3$, which contains ![]() $U/{\rm PGL}_3$ as an open set. It is well known that
$U/{\rm PGL}_3$ as an open set. It is well known that ![]() ${\mathcal {M}}_{\Lambda }^{0}$ is isomorphic to
${\mathcal {M}}_{\Lambda }^{0}$ is isomorphic to ![]() $U/{\rm PGL}_3$ by associating to a smooth plane sextic the double covers of
$U/{\rm PGL}_3$ by associating to a smooth plane sextic the double covers of ![]() $\mathbf{P}^2$ branched over it. Shah [Reference ShahSha80] has shown that this isomorphism extends to an open embedding
$\mathbf{P}^2$ branched over it. Shah [Reference ShahSha80] has shown that this isomorphism extends to an open embedding ![]() $V/{\rm PGL}_3 \hookrightarrow \mathcal {M}_{\Lambda }$ and that its image is contained in
$V/{\rm PGL}_3 \hookrightarrow \mathcal {M}_{\Lambda }$ and that its image is contained in ![]() ${\mathcal {M}}_{\Lambda }\setminus \bar {\mathcal {D}}_{\Lambda }^{+}$. Hence a holomorphic function on
${\mathcal {M}}_{\Lambda }\setminus \bar {\mathcal {D}}_{\Lambda }^{+}$. Hence a holomorphic function on ![]() ${\mathcal {M}}_{\Lambda }\setminus \bar {\mathcal {D}}_{\Lambda }^{+}$ gives one on
${\mathcal {M}}_{\Lambda }\setminus \bar {\mathcal {D}}_{\Lambda }^{+}$ gives one on ![]() $V/{\rm PGL}_3$, which in turn is pulled back to
$V/{\rm PGL}_3$, which in turn is pulled back to ![]() $V$. Since the complement of
$V$. Since the complement of ![]() $V$ in
$V$ in ![]() $|\mathcal {O}_{\mathbf{P}^2}(6)|$ is of codimension
$|\mathcal {O}_{\mathbf{P}^2}(6)|$ is of codimension ![]() $2$ in
$2$ in ![]() $|\mathcal {O}_{\mathbf{P}^2}(6)|$, a holomorphic function on
$|\mathcal {O}_{\mathbf{P}^2}(6)|$, a holomorphic function on ![]() $V$ extends to
$V$ extends to ![]() $|\mathcal {O}_{\mathbf{P}^2}(6)|$ holomorphically and so is a constant.
$|\mathcal {O}_{\mathbf{P}^2}(6)|$ holomorphically and so is a constant.
Remark 8.8 Let ![]() $(g,k)=(10,0)$. Since
$(g,k)=(10,0)$. Since ![]() $\varphi _{\Lambda }$ is constant when
$\varphi _{\Lambda }$ is constant when ![]() $\Lambda =({\Bbb A}_{1}^{+})^{\perp }$, we get
$\Lambda =({\Bbb A}_{1}^{+})^{\perp }$, we get
by (8.19). In particular, ![]() $J_{{\Bbb A}_{1}^{+}}^{*}\chi _{10}$ vanishes on
$J_{{\Bbb A}_{1}^{+}}^{*}\chi _{10}$ vanishes on ![]() ${\mathcal {D}}_{\Lambda }^{+}$. Since
${\mathcal {D}}_{\Lambda }^{+}$. Since ![]() ${\Bbb U}=[{\Bbb A}_{1}^{+}\oplus \textbf {Z}d]$ for any
${\Bbb U}=[{\Bbb A}_{1}^{+}\oplus \textbf {Z}d]$ for any ![]() $d\in \Delta _{\Lambda }^{+}$, this, together with (3.5), implies that
$d\in \Delta _{\Lambda }^{+}$, this, together with (3.5), implies that ![]() $J_{\Bbb U}^{*}\chi _{10}$ vanishes identically on
$J_{\Bbb U}^{*}\chi _{10}$ vanishes identically on ![]() $\Omega _{{\Bbb U}^{\perp }}$.
$\Omega _{{\Bbb U}^{\perp }}$.
9. The structure of  $\tau _{M}$: the case
$\tau _{M}$: the case  $\delta =0$
$\delta =0$
In this section ![]() $M\subset {\Bbb L}_{K3}$ is assumed to be a primitive
$M\subset {\Bbb L}_{K3}$ is assumed to be a primitive ![]() $2$-elementary Lorentzian sublattice with
$2$-elementary Lorentzian sublattice with ![]() $\delta =0$. As before, we set
$\delta =0$. As before, we set ![]() $\Lambda =M^{\perp }$.
$\Lambda =M^{\perp }$.
9.1 The structure of  $\Phi _{M}$: the case
$\Phi _{M}$: the case  $r\not =2,10$ and
$r\not =2,10$ and  $\delta =0$
$\delta =0$
Lemma 9.1 Let ![]() $\Lambda \cong {\Bbb U}\oplus {\Bbb U}(k)\oplus {\Bbb D}_{4}\oplus {\Bbb E}_{8}$ with
$\Lambda \cong {\Bbb U}\oplus {\Bbb U}(k)\oplus {\Bbb D}_{4}\oplus {\Bbb E}_{8}$ with ![]() $k=1,2$. Then the following equality of divisors on
$k=1,2$. Then the following equality of divisors on ![]() $\Omega _{\Lambda }$ holds:
$\Omega _{\Lambda }$ holds:
Proof. Recall that the lattice ![]() $\Lambda _{g,k}$ was defined in § 8. Since
$\Lambda _{g,k}$ was defined in § 8. Since ![]() $\Lambda _{g,k-1}\cong \Lambda \oplus {\Bbb A}_{1}$ by comparing the invariants
$\Lambda _{g,k-1}\cong \Lambda \oplus {\Bbb A}_{1}$ by comparing the invariants ![]() $(r,l,\delta )$, there is a root
$(r,l,\delta )$, there is a root ![]() $d\in \Delta _{\Lambda _{g,k-1}}^{+}$ with
$d\in \Delta _{\Lambda _{g,k-1}}^{+}$ with ![]() $\Lambda _{g,k-1}\cap d^{\perp }\cong \Lambda$. Since
$\Lambda _{g,k-1}\cap d^{\perp }\cong \Lambda$. Since ![]() $d\in \Delta _{\Lambda _{g,k-1}}^{+}$ we get, by (8.3), (8.8), (8.17) and Propositions 2.1 and 2.2,
$d\in \Delta _{\Lambda _{g,k-1}}^{+}$ we get, by (8.3), (8.8), (8.17) and Propositions 2.1 and 2.2,
 \begin{align*} {\rm div}(J_{M}^{*}\chi_{g}^{8}) &= {\rm div}(J_{M_{g,k-1}}^{*}\chi_{g}^{8})|_{\Omega_{\Lambda}} = \{ 2^{2g-1}{\mathcal{D}}_{\Lambda_{g,k-1}}^{-} + 2^{k+3}{\mathcal{H}}_{\Lambda_{g,k-1}} \}|_{\Omega_{\Lambda}}\\ &= 2^{2g-1}{\mathcal{D}}_{\Lambda}^{-} + 2^{k+4}{\mathcal{H}}_{\Lambda} = 2^{g-1}(2^{g}+1){\mathcal{D}}_{\Lambda}. \end{align*}
\begin{align*} {\rm div}(J_{M}^{*}\chi_{g}^{8}) &= {\rm div}(J_{M_{g,k-1}}^{*}\chi_{g}^{8})|_{\Omega_{\Lambda}} = \{ 2^{2g-1}{\mathcal{D}}_{\Lambda_{g,k-1}}^{-} + 2^{k+3}{\mathcal{H}}_{\Lambda_{g,k-1}} \}|_{\Omega_{\Lambda}}\\ &= 2^{2g-1}{\mathcal{D}}_{\Lambda}^{-} + 2^{k+4}{\mathcal{H}}_{\Lambda} = 2^{g-1}(2^{g}+1){\mathcal{D}}_{\Lambda}. \end{align*}
To get the last equality, we used ![]() $g-1=k+4$,
$g-1=k+4$, ![]() ${\mathcal {D}}_{\Lambda }^{+}=0$ and
${\mathcal {D}}_{\Lambda }^{+}=0$ and ![]() ${\mathcal {H}}_{\Lambda }={\mathcal {D}}_{\Lambda }$ for
${\mathcal {H}}_{\Lambda }={\mathcal {D}}_{\Lambda }$ for ![]() $\Lambda$, where the last two equalities follow from
$\Lambda$, where the last two equalities follow from ![]() $\varepsilon _{\Lambda }=-2$,
$\varepsilon _{\Lambda }=-2$, ![]() $\delta (\Lambda )=0$ and
$\delta (\Lambda )=0$ and ![]() $\textbf {1}_{\Lambda }=0$.
$\textbf {1}_{\Lambda }=0$.
Theorem 9.2 If ![]() $r\not =2,10$ and
$r\not =2,10$ and ![]() $\delta =0$, there is a constant
$\delta =0$, there is a constant ![]() $C_{M,\ell }>0$ depending only on
$C_{M,\ell }>0$ depending only on ![]() $M$ and
$M$ and ![]() $\ell$ such that the following equality of automorphic forms on
$\ell$ such that the following equality of automorphic forms on ![]() $\Omega _{\Lambda }$ holds:
$\Omega _{\Lambda }$ holds:
In particular, there is a constant ![]() $C_{M}>0$ depending only on
$C_{M}>0$ depending only on ![]() $M$ such that the following equality of automorphic forms on
$M$ such that the following equality of automorphic forms on ![]() $\Omega _{\Lambda }$ holds:
$\Omega _{\Lambda }$ holds:
Proof. For ![]() $r>10$, the result was proved in [Reference YoshikawaYos13, Theorem 9.1]. We may assume
$r>10$, the result was proved in [Reference YoshikawaYos13, Theorem 9.1]. We may assume ![]() $2 < r < 10$ and
$2 < r < 10$ and ![]() $\delta =0$. By Proposition 1.1, we get
$\delta =0$. By Proposition 1.1, we get ![]() $r=6$ and
$r=6$ and ![]() $\Lambda \cong {\Bbb U}\oplus {\Bbb U}(k)\oplus {\Bbb D}_{4}\oplus {\Bbb E}_{8}$,
$\Lambda \cong {\Bbb U}\oplus {\Bbb U}(k)\oplus {\Bbb D}_{4}\oplus {\Bbb E}_{8}$, ![]() $k=1,2$. Since
$k=1,2$. Since ![]() $\delta (\Lambda )=0$, we have
$\delta (\Lambda )=0$, we have ![]() ${\mathcal {D}}_{\Lambda }^{+}=0$ and
${\mathcal {D}}_{\Lambda }^{+}=0$ and ![]() $\textbf {1}_{\Lambda }=0$. Since
$\textbf {1}_{\Lambda }=0$. Since ![]() $r(\Lambda )=16$, we have
$r(\Lambda )=16$, we have ![]() $\varepsilon _{\Lambda }=-2$, which, together with
$\varepsilon _{\Lambda }=-2$, which, together with ![]() $\textbf {1}_{\Lambda }=0$, yields that
$\textbf {1}_{\Lambda }=0$, yields that ![]() ${\mathcal {H}}_{\Lambda }={\mathcal {D}}_{\Lambda }$. By Theorem 8.1, we get
${\mathcal {H}}_{\Lambda }={\mathcal {D}}_{\Lambda }$. By Theorem 8.1, we get ![]() ${\rm wt}(\Psi _{\Lambda }^{\ell })=0$ and
${\rm wt}(\Psi _{\Lambda }^{\ell })=0$ and
which implies that ![]() $\Psi _{\Lambda }$ is a non-zero constant function on
$\Psi _{\Lambda }$ is a non-zero constant function on ![]() $\Omega _{\Lambda }$.
$\Omega _{\Lambda }$.
Set ![]() $\varphi _{\Lambda }:=\Psi _{\Lambda }^{2^{g-1}\ell }\otimes J_{M}^{*}\chi _{g}^{8\ell }/\Phi _{M}^{2^{g-1}(2^{g}+1)}$. Since
$\varphi _{\Lambda }:=\Psi _{\Lambda }^{2^{g-1}\ell }\otimes J_{M}^{*}\chi _{g}^{8\ell }/\Phi _{M}^{2^{g-1}(2^{g}+1)}$. Since ![]() $\Psi _{\Lambda }$ is a non-zero constant, we deduce from Lemma 9.1 and
$\Psi _{\Lambda }$ is a non-zero constant, we deduce from Lemma 9.1 and ![]() ${\rm wt}(\Phi _{M})=(0,4\ell )$,
${\rm wt}(\Phi _{M})=(0,4\ell )$, ![]() ${\rm div}(\Phi _{M})=\ell {\mathcal {D}}_{\Lambda }$ that
${\rm div}(\Phi _{M})=\ell {\mathcal {D}}_{\Lambda }$ that
Hence ![]() $\varphi _{\Lambda }$ is a holomorphic function on
$\varphi _{\Lambda }$ is a holomorphic function on ![]() ${\mathcal {M}}_{\Lambda }$ by (9.1) and extends holomorphically to
${\mathcal {M}}_{\Lambda }$ by (9.1) and extends holomorphically to ![]() ${\mathcal {M}}_{\Lambda }^{*}$. Thus
${\mathcal {M}}_{\Lambda }^{*}$. Thus ![]() $\varphi _{\Lambda }$ is a non-zero constant.
$\varphi _{\Lambda }$ is a non-zero constant.
9.2 The structure of  $\Phi _{M}$: the case
$\Phi _{M}$: the case  $(r,\delta )=(10,0)$
$(r,\delta )=(10,0)$
In this subsection we assume that ![]() $M$ is non-exceptional and
$M$ is non-exceptional and
Then ![]() $0\leq l\leq 8$ and
$0\leq l\leq 8$ and ![]() $2\leq g\leq 6$. Since
$2\leq g\leq 6$. Since ![]() $J_{M}^{*}\chi _{g}$ vanishes identically on
$J_{M}^{*}\chi _{g}$ vanishes identically on ![]() $\Omega _{\Lambda }$ (e.g. [Reference YoshikawaYos13, Proposition 9.3]), Theorem 8.6 does not hold in this case. Identify
$\Omega _{\Lambda }$ (e.g. [Reference YoshikawaYos13, Proposition 9.3]), Theorem 8.6 does not hold in this case. Identify ![]() ${\frak M}_{g}$ with its image by the Torelli map
${\frak M}_{g}$ with its image by the Torelli map ![]() $j\colon {\frak M}_{g}\hookrightarrow {\mathcal {A}}_{g}$. Then
$j\colon {\frak M}_{g}\hookrightarrow {\mathcal {A}}_{g}$. Then ![]() $J_{M}\colon \Omega _{\Lambda }^{0}\to {\mathcal {A}}_{g}$ is identified with the map
$J_{M}\colon \Omega _{\Lambda }^{0}\to {\mathcal {A}}_{g}$ is identified with the map ![]() $\mu _{\Lambda }=j^{-1}\circ J_{M}\colon \Omega _{\Lambda }^{0}\to {\frak M}_{g}$. Write
$\mu _{\Lambda }=j^{-1}\circ J_{M}\colon \Omega _{\Lambda }^{0}\to {\frak M}_{g}$. Write ![]() ${\frak H}_{{\rm hyp},g}\subset {\frak M}_{g}$ for the hyperelliptic locus.
${\frak H}_{{\rm hyp},g}\subset {\frak M}_{g}$ for the hyperelliptic locus.
Proposition 9.3 Let ![]() $M$ be non-exceptional with
$M$ be non-exceptional with ![]() $(r,\delta )=(10,0)$. Then
$(r,\delta )=(10,0)$. Then ![]() $J_{M}^{*}\Upsilon _{g}$ does not vanish identically on
$J_{M}^{*}\Upsilon _{g}$ does not vanish identically on ![]() $\Omega _{\Lambda }^{0}$. Moreover, for any
$\Omega _{\Lambda }^{0}$. Moreover, for any ![]() $d\in \Delta _{\Lambda }$,
$d\in \Delta _{\Lambda }$, ![]() $J_{[M\perp d]}^{*}\chi _{g-1}$ is nowhere vanishing on
$J_{[M\perp d]}^{*}\chi _{g-1}$ is nowhere vanishing on ![]() $\Omega _{\Lambda \cap d^{\perp }}^{0}$.
$\Omega _{\Lambda \cap d^{\perp }}^{0}$.
Proof. For the first assertion, it suffices to prove ![]() $\mu _{\Lambda }(\Omega _{\Lambda }^{0})\not \subset {\rm div}(\Upsilon _{g})\cap {\frak M}_{g}$. Since
$\mu _{\Lambda }(\Omega _{\Lambda }^{0})\not \subset {\rm div}(\Upsilon _{g})\cap {\frak M}_{g}$. Since ![]() $\Upsilon _{2}$ is nowhere vanishing on the diagonal locus of
$\Upsilon _{2}$ is nowhere vanishing on the diagonal locus of ![]() ${\frak S}_{2}$ and since
${\frak S}_{2}$ and since ![]() $\mu _{\Lambda }(\Omega _{\Lambda }^{0})$ is the image of the diagonal locus by the projection
$\mu _{\Lambda }(\Omega _{\Lambda }^{0})$ is the image of the diagonal locus by the projection ![]() ${\frak S}_{2}\to {\mathcal {A}}_{2}$, we get
${\frak S}_{2}\to {\mathcal {A}}_{2}$, we get ![]() ${\rm div}(\Upsilon _{2})\cap \mu _{\Lambda }(\Omega _{\Lambda }^{0})=\emptyset$. Similarly, we have
${\rm div}(\Upsilon _{2})\cap \mu _{\Lambda }(\Omega _{\Lambda }^{0})=\emptyset$. Similarly, we have ![]() ${\rm div}(\Upsilon _{3})\cap \mu _{\Lambda }(\Omega _{\Lambda }^{0})=\emptyset$ by [Reference IgusaIgu67, Lemma 11]. Let
${\rm div}(\Upsilon _{3})\cap \mu _{\Lambda }(\Omega _{\Lambda }^{0})=\emptyset$ by [Reference IgusaIgu67, Lemma 11]. Let ![]() $g=4$. Since
$g=4$. Since ![]() $\mu _{\Lambda }(\Omega _{\Lambda }^{0})\subset {\rm div}(\chi _{4})$, the inclusion
$\mu _{\Lambda }(\Omega _{\Lambda }^{0})\subset {\rm div}(\chi _{4})$, the inclusion ![]() $\mu _{\Lambda }(\Omega _{\Lambda }^{0})\subset {\rm div}(\Upsilon _{4})\cap {\frak M}_{4}$ would imply
$\mu _{\Lambda }(\Omega _{\Lambda }^{0})\subset {\rm div}(\Upsilon _{4})\cap {\frak M}_{4}$ would imply ![]() $\mu _{\Lambda }(\Omega _{\Lambda }^{0})\subset {\rm div}(\chi _{4})\cap {\rm div}(\Upsilon _{4})\cap {\frak M}_{4}$. Since the right-hand side coincides with
$\mu _{\Lambda }(\Omega _{\Lambda }^{0})\subset {\rm div}(\chi _{4})\cap {\rm div}(\Upsilon _{4})\cap {\frak M}_{4}$. Since the right-hand side coincides with ![]() ${\frak H}_{\rm hyp,4}$ by [Reference IgusaIgu82, Corollary, p. 544], this last inclusion contradicts Lemma 7.3. Thus
${\frak H}_{\rm hyp,4}$ by [Reference IgusaIgu82, Corollary, p. 544], this last inclusion contradicts Lemma 7.3. Thus ![]() $\mu _{\Lambda }(\Omega _{\Lambda }^{0})\not \subset {\rm div}(\Upsilon _{4})\cap {\frak M}_{4}$. Let
$\mu _{\Lambda }(\Omega _{\Lambda }^{0})\not \subset {\rm div}(\Upsilon _{4})\cap {\frak M}_{4}$. Let ![]() $g=5$. Let
$g=5$. Let ![]() $F_{5}$ be the Schottky form in genus
$F_{5}$ be the Schottky form in genus ![]() $5$ (cf. [Reference Grushevsky and Salvati-ManniGS11, p. 1018]), whose zero divisor characterizes the (closure of) trigonal locus of
$5$ (cf. [Reference Grushevsky and Salvati-ManniGS11, p. 1018]), whose zero divisor characterizes the (closure of) trigonal locus of ![]() ${\frak M}_{5}$ (cf. [Reference Grushevsky and Salvati-ManniGS11, Corollary 18]). By [Reference KondōKon94], a general point of
${\frak M}_{5}$ (cf. [Reference Grushevsky and Salvati-ManniGS11, Corollary 18]). By [Reference KondōKon94], a general point of ![]() $\mu _{\Lambda }(\Omega _{\Lambda }^{0})$ is contained in the intersection of the theta-null divisor and the trigonal locus. Then the inclusion
$\mu _{\Lambda }(\Omega _{\Lambda }^{0})$ is contained in the intersection of the theta-null divisor and the trigonal locus. Then the inclusion ![]() $\mu _{\Lambda }(\Omega _{\Lambda }^{0})\subset {\rm div}(\Upsilon _{5})\cap {\frak M}_{5}$ would imply
$\mu _{\Lambda }(\Omega _{\Lambda }^{0})\subset {\rm div}(\Upsilon _{5})\cap {\frak M}_{5}$ would imply
Since the right-hand side coincides with ![]() ${\frak H}_{\rm hyp,5}$ by [Reference Fontanari and PascoluttiFP12, p. 67], this last inclusion contradicts Lemma 7.3. Thus
${\frak H}_{\rm hyp,5}$ by [Reference Fontanari and PascoluttiFP12, p. 67], this last inclusion contradicts Lemma 7.3. Thus ![]() $\mu _{\Lambda }(\Omega _{\Lambda }^{0})\not \subset {\rm div}(\Upsilon _{5})\cap {\frak M}_{5}$. When
$\mu _{\Lambda }(\Omega _{\Lambda }^{0})\not \subset {\rm div}(\Upsilon _{5})\cap {\frak M}_{5}$. When ![]() $g=6$, we get
$g=6$, we get ![]() $\mu _{\Lambda }(\Omega _{\Lambda }^{0})\not \subset {\rm div}(\Upsilon _{6})\cap {\frak M}_{6}$ by Lemmas 4.1 and 7.4. This proves the first assertion. Since
$\mu _{\Lambda }(\Omega _{\Lambda }^{0})\not \subset {\rm div}(\Upsilon _{6})\cap {\frak M}_{6}$ by Lemmas 4.1 and 7.4. This proves the first assertion. Since ![]() $r([M\perp d])>10$, the second assertion follows from [Reference YoshikawaYos13, Proposition 4.2 (1)]. This completes the proof.
$r([M\perp d])>10$, the second assertion follows from [Reference YoshikawaYos13, Proposition 4.2 (1)]. This completes the proof.
Theorem 9.4 Let ![]() $M$ be non-exceptional with
$M$ be non-exceptional with ![]() $(r,\delta )=(10,0)$. Then there is a constant
$(r,\delta )=(10,0)$. Then there is a constant ![]() $C_{M,\ell }>0$ depending only on
$C_{M,\ell }>0$ depending only on ![]() $M$ and
$M$ and ![]() $\ell$ such that the following equality of automorphic forms on
$\ell$ such that the following equality of automorphic forms on ![]() $\Omega _{\Lambda }$ holds:
$\Omega _{\Lambda }$ holds:
In particular, there is a constant ![]() $C_{M}>0$ depending only on
$C_{M}>0$ depending only on ![]() $M$ such that
$M$ such that
Proof. Since ![]() $(r,\delta )=(10,0)$, we get
$(r,\delta )=(10,0)$, we get ![]() $(r(\Lambda ),\delta (\Lambda ))=(12,0)$. By [Reference YoshikawaYos13, Theorem 8.1],
$(r(\Lambda ),\delta (\Lambda ))=(12,0)$. By [Reference YoshikawaYos13, Theorem 8.1],
Since ![]() $J_{M}^{*}\Upsilon _{g}$ does not vanish identically on
$J_{M}^{*}\Upsilon _{g}$ does not vanish identically on ![]() $\Omega _{\Lambda }^{0}$ by Proposition 9.3 and since
$\Omega _{\Lambda }^{0}$ by Proposition 9.3 and since ![]() $\bar {\mathcal {D}}_{\Lambda }$ is irreducible, there exist
$\bar {\mathcal {D}}_{\Lambda }$ is irreducible, there exist ![]() $a\in \textbf {Z}_{\geq 0}$ and an effective divisor
$a\in \textbf {Z}_{\geq 0}$ and an effective divisor ![]() ${\mathcal {E}}_{\Lambda }$ on
${\mathcal {E}}_{\Lambda }$ on ![]() $\Omega _{\Lambda }$ such that
$\Omega _{\Lambda }$ such that
Set ![]() $\varphi _{\Lambda }:=\Psi _{\Lambda }^{(2^{g-1}+1)\ell }\otimes J_{M}^{*}\Upsilon _{g}^{\ell }/\Phi _{M}^{(2^{g-1}+1)(2^{g}-1)}$. Comparing (9.2), (9.3) and
$\varphi _{\Lambda }:=\Psi _{\Lambda }^{(2^{g-1}+1)\ell }\otimes J_{M}^{*}\Upsilon _{g}^{\ell }/\Phi _{M}^{(2^{g-1}+1)(2^{g}-1)}$. Comparing (9.2), (9.3) and ![]() ${\rm wt}(\Phi _{M})=(4\ell ,4\ell )$,
${\rm wt}(\Phi _{M})=(4\ell ,4\ell )$, ![]() ${\rm div}(\Phi _{M})=\ell {\mathcal {D}}_{\Lambda }$, we get
${\rm div}(\Phi _{M})=\ell {\mathcal {D}}_{\Lambda }$, we get
By Proposition 9.3, we can apply Lemma 4.3 to a general curve ![]() $\gamma \colon \Delta \to {\mathcal {M}}_{\Lambda }$ intersecting
$\gamma \colon \Delta \to {\mathcal {M}}_{\Lambda }$ intersecting ![]() $\bar {\mathcal {D}}_{\Lambda }^{0}$ transversally. Since
$\bar {\mathcal {D}}_{\Lambda }^{0}$ transversally. Since ![]() $a\geq 2(2^{2(g-1)}-1)$ by Lemma 4.3, we get
$a\geq 2(2^{2(g-1)}-1)$ by Lemma 4.3, we get ![]() ${\rm div}(\varphi _{\Lambda })\geq 0$. By the Koecher principle,
${\rm div}(\varphi _{\Lambda })\geq 0$. By the Koecher principle, ![]() $\varphi _{\Lambda }$ is a non-zero constant.
$\varphi _{\Lambda }$ is a non-zero constant.
In the rest of this section we determine ![]() $\Phi _{M}$ for the remaining
$\Phi _{M}$ for the remaining ![]() $M$, that is, those
$M$, that is, those ![]() $M$ with
$M$ with ![]() $(r,\delta )=(2,0)$. Then, either
$(r,\delta )=(2,0)$. Then, either ![]() $M\cong {\Bbb U}$ or
$M\cong {\Bbb U}$ or ![]() ${\Bbb U}(2)$.
${\Bbb U}(2)$.
9.3 The structure of  $\Phi _{\Bbb U}$
$\Phi _{\Bbb U}$
In this subsection we set
Then ![]() $g=10$ and
$g=10$ and ![]() $J_{M}^{*}\chi _{10}$ vanishes identically on
$J_{M}^{*}\chi _{10}$ vanishes identically on ![]() $\Omega _{\Lambda }^{0}$.
$\Omega _{\Lambda }^{0}$.
Let ![]() $E_{4}(\tau )=\theta _{{\Bbb E}_{8}^{+}}(\tau )=1+240q+\cdots$ be the Eisenstein series of weight
$E_{4}(\tau )=\theta _{{\Bbb E}_{8}^{+}}(\tau )=1+240q+\cdots$ be the Eisenstein series of weight ![]() $4$ (or equivalently, the theta series of
$4$ (or equivalently, the theta series of ![]() ${\Bbb E}_{8}^{+}$) and set
${\Bbb E}_{8}^{+}$) and set
Then ![]() $f_{\Lambda }(\tau )$ is a modular form of weight
$f_{\Lambda }(\tau )$ is a modular form of weight ![]() $-8$. We prove the following theorem.
$-8$. We prove the following theorem.
Theorem 9.5 There exists a constant ![]() $C_{M,\ell }>0$ such that
$C_{M,\ell }>0$ such that
In particular, there is a constant ![]() $C_{M}>0$ depending only on
$C_{M}>0$ depending only on ![]() $M=\Bbb U$ such that
$M=\Bbb U$ such that
For the proof of Theorem 9.5, we first prove the following lemma.
Lemma 9.6 ![]() $J_{M}^{*}\Upsilon _{10}$ is nowhere vanishing on
$J_{M}^{*}\Upsilon _{10}$ is nowhere vanishing on ![]() $\Omega _{\Lambda }^{0}\setminus {\mathcal {H}}_{\Lambda }$.
$\Omega _{\Lambda }^{0}\setminus {\mathcal {H}}_{\Lambda }$.
Proof. Let ![]() $(X,\iota ,\alpha )$ be an arbitrary marked
$(X,\iota ,\alpha )$ be an arbitrary marked ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface of type
$K3$ surface of type ![]() $M={\Bbb U}$ with period in
$M={\Bbb U}$ with period in ![]() $\Omega _{\Lambda }\setminus {\mathcal {H}}_{\Lambda }$. Let
$\Omega _{\Lambda }\setminus {\mathcal {H}}_{\Lambda }$. Let ![]() $C$ be the component of genus
$C$ be the component of genus ![]() $10$ of
$10$ of ![]() $X^{\iota }$. Fix a symplectic basis of
$X^{\iota }$. Fix a symplectic basis of ![]() $H_{1}(C,\textbf {Z})$, so that
$H_{1}(C,\textbf {Z})$, so that ![]() $\Omega (C)\in {\frak S}_{10}$, where
$\Omega (C)\in {\frak S}_{10}$, where ![]() $\Omega (C)$ is the period of
$\Omega (C)$ is the period of ![]() $C$ with respect to the symplectic basis. By Proposition 7.1, there is a unique even pair
$C$ with respect to the symplectic basis. By Proposition 7.1, there is a unique even pair ![]() $(a_{0},b_{0})$,
$(a_{0},b_{0})$, ![]() $a_{0},b_{0}\in \{0,\frac {1}{2}\}^{10}$ such that
$a_{0},b_{0}\in \{0,\frac {1}{2}\}^{10}$ such that ![]() $\theta _{a_{0},b_{0}}(\Omega (C))=0$ and
$\theta _{a_{0},b_{0}}(\Omega (C))=0$ and ![]() $\theta _{a,b}(\Omega (C))\not =0$ for all even pairs
$\theta _{a,b}(\Omega (C))\not =0$ for all even pairs ![]() $(a,b)$ with
$(a,b)$ with ![]() $(a,b)\not =(a_{0},b_{0})$. Hence we get
$(a,b)\not =(a_{0},b_{0})$. Hence we get
This proves the lemma.
By Lemma 9.6, there exist ![]() $\alpha ,\beta \in \textbf {Z}_{>0}$ such that
$\alpha ,\beta \in \textbf {Z}_{>0}$ such that
To prove Theorem 9.5, we must determine ![]() $\beta$.
$\beta$.
We use the following notation. Set
Let ![]() $d\in \Delta ^{+}_{L}$ be a generator of
$d\in \Delta ^{+}_{L}$ be a generator of ![]() ${\Bbb A}_{1}$. Then
${\Bbb A}_{1}$. Then ![]() $\Lambda =L\cap d^{\perp }$,
$\Lambda =L\cap d^{\perp }$, ![]() $L^{\perp }={\Bbb A}_{1}^{+}$ and
$L^{\perp }={\Bbb A}_{1}^{+}$ and ![]() $A_{L}=\{0,\textbf {1}_{L}\}$, where
$A_{L}=\{0,\textbf {1}_{L}\}$, where ![]() $\textbf {1}_{L}=[d/2]$. As before, we make the identification
$\textbf {1}_{L}=[d/2]$. As before, we make the identification
Let ![]() $[\eta ]\in H_{d}^{0}$ be an arbitrary point. Let
$[\eta ]\in H_{d}^{0}$ be an arbitrary point. Let ![]() $U\cong \Delta ^{19}$ be a small neighborhood of
$U\cong \Delta ^{19}$ be a small neighborhood of ![]() $[\eta ]$ in
$[\eta ]$ in ![]() $\Omega _{L}$ equipped with a system of coordinates
$\Omega _{L}$ equipped with a system of coordinates ![]() $(t,s_{1},\ldots ,s_{18})$ such that
$(t,s_{1},\ldots ,s_{18})$ such that ![]() $U\cap {\mathcal {D}}_{L}=U\cap H_{d}=U\cap \Omega _{\Lambda }=\{(t,s)\in U;\,t=0\}\cong \Delta ^{18}$. Since
$U\cap {\mathcal {D}}_{L}=U\cap H_{d}=U\cap \Omega _{\Lambda }=\{(t,s)\in U;\,t=0\}\cong \Delta ^{18}$. Since ![]() $d\in \Delta ^{+}_{L}$ and hence
$d\in \Delta ^{+}_{L}$ and hence ![]() $g(L)=g(\Lambda )=10$ by [Reference YoshikawaYos13, Lemma 11.5], the Torelli map
$g(L)=g(\Lambda )=10$ by [Reference YoshikawaYos13, Lemma 11.5], the Torelli map ![]() $J_{{\Bbb A}_{1}^{+}}$ is a holomorphic map from
$J_{{\Bbb A}_{1}^{+}}$ is a holomorphic map from ![]() $U$ to
$U$ to ![]() ${\mathcal {A}}_{10}$ by Theorem 3.5. Let
${\mathcal {A}}_{10}$ by Theorem 3.5. Let ![]() $\Pi \colon {\frak S}_{10}\to {\mathcal {A}}_{10}$ be the projection. Since
$\Pi \colon {\frak S}_{10}\to {\mathcal {A}}_{10}$ be the projection. Since ![]() $U$ is contractible,
$U$ is contractible, ![]() $J_{{\Bbb A}_{1}^{+}}\colon U\to {\mathcal {A}}_{10}$ is liftable. Namely, there exists a holomorphic map
$J_{{\Bbb A}_{1}^{+}}\colon U\to {\mathcal {A}}_{10}$ is liftable. Namely, there exists a holomorphic map ![]() $\tilde {J}_{{\Bbb A}_{1}^{+}}\colon U\to {\frak S}_{10}$ such that
$\tilde {J}_{{\Bbb A}_{1}^{+}}\colon U\to {\frak S}_{10}$ such that
Since ![]() $\tilde {J}_{{\Bbb A}_{1}^{+}}$ takes its values in
$\tilde {J}_{{\Bbb A}_{1}^{+}}$ takes its values in ![]() ${\frak S}_{10}$, the value
${\frak S}_{10}$, the value ![]() $\theta _{a,b}(\tilde {J}_{{\Bbb A}_{1}^{+}}(t,s))$ makes sense for all
$\theta _{a,b}(\tilde {J}_{{\Bbb A}_{1}^{+}}(t,s))$ makes sense for all ![]() $(s,t)\in U$ and even
$(s,t)\in U$ and even ![]() $(a,b)$,
$(a,b)$, ![]() $a,b\in \{0,1/2\}^{10}$. Since
$a,b\in \{0,1/2\}^{10}$. Since ![]() $\tilde {J}_{{\Bbb A}_{1}^{+}}^{*}\chi _{10}=\prod _{(a,b)\,{\rm even}}\tilde {J}_{{\Bbb A}_{1}^{+}}^{*}\theta _{a,b}$ is nowhere vanishing on
$\tilde {J}_{{\Bbb A}_{1}^{+}}^{*}\chi _{10}=\prod _{(a,b)\,{\rm even}}\tilde {J}_{{\Bbb A}_{1}^{+}}^{*}\theta _{a,b}$ is nowhere vanishing on ![]() $U\setminus ({\mathcal {D}}_{L}\cup {\mathcal {H}}_{L})$ and since there exists by Proposition 7.1 a unique even theta constant
$U\setminus ({\mathcal {D}}_{L}\cup {\mathcal {H}}_{L})$ and since there exists by Proposition 7.1 a unique even theta constant ![]() $\theta _{a_{0},b_{0}}$ vanishing identically on
$\theta _{a_{0},b_{0}}$ vanishing identically on ![]() $H_{d}$, we get the following:
$H_{d}$, we get the following:
•
 $U\cap H_{d}$ is a component of
$U\cap H_{d}$ is a component of  $U\cap {\rm div}(\tilde {J}_{{\Bbb A}_{1}^{+}}^{*}\theta _{a_{0},b_{0}})$;
$U\cap {\rm div}(\tilde {J}_{{\Bbb A}_{1}^{+}}^{*}\theta _{a_{0},b_{0}})$;•
 $U\cap H_{d}$ is not a component of
$U\cap H_{d}$ is not a component of  $U\cap {\rm div}(\tilde {J}_{{\Bbb A}_{1}^{+}}^{*}\theta _{a,b})$ for any even
$U\cap {\rm div}(\tilde {J}_{{\Bbb A}_{1}^{+}}^{*}\theta _{a,b})$ for any even  $(a,b)\not =(a_{0},b_{0})$.
$(a,b)\not =(a_{0},b_{0})$.
Thus there exist ![]() $c\in \textbf {Z}_{>0}$,
$c\in \textbf {Z}_{>0}$, ![]() $c_{a,b}(\lambda )\in \textbf {Z}_{\geq 0}$ such that, for
$c_{a,b}(\lambda )\in \textbf {Z}_{\geq 0}$ such that, for ![]() $(a,b)=(a_{0},b_{0})$,
$(a,b)=(a_{0},b_{0})$,
and such that, for all ![]() $(a,b)\not =(a_{0},b_{0})$,
$(a,b)\not =(a_{0},b_{0})$,
Let ![]() $s_{d}\in O(L)$ be the reflection with respect to
$s_{d}\in O(L)$ be the reflection with respect to ![]() $d$. Since
$d$. Since ![]() $J_{{\Bbb A}_{1}^{+}}\circ s_{d}=J_{{\Bbb A}_{1}^{+}}$, we have
$J_{{\Bbb A}_{1}^{+}}\circ s_{d}=J_{{\Bbb A}_{1}^{+}}$, we have ![]() $s_{d}^{*}\circ (\tilde {J}_{{\Bbb A}_{1}^{+}})^{*}=(\tilde {J}_{{\Bbb A}_{1}^{+}})^{*}$, which implies the following equality for every even pair
$s_{d}^{*}\circ (\tilde {J}_{{\Bbb A}_{1}^{+}})^{*}=(\tilde {J}_{{\Bbb A}_{1}^{+}})^{*}$, which implies the following equality for every even pair ![]() $(a,b)$:
$(a,b)$:
Lemma 9.7 Let ![]() $\lambda \in L^{\lor }$ be such that
$\lambda \in L^{\lor }$ be such that ![]() $\lambda ^{2}=-9/2$,
$\lambda ^{2}=-9/2$, ![]() $|\langle \lambda ,d\rangle |=1$,
$|\langle \lambda ,d\rangle |=1$, ![]() $[\lambda ]=\textbf {1}_{L}$. If
$[\lambda ]=\textbf {1}_{L}$. If ![]() $c_{a_{0},b_{0}}(\lambda )>0$, then
$c_{a_{0},b_{0}}(\lambda )>0$, then ![]() $c_{a,b}(\lambda )=0$ for all
$c_{a,b}(\lambda )=0$ for all ![]() $(a,b)\not =(a_{0},b_{0})$.
$(a,b)\not =(a_{0},b_{0})$.
Proof. Assume ![]() $c_{a_{0},b_{0}}(\lambda )>0$ and
$c_{a_{0},b_{0}}(\lambda )>0$ and ![]() $c_{a',b'}(\lambda )>0$ for some even
$c_{a',b'}(\lambda )>0$ for some even ![]() $(a',b')\not =(a_{0},b_{0})$. Then, for every
$(a',b')\not =(a_{0},b_{0})$. Then, for every ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface
$K3$ surface ![]() $(X,\iota )$ of type
$(X,\iota )$ of type ![]() ${\Bbb A}_{1}^{+}$ whose period lies in
${\Bbb A}_{1}^{+}$ whose period lies in ![]() $U\cap H_{\lambda }\setminus H_{d}$,
$U\cap H_{\lambda }\setminus H_{d}$, ![]() $X^{\iota }$ has two distinct effective even half canonical bundles corresponding to
$X^{\iota }$ has two distinct effective even half canonical bundles corresponding to ![]() $(a_{0},b_{0})$ and
$(a_{0},b_{0})$ and ![]() $(a',b')$. This contradicts Remark 6.10.
$(a',b')$. This contradicts Remark 6.10.
Recall that ![]() $i\colon \Omega _{\Lambda }\hookrightarrow \Omega _{L}$ is the inclusion induced by that of lattices
$i\colon \Omega _{\Lambda }\hookrightarrow \Omega _{L}$ is the inclusion induced by that of lattices ![]() $\Lambda =L\cap d^{\perp }\subset L$. On
$\Lambda =L\cap d^{\perp }\subset L$. On ![]() $H_{d}^{0}\cap U$, set
$H_{d}^{0}\cap U$, set
By (3.5), we have ![]() $J_{M}=\Pi \circ \tilde {J}_{M}$.
$J_{M}=\Pi \circ \tilde {J}_{M}$.
Since ![]() $U\cap H_{d}\subset H_{d}^{0}=\Omega _{\Lambda }^{0}$, we have the following equality of divisors on
$U\cap H_{d}\subset H_{d}^{0}=\Omega _{\Lambda }^{0}$, we have the following equality of divisors on ![]() $U\cap \Omega _{\Lambda }^{0}$ by (9.6):
$U\cap \Omega _{\Lambda }^{0}$ by (9.6):
Lemma 9.8 For every ![]() $\lambda \in L^{\lor }$ with
$\lambda \in L^{\lor }$ with ![]() $\lambda ^{2}=-9/2$,
$\lambda ^{2}=-9/2$, ![]() $\langle \lambda ,d\rangle =\pm 1$,
$\langle \lambda ,d\rangle =\pm 1$, ![]() $\lambda \equiv \textbf {1}_{L}\bmod L$, the following equalities hold:
$\lambda \equiv \textbf {1}_{L}\bmod L$, the following equalities hold:
Proof. Since ![]() $\tilde {J}_{{\Bbb A}_{1}^{+}}^{*}(\chi _{10}/\theta _{a_{0},b_{0}})^{8}|_{U\cap H_{d}} = \tilde {J}_{{\Bbb A}_{1}^{+}}^{*}\Upsilon _{10}|_{U\cap H_{d}}$ by the definitions of
$\tilde {J}_{{\Bbb A}_{1}^{+}}^{*}(\chi _{10}/\theta _{a_{0},b_{0}})^{8}|_{U\cap H_{d}} = \tilde {J}_{{\Bbb A}_{1}^{+}}^{*}\Upsilon _{10}|_{U\cap H_{d}}$ by the definitions of ![]() $\Upsilon _{g}$ and
$\Upsilon _{g}$ and ![]() $\theta _{a_{0},b_{0}}$, we get the following equality of divisors on
$\theta _{a_{0},b_{0}}$, we get the following equality of divisors on ![]() $U\cap \Omega _{\Lambda }^{0}$:
$U\cap \Omega _{\Lambda }^{0}$:
where the second equality follows from (9.10). On the other hand we get, by (9.8),
 \[ {\rm div}(\tilde{J}_{{\Bbb A}_{1}^{+}}^{*}(\chi_{10}/\theta_{a_{0},b_{0}})^{8}|_{U}) = \sum_{\lambda\in L^{\lor}/\pm1, \lambda^{2}=-9/2, |\langle\lambda,d\rangle|=1, [\lambda]=\textbf{1}_{L}} \biggl(\sum_{(a,b)\not=(a_{0},b_{0})}c_{a,b}(\lambda)\biggr)\,H_{\lambda}, \]
\[ {\rm div}(\tilde{J}_{{\Bbb A}_{1}^{+}}^{*}(\chi_{10}/\theta_{a_{0},b_{0}})^{8}|_{U}) = \sum_{\lambda\in L^{\lor}/\pm1, \lambda^{2}=-9/2, |\langle\lambda,d\rangle|=1, [\lambda]=\textbf{1}_{L}} \biggl(\sum_{(a,b)\not=(a_{0},b_{0})}c_{a,b}(\lambda)\biggr)\,H_{\lambda}, \]
which, together with (2.2), yields the following equality of divisors on ![]() $U$:
$U$:
 \begin{equation}i^{*}{\rm div}\biggl(\tilde{J}_{{\Bbb A}_{1}^{+}}^{*}\biggl(\frac{\chi_{10}}{\theta_{a_{0},b_{0}}}\biggr)^{8}|_{U}\biggr) = \sum_{\mu\in\Lambda/\pm1, \mu^{2}=-4} \sum_{(a,b)\not=(a_{0},b_{0})} \left\{c_{a,b}\left(\mu+\frac{d}{2}\right)+c_{a,b}\left(\mu-\frac{d}{2}\right)\right\}\,H_{\mu}. \end{equation}
\begin{equation}i^{*}{\rm div}\biggl(\tilde{J}_{{\Bbb A}_{1}^{+}}^{*}\biggl(\frac{\chi_{10}}{\theta_{a_{0},b_{0}}}\biggr)^{8}|_{U}\biggr) = \sum_{\mu\in\Lambda/\pm1, \mu^{2}=-4} \sum_{(a,b)\not=(a_{0},b_{0})} \left\{c_{a,b}\left(\mu+\frac{d}{2}\right)+c_{a,b}\left(\mu-\frac{d}{2}\right)\right\}\,H_{\mu}. \end{equation}
Substituting (9.11), (9.13) into (9.12) and comparing the coefficients of ![]() $H_{\mu }$, we get
$H_{\mu }$, we get
 \begin{equation} \sum_{(a,b)\not=(a_{0},b_{0})}\left\{c_{a,b}\left(\mu+\frac{d}{2}\right) +c_{a,b}\left(\mu-\frac{d}{2}\right)\right\}=\beta. \end{equation}
\begin{equation} \sum_{(a,b)\not=(a_{0},b_{0})}\left\{c_{a,b}\left(\mu+\frac{d}{2}\right) +c_{a,b}\left(\mu-\frac{d}{2}\right)\right\}=\beta. \end{equation}
Since ![]() $c_{a,b}(\mu +{d}/{2})=c_{a,b}(\mu -{d}/{2})$ by (9.9), we get
$c_{a,b}(\mu +{d}/{2})=c_{a,b}(\mu -{d}/{2})$ by (9.9), we get ![]() $\sum _{(a,b)\not =(a_{0},b_{0})}c_{a,b}(\lambda )=\beta /2$ by (9.14). If
$\sum _{(a,b)\not =(a_{0},b_{0})}c_{a,b}(\lambda )=\beta /2$ by (9.14). If ![]() $c_{a_{0},b_{0}}(\lambda )>0$, then
$c_{a_{0},b_{0}}(\lambda )>0$, then ![]() $\sum _{(a,b)\not =(a_{0},b_{0})}c_{a,b}(\lambda )=0$ by Lemma 9.7. Since
$\sum _{(a,b)\not =(a_{0},b_{0})}c_{a,b}(\lambda )=0$ by Lemma 9.7. Since ![]() $\beta >0$, this contradicts the equality
$\beta >0$, this contradicts the equality ![]() $\sum _{(a,b)\not =(a_{0},b_{0})}c_{a,b}(\lambda )=\beta /2$. Thus
$\sum _{(a,b)\not =(a_{0},b_{0})}c_{a,b}(\lambda )=\beta /2$. Thus ![]() $c_{a_{0},b_{0}}(\lambda )=0$.
$c_{a_{0},b_{0}}(\lambda )=0$.
Lemma 9.9 One has the equality ![]() $\beta =2^{5}$.
$\beta =2^{5}$.
Proof. By (9.7), (9.8) and Lemma 9.8, we get on ![]() $U$,
$U$,
which yields the equality of divisors ![]() ${\rm div}(J_{{\Bbb A}_{1}^{+}}^{*}\chi _{10}^{8})=c {\mathcal {D}}_{L}^{+}+(\beta /2)\cdot {\mathcal {H}}_{L}$ on
${\rm div}(J_{{\Bbb A}_{1}^{+}}^{*}\chi _{10}^{8})=c {\mathcal {D}}_{L}^{+}+(\beta /2)\cdot {\mathcal {H}}_{L}$ on ![]() $U$. By Remark 8.8, we get
$U$. By Remark 8.8, we get ![]() $c=c_{10}=2^{4}\cdot 7$ and
$c=c_{10}=2^{4}\cdot 7$ and ![]() $\beta /2=b_{10}=2^{4}$. Thus
$\beta /2=b_{10}=2^{4}$. Thus ![]() $\beta =2^{5}$.
$\beta =2^{5}$.
Proof Proof of Theorem 9.5 By Theorem 8.1 (1), we have
By [Reference BorcherdsBor98, Theorem 13.3], we get
Set ![]() $\varphi _{\Lambda }:=\Psi _{\Lambda }(\cdot ,2^{g-1}F_{\Lambda } +f_{\Lambda })^{\ell }\otimes \Upsilon _{g}^{\ell }/\Phi _{M}^{(2^{g-1}+1)(2^{g}-1)}$. Since
$\varphi _{\Lambda }:=\Psi _{\Lambda }(\cdot ,2^{g-1}F_{\Lambda } +f_{\Lambda })^{\ell }\otimes \Upsilon _{g}^{\ell }/\Phi _{M}^{(2^{g-1}+1)(2^{g}-1)}$. Since ![]() ${\rm wt}(\Phi _{M})=(-4\ell ,4\ell )$ and
${\rm wt}(\Phi _{M})=(-4\ell ,4\ell )$ and ![]() ${\rm div}(\Phi _{M})=\ell {\mathcal {D}}_{\Lambda }$, we deduce from (9.17), (9.18) that
${\rm div}(\Phi _{M})=\ell {\mathcal {D}}_{\Lambda }$, we deduce from (9.17), (9.18) that ![]() ${\rm wt}(\varphi _{\Lambda })=(0,0)$ and
${\rm wt}(\varphi _{\Lambda })=(0,0)$ and
where we used Lemma 9.9 to get the second equality. By Lemma 9.6 and Theorem 8.6 for ![]() $[M\perp d]$,
$[M\perp d]$, ![]() $d\in \Delta _{\Lambda }$, Lemma 4.3 applies to a general curve
$d\in \Delta _{\Lambda }$, Lemma 4.3 applies to a general curve ![]() $\gamma \colon \Delta \to {\mathcal {M}}_{\Lambda }$ intersecting
$\gamma \colon \Delta \to {\mathcal {M}}_{\Lambda }$ intersecting ![]() $\bar {\mathcal {D}}_{\Lambda }^{0}$ transversally. Since
$\bar {\mathcal {D}}_{\Lambda }^{0}$ transversally. Since ![]() $\alpha \geq 2(2^{18}-1)$ by Lemma 4.3, we get
$\alpha \geq 2(2^{18}-1)$ by Lemma 4.3, we get ![]() ${\rm div}(\varphi _{\Lambda })\geq 0$. As before, this implies that
${\rm div}(\varphi _{\Lambda })\geq 0$. As before, this implies that ![]() $\varphi _{\Lambda }$ is a constant.
$\varphi _{\Lambda }$ is a constant.
9.4 The structure of  $\Phi _{{\Bbb U}(2)}$
$\Phi _{{\Bbb U}(2)}$
In this subsection we set
Then ![]() $g=9$ and
$g=9$ and ![]() $J_{M}^{*}\chi _{9}$ vanishes identically. Let
$J_{M}^{*}\chi _{9}$ vanishes identically. Let ![]() $\{{\frak e},{\frak f}\}$ be a basis of
$\{{\frak e},{\frak f}\}$ be a basis of ![]() $M={\Bbb U}(2)$ with
$M={\Bbb U}(2)$ with ![]() ${\frak e}^{2}={\frak f}^{2}=0$ and
${\frak e}^{2}={\frak f}^{2}=0$ and ![]() $\langle {\frak e},{\frak f}\rangle =2$. Hence
$\langle {\frak e},{\frak f}\rangle =2$. Hence ![]() $({\frak e}+{\frak f})/2\in A_{\Lambda }$ is the unique element with non-zero norm. Let
$({\frak e}+{\frak f})/2\in A_{\Lambda }$ is the unique element with non-zero norm. Let ![]() $\textbf {e}_{00},\textbf {e}_{01},\textbf {e}_{10},\textbf {e}_{11}$ be the standard basis of
$\textbf {e}_{00},\textbf {e}_{01},\textbf {e}_{10},\textbf {e}_{11}$ be the standard basis of ![]() $\textbf {C}[A_{\Lambda }]=\textbf {C}[A_{{\Bbb U}(2)}]$, where
$\textbf {C}[A_{\Lambda }]=\textbf {C}[A_{{\Bbb U}(2)}]$, where ![]() $\textbf {e}_{\alpha \beta }$ corresponds to
$\textbf {e}_{\alpha \beta }$ corresponds to ![]() $(\alpha \,{\frak e}+\beta \,{\frak f})/2\in A_{\Lambda }$. Applying the construction of [Reference BorcherdsBor00, Proof of Lemma 11.1] and [Reference ScheithauerSch06, Theorem 6.2] to the modular form
$(\alpha \,{\frak e}+\beta \,{\frak f})/2\in A_{\Lambda }$. Applying the construction of [Reference BorcherdsBor00, Proof of Lemma 11.1] and [Reference ScheithauerSch06, Theorem 6.2] to the modular form ![]() $\eta (\tau )^{-8}\eta (2\tau )^{-8}$, we define
$\eta (\tau )^{-8}\eta (2\tau )^{-8}$, we define
 \begin{align} f_{\Lambda}(\tau) &:= 8 \sum_{\gamma\in A_{\Lambda}} \biggl\{ \eta\biggl(\frac{\tau}{2}\biggr)^{-8}\eta(\tau)^{-8} + (-1)^{q_{\Lambda}(\gamma)}\eta\left(\frac{\tau+1}{2}\right)^{-8}\eta(\tau+1)^{-8} \biggr\} \textbf{e}_{\gamma}\nonumber\\ & \qquad +\eta(\tau)^{-8}\eta(2\tau)^{-8}\,\textbf{e}_{00}. \end{align}
\begin{align} f_{\Lambda}(\tau) &:= 8 \sum_{\gamma\in A_{\Lambda}} \biggl\{ \eta\biggl(\frac{\tau}{2}\biggr)^{-8}\eta(\tau)^{-8} + (-1)^{q_{\Lambda}(\gamma)}\eta\left(\frac{\tau+1}{2}\right)^{-8}\eta(\tau+1)^{-8} \biggr\} \textbf{e}_{\gamma}\nonumber\\ & \qquad +\eta(\tau)^{-8}\eta(2\tau)^{-8}\,\textbf{e}_{00}. \end{align}
Then ![]() $f_{\Lambda }(\tau )$ is an
$f_{\Lambda }(\tau )$ is an ![]() $O(A_{\Lambda })$-invariant modular form of weight
$O(A_{\Lambda })$-invariant modular form of weight ![]() $-8$ and of type
$-8$ and of type ![]() $\rho _{\Lambda }$ with principal part
$\rho _{\Lambda }$ with principal part
Since ![]() $O(q_{\Lambda })$ preserves
$O(q_{\Lambda })$ preserves ![]() $({\frak e}+{\frak f})/2$, the Heegner divisor of
$({\frak e}+{\frak f})/2$, the Heegner divisor of ![]() $\Omega _{\Lambda }$,
$\Omega _{\Lambda }$,
is ![]() $O^{+}(\Lambda )$-invariant. By [Reference BorcherdsBor98, Theorem 13.3], the Borcherds lift
$O^{+}(\Lambda )$-invariant. By [Reference BorcherdsBor98, Theorem 13.3], the Borcherds lift ![]() $\Psi _{\Lambda }(\cdot ,f_{\Lambda })$ is an automorphic form on
$\Psi _{\Lambda }(\cdot ,f_{\Lambda })$ is an automorphic form on ![]() $\Omega _{\Lambda }$ for
$\Omega _{\Lambda }$ for ![]() $O^{+}(\Lambda )$ such that
$O^{+}(\Lambda )$ such that
In this subsection we prove the following theorem.
Theorem 9.10 There exists a constant ![]() $C_{M,\ell }>0$ such that
$C_{M,\ell }>0$ such that
In particular, there is a constant ![]() $C_{M}>0$ depending only on
$C_{M}>0$ depending only on ![]() $M={\Bbb U}(2)$ such that
$M={\Bbb U}(2)$ such that
Define the reduced divisor ![]() ${\mathcal {H}}_{1}$ on
${\mathcal {H}}_{1}$ on ![]() $\Omega _{\Lambda }$ as
$\Omega _{\Lambda }$ as
The divisor ![]() $\bar {\mathcal {H}}_{1}\subset {\mathcal {M}}_{\Lambda }$ in § 7.2 is obtained as the quotient
$\bar {\mathcal {H}}_{1}\subset {\mathcal {M}}_{\Lambda }$ in § 7.2 is obtained as the quotient ![]() $\bar {\mathcal {H}}_{1}={\mathcal {H}}_{1}/O(\Lambda )$.
$\bar {\mathcal {H}}_{1}={\mathcal {H}}_{1}/O(\Lambda )$.
Lemma 9.11 ![]() $J_{M}^{*}\Upsilon _{9}$ is nowhere vanishing on
$J_{M}^{*}\Upsilon _{9}$ is nowhere vanishing on ![]() $\Omega _{\Lambda }^{0}\setminus {\mathcal {H}}_{1}$.
$\Omega _{\Lambda }^{0}\setminus {\mathcal {H}}_{1}$.
Proof. By using Proposition 7.2 instead of Proposition 7.1, the proof is parallel to that of Lemma 9.6.
By Lemma 9.11, there exist ![]() $\alpha ,\beta \in \textbf {Z}_{>0}$ such that
$\alpha ,\beta \in \textbf {Z}_{>0}$ such that
Lemma 9.12 One has the inequality ![]() $\beta \geq 2^{4}$.
$\beta \geq 2^{4}$.
Proof. Let ![]() $\lambda \in \Lambda$ be an arbitrary vector such that
$\lambda \in \Lambda$ be an arbitrary vector such that ![]() $\lambda ^{2}=-4$ and
$\lambda ^{2}=-4$ and ![]() ${\rm div}(\lambda )=1$. We set
${\rm div}(\lambda )=1$. We set
 \[ H_{\lambda}^{0} := H_{\lambda} \setminus \Bigg( {\mathcal{D}}_{\Lambda}\cup\bigcup_{\lambda'\in\Lambda, (\lambda')^{2}=-4, {\rm div}(\lambda')=1}H_{\lambda'} \Bigg). \]
\[ H_{\lambda}^{0} := H_{\lambda} \setminus \Bigg( {\mathcal{D}}_{\Lambda}\cup\bigcup_{\lambda'\in\Lambda, (\lambda')^{2}=-4, {\rm div}(\lambda')=1}H_{\lambda'} \Bigg). \]
Then ![]() $H_{\lambda }^{0}$ is a non-empty Zariski open subset of
$H_{\lambda }^{0}$ is a non-empty Zariski open subset of ![]() $H_{\lambda }$. Let
$H_{\lambda }$. Let ![]() $[\eta ]\in H_{\lambda }^{0}$ be an arbitrary point. Let
$[\eta ]\in H_{\lambda }^{0}$ be an arbitrary point. Let ![]() $U\cong \Delta ^{18}$ be a small neighborhood of
$U\cong \Delta ^{18}$ be a small neighborhood of ![]() $[\eta ]$ in
$[\eta ]$ in ![]() $\Omega _{\Lambda }$ such that
$\Omega _{\Lambda }$ such that ![]() $U\cap ({\mathcal {H}}_{1}\cup {\mathcal {D}}_{\Lambda })=U\cap H_{\lambda }^{0}\cong \Delta ^{17}$. Since
$U\cap ({\mathcal {H}}_{1}\cup {\mathcal {D}}_{\Lambda })=U\cap H_{\lambda }^{0}\cong \Delta ^{17}$. Since ![]() $U$ is small enough, there is a marked family of
$U$ is small enough, there is a marked family of ![]() $2$-elementary
$2$-elementary ![]() $K3$ surfaces
$K3$ surfaces ![]() $(p\colon ({\mathcal {X}},\iota )\to U,\alpha )$ of type
$(p\colon ({\mathcal {X}},\iota )\to U,\alpha )$ of type ![]() $M={\Bbb U}(2)$, whose period map is the inclusion
$M={\Bbb U}(2)$, whose period map is the inclusion ![]() $U\hookrightarrow \Omega _{\Lambda }$. Set
$U\hookrightarrow \Omega _{\Lambda }$. Set ![]() ${\mathcal {C}}:={\mathcal {X}}^{\iota }$. Then
${\mathcal {C}}:={\mathcal {X}}^{\iota }$. Then ![]() $p\colon {\mathcal {C}}\to U$ is a family of smooth curves of genus
$p\colon {\mathcal {C}}\to U$ is a family of smooth curves of genus ![]() $9$. Set
$9$. Set ![]() $C_{t}:=p^{-1}(t)\cap {\mathcal {C}}$ for
$C_{t}:=p^{-1}(t)\cap {\mathcal {C}}$ for ![]() $t\in U$. The period map
$t\in U$. The period map ![]() $J_{M}|_{U}$ is a holomorphic map from
$J_{M}|_{U}$ is a holomorphic map from ![]() $U$ to
$U$ to ![]() ${\mathcal {A}}_{9}$ such that
${\mathcal {A}}_{9}$ such that ![]() $J_{M}(t)=\Omega (C_{t})$. Since
$J_{M}(t)=\Omega (C_{t})$. Since ![]() $U$ is contractible, the local system
$U$ is contractible, the local system ![]() $R^{1}(p|_{\mathcal {C}})_{*}\textbf {Z}$ is trivial and admits a symplectic basis. Hence
$R^{1}(p|_{\mathcal {C}})_{*}\textbf {Z}$ is trivial and admits a symplectic basis. Hence ![]() $J_{M}\colon U\to {\mathcal {A}}_{9}$ lifts to a holomorphic map
$J_{M}\colon U\to {\mathcal {A}}_{9}$ lifts to a holomorphic map ![]() $\tilde {J}_{M}\colon U\to {\frak S}_{9}$ such that
$\tilde {J}_{M}\colon U\to {\frak S}_{9}$ such that ![]() $J_{M}=\Pi \circ \tilde {J}_{M}$, where
$J_{M}=\Pi \circ \tilde {J}_{M}$, where ![]() $\Pi \colon {\frak S}_{9}\to {\mathcal {A}}_{9}$ is the projection.
$\Pi \colon {\frak S}_{9}\to {\mathcal {A}}_{9}$ is the projection.
Since ![]() $\tilde {J}_{M}$ takes its values in
$\tilde {J}_{M}$ takes its values in ![]() ${\frak S}_{9}$, the value of the theta constant
${\frak S}_{9}$, the value of the theta constant ![]() $\theta _{a,b}(\tilde {J}_{M}(t))$ makes sense for all
$\theta _{a,b}(\tilde {J}_{M}(t))$ makes sense for all ![]() $t\in U$ and for every even pair
$t\in U$ and for every even pair ![]() $(a,b)$,
$(a,b)$, ![]() $a,b\in \{0,1/2\}^{9}$. Moreover, since the family
$a,b\in \{0,1/2\}^{9}$. Moreover, since the family ![]() $p\colon {\mathcal {C}}\to U$ admits a level
$p\colon {\mathcal {C}}\to U$ admits a level ![]() $4l$ structure for any
$4l$ structure for any ![]() $l\in \textbf {Z}_{>0}$, the square root
$l\in \textbf {Z}_{>0}$, the square root ![]() $\tilde {J}_{M}^{*}\sqrt {\theta _{a,b}}$ is a well-defined holomorphic section of a holomorphic line bundle on
$\tilde {J}_{M}^{*}\sqrt {\theta _{a,b}}$ is a well-defined holomorphic section of a holomorphic line bundle on ![]() $U$ for every even pair
$U$ for every even pair ![]() $(a,b)$ by [Reference TsuyumineTsu91, Theorem 1]. Since any holomorphic line bundle on
$(a,b)$ by [Reference TsuyumineTsu91, Theorem 1]. Since any holomorphic line bundle on ![]() $U$ is trivial, we may regard
$U$ is trivial, we may regard ![]() $\tilde {J}_{M}^{*}\sqrt {\theta _{a,b}}\in {\mathcal {O}}(U)$.
$\tilde {J}_{M}^{*}\sqrt {\theta _{a,b}}\in {\mathcal {O}}(U)$.
We deduce from Proposition 7.2 the existence of a unique even pair ![]() $(a_{0},b_{0})$ and at least one even pair
$(a_{0},b_{0})$ and at least one even pair ![]() $(a_{1},b_{1})$ with the following properties:
$(a_{1},b_{1})$ with the following properties:
(1)
 $\tilde {J}_{M}^{*}\theta _{a_{0},b_{0}}$ vanishes identically on
$\tilde {J}_{M}^{*}\theta _{a_{0},b_{0}}$ vanishes identically on  $U$;
$U$;(2) set-theoretically,
 $U\cap {\rm div}(\tilde {J}_{M}^{*}\theta _{a_{1},b_{1}})=U\cap H_{\lambda }$.
$U\cap {\rm div}(\tilde {J}_{M}^{*}\theta _{a_{1},b_{1}})=U\cap H_{\lambda }$.
By (2) and the fact that ![]() $\tilde {J}_{M}^{*}\sqrt {\theta _{a_{1},b_{1}}}\in {\mathcal {O}}(U)$, there exists
$\tilde {J}_{M}^{*}\sqrt {\theta _{a_{1},b_{1}}}\in {\mathcal {O}}(U)$, there exists ![]() $c\in \textbf {Z}_{>0}$ such that on
$c\in \textbf {Z}_{>0}$ such that on ![]() $U$,
$U$,
By (1) and the definition of ![]() $\Upsilon _{9}$, we have
$\Upsilon _{9}$, we have
Setting ![]() $E:={\rm div}(\prod _{(a,b)\not =(a_{0},b_{0}),(a_{1},b_{1})}\tilde {J}_{M}^{*}\theta _{a,b}^{8})$, we get the following equality of divisors on
$E:={\rm div}(\prod _{(a,b)\not =(a_{0},b_{0}),(a_{1},b_{1})}\tilde {J}_{M}^{*}\theta _{a,b}^{8})$, we get the following equality of divisors on ![]() $U$:
$U$:
Thus we get the desired inequality ![]() $\beta \geq 16c\geq 2^{4}$.
$\beta \geq 16c\geq 2^{4}$.
Proof Proof of Theorem 9.10 By Theorem 8.1 (2), we get
Since ![]() ${\rm wt}(J_{M}^{*}\Upsilon _{9})=(0,2^{2}(2^{8}+1)(2^{9}-1))$ and since
${\rm wt}(J_{M}^{*}\Upsilon _{9})=(0,2^{2}(2^{8}+1)(2^{9}-1))$ and since ![]() ${\rm div}(J_{M}^{*}\Upsilon _{9})=\alpha {\mathcal {D}}_{\Lambda }+\beta {\mathcal {H}}_{1}$ by (9.22), we get
${\rm div}(J_{M}^{*}\Upsilon _{9})=\alpha {\mathcal {D}}_{\Lambda }+\beta {\mathcal {H}}_{1}$ by (9.22), we get
 \begin{gather*} {\rm wt}( \Psi_{\Lambda}(\cdot,2^{8}F_{\Lambda}+f_{\Lambda})\otimes J_{M}^{*}\Upsilon_{9} ) = ( -4(2^{8}+1)(2^{9}-1),4(2^{8}+1)(2^{9}-1) ),\\ {\rm div}( \Psi_{\Lambda}(\cdot,2^{8}F_{\Lambda}+f_{\Lambda})\otimes J_{M}^{*}\Upsilon_{9} ) = (\alpha+2^{8}+1) {\mathcal{D}}_{\Lambda}+(\beta-2^{4}) {\mathcal{H}}_{1}. \end{gather*}
\begin{gather*} {\rm wt}( \Psi_{\Lambda}(\cdot,2^{8}F_{\Lambda}+f_{\Lambda})\otimes J_{M}^{*}\Upsilon_{9} ) = ( -4(2^{8}+1)(2^{9}-1),4(2^{8}+1)(2^{9}-1) ),\\ {\rm div}( \Psi_{\Lambda}(\cdot,2^{8}F_{\Lambda}+f_{\Lambda})\otimes J_{M}^{*}\Upsilon_{9} ) = (\alpha+2^{8}+1) {\mathcal{D}}_{\Lambda}+(\beta-2^{4}) {\mathcal{H}}_{1}. \end{gather*}
Since ![]() ${\rm wt}(\Phi _{M})=(-4\ell ,4\ell )$ and
${\rm wt}(\Phi _{M})=(-4\ell ,4\ell )$ and ![]() ${\rm div}(\Phi _{M})=\ell {\mathcal {D}}_{\Lambda }$,
${\rm div}(\Phi _{M})=\ell {\mathcal {D}}_{\Lambda }$,
is a meromorphic function on ![]() ${\mathcal {M}}_{\Lambda }$ with divisor
${\mathcal {M}}_{\Lambda }$ with divisor
By Lemma 9.11 and Theorem 8.6 for ![]() $[M\perp d]$,
$[M\perp d]$, ![]() $d\in \Delta _{\Lambda }$, Lemma 4.3 applies to a general curve
$d\in \Delta _{\Lambda }$, Lemma 4.3 applies to a general curve ![]() $\gamma \colon \Delta \to {\mathcal {M}}_{\Lambda }$ intersecting
$\gamma \colon \Delta \to {\mathcal {M}}_{\Lambda }$ intersecting ![]() $\bar {\mathcal {D}}_{\Lambda }^{0}$ transversally. Since
$\bar {\mathcal {D}}_{\Lambda }^{0}$ transversally. Since ![]() $\alpha \geq 2(2^{16}-1)$ and
$\alpha \geq 2(2^{16}-1)$ and ![]() $\beta \geq 2^{4}$ by Lemmas 4.3 and 9.12, we get
$\beta \geq 2^{4}$ by Lemmas 4.3 and 9.12, we get ![]() ${\rm div}(\varphi _{\Lambda })\geq 0$. Thus
${\rm div}(\varphi _{\Lambda })\geq 0$. Thus ![]() $\varphi _{\Lambda }$ is a constant.
$\varphi _{\Lambda }$ is a constant.
9.5 The divisors of  $J_{M}^{*}\chi _{g}^{8}$ and
$J_{M}^{*}\chi _{g}^{8}$ and  $J_{M}^{*}\Upsilon _{g}$
$J_{M}^{*}\Upsilon _{g}$
We now summarize the formulas for the divisors of ![]() $J_{M}^{*}\chi _{g}^{8}$ and
$J_{M}^{*}\chi _{g}^{8}$ and ![]() $J_{M}^{*}\Upsilon _{g}$ obtained so far. We also give a geometric interpretation of this result in terms of log Del Pezzo surfaces.
$J_{M}^{*}\Upsilon _{g}$ obtained so far. We also give a geometric interpretation of this result in terms of log Del Pezzo surfaces.
Theorem 9.13 Let ![]() $M$ be a non-exceptional primitive
$M$ be a non-exceptional primitive ![]() $2$-elementary Lorentzian sublattice of
$2$-elementary Lorentzian sublattice of ![]() ${\Bbb L}_{K3}$ with
${\Bbb L}_{K3}$ with ![]() $\Lambda =M^{\perp }$ and invariants
$\Lambda =M^{\perp }$ and invariants ![]() $(r,l,\delta )$. Then the following statements hold.
$(r,l,\delta )$. Then the following statements hold.
(1) If
 $g=0$ (i.e.
$g=0$ (i.e.  $r+l=22$) then
$r+l=22$) then  ${\rm div}(J_{M}^{*}\chi _{g}^{8})=0$.
${\rm div}(J_{M}^{*}\chi _{g}^{8})=0$.(2) If
 $r\geq 2$,
$r\geq 2$,  $\delta =1$ and
$\delta =1$ and  $1\leq g\leq 9$, then
$1\leq g\leq 9$, then  ${\rm div}(J_{M}^{*}\chi _{g}^{8})=2^{2g-1}{\mathcal {D}}_{\Lambda }^{-}+2^{k+4}{\mathcal {H}}_{\Lambda }$.
${\rm div}(J_{M}^{*}\chi _{g}^{8})=2^{2g-1}{\mathcal {D}}_{\Lambda }^{-}+2^{k+4}{\mathcal {H}}_{\Lambda }$.(3) If
 $(r,\delta )=(1,1)$, then
$(r,\delta )=(1,1)$, then  ${\rm div}(J_{M}^{*}\chi _{g}^{8})=2^{19}{\mathcal {D}}_{\Lambda }^{-}+2^{4}\cdot 7 {\mathcal {D}}_{\Lambda }^{+}+2^{4}{\mathcal {H}}_{\Lambda }$.
${\rm div}(J_{M}^{*}\chi _{g}^{8})=2^{19}{\mathcal {D}}_{\Lambda }^{-}+2^{4}\cdot 7 {\mathcal {D}}_{\Lambda }^{+}+2^{4}{\mathcal {H}}_{\Lambda }$.(4) If
 $\delta =0$ and
$\delta =0$ and  $r\not =2,10$, then
$r\not =2,10$, then  ${\rm div}(J_{M}^{*}\chi _{g}^{8})=2^{g-1}(2^{g}+1) {\mathcal {D}}_{\Lambda }$.
${\rm div}(J_{M}^{*}\chi _{g}^{8})=2^{g-1}(2^{g}+1) {\mathcal {D}}_{\Lambda }$.(5) If
 $(r,\delta )=(2,0)$ or
$(r,\delta )=(2,0)$ or  $(10,0)$, then
$(10,0)$, then  $J_{M}^{*}\chi _{g}^{8}$ vanishes identically on
$J_{M}^{*}\chi _{g}^{8}$ vanishes identically on  $\Omega _{\Lambda }$.
$\Omega _{\Lambda }$.(6) If
 $(r,\delta )=(10,0)$, then
$(r,\delta )=(10,0)$, then  ${\rm div}(J_{M}^{*}\Upsilon _{g})=2(2^{2(g-1)}-1) {\mathcal {D}}_{\Lambda }$.
${\rm div}(J_{M}^{*}\Upsilon _{g})=2(2^{2(g-1)}-1) {\mathcal {D}}_{\Lambda }$.(7) If
 $(r,l,\delta )=(2,0,0)$, then
$(r,l,\delta )=(2,0,0)$, then  ${\rm div}(J_{M}^{*}\Upsilon _{10})=2(2^{18}-1) {\mathcal {D}}_{\Lambda }+2^{5} {\mathcal {H}}_{\Lambda }$.
${\rm div}(J_{M}^{*}\Upsilon _{10})=2(2^{18}-1) {\mathcal {D}}_{\Lambda }+2^{5} {\mathcal {H}}_{\Lambda }$.(8) If
 $(r,l,\delta )=(2,2,0)$, then
$(r,l,\delta )=(2,2,0)$, then  ${\rm div}(J_{M}^{*}\Upsilon _{9})=2(2^{16}-1) {\mathcal {D}}_{\Lambda }+2^{4}\,\{{\mathcal {H}}_{\Lambda }-{\mathcal {H}}_{\Lambda }(-1,\textbf {e}_{11})\}$.
${\rm div}(J_{M}^{*}\Upsilon _{9})=2(2^{16}-1) {\mathcal {D}}_{\Lambda }+2^{4}\,\{{\mathcal {H}}_{\Lambda }-{\mathcal {H}}_{\Lambda }(-1,\textbf {e}_{11})\}$.
Proof. Assertion (1) is obvious since ![]() $\chi _{g}=1$ for
$\chi _{g}=1$ for ![]() $g=0$. For
$g=0$. For ![]() $g=1,2$ (respectively,
$g=1,2$ (respectively, ![]() $3\leq g\leq 9$), we get (2) by [Reference YoshikawaYos13, Proposition 4.2 (2), (3)] (respectively, Lemma 8.3, Proposition 8.4, (8.17)). We get (3) by Proposition 8.4, (8.17) and (8.20). When
$3\leq g\leq 9$), we get (2) by [Reference YoshikawaYos13, Proposition 4.2 (2), (3)] (respectively, Lemma 8.3, Proposition 8.4, (8.17)). We get (3) by Proposition 8.4, (8.17) and (8.20). When ![]() $r > 10$ (respectively,
$r > 10$ (respectively, ![]() $2 < r < 10$), we get (4) by [Reference YoshikawaYos13, (9.3)] and the equality
$2 < r < 10$), we get (4) by [Reference YoshikawaYos13, (9.3)] and the equality ![]() $a=E=0$ in [Reference YoshikawaYos13, Proof of Theorem 9.1] (respectively, Lemma 9.1). We get (5) by [Reference YoshikawaYos13, Proposition 9.3] when
$a=E=0$ in [Reference YoshikawaYos13, Proof of Theorem 9.1] (respectively, Lemma 9.1). We get (5) by [Reference YoshikawaYos13, Proposition 9.3] when ![]() $r=10$. When
$r=10$. When ![]() $r=2$,
$r=2$, ![]() $\delta =0$, there are two possible cases:
$\delta =0$, there are two possible cases: ![]() $g=10$ and
$g=10$ and ![]() $g=9$. For
$g=9$. For ![]() $g=10$, (5) was proved in Remark 8.8. For
$g=10$, (5) was proved in Remark 8.8. For ![]() $g=9$, (5) was proved in § 7.2. This proves (5). We get (6) by (9.3) and the equality
$g=9$, (5) was proved in § 7.2. This proves (5). We get (6) by (9.3) and the equality ![]() $a=2(2^{2(g-1)}-1)$ in the proof of Theorem 9.4. We get (7) by (9.6), since
$a=2(2^{2(g-1)}-1)$ in the proof of Theorem 9.4. We get (7) by (9.6), since ![]() $\beta =2^{5}$ and
$\beta =2^{5}$ and ![]() $\alpha =2(2^{18}-1)$ in the proof of Theorem 9.5. We get (8) by (9.22), since the equalities
$\alpha =2(2^{18}-1)$ in the proof of Theorem 9.5. We get (8) by (9.22), since the equalities ![]() $\alpha =2(2^{16}-1)$ and
$\alpha =2(2^{16}-1)$ and ![]() $\beta =2^{4}$ follow from the proof of Theorem 9.10. This completes the proof.
$\beta =2^{4}$ follow from the proof of Theorem 9.10. This completes the proof.
Corollary 9.14 For ![]() $(r,l,\delta )=(10,2,0),(10,4,0)$,
$(r,l,\delta )=(10,2,0),(10,4,0)$, ![]() $J_{M}(\Omega _{\Lambda }^{0})$ is disjoint from the hyperelliptic locus. For
$J_{M}(\Omega _{\Lambda }^{0})$ is disjoint from the hyperelliptic locus. For ![]() $(r,l,\delta )=(10,0,0)$, every member of
$(r,l,\delta )=(10,0,0)$, every member of ![]() $J_{M}(\Omega _{\Lambda }^{0})$ has exactly one effective even theta characteristic.
$J_{M}(\Omega _{\Lambda }^{0})$ has exactly one effective even theta characteristic.
Proof. Set-theoretically, ![]() ${\frak H}_{{\rm hyp},4}$ (respectively,
${\frak H}_{{\rm hyp},4}$ (respectively, ![]() ${\frak H}_{{\rm hyp},5}$) is given by
${\frak H}_{{\rm hyp},5}$) is given by ![]() ${\rm div}(\chi _{4})\cap {\rm div}(\Upsilon _{4})$ (respectively,
${\rm div}(\chi _{4})\cap {\rm div}(\Upsilon _{4})$ (respectively, ![]() ${\rm div}(\chi _{5})\cap {\rm div}(\Upsilon _{5})\cap {\rm div}(F_{5})$) on
${\rm div}(\chi _{5})\cap {\rm div}(\Upsilon _{5})\cap {\rm div}(F_{5})$) on ![]() ${\frak M}_{4}$ (respectively,
${\frak M}_{4}$ (respectively, ![]() ${\frak M}_{5}$). Since
${\frak M}_{5}$). Since ![]() $J_{M}^{*}\Upsilon _{4}$ (respectively,
$J_{M}^{*}\Upsilon _{4}$ (respectively, ![]() $J_{M}^{*}\Upsilon _{5}$) is nowhere vanishing on
$J_{M}^{*}\Upsilon _{5}$) is nowhere vanishing on ![]() $\Omega _{\Lambda }^{0}$ by Theorem 9.13 (6) for
$\Omega _{\Lambda }^{0}$ by Theorem 9.13 (6) for ![]() $(r,l,\delta )=(10,4,0)$ (respectively,
$(r,l,\delta )=(10,4,0)$ (respectively, ![]() $(10,2,0)$), we get the first assertion. When
$(10,2,0)$), we get the first assertion. When ![]() $(r,l,\delta )=(10,0,0)$,
$(r,l,\delta )=(10,0,0)$, ![]() $J_{M}^{*}\chi _{6}$ vanishes identically on
$J_{M}^{*}\chi _{6}$ vanishes identically on ![]() $\Omega _{\Lambda }^{0}$ and
$\Omega _{\Lambda }^{0}$ and ![]() $J_{M}^{*}\Upsilon _{6}$ is nowhere vanishing on
$J_{M}^{*}\Upsilon _{6}$ is nowhere vanishing on ![]() $\Omega _{\Lambda }^{0}$ by Theorem 9.13 (5), (6). This, together with Lemma 4.1, implies the second assertion.
$\Omega _{\Lambda }^{0}$ by Theorem 9.13 (5), (6). This, together with Lemma 4.1, implies the second assertion.
Let us give a geometric interpretation of Theorem 9.13, where we use the notion of log Del Pezzo surfaces of index at most ![]() $2$. We refer to [Reference Alexeev and NikulinAN06] for this notion. Let
$2$. We refer to [Reference Alexeev and NikulinAN06] for this notion. Let ![]() $S$ be a log Del Pezzo surface of index at most
$S$ be a log Del Pezzo surface of index at most ![]() $2$. By [Reference Alexeev and NikulinAN06, Theorem 1.5], the bi-anticanonical system of
$2$. By [Reference Alexeev and NikulinAN06, Theorem 1.5], the bi-anticanonical system of ![]() $S$ contains a smooth member. For any smooth member
$S$ contains a smooth member. For any smooth member ![]() $C\in |-2K_{S}|$, one can canonically associate a
$C\in |-2K_{S}|$, one can canonically associate a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface
$K3$ surface ![]() $(X_{(S,C)},\iota _{(S,C)})$ whose quotient
$(X_{(S,C)},\iota _{(S,C)})$ whose quotient ![]() $X_{(S,C)}/\iota _{(S,C)}$ is the right resolution of
$X_{(S,C)}/\iota _{(S,C)}$ is the right resolution of ![]() $S$ (see [Reference Alexeev and NikulinAN06, § 2.1]). We define the invariant
$S$ (see [Reference Alexeev and NikulinAN06, § 2.1]). We define the invariant ![]() $\delta (S)\in \{0,1\}$ as that of the
$\delta (S)\in \{0,1\}$ as that of the ![]() $2$-elementary lattice
$2$-elementary lattice ![]() $H^{2}(X_{(S,C)},\textbf {Z})_{+}$. Then
$H^{2}(X_{(S,C)},\textbf {Z})_{+}$. Then ![]() $\delta (S)$ is independent of the choice of a smooth member
$\delta (S)$ is independent of the choice of a smooth member ![]() $C\in |-2K_{S}|$.
$C\in |-2K_{S}|$.
Corollary 9.15 Let ![]() $S$ be a log Del Pezzo surface of index at most
$S$ be a log Del Pezzo surface of index at most ![]() $2$ and let
$2$ and let ![]() $C\in |-2K_{S}|$ be a smooth member. If
$C\in |-2K_{S}|$ be a smooth member. If ![]() $S\not \cong \mathbf{F}_{0},\mathbf{P}(1,1,2)$, then the following statements hold.
$S\not \cong \mathbf{F}_{0},\mathbf{P}(1,1,2)$, then the following statements hold.
(1) When
 $(\rho (S),\delta (S))\not =(2,0),(10,0)$,
$(\rho (S),\delta (S))\not =(2,0),(10,0)$,  $C$ has an effective even theta characteristic if and only if the period of
$C$ has an effective even theta characteristic if and only if the period of  $(X_{(S,C)},\iota _{(S,C)})$ lies in the characteristic Heegner divisor.
$(X_{(S,C)},\iota _{(S,C)})$ lies in the characteristic Heegner divisor.(2) When
 $(\rho (S),\delta (S))=(2,0)$ or
$(\rho (S),\delta (S))=(2,0)$ or  $(10,0)$,
$(10,0)$,  $C$ always has an effective even theta characteristic. Moreover,
$C$ always has an effective even theta characteristic. Moreover,  $C$ has at least two effective even theta characteristics if and only if the period of
$C$ has at least two effective even theta characteristics if and only if the period of  $(X_{(S,C)},\iota _{(S,C)})$ lies in the characteristic Heegner divisor.
$(X_{(S,C)},\iota _{(S,C)})$ lies in the characteristic Heegner divisor.
Proof. Since the period of ![]() $C$ is exactly the image of
$C$ is exactly the image of ![]() $(X_{(S,C)},\iota _{(S,C)})$ by the Torelli map, the result follows from Theorem 9.13.
$(X_{(S,C)},\iota _{(S,C)})$ by the Torelli map, the result follows from Theorem 9.13.
9.6 The quasi-affinity of  ${\mathcal {M}}_{\Lambda }^{0}$
${\mathcal {M}}_{\Lambda }^{0}$
As an application of the results in this and the previous section, we obtain the quasi-affinity of ![]() ${\mathcal {M}}_{\Lambda }^{0}$ for a wide range of
${\mathcal {M}}_{\Lambda }^{0}$ for a wide range of ![]() $\Lambda$ as follows.
$\Lambda$ as follows.
Theorem 9.16 If ![]() $\Lambda$ is a primitive
$\Lambda$ is a primitive ![]() $2$-elementary sublattice of
$2$-elementary sublattice of ![]() ${\Bbb L}_{K3}$ with
${\Bbb L}_{K3}$ with ![]() $r(\Lambda )<16$ and signature
$r(\Lambda )<16$ and signature ![]() $(2,r(\Lambda )-2)$, then
$(2,r(\Lambda )-2)$, then ![]() ${\mathcal {M}}_{\Lambda }^{0}$ is quasi-affine.
${\mathcal {M}}_{\Lambda }^{0}$ is quasi-affine.
Proof. By [Reference YoshikawaYos13, Proposition 2.2], ![]() $\bar {J}_{M}^{0}$ extends to a meromorphic map from
$\bar {J}_{M}^{0}$ extends to a meromorphic map from ![]() ${\mathcal {M}}_{\Lambda }^{*}$ to
${\mathcal {M}}_{\Lambda }^{*}$ to ![]() ${\mathcal {A}}_{g}^{*}$. We regard
${\mathcal {A}}_{g}^{*}$. We regard ![]() ${\mathcal {M}}_{\Lambda }^{0}$ as a Zariski open subset of a subvariety of
${\mathcal {M}}_{\Lambda }^{0}$ as a Zariski open subset of a subvariety of ![]() ${\mathcal {M}}_{\Lambda }^{*}\times {\mathcal {A}}_{g}^{*}$ via the embedding
${\mathcal {M}}_{\Lambda }^{*}\times {\mathcal {A}}_{g}^{*}$ via the embedding ![]() ${\rm id}_{{\mathcal {M}}_{\Lambda }^{0}}\times \bar {J}_{M}^{0}$. It suffices to prove the existence of a meromorphic section of an ample line bundle on
${\rm id}_{{\mathcal {M}}_{\Lambda }^{0}}\times \bar {J}_{M}^{0}$. It suffices to prove the existence of a meromorphic section of an ample line bundle on ![]() ${\mathcal {M}}_{\Lambda }^{*}\times {\mathcal {A}}_{g}^{*}$, which is nowhere vanishing on
${\mathcal {M}}_{\Lambda }^{*}\times {\mathcal {A}}_{g}^{*}$, which is nowhere vanishing on ![]() ${\mathcal {M}}_{\Lambda }^{0}$ [Reference GrothenidieckGro61, Proposition 5.1.2]. Let
${\mathcal {M}}_{\Lambda }^{0}$ [Reference GrothenidieckGro61, Proposition 5.1.2]. Let ![]() $\lambda _{\Lambda }$ be the Hodge bundle on
$\lambda _{\Lambda }$ be the Hodge bundle on ![]() ${\mathcal {M}}_{\Lambda }^{*}$. By Baily and Borel, the line bundle
${\mathcal {M}}_{\Lambda }^{*}$. By Baily and Borel, the line bundle ![]() $\lambda _{\Lambda }^{\otimes a}\boxtimes {\mathcal {F}}_{g}^{\otimes b}$ on
$\lambda _{\Lambda }^{\otimes a}\boxtimes {\mathcal {F}}_{g}^{\otimes b}$ on ![]() ${\mathcal {M}}_{\Lambda }^{*}\times {\mathcal {A}}_{g}^{*}$ is ample if
${\mathcal {M}}_{\Lambda }^{*}\times {\mathcal {A}}_{g}^{*}$ is ample if ![]() $a>0$ and
$a>0$ and ![]() $b>0$. Under the assumption
$b>0$. Under the assumption ![]() $r>6$, it follows from Theorems 8.6, 9.2 and 9.4 that
$r>6$, it follows from Theorems 8.6, 9.2 and 9.4 that ![]() $\Phi _{M}^{\nu }$ is a meromorphic section of
$\Phi _{M}^{\nu }$ is a meromorphic section of ![]() $\lambda _{\Lambda }^{\otimes a}\boxtimes {\mathcal {F}}_{g}^{\otimes b}$ for some
$\lambda _{\Lambda }^{\otimes a}\boxtimes {\mathcal {F}}_{g}^{\otimes b}$ for some ![]() $a,b,\nu \in {\mathbf {Z}}_{>0}$. Since
$a,b,\nu \in {\mathbf {Z}}_{>0}$. Since ![]() $\Phi _{M}^{\nu }$ is nowhere vanishing on
$\Phi _{M}^{\nu }$ is nowhere vanishing on ![]() ${\mathcal {M}}_{\Lambda }^{0}$ by Theorem 5.1,
${\mathcal {M}}_{\Lambda }^{0}$ by Theorem 5.1, ![]() $\Phi _{M}^{\nu }$ is a desired section.
$\Phi _{M}^{\nu }$ is a desired section.
By [Reference Borcherds, Katzarkov, Pantev and Shepherd-BarronBKPS98], it is known that ![]() ${\mathcal {M}}_{\Lambda }^{0}$ is quasi-affine when
${\mathcal {M}}_{\Lambda }^{0}$ is quasi-affine when ![]() $\Lambda ={\Bbb U}^{\oplus 2}\oplus {\Bbb E}_{8}^{\oplus 2}\oplus {\Bbb A}_{1}$,
$\Lambda ={\Bbb U}^{\oplus 2}\oplus {\Bbb E}_{8}^{\oplus 2}\oplus {\Bbb A}_{1}$, ![]() ${\Bbb U}^{\oplus 2}\oplus {\Bbb E}_{8}^{\oplus 2}$. This, together with Theorem 9.16, implies that
${\Bbb U}^{\oplus 2}\oplus {\Bbb E}_{8}^{\oplus 2}$. This, together with Theorem 9.16, implies that ![]() ${\mathcal {M}}_{\Lambda }^{0}$ is quasi-affine, possibly except for
${\mathcal {M}}_{\Lambda }^{0}$ is quasi-affine, possibly except for ![]() $12$ isometry classes of primitive
$12$ isometry classes of primitive ![]() $2$-elementary sublattices of
$2$-elementary sublattices of ![]() ${\Bbb L}_{K3}$.
${\Bbb L}_{K3}$.
10. Spin- $1/2$ bosonization formula and a factorization of
$1/2$ bosonization formula and a factorization of  $\tau _{M}$
$\tau _{M}$
In this section we introduce a twisted version ![]() $\tau _{M}^{{\rm spin}}$ of
$\tau _{M}^{{\rm spin}}$ of ![]() $\tau _{M}$ and give its explicit formula purely in terms of Borcherds products. The relations (10.5) and (10.6) below provide a factorization of
$\tau _{M}$ and give its explicit formula purely in terms of Borcherds products. The relations (10.5) and (10.6) below provide a factorization of ![]() $\tau _{M}$ at the level of holomorphic torsion invariants.
$\tau _{M}$ at the level of holomorphic torsion invariants.
10.1 Spin- $1/2$ bosonization formula
$1/2$ bosonization formula
Let ![]() $C$ be a smooth projective curve of genus
$C$ be a smooth projective curve of genus ![]() $g$ and let
$g$ and let ![]() $\Sigma$ be a theta characteristic. The pair
$\Sigma$ be a theta characteristic. The pair ![]() $(C,\Sigma )$ is called a spin curve. A theta characteristic
$(C,\Sigma )$ is called a spin curve. A theta characteristic ![]() $\Sigma$ is ineffective if
$\Sigma$ is ineffective if ![]() $h^{0}(\Sigma )=0$. Let
$h^{0}(\Sigma )=0$. Let ![]() $\omega$ be a Kähler form on
$\omega$ be a Kähler form on ![]() $C$. Then
$C$. Then ![]() $\Sigma$ is equipped with the Hermitian metric induced by
$\Sigma$ is equipped with the Hermitian metric induced by ![]() $\omega$. Let
$\omega$. Let ![]() $\tau (C,\Sigma ;\omega )$ be the analytic torsion of
$\tau (C,\Sigma ;\omega )$ be the analytic torsion of ![]() $\Sigma$ with respect to
$\Sigma$ with respect to ![]() $\omega$. Recall that
$\omega$. Recall that ![]() ${\rm vol}(C,\omega )=\int _{C}\omega /2\pi$. We set
${\rm vol}(C,\omega )=\int _{C}\omega /2\pi$. We set
By the anomaly formula for Quillen metrics [Reference Bismut, Gillet and SouléBGS88], if ![]() $\Sigma$ is ineffective,
$\Sigma$ is ineffective, ![]() $\tilde {\tau }_{g}(C,\Sigma )$ is independent of the choice of a Kähler form
$\tilde {\tau }_{g}(C,\Sigma )$ is independent of the choice of a Kähler form ![]() $\omega$ on
$\omega$ on ![]() $C$. Thus we get an invariant
$C$. Thus we get an invariant ![]() $\tilde {\tau }_{g}$ of ineffective spin curves of genus
$\tilde {\tau }_{g}$ of ineffective spin curves of genus ![]() $g$. In this subsection we recall the spin-
$g$. In this subsection we recall the spin-![]() $1/2$ bosonization formula [Reference Alvarez-Gaumé, Moore and VafaAMV86, Reference Bost and NelsonBN86, Reference FayFay92], which gives an explicit formula for
$1/2$ bosonization formula [Reference Alvarez-Gaumé, Moore and VafaAMV86, Reference Bost and NelsonBN86, Reference FayFay92], which gives an explicit formula for ![]() $\tilde {\tau }_{g}$ viewed as a function on the moduli space of ineffective spin curves of genus
$\tilde {\tau }_{g}$ viewed as a function on the moduli space of ineffective spin curves of genus ![]() $g$ with level
$g$ with level ![]() $2$ structure.
$2$ structure.
Let ![]() $V$ be a fixed symplectic vector space of rank
$V$ be a fixed symplectic vector space of rank ![]() $2g$ over
$2g$ over ![]() $\mathbf{F}_{2}$ equipped with a fixed symplectic basis
$\mathbf{F}_{2}$ equipped with a fixed symplectic basis ![]() $\{{\frak e}_{1},\ldots ,{\frak e}_{g},{\frak f}_{1},\ldots ,{\frak f}_{g}\}$. A level
$\{{\frak e}_{1},\ldots ,{\frak e}_{g},{\frak f}_{1},\ldots ,{\frak f}_{g}\}$. A level ![]() $2$ structure on
$2$ structure on ![]() $C\in {\frak M}_{g}$ is defined as an isomorphism of symplectic vector spaces
$C\in {\frak M}_{g}$ is defined as an isomorphism of symplectic vector spaces ![]() $\alpha \colon V\cong H_{1}(C,\mathbf{F}_{2})$, where
$\alpha \colon V\cong H_{1}(C,\mathbf{F}_{2})$, where ![]() $H_{1}(C,\mathbf{F}_{2})$ is equipped with the intersection pairing. Let
$H_{1}(C,\mathbf{F}_{2})$ is equipped with the intersection pairing. Let ![]() ${\rm Alb}(C)[2]$ (respectively,
${\rm Alb}(C)[2]$ (respectively, ![]() ${\rm Pic}^{0}(C)[2]$) be the
${\rm Pic}^{0}(C)[2]$) be the ![]() $2$-division points of the Albanese variety
$2$-division points of the Albanese variety ![]() ${\rm Alb}(C)$ (respectively, Picard variety
${\rm Alb}(C)$ (respectively, Picard variety ![]() ${\rm Pic}^{0}(C)$). By the canonical isomorphism
${\rm Pic}^{0}(C)$). By the canonical isomorphism ![]() $H_{1}(C,\mathbf{F}_{2})\cong \frac {1}{2}H_{1}(C,\textbf {Z})/H_{1}(C,\textbf {Z})\cong {\rm Alb}(C)[2]$ and the Abel–Jacobi isomorphism
$H_{1}(C,\mathbf{F}_{2})\cong \frac {1}{2}H_{1}(C,\textbf {Z})/H_{1}(C,\textbf {Z})\cong {\rm Alb}(C)[2]$ and the Abel–Jacobi isomorphism ![]() ${\rm Pic}^{0}(C)\cong {\rm Alb}(C)$, a level
${\rm Pic}^{0}(C)\cong {\rm Alb}(C)$, a level ![]() $2$ structure on
$2$ structure on ![]() $C$ is identified with a symplectic basis of
$C$ is identified with a symplectic basis of ![]() ${\rm Pic}^{0}(C)[2]$ with respect to the Weil pairing.
${\rm Pic}^{0}(C)[2]$ with respect to the Weil pairing.
Let ![]() ${\frak M}_{g}(2)$ be the moduli space of projective curves of genus
${\frak M}_{g}(2)$ be the moduli space of projective curves of genus ![]() $g$ with level
$g$ with level ![]() $2$ structure and let
$2$ structure and let ![]() $p\colon {\frak M}_{g}(2)\to {\frak M}_{g}$ be the natural projection. Let
$p\colon {\frak M}_{g}(2)\to {\frak M}_{g}$ be the natural projection. Let ![]() ${\mathcal {S}}_{g}^{+}$ be the moduli space of even spin curves of genus
${\mathcal {S}}_{g}^{+}$ be the moduli space of even spin curves of genus ![]() $g$ and let
$g$ and let ![]() $\pi \colon {\mathcal {S}}_{g}^{+}\to {\frak M}_{g}$ be the natural projection. We define
$\pi \colon {\mathcal {S}}_{g}^{+}\to {\frak M}_{g}$ be the natural projection. We define ![]() ${\mathcal {S}}_{g}^{+}(2)$ as the fiber product
${\mathcal {S}}_{g}^{+}(2)$ as the fiber product ![]() ${\mathcal {S}}_{g}^{+}\times _{{\frak M}_{g}}{\frak M}_{g}(2)$. The projection from
${\mathcal {S}}_{g}^{+}\times _{{\frak M}_{g}}{\frak M}_{g}(2)$. The projection from ![]() ${\mathcal {S}}_{g}^{+}(2)$ to
${\mathcal {S}}_{g}^{+}(2)$ to ![]() ${\frak M}_{g}(2)$ (respectively,
${\frak M}_{g}(2)$ (respectively, ![]() ${\mathcal {S}}_{g}^{+}$) is denoted again by
${\mathcal {S}}_{g}^{+}$) is denoted again by ![]() $p$ (respectively,
$p$ (respectively, ![]() $\pi$). The covering
$\pi$). The covering ![]() $p\colon {\mathcal {S}}_{g}^{+}(2)\to {\frak M}_{g}(2)$ of degree
$p\colon {\mathcal {S}}_{g}^{+}(2)\to {\frak M}_{g}(2)$ of degree ![]() $2^{g-1}(2^{g}+1)$ is trivial as follows. On
$2^{g-1}(2^{g}+1)$ is trivial as follows. On ![]() $(C,\alpha )\in {\frak M}_{g}(2)$, there is a distinguished even theta characteristic
$(C,\alpha )\in {\frak M}_{g}(2)$, there is a distinguished even theta characteristic ![]() $\kappa \in {\rm Pic}^{g-1}(C)$ called Riemann's constant (e.g. [Reference FayFay92, p. 6 and Lemma 1.5]). For every even pair
$\kappa \in {\rm Pic}^{g-1}(C)$ called Riemann's constant (e.g. [Reference FayFay92, p. 6 and Lemma 1.5]). For every even pair ![]() $(a,b)$,
$(a,b)$, ![]() $a,b\in \{0,1/2\}^{g}$, we define a section
$a,b\in \{0,1/2\}^{g}$, we define a section ![]() $\sigma _{a,b}\colon {\frak M}_{g}(2)\to {\mathcal {S}}_{g}^{+}(2)$ by
$\sigma _{a,b}\colon {\frak M}_{g}(2)\to {\mathcal {S}}_{g}^{+}(2)$ by ![]() $\sigma _{a,b}(C,\alpha ):=(C,\kappa \otimes \chi _{a,b},\alpha )$, where
$\sigma _{a,b}(C,\alpha ):=(C,\kappa \otimes \chi _{a,b},\alpha )$, where ![]() $\chi _{a,b}\in {\rm Pic}^{0}(C)[2]$ is the point corresponding to
$\chi _{a,b}\in {\rm Pic}^{0}(C)[2]$ is the point corresponding to ![]() $\sum _{i}2a_{i}{\frak e}_{i}+\sum _{j}2b_{j}{\frak f}_{j}\in \mathbf{F}_{2}^{2g}$ via the isomorphism
$\sum _{i}2a_{i}{\frak e}_{i}+\sum _{j}2b_{j}{\frak f}_{j}\in \mathbf{F}_{2}^{2g}$ via the isomorphism ![]() $\mathbf{F}_{2}^{2g}\cong {\rm Pic}^{0}(C)[2]$ induced by
$\mathbf{F}_{2}^{2g}\cong {\rm Pic}^{0}(C)[2]$ induced by ![]() $\alpha$. In this way, we get a decomposition
$\alpha$. In this way, we get a decomposition ![]() ${\mathcal {S}}_{g}^{+}(2)=\amalg _{(a,b)\,{\rm even}}\sigma _{a,b}({\frak M}_{g}(2))$. We set
${\mathcal {S}}_{g}^{+}(2)=\amalg _{(a,b)\,{\rm even}}\sigma _{a,b}({\frak M}_{g}(2))$. We set ![]() ${\mathcal {S}}_{g}^{+,0}(2):=\amalg _{(a,b)\,{\rm even}}\sigma _{a,b}({\frak M}_{g}(2)\setminus {\rm div}(\theta _{a,b}))$ and
${\mathcal {S}}_{g}^{+,0}(2):=\amalg _{(a,b)\,{\rm even}}\sigma _{a,b}({\frak M}_{g}(2)\setminus {\rm div}(\theta _{a,b}))$ and ![]() ${\mathcal {S}}_{g}^{+,0}:=\pi ({\mathcal {S}}_{g}^{+,0}(2))=\bigcup _{(a,b)\,{\rm even}} \pi (\sigma _{a,b}({\frak M}_{g}(2)\setminus {\rm div}(\theta _{a,b})))$. Since
${\mathcal {S}}_{g}^{+,0}:=\pi ({\mathcal {S}}_{g}^{+,0}(2))=\bigcup _{(a,b)\,{\rm even}} \pi (\sigma _{a,b}({\frak M}_{g}(2)\setminus {\rm div}(\theta _{a,b})))$. Since ![]() $h^{0}(\kappa \otimes \chi _{a,b})=0$ if and only if
$h^{0}(\kappa \otimes \chi _{a,b})=0$ if and only if ![]() $\theta _{a,b}(\Omega (C))\not =0$ for
$\theta _{a,b}(\Omega (C))\not =0$ for ![]() $(C,\alpha )\in {\frak M}_{g}(2)$,
$(C,\alpha )\in {\frak M}_{g}(2)$, ![]() $\tilde {\tau }_{g}$ is a function on
$\tilde {\tau }_{g}$ is a function on ![]() ${\mathcal {S}}_{g}^{+,0}$.
${\mathcal {S}}_{g}^{+,0}$.
On the other hand, for every even pair ![]() $(a,b)$, the theta constant
$(a,b)$, the theta constant ![]() $\theta _{a,b}$ is a section of a certain line bundle on
$\theta _{a,b}$ is a section of a certain line bundle on ![]() ${\frak M}_{g}(2)$ and its Petersson norm
${\frak M}_{g}(2)$ and its Petersson norm ![]() $\|\theta _{a,b}\|$ is a function on
$\|\theta _{a,b}\|$ is a function on ![]() ${\frak M}_{g}(2)$. For
${\frak M}_{g}(2)$. For ![]() $g=0$, we define
$g=0$, we define ![]() $\|\theta _{a,b}\|:=1$. Let
$\|\theta _{a,b}\|:=1$. Let ![]() $\zeta _\textbf {Q}(s)$ be the Riemann zeta function. By the spin-
$\zeta _\textbf {Q}(s)$ be the Riemann zeta function. By the spin-![]() $1/2$ bosonization formula ([Reference Alvarez-Gaumé, Moore and VafaAMV86, Reference Bost and NelsonBN86], [Reference FayFay92, Theorem 4.9 (i), p. 94 (4.58), p. 97 (5.7)]), the following equality of functions on
$1/2$ bosonization formula ([Reference Alvarez-Gaumé, Moore and VafaAMV86, Reference Bost and NelsonBN86], [Reference FayFay92, Theorem 4.9 (i), p. 94 (4.58), p. 97 (5.7)]), the following equality of functions on ![]() ${\frak M}_{g}(2)\setminus {\rm div}(\theta _{a,b})$ holds:
${\frak M}_{g}(2)\setminus {\rm div}(\theta _{a,b})$ holds:
where ![]() ${\frak c}_{g}$ is evaluated by the arithmetic Riemann–Roch theorem [Reference Gillet and SouléGS92] for
${\frak c}_{g}$ is evaluated by the arithmetic Riemann–Roch theorem [Reference Gillet and SouléGS92] for ![]() $g=0$, by Kronecker's limit formula and Ray and Singer's formula [Reference Ray and SingerRS73, Theorem 4.1] for
$g=0$, by Kronecker's limit formula and Ray and Singer's formula [Reference Ray and SingerRS73, Theorem 4.1] for ![]() $g=1$, and by Wentworth's formula [Reference WentworthWen12, (1.1) and Corollary 1.1] for
$g=1$, and by Wentworth's formula [Reference WentworthWen12, (1.1) and Corollary 1.1] for ![]() $g\geq 2$. In other words,
$g\geq 2$. In other words,
for all ![]() $(C,\alpha )\in {\frak M}_{g}(2)\setminus {\rm div}(\theta _{a,b})$ and even pairs
$(C,\alpha )\in {\frak M}_{g}(2)\setminus {\rm div}(\theta _{a,b})$ and even pairs ![]() $(a,b)$. Notice that the Laplacians (respectively, volume) in [Reference WentworthWen12] differ (respectively, differs) from ours by the scaling factor
$(a,b)$. Notice that the Laplacians (respectively, volume) in [Reference WentworthWen12] differ (respectively, differs) from ours by the scaling factor ![]() $2$ (respectively,
$2$ (respectively, ![]() $2\pi$). Hence Wentworth's formula [Reference WentworthWen12, (1.1) and Corollary 1.1] reads
$2\pi$). Hence Wentworth's formula [Reference WentworthWen12, (1.1) and Corollary 1.1] reads
 \begin{align} &\textrm{Area}(C,\omega)2^{-\zeta_{{\mathcal{O}}_{C}}(0)}\tau(C,\omega)2^{-\zeta_{\Sigma}(0)}\tau(C,\kappa\otimes\chi_{a,b};\omega)^{2}\nonumber\\ &\quad = (4\pi e^{6(2\zeta_\textbf{Q}'(-1)+\zeta_\textbf{Q}(-1))})^{1-g} \|\theta_{a,b}(\Omega(C))\|^{-4}, \end{align}
\begin{align} &\textrm{Area}(C,\omega)2^{-\zeta_{{\mathcal{O}}_{C}}(0)}\tau(C,\omega)2^{-\zeta_{\Sigma}(0)}\tau(C,\kappa\otimes\chi_{a,b};\omega)^{2}\nonumber\\ &\quad = (4\pi e^{6(2\zeta_\textbf{Q}'(-1)+\zeta_\textbf{Q}(-1))})^{1-g} \|\theta_{a,b}(\Omega(C))\|^{-4}, \end{align}
where ![]() $\zeta _{{\mathcal {O}}_{C}}(s)$ (respectively,
$\zeta _{{\mathcal {O}}_{C}}(s)$ (respectively, ![]() $\zeta _{\Sigma }(s)$) is the spectral zeta function of the Laplacian
$\zeta _{\Sigma }(s)$) is the spectral zeta function of the Laplacian ![]() $(\bar {\partial }+\bar {\partial }^{*})^{2}$ acting on the smooth sections of
$(\bar {\partial }+\bar {\partial }^{*})^{2}$ acting on the smooth sections of ![]() ${\mathcal {O}}_{C}$ (respectively,
${\mathcal {O}}_{C}$ (respectively, ![]() $\Sigma$) and
$\Sigma$) and ![]() ${\rm Area}(C,\omega ):=\int _{C}\omega$. Since
${\rm Area}(C,\omega ):=\int _{C}\omega$. Since
by [Reference FayFay92, p. 37, line 16] and since ![]() ${\rm Vol}(C,\omega )={\rm Area}(C,\omega )/2\pi$, we get the value
${\rm Vol}(C,\omega )={\rm Area}(C,\omega )/2\pi$, we get the value ![]() ${\frak c}_{g}$ in (10.1).
${\frak c}_{g}$ in (10.1).
Let us extend the definition of ![]() $\tilde {\tau }_{g}$ to disconnected curves as follows. A line bundle on a disconnected curve is a theta characteristic if it is a componentwise theta characteristic. Similarly, a theta characteristic on a disconnected curve is ineffective if it is componentwise ineffective. In what follows, for a disjoint union of smooth projective curves
$\tilde {\tau }_{g}$ to disconnected curves as follows. A line bundle on a disconnected curve is a theta characteristic if it is a componentwise theta characteristic. Similarly, a theta characteristic on a disconnected curve is ineffective if it is componentwise ineffective. In what follows, for a disjoint union of smooth projective curves ![]() $C=\amalg _{i\in I}C_{i}$ with
$C=\amalg _{i\in I}C_{i}$ with ![]() $g(C_{i}):=g_{i}$ and an ineffective theta characteristic
$g(C_{i}):=g_{i}$ and an ineffective theta characteristic ![]() $\Sigma =\{\Sigma _{i}\}_{i\in I}$ on
$\Sigma =\{\Sigma _{i}\}_{i\in I}$ on ![]() $C$, we define
$C$, we define
where ![]() $g:=\sum _{i\in I}g_{i}$ is the total genus of
$g:=\sum _{i\in I}g_{i}$ is the total genus of ![]() $C$.
$C$.
10.2 A factorization of  $\tau _{M}$
$\tau _{M}$
We introduce the following twisted version of ![]() $\tau _{M}$.
$\tau _{M}$.
Definition 10.1 Let ![]() $(X,\iota )$ be a
$(X,\iota )$ be a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface of type
$K3$ surface of type ![]() $M$ and let
$M$ and let ![]() $\gamma$ be an
$\gamma$ be an ![]() $\iota$-invariant Kähler form on
$\iota$-invariant Kähler form on ![]() $X$. If
$X$. If ![]() $M\not \cong {\Bbb U}(2)\oplus {\Bbb E}_{8}(2)$, define
$M\not \cong {\Bbb U}(2)\oplus {\Bbb E}_{8}(2)$, define
 \begin{align*} \tau_{M}^{{\rm spin}}(X,\iota) &:= \prod_{\Sigma^{2}=K_{X^{\iota}}, h^{0}(\Sigma)=0} \biggl\{ {\rm Vol}(X,\gamma)^{({14-r})/{4}} \tau_{\textbf{Z}_{2}}(X,\gamma)(\iota)\, \tau(X^{\iota},\Sigma;\gamma|_{X^{\iota}})^{-2} \\ &\quad \times \exp\biggl[ \frac{1}{8}\int_{X^{\iota}} \log\left.\left(\frac{\eta\wedge\bar{\eta}} {\gamma^{2}/2!}\cdot\frac{{\rm Vol}(X,\gamma)}{\|\eta\|_{L^{2}}^{2}} \right)\right|_{X^{\iota}} c_{1}(X^{\iota},\gamma|_{X^{\iota}}) \biggr] \biggr\}, \end{align*}
\begin{align*} \tau_{M}^{{\rm spin}}(X,\iota) &:= \prod_{\Sigma^{2}=K_{X^{\iota}}, h^{0}(\Sigma)=0} \biggl\{ {\rm Vol}(X,\gamma)^{({14-r})/{4}} \tau_{\textbf{Z}_{2}}(X,\gamma)(\iota)\, \tau(X^{\iota},\Sigma;\gamma|_{X^{\iota}})^{-2} \\ &\quad \times \exp\biggl[ \frac{1}{8}\int_{X^{\iota}} \log\left.\left(\frac{\eta\wedge\bar{\eta}} {\gamma^{2}/2!}\cdot\frac{{\rm Vol}(X,\gamma)}{\|\eta\|_{L^{2}}^{2}} \right)\right|_{X^{\iota}} c_{1}(X^{\iota},\gamma|_{X^{\iota}}) \biggr] \biggr\}, \end{align*}
where ![]() $\Sigma$ runs over all ineffective theta characteristics on
$\Sigma$ runs over all ineffective theta characteristics on ![]() $X^{\iota }$. If
$X^{\iota }$. If ![]() $M\cong {\Bbb U}(2)\oplus {\Bbb E}_{8}(2)$ and hence
$M\cong {\Bbb U}(2)\oplus {\Bbb E}_{8}(2)$ and hence ![]() $X^{\iota }=\emptyset$, define
$X^{\iota }=\emptyset$, define
Recall that the vector-valued modular form ![]() $f_{\Lambda }$ of type
$f_{\Lambda }$ of type ![]() $\rho _{\Lambda }$ was defined by (9.5) and (9.19) when
$\rho _{\Lambda }$ was defined by (9.5) and (9.19) when ![]() $r=22-r(\Lambda )=2$. We extend its definition to the case
$r=22-r(\Lambda )=2$. We extend its definition to the case ![]() $r\not =2$ by setting
$r\not =2$ by setting
Then Theorem 0.1 is interpreted as the modularity of ![]() $\tau _{M}^{{\rm spin}}$ as follows.
$\tau _{M}^{{\rm spin}}$ as follows.
Theorem 10.2 There exists a constant ![]() $C'_{M}>0$ depending only on
$C'_{M}>0$ depending only on ![]() $M$ such that the following equality of functions on
$M$ such that the following equality of functions on ![]() ${\mathcal {M}}_{\Lambda }^{0}\setminus {\mathcal {H}}_{\Lambda }$ holds:
${\mathcal {M}}_{\Lambda }^{0}\setminus {\mathcal {H}}_{\Lambda }$ holds:
Proof. For a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface
$K3$ surface ![]() $(X,\iota )$ of type
$(X,\iota )$ of type ![]() $M$ with
$M$ with ![]() $(r,l,\delta )\not =(10,10,0),(10,8,0)$, recall that
$(r,l,\delta )\not =(10,10,0),(10,8,0)$, recall that ![]() $X^{\iota }$ consists of a curve of genus
$X^{\iota }$ consists of a curve of genus ![]() $g=g(M)$ and
$g=g(M)$ and ![]() $k=k(M)$ smooth rational curves (cf. § 3.2).
$k=k(M)$ smooth rational curves (cf. § 3.2).
Case 1. If ![]() $(r,\delta )\not =(2,0),(10,0)$ and
$(r,\delta )\not =(2,0),(10,0)$ and ![]() $X^{\iota }$ has no effective even theta characteristics, we get
$X^{\iota }$ has no effective even theta characteristics, we get
 \begin{align} \tau_{M}^{{\rm spin}}(X,\iota) &= \frac {\tau_{M}(X,\iota)^{2^{g-1}(2^{g}+1)}} {\prod_{\Sigma^{2}=K_{X^{\iota}}, h^{0}(\Sigma)=0}\tilde{\tau}_{g}(X^{\iota},\Sigma)} = \frac {\tau_{M}(X,\iota)^{2^{g-1}(2^{g}+1)}} {\prod_{(a,b)\,{\rm even}}{\frak c}_{g}{\frak c}_{0}^{k}\|\theta_{a,b}(\Omega(X^{\iota}))\|^{-4}}\nonumber\\ &= c_{M} \tau_{M}(X,\iota)^{2^{g-1}(2^{g}+1)}\|\chi_{g}(\Omega(X^{\iota}))^{8}\|^{1/2}, \end{align}
\begin{align} \tau_{M}^{{\rm spin}}(X,\iota) &= \frac {\tau_{M}(X,\iota)^{2^{g-1}(2^{g}+1)}} {\prod_{\Sigma^{2}=K_{X^{\iota}}, h^{0}(\Sigma)=0}\tilde{\tau}_{g}(X^{\iota},\Sigma)} = \frac {\tau_{M}(X,\iota)^{2^{g-1}(2^{g}+1)}} {\prod_{(a,b)\,{\rm even}}{\frak c}_{g}{\frak c}_{0}^{k}\|\theta_{a,b}(\Omega(X^{\iota}))\|^{-4}}\nonumber\\ &= c_{M} \tau_{M}(X,\iota)^{2^{g-1}(2^{g}+1)}\|\chi_{g}(\Omega(X^{\iota}))^{8}\|^{1/2}, \end{align}with
Here the first equality of (10.5) follows from Definition 10.1 and the second follows from (10.2). Comparing Theorem 0.1 and (10.5), we get (10.4) with ![]() $(C'_{M})^{2}:=c_{M}^{2}/C_{M}$ in this case.
$(C'_{M})^{2}:=c_{M}^{2}/C_{M}$ in this case.
Case 2. If ![]() $(r,\delta )=(2,0),(10,0)$ with
$(r,\delta )=(2,0),(10,0)$ with ![]() $(r,l,\delta )\not =(10,10,0),(10,8,0)$ and if
$(r,l,\delta )\not =(10,10,0),(10,8,0)$ and if ![]() $X^{\iota }$ has a unique effective even theta characteristic corresponding to a theta constant
$X^{\iota }$ has a unique effective even theta characteristic corresponding to a theta constant ![]() $\theta _{a_{0},b_{0}}(\Omega (X^{\iota }))$ with respect to a suitable level
$\theta _{a_{0},b_{0}}(\Omega (X^{\iota }))$ with respect to a suitable level ![]() $2$ structure, we get in the same way
$2$ structure, we get in the same way
 \begin{align} \tau_{M}^{{\rm spin}}(X,\iota) &= \frac {\tau_{M}(X,\iota)^{(2^{g}-1)(2^{g-1}+1)}} {\prod_{\Sigma^{2}=K_{X^{\iota}}, h^{0}(\Sigma)=0}\tilde{\tau}(X^{\iota},\Sigma)} = \frac {\tau_{M}(X,\iota)^{(2^{g}-1)(2^{g-1}+1)}} {\prod_{(a,b)\not=(a_{0},b_{0}),{\rm even}}{\frak c}_{0}^{k}{\frak c}_{g}\|\theta_{a,b}(\Omega(X^{\iota}))\|^{-4}}\nonumber\\ &= c_{M} \tau_{M}(X,\iota)^{(2^{g}-1)(2^{g-1}+1)} \|\Upsilon_{g}(\Omega(X^{\iota}))\|^{1/2}, \end{align}
\begin{align} \tau_{M}^{{\rm spin}}(X,\iota) &= \frac {\tau_{M}(X,\iota)^{(2^{g}-1)(2^{g-1}+1)}} {\prod_{\Sigma^{2}=K_{X^{\iota}}, h^{0}(\Sigma)=0}\tilde{\tau}(X^{\iota},\Sigma)} = \frac {\tau_{M}(X,\iota)^{(2^{g}-1)(2^{g-1}+1)}} {\prod_{(a,b)\not=(a_{0},b_{0}),{\rm even}}{\frak c}_{0}^{k}{\frak c}_{g}\|\theta_{a,b}(\Omega(X^{\iota}))\|^{-4}}\nonumber\\ &= c_{M} \tau_{M}(X,\iota)^{(2^{g}-1)(2^{g-1}+1)} \|\Upsilon_{g}(\Omega(X^{\iota}))\|^{1/2}, \end{align}with
By Theorem 0.1 and (10.6), we get (10.4) with ![]() $(C'_{M})^{2}:=c_{M}^{2}/C_{M}$ in this case.
$(C'_{M})^{2}:=c_{M}^{2}/C_{M}$ in this case.
Case 3. If ![]() $(r,l,\delta )=(10,10,0)$, then
$(r,l,\delta )=(10,10,0)$, then ![]() $X^{\iota }=\emptyset$. Since we defined
$X^{\iota }=\emptyset$. Since we defined ![]() $g=1$ in this case, we get (10.4) with
$g=1$ in this case, we get (10.4) with ![]() $(C'_{M})^{2}:=C_{M}^{-1}$ by Definition 10.1 and Theorem 0.1. If
$(C'_{M})^{2}:=C_{M}^{-1}$ by Definition 10.1 and Theorem 0.1. If ![]() $(r,l,\delta )=(10,8,0)$, then
$(r,l,\delta )=(10,8,0)$, then ![]() $X^{\iota }$ consists of two disjoint elliptic curves. In the same way as in (10.6), we get (10.4) with
$X^{\iota }$ consists of two disjoint elliptic curves. In the same way as in (10.6), we get (10.4) with ![]() $(C'_{M})^{2}:=c_{M}^{2}/C_{M}$,
$(C'_{M})^{2}:=c_{M}^{2}/C_{M}$, ![]() $c_{M}=({\frak c}_{1}^{-2})^{9}=(4\pi )^{-18}$ in this case. This completes the proof.
$c_{M}=({\frak c}_{1}^{-2})^{9}=(4\pi )^{-18}$ in this case. This completes the proof.
Remark 10.3 Assume ![]() ${\mathcal {H}}_{\Lambda }\not =\emptyset$. As the period of a
${\mathcal {H}}_{\Lambda }\not =\emptyset$. As the period of a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface of type
$K3$ surface of type ![]() $M$ approaches a point of
$M$ approaches a point of ![]() ${\mathcal {H}}_{\Lambda }$, one of the ineffective even theta characteristics on its fixed curve becomes effective in the limit and the value
${\mathcal {H}}_{\Lambda }$, one of the ineffective even theta characteristics on its fixed curve becomes effective in the limit and the value ![]() $\tau _{M}^{{\rm spin}}$ jumps there. Because of this jumping,
$\tau _{M}^{{\rm spin}}$ jumps there. Because of this jumping, ![]() $\tau _{M}^{{\rm spin}}$ is a discontinuous function on
$\tau _{M}^{{\rm spin}}$ is a discontinuous function on ![]() ${\mathcal {M}}_{\Lambda }^{0}$. Since
${\mathcal {M}}_{\Lambda }^{0}$. Since ![]() $\|\Psi _{\Lambda }(\cdot ,2^{g-1}F_{\Lambda }+f_{\Lambda })\|$ is also discontinuous along
$\|\Psi _{\Lambda }(\cdot ,2^{g-1}F_{\Lambda }+f_{\Lambda })\|$ is also discontinuous along ![]() ${\mathcal {H}}_{\Lambda }$ by [Reference SchoferSch09, Theorem 1.1 (i)], it is an interesting problem to compare
${\mathcal {H}}_{\Lambda }$ by [Reference SchoferSch09, Theorem 1.1 (i)], it is an interesting problem to compare ![]() $\tau _{M}^{{\rm spin}}$ and
$\tau _{M}^{{\rm spin}}$ and ![]() $\|\Psi _{\Lambda }(\cdot ,2^{g-1}F_{\Lambda }+f_{\Lambda })\|$ on the locus
$\|\Psi _{\Lambda }(\cdot ,2^{g-1}F_{\Lambda }+f_{\Lambda })\|$ on the locus ![]() ${\mathcal {H}}_{\Lambda }$.
${\mathcal {H}}_{\Lambda }$.
Remark 10.4 As suggested by a referee, it is possible to express the invariants ![]() $\tau _{M}(X,\iota )$ and
$\tau _{M}(X,\iota )$ and ![]() $\tau _{M}^{{\rm spin}}(X,\iota )$ in terms of X. Ma's orbifold analytic torsions [Reference MaMa05] for
$\tau _{M}^{{\rm spin}}(X,\iota )$ in terms of X. Ma's orbifold analytic torsions [Reference MaMa05] for ![]() $X/\iota$ and the twisted sector
$X/\iota$ and the twisted sector ![]() $\Sigma (X/\iota )=X^{\iota }$. Here
$\Sigma (X/\iota )=X^{\iota }$. Here ![]() $X/\iota$ is a smooth surface with non-trivial orbifold structure. In this direction, it is possible to construct a holomorphic torsion invariant for log-Enriques surfaces by making use of orbifold analytic torsion and give its explicit formula as an automorphic function on the moduli space (in a forthcoming paper by Dai and Yoshikawa).
$X/\iota$ is a smooth surface with non-trivial orbifold structure. In this direction, it is possible to construct a holomorphic torsion invariant for log-Enriques surfaces by making use of orbifold analytic torsion and give its explicit formula as an automorphic function on the moduli space (in a forthcoming paper by Dai and Yoshikawa).
10.3 A uniqueness of elliptic modular form corresponding to  $\tau _{M}^{{\rm spin}}$
$\tau _{M}^{{\rm spin}}$
Set
Since ![]() $\tau _{M}^{{\rm spin}}=C'_{M}\|\Phi _{M}^{{\rm spin}}\|^{-1/2}$,
$\tau _{M}^{{\rm spin}}=C'_{M}\|\Phi _{M}^{{\rm spin}}\|^{-1/2}$, ![]() $\Phi _{M}^{{\rm spin}}$ can be identified with
$\Phi _{M}^{{\rm spin}}$ can be identified with ![]() $\tau _{M}^{{\rm spin}}$. In this subsection we study the uniqueness of elliptic modular form whose Borcherds lift is
$\tau _{M}^{{\rm spin}}$. In this subsection we study the uniqueness of elliptic modular form whose Borcherds lift is ![]() $\Phi _{M}^{{\rm spin}}$.
$\Phi _{M}^{{\rm spin}}$.
For a modular form ![]() $\varphi (\tau )$ of type
$\varphi (\tau )$ of type ![]() $\rho _{\Lambda }$ with weight
$\rho _{\Lambda }$ with weight ![]() $1-b^{-}(\Lambda )/2$, we write
$1-b^{-}(\Lambda )/2$, we write
for its Fourier expansion. The principal part of ![]() $\varphi$ is the Laurent polynomial defined as
$\varphi$ is the Laurent polynomial defined as
Notice that we used the notation ![]() ${\mathcal {P}}_{\leq 0}[\varphi ]=\sum _{\gamma \in A_{\Lambda }}\textbf {e}_{\gamma }\sum _{n\in \gamma ^{2}/2+\textbf {Z}, n\leq 0}c_{\gamma }(n;\varphi )q^{n}$ in the previous sections. Obviously,
${\mathcal {P}}_{\leq 0}[\varphi ]=\sum _{\gamma \in A_{\Lambda }}\textbf {e}_{\gamma }\sum _{n\in \gamma ^{2}/2+\textbf {Z}, n\leq 0}c_{\gamma }(n;\varphi )q^{n}$ in the previous sections. Obviously, ![]() ${\mathcal {P}}_{\leq 0}[\varphi ]-{\mathcal {P}}[\varphi ]\in \textbf {C}[A_{\Lambda }]$ is the constant term of
${\mathcal {P}}_{\leq 0}[\varphi ]-{\mathcal {P}}[\varphi ]\in \textbf {C}[A_{\Lambda }]$ is the constant term of ![]() $\varphi$.
$\varphi$.
Similarly, for a Heegner divisor ![]() $H=\sum _{\gamma \in A_{\Lambda }}\sum _{n\in \gamma ^{2}/2+\textbf {Z}, n<0}a_{\gamma }(n)\,H(n,\gamma )$ on
$H=\sum _{\gamma \in A_{\Lambda }}\sum _{n\in \gamma ^{2}/2+\textbf {Z}, n<0}a_{\gamma }(n)\,H(n,\gamma )$ on ![]() $\Omega _{\Lambda }$, where
$\Omega _{\Lambda }$, where ![]() $H(n,\gamma ):=\sum _{\lambda \in (\gamma +\Lambda )/\pm 1, \lambda ^{2}=2n}H_{\lambda }$,
$H(n,\gamma ):=\sum _{\lambda \in (\gamma +\Lambda )/\pm 1, \lambda ^{2}=2n}H_{\lambda }$, ![]() $n\in \textbf {Q}$,
$n\in \textbf {Q}$, ![]() $\gamma \in A_{\Lambda }$, we define
$\gamma \in A_{\Lambda }$, we define
Comparing (8.1), (9.5), (9.20) with Theorem 8.1, (9.18), (9.24), we have the equality
if ![]() $\Lambda \not \cong {\Bbb U}(2)^{\oplus 2},({\Bbb A}_{1}^{+})^{\oplus 2}$ or equivalently
$\Lambda \not \cong {\Bbb U}(2)^{\oplus 2},({\Bbb A}_{1}^{+})^{\oplus 2}$ or equivalently ![]() ${\mathcal {D}}_{\Lambda }\not =0$. When
${\mathcal {D}}_{\Lambda }\not =0$. When ![]() $\Lambda \cong {\Bbb U}(2)^{\oplus 2}$ or
$\Lambda \cong {\Bbb U}(2)^{\oplus 2}$ or ![]() $({\Bbb A}_{1}^{+})^{\oplus 2}$, we have
$({\Bbb A}_{1}^{+})^{\oplus 2}$, we have ![]() ${\mathcal {P}}[2^{g-1}F_{\Lambda }+f_{\Lambda }]\not =0$ but
${\mathcal {P}}[2^{g-1}F_{\Lambda }+f_{\Lambda }]\not =0$ but ![]() ${\frak P}[{\rm div}(\Phi _{M}^{{\rm spin}})]=0$. Thus (10.8) does not hold in these two cases. Except for them, the elliptic modular form
${\frak P}[{\rm div}(\Phi _{M}^{{\rm spin}})]=0$. Thus (10.8) does not hold in these two cases. Except for them, the elliptic modular form ![]() $2^{g-1}F_{\Lambda }+f_{\Lambda }$ is characterized uniquely by the holomorphic torsion invariant
$2^{g-1}F_{\Lambda }+f_{\Lambda }$ is characterized uniquely by the holomorphic torsion invariant ![]() $\tau _{M}^{{\rm spin}}$ as follows.
$\tau _{M}^{{\rm spin}}$ as follows.
Theorem 10.5 If ![]() $\Lambda \not \cong {\Bbb U}(2)^{\oplus 2},({\Bbb A}_{1}^{+})^{\oplus 2}$, then there exists a unique
$\Lambda \not \cong {\Bbb U}(2)^{\oplus 2},({\Bbb A}_{1}^{+})^{\oplus 2}$, then there exists a unique ![]() $O(q_{\Lambda })$-invariant elliptic modular form
$O(q_{\Lambda })$-invariant elliptic modular form ![]() $\varphi _{\Lambda }$ of type
$\varphi _{\Lambda }$ of type ![]() $\rho _{\Lambda }$ with weight
$\rho _{\Lambda }$ with weight ![]() $1-b^{-}(\Lambda )/2$ such that
$1-b^{-}(\Lambda )/2$ such that
In particular, the ![]() $O(q_{\Lambda })$-invariance and (10.9) characterize
$O(q_{\Lambda })$-invariance and (10.9) characterize ![]() $2^{g-1}F_{\Lambda }+f_{\Lambda }$ uniquely.
$2^{g-1}F_{\Lambda }+f_{\Lambda }$ uniquely.
Proof. Let ![]() $\varphi _{\Lambda }$ be an
$\varphi _{\Lambda }$ be an ![]() $O(q_{\Lambda })$-invariant modular form satisfying (10.9). Set
$O(q_{\Lambda })$-invariant modular form satisfying (10.9). Set ![]() $\psi :=\varphi _{\Lambda }-(2^{g-1}F_{\Lambda }+f_{\Lambda })$. This is a modular form of type
$\psi :=\varphi _{\Lambda }-(2^{g-1}F_{\Lambda }+f_{\Lambda })$. This is a modular form of type ![]() $\rho _{\Lambda }$ and weight
$\rho _{\Lambda }$ and weight ![]() $1-b^{-}(\Lambda )/2$ which is holomorphic at the cusp, is
$1-b^{-}(\Lambda )/2$ which is holomorphic at the cusp, is ![]() $O(q_{\Lambda })$-invariant, and satisfies
$O(q_{\Lambda })$-invariant, and satisfies ![]() $c_{0}(0; \psi )=0$. We must prove
$c_{0}(0; \psi )=0$. We must prove ![]() $\psi =0$. When
$\psi =0$. When ![]() $b^{-}(\Lambda )>2$,
$b^{-}(\Lambda )>2$, ![]() $\psi$ has negative weight and hence
$\psi$ has negative weight and hence ![]() $\psi =0$.
$\psi =0$.
Let ![]() $b^{-}(\Lambda )=2$. Then
$b^{-}(\Lambda )=2$. Then ![]() $\psi$ has weight
$\psi$ has weight ![]() $0$, so it must be a constant vector of
$0$, so it must be a constant vector of ![]() $\textbf {C}[A_{\Lambda }]$. From [Reference NikulinNik80, Lemma 3.9.1] and [Reference SkoruppaSko08, Theorem 1], we deduce that
$\textbf {C}[A_{\Lambda }]$. From [Reference NikulinNik80, Lemma 3.9.1] and [Reference SkoruppaSko08, Theorem 1], we deduce that ![]() ${\rm Mp}_{2}(\textbf {Z})\times O(q_{\Lambda })$-invariant vectors in
${\rm Mp}_{2}(\textbf {Z})\times O(q_{\Lambda })$-invariant vectors in ![]() ${\mathbf {C}}[A_{\Lambda }]$ are scalar multiples of
${\mathbf {C}}[A_{\Lambda }]$ are scalar multiples of ![]() $\nu _{\Lambda }\textbf {e}_{0}+\textbf {v}_{\Lambda }+\nu _{\Lambda }\delta (\Lambda )\textbf {e}_{\textbf {1}_{\Lambda }}$ for some
$\nu _{\Lambda }\textbf {e}_{0}+\textbf {v}_{\Lambda }+\nu _{\Lambda }\delta (\Lambda )\textbf {e}_{\textbf {1}_{\Lambda }}$ for some ![]() $\nu _{\Lambda }\in \textbf {Z}_{>0}$, where
$\nu _{\Lambda }\in \textbf {Z}_{>0}$, where ![]() ${\mathbf {v}}_{\Lambda } =\sum _{\gamma \ne 0,\textbf {1}_{\Lambda },\gamma ^{2}\equiv 0}\textbf {e}_{\gamma }$. Since
${\mathbf {v}}_{\Lambda } =\sum _{\gamma \ne 0,\textbf {1}_{\Lambda },\gamma ^{2}\equiv 0}\textbf {e}_{\gamma }$. Since ![]() $c_{0}(0; \psi )=0$, we have
$c_{0}(0; \psi )=0$, we have ![]() $\psi =0$.
$\psi =0$.
Let ![]() $b^{-}(\Lambda )=1$. By [Reference SkoruppaSko08, Theorems 5 and 9] there is a canonical isomorphism between the space of modular forms of type
$b^{-}(\Lambda )=1$. By [Reference SkoruppaSko08, Theorems 5 and 9] there is a canonical isomorphism between the space of modular forms of type ![]() $\rho _{\Lambda }$ and weight
$\rho _{\Lambda }$ and weight ![]() $1/2$ with the space of
$1/2$ with the space of ![]() ${\rm Mp}_{2}({\mathbf {Z}})$-invariant vectors in
${\rm Mp}_{2}({\mathbf {Z}})$-invariant vectors in ![]() ${\mathbf {C}}[A_{{\Bbb A}_{1}}]\otimes {\mathbf {C}}[A_{\Lambda }] \simeq {\mathbf {C}}[A_{{\Bbb A}_{1}\oplus \Lambda }]$. By [Reference SkoruppaSko08, Theorem 1], the latter is generated by the vectors
${\mathbf {C}}[A_{{\Bbb A}_{1}}]\otimes {\mathbf {C}}[A_{\Lambda }] \simeq {\mathbf {C}}[A_{{\Bbb A}_{1}\oplus \Lambda }]$. By [Reference SkoruppaSko08, Theorem 1], the latter is generated by the vectors ![]() $I_{U}=\sum _{\gamma \in U}\textbf {e}_{\gamma }$ where
$I_{U}=\sum _{\gamma \in U}\textbf {e}_{\gamma }$ where ![]() $U$ runs over self-dual isotropic subgroups of
$U$ runs over self-dual isotropic subgroups of ![]() $A_{{\Bbb A}_{1}\oplus \Lambda }$. In this isomorphism the modular form corresponding to
$A_{{\Bbb A}_{1}\oplus \Lambda }$. In this isomorphism the modular form corresponding to ![]() $I_{U}$ is given by
$I_{U}$ is given by ![]() $\sum _{\gamma \in U}\theta _{{\Bbb A}_{1}^{+}+\gamma _{1}}\textbf {e}_{\gamma _{2}}$ where
$\sum _{\gamma \in U}\theta _{{\Bbb A}_{1}^{+}+\gamma _{1}}\textbf {e}_{\gamma _{2}}$ where ![]() $\gamma =(\gamma _{1}, \gamma _{2})\in A_{{\Bbb A}_{1}\oplus \Lambda }$ (see [Reference SkoruppaSko08, Theorem 8]). Now we have
$\gamma =(\gamma _{1}, \gamma _{2})\in A_{{\Bbb A}_{1}\oplus \Lambda }$ (see [Reference SkoruppaSko08, Theorem 8]). Now we have ![]() $\Lambda \cong {\Bbb A}_{1}^{+}\oplus {\Bbb U}$ or
$\Lambda \cong {\Bbb A}_{1}^{+}\oplus {\Bbb U}$ or ![]() $({\Bbb A}_{1}^{+})^{\oplus 2}\oplus {\Bbb A}_{1}$. In the first case,
$({\Bbb A}_{1}^{+})^{\oplus 2}\oplus {\Bbb A}_{1}$. In the first case, ![]() $A_{{\Bbb A}_{1}\oplus \Lambda }$ contains a unique non-zero isotropic element, and the corresponding modular form
$A_{{\Bbb A}_{1}\oplus \Lambda }$ contains a unique non-zero isotropic element, and the corresponding modular form ![]() $\varphi$ has
$\varphi$ has ![]() $c_{0}(0; \varphi )\ne 0$. In the second case,
$c_{0}(0; \varphi )\ne 0$. In the second case, ![]() $A_{{\Bbb A}_{1}\oplus \Lambda }$ contains exactly two isotropic subgroups of rank
$A_{{\Bbb A}_{1}\oplus \Lambda }$ contains exactly two isotropic subgroups of rank ![]() $2$, which can be switched by an element of
$2$, which can be switched by an element of ![]() $O(q_{\Lambda })$. If
$O(q_{\Lambda })$. If ![]() $\varphi _{1}$ and
$\varphi _{1}$ and ![]() $\varphi _{2}$ are the corresponding modular forms, then
$\varphi _{2}$ are the corresponding modular forms, then ![]() $\psi$ must be a scalar multiple of
$\psi$ must be a scalar multiple of ![]() $\varphi _{1}+\varphi _{2}$. Again we have
$\varphi _{1}+\varphi _{2}$. Again we have ![]() $c_{0}(0; \varphi _{1}+\varphi _{2})\ne 0$, so
$c_{0}(0; \varphi _{1}+\varphi _{2})\ne 0$, so ![]() $\psi =0$.
$\psi =0$.
11. An equivariant analogue of Borcherds’ conjecture
In this section we study an equivariant analogue of Borcherds’ conjecture [Reference BorcherdsBor98]. Let us briefly explain this conjecture. Let ![]() $X_{K3}$ be the oriented
$X_{K3}$ be the oriented ![]() $4$-manifold underlying a
$4$-manifold underlying a ![]() $K3$ surface. Let
$K3$ surface. Let ![]() ${\mathcal {E}}$ be the set of Ricci-flat Riemannian metrics on
${\mathcal {E}}$ be the set of Ricci-flat Riemannian metrics on ![]() $X_{K3}$ with normalized volume
$X_{K3}$ with normalized volume ![]() $1$ (cf. [Reference YauYau78]). For
$1$ (cf. [Reference YauYau78]). For ![]() $\gamma \in {\mathcal {E}}$, let
$\gamma \in {\mathcal {E}}$, let ![]() $\Delta _{\gamma }$ be the Laplacian of
$\Delta _{\gamma }$ be the Laplacian of ![]() $(X_{K3},\gamma )$ acting on
$(X_{K3},\gamma )$ acting on ![]() $C^{\infty }(X_{K3})$. Let
$C^{\infty }(X_{K3})$. Let ![]() $\det \Delta _{\gamma }$ be the regularized determinant of
$\det \Delta _{\gamma }$ be the regularized determinant of ![]() $\Delta _{\gamma }$. Then the assignment
$\Delta _{\gamma }$. Then the assignment ![]() $\det \Delta \colon {\mathcal {E}}\ni \gamma \to \det \Delta _{\gamma }\in {\mathbf {R}}$ is a function on
$\det \Delta \colon {\mathcal {E}}\ni \gamma \to \det \Delta _{\gamma }\in {\mathbf {R}}$ is a function on ![]() ${\mathcal {E}}$. In [Reference BorcherdsBor98, Example 15.2], Borcherds conjectured that
${\mathcal {E}}$. In [Reference BorcherdsBor98, Example 15.2], Borcherds conjectured that ![]() $\det \Delta$ is given by the automorphic form
$\det \Delta$ is given by the automorphic form ![]() $\Phi _{{\Bbb L}_{K3}}(\cdot ,1,E_{4}/\eta ^{24})$ on
$\Phi _{{\Bbb L}_{K3}}(\cdot ,1,E_{4}/\eta ^{24})$ on ![]() $G({\Bbb L}_{K3})$, the period space of
$G({\Bbb L}_{K3})$, the period space of ![]() ${\mathcal {E}}$, where
${\mathcal {E}}$, where ![]() $E_{4}(\tau )$ is the Eisenstein series of weight
$E_{4}(\tau )$ is the Eisenstein series of weight ![]() $4$. To our knowledge, this conjecture is still open. Here, instead of the original Borcherds conjecture, we study its equivariant analogue.
$4$. To our knowledge, this conjecture is still open. Here, instead of the original Borcherds conjecture, we study its equivariant analogue.
Let ![]() $\iota \colon X_{K3}\to X_{K3}$ be a
$\iota \colon X_{K3}\to X_{K3}$ be a ![]() $C^{\infty }$ involution. We define the lattices
$C^{\infty }$ involution. We define the lattices ![]() $H^{2}(X_{K3},{\mathbf {Z}})_{\pm }$ as in the preceding sections. Then
$H^{2}(X_{K3},{\mathbf {Z}})_{\pm }$ as in the preceding sections. Then ![]() $\iota$ is called hyperbolic if
$\iota$ is called hyperbolic if ![]() $H^{2}(X_{K3},{\mathbf {Z}})_{+}$ is Lorentzian. Let
$H^{2}(X_{K3},{\mathbf {Z}})_{+}$ is Lorentzian. Let ![]() ${\mathcal {E}}^{\iota }$ be the set of
${\mathcal {E}}^{\iota }$ be the set of ![]() $\iota$-invariant Ricci-flat Riemannian metrics on
$\iota$-invariant Ricci-flat Riemannian metrics on ![]() $X_{K3}$ with volume
$X_{K3}$ with volume ![]() $1$. Since we are interested in an equivariant analogue of Borcherds’ conjecture, throughout this section, we restrict our consideration to those involutions
$1$. Since we are interested in an equivariant analogue of Borcherds’ conjecture, throughout this section, we restrict our consideration to those involutions ![]() $\iota$ satisfying
$\iota$ satisfying
By [Reference YoshikawaYos08, Propisitions 3.4, 3.6], if ![]() $\iota$ is hyperbolic, then (11.1) is equivalent to the existence of a complex structure
$\iota$ is hyperbolic, then (11.1) is equivalent to the existence of a complex structure ![]() $I$ on
$I$ on ![]() $X_{K3}$ such that
$X_{K3}$ such that ![]() $\iota$ is an anti-symplectic holomorphic involution on
$\iota$ is an anti-symplectic holomorphic involution on ![]() $(X_{K3},I)$. In particular, if
$(X_{K3},I)$. In particular, if ![]() $\iota$ is hyperbolic with (11.1), then
$\iota$ is hyperbolic with (11.1), then ![]() $X_{K3}^{\iota }$ is a disjoint union of (possibly empty) smooth compact real surfaces.
$X_{K3}^{\iota }$ is a disjoint union of (possibly empty) smooth compact real surfaces.
Let ![]() $\iota$ be a hyperbolic involution on
$\iota$ be a hyperbolic involution on ![]() $X_{K3}$ with (11.1). Its type is defined as the isometry class of
$X_{K3}$ with (11.1). Its type is defined as the isometry class of ![]() $H^{2}(X_{K3},{\mathbf {Z}})_{+}$. Let
$H^{2}(X_{K3},{\mathbf {Z}})_{+}$. Let ![]() $M$ be the type of
$M$ be the type of ![]() $\iota$ and set
$\iota$ and set ![]() $\Lambda :=M^{\perp _{{\Bbb L}_{K3}}}$. Then
$\Lambda :=M^{\perp _{{\Bbb L}_{K3}}}$. Then ![]() $M$ and
$M$ and ![]() $\Lambda$ are primitive
$\Lambda$ are primitive ![]() $2$-elementary sublattices of
$2$-elementary sublattices of ![]() ${\Bbb L}_{K3}$. To formulate an equivariant analogue of Borcherds’ conjecture, we construct two functions on
${\Bbb L}_{K3}$. To formulate an equivariant analogue of Borcherds’ conjecture, we construct two functions on ![]() ${\mathcal {E}}^{\iota }$.
${\mathcal {E}}^{\iota }$.
Let ![]() $\gamma \in {\mathcal {E}}^{\iota }$. Let
$\gamma \in {\mathcal {E}}^{\iota }$. Let ![]() $C^{\infty }(X_{K3})_{\pm }$ be the
$C^{\infty }(X_{K3})_{\pm }$ be the ![]() $\pm 1$-eigenspace of the
$\pm 1$-eigenspace of the ![]() $\iota$-action on
$\iota$-action on ![]() $C^{\infty }(X_{K3})$. Since
$C^{\infty }(X_{K3})$. Since ![]() $\Delta _{\gamma }$ preserves
$\Delta _{\gamma }$ preserves ![]() $C^{\infty }(X_{K3})_{\pm }$, we can define
$C^{\infty }(X_{K3})_{\pm }$, we can define ![]() $\Delta _{\gamma ,\pm }:=\Delta _{\gamma }|_{C^{\infty }(X_{K3})_{\pm }}$. Let
$\Delta _{\gamma ,\pm }:=\Delta _{\gamma }|_{C^{\infty }(X_{K3})_{\pm }}$. Let ![]() $\zeta _{\pm }(s)$ be the spectral zeta function of
$\zeta _{\pm }(s)$ be the spectral zeta function of ![]() $\Delta _{\gamma ,\pm }$. The equivariant determinant of
$\Delta _{\gamma ,\pm }$. The equivariant determinant of ![]() $\Delta _{\gamma }$ is defined as (cf. [Reference BismutBis95])
$\Delta _{\gamma }$ is defined as (cf. [Reference BismutBis95])
Assume ![]() $X_{K3}^{\iota }\not =\emptyset$. Let
$X_{K3}^{\iota }\not =\emptyset$. Let ![]() $S_{\gamma }$ be a spinor bundle on the fixed point set
$S_{\gamma }$ be a spinor bundle on the fixed point set ![]() $(X_{K3}^{\iota }, \gamma |_{X^{\iota }_{K3}})$. Let
$(X_{K3}^{\iota }, \gamma |_{X^{\iota }_{K3}})$. Let ![]() $D_{S_{\gamma }}$ be the Dirac operator acting on
$D_{S_{\gamma }}$ be the Dirac operator acting on ![]() $C^{\infty }(S_{\gamma })$. Let
$C^{\infty }(S_{\gamma })$. Let ![]() $\det D_{S_{\gamma }}^{2}$ be the regularized determinant of
$\det D_{S_{\gamma }}^{2}$ be the regularized determinant of ![]() $D_{S_{\gamma }}^{2}$. If
$D_{S_{\gamma }}^{2}$. If ![]() $\zeta _{D_{S_{\gamma }}^{2}}(s)$ denotes the spectral zeta function of
$\zeta _{D_{S_{\gamma }}^{2}}(s)$ denotes the spectral zeta function of ![]() $D_{S_{\gamma }}^{2}$, then
$D_{S_{\gamma }}^{2}$, then
When ![]() $X_{K3}^{\iota }=\emptyset$, we define
$X_{K3}^{\iota }=\emptyset$, we define ![]() $\det D_{S_{\gamma }}^{2}:=1$. As an equivariant analogue of the function
$\det D_{S_{\gamma }}^{2}:=1$. As an equivariant analogue of the function ![]() $\det \Delta$ on
$\det \Delta$ on ![]() ${\mathcal {E}}$, we consider the following function on
${\mathcal {E}}$, we consider the following function on ![]() ${\mathcal {E}}^{\iota }$.
${\mathcal {E}}^{\iota }$.
Definition 11.1 For ![]() $\gamma \in {\mathcal {E}}^{\iota }$, define
$\gamma \in {\mathcal {E}}^{\iota }$, define
where ![]() $S_{\gamma }$ runs over the spinor bundles on
$S_{\gamma }$ runs over the spinor bundles on ![]() $(X_{K3}^{\iota }, \gamma |_{X^{\iota }_{K3}})$ with
$(X_{K3}^{\iota }, \gamma |_{X^{\iota }_{K3}})$ with ![]() $\ker D_{S_{\gamma }}=0$.
$\ker D_{S_{\gamma }}=0$.
Let us construct an automorphic function on the period space of ![]() ${\mathcal {E}}^{\iota }$. By [Reference YoshikawaYos08, Proposition 3.6], for example, there exists a hyperkähler structure
${\mathcal {E}}^{\iota }$. By [Reference YoshikawaYos08, Proposition 3.6], for example, there exists a hyperkähler structure ![]() $(I,J,K)$ on
$(I,J,K)$ on ![]() $(X_{K3},\gamma )$ such that
$(X_{K3},\gamma )$ such that
By [Reference YoshikawaYos08, Lemma 3.17], the pair of conjugate points of ![]() ${\mathcal {M}}_{\Lambda }$ defined as
${\mathcal {M}}_{\Lambda }$ defined as
is independent of the choice of a triplet ![]() $(I,J,K)$ satisfying (11.2) and a marking, that is, an isometry
$(I,J,K)$ satisfying (11.2) and a marking, that is, an isometry ![]() $\alpha \colon H^{2}(X_{K3},{\mathbf {Z}})\to {\Bbb L}_{K3}$ satisfying
$\alpha \colon H^{2}(X_{K3},{\mathbf {Z}})\to {\Bbb L}_{K3}$ satisfying ![]() $\alpha (H^{2}(X,{\mathbf {Z}})_{+})=M$. The pair of conjugate points
$\alpha (H^{2}(X,{\mathbf {Z}})_{+})=M$. The pair of conjugate points ![]() $\pi _{\iota }(\gamma )\in {\mathcal {M}}_{\Lambda }$ is called the period of
$\pi _{\iota }(\gamma )\in {\mathcal {M}}_{\Lambda }$ is called the period of ![]() $\gamma \in {\mathcal {E}}^{\iota }$.
$\gamma \in {\mathcal {E}}^{\iota }$.
Lemma 11.2 ![]() $\pi _{\iota }^{*}\|\Psi _{\Lambda }(\cdot ,2^{g-1}F_{\Lambda }+f_{\Lambda })\|$ is a well-defined function on
$\pi _{\iota }^{*}\|\Psi _{\Lambda }(\cdot ,2^{g-1}F_{\Lambda }+f_{\Lambda })\|$ is a well-defined function on ![]() ${\mathcal {E}}^{\iota }$.
${\mathcal {E}}^{\iota }$.
Proof. Write ![]() $\Lambda ={\Bbb U}(-N)\oplus L$,
$\Lambda ={\Bbb U}(-N)\oplus L$, ![]() $N\in \{1,2\}$, where
$N\in \{1,2\}$, where ![]() $L$ is a Lorentzian lattice. Set
$L$ is a Lorentzian lattice. Set ![]() $C_{L}:=\{x\in L\otimes {\mathbf {R}};\,\langle x,x\rangle >0\}$. Since
$C_{L}:=\{x\in L\otimes {\mathbf {R}};\,\langle x,x\rangle >0\}$. Since ![]() $L$ is Lorentzian,
$L$ is Lorentzian, ![]() $C_{L}$ consists of two components
$C_{L}$ consists of two components ![]() $C_{L}^{\pm }$ with
$C_{L}^{\pm }$ with ![]() $C_{L}^{-}=-C_{L}^{+}$. Then
$C_{L}^{-}=-C_{L}^{+}$. Then ![]() $L\otimes {\mathbf {R}}+\sqrt {-1}C_{L}\subset L\otimes {\mathbf {C}}$ is isomorphic to
$L\otimes {\mathbf {R}}+\sqrt {-1}C_{L}\subset L\otimes {\mathbf {C}}$ is isomorphic to ![]() $\Omega _{\Lambda }$ via the map
$\Omega _{\Lambda }$ via the map
Since ![]() $\exp _{N}\circ (-1_{L})=(1_{{\Bbb U}(-N)}\oplus -1_{L})\circ \exp _{N}$ and since
$\exp _{N}\circ (-1_{L})=(1_{{\Bbb U}(-N)}\oplus -1_{L})\circ \exp _{N}$ and since ![]() $-1_{L}$ exchanges the components of
$-1_{L}$ exchanges the components of ![]() $C_{L}$,
$C_{L}$, ![]() $1_{{\Bbb U}(-N)}\oplus -1_{L}\in O(\Lambda )$ exchanges the components of
$1_{{\Bbb U}(-N)}\oplus -1_{L}\in O(\Lambda )$ exchanges the components of ![]() $\Omega _{\Lambda }$.
$\Omega _{\Lambda }$.
Set ![]() $\eta :=\alpha (\omega _{J}+\sqrt {-1}\omega _{K})$. Let
$\eta :=\alpha (\omega _{J}+\sqrt {-1}\omega _{K})$. Let ![]() $z\in L\otimes {\mathbf {R}}+\sqrt {-1}C_{L}$ be such that
$z\in L\otimes {\mathbf {R}}+\sqrt {-1}C_{L}$ be such that ![]() $[\eta ]=\exp _{N}(z)$. Then
$[\eta ]=\exp _{N}(z)$. Then ![]() $\bar {\eta }=\alpha (\omega _{J}-\sqrt {-1}\omega _{K})$ and
$\bar {\eta }=\alpha (\omega _{J}-\sqrt {-1}\omega _{K})$ and ![]() $[\bar {\eta }]=\exp _{N}(\bar {z})$. Let
$[\bar {\eta }]=\exp _{N}(\bar {z})$. Let ![]() $\Omega _{\Lambda }^{+}$ be the component of
$\Omega _{\Lambda }^{+}$ be the component of ![]() $\Omega _{\Lambda }$ such that
$\Omega _{\Lambda }$ such that ![]() $[\eta ]\in \Omega _{\Lambda }^{+}$. Let
$[\eta ]\in \Omega _{\Lambda }^{+}$. Let ![]() $\Omega _{\Lambda }^{-}$ be the remaining component. Then
$\Omega _{\Lambda }^{-}$ be the remaining component. Then ![]() $\Omega _{\Lambda }^{-}=\overline {\Omega _{\Lambda }^{+}}$ and
$\Omega _{\Lambda }^{-}=\overline {\Omega _{\Lambda }^{+}}$ and ![]() $[\bar {\eta }]\in \Omega _{\Lambda }^{-}$. Since
$[\bar {\eta }]\in \Omega _{\Lambda }^{-}$. Since ![]() $(1_{{\Bbb U}(-N)}\oplus -1_{L})[\bar {\eta }] = [(1_{{\Bbb U}(-N)}\oplus -1_{L})(\exp _{N}(\bar {z}))] = [\exp _{N}(-\bar {z})] \in \Omega _{\Lambda }^{+}$, the point of
$(1_{{\Bbb U}(-N)}\oplus -1_{L})[\bar {\eta }] = [(1_{{\Bbb U}(-N)}\oplus -1_{L})(\exp _{N}(\bar {z}))] = [\exp _{N}(-\bar {z})] \in \Omega _{\Lambda }^{+}$, the point of ![]() $\Omega _{\Lambda }^{+}/O^{+}(\Lambda )$ corresponding to
$\Omega _{\Lambda }^{+}/O^{+}(\Lambda )$ corresponding to ![]() $[\bar {\eta }]$ is represented by
$[\bar {\eta }]$ is represented by ![]() $[\exp _{N}(-\bar {z})]$.
$[\exp _{N}(-\bar {z})]$.
For simplicity, write ![]() $\Psi (\cdot )$ for
$\Psi (\cdot )$ for ![]() $\Psi _{\Lambda }(\cdot ,2^{g-1}F_{\Lambda }+f_{\Lambda })$. Let
$\Psi _{\Lambda }(\cdot ,2^{g-1}F_{\Lambda }+f_{\Lambda })$. Let ![]() $w$ be its weight. Then
$w$ be its weight. Then ![]() $\Psi \in {\mathcal {O}}(L\otimes {\mathbf {R}}+\sqrt {-1}C_{L}^{+})$. By the definition of Petersson norm (cf. § 4.2),
$\Psi \in {\mathcal {O}}(L\otimes {\mathbf {R}}+\sqrt {-1}C_{L}^{+})$. By the definition of Petersson norm (cf. § 4.2),
Since ![]() $\Psi$ is a Borcherds product, it is expressed as a Fourier series
$\Psi$ is a Borcherds product, it is expressed as a Fourier series
with ![]() $a(\lambda )\in {\mathbf {Z}}$. Since
$a(\lambda )\in {\mathbf {Z}}$. Since ![]() $\overline {e^{2\pi i\langle l,z\rangle }}=e^{2\pi i\langle l,-\bar {z}\rangle }$ and
$\overline {e^{2\pi i\langle l,z\rangle }}=e^{2\pi i\langle l,-\bar {z}\rangle }$ and ![]() $a(l)\in {\mathbf {Z}}$ for all
$a(l)\in {\mathbf {Z}}$ for all ![]() $l\in L^{\lor }$ and hence
$l\in L^{\lor }$ and hence ![]() $\overline {\Psi (z)}=\Psi (-\bar {z})$, we deduce from (11.4) and (11.5) that
$\overline {\Psi (z)}=\Psi (-\bar {z})$, we deduce from (11.4) and (11.5) that ![]() $\|\Psi ([\eta ])\|^{2}=\|\Psi ([\bar {\eta }])\|^{2}$.
$\|\Psi ([\eta ])\|^{2}=\|\Psi ([\bar {\eta }])\|^{2}$.
Now we can formulate an equivariant analogue of Borcherds’ conjecture as the coincidence of the two functions ![]() $\tau _{\iota }^{{\rm spin}}$ and
$\tau _{\iota }^{{\rm spin}}$ and ![]() $\pi _{\iota }^{*}\|\Psi _{\Lambda }(\cdot ,2^{g-1}F_{\Lambda }+f_{\Lambda })\|$ on
$\pi _{\iota }^{*}\|\Psi _{\Lambda }(\cdot ,2^{g-1}F_{\Lambda }+f_{\Lambda })\|$ on ![]() ${\mathcal {E}}^{\iota }$. By Theorem 10.2, we have an affirmative answer to this problem.
${\mathcal {E}}^{\iota }$. By Theorem 10.2, we have an affirmative answer to this problem.
Theorem 11.3 Let ![]() $\iota$ be a hyperbolic involution on
$\iota$ be a hyperbolic involution on ![]() $X_{K3}$ with
$X_{K3}$ with ![]() ${\mathcal {E}}^{\iota }\not =\emptyset$. Then the following equality of functions on
${\mathcal {E}}^{\iota }\not =\emptyset$. Then the following equality of functions on ![]() $\pi _{\iota }^{-1}({\mathcal {M}}_{\Lambda }^{0}\setminus {\mathcal {H}}_{\Lambda })\subset {\mathcal {E}}^{\iota }$ holds:
$\pi _{\iota }^{-1}({\mathcal {M}}_{\Lambda }^{0}\setminus {\mathcal {H}}_{\Lambda })\subset {\mathcal {E}}^{\iota }$ holds:
where ![]() $C''_{M}$ is a constant depending only on
$C''_{M}$ is a constant depending only on ![]() $M$.
$M$.
Proof. Let ![]() $\gamma \in {\mathcal {E}}^{\iota }$. Let
$\gamma \in {\mathcal {E}}^{\iota }$. Let ![]() $(I,J,K)$ be a hyperkähler structure on
$(I,J,K)$ be a hyperkähler structure on ![]() $(X_{K3},\gamma )$ with (11.2) and set
$(X_{K3},\gamma )$ with (11.2) and set ![]() $X_{I}:=(X_{K3},I)$. Then
$X_{I}:=(X_{K3},I)$. Then ![]() $(X_{I},\iota )$ is a
$(X_{I},\iota )$ is a ![]() $2$-elementary
$2$-elementary ![]() $K3$ surface of type
$K3$ surface of type ![]() $M$. By [Reference YoshikawaYos08, Lemma 4.3], we have
$M$. By [Reference YoshikawaYos08, Lemma 4.3], we have
On the other hand, it is classical that ![]() $D_{S_{\gamma }}$ can be identified with the Dolbeault operator
$D_{S_{\gamma }}$ can be identified with the Dolbeault operator ![]() $\sqrt {2}(\bar {\partial }+\bar {\partial }^{*})$ acting on
$\sqrt {2}(\bar {\partial }+\bar {\partial }^{*})$ acting on ![]() $A^{0,*}(X_{K3}^{\iota },\Sigma _{S_{\gamma }})$, where
$A^{0,*}(X_{K3}^{\iota },\Sigma _{S_{\gamma }})$, where ![]() $\Sigma _{S_{\gamma }}$ is the theta characteristic on
$\Sigma _{S_{\gamma }}$ is the theta characteristic on ![]() $X_{K3}^{\iota }$ corresponding to
$X_{K3}^{\iota }$ corresponding to ![]() $S_{\gamma }$. Here
$S_{\gamma }$. Here ![]() $X_{K3}^{\iota }$ is endowed with the complex structure induced by
$X_{K3}^{\iota }$ is endowed with the complex structure induced by ![]() $\gamma$. Since
$\gamma$. Since ![]() $D_{S_{\gamma }}^{2}=2(\bar {\partial }+\bar {\partial }^{*})^{2}$ by this identification, we have
$D_{S_{\gamma }}^{2}=2(\bar {\partial }+\bar {\partial }^{*})^{2}$ by this identification, we have ![]() $\zeta _{D_{S_{\gamma }}^{2}}(s)=2^{-s+1}\zeta _{\Sigma _{S_{\gamma }}}(s)$, where
$\zeta _{D_{S_{\gamma }}^{2}}(s)=2^{-s+1}\zeta _{\Sigma _{S_{\gamma }}}(s)$, where ![]() $\zeta _{\Sigma _{S_{\gamma }}}(s)$ is the spectral zeta function of
$\zeta _{\Sigma _{S_{\gamma }}}(s)$ is the spectral zeta function of ![]() $(\bar {\partial }+\bar {\partial }^{*})^{2}|_{A^{0,0}(\Sigma _{S_{\gamma }})}$ as in § 10.1. Hence
$(\bar {\partial }+\bar {\partial }^{*})^{2}|_{A^{0,0}(\Sigma _{S_{\gamma }})}$ as in § 10.1. Hence
By (11.6), (11.7) and the definitions of ![]() $\tau ^{{\rm spin}}_{M}$ and
$\tau ^{{\rm spin}}_{M}$ and ![]() $\tau ^{{\rm spin}}_{\iota }$, we get
$\tau ^{{\rm spin}}_{\iota }$, we get
where ![]() $N(\gamma ,\iota )$ is the number of ineffective spinor bundles on
$N(\gamma ,\iota )$ is the number of ineffective spinor bundles on ![]() $(X_{K3}^{\iota },\gamma )$.
$(X_{K3}^{\iota },\gamma )$.
Let ![]() $\gamma \in \pi _{\iota }^{-1}({\mathcal {M}}_{\Lambda }^{0}\setminus {\mathcal {H}}_{\Lambda })$. Since
$\gamma \in \pi _{\iota }^{-1}({\mathcal {M}}_{\Lambda }^{0}\setminus {\mathcal {H}}_{\Lambda })$. Since ![]() $N(\gamma ,\iota )$ is a constant function on
$N(\gamma ,\iota )$ is a constant function on ![]() $\pi _{\iota }^{-1}({\mathcal {M}}_{\Lambda }^{0}\setminus {\mathcal {H}}_{\Lambda })$ by Theorem 9.13 and (11.3) and since
$\pi _{\iota }^{-1}({\mathcal {M}}_{\Lambda }^{0}\setminus {\mathcal {H}}_{\Lambda })$ by Theorem 9.13 and (11.3) and since ![]() $\pi _{\iota }(\gamma )$ is given by the pair of
$\pi _{\iota }(\gamma )$ is given by the pair of ![]() $\bar {\pi }_{M}(X_{I},\iota )$ and its conjugate point by (11.3), the result follows from Theorem 10.2 and (11.8).
$\bar {\pi }_{M}(X_{I},\iota )$ and its conjugate point by (11.3), the result follows from Theorem 10.2 and (11.8).
As in [Reference YoshikawaYos08] and [Reference YoshikawaYos13, § 10], we obtain, as a corollary of Theorem 11.3, an interpretation of Theorem 10.2 on the mirror side, that is, in terms of real ![]() $K3$ surfaces. Recall that a pair consisting of a
$K3$ surfaces. Recall that a pair consisting of a ![]() $K3$ surface and an anti-holomorphic involution is called a real
$K3$ surface and an anti-holomorphic involution is called a real ![]() $K3$ surface. The set of fixed points of the involution on a real
$K3$ surface. The set of fixed points of the involution on a real ![]() $K3$ surface is the set of real points. A holomorphic
$K3$ surface is the set of real points. A holomorphic ![]() $2$-form on a real
$2$-form on a real ![]() $K3$ surface is said to be defined over
$K3$ surface is said to be defined over ![]() ${\mathbf {R}}$ if it is mapped to its complex conjugation by the involution. In view of mirror symmetry for
${\mathbf {R}}$ if it is mapped to its complex conjugation by the involution. In view of mirror symmetry for ![]() $K3$ surfaces with involution [Reference Gross and WilsonGW97, § 2], the following corollary is a counterpart of Theorem 10.2 in mirror symmetry.
$K3$ surfaces with involution [Reference Gross and WilsonGW97, § 2], the following corollary is a counterpart of Theorem 10.2 in mirror symmetry.
Corollary 11.4 Let ![]() $(Y,\sigma )$ be a real
$(Y,\sigma )$ be a real ![]() $K3$ surface. Let
$K3$ surface. Let ![]() $M$ be the type of
$M$ be the type of ![]() $\sigma$ and let
$\sigma$ and let ![]() $\alpha$ be a marking with
$\alpha$ be a marking with ![]() $\alpha (H^{2}(X,{\mathbf {Z}})_{+})=M$. Let
$\alpha (H^{2}(X,{\mathbf {Z}})_{+})=M$. Let ![]() $\gamma$ be a
$\gamma$ be a ![]() $\sigma$-invariant Ricci-flat Kähler metric on
$\sigma$-invariant Ricci-flat Kähler metric on ![]() $Y$ with volume
$Y$ with volume ![]() $1$. Let
$1$. Let ![]() $\omega _{\gamma }$ be the Kähler form of
$\omega _{\gamma }$ be the Kähler form of ![]() $\gamma$ and let
$\gamma$ and let ![]() $\eta _{\gamma }$ be a holomorphic
$\eta _{\gamma }$ be a holomorphic ![]() $2$-form on
$2$-form on ![]() $Y$ defined over
$Y$ defined over ![]() ${\mathbf {R}}$ such that
${\mathbf {R}}$ such that ![]() $\eta _{\gamma }\wedge \bar {\eta }_{\gamma }=2\omega _{\gamma }^{2}$. Then
$\eta _{\gamma }\wedge \bar {\eta }_{\gamma }=2\omega _{\gamma }^{2}$. Then
where ![]() $\Im (\eta _{\gamma })+\sqrt {-1}\omega _{\gamma }\in H^{2}(Y,{\mathbf {R}})+\sqrt {-1}{\mathcal {K}}_{Y}$ is a point of the complexified Kähler cone of the Kähler surface
$\Im (\eta _{\gamma })+\sqrt {-1}\omega _{\gamma }\in H^{2}(Y,{\mathbf {R}})+\sqrt {-1}{\mathcal {K}}_{Y}$ is a point of the complexified Kähler cone of the Kähler surface ![]() $(Y,\omega _{\gamma })$ with
$(Y,\omega _{\gamma })$ with ![]() $B$-field
$B$-field ![]() $\Im (\eta _{\gamma })$.
$\Im (\eta _{\gamma })$.
Proof. Set ![]() $I'=K$,
$I'=K$, ![]() $J'=-J$,
$J'=-J$, ![]() $K'=I$, where
$K'=I$, where ![]() $(I,J,K)$ is a hyperkähler structure on
$(I,J,K)$ is a hyperkähler structure on ![]() $(X_{K3},\gamma )$ satisfying (11.2) for
$(X_{K3},\gamma )$ satisfying (11.2) for ![]() $\sigma$. Then
$\sigma$. Then ![]() $(I',J',K')$ is a hyperkähler structure on
$(I',J',K')$ is a hyperkähler structure on ![]() $(X_{K3},\gamma )$ such that
$(X_{K3},\gamma )$ such that ![]() $\sigma _{*}I'=-I'\sigma _{*}$,
$\sigma _{*}I'=-I'\sigma _{*}$, ![]() $\sigma _{*}J'=-J'\sigma _{*}$,
$\sigma _{*}J'=-J'\sigma _{*}$, ![]() $\sigma _{*}K'=K'\sigma _{*}$. Set
$\sigma _{*}K'=K'\sigma _{*}$. Set ![]() $Y=(X_{K3},I')$. Then
$Y=(X_{K3},I')$. Then ![]() $\sigma$ is an anti-holomorphic involution on
$\sigma$ is an anti-holomorphic involution on ![]() $Y$. On the other hand,
$Y$. On the other hand, ![]() $\sigma$ is an anti-symplectic holomorphic involution on
$\sigma$ is an anti-symplectic holomorphic involution on ![]() $(X_{K3},K')$. By [Reference Gross and WilsonGW97, p. 514], we see that
$(X_{K3},K')$. By [Reference Gross and WilsonGW97, p. 514], we see that ![]() $\Re (\eta _{\gamma })$ and
$\Re (\eta _{\gamma })$ and ![]() $\Im (\eta _{\gamma })+\sqrt {-1}\omega _{\gamma }$ are a Kähler form and a holomorphic
$\Im (\eta _{\gamma })+\sqrt {-1}\omega _{\gamma }$ are a Kähler form and a holomorphic ![]() $2$-form on
$2$-form on ![]() $(X_{K3},K')$, respectively. From this interpretation and Theorem 11.3, the result follows.
$(X_{K3},K')$, respectively. From this interpretation and Theorem 11.3, the result follows.
Is it possible to prove Corollary 11.4 without passing through algebraic geometry? Such a proof will provide a new understanding of Theorem 10.2.
Acknowledgements
The first-named author is partially supported by JSPS KAKENHI grants 17K14158 and 20H00112. The second-named author is partially supported by JSPS KAKENHI grants 16H03935 and 16H06335. He is grateful to Professor Jean-Michel Bismut for helpful discussions and to Professor Riccardo Salvati Manni for answering his questions. The authors are grateful to the referee for a careful reading of the paper and helpful comments.