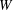Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-11T02:41:04.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of finite-dimensional irreducible modules over $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}W$-algebras

Part of: Lie algebras and Lie superalgebras Representation theory of rings and algebras

Published online by Cambridge University Press:  07 April 2014

Ivan Losev  and
Victor Ostrik
Ivan Losev
Affiliation:
Department of Mathematics, Northeastern University, Boston, MA 02115, USA email i.loseu@neu.edu
Victor Ostrik
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR 97403, USA email vostrik@darkwing.uoregon.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Finite 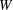$W$-algebras are certain associative algebras arising in Lie theory. Each 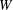$W$-algebra is constructed from a pair of a semisimple Lie algebra 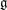${\mathfrak{g}}$ (our base field is algebraically closed and of characteristic 0) and its nilpotent element $e$. In this paper we classify finite-dimensional irreducible modules with integral central character over 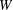$W$-algebras. In more detail, in a previous paper the first author proved that the component group 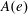$A(e)$ of the centralizer of the nilpotent element under consideration acts on the set of finite-dimensional irreducible modules over the 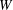$W$-algebra and the quotient set is naturally identified with the set of primitive ideals in 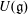$U({\mathfrak{g}})$ whose associated variety is the closure of the adjoint orbit of $e$. In this paper, for a given primitive ideal with integral central character, we compute the corresponding 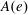$A(e)$-orbit. The answer is that the stabilizer of that orbit is basically a subgroup of 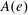$A(e)$ introduced by G. Lusztig. In the proof we use a variety of different ingredients: the structure theory of primitive ideals and Harish-Chandra bimodules for semisimple Lie algebras, the representation theory of 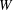$W$-algebras, the structure theory of cells and Springer representations, and multi-fusion monoidal categories.

Keywords

W-algebrasemisimple Lie algebranilpotent orbitprimitive idealHarish-Chandra bimodulecells in Weyl groupsSpringer representationLusztig’s subgroupsasymptotic Hecke algebra

MSC classification

Secondary: 16G99: None of the above, but in this section 17B35: Universal enveloping (super)algebras
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 6 , June 2014 , pp. 1024 - 1076
Copyright
© The Author(s) 2014 

References

Barbash, D. and Vogan, D., Primitive ideals and orbital integrals in complex classical groups, Math. Ann. 249 (1982), 153–199.CrossRefGoogle Scholar
Bernstein, J. and Gelfand, S., Tensor products of finite and infinite-dimensional representations of semisimple Lie algebras, Compositio Math. 41 (1980), 245–285.Google Scholar
Bezrukavnikov, R. and Ostrik, V., On tensor categories attached to cells in affine Weyl groups, II, in Representation theory of algebraic groups and quantum groups, Advanced Studies in Pure Mathematics, vol. 40 (Mathematical Society of Japan, 2004), 101–119.CrossRefGoogle Scholar
Bezrukavnikov, R., Finkelberg, M. and Ostrik, V., Character D-modules via Drinfeld center of Harish-Chandra bimodules, Invent. Math. 188 (2012), 589–620.CrossRefGoogle Scholar
Bezrukavnikov, R., Finkelberg, M. and Ostrik, V., On tensor categories attached to cells in affine Weyl groups, III, Israel J. Math. 170 (2009), 207–234.Google Scholar
Borho, W. and Brylinski, J.-L., Differential operators on homogeneous spaces I. Irreducibility of associated variety for annihilators of induced modules, Invent. Math 69 (1982), 437–476.Google Scholar
Brown, J. and Goodwin, S., Finite dimensional irreducible representations of finite W-algebras associated to even multiplicity nilpotent orbits in classical Lie algebras, Math. Z. 273 (2013), 123–160.Google Scholar
Brown, J. and Goodwin, S., Non-integral representation theory of even multiplicity finite W-algebras, J. Algebra 380 (2013), 30–45.CrossRefGoogle Scholar
Brundan, J., Goodwin, S. and Kleshchev, A., Highest weight theory for finite W-algebras, Int. Math. Res. Not. IMRN 2008 (2008), doi:10.1093/imrn/rnn051.CrossRefGoogle Scholar
Brundan, J. and Kleshchev, A., Representations of shifted Yangians and finite W-algebras, Mem. Amer. Math. Soc. 196 (2008).Google Scholar
Carter, R., Finite groups of Lie type. Conjugacy classes and complex characters, second edition (John Wiley and sons, 1993).Google Scholar
Collingwood, D. and McGovern, W., Nilpotent orbits in semisimple Lie algebras (Chapman and Hall, London, 1993).Google Scholar
Dodd, C., Injectivity of a certain cycle map for finite dimensional W-algebras, Int. Math. Res. Not. IMRN 2013 (2013), doi:10.1093/imrn/rnt106.Google Scholar
Etingof, P. and Gelaki, Sh., Isocategorical groups, Int. Math. Res. Not. IMRN 2 (2001), 59–76.CrossRefGoogle Scholar
Etingof, P., Ostrik, V. and Nikshych, D., On fusion categories, Ann. of Math. (2) 162 (2005), 581–642.CrossRefGoogle Scholar
Gabber, O. and Joseph, A., On the Bernstein–Gelfand–Gelfand resolution and the Duflo sum formula, Compositio Math. 43 (1981), 107–131.Google Scholar
Garfinkle, D., On the classification of primitive ideals for complex classical Lie algebras, I, Compositio Math. 75 (1990), 135–169.Google Scholar
Goodman, F. and Wenzl, H., Ideals in Temperley–Lieb Category, Comm. Math. Phys. 234 (2003), 172–181.Google Scholar
Goodwin, S., Translation for finite W-algebras, Represent. Theory 15 (2011), 307–346.Google Scholar
Jantzen, J. C., Einhüllende Algebren halbeinfacher Lie-Algebren, Ergebnisse der Mathematic, vol. 3 (Springer, 1983).Google Scholar
Joseph, A., On the associated variety of a primitive ideal, J. Algebra 93 (1985), 509–523.Google Scholar
Joseph, A., On the cyclicity of vectors associated with Duflo involutions, Lecture Notes in Mathematics, vol. 1243 (Springer, Berlin, 1987), 144–188.Google Scholar
Losev, I., Quantized symplectic actions and W-algebras, J. Amer. Math. Soc 23 (2010), 34–59.Google Scholar
Losev, I., Finite $W$-algebras, Proceedings of the International Congress of Mathematicians, Hyderabad, India (Hindustan Book Agency, New Delhi, 2010), 1281–1307.Google Scholar
Losev, I., Finite dimensional representations of W-algebras, Duke Math. J. 159 (2011), 99–143.Google Scholar
Losev, I., Parabolic induction and one-dimensional representations of W-algebras, Adv. Math. 226 (2011), 4841–4883.Google Scholar
Losev, I., Dimensions of irreducible modules over W-algebras and Goldie ranks, Preprint (2012), arXiv:1209.1083.Google Scholar
Losev, I., On the structure of the category 𝓞 for W-algebras, Sémin. Congr. 24 (2012), 351–368.Google Scholar
Lusztig, G., A class of irreducible representations of a Weyl group, II, Proc. Kon. Nederl. Akad., Ser. A 85 (1982), 219–226.Google Scholar
Lusztig, G., Characters of reductive groups over a finite field, Annals of Mathematics Studies, vol. 107 (Princeton University Press, Princeton, NJ, 1984).Google Scholar
Lusztig, G., Sur les cellules gauches des groupes de Weyl, C. R. Acad. Sci. Paris 1 (1986), 5–8.Google Scholar
Lusztig, G., Leading coefficients of character values of Hecke algebras, in The Arcata conference on representations of finite groups, Part 2, Proceedings of Symposia in Pure Mathematics, vol. 47 (American Mathematical Society, Providence, RI, 1987), 235–262.Google Scholar
Lusztig, G., Cells in affine Weyl groups, IV, J. Fac. Sci. Univ. Tokyo Sect. IA, Math. 36 (1989), 297–328.Google Scholar
Lusztig, G., Cells in affine Weyl groups and tensor categories, Adv. Math. 129 (1997), 85–98.Google Scholar
Lusztig, G., Unipotent classes and special Weyl group representations, J. Algebra 321 (2009), 3418–3449.Google Scholar
Lusztig, G., Families and Springer’s correspondence, Pacific J. Math., to appear, arXiv:1201.5593.Google Scholar
McGovern, W., Left cells and domino tableaux in classical Weyl groups, Compositio Math. 101 (1996), 77–98.Google Scholar
Mazorchuk, V., Lectures on algebraic categorification, The QGM Master Class Series (European Mathematical Society, 2012).Google Scholar
Ostrik, V., Module categories, weak Hopf algebras and modular invariants, Transform. Groups 8 (2003), 177–206.Google Scholar
Ostrik, V., Module categories over the Drinfeld double of a finite group, Int. Math. Res. Not. IMRN 27 (2003), 1507–1520.Google Scholar
Ostrik, V., Tensor categories attached to exceptional cells in Weyl groups, Int. Math. Res. Not. IMRN 2013 (2013), doi:10.1093/imrn/rnt086.Google Scholar
Premet, A., Special transverse slices and their enveloping algebras, Adv. Math. 170 (2002), 1–55.Google Scholar
Premet, A., Enveloping algebras of Slodowy slices and the Joseph ideal, J. Eur. Math. Soc. 9 (2007), 487–543.Google Scholar
Vinberg, E., On invariants of a set of matrices, J. Lie Theory 6 (1996), 249–269.Google Scholar
Wang, W., Nilpotent orbits and W-algebras, Fields Institute Communications Series, vol. 59 (American Mathematical Society, Providence, RI, 2011), 71–105.Google Scholar