Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-14T09:26:36.773Z Has data issue: false hasContentIssue false
  • English
  • Français

Central elements in affine mod p Hecke algebras via perverse 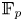$\mathbb {F}_p$-sheaves

Part of: Special varieties Representation theory of groups (Co)homology theory

Published online by Cambridge University Press:  14 September 2021

Robert Cass
Robert Cass*
Affiliation:
Department of Mathematics, Harvard University, Cambridge, MA02138, USArcass@math.harvard.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 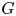$G$ be a split connected reductive group over a finite field of characteristic 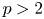$p > 2$ such that 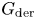$G_\text {der}$ is absolutely almost simple. We give a geometric construction of perverse 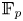$\mathbb {F}_p$-sheaves on the Iwahori affine flag variety of 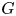$G$ which are central with respect to the convolution product. We deduce an explicit formula for an isomorphism from the spherical mod 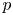$p$ Hecke algebra to the center of the Iwahori mod 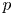$p$ Hecke algebra. We also give a formula for the central integral Bernstein elements in the Iwahori mod 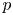$p$ Hecke algebra. To accomplish these goals we construct a nearby cycles functor for perverse $\mathbb {F}_p$-sheaves and we use Frobenius splitting techniques to prove some properties of this functor. We also prove that certain equal characteristic analogues of local models of Shimura varieties are strongly 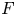$F$-regular, and hence they are $F$-rational and have pseudo-rational singularities.

Keywords

Hecke algebraslocal modelsperverse sheavesF-singularities

MSC classification

Primary: 14M15: Grassmannians, Schubert varieties, flag manifolds
Secondary: 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials 20C08: Hecke algebras and their representations
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 10 , October 2021 , pp. 2215 - 2241
Check for updates
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Current address: Department of Mathematics, California Institute of Technology, Pasadena, CA 91125, USA; rcass@caltech.edu

References

Aberbach, I. M., Extension of weakly and strongly F-regular rings by flat maps, J. Algebra 241 (2001), 799–807.CrossRefGoogle Scholar
Beauville, A. and Laszlo, Y., Un lemme de descente, C. R. Math. Acad. Sci. Paris 320 (1995), 335–340.Google Scholar
Beilinson, A. A., Bernstein, J. and Deligne, P., Faisceaux pervers, in Analysis and topology on singular spaces, I (Luminy, 1981), Astérisque, vol. 100 (Société Mathématique de France, Paris, 1982), 5–171.Google Scholar
Bezrukavnikov, R., On two geometric realizations of an affine Hecke algebra, Publ. Math. Inst. Hautes Études Sci. 123 (2016), 1–67.CrossRefGoogle Scholar
Blickle, M. and Schwede, K., $p^{-1}$-linear maps in algebra and geometry, in Commutative algebra (Springer, New York, 2013), 123–205.CrossRefGoogle Scholar
Brion, M. and Kumar, S., Frobenius splitting methods in geometry and representation theory, Progress in Mathematics, vol. 231 (Birkhäuser, Boston, 2005).CrossRefGoogle Scholar
Cass, R., Perverse $\mathbb {F}_p$-sheaves on the affine Grassmannian, Preprint (2019), arXiv:1910.03377v3.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique: III. Étude cohomologique des faisceaux cohérents: I, Publ. Math. Inst. Hautes Études Sci. 11 (1961), 167.Google Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas: II, Publ. Math. Inst. Hautes Études Sci. 24 (1965), 231.Google Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas: III, Publ. Math. Inst. Hautes Études Sci. 28 (1966), 255.CrossRefGoogle Scholar
Faltings, G., Algebraic loop groups and moduli spaces of bundles, J. Eur. Math. Soc. (JEMS) 5 (2003), 41–68.CrossRefGoogle Scholar
Gaitsgory, D., Construction of central elements in the affine Hecke algebra via nearby cycles, Invent. Math. 144 (2001), 253–280.CrossRefGoogle Scholar
Görtz, U., Affine Springer fibers and affine Deligne-Lusztig varieties, in Affine flag manifolds and principal bundles, Trends Math. (Birkhäuser, Basel, 2010), 1–50.Google Scholar
Grosse-Klönne, E., From pro-$p$ Iwahori-Hecke modules to $(\varphi , \Gamma )$-modules, I, Duke Math. J. 165 (2016), 1529–1595.CrossRefGoogle Scholar
Haines, T. J. and Richarz, T., Normality and Cohen-Macaulayness of parahoric local models, J. Eur. Math. Soc. (JEMS), to appear. Preprint (2019), arXiv:1903.10585v4.Google Scholar
Haines, T. J. and Richarz, T., The test function conjecture for local models of Weil-restricted groups, Compos. Math. 156 (2020), 1348–1404.CrossRefGoogle Scholar
Hamacher, P. and Viehmann, E., Irreducible components of minuscule affine Deligne-Lusztig varieties, Algebra Number Theory 12 (2018), 1611–1634.CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York-Heidelberg, 1977).CrossRefGoogle Scholar
Hashimoto, M., Surjectivity of multiplication and F-regularity of multigraded rings, in Commutative algebra (Grenoble/Lyon, 2001), Contemporary Mathematics, vol. 331 (American Mathematical Society, Providence, RI, 2003), 153–170.CrossRefGoogle Scholar
Henniart, G. and Vignéras, M.-F., A Satake isomorphism for representations modulo $p$ of reductive groups over local fields, J. Reine Angew. Math. 701 (2015), 33–75.Google Scholar
Herzig, F., The classification of irreducible admissible mod $p$ representations of a $p$-adic ${\rm GL_n}$, Invent. Math. 186 (2011), 373–434.CrossRefGoogle Scholar
Herzig, F., A Satake isomorphism in characteristic $p$, Compos. Math. 147 (2011), 263–283.CrossRefGoogle Scholar
Hochster, M. and Huneke, C., Tight closure and strong $F$-regularity, Mém. Soc. Math. Fr. (N.S.) 38 (1989), 119–113.Google Scholar
Hochster, M. and Huneke, C., $F$-regularity, test elements, and smooth base change, Trans. Amer. Math. Soc. 346 (1994), 1–62.Google Scholar
Illusie, L., Exposé I : Autour du théorème de monodromie locale, in Périodes p-adiques – Séminaire de Bures, 1988, Astérisque, vol. 223 (Société mathématique de France, 1994), 9–57.Google Scholar
Kovács, S. J., Rational singularities, Preprint (2017), arXiv:1703.02269v8.Google Scholar
Kunz, E., On Noetherian rings of characteristic $p$, Amer. J. Math. 98 (1976), 999–1013.CrossRefGoogle Scholar
Milne, J. S. and Shih, K. Y., Conjugates of Shimura varieties, in Hodge cycles, motives, and shimura varieties, Lecture Notes in Mathematics, vol. 900 (Springer, Berlin, 1982), 280–356.CrossRefGoogle Scholar
Ollivier, R., Compatibility between Satake and Bernstein isomorphisms in characteristic $p$, Algebra Number Theory 8 (2014), 1071–1111.CrossRefGoogle Scholar
Ollivier, R., An inverse Satake isomorphism in characteristic $p$, Selecta Math. (N.S.) 21 (2015), 727–761.CrossRefGoogle Scholar
Pappas, G. and Rapoport, M., Twisted loop groups and their affine flag varieties, Adv. Math. 219 (2008), 118–198. With an appendix by T. Haines and Rapoport.CrossRefGoogle Scholar
Pappas, G. and Zhu, X., Local models of Shimura varieties and a conjecture of Kottwitz, Invent. Math. 194 (2013), 147–254.CrossRefGoogle Scholar
Pépin, C. and Schmidt, T., Generic and Mod p Kazhdan-Lusztig Theory for ${GL}_2$, Preprint (2020), arXiv:2007.01364v1.Google Scholar
Deligne, P., Séminaire de Géométrie Algébrique du Bois-Marie – Cohomologie étale – SGA $4\frac {1}2$, Lecture Notes in Mathematics, vol. 569 (Springer, Berlin, 1977).CrossRefGoogle Scholar
Deligne, P. and Katz, N., Séminaire de Géométrie Algébrique du Bois-Marie 1967–1969 – Groupes de monodromie en géométrie algébrique. II – (SGA7), Lecture Notes in Mathematics, vol. 340 (Springer, Berlin, 1973).Google Scholar
Smith, K. E., $F$-rational rings have rational singularities, Amer. J. Math. 119 (1997), 159–180.CrossRefGoogle Scholar
Smith, K. E., Globally F-regular varieties: applications to vanishing theorems for quotients of Fano varieties, Michigan Math. J. 48 (2000), 553–572.CrossRefGoogle Scholar
The Stacks Project Authors, Stacks Project (2021), https://stacks.math.columbia.edu.Google Scholar
Vignéras, M.-F., Pro-$p$-Iwahori Hecke ring and supersingular $\overline {\mathbf {F}}_p$-representations, Math. Ann. 331 (2005), 523–556.CrossRefGoogle Scholar
Zhu, X., Affine Demazure modules and $T$-fixed point subschemes in the affine Grassmannian, Adv. Math. 221 (2009), 570–600.CrossRefGoogle Scholar
Zhu, X., On the coherence conjecture of Pappas and Rapoport, Ann. of Math. (2) 180 (2014), 1–85.CrossRefGoogle Scholar
Zhu, X., An introduction to affine Grassmannians and the geometric Satake equivalence, in Geometry of moduli spaces and representation theory, IAS/Park City Mathematics Series, vol. 24 (American Mathematical Society, Providence, RI, 2017), 59–154.CrossRefGoogle Scholar
Zhu, X., A note on integral Satake isomorphisms, Preprint (2020), arXiv:2005.13056v3.Google Scholar