Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-19T03:58:02.535Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational points and derived equivalence

Part of: Surfaces and higher-dimensional varieties Curves Arithmetic problems. Diophantine geometry Families, fibrations

Published online by Cambridge University Press:  30 April 2021

Nicolas Addington ,
Benjamin Antieau ,
Katrina Honigs  and
Sarah Frei
Nicolas Addington
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR97403-1222, USAadding@uoregon.edu
Benjamin Antieau
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Road, Evanston, IL60208, USAantieau@northwestern.edu
Katrina Honigs
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR97403-1222, USAhonigs@uoregon.edu
Sarah Frei
Affiliation:
Department of Mathematics, Rice University, 6100 Main Street, Houston, TX77005-1892, USAsarah.frei@rice.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We give the first examples of derived equivalences between varieties defined over non-closed fields where one has a rational point and the other does not. We begin with torsors over Jacobians of curves over 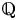$\mathbb {Q}$ and $\mathbb {F}_q(t)$, and conclude with a pair of hyperkähler 4-folds over 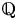$\mathbb {Q}$. The latter is independently interesting as a new example of a transcendental Brauer–Manin obstruction to the Hasse principle. The source code for the various computations is supplied as supplementary material with the online version of this article.

Keywords

derived categories of coherent sheavesrational pointsBrauer–Manin obstructionsmoduli spaces of sheavesK3 surfacesholomorphic symplectic varieties

MSC classification

Primary: 14D20: Algebraic moduli problems, moduli of vector bundles 14G05: Rational points 14H40: Jacobians, Prym varieties 14J28: $K3$ surfaces and Enriques surfaces
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 5 , May 2021 , pp. 1036 - 1050
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Addington, N., Donovan, W. and Meachan, C., Moduli spaces of torsion sheaves on K3 surfaces and derived equivalences, J. Lond. Math. Soc. (2) 93 (2016), 846–865.10.1112/jlms/jdw022CrossRefGoogle Scholar
Antieau, B., Krashen, D. and Ward, M., Derived categories of torsors for abelian schemes, Adv. Math. 306 (2017), 1–23.10.1016/j.aim.2016.09.037CrossRefGoogle Scholar
Arinkin, D., Autoduality of compactified Jacobians for curves with plane singularities, J. Algebraic Geom. 22 (2013), 363–388.10.1090/S1056-3911-2012-00596-7CrossRefGoogle Scholar
Ascher, K., Dasaratha, K., Perry, A. and Zhou, R., Rational points on twisted K3 surfaces and derived equivalences, in Brauer groups and obstruction problems, Progress in Mathematics, vol. 320 (Birkhäuser, Cham, 2017), 13–28.10.1007/978-3-319-46852-5_3CrossRefGoogle Scholar
Auel, A. and Bernardara, M., Semiorthogonal decompositions and birational geometry of del Pezzo surfaces over arbitrary fields, Proc. Lond. Math. Soc. (3) 117 (2018), 1–64.10.1112/plms.12119CrossRefGoogle Scholar
Berg, J. and Várilly-Alvarado, A., Odd order obstructions to the Hasse principle on general K3 surfaces, Math. Comp. 89 (2020), 1395–1416.10.1090/mcom/3485CrossRefGoogle Scholar
Bhargava, M., Gross, B. and Wang, X., A positive proportion of locally soluble hyperelliptic curves over $\mathbb {Q}$ have no point over any odd degree extension, J. Amer. Math. Soc. 30 (2017), 451–493. With an appendix by T. Dokchitser and V. Dokchitser.10.1090/jams/863CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., The Magma algebra system. I. The user language, J. Symbolic Comput. 24 (1997), 235–265.10.1006/jsco.1996.0125CrossRefGoogle Scholar
Charles, F., Birational boundedness for holomorphic symplectic varieties, Zarhin's trick for K3 surfaces, and the Tate conjecture, Ann. of Math. (2) 184 (2016), 487–526.10.4007/annals.2016.184.2.4CrossRefGoogle Scholar
Coray, D. and Manoil, C., On large Picard groups and the Hasse principle for curves and K3 surfaces, Acta Arith. 76 (1996), 165–189.10.4064/aa-76-2-165-189CrossRefGoogle Scholar
Elsenhans, A.-S. and Jahnel, J., K3 surfaces of Picard rank one and degree two, in Algorithmic number theory, Lecture Notes in Computer Science, vol. 5011 (Springer, Berlin, 2008), 212–225.10.1007/978-3-540-79456-1_14CrossRefGoogle Scholar
Frei, S., Moduli spaces of sheaves on K3 surfaces and Galois representations, Selecta Math. (N.S.) 26 (2020), Paper No. 6.10.1007/s00029-019-0530-7CrossRefGoogle Scholar
Hassett, B. and Tschinkel, Y., Rational points on K3 surfaces and derived equivalence, in Brauer groups and obstruction problems, Progress in Mathematics, vol. 320 (Birkhäuser, Cham, 2017), 87–113.10.1007/978-3-319-46852-5_6CrossRefGoogle Scholar
Hassett, B. and Várilly-Alvarado, A., Failure of the Hasse principle on general K3 surfaces, J. Inst. Math. Jussieu 12 (2013), 853–877.10.1017/S1474748012000904CrossRefGoogle Scholar
Honigs, K., Derived equivalent surfaces and abelian varieties, and their zeta functions, Proc. Amer. Math. Soc. 143 (2015), 4161–4166.10.1090/proc/12522CrossRefGoogle Scholar
Honigs, K., Derived equivalence, Albanese varieties, and the zeta functions of 3-dimensional varieties, Proc. Amer. Math. Soc. 146 (2018), 1005–1013, with an appendix by J. Achter, S. Casalaina-Martin, K. Honigs, and C. Vial.10.1090/proc/13810CrossRefGoogle Scholar
Huybrechts, D., Fourier–Mukai transforms in algebraic geometry, Oxford Mathematical Monographs (Clarendon Press, Oxford, 2006).Google Scholar
Huybrechts, D. and Lehn, M., The geometry of moduli spaces of sheaves, second edition, Cambridge Mathematical Library (Cambridge University Press, Cambridge, 2010).10.1017/CBO9780511711985CrossRefGoogle Scholar
Kleiman, S., The Picard scheme, in Fundamental algebraic geometry, Mathematical Surveys and Monographs, vol. 123 (American Mathematical Society, Providence, RI, 2005), 235–321.Google Scholar
Langer, A., Moduli spaces of sheaves in mixed characteristic, Duke Math. J. 124 (2004), 571–586.10.1215/S0012-7094-04-12434-0CrossRefGoogle Scholar
Langer, A., Semistable sheaves in positive characteristic, Ann. of Math. (2) 159 (2004), 251–276.10.4007/annals.2004.159.251CrossRefGoogle Scholar
Lichtenbaum, S., Duality theorems for curves over $p$-adic fields, Invent. Math. 7 (1969), 120–136.10.1007/BF01389795CrossRefGoogle Scholar
Lieblich, M., Moduli of complexes on a proper morphism, J. Algebraic Geom. 15 (2006), 175–206.10.1090/S1056-3911-05-00418-2CrossRefGoogle Scholar
Mukai, S., Duality between $D(X)$ and $D(\hat {X})$ with its application to Picard sheaves, Nagoya Math. J. 81 (1981), 153–175.10.1017/S002776300001922XCrossRefGoogle Scholar
Mukai, S., Symplectic structure of the moduli space of sheaves on an abelian or K3 surface, Invent. Math. 77 (1984), 101–116.10.1007/BF01389137CrossRefGoogle Scholar
Orlov, D., Derived categories of coherent sheaves on abelian varieties and equivalences between them, Izv. Ross. Akad. Nauk Ser. Mat. 66 (2002), 131–158.Google Scholar
Orlov, D., Derived categories of coherent sheaves, and motives, Uspekhi Mat. Nauk 60 (2005), 231–232.Google Scholar
Polishchuk, A., Abelian varieties, theta functions and the Fourier transform, Cambridge Tracts in Mathematics, vol. 153 (Cambridge University Press, Cambridge, 2003).10.1017/CBO9780511546532CrossRefGoogle Scholar
Poonen, B., Rational points on varieties, Graduate Studies in Mathematics, vol. 186 (American Mathematical Society, Providence, RI, 2017). Also http://math.mit.edu/~poonen/papers/Qpoints.pdf.10.1090/gsm/186CrossRefGoogle Scholar
Poonen, B. and Stoll, M., The Cassels-Tate pairing on polarized abelian varieties, Ann. of Math. (2) 150 (1999), 1109–1149.10.2307/121064CrossRefGoogle Scholar
Sawon, J., Twisted Fourier–Mukai transforms for holomorphic symplectic four-folds, Adv. Math. 218 (2008), 828–864.10.1016/j.aim.2008.01.013CrossRefGoogle Scholar
The Stacks Project Authors, Stacks Project (2018), https://stacks.math.columbia.edu.Google Scholar
Supplementary material: File

Addington et al. supplementary material

Addington et al. supplementary material

Download Addington et al. supplementary material(File)
File 4.3 KB