Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-14T09:16:15.816Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower bounds for Maass forms on semisimple groups

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  17 April 2020

Farrell Brumley  and
Simon Marshall
Farrell Brumley
Affiliation:
Université Sorbonne Paris Nord, Laboratoire de Géométrie, Analyse et Applications, LAGA, CNRS, UMR 7539, F-93430, Villetaneuse, France email brumley@math.univ-paris13.fr
Simon Marshall
Affiliation:
Department of Mathematics, University of Wisconsin – Madison, 480 Lincoln Drive,MadisonWI 53706, USA email marshall@math.wisc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 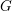$G$ be an anisotropic semisimple group over a totally real number field 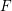$F$. Suppose that 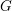$G$ is compact at all but one infinite place 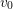$v_{0}$. In addition, suppose that 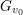$G_{v_{0}}$ is 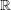$\mathbb{R}$-almost simple, not split, and has a Cartan involution defined over 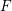$F$. If 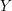$Y$ is a congruence arithmetic manifold of non-positive curvature associated with 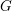$G$, we prove that there exists a sequence of Laplace eigenfunctions on 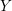$Y$ whose sup norms grow like a power of the eigenvalue.

Keywords

sup normsMaass formssymmetric varietiestrace formulaautomorphic periods

MSC classification

Primary: 11F03: Modular and automorphic functions
Secondary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields 11F72: Spectral theory; Selberg trace formula
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 5 , May 2020 , pp. 959 - 1003
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

FB is supported by ANR grant 14-CE25 and SM is supported by NSF grant DMS-1902173.

References

Avacumović, G. V., Über die Eigenfunktionen auf geschlossenen Riemannschen Mannigfaltig-keiten, Math. Z. 65 (1956), 327–344.CrossRefGoogle Scholar
Blomer, V. and Pohl, A., The sup-norm problem on the Siegel modular space of rank two, Amer. J. Math. 138 (2016), 999–1027.CrossRefGoogle Scholar
Borel, A., Compact Clifford–Klein forms of symmetric spaces, Topology 2 (1963), 111–122.CrossRefGoogle Scholar
Borel, A., Linear algebraic groups, Graduate Texts in Mathematics, vol. 126, second edition (Springer, New York, 1991).CrossRefGoogle Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local: II. Schémas en groupes. Existence d’une donnée radicielle valué, Publ. Math. Inst. Hautes Études Sci. 60 (1984), 5–184.CrossRefGoogle Scholar
Casselman, W., The unramified principal series of p-adic groups I, Compos. Math. 40 (1980), 387–406.Google Scholar
Colin de Verdière, Y., Ergodicité et fonctions propres du Laplacien, Comm. Math. Phys. 102 (1985), 497–502.CrossRefGoogle Scholar
Donnelly, H., Exceptional sequences of eigenfunctions for hyperbolic manifolds, Proc. Amer. Math. Soc. 135 (2007), 1551–1555.CrossRefGoogle Scholar
Duistermaat, J. J., Kolk, J. A. C. and Varadarajan, V. S., Spectra of compact locally symmetric manifolds of negative curvature, Invent. Math. 52 (1979), 27–93.CrossRefGoogle Scholar
Feigon, B., Lapid, E. and Offen, O., On representations distinguished by unitary groups, Publ. Math. Inst. Hautes Études Sci. 115 (2012), 185–323.CrossRefGoogle Scholar
Finis, T. and Lapid, E., An approximation principle for congruence subgroups, J. Eur. Math. Soc. (JEMS) 20 (2018), 1075–1138.CrossRefGoogle Scholar
Gangolli, R., On the Plancherel formula and the Paley–Wiener theorem for spherical functions on semisimple Lie groups, Ann. of Math. (2) 93 (1971), 105–165.Google Scholar
Gross, B., On the Satake isomorphism, in Galois representations in arithmetic algebraic geometry (Durham, 1996), London Mathematical Society Lecture Note Series, vol. 254 (Cambridge University Press, Cambridge), 223–238.Google Scholar
Gross, B., On the motive of a reductive group, Invent. Math. 130 (1997), 287–313.CrossRefGoogle Scholar
Harish-Chandra, A formula for semisimple Lie groups, Amer. J. Math. 79 (1957), 733–760.CrossRefGoogle Scholar
Harish-Chandra, Some results on an invariant integral on a semi-simple Lie algebra, Ann. of Math. (2) 80 (1964), 551–593.CrossRefGoogle Scholar
Harish-Chandra, Discrete series for semisimple Lie groups II, Acta Math. 116 (1966), 1–111.CrossRefGoogle Scholar
Helgason, S., Groups and geometric analysis, Mathematical Surveys and Monographs, vol. 83. (American Mathematical Society, Providence, RI, 2000).CrossRefGoogle Scholar
Helgason, S., Differential geometry, Lie groups, and symmetric spaces, Graduate Studies in Mathematics, vol. 34 (American Mathematical Society, Providence, RI, 2001).CrossRefGoogle Scholar
Helgason, S., Geometric analysis on symmetric spaces, Mathematical Surveys and Monographs, vol. 39 (American Mathematical Society, 2008).CrossRefGoogle Scholar
Helminck, A. G. and Wang, S. P., On rationality properties of involutions of reductive groups, Adv. Math. 99 (1993), 26–97.CrossRefGoogle Scholar
Iwaniec, H. and Sarnak, P., L ∞ norms of eigenfunctions of arithmetic surfaces, Ann. of Math. (2) 141 (1995), 301–320.CrossRefGoogle Scholar
Jacquet, H., Kloosterman identities over a quadratic extension II, Ann. Sci. Éc. Norm. Supér. (4) 38 (2005), 609–669.CrossRefGoogle Scholar
Jacquet, H., Lai, K. and Rallis, S., A trace formula for symmetric spaces, Duke Math. J. 70 (1993), 305–372.CrossRefGoogle Scholar
Knapp, A., Lie groups beyond an introduction, Progress in Mathematics, vol. 140 (Birkhäuser, Boston, 2002).Google Scholar
Kottwitz, R., Stable trace formula: elliptic singular terms, Math. Ann. 275 (1986), 365–400.CrossRefGoogle Scholar
Kottwitz, R., Tamagawa numbers, Ann. of Math. (2) 127 (1988), 629–646.CrossRefGoogle Scholar
Lapid, E. and Offen, O., Compact unitary periods, Compos. Math. 143 (2007), 323–338.CrossRefGoogle Scholar
Levitan, B. M., On the asymptoptic behavior of the spectral function of a self-adjoint differential equation of second order, Isv. Akad. Nauk SSSR Ser. Mat. 16 (1952), 325–352.Google Scholar
Macdonald, I. G., Spherical functions on a group of p-adic type, Publications of the Ramanujan Institute no. 2 (Ramanujan Institute, Centre for Advanced Study in Mathematics, University of Madras, Madras, 1971).Google Scholar
Maclachlan, C. and Reid, A. W., The arithmetic of hyperbolic 3-manifolds (Springer, New York, 2003).CrossRefGoogle Scholar
Marshall, S., Upper bounds for Maass forms on semisimple groups, Preprint (2014),arXiv:1405.7033.Google Scholar
Matz, J. and Templier, N., Sato–Tate equidistribution for families of Hecke–Maass forms on $\text{SL}(n,\mathbb{R})/\text{SO}(n)$, Preprint (2015), arXiv:1505.07285.Google Scholar
Milicevic, D., Large values of eigenfunctions on arithmetic hyperbolic 3-manifolds, Geom. Funct. Anal. 21 (2011), 1375–1418.CrossRefGoogle Scholar
Nadler, D., Perverse sheaves on real loop Grassmannians, Invent. Math. 159 (2005), 1–73.CrossRefGoogle Scholar
Onishchik, A. and Vinberg, E., Lie groups and Lie algebras III, Encyclopaedia of Mathematical Sciences, vol. 41 (Springer, Berlin, 1994).CrossRefGoogle Scholar
Rudnick, Z. and Sarnak, P., The behaviour of eigenstates of arithmetic hyperbolic manifolds, Comm. Math. Phys. 161 (1994), 195–213.CrossRefGoogle Scholar
Saha, A., Large values of newforms on GL (2) with highly ramified central character, Int. Math. Res. Not. IMRN 2016 (2016), 4103–4131.CrossRefGoogle Scholar
Sakellaridis, Y., On the unramified spectrum of spherical varieties over p-adic fields, Compos. Math. 144 (2008), 978–1016.CrossRefGoogle Scholar
Sakellaridis, Y., Spherical functions on spherical varieties, Amer. J. Math. 135 (2013), 1291–1381.CrossRefGoogle Scholar
Sakellaridis, Y. and Venkatesh, A., Periods and harmonic analysis on spherical varieties, Astérisque 396 (2017).Google Scholar
Sarnak, P., Arithmetic quantum chaos, Israel Mathematical Conference Proceedings, Schur Lectures (Bar-Ilan University, Ramat-Gan, Israel, 1995).Google Scholar
Sarnak, P., Letter to Morawetz, available at http://publications.ias.edu/sarnak/paper/480.Google Scholar
Schnirelman, A. I., Ergodic properties of eigenfunctions, Uspekhi Mat. Nauk 29 (1974), 181–182.Google Scholar
Shin, S.-W. and Templier, N., Sato–Tate theorem for families and low-lying zeros of automorphic L-functions, Invent. Math. 203 (2016), 1–177.CrossRefGoogle Scholar
Sogge, C. and Zelditch, S., Riemannian manifolds with maximal eigenfunction growth, Duke Math. J. 114 (2002), 387–437.Google Scholar
Steinberg, R., Endomorphisms of linear algebraic groups, Mem. Amer. Math. Soc. 80 (1968).Google Scholar
Templier, N., Large values of modular forms, Camb. J. Math. 2 (2014), 91–116.CrossRefGoogle Scholar
Tits, J, Reductive groups over local fields, in Automorphic forms, representations and L-functions, Proceedings of Symposia in Pure Mathematics, vol. 33 (American Mathematical Society, Providence, RI, 1979), 29–70; Part 1.CrossRefGoogle Scholar
Vust, T., Opération de groupes réductifs dans un type de cônes presque homogènes, Bull. Soc. Math. France 102 (1974), 317–333.CrossRefGoogle Scholar
Zelditch, S., Uniform distribution of eigenfunctions on compact hyperbolic surfaces, Duke Math. J. 55 (1987), 919–941.CrossRefGoogle Scholar