Clay characterization

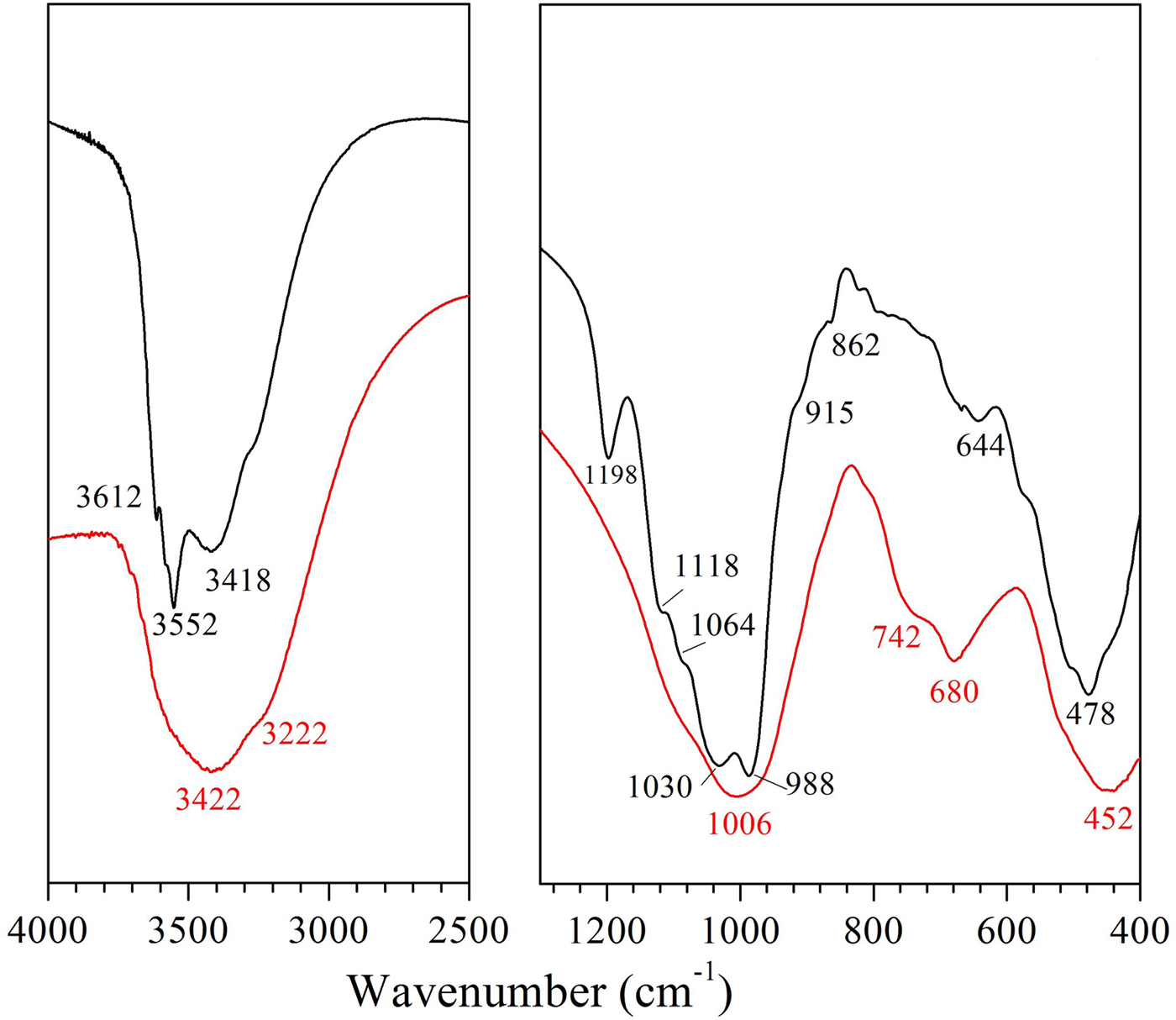
Examination of the XRD patterns (Fig. 1) showed that ATP consists mainly of palygorskite (92%), minor nontronite (5%) and quartz (3%), while in the VRM sample, vermiculite (72%) along with mixed-layer biotite-vermiculite (hydrobiotite, 17%) and chlorite-vermiculite (corrensite, 11%) were detected. The XRD results were confirmed by the FTIR analysis (Fig. 2). The FTIR spectrum (Fig. 2) of ATP is typical of Fe-rich palygorskite exhibiting two bands at 3612 and 3552 cm⁻¹ attributed to the structural OH-stretching vibrations of Al and Fe, while the stretching vibration at 3418 cm⁻¹ was due to water in the palygorskite channels (Chahi et al., Reference Chahi, Petit and Decarreau2002; Suárez & García-Romero, Reference Suárez and García-Romero2006). Also, a very characteristic Si–O stretching pattern for palygorskite was presented with a high-frequency component at 1198 cm⁻¹ and a doublet of low-frequency vibrations at 1030 and 988 cm⁻¹ (Mendelovici, Reference Mendelovici1973; Frost et al., Reference Frost, Locos, Ruan and Kloprogge2001; Madejová et al., Reference Madejová, Balan, Petit and Christidis2011). The structural OH-stretching band at 3612 cm⁻¹ along with the well-defined Al₂OH deformation band at 915 cm⁻¹ and a slight inflection near 862 cm⁻¹ (AlMgOH) reflect the dominantly dioctahedral character of the ATP sample (Madejová & Komadel, Reference Madejová and Komadel2001). Additionally, the bands at 3552 cm⁻¹ and 820 cm⁻¹ assigned to Fe₂OH stretching and bending, respectively, validated the presence of dioctahedral smectite (nontronite) in the ATP sample (Christidis et al., Reference Christidis, Katsiki, Pratikakis and Kacandes2010) and not trioctahedral smectite (saponite) as was assumed in earlier studies (Kastritis et al., Reference Kastritis, Kacandes, Mposkos and Eliopoulos2003). Quartz admixture (790 cm⁻¹) was also revealed in ATP spectra. On the other hand, the spectrum of vermiculite (VRM) showed a strong, broad OH-stretching band at 3422 cm⁻¹ characteristic of mixed-layer vermiculite samples (Muiambo et al., Reference Muiambo, Focke, Atanasova, Van Der Westhuizen and Tiedt2010). The band at 1006 cm⁻¹ was ascribed to a Si-O-Si stretching.

Fig. 1. XRD patterns of the natural clays studied: palygorskite (upper) and vermiculite (lower). Inset are the patterns of the oriented (black line), glycolated (red line) and heated (blue line) samples. Pal: palygorskite (JCPDS card No. 31-0783), Sm: smectite (JCPDS card No. 29-1497), Q: quartz (JCPDS card No. 46-1045), VRM: vermiculite (JCPDS card 16-0613).

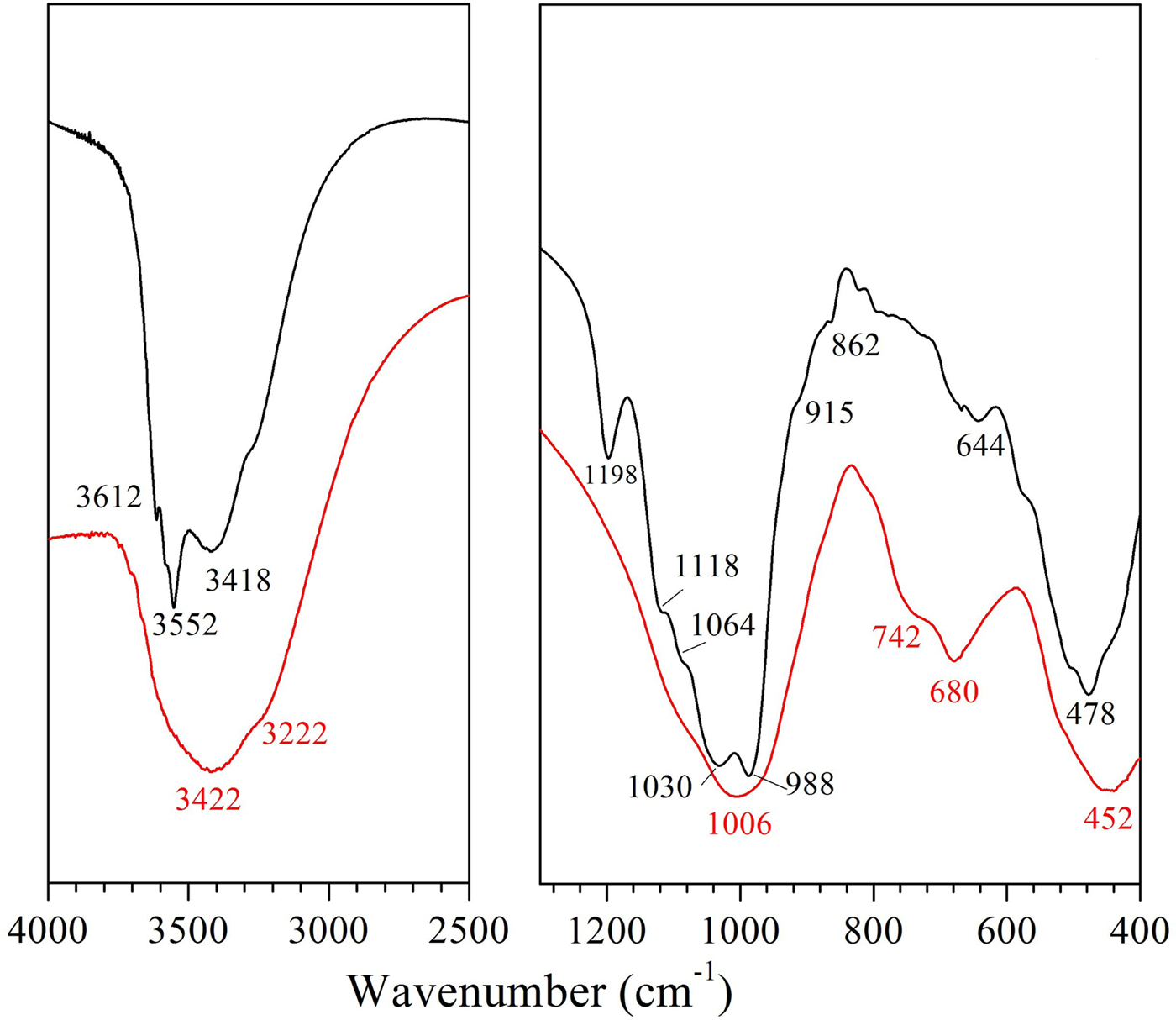
Fig. 2. FTIR spectra of the natural clays studied: palygorskite (ATP, black line) and vermiculite (VRM, red line).

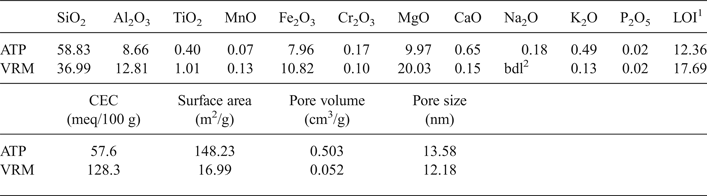
The SEM images show a typical fibrous texture for attapulgite (ATP), while in the VRM, the mixed-layer phases were presented as brighter and darker regions (Fig. 3). The chemical compositions of the natural clays used, the CEC values and the textural properties of the clays are listed in Table 1.

Fig. 3. SEM images of the palygorskite (ATP, left) and vermiculite (VRM, right).

Table 1. Chemical composition (wt. %), CEC and textural properties of the natural clays studied.

¹ LOI: loss on ignition, ² bdl: below detection limit.

Effects of various parameters on the ability of adsorbents to remove Cu and Ni

Effect of pH

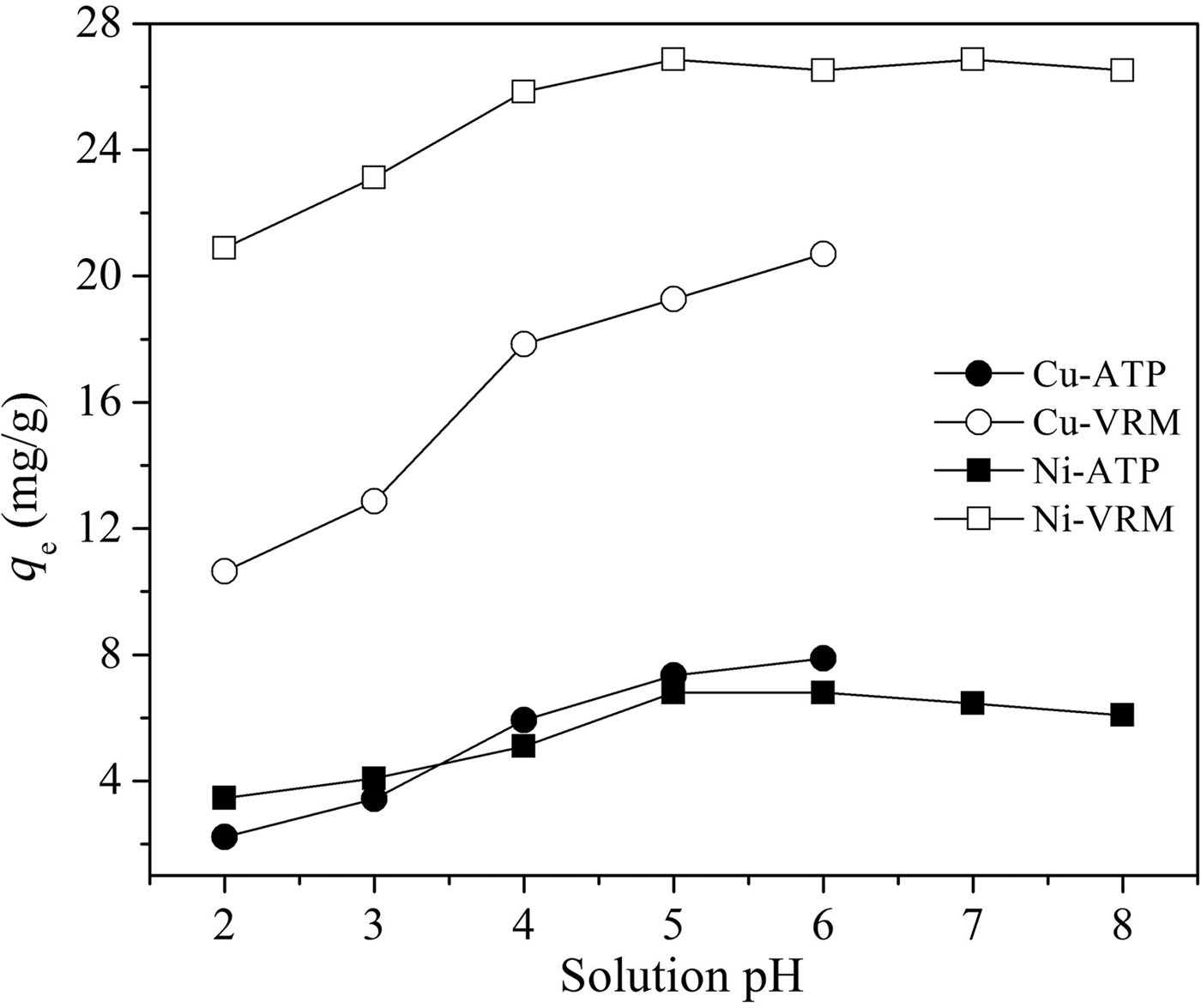
The initial pH value of the metal aqueous solution is a significant factor in the adsorption process and this controls the uptake of the metal ions at the adsorbent–clay interfaces. The effect of solution pH was investigated in the range 2–6 for copper and 2–8 for nickel, which avoids metal precipitation in hydroxide forms and maintains their cationic species (Bayat, Reference Bayat2002; Sen Gupta & Bhattacharyya, Reference Sen Gupta and Bhattacharyya2008); results are shown in Fig. 4. The adsorption of Cu²⁺ and Ni²⁺ ions was highly pH-dependent, and increased adsorption capacities, q _e (mg g⁻¹) with increasing pH were observed. As far as the efficiency of the studied clays is concerned, vermiculite took up more Cu²⁺ and Ni²⁺ ions at a given pH than palygorskite. The differences in amount adsorbed with pH, and particularly the reduced removal efficiencies for all studied cases at low pH, could be ascribed to: (1) the antagonism between the metal and H₃O⁺ ions for the vacant adsorption sites on clay surfaces at substantially low pH values; and (2) surface protonation reactions lead to positively charged clay surfaces at lower pH and hence to increased repulsion forces between metal ions and clay surfaces, which prevent metal ions from accessing the surface binding sites. This ultimately leads to lower adsorption efficiency (Mathialagan & Viraraghavan, Reference Mathialagan and Viraraghavan2003; Sen Gupta & Bhattacharyya, Reference Sen Gupta and Bhattacharyya2008).

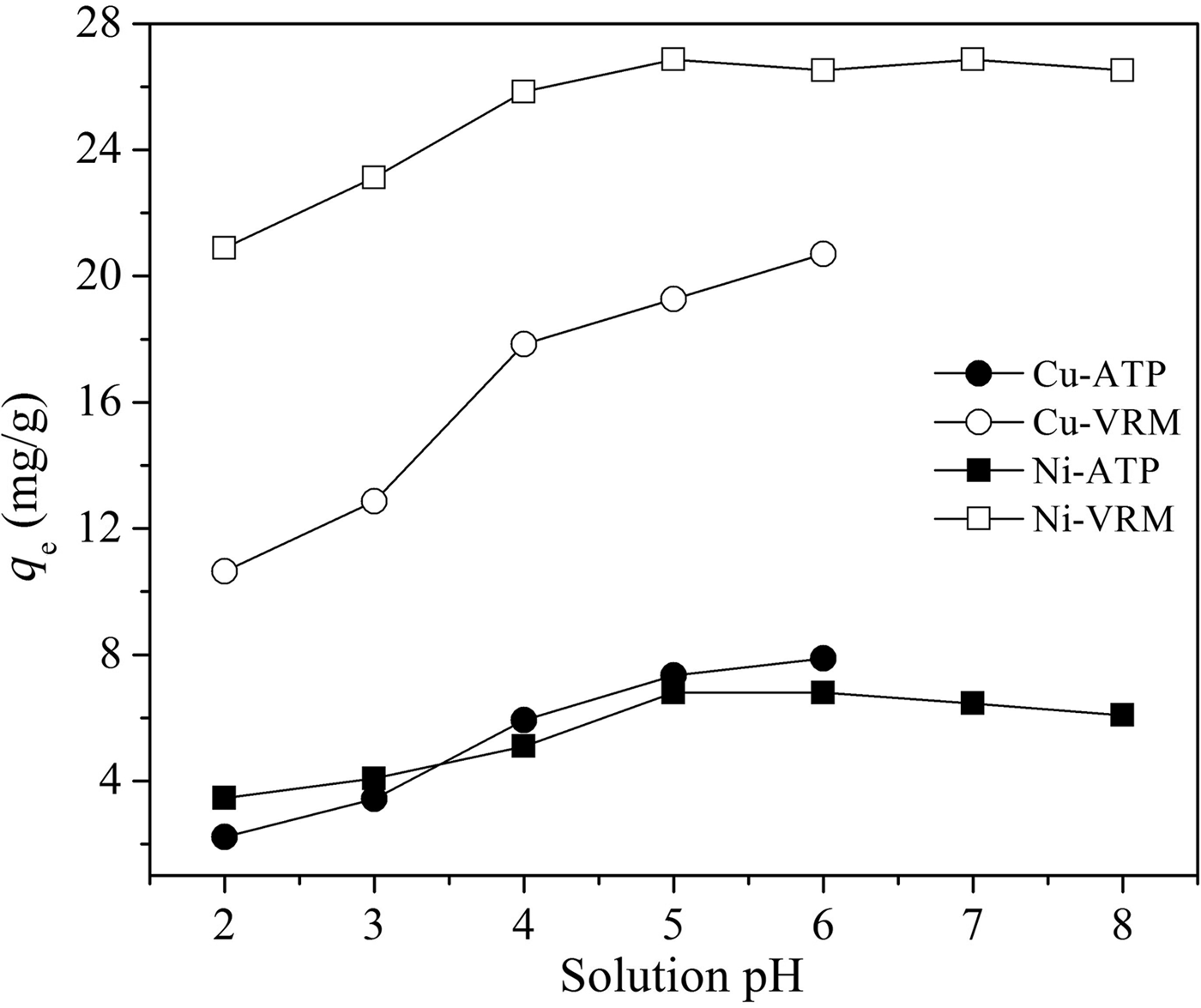
Fig. 4. Effect of pH on Cu²⁺, and Ni²⁺ adsorption by the natural clays studied. Contact time: 120 min; adsorbent dosage: 1 g L⁻¹; initial metal concentration: 50 mg L⁻¹.

Effect of clay amount

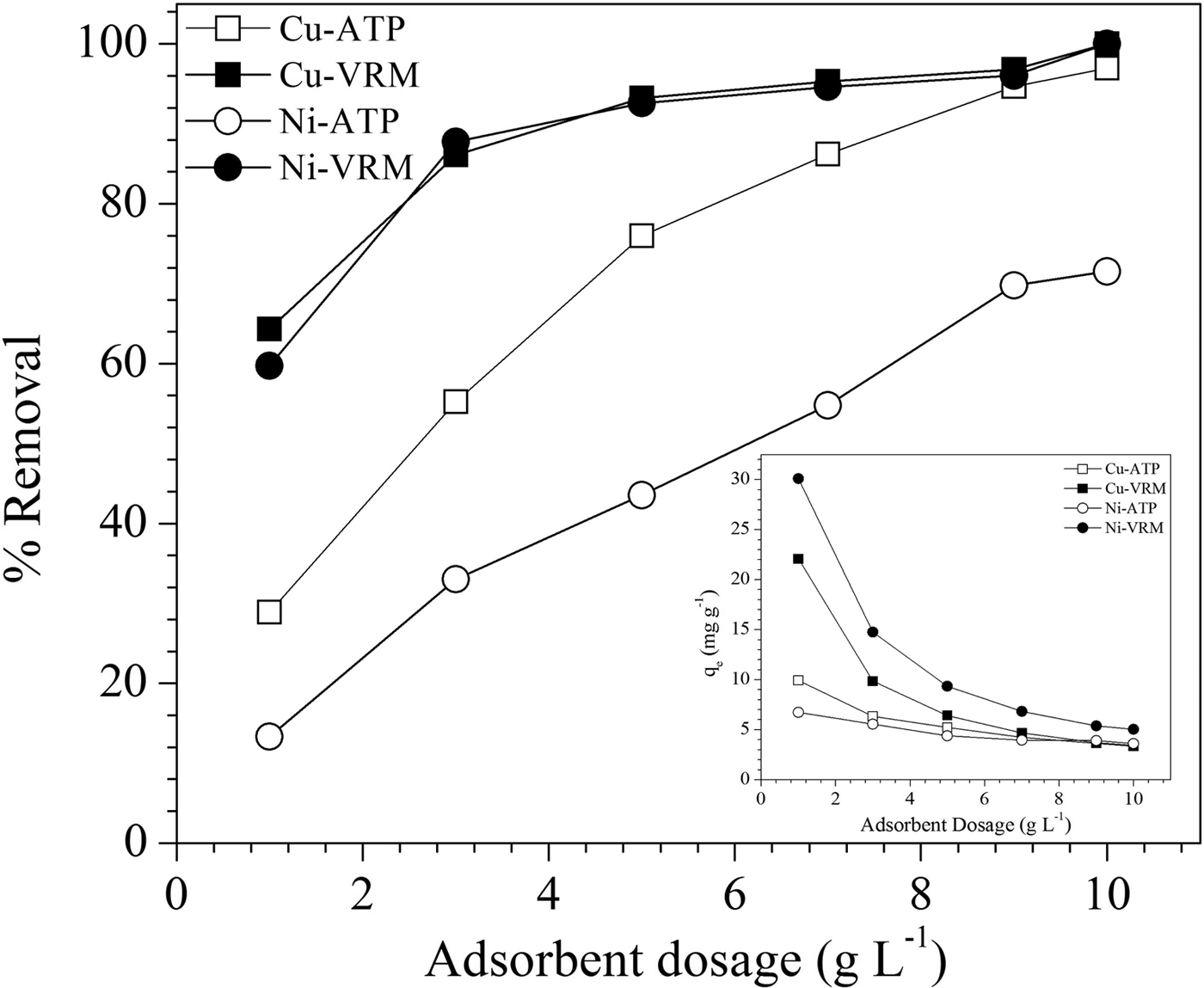
The effect of clay amount was studied by variation of dosages from 0.1 to 1 g L⁻¹ and the results are presented in Fig. 5. In VRM a dose of 5 g L⁻¹ exhibited removal efficiency of >90% for both Cu²⁺ and Ni²⁺ ions, while for ATP larger amounts are necessary to achieve satisfactory removal efficiencies. Generally, the adsorption extent, calculated as the % removal of Cu²⁺ and Ni²⁺ ions, increased with increasing clay dosage. This might be ascribed to the larger surface area and more binding sites available as the clay amount increased (Liu & Zhou, Reference Liu and Zhou2010; Sen & Gomez, Reference Sen and Gomez2011). A reverse trend was observed in adsorption capacity (q _e) which decreased gradually with the increase in clay amount. This might be explained by: (1) the large clay quantities efficiently diminish the saturation of the adsorption sites resulting in the reduction of covered sites per unit mass and therefore to a lesser adsorption capacity; and (2) higher clay dosages led to aggregation phenomena which result in lower total surface area, and increased divisional path length, both of which lead to decreased adsorption capacity (Shukla et al., Reference Shukla, Zhang, Dubey, Margrave and Shukla2002).

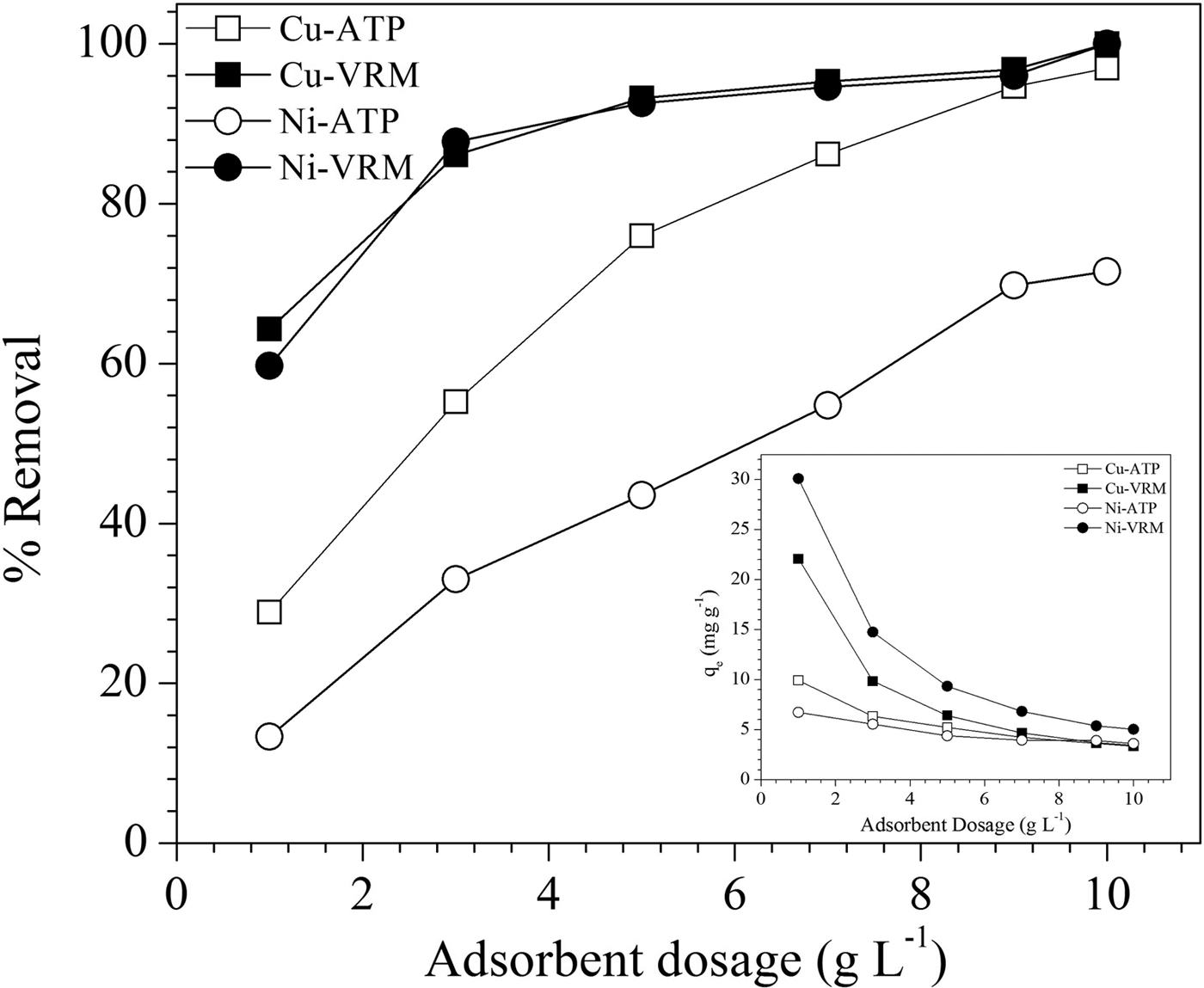
Fig. 5. Effect of adsorbent dosage on Cu²⁺ and Ni²⁺ adsorption by the natural clays studied. Contact time: 120 min; initial pH: pH_Cu 5.10, pH_Ni 4.85; initial metal concentration: 50 mg L⁻¹.

Effect of contact time and adsorption kinetics

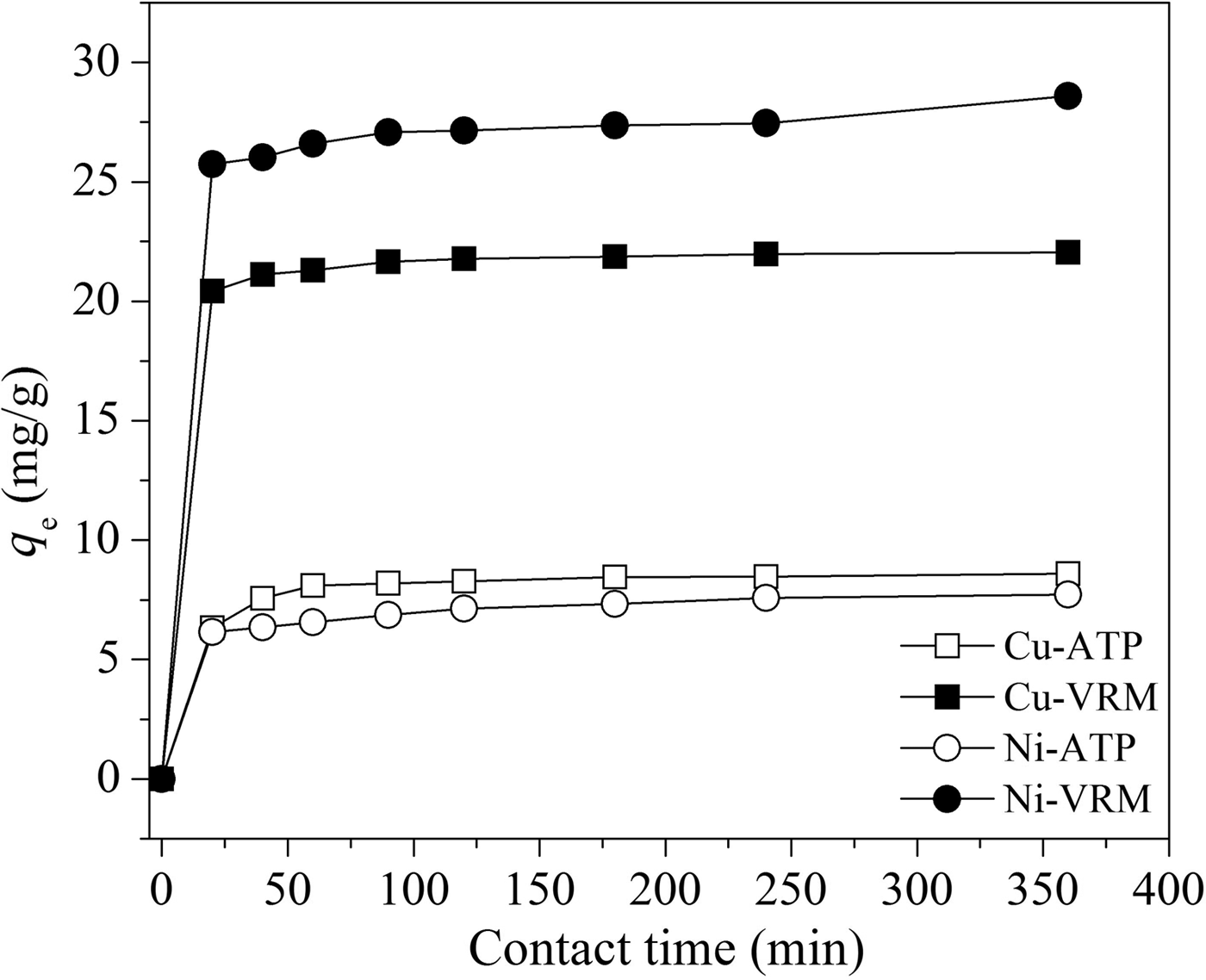
The effect of contact time on the adsorption of Cu²⁺ and Ni²⁺ ions was investigated at various time intervals in the range 20–360 min and the results are presented in Fig. 6. The removal of Cu²⁺ and Ni²⁺ ions increased rapidly in both clays in the first 20 min of adsorption, while negligible differences in the removal of metal ions were noted after ~60 min of contact, indicating that adsorption equilibrium was established. This might be attributed to the high rate at which adsorption takes place on the free surface in the first stage of adsorption, while, as the sites were filled with the metal ions, the rate decreased (Srivastava et al., Reference Srivastava, Mall and Mishra2008). The adsorption capacities recorded for vermiculite were significantly higher than those for palygorskite, indicating its better applicability.

Fig. 6. Effect of contact time on Cu²⁺, and Ni²⁺ adsorption by the natural clays studied. Initial metal concentration: 50 mg L⁻¹; initial pH: pH_Cu 5.10, pH_Ni 4.85; adsorbent dosage: 1 g L⁻¹.

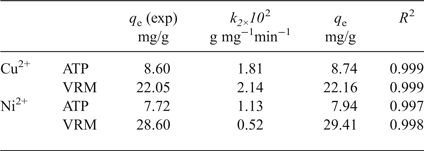
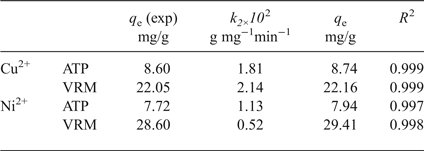
In order to investigate the adsorption mechanism, and particularly the adsorption rate, various kinetic models (data not shown) were used. The best-fit kinetic model was evaluated by the linear coefficient of determination (R ²) and the experimental (q _e,exp) and calculated (q _e,cal) adsorption capacities. Larger R ² values and the smaller variations in q _e values were observed for a pseudo-second-order kinetic model (Table 2), which is expressed by equation 3 (Ho & McKay, Reference Ho and McKay1998) as follows:

(3)$$\displaystyle{t \over {q_{\rm t}}} = \displaystyle{1 \over {(k_2q_{\rm e}^2 )}} + \displaystyle{1 \over {q_{\rm e}}}t$$

where q _t and q _e are the adsorption capacities at time t (min) and equilibrium time (mg g⁻¹), respectively and k ₂ (g mg⁻¹ min⁻¹) is the rate constant of the pseudo-second-order adsorption, which better described the experimental kinetic data.

Table 2. Parameters of the pseudo-second-order kinetic model for adsorption of Cu²⁺ and Ni²⁺ ions by the natural clays studied.

Adsorption isotherms

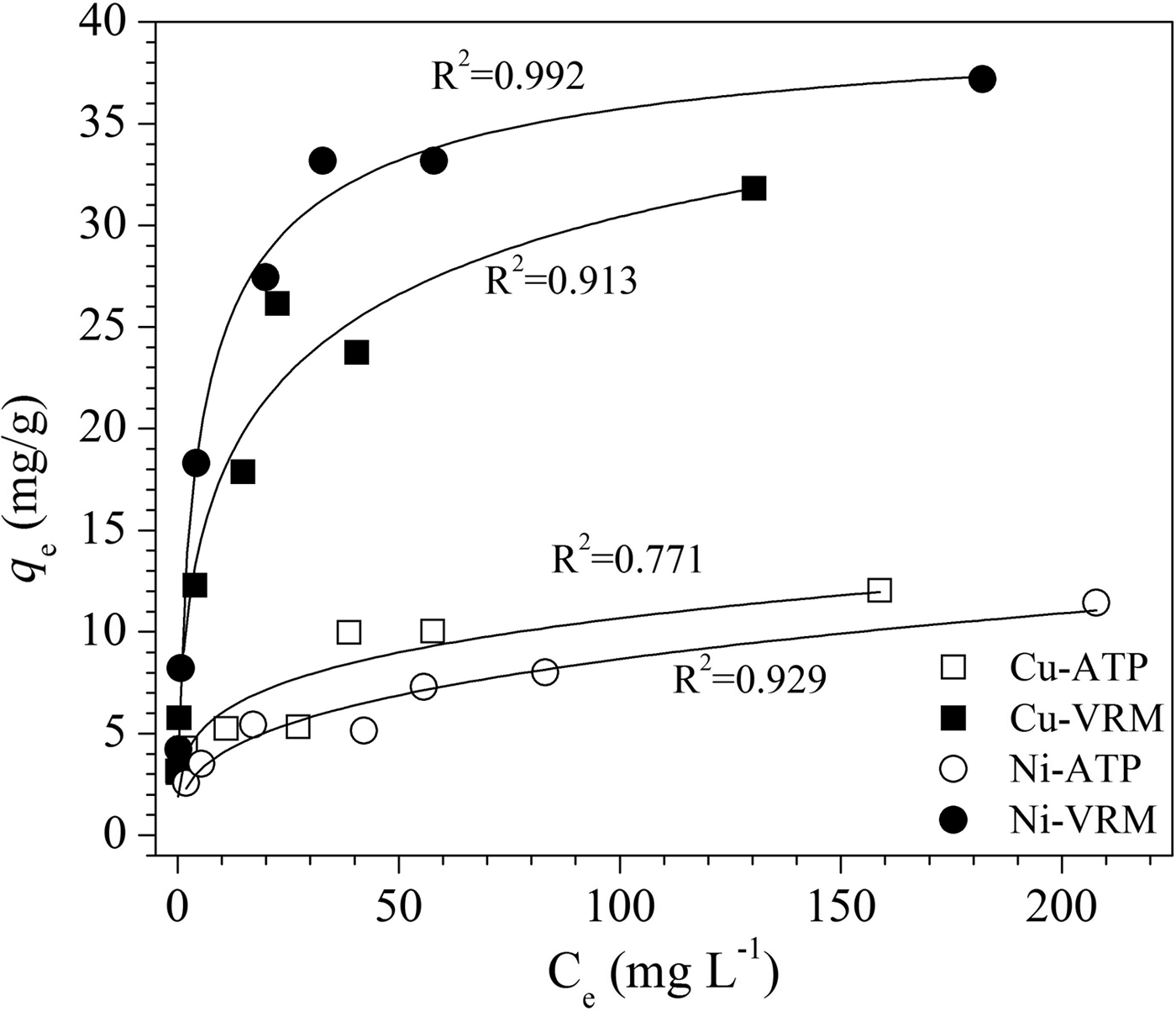
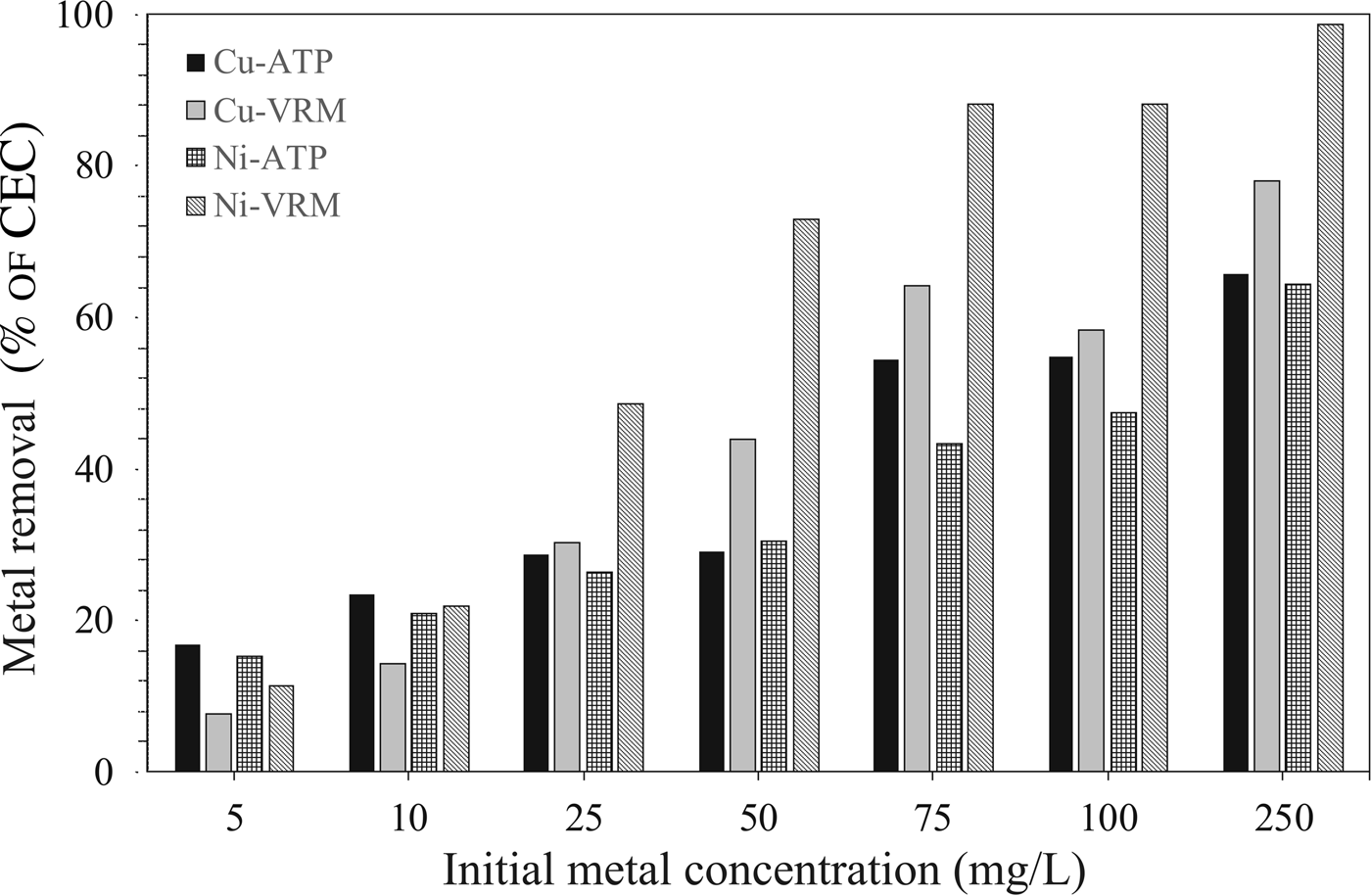
The experimental data obtained from the adsorption isotherm studies are essential for assessment of the surface properties and the affinity of an adsorbent for a specific sorbate, both of which are critical in optimizing its usage. The adsorption isotherms for Cu²⁺ and Ni²⁺ are presented in Fig. 7. The increase in the initial metal concentration resulted in an increase of the adsorption capacity. The isotherms were of L-type (Giles et al., Reference Giles, Smith and Huitson1974) indicating a high affinity between sorbent and solute. Τhe Cu²⁺ and Ni²⁺ ions adsorbed per unit mass of the natural clays studied were expressed as a percentage of the CEC and the results are given in Fig. 8. Even for an initial Cu²⁺ concentration of 250 mg/L, almost 66% and 78% of the available exchangeable sites of ATP and VRM samples were covered, respectively. Correspondingly, almost 64% and 98% of the available sites of ATP and VRM were covered with Ni²⁺, respectively.

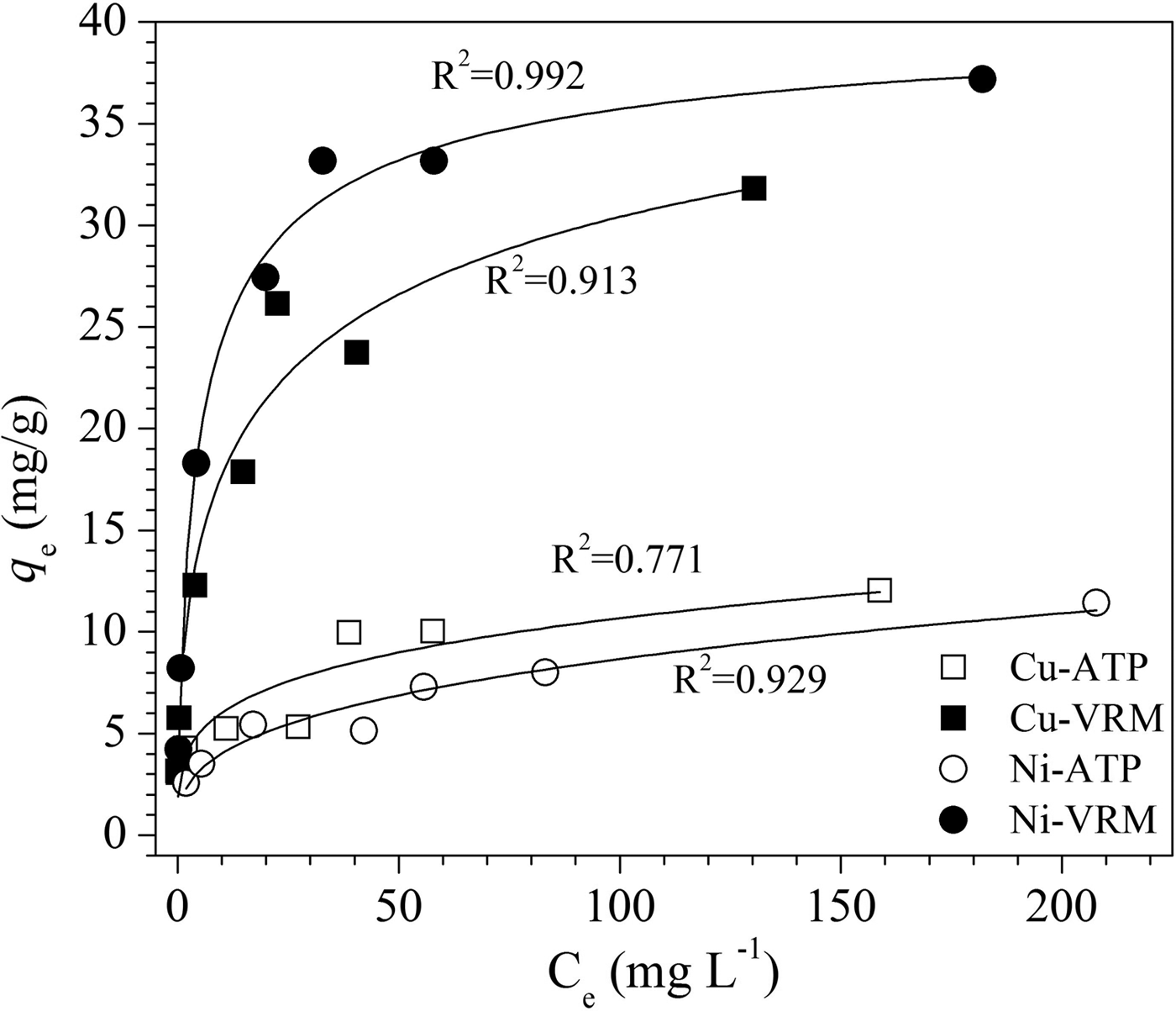
Fig. 7. Adsorption isotherms for Cu²⁺ and Ni²⁺ ions. The lines represent a non-linear fit of the Langmuir isotherm.

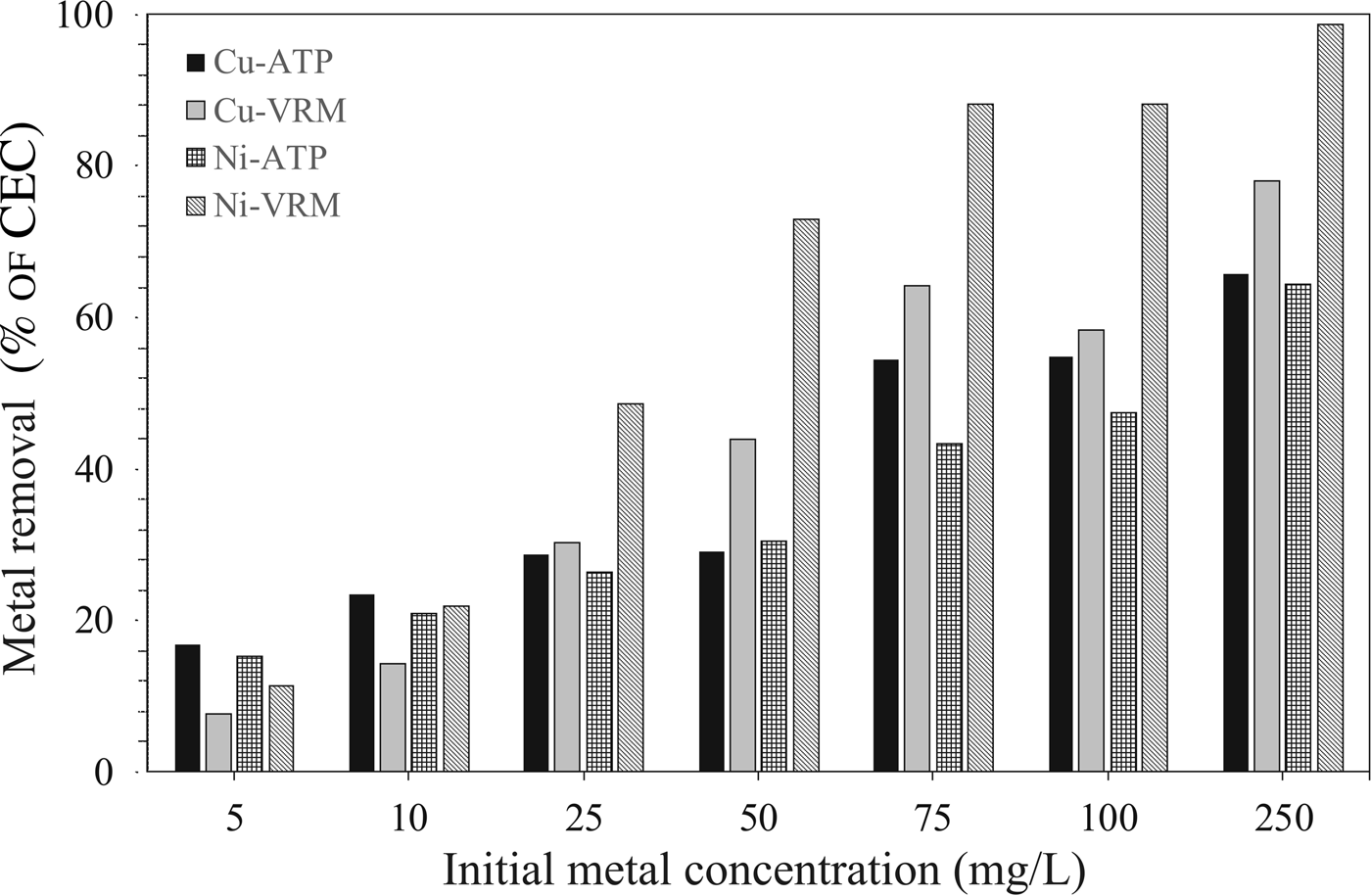
Fig. 8. The amounts of Cu²⁺ and Ni²⁺ ions adsorbed in different initial concentrations, expressed as a percentage (%) of the CEC of the natural clays studied.

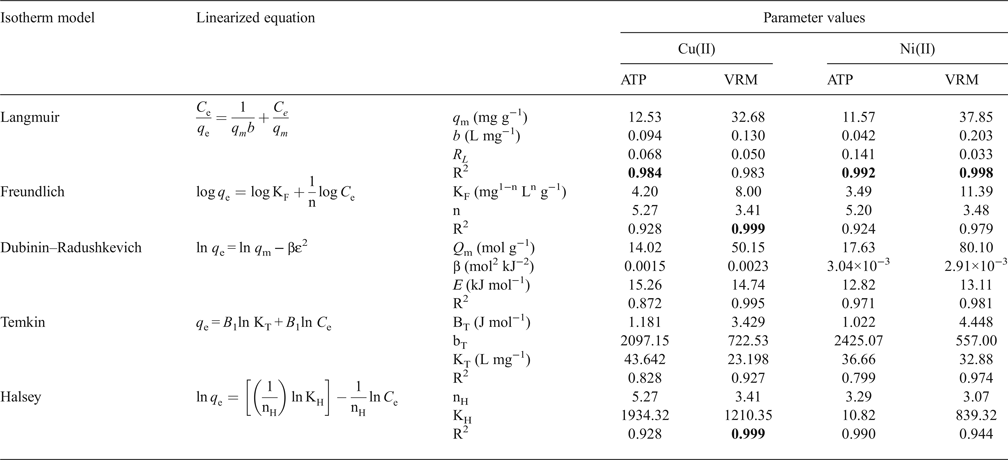
With a view to understanding the mechanism of Cu²⁺ and Ni²⁺ adsorption onto the ATP and VRM samples, the experimental data obtained were tested with the Langmuir, Freundlich, Dubinin–Radushkevich (D–R), Temkin and Halsey isotherm models. The adsorption isotherm models equations are shown below (equations 4–8):

(4)$$q_{\rm e} = \displaystyle{{q_{\rm m}{\rm b}C_{\rm e}} \over {(1 + bC_{\rm e})}}$$

where q _e (mg g⁻¹) is the adsorption capacity at equilibrium, C _e (mg L⁻¹) is the concentration of the sorbate at equilibrium, b (L mg⁻¹) is the Langmuir equilibrium constant associated to the energy of adsorption and q _m (mg g⁻¹) denotes the theoretical Langmuir monolayer adsorption capacity.

(5)$$q_{\rm e} = K_FC_{\rm e}^{1/{\rm n}} $$

where K_F (mg¹⁻ⁿ Lⁿ g⁻¹) and n (dimensionless) are Freundlich constants related to adsorption capacity and sorption intensity, respectively.

(6)$$q_{\rm e} = Q_{\rm m}e^{ - {\rm \beta \varepsilon} ^2}$$

where Q _m (mol g⁻¹) is the Dubinin–Radushkevich monolayer capacity, β (mol² kJ⁻²) is a constant related to sorption energy, and ε represents the Polanyi potential constant which is related to the equilibrium concentration and is given as $\varepsilon = {\rm R}T\ln (1 + \displaystyle{1 \over {C_{\rm e}}})$, where R is the gas constant (8.314.10⁻³ kJ mol⁻¹ K⁻¹) and T is the absolute temperature (K). Constant β gives the mean adsorption energy, E, of sorption per molecule of the sorbate when it is transferred to the surface of the solid from infinity in the solution and can be computed as $E = \displaystyle{1 \over {\sqrt {2{\rm\beta}}}} $

(7)$$q_{\rm e} = B_T\ln (\hbox{K}_{\rm T}C_{\rm e})$$

where B _T (J mol⁻¹) is related to the heat of adsorption and is given as $B_T = \displaystyle{{{\rm R}T} \over {\hbox{b}_{\rm T}}}$, while b_T is the Temkin isotherm constant and K_T (L mg⁻¹) is the equilibrium binding constant.

(8)$$q_{\rm e} = e^{\left[ {\displaystyle{{\left( {\ln {\rm K}_{\rm H} - \ln C_{\rm e}} \right)} \over {{\rm n}_{\rm H}}}} \right]}$$

where K_H and n_H are the Halsey isotherm constants.

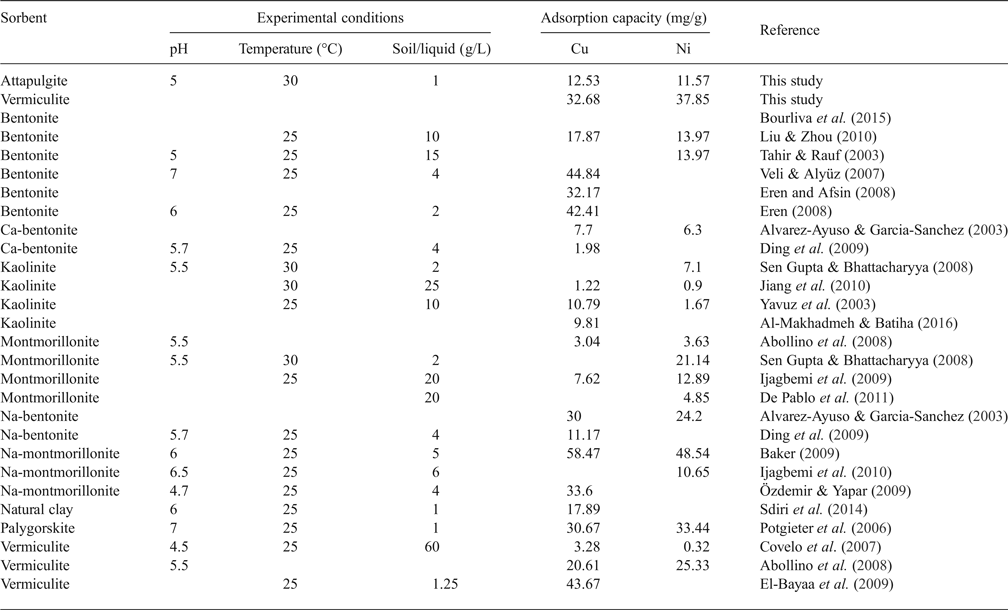
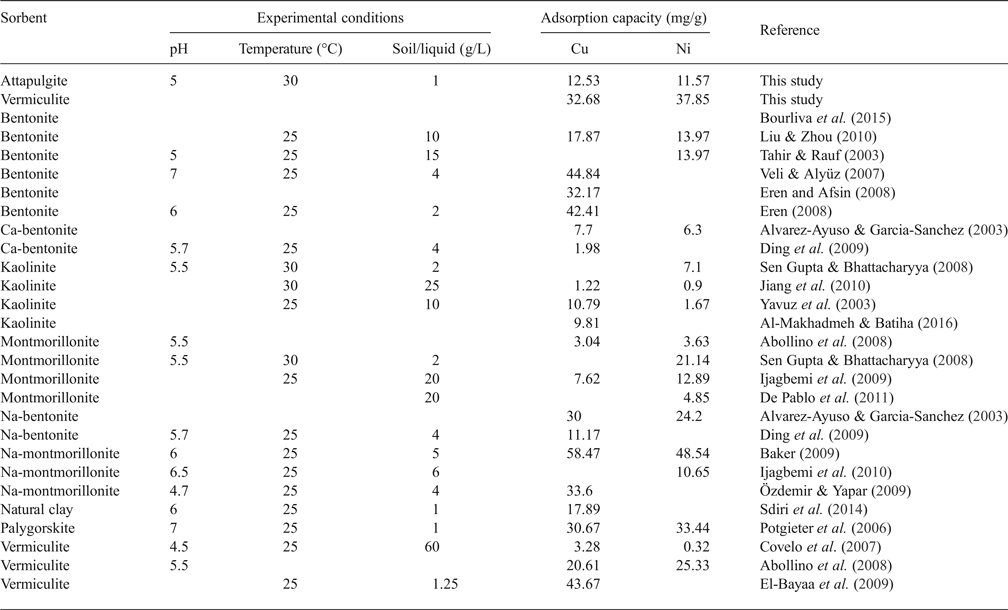
The linear coefficient of determination, R², was used to confirm the good fitness of each isotherm model to the experimental data, and the values along with the isotherms’ parameters are presented in Table 3. The highest values of R² were observed for the Langmuir isotherm with the exception of Cu²⁺ adsorption onto VRM which follows the Freundlich isotherm model. The Langmuir equilibrium coefficient, b, was large with values of 42–94 L g⁻¹ (Table 3) for the metal-ATP systems and even larger (130–203 L g⁻¹) for the metal ion-VRM systems. The higher value of b (203 L g⁻¹) for the adsorption of Ni²⁺ ions onto vermiculite showed that the interactions were stronger between nickel ions and vermiculite. The maximum adsorption capacity q _m was 12.53 mg g⁻¹ and 32.68 mg g⁻¹ for Cu²⁺ for ATP and VRM, respectively, while for Ni²⁺ ions it was 11.57 mg g⁻¹ and 37.85 mg g⁻¹, respectively for ATP and VRM. The maximum adsorption capacities determined were higher in VRM than in ATP for both the Cu²⁺ and Ni²⁺ ions. Although the different experimental conditions applied make direct comparison between various adsorbents difficult, the adsorption capacities of the natural clays utilized in this study were notably higher than values reported from similar studies (Table 4). The separation factor, R_L, values calculated by the equation R_L=1/(1+bC ₀), where C ₀ (mg L⁻¹) is the initial Cu²⁺ or Ni²⁺ concentration in the solution and b (L mg⁻¹) is the Langmuir constant, varied between 0.33 and 0.141 indicating favourable adsorption.

Table 3. Adsorption isotherm models and parameter values for the adsorption of Cu²⁺ and Ni²⁺ ions on the studied clays.

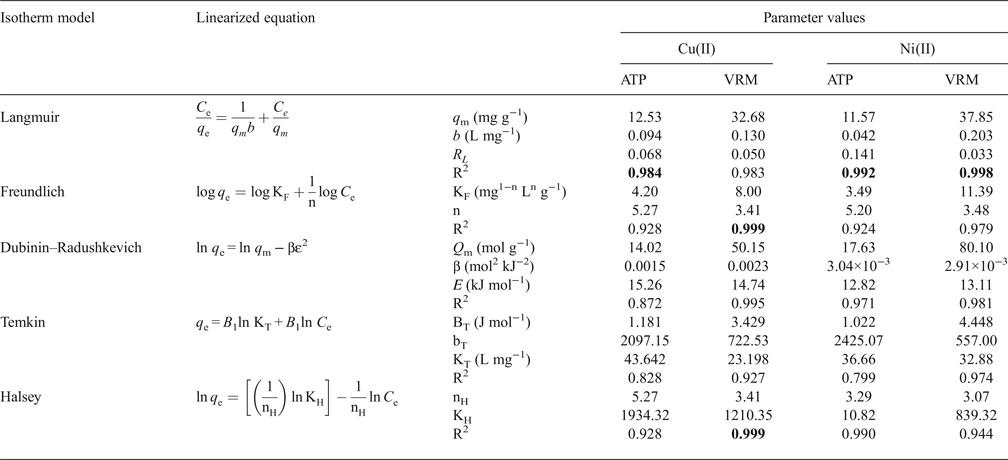
Significant R² values are marked in bold.

Table 4. Reported results on the adsorption capacities of various clay minerals for Cu²⁺ and Ni²⁺ ions.

The Freundlich isotherm model, based on multilayer adsorption, exhibited good applicability (R² = 0.924–0.999). The estimated Freundlich adsorption constant (K_F) was higher for vermiculite (Cu²⁺: 8.00, Ni²⁺: 11.39 mg¹⁻ⁿ Lⁿ g⁻¹) compared to that of palygorskite (Cu²⁺: 4.20, Ni²⁺: 3.49 mg¹⁻ⁿ Lⁿ g⁻¹). This is in accordance with the experimental results in which vermiculite exhibited higher adsorption capacities than palygorskite. The Freundlich coefficient n values ranging from 1 to 10 (3.41–5.27) support the favourable adsorption of Cu²⁺ and Ni²⁺ ions onto the studied natural clays.

The D–R model described the experimental data well with the exception of Cu²⁺ adsorption onto ATP which presented a lower R² value (0.872) (Table 3). Within D–R parameters, the mean free energy (E) offers valuable information on the mechanism of adsorption. The E values were >8 kJ mol⁻¹ (range 12.82–18.26 kJ mol⁻¹) in all cases, suggesting the dominance of chemical adsorption of Cu²⁺ and Ni²⁺ ions onto ATP and VRM. The comparison of D–R and Langmuir models’ maximum monolayer capacity showed that the Langmuir model fitted the experimental data better than D–R isotherm. The Langmuir parameter (q _m) was closer to the experimental capacity determined compared with the corresponding D–R parameter (Q _m) which is higher than the experimental capacity value determined. Consequently, the Langmuir model explained better the Cu²⁺ and Ni²⁺ ions’ adsorption onto the studied natural clays than the Dubinin–Radushkevich model.

The Temkin isotherm (data not shown) provides a close fit to the data for adsorption of Cu²⁺ and Ni²⁺ onto vermiculite, but the experimental data for the adsorption of the metal ions studied onto ATP did not fit well in the concentration range studied (Table 3). The values of the Temkin constants B_T, b_T and K_T are listed in Table 2. The B_T values which are indicative of the heat of metal adsorption onto the studied natural clays were positive (1.022–4.448 J mol⁻¹) suggesting an endothermic adsorption reaction. On the other hand, the Halsey isotherm plots for the adsorption of Cu²⁺ and Ni²⁺ ions onto the studied natural clays (data not shown) exhibited high R² values (0.928–0.998) indicating a good fit of the experimental data and an accurate description of the sorption behaviour of Cu²⁺ and Ni²⁺ ions onto the studied clays (ATP and VRM) by the Halsey isotherm. The n _H values of the adsorption of Cu²⁺ ions onto ATP and VRM were 5.27 and 3.41, respectively, while those for the adsorption of Ni²⁺ ions were 3.29 and 3.07, respectively, suggesting that the adsorbed molecules may form multilayers (Tang et al., Reference Tang, Chew, Chan and Raper2003).

Evaluation of adsorption mechanism

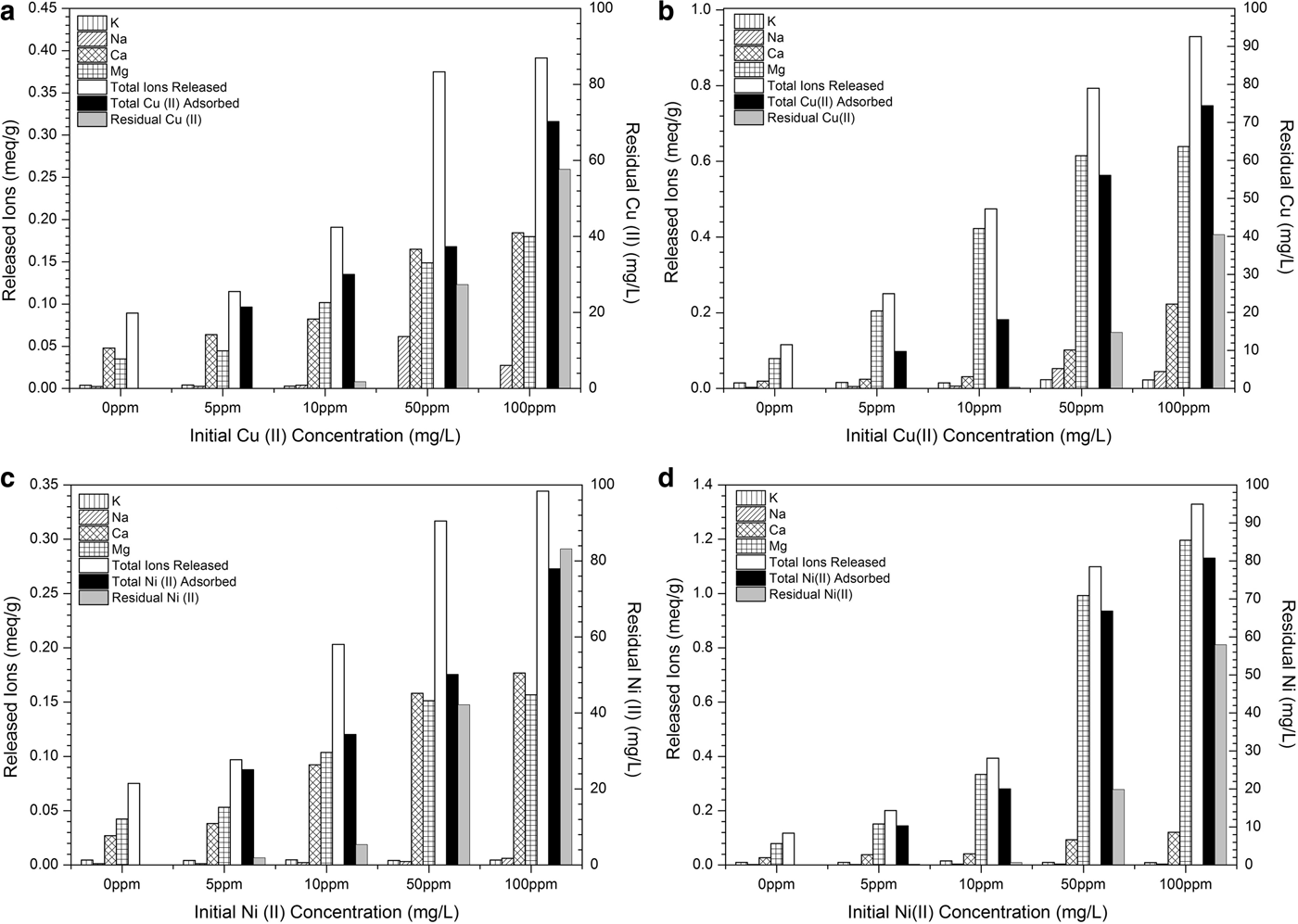
The retention of Cu²⁺ and Ni²⁺ ions by the clays is clearly an ion exchange process which is validated by the determination of Ca²⁺, Mg²⁺, Na⁺ and K⁺ ions released during Cu and Ni adsorption, in relation to the initial concentrations (Fig. 9). Also, the total release of positively charged ions (sum of Ca²⁺, Mg²⁺, Na⁺ and K⁺ ions) from the two clay adsorbents along with the total adsorbed and the residual Cu²⁺ and Ni²⁺ ions are shown.

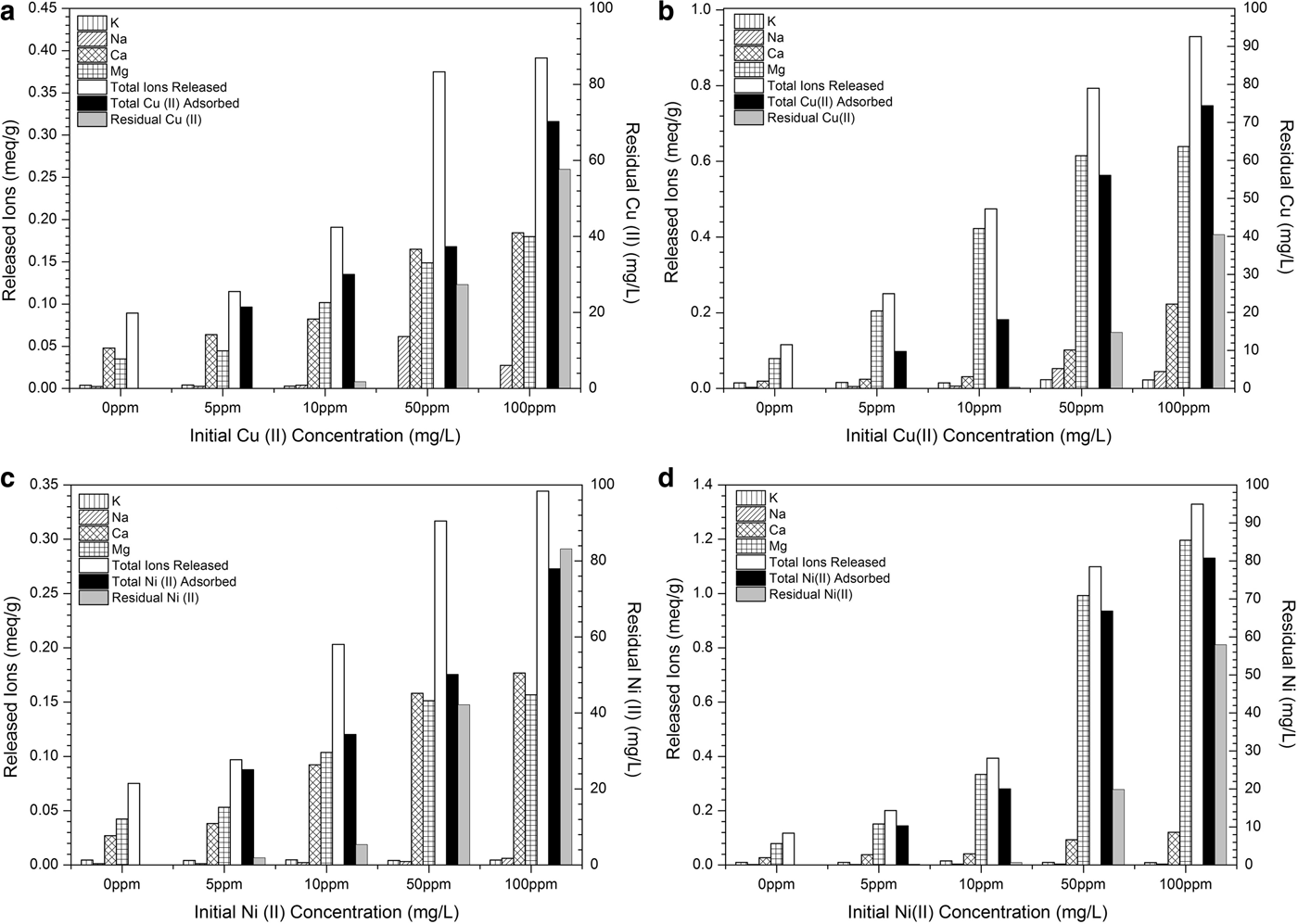
Fig. 9. Concentrations of released K⁺, Na⁺, Ca²⁺, Mg²⁺ ions and total released cations (sum of K⁺ + Na⁺+ Ca²⁺+ Mg²⁺ ions) during Cu²⁺ (up), and Ni²⁺ (down) adsorption (adsorbed-residual) by palygorskite (a, c) and vermiculite (b, d). The contact time applied was 120 min. The measured CECs were ~0.58 meq/g for ATP and ~1.28 meq/g for VRM.

Briefly, in both the ATP and VRM clays, the amounts of Na⁺ and K⁺ ions released are small and remain almost invariable during Cu and Ni adsorption for the initial concentrations studied, indicating that they were not affected by the Cu and Ni adsorption. On the other hand, the amounts of the Ca²⁺ and Mg²⁺ ions released from the surfaces of both clays are greater, with the total released Ca²⁺ and Mg²⁺ contents from sample VRM being significantly greater than those from ATP. This is in accordance with the experimental results which showed higher adsorption capacity of the VRM for Cu²⁺ and Ni²⁺ ions than the ATP. The amounts of both Ca²⁺ and Mg²⁺ released from palygorskite increased with increasing initial metal concentration, while in vermiculite an increase in mainly Mg²⁺ ions was observed. The main reason for the increase in the release of Ca²⁺ and Mg²⁺ is the larger amounts of adsorbed Cu²⁺ and Ni²⁺ ions on the two clays by increasing their initial metal concentrations. Both clay adsorbents adsorbed successfully even higher Cu²⁺ and Ni²⁺ concentrations with simultaneous increase in Ca²⁺ and/or Mg²⁺ release.

In all studied cases, more cations were released than were metals adsorbed, indicating that ion-exchange reactions were more likely to predominate in Cu²⁺ and Ni²⁺ adsorption by both palygorskite and vermiculite (Fig. 9). Moreover, taking into account the CEC values of the natural clays (~0.58 meq/g for ATP and ~1.28 meq/g for VRM), it was clear that saturation was not reached. This observation indicated that Cu²⁺ and Ni²⁺ species occupy the exchange sites, forcing directly the release of counterbalanced ions through an ion exchange process and form outer-sphere complexes (Stumm, Reference Stumm1991):

$$\left( { \equiv S - O^ -} \right)_2...C_{3 - n}^{n +} + M^{2 +} \rightleftharpoons \left( { \equiv S - O^ -} \right)_2...M^{2 +} + \left( {3 - n} \right)C^{n +}, $$

where S corresponds to framework Si or Al, C is the counterbalanced ion with charge n ⁺ (n = 1 or 2) and M is the studied metal Cu²⁺ or Ni²⁺.

A more detailed analysis of the chemical compositions of the surfaces of the natural clays used and the presence of Cu and Ni were investigated by elemental mapping using energy dispersive X-ray (EDX) (Fig. 10). The Si, Al, Fe and Mg corresponding micrographs for the two natural clays indicated the distribution of the functional groups formed on the surface. The presence of copper and nickel adsorbed on attapulgite and vermiculite showed uniform distribution in all cases (Fig. 10).

Fig. 10. SEM-EDX mapping images of the natural clays studied after (a) Cu²⁺ and (b) Ni²⁺ adsorption.