INTRODUCTION
Illite age analysis (IAA) is a method developed to help constrain the age of authigenic illite formation in shales (Pevear, Reference Pevear1999) while acknowledging that, with the rare exception of bentonite beds, almost all size fractions of all shales will contain mixtures of authigenic and detrital illite components. The method assumes that authigenic (usually 1M and 1M d illite, often still interstratified with smectite) and detrital components (1M and 2M 1 illites; note that if 1M illite is the detrital component, then authigenic illite must be in mixed-layer illite-smectite [I-S]) can be identified and quantified from an X-ray diffraction (XRD) scan and that any size fraction of a shale consists of just these two K-bearing components. Failure to account for the proportion of detrital illite will create a systematic error in the authigenic age interpretation, and in some instances this error can be an order of magnitude or more greater than the analytical error. Pevear (Reference Pevear1999) has shown how IAA is applied in the context of a kinetic model of smectite–illite reaction and in combination with other palaeothermometers (e.g. vitrinite reflectance and apatite fission track analysis) to define model-independent temperature histories that provide critical constraints for more accurate thermal models useful for petroleum exploration. IAA is based on the long-standing recognition of the prograde diagenetic reaction of smectite to create illite (Maxwell & Hower, Reference Maxwell and Hower1967) common in sedimentary basins. Although IAA results in a single age, that age represents a spectrum of ages resulting from the progressive transformation of smectite to illite over a finite time interval and yielding a weighted average of the age of all illite particles formed (note: in some instances where K is unevenly distributed, this statement is no longer strictly true, but except in extreme circumstances, this problem has a minor effect on the age derived).
With the established IAA methodology in place, the question arose in the early 1990s about whether the IAA method could be extended to another petroleum exploration risk – the timing of structural trap formation in a fold-and-thrust belt with respect to the timing of gas generation. To address this question, we reasoned that dating fault gouges that created folded structural traps was the most certain approach, and that this information could help better assign appropriate risk factors to traps formed after the end of gas generation and differentiate them from traps that formed while gas was still undergoing generation. At the time that research began, there was scant literature available to suggest that such an approach might succeed; only Lyon & Snellenburg (Reference Lyons and Snellenberg1971) and Kralik et al. (Reference Kralik, Klima and Riedmueller1987) suggested that clays in faults could be dated and those dates applied in a tectonic interpretation. This paper is intended to review how the IAA method came to be applied to fault gouge dating, both the original industry research and later academic research, and leaves aside any review of how the IAA method evolved after Pevear (Reference Pevear1999).
Basis for review
This review pursues two goals: (1) outline the original research undertaken at Exxon Production Research Company in the early 1990s; and (2) review the considerable development and application of the methods in the 25 years since our work was undertaken. Because the Exxon research is proprietary, only specific elements focusing on fault processes have been published, although additional information was published in abstracts and presented in conferences. The early Exxon research provided motivation, samples and knowledge for the original academic research (van der Pluijm et al., Reference van der Pluijm, Hall, Vrolijk, Pevear and Covey2001), which has since grown substantially. Many of the Exxon results discussed here have no academic publication history to cite, and the imperative to create that record has been superseded by subsequent research and publications by others, often with superior methods. It is the purpose of this review to summarize that subsequent research. Nevertheless, early industry research results were crucial for establishing the feasibility of the approach and persuading others to undertake these costly, labour-intensive analyses that yield important geological insights.
This review complements that by Tagami (Reference Tagami2012) and delves more deeply into one of the many dating methods discussed in that paper. In a final section, we speculate on where future research will be most effective.
Definitions
The term ‘clay gouge’ is used in this review in the same way as in Vrolijk & van der Pluijm (Reference Vrolijk and van der Pluijm1999) – a field descriptive term that describes a light- to dark-coloured, clay-rich (often clay mineral-rich) material that becomes sticky mud when wet. This term implies no formation mechanisms of the gouge.
The best terminology for the interpretive product, which is a radiometric age of authigenically produced illite produced during deformation in a high-shear strain fault zone, is also open to debate. This description is cumbersome, and while others have used many different terms (e.g. fault dating, dating of fault gouge, dating of shallow faults, timing of brittle deformation and variations on these terms), the term dating of fault gouge (or fault gouge dating or simply gouge dating) is used in this review to convey the primary purpose of the analysis, relying upon textural arguments to deduce that gouge formation is associated with neoformation of illite that is related to strain rate in the fault zone (i.e. more neoformation during higher shear strain-rates). Importantly, the resulting fault age likely reflects an aggregate age of the entire shear strain history, just like IAA yields an aggregate age of illite authigenesis.
FIRST STEPS
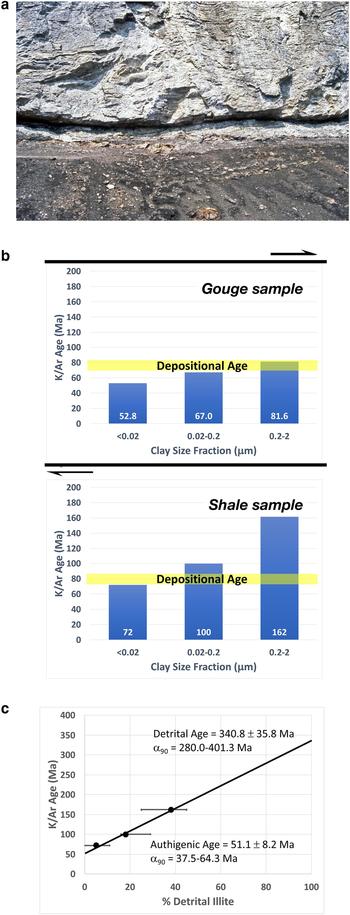
To test the feasibility of dating fault gouges, an initial test was conducted on samples from four thrust fault outcrops in the Front Ranges of the Canadian Rockies west of Calgary. For the McConnell Thrust exposed on Mt Yamnuska, just north of the Trans-Canada Highway west of Calgary, samples were collected from the thrust fault exposed in a thrust-ramp setting in which Cambrian Eldon Fm. limestones overlie Upper Cretaceous Belly River shales. The resulting ages decrease with decreasing size fractions (2.0–0.2, 0.20–0.02 and <0.02 µm), and the ages of the fine and medium-sized fractions are younger than the depositional age of the Belly River shale (Fig. 1b; the age of the coarse fraction is equivalent to the depositional age). The underlying Belly River shale sample defines a similarly inclined age distribution, as expected for undeformed shale samples in which the age of the fine fraction is less than the depositional age, while the medium and coarse fractions are older. Importantly, the age of any individual size fraction in the gouge sample is younger than its counterpart in the shale. When modelling the amount of authigenic (mixed-layer I-S) versus detrital discrete illite in the undeformed shale using the NewMod program (Moore & Reynolds, Reference Moore and Reynolds1989), the resulting IAA plot (Fig. 1c) yields an interpreted authigenic illite age of 51.1 ± 8.2 Ma (1σ errors; ages defined at the 90% confidence level using Monte Carlo simulation of linear regression through the measured data points, and their associated analytical uncertainties yield an age range of 37.5–64.3 Ma).
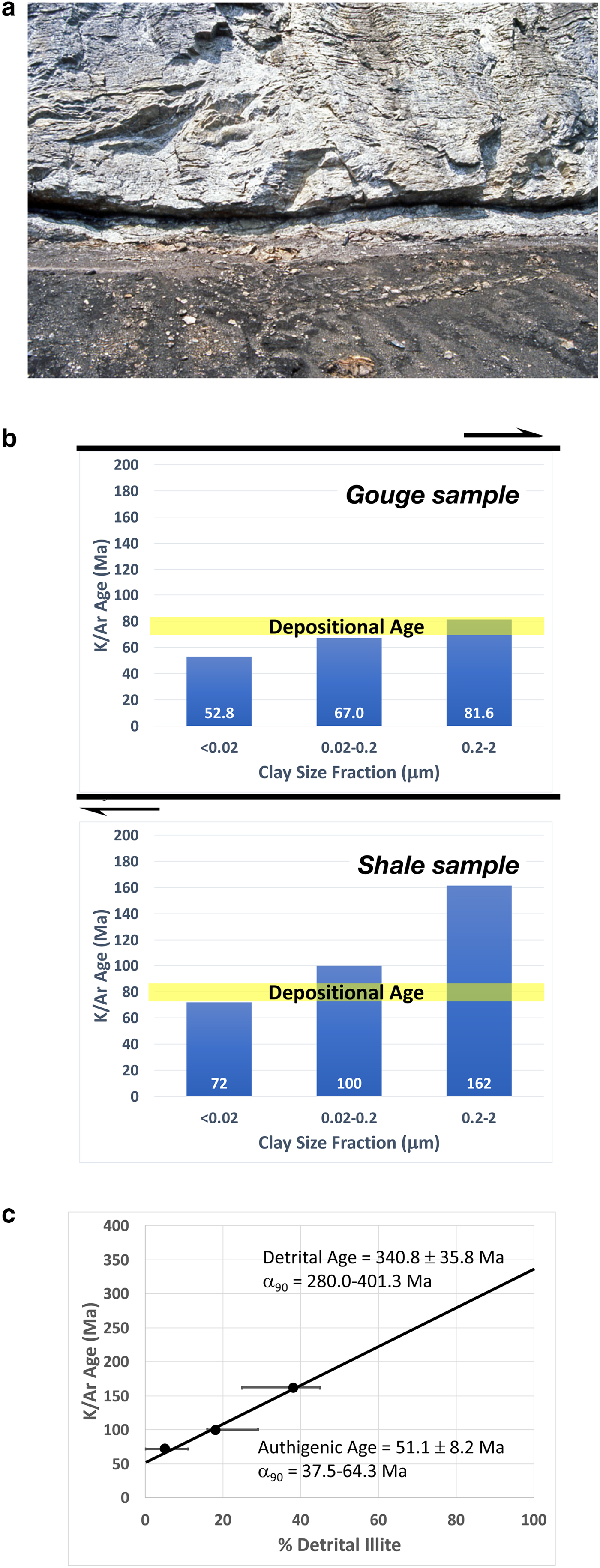
Fig. 1. McConnell thrust exposed at Mt Yamnuska with initial fault (thrust gouge) and shale (Belly River shale) age data below. (a) Field outcrop photo. Outcrop height ≈ 6 m (b) Age–size distributions for fine-, medium- and coarse-sized fractions between gouge sample (above) and shale sample (below). Note the significant difference in distribution of ages and absolute age values, especially when referenced against depositional age. (c) IAA authigenic age regression for undeformed Belly River shale. Note that no comparable IAA plot was possible for the gouge sample because each size fraction contained only discrete illite, and at the time of the original interpretation, there existed no method (e.g. Wildfire) to distinguish diagenetic from detrital clays.
Several aspects of this first analysis were unexpected but encouraged us to continue. First, as Pevear (Reference Pevear1999) showed, three types of age distributions are encountered in shale analyses: (1) an inclined spectrum like that for the Belly River shale – this is encountered in almost all shales; (2) a bench spectrum encountered when dating illites in sandstones – in this instance, the medium and fine fractions are interpreted as including only authigenic illite components, while the coarse fraction also contains a detrital component; and (3) a flat spectrum, which is encountered in bentonite beds, has the same age across all size fractions and is interpreted as including only authigenic illite. Finding the rare, flat age spectrum (e.g. the second McConnell Thrust sample from Compression Ridge; Table 1) encouraged us to think that the ages reflected an interpretable geological event. Second, direct comparison of glycolated fine-fraction XRD scans (Fig. 2) shows that the degree of smectite–illite reaction is far advanced in the fault sample, even though the fault sample was obtained only 500 m stratigraphically above the shale sample.
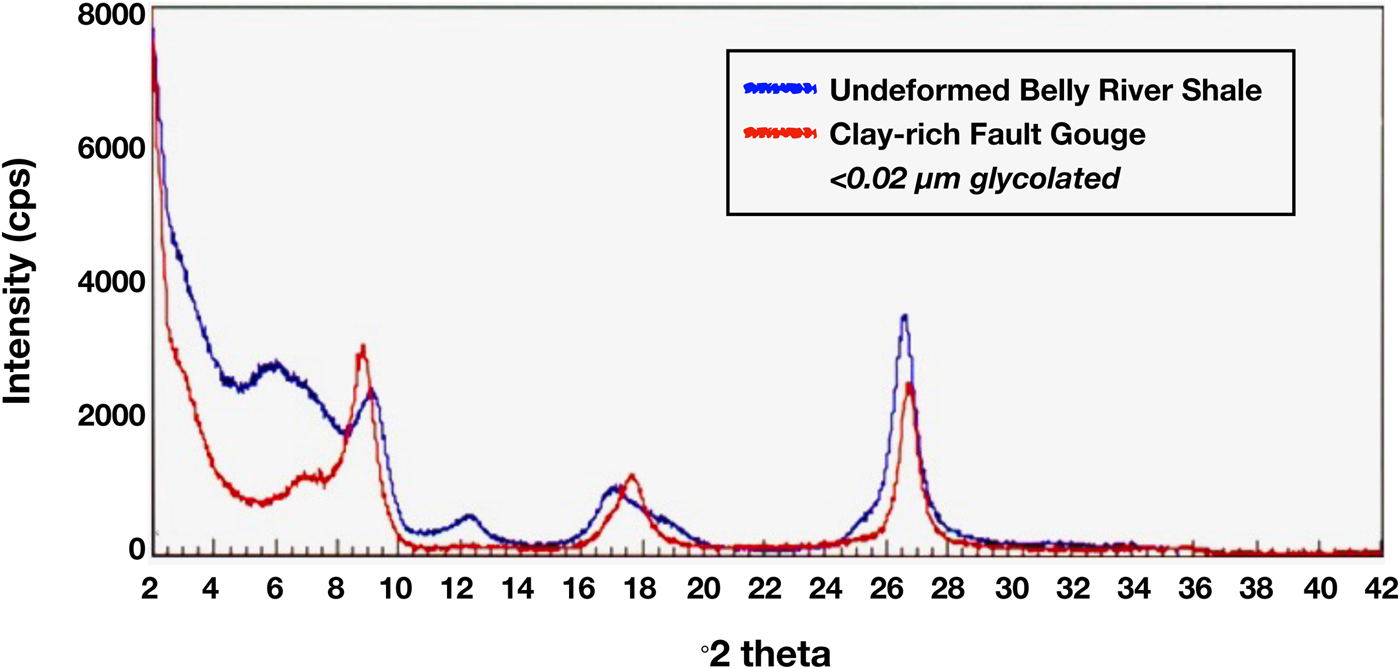
Fig. 2. XRD patterns of glycolated fine (<0.02 µm) size fraction comparing gouge and shale samples from Mt Yamnuska. Note the vast advancement of smectite–illite reaction progress in the gouge sample.
Table 1. Summary of fault outcrop age results.

What is surprising and perhaps serendipitous is that the first samples revealed many of the important attributes that helped persuade us that dating fault gouges is possible, and many of the observations and inferences drawn after completion of these first tests held up and were reported (Vrolijk & van der Pluijm, Reference Vrolijk and van der Pluijm1999) after far more samples were evaluated.
METHOD REFINEMENT AND TESTING
Based on the positive initial results, a more comprehensive analysis of a series of faults across the Front Ranges of the Rockies through Kananaskis Country was undertaken, spanning the thrust-belt from the Sulphur Mountain thrust in the west to the Moose Mountain thrust in the east. Samples were also taken along strike from the Bow River in the north to Crowsnest Pass in the south.
Multiple types of age distributions occur in the fault samples analysed (Table 1). Each sample contained a substantial amount of authigenic illite because the measured age of most size fractions is less than the depositional age, and in all instances the age of any individual size fraction is less than the age of the corresponding size fraction in the undeformed sample from the same stratigraphic unit adjacent to the fault. We found it critical to analyse undeformed footwall samples that were similar to the deformed lithologies in order to develop confidence in the interpreted fault ages.
Only faults in the frontal part of the fold-and-thrust belt allowed authigenic age extrapolation because at the time of this work only the NewMod analytical approach was available. A genetic algorithm method based on the NewMod algorithms and similar to the approach described by Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) was employed, but these methods are only able to distinguish mixed-layer I-S from discrete illite. In one instance (Sulphur Mountain thrust), a preliminary attempt was made to define proportions of 2M 1 mica in samples using an oblique texture electron diffraction method (Tsipursky & Drits, Reference Tsipursky and Drits1984; Plançon et al., Reference Plançon, Tsipurski and Drits1985) that was under development at the time (Wildfire was yet to be developed), but in that instance, the extrapolated results yielded only a small change in the interpreted authigenic age. When confronted with illite-dominated samples like the McConnell thrust at Mt Yamnuska, only upper age constraints on the fault age could be inferred. We were thus more confident in fault ages defined by bench or flat spectra and used the average of overlapping K/Ar ages to define the fault age.
Samples defined in structural context
Extensive petrographic work was pursued to help ensure that dated clays were pre- or syn-kinematic (i.e. all clay mineral particles have microfabrics consistent with shear deformation), using both transmitted light petrography to evaluate preferred alignment networks consistent with shear fabrics and scanning electron microscopy analyses to document particle-size fabrics (Fig. 3). In one sample (Moose Mountain; Table 1), no deformation fabrics were observed in thin section, and the ages obtained were identical to the undeformed shale even though the sample was collected from a shear zone. Transmission electron microscopy analyses of size-separated samples was also undertaken to examine illite crystal morphologies (Fig. 4), and in some instances long-lath crystals were found that are rare in shales, although this is a common form developed in sandstones where crystals can grow into void spaces. All of these observations were used to support the interpretation that the gouge samples underwent a different dissolution–precipitation history than similar shales subjected only to burial diagenesis. We posited that the observation of deformation fabrics in clays and the identification of illite morphologies that are unusual in shales provided a necessary but insufficient test of the hypothesis that an absolute date of fault deformation was being obtained.

Fig. 3. Photomicrograph of sample KKF-1a, Rundle thrust, Mt Kidd, cross-polarized light. Note distinct, strongly preferred alignment of clay minerals from upper-right to lower-left, sometimes bending around detrital quartz (Q) and rock fragment (RF) silt grains, and weaker texture trending upper-left to lower-right. Such fabrics often associated with shear zones in clay-rich rocks and help confirm the pre- to syn-tectonic origin of clay minerals.

Fig. 4. Transmission electron photomicrograph of coarse (2.0–0.2 µm) size fraction of the Lewis thrust, Gould Dome. Note abundance of lath morphologies in the sample.
Method precision
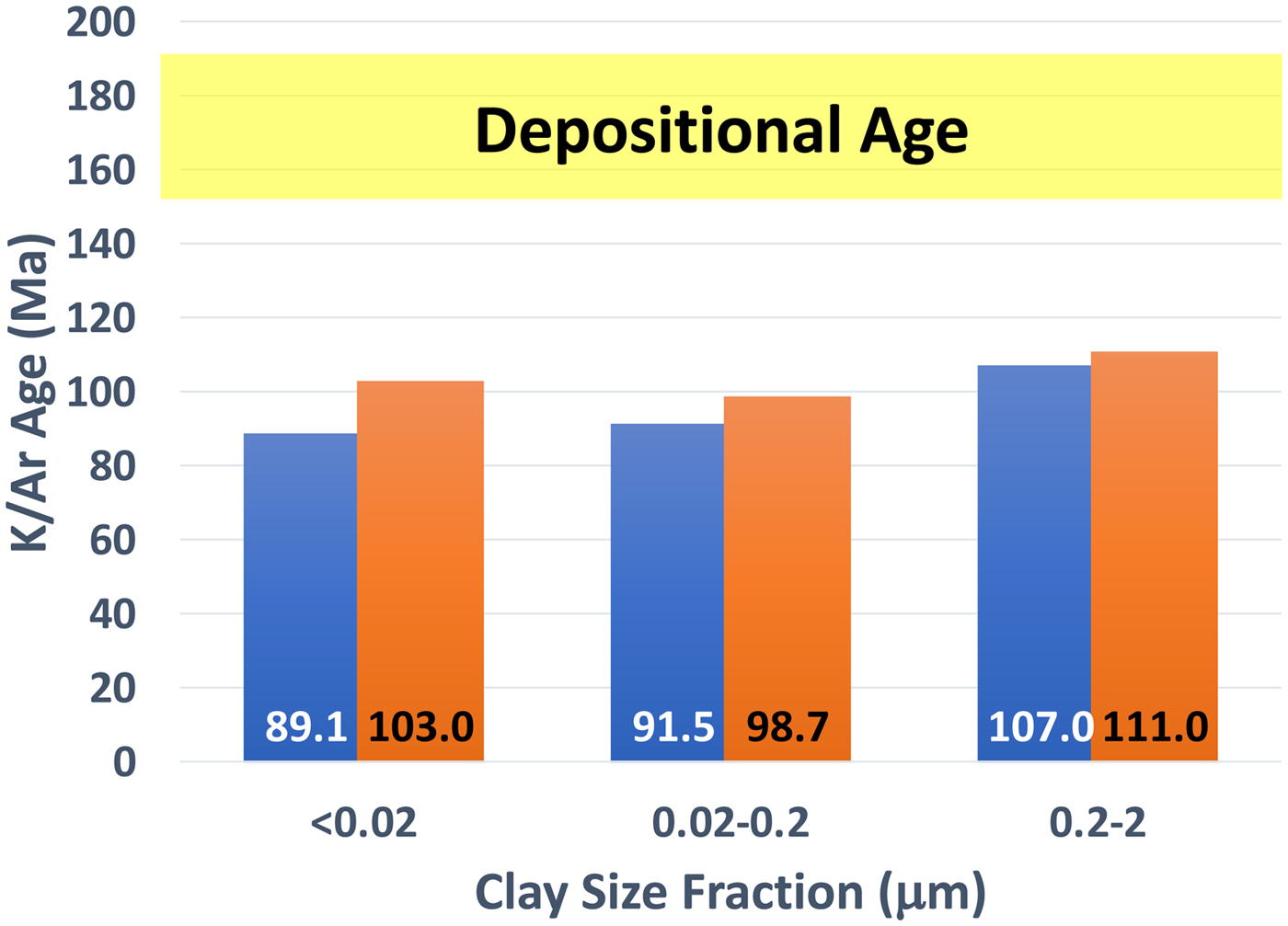
An additional test of the IAA method applied to faults involved evaluating reproducibility by processing and analysing two or more samples from the same outcrop (Fig. 5). Although reasonable reproducibility was recorded between samples, significant deviations often arose. In Fig. 5, two samples of the Rundle thrust yielded the same age for the coarse fractions within analytical uncertainty (1σ = 3 m.y.). Ages of medium and fine fractions differ by values beyond the 1σ age error, but the correspondence between the ages of medium and fine fractions is smaller than the difference between samples. With the benefit of hindsight, it is now possible to conclude that the initial analysis was incomplete and that the age difference was the result of differing amounts of detrital 2M 1 contributions to each of these samples. This is a crucial experiment because it is the key to assessing the precision of the method (assuming a single sample reflects the integrated history of a simple fault history) or alternatively a complex fault history in which each size fraction represents a different part of that history (e.g. Zwingmann et al., Reference Zwingmann, Yamada and Tagami2010a).
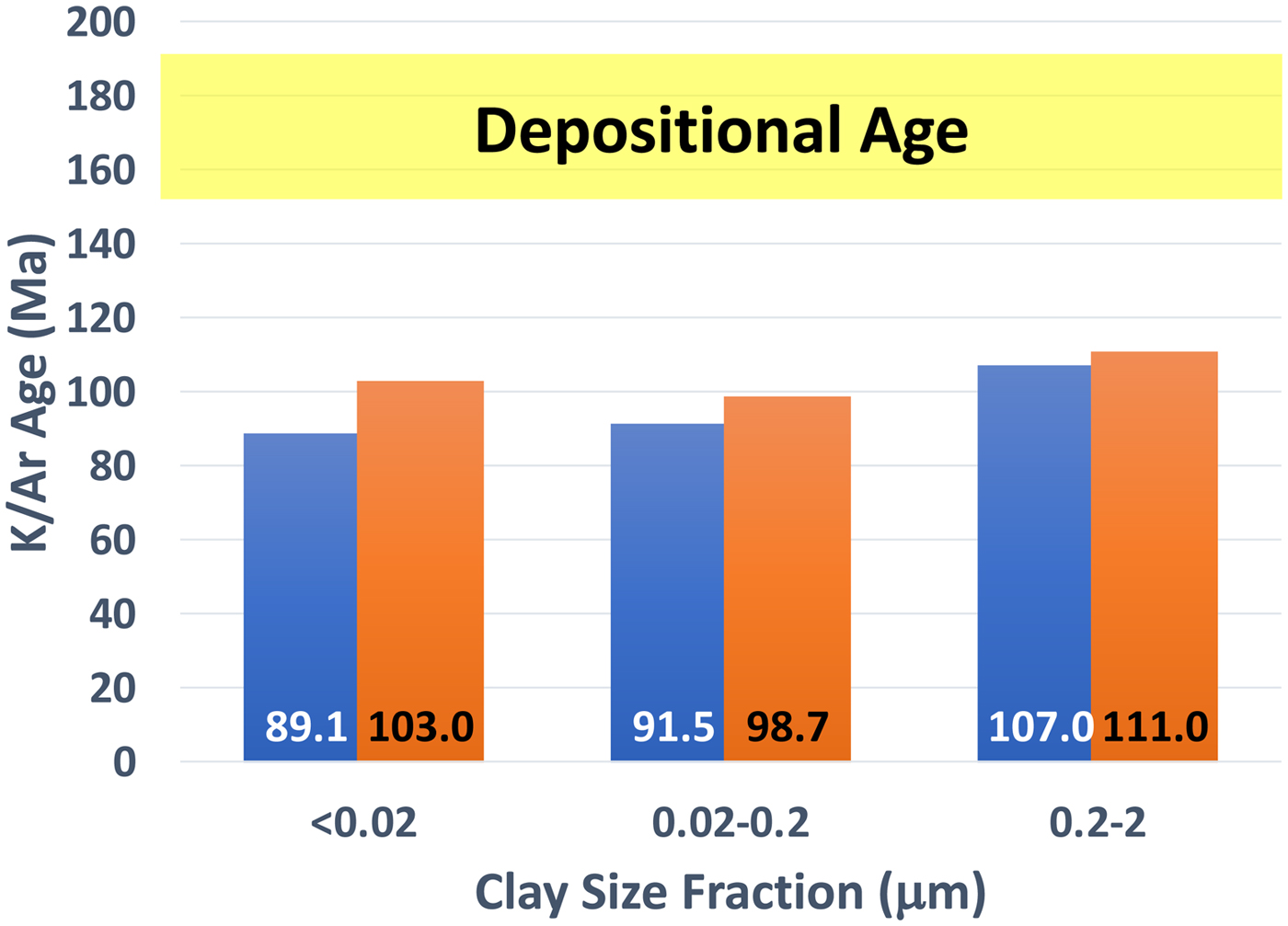
Fig. 5. Replicate K/Ar ages for two samples collected from the Sulphur Mountain thrust. Note the significant age differences in fine and medium fractions. Subsequent work led to the inference that the amount of 2M 1 mica differs between samples.
Our best test of reproducibility involved extrapolated ages for four samples from the Lewis thrust (Gould Dome) within 1 m of the thrust as described in Vrolijk & van der Pluijm (Reference Vrolijk and van der Pluijm1999). In order of distance from fault surface with overlying Devonian Palliser Fm. carbonate rocks, interpreted ages are 53.3 ± 5.3 Ma (10 cm), 54.8 ± 15.4 Ma (40 cm), 65.9 ± 11.2 Ma (60 cm) and 57.3 ± 5.3 Ma (65 cm). All of these ages overlap within the 1σ error of the extrapolated age. Note that three of these four samples were described in the field as bentonites with no more than 25% detrital illite in the finest size fraction, and the sample described as a scaly mudstone (40 cm) has more detrital material in the fine fraction, which leads to a large error in the age extrapolation.
Precision was further tested by comparing ages across a transect of faults (Fig. 6). In this evaluation, the progression of faults interpreted from structural geometric and kinematic perspectives indicates that each successive fault from the hinterland to the foreland should be younger. The progression of fault ages honoured a foreland–younging progression and suggests that the precision of the method is less than the age difference between the faults analysed (4–17 m.y.). If precision was less than this age difference, then ages would probably both increase and decrease progressing from hinterland to foreland.
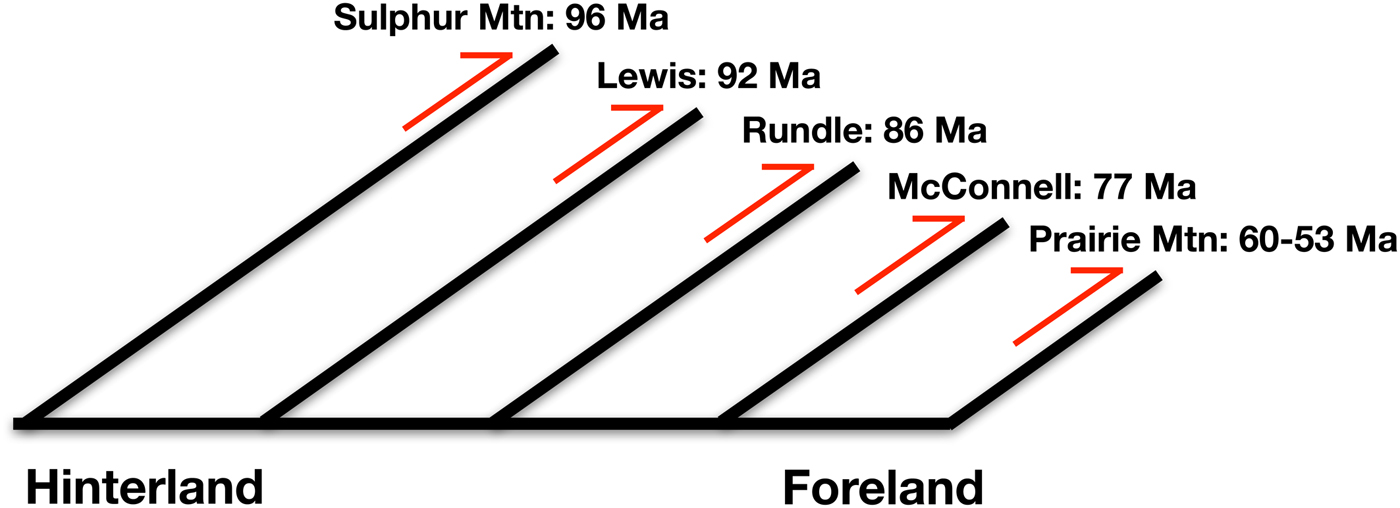
Fig. 6. Interpreted K/Ar ages for a series of five thrust faults that young progressively towards the foreland, consistent with the structural geometric and kinematic interpretation of in-sequence thrusting.
Method accuracy
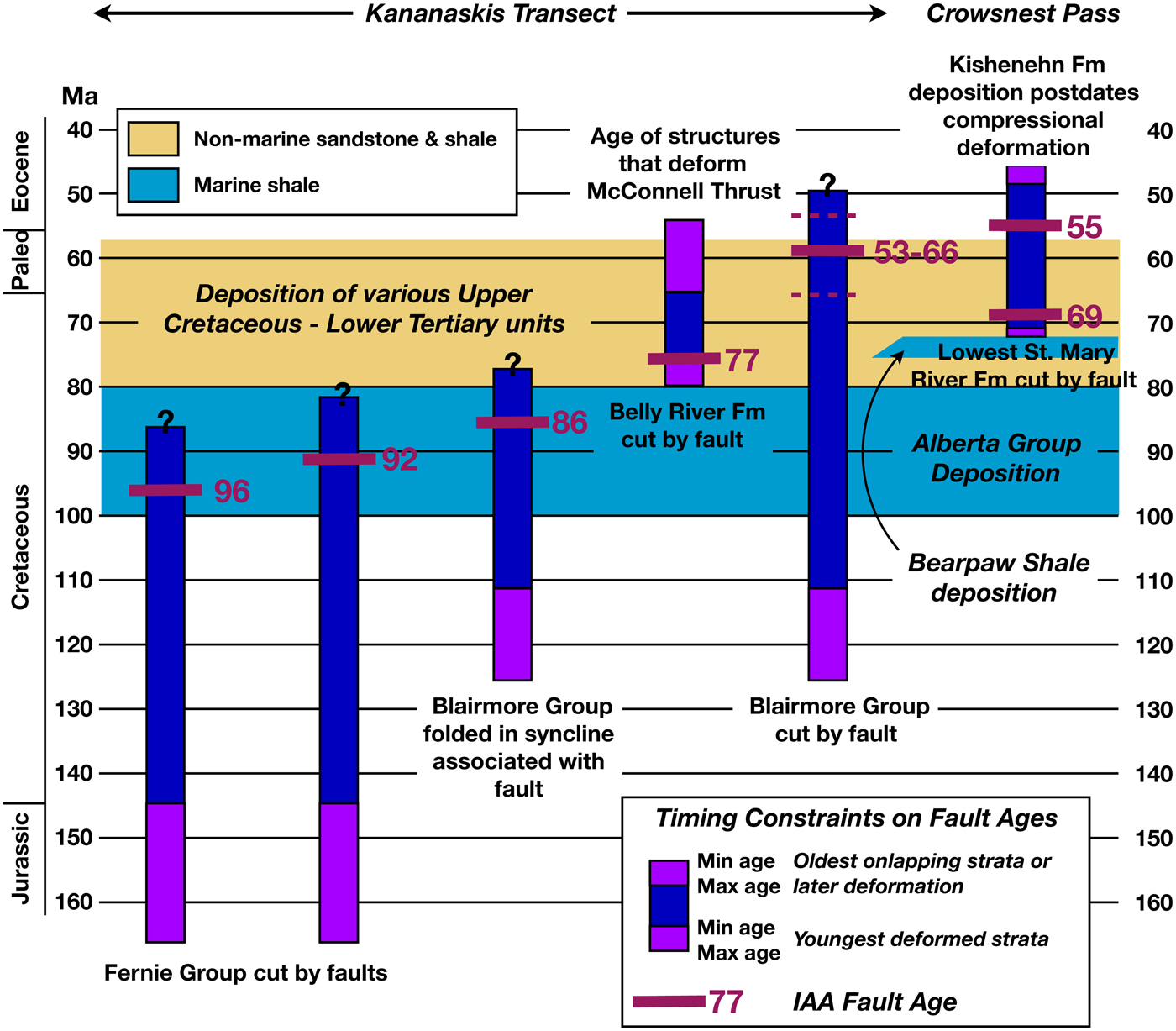
Accuracy of geological methods is extraordinarily difficult to evaluate because a precise reference to compare with rarely exists, and yet this step is crucial to the successful development of any method. This problem is acute here because, as discussed in the next section, dissolution/precipitation processes beyond the realm of burial diagenesis appear important, and there is no easy way to simulate these processes in the laboratory. Moreover, the notion that the age of illite neoformation is associated with a fault deformation history can only be tested by comparison with field relationships. The fault gouge-dating method was developed and tested in southern Alberta because available stratigraphic and geological evidence provide limits on the possible fault gouge ages under investigation. A compilation of the available data at the time of our work (Fig. 7) reveals interpreted fault ages that fall within the permissible age constraints, each of which also contains some uncertainty. This analysis reveals that the interpreted ages are accurate to within at least a few million years, but it was impossible to quantify accuracy further, or to define any systematic bias in the measured ages.
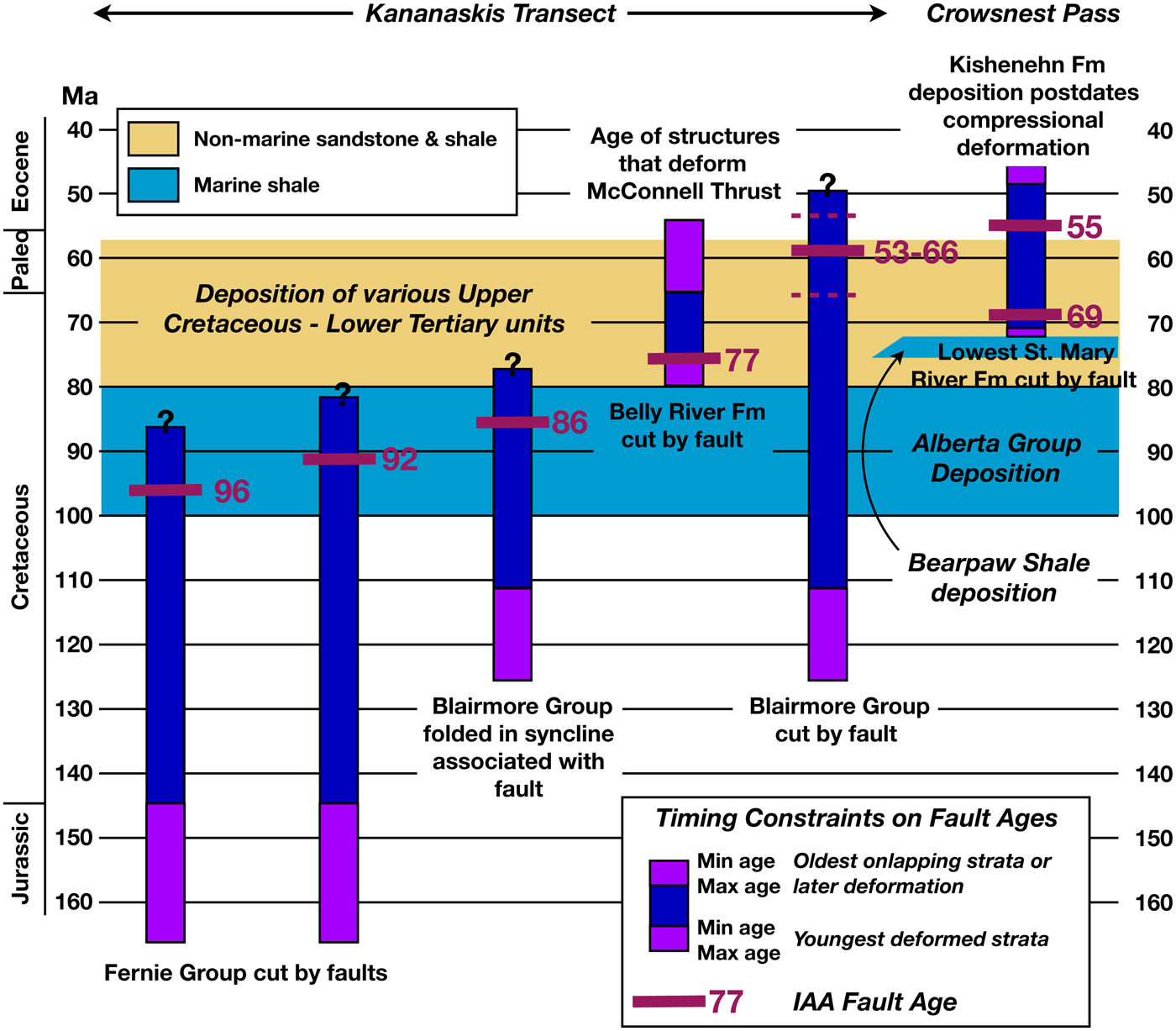
Fig. 7. Compilation of available (~1992) stratigraphic and geological age constraints for thrust faults in southern Alberta with interpreted fault ages posted. Note that all fault ages fall within the span of available age constraints, although in some instances constraints remain broad. Kananaskis Transect includes (left to right; hinterland to foreland): Sulphur Mountain thrust, Rundle thrust, Lewis thrust, McConnell Thrust and Prairie Mountain thrust. Two fault outcrops were analysed in Crowsnest Pass area where the Lewis thrust is geometrically out of sequence.
Fault process interpretations
To further test the veracity of the dating method applied to fault gouges, experiments were undertaken with samples intended to elucidate the fault processes that would make dating feasible. The most important observations made were that footwall shales that contain modest amounts of illite in mixed-layer I-S are transformed into gouge with substantial amounts of 1M d illite. This was observed in the present simple sample comparison test (Fig. 2) and in clay mineral profiles into the footwall below the Lewis thrust (Vrolijk & van der Pluijm, Reference Vrolijk and van der Pluijm1999). Viewing the smectite–illite reaction as an irreversible, prograde mineral reaction limited by kinetics in the low-temperature environment of the Canadian Front Ranges (footwall vitrinite reflectance values range from 0.6 to 1.7), we interpreted the clays in faults to be dominated by deformation-driven dissolution–precipitation reactions (Vrolijk & van der Pluijm, Reference Vrolijk and van der Pluijm1999).
Oxygen isotope ratios of most clay fractions (analyses performed by Fred Longstaffe) are consistent with an interpretation of dissolution–precipitation in a rock-dominated system. In particular, end-member oxygen isotope ratios of authigenic and detrital components were defined in the same way as ages, and in one example, the fine fraction was 3.4‰ lighter than the course fraction, and for any given size fraction the gouge sample was 3–6‰ heavier than the undeformed shale, which has also undergone a lesser degree of smectite–illite reaction progress. Given the complexities of additional oxygen-bearing mineral phases (e.g. quartz) in each sample, it seemed unwarranted to pursue interpretation of this dataset further, although the potential for oxygen and other stable isotope ratios to augment fault gouge process interpretations appears possible under the right circumstances (e.g. where the isotopic composition of contaminant phases is irrelevant to the interpretation). In rare instances where samples contained sufficient mixed-layer I-S to model the amount of detrital illite, end-member authigenic and detrital values were extrapolated, and the authigenic component had a lower oxygen isotope ratio than the detrital component, but this was done without attempting to account for the isotopic effects of other oxygen-bearing mineral phases.
In one sample (McConnell Thrust, Compression Ridge), an Rb/Sr age assessment was attempted from two samples from the same outcrop locality. The coarse fractions had the lowest 87Sr/86Sr and 87Rb/86Sr values and the fine fractions the highest values, and the 87Sr/86Sr value of the coarse fraction is greater than the value of the Devonian Palliser Fm. carbonate in the hanging wall of the thrust. The measured data plot along a well-defined line with an isochron age of 50.0 ± 3.5 Ma, which was 27 m.y. younger than our interpreted age from K/Ar. Because the isochron age fell outside of the range of permissible ages (Fig. 7), we discarded the age obtained from the Rb/Sr method and no longer pursued the Rb/Sr method because of the greater time requirements and expense of this method. At the time, the spurious Rb/Sr age was speculatively attributed to the massive amount of Sr in the Palaeozoic carbonate platform sequence in the hanging wall, possibly introducing unrecognized Sr-bearing phases in our samples, but subsequent age determinations on these samples with the 40Ar/39Ar method yielded a more similar interpreted age (van der Pluijm, et al., Reference van der Pluijm, Vrolijk, Pevear, Hall and Solum2006; see below). Regardless, based on the distribution of Rb/Sr isotopic data from the variously sized fractions, the definition of at least a pseudo-isochron is compatible with dissolution–precipitation reactions.
Method evolution and transition to academic research
By the mid-1990s, the development of the fault gouge-dating method was sufficient for commercial application and further Exxon research ended. This timing was fortuitous because important developments were on the horizon: the development of a micro-encapsulation method for the successful 40Ar/39Ar dating of illites (e.g. Foland et al., Reference Foland, Hubacher and Arehartet1992; Onstott et al., Reference Onstott, Mueller, Vrolijk and Pevear1997) and the development of the Wildfire program (Grathoff & Moore, Reference Grathoff and Moore1996) for the modelling of illite polytypes. These two methods would have a large impact on subsequent academic research.
Because our research had resulted in the confirmation of a useful dating method, and because the interpreted fault processes seemed to be important for better understanding the mechanical behaviour (i.e. deformation behaviour under conditions of dissolution–reprecipitation) and could be seen as an under-considered aspect of earthquake studies, a series of meeting abstracts and presentations were released, which raised the interest of Ben van der Pluijm (University of Michigan). An informal collaboration arose that resulted in publication (Vrolijk & van der Pluijm, Reference Vrolijk and van der Pluijm1999) and the release to the University of Michigan group of splits of our size-separated samples and the associated mineralogical characterization and geological context. These steps concluded the involvement of Exxon in fault gouge-dating research. It is important to realize, however, that the proprietary nature of the Exxon research prevented us from revealing detailed results, and van der Pluijm and the University of Michigan group needed to reinvent and improve upon the existing technique. What was perhaps unusual in our collaboration was that we could provide assurances that pursuit of this research would yield fruitful and significant results.
SIXTEEN YEARS OF FAULT GOUGE-DATING STUDIES
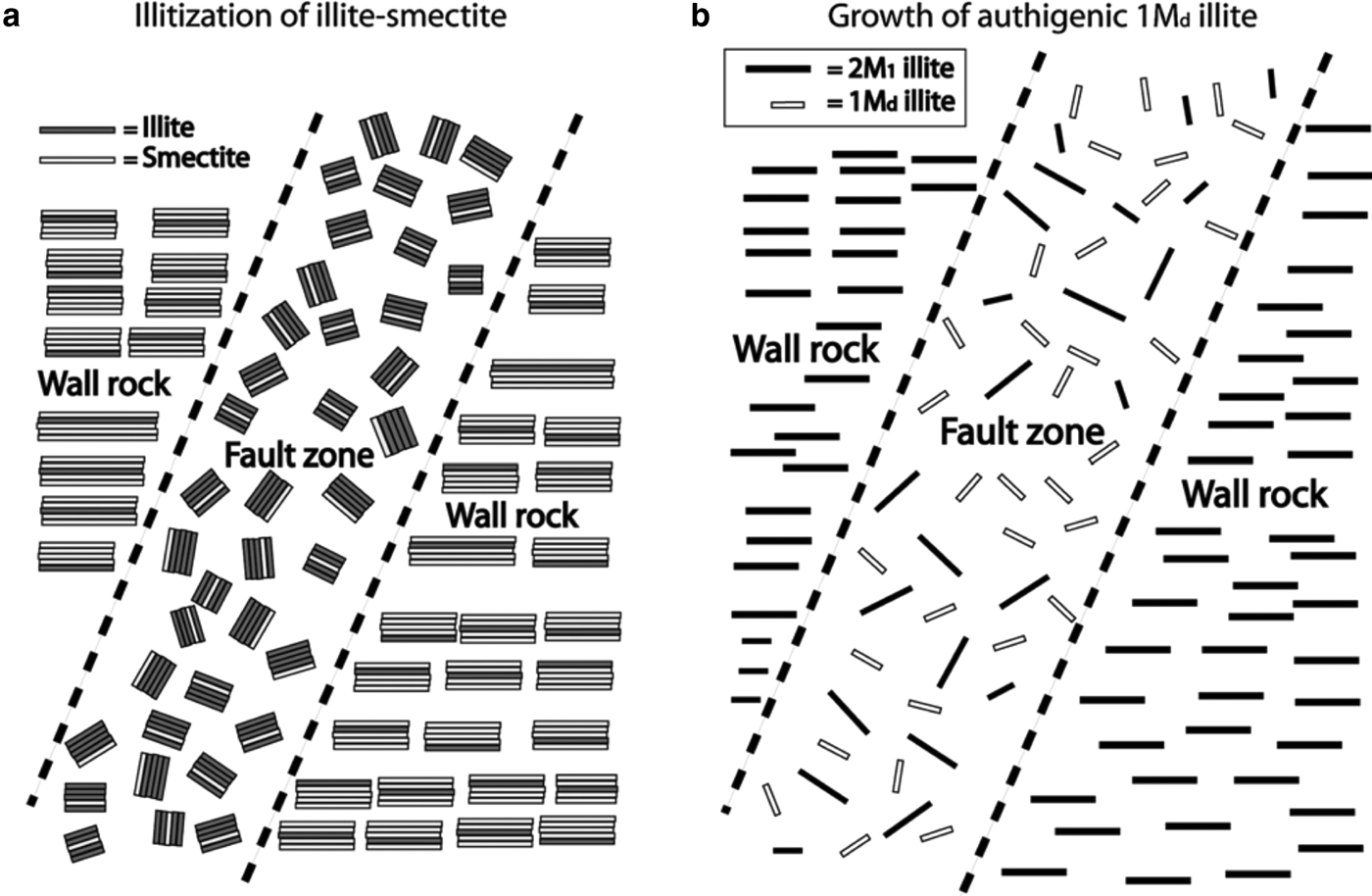
Research into methods to date fault gouge has developed along several lines in the past 16 years, and two people are responsible for participating in most of the studies: Ben van der Pluijm and Horst Zwingmann, either working with students or collaborators. The research falls into two categories defined by Haines & van der Pluijm (Reference Haines and van der Pluijm2008): prograde and retrograde mineral reactions (Fig. 8). Fault gouge dating in the Canadian Rockies is an example of dating prograde smectite–illite reactions, but gouge dating in settings where no low-temperature 1M d illite is present in the rocks cut by faults has emerged as an additional useful dating application. Published studies include reports of method testing and validation, application for the development of improved tectonic insights, and fault process studies; published reports often address more than one of these categories. These themes provide the framework for this review.
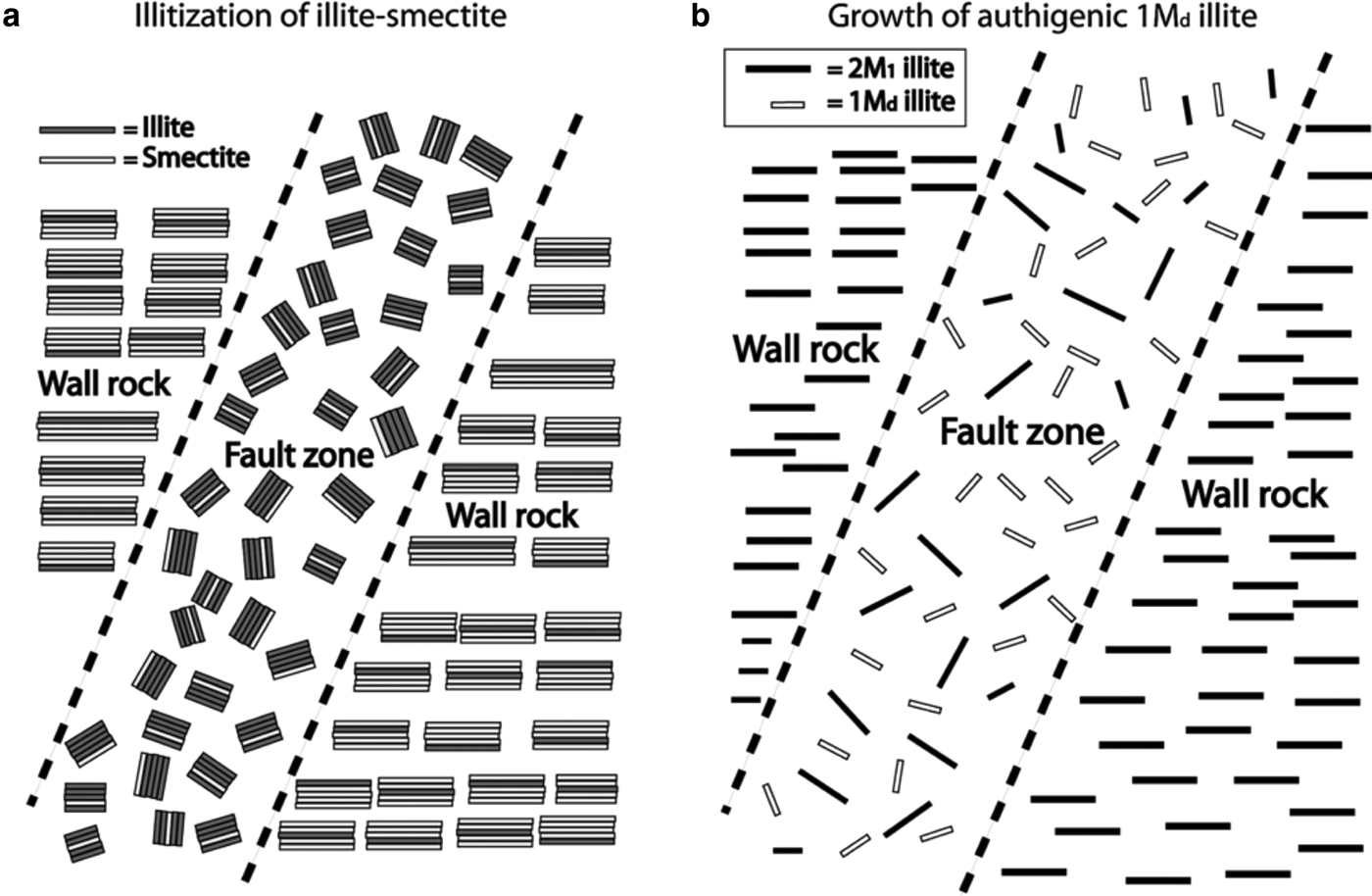
Fig. 8. Two types of clay gouge. (a) Prograde fault zone in which mixed-layer I-S in wall rock becomes more illitic in fault. (b) Retrograde fault in which low-temperature 1M d illite in fault contrasts with crystalline 2M 1 mica (muscovite) in wall rock. From Haines & van der Pluijm (Reference Haines and van der Pluijm2008).
Fault gouge dating of prograde mineral reactions
Van der Pluijm et al. (Reference van der Pluijm, Hall, Vrolijk, Pevear and Covey2001) applied 40Ar/39Ar micro-encapsulation methods for the first time to obtain fault gouge ages. They observed a decrease in total gas ages with decreasing grain size, but independent modelling of the amount of detrital illite in each size fraction regressed an interpreted authigenic age of 51.5 ± 3.5 Ma, which is the same age obtained at Exxon using K/Ar methods. This work established the feasibility of gouge dating even when the gouge contains remnants of detrital clay minerals in the wall rock contributing to the measured age in any particular size fraction.
Coincident with the application of 40Ar/39Ar methods is a formal treatment of the fact that because the age-decay model is non-linear, linear mixing of ages with variable amounts of detrital illite yields only a first-order estimate of the extrapolated age. Van der Pluijm et al. (Reference van der Pluijm, Hall, Vrolijk, Pevear and Covey2001) introduced the use of e λt – 1 as the appropriate age formulation for linear mixing, although in many cases the difference between the approximate and precise methods is small, being smaller than the uncertainty in the amount of detrital illite. This particular issue is a good illustration of the difference between applied industry research that preceded this point, where this age error was recognized, understood to be small and overlooked in light of the questions being addressed, and academic research, where errors are eliminated if a solution can be found.
The second advancement in the gouge-dating method followed with Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) reporting Wildfire (Grathoff & Moore, Reference Grathoff and Moore1996) results from samples in the Exxon IAA collection, including a gouge sample from the Rundle thrust. In previous work, this sample was among those considered too illite-rich to model the percentage of detrital illite in the samples with NewMod, and thus had an interpreted age of 86.5 Ma based on similar ages in the fine and medium-sized fractions (bench age spectrum). Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) showed that these samples still contained some detrital 2M 1 mica and defined an age based on regression that is 7.3 m.y. younger, although the uncertainty ranges overlap. Note that the Rundle fault sample reported by Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) is the same sample described by Vrolijk & van der Pluijm (Reference Vrolijk and van der Pluijm1999), but that the earlier work used results from an experimental oblique texture electron diffraction method (Tsipursky et al., Reference Tsipursky and Drits1984; Plançon et al., Reference Plançon, Tsipurski and Drits1985) that yielded different results. The work by Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) illustrates the value and importance of polytype modelling applied to gouge-dating studies.
Solum et al. (Reference Solum, van der Pluijm and Peacor2005) used a combined Wildfire and NewMod approach for unravelling illite-rich gouge samples from the Moab normal fault, and ages were obtained with 40Ar/39Ar micro-encapsulation methods. These results were presented in a comprehensive fault study and yield interpreted fault ages of 60–63 Ma. Even though Solum et al. (Reference Solum, van der Pluijm and Peacor2005) used newly collected fault samples in a different location from samples reported by Pevear et al. (Reference Pevear, Vrolijk, Longstaffe, Hendry, Carey, Parnell, Ruffell and Worden1997) on the same fault, 40Ar/39Ar instead of K/Ar methods and a modified method of defining the amount of detrital illite, his interpreted fault ages overlap with the range of ages described by Pevear et al. (Reference Pevear, Vrolijk, Longstaffe, Hendry, Carey, Parnell, Ruffell and Worden1997), a testament to the strength of the fault gouge-dating method (i.e. it yields reproducible results).
Van der Pluijm et al. (Reference van der Pluijm, Vrolijk, Pevear, Hall and Solum2006) expanded the application of the 40Ar/39Ar method and the use of Wildfire to the Exxon Canadian fault collection. The 40Ar/39Ar ages reported by van der Pluijm et al. (Reference van der Pluijm, Vrolijk, Pevear, Hall and Solum2006) are generally younger than the K/Ar ages measured by Exxon and range from an insignificant difference (i.e. within expected analytical uncertainty) to ages that are up to 20% younger by the 40Ar/39Ar method. A comparison of ages based on sample and size fraction (Fig. 9) reveals a systematic bias of older K/Ar ages with respect to 40Ar/39Ar ages; note that with the total gas ages derived from the 40Ar/39Ar method, those ages should be the same as K/Ar ages (see Supplementary Data Table). The average age difference is 8.65 ± 7.50 m.y., which indicates that the systematic bias is greater than the random error (1σ). Some discrepancies arose in samples where the K/Ar ages appeared suspicious based on low Ar yields in the coarse fraction, so part of the difference is explained by a likely superior 40Ar/39Ar method (i.e. in the context of sample size requirements at the time the analyses were performed, application of modern methods might lead to a different outcome). The systematic bias is probably a laboratory problem that was never resolved, but we are willing to speculate that the 40Ar/39Ar ages are accurate; it would be interesting to see if this bias persists with modern dating procedures. An important perspective to maintain, however, is that although the interpreted Rundle thrust ages differ between Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) and van der Pluijm et al. (Reference van der Pluijm, Vrolijk, Pevear, Hall and Solum2006), the interpreted fault ages and their specified uncertainty overlap, and that uncertainty is driven by the uncertainty in the mineralogical characterization (% detrital illite). The ages interpreted by van der Pluijm et al. (Reference van der Pluijm, Vrolijk, Pevear, Hall and Solum2006) describe a thrust belt that shortened in two distinct phases separated by 20 m.y.
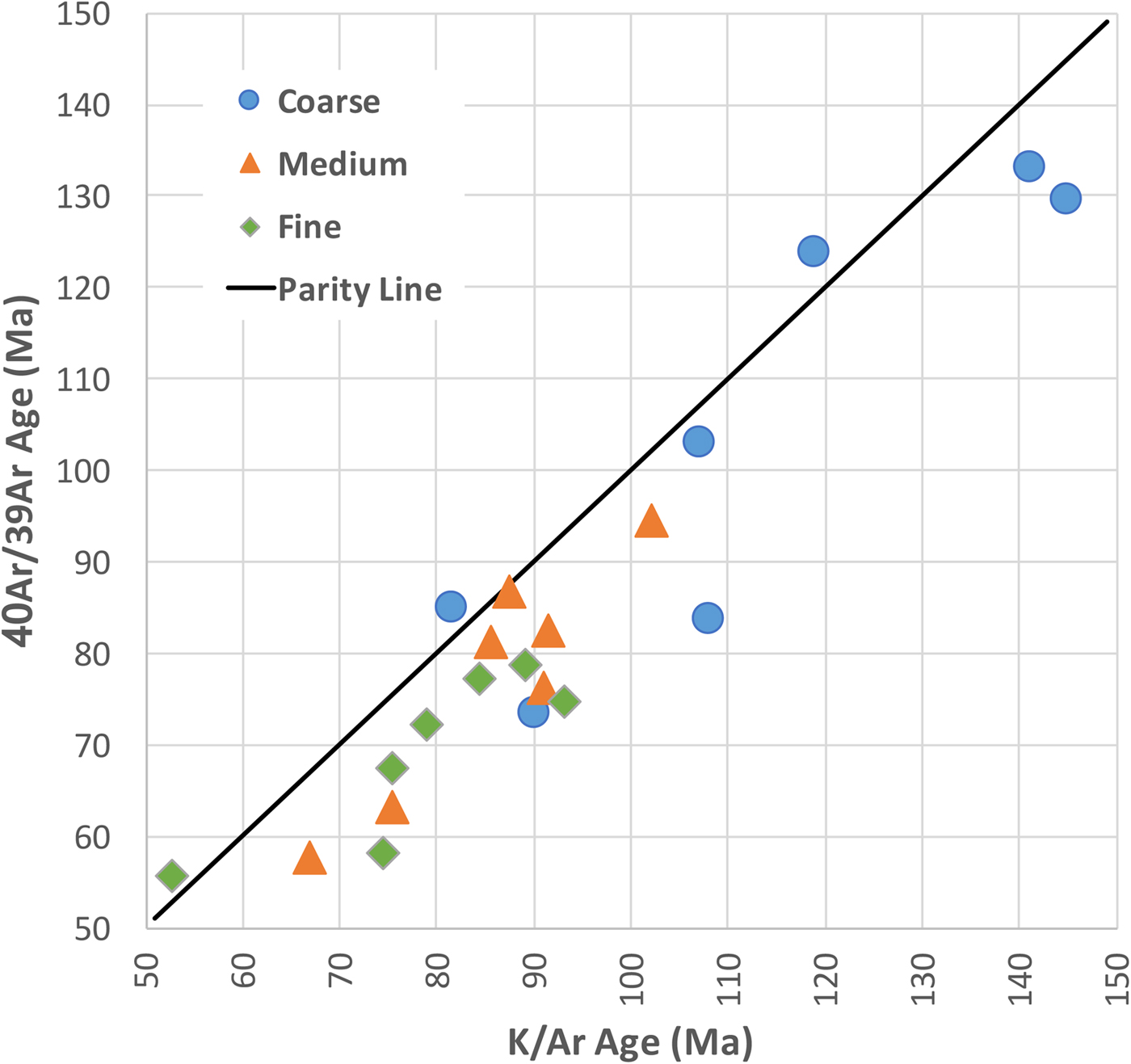
Fig. 9. Comparison of K/Ar and 40Ar/39Ar ages for splits from same sample preparations. Note systematic bias of older K/Ar ages. Source of bias was never addressed or resolved.
The paper by van der Pluijm et al. (Reference van der Pluijm, Vrolijk, Pevear, Hall and Solum2006) invites the question of whether a K/Ar age on a large sample is better or worse than a 40Ar/39Ar age on a small sample. In our opinion, there is no easy answer to this question, and Clauer et al. (Reference Clauer, Zwingmann, Liewig and Wendling2012) provide a helpful review of this issue. The debate over the best dating method persists, and a modern researcher would be well served to consider all method advancements in the context of the samples to be analysed and the questions being asked of the samples.
Solum & van der Pluijm (Reference Solum, van der Pluijm, Sears, Harms and Evenchick2007) then used the updated IAA method to date thrusts in the Sevier thrust belt of Wyoming and discovered that the similarity in ages between faults suggests that they deformed more or less synchronously (i.e. within the limits of age uncertainty) in the manner of a critically stressed wedge. This application, together with that of van der Pluijm et al. (Reference van der Pluijm, Vrolijk, Pevear, Hall and Solum2006), reveals how the IAA gouge-dating method is used as a tool to probe tectonic problems.
Zwingmann et al. (Reference Zwingmann, Offler, Wilson and Cox2004) published ages from normal fault gouges in the Sydney Basin, Australia, and interpreted a multi-stage history based on multiple samples and size fractions obtained from a single outcrop. They found gouge ages to be consistently younger than clays in the host rock and the expected younging of ages with decreasing grain size. Although Zwingmann et al. (Reference Zwingmann, Offler, Wilson and Cox2004) interpreted no detrital mica in their finest-sized fractions and thus interpreted those ages as pure authigenic fault ages, they used an alternative XRD quantification method of the intensity ratios of two peaks expressed on orientated clay samples (method of Maxwell & Hower, Reference Maxwell and Hower1967). Several aspects distinguish this paper, including: (1) faults all have small offsets (<10 m) and represent the smallest faults evaluated to date; (2) several faults were sampled in a single outcrop, which should improve the chances of working out a multi-stage history; and (3) grain size fractions used in this study are coarser than previous studies (coarsest fraction is 6–10 µm and finest is <0.1 µm). Zwingmann et al. (Reference Zwingmann, Offler, Wilson and Cox2004) introduced the complexity into fault gouge dating that illites grown over a protracted deformation period may yield ages that are distinguishable by dating, in addition to the spectrum of ages created by mixing of end-member component ages, but they correctly regard their ages as maximum fault ages.
Rahl et al. (Reference Rahl, Haines and van der Pluijm2011) integrated fault ages with other geological constraints in the Spanish Pyrenees to further elucidate the history of fold-and-thrust deformation and especially helped distinguish out-of-sequence thrusting. Pană & van der Pluijm (Reference Pană and van der Pluijm2015) expanded fault ages in the Canadian Rockies northward from the previous studies and tied this history to depositional patterns in the foreland basin. Similarly, Fitz-Diaz et al. (Reference Fitz-Diaz, Hudleston, Tolson and van der Pluijm2014) used fault ages in the Mexican fold belt to describe progressive but episodic deformation towards the foreland. This work touched on an issue taken up by Hnat & van der Pluijm (Reference Hnat and van der Pluijm2014) regarding the applicability of total gas versus retention ages from the 40Ar/39Ar analysis to provide guidelines dependent on crystallite thickness.
Fault gouge dating of retrograde mineral reactions
There are two approaches to evaluating clay gouge ages derived from higher-temperature metamorphic or igneous rocks: (1) assume that all clays are formed by faulting processes with qualitative evaluation of clay mineral and polytype proportions; or (2) make no assumptions and quantitatively model random XRD patterns to integrate the results with associated ages. Zwingmann & Mancktelow (Reference Zwingmann and Mancktelow2004) examined clay gouges derived from retrograde hydration reactions of high-grade metamorphic and igneous rocks in the Alps along young faults related to the Periadriatic fault. Given the abundance of independent geological constraints, this application served as a test of the methodology without mineralogical quantification. While the young ages generated are consistent with all clays being formed during faulting, it is difficult to distinguish authigenic 2M 1 mica from cataclastically deformed mica, especially where the age of mica in the wall rock is unknown.
The same approach was adopted by Davids et al. (Reference Davids, Wemmer, Zwingmann, Kohlmann, Jacobs and Bergh2013) to interpret Permian–Jurassic normal- and oblique-slip fault histories in Norway in which fault ages augmented fission track data. Pleuger et al. (Reference Pleuger, Mancktelow, Zwingmann and Manser2012) used fault ages to investigate neotectonic fault histories related to exhumation in the Alps. In both instances, the interpreted ages were used to refine an existing tectonic history. Torgersen et al. (Reference Torgersen, Viola, Zwingmann and Harris2014) applied similar logic to clay gouge in faults cutting greenschist–amphibolite facies metamorphic rocks in Norway and concluded that the age of the finest fraction represents the most recent fault history, and Torgersen et al. (Reference Torgersen, Viola, Zwingmann and Henderson2015) dated clay gouge in a fault in quartz diorite gneiss in the Oslo Graben. In this instance, Torgersen et al. (Reference Torgersen, Viola, Zwingmann and Henderson2015) did recognize amphibole in coarse-sized fractions and illustrated through mass balance modelling how the presence of amphibole from the host rock increased the measured age of the 2–6 and 6–10 µm size fractions.
In contrast, the second approach pursued by Haines & van der Pluijm (Reference Haines and van der Pluijm2008) carefully evaluates each part of the IAA procedure, including quantitative evaluation of illite polytypes, which they then applied to a low-angle normal fault in Mexico, where independent age constraints also limited the age of faulting. They deviated from the polytype modelling approach employed by Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) for matching the hkl patterns in order to determine the amount of 2M 1 mica and concentrate on matching specific peaks rather than the entire pattern. Haines & van der Pluijm (Reference Haines and van der Pluijm2008) showed that the results from the two approaches are similar for small amounts of 2M 1 mica, but the discrete peak-matching method results in much higher values of 2M 1 mica for 2M 1-rich samples. The implications of this difference are that interpreted ages will be the same when mixing lines are defined by samples dominated by 1M/1M d clays, but using Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) results in much older interpreted ages if the sample is dominated by 2M 1 mica. Haines & van der Pluijm (Reference Grathoff and Moore2008) interpreted the ‘detrital’ age defined by their unmixing as representing the emergence of the fault from the ductile regime and thus, like Zwingmann & Mancktelow (Reference Zwingmann and Mancktelow2004), sought to interpret multiple stages in the fault history. Zwingmann et al. (Reference Zwingmann, Mancktelow, Antognini and Lucchini2010b) demonstrated to a high degree of certainty that entire gouge samples from the AlpTransit tunnel can consist entirely of newly formed clays and that end-member ages can reflect different parts of the fault history. Results from the Nojima fault zone, Japan (Zwingmann et al., Reference Zwingmann, Yamada and Tagami2010a) and Toki granite (Yamasaki et al., Reference Yamasaki, Zwingmann, Yamada, Tagami and Umeda2013) led to the same conclusion, which was an important realization for gouge-dating studies.
The two separate approaches come to the same conclusion – that ages from faults with retrograde mineral reactions document different parts of the fault history. This outcome is compatible with earlier work for low-grade, prograde mica growth discussed by Kirschner et al. (Reference Kirschner, Cosca, Masson and Hunziker1996) where the range of ages for white micas in a carbonate mylonite in the Morcles–Doldenhorn nappe was interpreted as reflecting a protracted ductile deformation.
Haines & van der Pluijm (Reference Haines and van der Pluijm2010) examined the Ruby detachment fault with gouge-dating methods to further refine the unroofing and associated brittle fault history and calculated a strain rate based on the acquired ages. An important contribution from this work is a critical evaluation of how the gouge clays differ from clays in the hanging wall and footwall rocks of a high-angle normal fault that soles into the detachment in order to develop confidence that the interpreted ages reflect deformation rather than a non-tectonic event like a hydrothermal episode. The comprehensive method employed by Haines & van der Pluijm (Reference Haines and van der Pluijm2010) appears to be a more complete and reliable approach than the one without quantitative mineralogical analysis because it offers a richer and more confident interpretation, yet from a pragmatic point of view, a semi-quantitative approach can still yield important geological insights.
The more comprehensive approach paid dividends, however, in the work of Verdel et al. (Reference Verdel, Niemi and van der Pluijm2011), because the clay mineralogy and polytype analysis demonstrated that clays found in the gouge of a low-angle normal fault are the same as those in hanging wall sediments. Verdel et al. (Reference Verdel, Niemi and van der Pluijm2011) concluded from these data that clays were mechanically incorporated into the fault via a clay smear mechanism (e.g. Vrolijk et al., Reference Vrolijk, Urai and Kettermann2016), and subsequent deformation was at such a low temperature that no further mineral reactions were possible (low temperature confirmed by apatite fission track ages and track length distributions).
In spite of differences in the amount of analytical thoroughness applied by different groups, the gouge-dating method has quickly found acceptance as a useful tool for fault tectonic studies. Additional gouge-dating studies have been undertaken in Asia to elucidate aspects of the Himalayan collision history (Biu et al., Reference Bui, Ngo, Khuong, Golonka, Nguyen, Song, Itaya and Yagi2017; Duvall et al., Reference Duvall, Clark, van der Pluijm and Li2011), the Late Phanerozoic tectonic history of northeast Asia (Song et al., Reference Song, Chung, Choi, Kang, Park, Itaya and Yi2014), Cretaceous fault reactivation in South Korea (Zwingmann et al., Reference Zwingmann, Han and Ree2011), the Alps (Surace et al., Reference Surace, Clauer, Thélin and Pfeifer2011), the North Anatolian Fault system (Uysal et al., Reference Uysal, Mutlu, Altunel, Karabacak and Golding2006) and Atlantic rifting in Norway (Viola et al., Reference Viola, Zwingmann, Mattila and Käpyaho2016). In each of these studies, gouge dating was used as part of a more complete geological evaluation, and the diversity of tectonic problems addressed attests to the general utility of the methods.
Fault processes and mechanics
In addition to revealing more detailed tectonic histories, gouge-dating studies also reveal information about the processes and mechanics of fault deformation based on mineral reaction rates, strain rates and fluid flow history. Vrolijk & van der Pluijm (Reference Vrolijk and van der Pluijm1999) interpreted accelerated prograde clay mineral reactions in thrust and normal fault settings and considered that shear heating is insufficient to drive the degree of reaction progress observed based on a kinetic model of smectite–illite reaction. Additional factors, outlined below, may also contribute to the observed acceleration of reaction progress.
An aspect of the gouge-dating process that perhaps illuminates the success of the methods applied includes the formation of nanoparticles in fault zones. Kameda et al. (Reference Kameda, Shimizu, Ujiie, Hirose, Ikari, Mori, Oohashi and Kimura2015) interpreted neoformation of smectite on the thrust that generated the giant Tohoku earthquake, and Smeraglia et al. (Reference Smeraglia, Billi, Carminati, Cavallo and Doglioni2017) suggested that nanospherules and nanotubes of illite influence fault mechanics. Schleicher et al. (Reference Schleicher, van der Pluijm and Warr2010) obtained ages of 8 Ma on a relic fault strand and 4 Ma on the current strand of the San Andreas Fault sampled in the San Andreas Fault Observatory at Depth (SAFOD) borehole, although there is a 2–3% chance that the younger age is 0 Ma, confirming the association of faulting and clay recrystallization. Schleicher et al. (Reference Schleicher, Boles and van Der Pluijm2015) deduced from laboratory friction experiments that smectite collapses under the effects of shear heating, but recovers soon after the end of deformation, which could have implications for velocity weakening versus strengthening behaviour. Mancketelow et al. (Reference Mancktelow, Zwingmann and Mulch2016) inferred that the development of clay gouge on the Naxos detachment may have contributed to fault weakening, thus aiding the rate of exhumation and cooling of the footwall. These studies (and many others) point to the importance of deformation-driven clay mineral reactions in active and seismogenic faults, just as deformation-driven reactions appear crucial for dating studies, but the effects of syn-deformation reactions on fault properties are underexplored.
Haines & van der Pluijm (Reference Haines and van der Pluijm2008, Reference Haines and van der Pluijm2010) interpreted strain rates on low-angle normal faults in the brittle regime, where clays are formed, as being the same as the deformation in the ductile realm, suggesting that the localization processes developed across a wide range of temperatures can be comparable.
Fluid flow issues focus on chemical open versus closed systems, with an end-member open system characterized by meteoric water infiltration. Solum et al. (Reference Solum, Davatzes and Lockner2010) deduced open system behaviour based on elemental comparisons of deformed and undeformed rocks, identified fault segments dominated by mechanical processes (i.e. a closed system) and inferred how the incorporation and evolution of clays influenced fault strength based on laboratory deformation experiments. Recent normal faulting in the Menderes Massif (Hetzel et al., Reference Hetzel, Zwingmann, Mulch, Gessner, Akal, Hampel, Güngör, Petschick, Mikes and Wedin2013) is interpreted to have developed under conditions of meteoric water based on hydrogen isotope ratios of clays. Haines et al. (Reference Haines, Mulch, Valley and van der Pluijm2016) also interprets meteoric water infiltration for normal faults active at upper to mid-crustal levels, linking observations in clay gouge to inferences from mineral reactions in mylonites. Boles et al. (Reference Boles, van der Pluijm, Mulch, Mutlu, Uysal and Warr2015) inferred protracted meteoric infiltration on the North Anatolian Fault based on combined age dating and hydrogen isotope measurements of clays.
In a comprehensive review of clay mineral reactions in low-angle normal faults, Haines & van der Pluijm (Reference Haines and van der Pluijm2012) reflected on four characteristics of the gouges they have investigated, including:
1. Growth of 1M d illite from fragments of 2M 1 illite or K-feldspar dissolution. They view this as less common in this environment than in sedimentary rocks with mixed-layer I-S.
2. ‘Retrograde diagenesis’ to form new chlorite–smectite or saponite from an initial, mechanically derived, chlorite-rich gouge.
3. Reaction of chlorite-rich gouge with Mg-rich fluids to produce pods of unique mineral assemblages.
4. Alteration of acidic volcanic wall rocks to form authigenic di-octahedral smectite.
This work tackles the complex problem of relating authigenic mineral assemblages in gouges to the heterolithic lithology of rocks incorporated into low-angle normal faults, the effects of mechanical comminution processes and the contribution of externally derived fluids out of chemical equilibrium with the local environment. This kind of mineral reaction framework is invaluable in relating the age of any particular K-bearing mineral phase to the deformation and associated mineral reaction history of a fault.
Finally, one aspect of fault processes reflects back on the success of gouge dating – shear heating or warm fluid intrusion resulting in Ar loss. Tonai et al. (Reference Tonai, Ito, Hashimoto, Tamura and Tomioka2016) interpreted complete Ar loss based on fault ages younger than diagenetic ages in deformed shales and attributed that loss to shear heating, although it is difficult to see how fault-activated recrystallization can be ruled out with the observations presented. Och et al. (Reference Och, Offler and Zwingmann2014) similarly interpreted Ar loss from heating related to Cretaceous intrusions based on equivalent ages from fault gouge and undeformed rocks, although gouge was sampled from faults with only metres of offset. Moreover, without any detailed mineralogical and polytype analysis, it is difficult to evaluate how similar ages are and whether a younger fault age could be extrapolated based on these data.
The problem with invoking an Ar diffusion argument is that it is difficult to derive a strong test of this hypothesis. By accepting that fault samples are a mixture of components derived either from authigenic and inherited (detrital) components or different stages in a fault evolution or possibly a combination of both and then invoking Ar diffusion, the number or degrees of freedom probably preclude a useful interpretation. The evidence for pervasive recrystallization during faulting is compelling, while the corresponding evidence for Ar diffusion seems much weaker. In our opinion, a researcher should remain mindful of this process in fault age interpretations, but invoke it only reluctantly or when there is strong evidence to support it.
Fold dating
The gouge-dating method has been extended to the structurally related problem of folding. Fitz-Diaz & van der Pluijm (Reference Fitz-Diaz and van der Pluijm2013) first dated clay layers between limestone beds that were intensely folded in the Mexican fold-and-thrust belt. These samples are notable for the amount of authigenic illite they contain, with only 0–20% of each sample consisting of detrital illite. It is interesting to ponder how much of the shale layer thickening in the tight chevron-fold axes might be related to dissolution, local limb-to-hinge transport and reprecipitation processes. This approach was expanded by Fitz-Diaz et al. (Reference Fitz-Diaz, Hudleston, Tolson and van der Pluijm2014) to a more regional evaluation of deformation timing in the Mexican fold-and-thrust belt.
Wang et al. (Reference Wang, Zwingmann, Zhou, Lo, Viola and Hao2016) described Late Jurassic and Early Cretaceous muscovite ages in fold hinges related to subduction-driven tectonic activity, and they compared these ages to Neoproterozoic detrital ages in the Proterozoic–Cambrian host rocks. This study does an excellent job of relating the dated muscovites from deformation fabrics defined at the outcrop to the microscope scale, which is easier for the larger muscovite crystal sizes. Given the low-grade metamorphic conditions of this study, the results compare with the interpretation of results offered by Kirschner et al. (Reference Kirschner, Cosca, Masson and Hunziker1996) more than results from van der Pluijm et al. (Reference van der Pluijm, Hall, Vrolijk, Pevear and Covey2001), which are derived from a diagenetic to very-low-grade metamorphic environment.
Nemkin et al. (Reference Nemkin, Fitz-Díaz, van der Pluijm and van der Voo2015) combined dates derived from folds with palaeomagnetic data to better constrain the timing of remagnetization related to folding. Although the growth of illites and magnetite were implicitly assumed to be related, there was no attempt in this paper to derive a series of linked chemical reactions that would explicitly relate the two processes.
Although fold dating based on the deformation-related growth of authigenic illite has been less widely applied than gouge dating, it appears to be feasible and successful. A successful study appears to rely upon the same elements that contribute to a successful fault study: careful sample selection in the field; detailed petrographic analysis to relate the particles being dated to microstructures tied to structures observed in the field; detailed mineralogical characterization and polytype quantification; and careful geochronological work. Although folds are often better exposed than faults, it is possible that only high-strain folds like those analysed to date may yield successful ages, but this speculation requires testing.
ISSUES AND QUESTIONS: CONCLUDING REMARKS
Fault gouge dating in sub-metamorphic, diagenetic environments has become an established geological practice. Successful gouge-dating studies rely upon the application and integration of a suite of established geological work practices: structural field mapping and analysis; microstructural petrography; XRD mineral identification; XRD clay mineral quantification; and radiometric age dating based on the K/Ar system (either K/Ar or 40Ar/39Ar methods). The results of fault gouge-dating studies have been used to refine fault and tectonic histories in a range of structural settings, including fold-and-thrust belts, normal fault terrains (including low-angle normal faults) and strike-slip faults spanning recent to Palaeozoic fault histories. The method has also been extended to folds, although the application in folds may be limited to high-strain folds.
Although the initial application of gouge dating grew out of applied industry research in a fold-and-thrust setting, it spread to a much broader range of settings and applications in academic research, including the application of gouge dating in retrograde clay gouge formed from fault processes in igneous or metamorphic rocks that contain no clays. Moreover, academic research, particularly work at the University of Michigan, incorporated two critical components into the analysis that were unavailable during the industry research phase: 40Ar/39Ar micro-encapsulation methods in addition to existing K/Ar methods; and quantification of illite polytypes and their abundances using Wildfire. Many of the published applications reviewed here would have been impossible without these subsequent developments, and a great deal of credit is due to van der Pluijm and his students for pursuing these developments.
The history of the interpretation of the Rundle thrust traced through this manuscript is a good illustration of the importance of subsequent developments. Initial ages from size fractions that were illite-rich and for which there was no means to evaluate the amount of inherited detrital material yielded older ages than subsequent interpretations. The working model assumed that if ages in fine and medium-sized fractions are the same within the analytical uncertainty, then this might approximate a pure authigenic end-member defined by the ‘bench spectrum’. However, polytype modelling by Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) showed this interpretation to be incorrect and lowered the interpreted fault age by 7.3 m.y. (<10%), and the application of 40Ar/39Ar methods (van der Pluijm et al., Reference van der Pluijm, Vrolijk, Pevear, Hall and Solum2006) lowered the age by another 6.5 m.y. (<10%). The analysis by Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) showed the critical importance of modelling the clay mineral polytypes in order to achieve a reliable fault age, and this example provides a basis for concern that studies of retrograde faults, in particular faults that could have incorporated illite at some point in the displacement history, skip this step and assume that the smallest size fraction dates the most recent fault history. There is no comprehensive understanding for why the use of 40Ar/39Ar methods results in a different age from the K/Ar method that applies to all situations. The size of the age change from Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) to van der Pluijm et al. (Reference van der Pluijm, Vrolijk, Pevear, Hall and Solum2006) is accentuated by the fact that the fine fraction is younger and the coarse fraction older by the 40Ar/39Ar method. Reconciling these two dating systems further is an area of potential future research, particularly in light of analytical advancements that reduce the sample size for K/Ar measurements.
The precision and accuracy of the method also requires further evaluation. Whereas Solum et al. (Reference Solum, van der Pluijm and Peacor2005) assumed a small (±3%) uncertainty in the interpretation of the amount of the 2M 1 polytype in a sample based on Grathoff & Moore (Reference Grathoff and Moore1996), our experience at Exxon was that some samples are better matched than others, and some samples therefore have greater uncertainty in the amount of detrital mica. Others (e.g. A.M. Schleicher, 2017, pers. comm.) have also experienced difficulties in achieving good matches between modelled and measured XRD patterns, for which there can be a myriad of mineralogical and sample preparation causes. What constitutes the best fit between measured and modelled patterns, as the divergence in approaches between Haines & van der Pluijm (Reference Haines and van der Pluijm2008) and Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) illustrates? Is the genetic algorithm approach described by Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002) a more objective approach compared to more manual analyses, particularly when it comes to defining uncertainty ranges? The Exxon method describes the full probability density function of mineralogical uncertainty in order to use that information in Monte Carlo simulations of linear regression of the data so as to define the uncertainty of the extrapolated diagenetic and detrital ages. More recent work (Mahon, Reference Mahon1996) introduced the York regression method for evaluating uncertainty in X and Y variables and demonstrated good correspondence with Monte Carlo methods. In our view, mineralogical uncertainty (i.e. the proportion of authigenic and detrital components in any size-separated sample) may remain the most important and underappreciated part of the analysis, and we would welcome further research to better define uncertainty in the mineralogical interpretation.
The distribution of extrapolated age probabilities is crucial for geological interpretation. For example, Schleicher et al. (Reference Schleicher, van der Pluijm and Warr2010) interpreted a 4 ± 4.9 Ma age for samples taken from the San Andreas Fault, yet the uncertainty range includes a zero age. While L.N. Warr (2017, pers. comm.) prefers a non-zero age interpretation for this sample, it is only possible to evaluate this viewpoint knowing the probability of the zero age (i.e. is it defined at the 1σ, 2σ, 3σ or 4σ level?). The discussion of precision, accuracy and uncertainty is critical because if too high a precision is assumed, then results that seem to contradict other observations will throw the method into doubt. Alternatively, if too large an uncertainty is assumed, then the method will cease to provide useful age constraints for some samples. In considering many samples processed in the Exxon laboratories, the following guidelines for considering uncertainty were developed:
• Samples with less detrital (2M 1) illite, particularly in the fine and medium fractions, yield less uncertainty from the linear regression.
• Samples with less difference between diagenetic and detrital end-member ages yield smaller extrapolation uncertainties (the tail-wagging-the-dog phenomenon, which helped lead us to the idea that flat and bench fault age spectra might be meaningful).
• Mineralogical uncertainty (% detrital illite) is greater than radiometric age uncertainty and thus has a bigger effect on diagenetic age uncertainty.
These guidelines were established to address and minimize potential complications identified in the literature. For example, there are many different ways to achieve clay mineral quantification (see, e.g. Środoń [Reference Środoń2002] and Zhou et al. [2018] for recent summaries and references to the history of this subject). NewMod and Wildfire have been used in fault gouge-dating studies, in part because they are well suited to distinguishing different illite phases (and illite is the predominant K-bearing clay mineral, which is essential for dating with the K/Ar system). Alternative quantification approaches may also prove useful (e.g. Środoń et al., Reference Środoń, Drits, McCarty, Hsieh and Eberl2001). In addition, linear unmixing of end-member ages is strictly incorrect, and a number of issues can influence the extrapolated age (e.g. Środoń et al., Reference Środoń, Clauer and Eberl2002). However, if extrapolation is small, then the errors become negligible, and the adaptation of simplifying assumptions like linear mixing can aid the processing of large sample datasets necessary to gain useful tectonic insights.
Given the history of research into fault gouge dating, was the Exxon research necessary to launch the subsequent research? While there were no conceptual advantages to pursuing this work in an industry laboratory, there were substantial logistical advantages. Gouge dating is a labour- and resource-intensive effort. A lot of time, equipment and expertise are required for sample preparation, analysis and interpretation. To marshal these resources in order to try to obtain an absolute age for faults without any certainty of success is a risky undertaking and may be why when work started at Exxon only the publications of Lyons & Snellenberg (Reference Lyons and Snellenberg1971) and Kralik et al. (Reference Kralik, Klima and Riedmueller1987) were available in the literature. Fault gouge-dating research occurred at Exxon because the analytical infrastructure was established and functioning for other purposes.
The certainty of success that van der Pluijm could observe, as well as size-separated and characterized samples for initial analyses, may have been a strong motivator for the early academic research. If true, what other research developments might languish because of logistical hurdles that seem too high to surmount in the current research environment? How do we recognize fruitful research opportunities? Do we need to become more tolerant of research ‘failures’ to help reduce the hurdles to trying new things? How do we recognize and develop unique research collaborations to further reduce these hurdles? There may be no simple answers to these questions; their solutions may simply depend on scientists being principally interested in scientific advancement.
Fault gouge-dating methods have achieved a routine, standard set of steps, and as the literature shows, many different groups can undertake gouge-dating studies. However, some nuanced judgement remains in the method, issues that experienced practitioners need to remain mindful of and new users must consider carefully. For example, Haines & van der Pluijm (Reference Grathoff and Moore2008) introduced an alternative method for modelling hkl patterns of random samples than the one used by Ylagan et al. (Reference Ylagan, Kim, Pevear and Vrolijk2002). While arguments can be made both for and against each approach, the important thing is to consider when the two methods yield the same result and under what conditions they are different, as Haines & van der Pluijm (Reference Haines and van der Pluijm2008) described. When they are different, we must consider the implications for the question(s) under consideration. Similarly, there are nuances in the choice of dating method, as Clauer et al. (Reference Clauer, Zwingmann, Liewig and Wendling2012) have described, and even within the application of the 40Ar/39Ar method, information about particle thicknesses should affect how the ages are interpreted (Hnat & van der Pluijm, Reference Hnat and van der Pluijm2014).
The matter of fault processes and the impact of syn-deformation clay mineral reactions, particularly as they relate to earthquake studies, is an area where there has been some effort, but in our opinion, there is an opportunity for an expanded effort and resulting insights. For example, detailed micro-structural analyses of recently seismic faults (e.g. Schleicher et al., Reference Schleicher, van der Pluijm and Warr2010, Reference Schleicher, Boles and van Der Pluijm2015; Smeraglia et al., Reference Smeraglia, Billi, Carminati, Cavallo and Doglioni2017) have revealed both mixed-layer I-S in some fault zones and dioctahedral smectite in other faults. What controls the mineral phase that is precipitated, and how does that affect the mechanical properties of the fault? Haines & van der Pluijm (Reference Haines and van der Pluijm2012) offered a clear example of how an approach identifying the product and reactant yields deeper insights into fault processes. Perhaps the answer to the question posed above rests in more emphasis being placed on reactants – could the presence or absence of dissolution of K-bearing phases control the precipitation of smectite versus mixed-layer I-S?
Lastly, additional instances of fault structural and tectonic insights generated by new gouge-dating studies should be on the horizon. The existing literature has shown the benefit of sampling at scales ranging from a single outcrop (metre-scale) to the regional scale (1000 km), and continued benefits will arise from a multitude of scales of investigation. The methods may be established, but there is a lot of geology yet to explore.
SUMMARY
Fault-gouge dating by application of the IAA method has become an accepted tool for probing fault structural and tectonic histories. IAA offers the means to unmix natural samples that contain two forms of illite developed as mixed-layer I-S, discrete 1M d illite or 2M 1 illite (muscovite). Although the original method was developed at Exxon Production Research Company to address a specific problem of trap timing in the fold-and-thrust belt of the Canadian Rockies, its use in academic research has spread to include all fault settings and types, as well as conditions marked by no mineral reactions up to metamorphic conditions. Academic research has contributed two significant modifications to the method: (1) the application of the 40Ar/39Ar method to augment K/Ar dating; and (2) the widespread application of Wildfire for modelling illite polytypes in illite-dominated samples. The method has also been applied successfully to date the age of fold development in a fold-and-thrust belt.
The application of IAA fault gouge dating has also spread to retrograde clay gouge, which develops in faults cutting igneous or metamorphic rocks that contain no clays to begin with. This development augments the original application developed for prograde clay gouge in which the sedimentary section cut by faults has a more limited degree of reaction progress (e.g. smectite–illite) than fault samples. In both instances, though, the development and evolution of clays is seen as an integral part of fault processes.
Although a fair investment towards establishing laboratory and interpretation procedures is required to apply the fault gouge-dating method, collaboration can help overcome some of these obstacles, which the literature record illustrates is happening. We expect to continue to see gouge-dating applications helping to address fault structural and tectonic questions, but the opportunity to apply the methods to studies of fault processes, and in particular earthquake studies, is greatly anticipated.
SUPPLEMENTARY MATERIAL
The supplementary material for this article can be found at https://doi.org/10.1180/clm.2018.22.
ACKNOWLEDGMENTS
The authors are first and foremost indebted to the Exxon lab support staff who contributed weeks and months to sample preparation and analysis: a huge debt of gratitude is owed to Tom Phillips, who processed all of the samples used in this study and preserved them in a way that made it easy to provide them to the Michigan group; Roy Brown spent countless hours helping to document deformation textures under the scanning electron microscope; GeorgAnn Robinson, who collected transmission electron microscopy images of the illite particles; and to Simon Tsipursky, who helped with the initial steps towards illite-polytype quantification. Three anonymous reviewers provided additional insights and perspectives that truly helped to improve the final manuscript.