Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T17:14:57.393Z Has data issue: false hasContentIssue false
  • English
  • Français

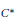Weakly Stable Relations and Inductive Limits of ${{C}^{*}}$-algebras

Published online by Cambridge University Press:  20 November 2018

Martha Salerno Monteiro
Martha Salerno Monteiro*
Affiliation:
Departamento de Matemática—IME Universidade de São Paulo Rua do Matão, 1010 CEP 05508-900 São Paulo—SP Brasil, e-mail: martha@ime.usp.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if 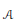$\mathcal{A}$ is a class of 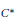${{C}^{*}}$-algebras for which the set of formal relations 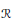$\mathcal{R}$ is weakly stable, then 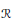$\mathcal{R}$ is weakly stable for the class 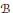$B$ that contains 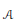$\mathcal{A}$ and all the inductive limits that can be constructed with the 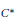${{C}^{*}}$-algebras in 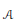$\mathcal{A}$.

A set of formal relations 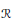$\mathcal{R}$ is said to be weakly stable for a class 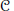$\mathcal{C}$ of 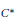${{C}^{*}}$-algebras if, in any 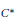${{C}^{*}}$-algebra 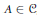$A\,\in \,\mathcal{C}$, close to an approximate representation of the set 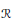$\mathcal{R}$ in 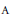$A$ there is an exact representation of 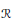$\mathcal{R}$ in 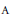$A$.

Keywords

46L05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 4 , 01 December 2003 , pp. 588 - 596
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Blackadar, B., Shape Theory for C*-Algebras. Math. Scand. 56 (1985), 249–275.Google Scholar
[2] Brown, L., Ext of certain free product C*-algebras. J. Operator Theory 6 (1981), 135–141.Google Scholar
[3] Cerri, C., Non-commutative Deformation of C(T2) and K-theory. Internat. J. Math. (5) 8 (1997), 555–571.Google Scholar
[4] Coburn, L. A., The C*-algebra generated by an Isometry. Bull. Amer.Math. Soc. 73 (1967), 722–726.Google Scholar
[5] Cuntz, J., K-Theory for certain C*-algebras. Ann. of Math. 113 (1981), 181–197.Google Scholar
[6] Eilers, S. and Loring, T. A. and Pedersen, G. K., Stability of Anticommutation Relations. An Application of Noncommutative CW complexes. J. Reine Angew.Math. 499 (1998), 101–143.Google Scholar
[7] Friis, P. and Rørdam, M., Almost commuting self-adjoint matrices.a short proof of Huaxin Lin's theorem. J. Reine Angew.Math. 479 (1996), 121–131.Google Scholar
[8] Hadwin, D. W., Closures of direct sums of classes of operators. Proc. Amer.Math. Soc. 121 (1994), 697–701.Google Scholar
[9] Lin, H., Almost commuting selfadjoint matrices and applications. Operator algebras and their applications, Amer.Math. Soc. 13, Fields Inst. Commun., 193–233.Google Scholar
[10] Loring, T. A., C*-Algebras generated by stable relations. J. Funct. Anal. 112 (1993), 159–201.Google Scholar
[11] Loring, T. A., Lifting Solutions to Perturbing Problem in C*-Algebras. Amer.Math. Soc. 81997, Fields Institute Monographs.Google Scholar
[12] Monteiro, M. S.,Weakly Stable Relations and Inductive Limits of C*-algebras. University of New Mexico, July, 2000.Google Scholar
[13] Murphy, G. J., C*-Algebras and Operator Theory. Academic Press, New York, 1990.Google Scholar
[14] Phillips, N. C., Inverse limit of C*-algebras and applications. Operator algebras and applications 1, Cambridge Univ. Press 135, LondonMath. Soc. Lecture Note. Ser. 1988, 127–185.Google Scholar