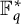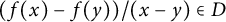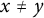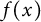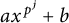1 Introduction
Throughout this paper, let p be a prime. Let
$q=p^n$
and
$\mathbb {F}_q$
be the finite field with q elements with
$\mathbb {F}_q^*=\mathbb {F}_q \setminus \{0\}$
.
A celebrated result of McConnel [Reference McConnel15] states that if D is a proper subgroup of
$\mathbb {F}_q^*$
, and
$f:\mathbb {F}_q \to \mathbb {F}_q$
is a function such that
$$ \begin{align} \frac{f(x)-f(y)}{x-y} \in D \end{align} $$
whenever
$x,y \in \mathbb {F}_q$
with
$x \neq y$
, then there are
$a,b \in \mathbb {F}_q$
and an integer
$0 \leq j \leq n-1$
, such that
$f(x)=a x^{p^j}+b$
for all
$x \in \mathbb {F}_q$
. This result was first proved by Carlitz [Reference Carlitz7] when q is odd and D consists of squares in
$\mathbb {F}_q^*$
, that is, D is the subgroup of index
$2$
. Carlitz’s theorem and McConnel’s theorem have various connections with finite geometry, graph theory, and group theory; we refer to a nice survey by Jones [Reference Jones11, Section 9]. In particular, they have many applications in finite geometry; see, for example, [Reference Blokhuis, Seress and Wilbrink5, Reference Knarr and Stroppel12]. We also refer to variations of McConnel’s theorem in [Reference Bruen and Levinger6, Reference Grundhöfer10, Reference Lenstra13] via tools from group theory.
One may wonder, if the assumption that D is a multiplicative subgroup plays an important role in McConnel’s theorem and if it is possible to weaken this assumption. Inspired by this natural question, in this paper, we find a sufficient condition on D so that if condition (1.1) holds for a function
$f:\mathbb {F}_q \to \mathbb {F}_q$
, then f necessarily has the form
$f(x)=a x^{p^j}+b$
. In particular, our main result (Theorem 1.2) strengthens McConnel’s theorem.
Before stating our results, we introduce some motivations and backgrounds from the theory of directions and their applications. Let
$AG(2,q)$
denote the affine Galois plane over the finite field
$\mathbb {F}_q$
. Let U be a subset of points in
$AG(2,q)$
; we use Cartesian coordinates in
$AG(2,q)$
so that
$U=\{(x_i,y_i):1 \leq i \leq |U|\}$
. The set of directions determined by
$U \subset AG(2, q)$
is
$$\begin{align*}\mathcal{D}_U=\left\{ \frac{y_j-y_i}{x_j-x_i} \colon 1\leq i <j \leq |U| \right \} \subset \mathbb{F}_q \cup \{\infty\},\end{align*}$$
where
$\infty $
is the vertical direction. If
$f:\mathbb {F}_q \to \mathbb {F}_q$
is a function, we can naturally consider its graph
$U(f)=\{(x,f(x)): x \in \mathbb {F}_q\}$
and the set of directions determined by f is
$\mathcal {D}_f:=\mathcal {D}_{U(f)}$
. Indeed,
$\mathcal {D}_f$
precisely computes the set of slopes of tangent lines joining two points on
$U(f)$
. Using this terminology, condition (1.1) is equivalent to
$\mathcal {D}_f \subset D$
.
The following well-known result is due to Blokhuis, Ball, Brouwer, Storme, and Szőnyi [Reference Ball3, Reference Blokhuis, Ball, Brouwer, Storme and Szőnyi4].
Theorem 1.1 Let p be a prime and let
$q=p^n$
. Let
$f:\mathbb {F}_q \to \mathbb {F}_q$
be a function such that
$f(0)=0$
. If
$|\mathcal {D}_f|\leq \frac {q+1}{2}$
, then f is a linearized polynomial, that is, there are
$\alpha _0,\alpha _1, \ldots , \alpha _{n-1}\in \mathbb {F}_q$
, such that
$$ \begin{align*}f(x)=\sum_{j=0}^{n-1} \alpha_j x^{p^j}, \quad \forall x \in \mathbb{F}_q. \end{align*} $$
In particular, when
$q=p$
is a prime, Theorem 1.1 implies McConnel’s theorem; this was first observed by Lovász and Schrijver [Reference Lovász and Schrijver14]. We remark that when
$q=p$
is a prime, Müller [Reference Müller16] showed a stronger result, namely, if D is a non-empty proper subset of
$\mathbb {F}_p^*$
such that
$f(x)-f(y)\in D$
whenever
$x-y \in D$
, then there are
$a,b \in \mathbb {F}_p$
such that
$f(x)=ax+b$
for all
$x \in \mathbb {F}_p$
. For a general prime power q, Theorem 1.1 does not imply McConnel’s theorem directly. However, using the idea of directions, Muzychuk [Reference Muzychuk17] provided a self-contained proof of McConnel’s theorem.
While Theorem 1.1 is already quite powerful, in many applications, if some extra information on
$\mathcal {D}_f$
is given, it is desirable to obtain a stronger conclusion, namely,
$f(x)$
is of the form
$ax^{p^j}+b$
for some j, or even
$f(x)$
must have the form
$ax+b$
. As an illustration, we mention two recent works in applying a stronger version of Theorem 1.1 to prove analogs of the Erdős–Ko–Rado (EKR) theorem in the finite field setting [Reference Aguglia, Csajbók and Weiner1, Reference Asgarli and Yip2]. Asgarli and Yip [Reference Asgarli and Yip2] proved the EKR theorem for a family of pseudo-Paley graphs of square order, and their main result roughly states that if
$\mathcal {D}_f$
arises from a Cayley graph with “nice multiplicative properties” on its connection set, then
$f(x)$
has the form
$ax+b$
; see [Reference Yip19] for more discussions. As another example, very recently, Aguglia, Csajbók, and Weiner proved several EKR theorems for polynomials over finite fields [Reference Aguglia, Csajbók and Weiner1]. Again, one key ingredient in their proof is a strengthening of Theorem 1.1. In [Reference Aguglia, Csajbók and Weiner1, Theorem 2.2], they showed that if
$\mathcal {D}_f$
is a proper
$\mathbb {F}_p$
-subspace of
$\mathbb {F}_q$
, then
$f(x)$
has the form
$ax+b$
; in [Reference Aguglia, Csajbók and Weiner1, Theorem 2.13] (see also [Reference Göloğlu and McGuire9]), they showed that if
$\mathcal {D}_f\setminus \{0\}$
is a subset of a coset of K, where K is the subgroup of
$\mathbb {F}_q^*$
with index
$2$
, then
$f(x)$
has the form
$ax^{p^j}+b$
for some j.
Inspired by the connection above between the theory of directions and McConnel’s theorem, we establish the following result.
Theorem 1.2 Let p be a prime. Let
$q=p^n$
and
$D \subset \mathbb {F}_q^*$
. Suppose
$f:\mathbb {F}_q \to \mathbb {F}_q$
is a function such that
$$ \begin{align*}\frac{f(x)-f(y)}{x-y} \in D \end{align*} $$
whenever
$x,y \in \mathbb {F}_q$
with
$x \neq y$
. If
$$ \begin{align} |DD^{-1}D^{-1}|\leq \frac{q+1}{2}, \end{align} $$
then there are
$a,b \in \mathbb {F}_q$
and an integer
$0 \leq j \leq n-1$
, such that
$f(x)=a x^{p^j}+b$
for all
$x \in \mathbb {F}_q$
. In particular, if
$c>0$
is a real number such that
$|DD|\leq c|D|$
, and
$c^3|D|\leq \frac {q+1}{2}$
, then the same conclusion holds.
If D is a proper subgroup of
$\mathbb {F}_q^*$
, then clearly
$DD^{-1}D^{-1}=D$
and thus Theorem 1.2 recovers McConnel’s theorem. Indeed, in this case, the doubling constant of D is simply
$|DD|/|D|=1$
. Our result shows that if the doubling constant
$|DD|/|D|$
of D is small, and
$|D|$
is not too large, then the analog of McConnel’s theorem still holds. There are many ways to construct a set
$D \subset \mathbb {F}_q^*$
with small doubling. For example, we can set
$D=K \cup E$
, where K is a subgroup of
$\mathbb {F}_q^*$
, and E is an arbitrary subset of
$\mathbb {F}_q^*$
such that
$|E|$
is small; alternatively, D can be taken to be the union of some cosets of a fixed subgroup K of
$\mathbb {F}_q^*$
.
For a linearized polynomial
$f(x)$
, note that
$\mathcal {D}_f=\operatorname {Im}(f(x)/x)$
. We refer to [Reference Csajbók, Marino and Polverino8] and references therein on the study of
$\operatorname {Im}(f(x)/x)$
for linearized polynomials f. In particular, it is an open question to determine all the possible sizes of
$\operatorname {Im}(f(x)/x)$
among linearized polynomials f [Reference Csajbók, Marino and Polverino8, Section 6]. Theorem 1.2 implies the following corollary, which partially addresses this question. It states that if D is such an image set and D satisfies inequality (1.2), then D is necessarily a coset of a subgroup of
$\mathbb {F}_{q}^*$
with a restricted index.
Corollary 1.3 Let p be a prime and let
$q=p^n$
. If
$D \subset \mathbb {F}_q^*$
and
$|DD^{-1}D^{-1}|\leq \frac {q+1}{2}$
, then
$D=\mathcal {D}_f$
for some function
$f: \mathbb {F}_q \to \mathbb {F}_q$
with
$f(0)=0$
if and only if
$D=aK$
, where
$a \in \mathbb {F}_q^*$
and K is a subgroup of
$\mathbb {F}_{q}^*$
with index
$p^r-1$
, where r is a divisor of n.
Notations. We follow standard notations for arithmetic operations among sets. Given two sets A and B, we write
$AB=\{ab: a \in A, b \in B\}$
,
$A^{-1}=\{a^{-1}: a \in A\}$
.
2 Proofs
We start by proving Theorem 1.2. Our proof is inspired by several arguments used in [Reference Lovász and Schrijver14, Reference Muzychuk17].
Proof (Proof of Theorem 1.2) Without loss of generality, by replacing the function
$f(x)$
with
$f(x)-f(0)$
, we may assume that
$f(0)=0$
. Since
$|\mathcal {D}_f|\leq \frac {q+1}{2}$
, Theorem 1.1 implies that f is linearized. Let
$g(x)=1/f(x^{-1})$
for
$x \in \mathbb {F}_q \setminus \{0\}$
and set
$g(0)=0$
. We claim that g is also linearized.
Let
$x,y \in \mathbb {F}_q^*$
with
$x \neq y$
. Then,
$$ \begin{align*}\frac{g(x)-g(y)}{x-y}=\frac{\frac{1}{f(x^{-1})}-\frac{1}{f(y^{-1})}}{x-y}=\frac{f(y^{-1})-f(x^{-1})}{(x-y)f(x^{-1})f(y^{-1})}=\frac{f(y^{-1}-x^{-1})}{(x-y)f(x^{-1})f(y^{-1})} \end{align*} $$
since f is linearized. It follows that
$$ \begin{align*}\frac{g(x)-g(y)}{x-y}=\frac{f(\frac{x-y}{xy})}{(x-y)f(x^{-1})f(y^{-1})}=\frac{f(\frac{x-y}{xy})}{\frac{x-y}{xy}} \cdot \frac{x^{-1}}{f(x^{-1})} \cdot \frac{y^{-1}}{f(y^{-1})} \in DD^{-1}D^{-1}. \end{align*} $$
On the other hand, if
$x \in \mathbb {F}_q^*$
, then
$$ \begin{align*}\frac{g(x)-g(0)}{x-0}=\frac{g(x)}{x}=\frac{1}{xf(x^{-1})}=\frac{x^{-1}}{f(x^{-1})} \in D^{-1}. \end{align*} $$
We conclude that
$$ \begin{align*}\mathcal{D}_g \subset DD^{-1}D^{-1} \cup D^{-1}=DD^{-1}D^{-1}. \end{align*} $$
Then inequality (1.2) implies that
$|\mathcal {D}_g|\leq \frac {q+1}{2}$
, and Theorem 1.1 implies that g is also linearized.
Since f and g are both linearized, we can find
$\alpha _0, \beta _0, \ldots , \alpha _{n-1}, \beta _{n-1} \in \mathbb {F}_q$
, such that
$$ \begin{align*}f(x)=\sum_{j=0}^{n-1} \alpha_j x^{p^j}, \quad \text{and} \quad g(x)=\sum_{j=0}^{n-1} \beta_j x^{p^j}, \quad \forall x \in \mathbb{F}_q. \end{align*} $$
By the definition of g, we have
$f(x^{-1})g(x)=1$
for each
$x \in \mathbb {F}_q^*$
, and thus
$(x^{p^{n-1}}f(x^{-1})) (g(x)/x)=x^{p^{n-1}-1}$
for all
$x \in \mathbb {F}_q^*$
. Equivalently,
$$ \begin{align} h(x):=\bigg(\sum_{j=0}^{n-1} \alpha_j x^{p^{n-1}-p^j}\bigg) \bigg(\sum_{j=0}^{n-1} \beta_j x^{p^j-1} \bigg)=x^{p^{n-1}-1} \end{align} $$
holds for all
$x \in \mathbb {F}_q^*$
. Note that
$h(x)-x^{p^{n-1}-1}$
is a polynomial with degree at most
$2(p^{n-1}-1)\leq p^n-1=q-1$
, and
$h(x)-x^{p^{n-1}-1}$
vanishes on
$\mathbb {F}_q^*$
. It follows that there is a constant
$C \in \mathbb {F}_q$
, such that
$h(x)-x^{p^{n-1}-1}=C(x^{q-1}-1)$
as polynomials. By setting
$x=0$
, we get
$C=0$
. Therefore,
$h(x)=x^{p^{n-1}-1}$
as polynomials. In particular,
$g(x)$
is a factor of
$x^{p^{n-1}}$
. Thus, there are
$\gamma \in \mathbb {F}_q^*$
and
$0 \leq j \leq n-1$
such that
$g(x)=\gamma x^{p^j}$
for all
$x \in \mathbb {F}_q$
, and it follows that
$f(x)=\gamma ^{-1} x^{p^j}$
for all
$x \in \mathbb {F}_q$
, as required.
Finally, assume that
$|DD|\leq c|D|$
, and
$c^3|D|\leq \frac {q+1}{2}$
. Then the Plünnecke–Ruzsa inequality (see, for example, [Reference Petridis18, Theorem 1.2]) implies that
$$ \begin{align*}|DD^{-1}D^{-1}|\leq c^3|D| \leq \frac{q+1}{2}, \end{align*} $$
and thus the same conclusion holds.
Now we use Theorem 1.2 to deduce Corollary 1.3.
Proof (Proof of Corollary 1.3) Assume that
$f:\mathbb {F}_q \to \mathbb {F}_q$
is a function such that
$f(0)=0$
and
$\mathcal {D}_f=D$
. Since
$D \subset \mathbb {F}_q^*$
and
$|DD^{-1}D^{-1}|\leq \frac {q+1}{2}$
, Theorem 1.2 implies that there exist
$a \in \mathbb {F}_q^*$
and an integer
$0 \leq j \leq n-1$
, such that
$f(x)=ax^{p^j}$
for all
$x \in \mathbb {F}_q$
. Therefore,
$D=\mathcal {D}_f=\{ax^{p^j-1}: x \in \mathbb {F}_q^*\}.$
Note that
$$ \begin{align*}\gcd(p^j-1, q-1)=\gcd(p^j-1, p^n-1)=p^{\gcd(j,n)}-1.\end{align*} $$
It follows that
$$ \begin{align*}D=\{ax^{p^{\gcd(j,n)}-1}: x \in \mathbb{F}_q^*\}=aK,\end{align*} $$
where K is the subgroup of
$\mathbb {F}_q^*$
with index
$p^{\gcd (j,n)}-1$
.
Conversely, let r be a divisor of n and
$a \in \mathbb {F}_q^*$
. Let
$f(x)=ax^{p^r}$
for all
$x \in \mathbb {F}_q$
. Then we have
$\mathcal {D}_f=\{ax^{p^r-1}: x \in \mathbb {F}_q^*\}=aK$
, where K is the subgroup of
$\mathbb {F}_q^*$
with index
$p^{r}-1$
.
Acknowledgments
The author thanks Bence Csajbók for helpful discussions. The author is also grateful to anonymous referees for their valuable comments and suggestions.
