Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-11T14:52:35.554Z Has data issue: false hasContentIssue false
  • English
  • Français

A Sharp Bound on RIC in Generalized Orthogonal Matching Pursuit

Published online by Cambridge University Press:  20 November 2018

Wengu Chen  and
Huanmin Ge
Wengu Chen
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing, 100088, China, e-mail: chenwg@iapcm.ac.cn
Huanmin Ge
Affiliation:
Graduate School, China Academy of Engineering Physics, Beijing, 100088, China, e-mail: gehuanmin@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The generalized orthogonal matching pursuit 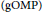$\left( \text{gOMP} \right)$ algorithm has received much attention in recent years as a natural extension of the orthogonal matching pursuit 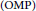$\left( \text{OMP} \right)$. It is used to recover sparse signals in compressive sensing. In this paper, a new bound is obtained for the exact reconstruction of every $K$-sparse signal via the 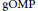$\text{gOMP}$ algorithm in the noiseless case. That is, if the restricted isometry constant 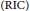$\left( \text{RIC} \right)$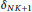${{\delta }_{NK+1}}$ of the sensing matrix $A$ satisfies

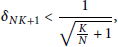${{\delta }_{NK+1}}\,<\frac{1}{\sqrt{\frac{K}{N}+\,1}},$

then the 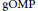$\text{gOMP}$ can perfectly recover every $K$-sparse signal $x$ from 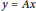$y\,=\,Ax$. Furthermore, the bound is proved to be sharp. In the noisy case, the above bound on $\text{RIC}$ combining with an extra condition on the minimum magnitude of the nonzero components of $K$-sparse signals can guarantee that the 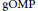$\text{gOMP}$ selects all of the support indices of the $K$-sparse signals.

Keywords

65D1565J2268W40sensing matrixgeneralized orthogonal matching pursuitrestricted isometry constantsparse signal
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 1 , 01 March 2018 , pp. 40 - 54
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Baraniuk, R., Davenport, M., Devore, R., and Wakin, M., A simple proof of the restricted isometry propertyfor random matrices. Constr. Approx. 28 (2008), no. 3, 253–263. http://dx.doi.org/10.1007/s00365-007-9003-x.Google Scholar
[2] Cai, T. T., Wang, L., and Xu, G. W., Shifting inequality and recovery ofsparse Signals. IEEE Trans. Signal Process. 58 (2010), 1300–1308. http://dx.doi.Org/10.1109/TSP.2009.2034936.Google Scholar
[3] Cai, T. T., Wang, L., and Xu, G. W., New boundsfor restricted isometry constants. IEEE Trans. Inf. Theory. 56 (2010), no. 9, 4388–4394. http://dx.doi.Org/10.1109/TIT.2O10.2054730.Google Scholar
[4] Cai, T. T. and Zhang, A. R., Compressed sensing and affine rank minimization under restricted isometry. IEEE Trans. Signal Process. 61 (2013), no. 13, 3279–3290. http://dx.doi.org/10.1109/TSP.2013.2259164.Google Scholar
[5] Cai, T. T. and Zhang, A. R., Sparse representation ofa polytope and recovery ofsparse Signals and low-rank matrices. IEEE Trans. Inf. Theory. 60 (2014), no. 1, 122–132. http://dx.doi.Org/10.11O9/TIT.2O13.2288639.Google Scholar
[6] Cai, T. T. and Zhang, A. R., Sharp RIP bound for sparse signal and low rank matrix recovery. Appl. Comput. Harmon. Anal. 35 (2013), 74–93. http://dx.doi.Org/10.1016/j.acha.2O12.07.010.Google Scholar
[7] Candes, E. J., The restricted isometry property and its implications for compressed sensing. C. R. Math. Acad. Sei. Paris 346(2008), no. 9-10, 589–592. http://dx.doi.Org/10.1016/j.crma.2008.03.014.Google Scholar
[8] Candes, E. J. and Tao, T., Decoding by linearprogramming. IEEE Trans. Inf. Theory 51 (2005), no. 12, 4203–4215. http://dx.doi.Org/10.11O9/TIT.2OO5.858979.Google Scholar
[9] Chang, L.-H. and Wu, J.-Y., An improved RIP-based Performance guarantee for sparse signal recovery via orthogonal matching pursuit. IEEE Trans. Inf. Theory. 60 (2014), no. 9, 5702–5715. http://dx.doi.org/10.1109/TIT.2014.2338314.Google Scholar
[10] Chartrand, R., Exact reconstruetion of sparse Signals via nonconvex minimization. IEEE Signal Proc. Lett. 14 (2007), no. 10, 707–710.Google Scholar
[11] Chen, S., Billings, S. A., and Luo, W., Orthogonal least Squares methods and their application to non-linear System identification. Internat. J. Control 50 (1989), no. 5, 1873–1896. http://dx.doi.Org/10.1080/00207178908953472.Google Scholar
[12] Dan, W. and Wang, R. H., Robustness of orthogonal matching pursuit under restricted isometry property. Sei. China Math. 57 (2014), no. 3, 627–634. http://dx.doi.Org/10.1007/s11425-013-4655-4.Google Scholar
[13] Dai, W. and Milenkovic, O., Subspace pursuit for compressive sensing signal reconstruetion. IEEE Trans. Inf. Theory 55 (2009), no. 5, 2230–2249. http://dx.doi.Org/10.1109/TIT.2OO9.2O16006.Google Scholar
[14] Davenport, M. A. and Wakin, M. B., Analysis of orthogonal matching pursuit using the restricted isometry property. IEEE Trans. Inf. Theory 56 (2010), 4395–4401. http://dx.doi.org/10.1109/TIT.2010.2054653.Google Scholar
[15] Donoho, D. L., Compressed sensing. IEEE Trans. Inf. Theory 56 (2006), no. 4, 1289–1306. http://dx.doi.Org/10.1109/TIT.2006.871 582.Google Scholar
[16] Donoho, D. L., Drori, I., Tsaig, Y., and Starck, J. L., Sparse solution of underdetermined linear equations by stagewise orthogonal matching pursuit. IEEE Trans. Inf. Theory 58 (2012), no. 2, 1094–1121. http://dx.doi.Org/10.1109/TIT.2O11.21 73241.Google Scholar
[17] Huang, S. S. and Zhu, J. B., Recovery ofsparse Signals using OMP and its variants: Convergence analysis based on RIP. Inverse Problems. 27(2011), no. 3, 035003,14/ http://dx.doi.Org/10.1088/0266-5611/27/3/035003.Google Scholar
[18] Liu, E. and Temlyakov, V. N., The orthogonal super greedy algorithm and applications in compressed sensing. IEEE Trans. Inf. Theory 58 (2012), no. 4, 2040–2047. http://dx.doi.Org/1 0.1109/TIT.2O11.21 77632.Google Scholar
[19] Mo, Q., A sharp restricted isometry constant bound of orthogonal matching pursuit. arxiv:1501.01708v1.Google Scholar
[20] Mo, Q. and Li, S., New bounds on the restricted isometry constant S2k- Appl. Comput. Harmon. Anal. 31 (2011), no. 3, 460–468. http://dx.doi.Org/10.1016/j.acha.2O11.04.005.Google Scholar
[21] Mo, Q. and Shen, Y., A remark on the restricted isometry property in orthogonal matching pursuit. IEEE Trans. Inform. Theory. 58 (2012), no. 6, 3654–3656. http://dx.doi.Org/10.1109/TIT.2O12.2185923.Google Scholar
[22] Needell, D. and Troop, J. A., CoSaMP: Iterative signal recovery from incomplete and inaecurate samples. Appl. Comput. Harmon. Anal. 26 (2009), no. 3, 301–321. http://dx.doi.Org/10.1016/j.acha.2008.07.00254Google Scholar
[23] Needell, D. and Vershynin, R., Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matchingpursuit. IEEE J. Sei. Topics Signal Process. 4 (2010), no. 2, 310–316.Google Scholar
[24] Satpathi, S., Das, R. L., and Chakraborty, M., Improving the bound on the RIP constant in generalized orthogonal matching pursuit. IEEE Signal Proc. Lett. 20 (2013), no. 20, 1074–1077.Google Scholar
[25] Shen, Y. and Li, S., Sparse Signals recovery from noise measurements by orthogonal matching pursuit. Inverse Probl. Imaging. 9 (2015), no. 1, 231–238. http://dx.doi.org/10.3934/ipi.2015.9.231.Google Scholar
[26] Tropp, J. A., Greed is good: Algorithmic results for sparse approximation. IEEE Trans. Inf. Theory. 50 (2004), 2231–2242. http://dx.doi.Org/10.1109/TIT.2004.834793.Google Scholar
[27] Tropp, J. A. and Gilbert, A. C., Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory. 53 (2007), no. 12, 4655–4666. http://dx.doi.Org/1 0.1109/TIT.2007.909108.Google Scholar
[28] Wang, J., Kwon, S., and Shim, B., Generalized orthogonal matching pursuit. IEEE Trans. Signal Process. 60 (2012), no. 12, 6202–6216. http://dx.doi.org/10.1109/TSP.2012.2218810.Google Scholar
[29] Wang, J. and Shim, B., On the recovery limit of sparse Signals using orthogonal matching pursuit. IEEE Trans. Signal Process. 60 (2012), no. 9, 4973–4976. http://dx.doi.org/10.1109/TSP.2012.2203124.Google Scholar
[30] Wen, J. M., Zhu, X. M., and Li, D. F., Improved bounds on restricted isometry constant for orthogonal matching pursuit. Electronic letters. 49 (2013), no. 23, 1487–1489.Google Scholar
[31] Wu, R., Huang, W., and Chen, D. R., The exact support recovery of sparse Signals with noise via orthogonal matching pursuit. IEEE Signal Proc. Lett. 20 (2013), no. 4, 403–406.Google Scholar
[32] Xu, Z. Q., The Performance of orthogonal multi-matching pursuit under RIP. Computer Science 33 (2015), 495–516.Google Scholar