Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-05T09:52:50.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Root Closure in Integral Domains, III

Published online by Cambridge University Press:  20 November 2018

David F. Anderson  and
David E. Dobbs
David F. Anderson
Affiliation:
Department of Mathematics The University of Tennessee Knoxville, TN 37996-1300, USA, (email: anderson@novell.math.utk.edu)
David E. Dobbs
Affiliation:
Department of Mathematics The University of Tennessee Knoxville, TN 37996-1300, USA, (email: dobbs@novell.math.utk.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If $A$ is a subring of a commutative ring 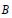$B$ and if $n$ is a positive integer, a number of sufficient conditions are given for “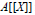$A[[X]]$ is $n$-root closed in 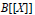$B[[X]]$” to be equivalent to “$A$ is $n$-root closed in 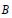$B$.” In addition, it is shown that if 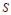$S$ is a multiplicative submonoid of the positive integers 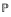$\mathbb{P}$ which is generated by primes, then there exists a one-dimensional quasilocal integral domain $A$ (resp., a von Neumann regular ring $A$) such that 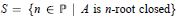$S=\{n\in \mathbb{P}|A\,\,\text{is}\,n-\text{root}\,\text{closed}\}$ (resp., 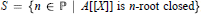$S=\{n\in \mathbb{P}\,|\,\,A[[X]]\,\,\text{is}\,n-\text{root}\,\text{closed}\}$).

Keywords

13G0513F2513C1513F4513B9912D99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 1 , 01 March 1998 , pp. 3 - 9
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Anderson, D. F., Root closure in integral domains. J. Algebra 79 (1982), 51–59.Google Scholar
2. Anderson, D. F., Root closure in integral domains, II. Glasgow Math. J. 31 (1989), 127–130.Google Scholar
3. Anderson, D. F. and Dobbs, D. E., Fields in which seminormality implies normality. Houston J. Math. 16 (1990), 231–247.Google Scholar
4. Anderson, D. F., Dobbs, D. E., and Roitman, M., Root closure in commutative rings. Ann. Sci.Univ. Clermont II, Sér.Math. 26 (1990), 1–11.Google Scholar
5. Anderson, D. F., Dobbs, D. E., and Roitman, M., When is a power series ring n-root closed?. J. Pure Appl. Algebra. 114 (1997), 111–131.Google Scholar
6. Angermüller, G., On the root and integral closure of noetherian domains of dimension one. J. Algebra 83 (1983), 437–441.Google Scholar
7. Angermüller, G., Root closure, J.Algebra 90 (1984), 189–197.Google Scholar
8. Brewer, J. W., Costa, D. L., and K. McCrimmon, Seminormality and root closure in polynomial rings and algebraic curves. J. Algebra 58 (1979), 217–226.Google Scholar
9. Brewer, J. W. and Nichols, W. D., Seminormality in power series rings. J.Algebra 82 (1983), 478–495.Google Scholar
10. Gilmer, R., Multiplicative Ideal Theory. Marcel Dekker, New York, 1972.Google Scholar
11. Lang, S., Algebra, Third Edition. Addison-Wesley, Reading, Massachusetts, 1993.Google Scholar
12. Ohm, J., Some counterexamples related to integral closure in D[[X]]. Trans. Amer. Math. Soc. 122 (1966), 321–333.Google Scholar
13. Seidenberg, A., Derivations and integral closure. Pac. J. Math. 16 (1966), 167–173.Google Scholar
14. Watkins, J. J., Root and integral closure for R[[X]]. J. Algebra 75 (1982), 43–58.Google Scholar