Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-11T07:48:19.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Real Hypersurfaces in Complex Two-plane Grassmannians with Reeb Parallel Ricci Tensor in the GTW Connection

Published online by Cambridge University Press:  20 November 2018

Juan de Dios Pérez ,
Hyunjin Lee ,
Young Jin Suh  and
Changhwa Woo
Juan de Dios Pérez
Affiliation:
Departamento de Geometria y Topologia, Universidad de Granada, 18071-Granada, Spain e-mail: jdperez@ugr.es
Hyunjin Lee
Affiliation:
Research Institute of Real and Complex Manifold, Kyungpook National University, Daegu 702-701, Republic of Korea e-mail: lhjibis@hanmail.net
Young Jin Suh
Affiliation:
Department of Mathematics and Research Institute of Real and Complex Manifold, Kyungpook National University, Daegu 702-701, Republic of Korea e-mail: yjsuh@knu.ac.kr
Changhwa Woo
Affiliation:
Department of Mathematics, Kyungpook National University, Daegu 702-701, Republic of Korea e-mail: legalgwch@naver.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There are several kinds of classification problems for real hypersurfaces in complex two-plane Grassmannians ${{G}_{2}}\left( {{\mathbb{C}}^{m+2}} \right)$. Among them, Suh classified Hopf hypersurfaces in ${{G}_{2}}\left( {{\mathbb{C}}^{m+2}} \right)$ with Reeb parallel Ricci tensor in Levi–Civita connection. In this paper, we introduce the notion of generalized Tanaka–Webster 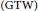$\left( \text{GTW} \right)$ Reeb parallel Ricci tensor for Hopf hypersurfaces in ${{G}_{2}}\left( {{\mathbb{C}}^{m+2}} \right)$. Next, we give a complete classification of Hopf hypersurfaces in ${{G}_{2}}\left( {{\mathbb{C}}^{m+2}} \right)$ with 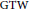$\text{GTW}$ Reeb parallel Ricci tensor.

Keywords

53C4053C15complex two-plane Grassmannianreal hypersurfaceHopf hypersurfacegeneralized Tanaka-Webster connectionparallelismReeb parallelismRicci tensor
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 4 , 01 December 2016 , pp. 721 - 733
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Cho, J. T., CR structures on real hypersurfaces of a complex space form. Publ. Math. Debrecen 54(1999), no. 3-4, 473–487.Google Scholar
[2] Cho, J. T., Levi-parallel hypersurfaces in a complex space form. Tsukuba J. Math. 30(2006), no. 2, 329–343.Google Scholar
[3] Cho, J. T. and Kimura, M., Reebflow symmetry on almost contact three-manifolds. Differential Geom. Appl. 35(2014), 266–273. http://dx.doi.Org/10.1016/j.difgeo.2014.05.002 Google Scholar
[4] Cho, J. T. and Kon, M., The Tanaka-Webster connection and real hypersurfaces in a complex space form. Kodai Math. J. 34(2011), no. 3, 474–484. http://dx.doi.Org/10.2996/kmj/1320935554 Google Scholar
[5] Jeong, I., Kimura, M., Lee, H., and Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with generalized Tanaka-Webster Reeb parallel shape operator. Monatsh. Math. 171(2013), no. 3-4, 357–376. http://dx.doi.Org/10.1007/s00605-013-0475-4 Google Scholar
[6] Jeong, I., Lee, H., and Suh, Y. J., Levi-dvita and generalized Tanaka-Webster covariant derivatives for real hypersurfaces in complex two-plane Grassmannians. Ann. Mat. Pura Appl. 194(2015), no. 3, 919–930. http://dx.doi.Org/10.1007/s10231-014-0405-7 Google Scholar
[7] Jeong, I., Machado, C. J. G., Perez, J. D., and Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with D1-parallel structure facobi operator. Internat J. Math. 22(2011), no. 5, 655–673. http://dx.doi.Org/10.1142/S0129167X11006957 Google Scholar
[8] Kimura, M., Sectional curvatures of holomorphicplanes on a real hypersurface in P“(C). Math. Ann. 276(1987), no. 3, 487–497. http://dx.doi.Org/10.1007/BF01450843 Google Scholar
[9] Kon, M., On a Hopf hypersurface of a complex space form. Differential Geom. Appl. 28(2010), no. 3, 295–300. http://dx.doi.Org/10.1016/j.difgeo.2009.10.012 Google Scholar
[10] Lee, H., Choi, Y. S., and Woo, C., Hopf hypersurfaces in complex two-plane Grassmannians with Reeb parallel shape operator. Bull. Malays. Math. Soc. 38(2015), no. 2, 617–634. http://dx.doi.Org/10.1007/s40840-014-0039-3 Google Scholar
[11] Lee, H. and Suh, Y. J., Real hypersurfaces of type B in complex two-plane Grassmannians related to the Reeb vector. Bull. Korean Math. Soc. 47(2010), no. 3, 551–561. http://dx.doi.Org/10.4134/BKMS.2010.473.551 Google Scholar
[12] Machado, C. J. G., Perez, J. D., and Suh, Y. J., Commuting structure Jacobi operator for real hypersurfaces in complex two-plane Grassmannians. Acta Math. Sin. 31(2015), no. 1,111-122. http://dx.doi.Org/!0.1007/s10114-015-1765-7 Google Scholar
[13] Pak, E., Suh, Y. J., and Woo, C., Restricted Ricci conditions for real hypersurfaces in complex two-plane Grassmannians. Houston J. Math. 41(2015), no. 3 767–783.Google Scholar
[14] Perez, J. D. and Suh, Y. J., The Ricci tensor of real hypersurfaces in complex two-plane Grassmannians. J. Korean Math. Soc. 44(2007), 211–235. http://dx.doi.Org/10.4134/JKMS.2007.44.1.211 Google Scholar
[15] Perez, J. D. and Suh, Y. J., and Watanabe, Y., Generalized Einstein real hypersurfaces in complex two-plane Grassmannians. J. Geom. Phys. 60(2010), 1806–1818. http://dx.doi.Org/10.1016/j.geomphys.2010.06.017 Google Scholar
[16] Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with commuting Ricci tensor. J. Geom. Phys. 60(2010), 1792–1805. http://dx.doi.Org/10.1016/j.geomphys.2010.06.007 Google Scholar
[17] Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with parallel Ricci tensor. Proc. Roy. Soc. Edinburgh Sect. A. 142(2012), 1309–1324. http://dx.doi.Org/10.1017/S0308210510001472 Google Scholar
[18] Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with Reeb parallel Ricci tensor. J. Geom. Phys. 64(2013), 1–11. http://dx.doi.Org/10.1016/j.geomphys.2012.10.005 Google Scholar
[19] Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with harmonic curvature. J. Math. Pures Appl. 100(2013), no. 1, 16–33. http://dx.doi.Org/10.1016/j.matpur.2O12.10.010 Google Scholar
[20] Suh, Y. J., Hypersurfaces with isometric Reeb flow in complex hyperbolic two-plane Grassmannians. Adv. in Appl. Math. 50(2013), no. 4, 645–659. http://dx.doi.Org/10.1016/j.aam.2O13.01.001 Google Scholar
[21] Suh, Y. J., Real hypersurfaces in complex hyperbolic two-plane Grassmannians with Reeb vector field. Adv. in Appl. Math. 55(2014), 131–145. http://dx.doi.Org/10.1016/j.aam.2O14.01.005 Google Scholar
[22] Suh, Y. J., Real hypersurfaces in the complex quadric with parallel Ricci tensor. Adv. in Math. 281(2015), 886–905. http://dx.doi.Org/!0.1016/j.aim.2O15.05.012 Google Scholar