Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-11T07:20:52.677Z Has data issue: false hasContentIssue false
  • English
  • Français

Rationality and Orbit Closures

Published online by Cambridge University Press:  20 November 2018

Jason Levy
Jason Levy*
Affiliation:
Department of Mathematics and Statistics, University of Ottawa, 585 King Edward, Ottawa, Ontario K1N 6N5, email: jlevy@science.uottawa.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose we are given a finite-dimensional vector space 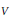$V$ equipped with an $F$-rational action of a linearly algebraic group 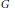$G$, with $F$ a characteristic zero field. We conjecture the following: to each vector 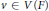$v\,\in \,V(F)$ there corresponds a canonical 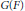$G(F)$-orbit of semisimple vectors of 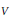$V$. In the case of the adjoint action, this orbit is the 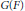$G(F)$-orbit of the semisimple part of $v$, so this conjecture can be considered a generalization of the Jordan decomposition. We prove some cases of the conjecture.

Keywords

14L2420G15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 2 , 01 June 2003 , pp. 204 - 215
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Birkes, David, Orbits of linear algebraic groups. Ann. of Math. (2) 93 (1971), 459–475.Google Scholar
[2] Borel, Armand, Linear algebraic groups. 2nd edition, Graduate Texts in Math. 126, Springer-Verlag, New York, 1991.Google Scholar
[3] Hesselink, W. H., Concentration under actions of algebraic groups. Lecture Notes in Math. 867, Springer, Berlin, 1981, 55–89.Google Scholar
[4] Kempf, G., Instability in invariant theory. Ann. of Math. (2) 108 (1978), 299–316.Google Scholar
[5] Levy, J., A truncated integral of the Poisson summation formula. Canad. J. Math. 53 (2001), 122–160.Google Scholar
[6] Luna, D., Sur certaines opérations différentiables des groupes de Lie. Amer. J. Math. 97 (1975), 172–181.Google Scholar
[7] Ness, L., A stratification of the null cone via the moment map. Amer. J. Math. 106 (1984), 1281–1329.Google Scholar
[8] Rader, Cary and Rallis, Steve, Spherical characters on p-adic symmetric spaces. Amer. J. Math. 118 (1996), 91–178.Google Scholar
[9] Raghunathan, M. S., A note on orbits of reductive groups. J. IndianMath. Soc. (N.S.) 38 (1974), 65–70.Google Scholar
[10] Richardson, R. W., On orbits of algebraic groups and Lie groups. Bull. Austral. Math. Soc. 25 (1982), 1–29.Google Scholar
[11] Richardson, R. W., Conjugacy classes of n-tuples in Lie algebras and algebraic groups. Duke Math. J. 57 (1988), 1–35.Google Scholar
[12] Springer, T. A., Galois cohomology of linear algebraic groups. Proc. Sympos. Pure Math. 9, Amer. Math. Soc., Providence, RI, 1966, 149–158.Google Scholar