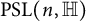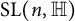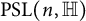1 Introduction
Symmetry is a widely studied concept in various areas of science where dynamical systems or geometric automorphisms are involved. Symmetries are formulated mathematically using the notion of groups. Let G be a group. An element
$\iota $
of order at most two in G is called an involution, i.e.,
$\iota ^2=e$
. It is a problem of potential applications in several areas of mathematics to decompose an element into a product of involutions; see [Reference Basmajian and MaskitBM, Reference DjokovićDj, Reference EllersEl, Reference Hoffman and PaigeHP, Reference Roche and VinrootRV, Reference WonenburgerWo]. Particularly interesting elements are those that are products of two involutions. In the literature, an element
$g \in G$
is called reversible or real if g is conjugate to
$g^{-1}$
in G. An element
$g \in G$
is called strongly reversible or strongly real if g is conjugate to
$g^{-1}$
by an involution in G. Equivalently, an element
$g \in G$
is strongly reversible if and only if it can be written as a product of two involutions in G; see [Reference O’Farrell and ShortOS]. An element that conjugates g to
$g^{-1}$
is also known as ‘reversing symmetry’ of g; see [Reference Baake and RobertsBR, Reference Lamb and RobertsLR]. We refer to [Reference BaakeBa] for a brief survey on symmetries and reversing symmetries in dynamical systems.
By reversibility in a group G, we mean a classification of reversible and strongly reversible elements in G. The reversible and strongly reversible elements appear in various areas of mathematics, such as classical dynamics, mechanics, group theory, representation theory, geometry, complex analysis, and functional equations; see [Reference Arnol’d and AvezAA, Reference Lamb and RobertsLR, Reference O’FarrellO’Fa, Reference Tiep and ZalesskiTZ]. Classifying the reversible and strongly reversible elements in a group has been a problem of broad interest; see the monograph [Reference O’Farrell and ShortOS] for a survey on this theme. In spite of many works, complete and concrete classifications of reversible and strongly reversible elements are not known for many families of groups. The aim of this article is to investigate reversibility in the group
$\mathrm {SL}(n, \mathbb {H})$
,
$n \times n$
matrices over the skew-field
$\mathbb {H}$
of Hamilton’s quaternions with quaternionic determinant one.
The group of projective automorphisms of the n-dimensional quaternionic projective space
$ \mathbb P_{\mathbb {H}}^n$
is the projective linear group
$\mathrm {PSL}(n, \mathbb {H})= \mathrm {SL}(n,\mathbb {H})/\{\pm \mathrm {I}_{n}\}$
. When
$n=2$
, this is related to the geometry of the five-dimensional hyperbolic space or the Möbius geometry of the four-dimensional sphere; see [Reference GongopadhyayGo1, Reference Parker and ShortPS]. Reversibility is a natural problem in this context from a geometric point of view. Using the action of
$\mathrm {SL}(2, \mathbb {H})$
on
$ \mathbb P_{\mathbb {H}}^1$
by Möbius transformations, Lávička, O’Farrell, and Short classified the reversible and strongly reversible elements in
$\mathrm {PSL}(2, \mathbb {H})$
in [Reference Lávička, O’Farrell and ShortLOS]. This work was generalized to the Möbius group
$\mathrm {SO}_o(n,1)$
independently in the works [Reference GongopadhyayGo2] and [Reference ShortSho], also see [Reference Basmajian and MaskitBM]. However, not much has been investigated for the problem in
$\mathrm {SL}(n, \mathbb {H})$
. On the other hand, reversibility in
$\mathrm {SL}(n, \mathrm {\mathbb {F}})$
, where
$\mathrm {\mathbb {F}}$
is a field, has been investigated by many authors, e.g., [Reference Gongopadhyay and MaityGM, Reference Gill and SinghGS, Reference Singh and ThakurST, Reference WonenburgerWo], and also see [Reference O’Farrell and ShortOS, p. 77]. In spite of these works, a complete list of the reversible and strongly reversible elements in
$\mathrm {SL}(n, \mathbb {C})$
has been obtained only recently by the authors in [Reference Gongopadhyay, Lohan and MaityGLM2].
It is a natural question to ask for reversibility in
$\mathrm {SL}(n, \mathbb {H})$
and
$\mathrm {PSL}(n, \mathbb {H})$
generalizing these works. In [Reference Dutta, Gongopadhyay and LohanDGL], reversible and strongly reversible elements in
$\mathrm {PSL}(3, \mathbb {H})$
have been classified. They were further applied to provide an algebraic characterization of the dynamical types of
$\mathrm {PSL}(3, \mathbb {H})$
, which generalizes the results in the context of
$\mathrm {PSL}(2, \mathbb {H})$
, e.g., in [Reference GongopadhyayGo1, Reference Parker and ShortPS].
In this paper, we solve the reversibility problem for the group
$\mathrm {SL}(n, \mathbb {H})$
for arbitrary n. The following theorem extends [Reference Dutta, Gongopadhyay and LohanDGL, Theorem 1.1] and also the work [Reference Lávička, O’Farrell and ShortLOS].
Theorem 1.1 An element of
$ \mathrm {PSL}(n,\mathbb {H})$
is reversible if and only if it is strongly reversible.
Note that every element
$[g]$
in
$\mathrm {PSL}(n, \mathbb {H})$
has two lifts, g and
$-g$
, in
$\mathrm {SL}(n, \mathbb {H})$
. Therefore, an element
$[g] \in \mathrm {PSL}(n, \mathbb {H})$
is conjugate to its inverse if and only if either g is conjugate to
$g^{-1}$
or g is conjugate to
$-g^{-1} $
in
$\mathrm {SL}(n, \mathbb {H})$
. To classify reversible (resp. strongly reversible) elements in
$\mathrm {PSL}(n, \mathbb {H})$
, we first need to classify reversible (resp. strongly reversible) elements in
$\mathrm {SL}(n, \mathbb {H})$
. However, this alone does not completely classify these elements in
$\mathrm {PSL}(n, \mathbb {H})$
. Following [Reference Dutta, Gongopadhyay and LohanDGL], to obtain a complete classification of reversible (resp. strongly reversible) elements in
$\mathrm {PSL}(n, \mathbb {H})$
, investigation of the following equation is required:
$hgh^{-1}=-g^{-1}$
, where
$g, h \in \mathrm {SL}(n, \mathbb {H})$
.
We investigated the reversibility in the group
$\mathrm {GL}(n,\mathbb {H})$
in [Reference Gongopadhyay, Lohan, Maity and PapadopoulosGLM1]. Note that if two matrices are conjugate by an element of
$\mathrm {GL}(n,\mathbb {H})$
, then by a suitable scaling of the conjugating element, we can assume that both the matrices are conjugate by an element of
$ \mathrm {SL}(n,\mathbb {H})$
, cf. [Reference Dutta, Gongopadhyay and LohanDGL, Remark 2.4]. Therefore, the classification of reversible elements in
$ \mathrm {SL }(n,\mathbb {H})$
reduces to that of
$ \mathrm {GL }(n,\mathbb {H})$
and is given by the following result. We refer to Lemma 2.4 for the Jordan decomposition of quaternionic matrices.
Theorem 1.2 ([Reference Gongopadhyay, Lohan, Maity and PapadopoulosGLM1, Theorem 5.1])
An element
$A \in \mathrm {SL }(n,\mathbb {H})$
is reversible if and only if the Jordan blocks in the Jordan decomposition of A can be partitioned into pairs
$ \{ \mathrm {J}(\lambda , s),\mathrm {J}(\lambda ^{-1}, s)\} $
or singletons
$\{\mathrm {J}(\mu , t )\}$
, where
$\lambda , \mu \in \mathbb {C} \setminus \{0\}$
with non-negative imaginary parts such that
$|\lambda | \neq 1$
and
$ |\mu | = 1$
.
Note that if
$g \in \mathrm {GL }(n,\mathbb {H})$
is an involution, then
$ g \in \mathrm {SL }(n,\mathbb {H})$
; see [Reference RodmanRo, Theorem 5.9.2]. Therefore, if an element of
$\mathrm {SL }(n,\mathbb {H})$
is strongly reversible in
$\mathrm {GL }(n,\mathbb {H})$
, then it will also be strongly reversible in
$\mathrm {SL }(n,\mathbb {H})$
. This implies that the classification of strongly reversible elements in
$\mathrm {SL }(n,\mathbb {H})$
follows from the corresponding classification in
$\mathrm {GL }(n,\mathbb {H})$
. Unlike the general linear group
$\mathrm {GL}(n,\mathbb {F})$
over a field
$\mathbb {F}$
, not every reversible element of
$\mathrm {GL}(n,\mathbb {H})$
is strongly reversible in
$\mathrm {GL}(n,\mathbb {H})$
; see [Reference EllersEl]. For example, while
$\mathbf {i} \in \mathrm {GL}(1,\mathbb {H})$
is reversible (because
$\mathbf {j} \mathbf {i} \mathbf {j}^{-1} =-\mathbf {i}$
), it is not strongly reversible since
$\{\pm 1 \}$
are only two involutions in
$\mathrm {GL}(1,\mathbb {H})$
. In [Reference Gongopadhyay, Lohan, Maity and PapadopoulosGLM1, Theorem 5.4], we gave a sufficient criterion for strong reversibility of the reversible elements in
$\mathrm {GL}(n,\mathbb {H})$
. In this article, we will show that these conditions are also necessary. We prove the following result, which classifies the strongly reversible elements in
$\mathrm {SL}(n,\mathbb {H})$
, and hence in
$\mathrm {GL}(n,\mathbb {H})$
.
Theorem 1.3 Let
$A \in \mathrm {SL}(n,\mathbb {H})$
be a reversible element. Then A is strongly reversible in
$\mathrm {SL }(n,\mathbb {H})$
if and only if, in the Jordan decomposition of A, every Jordan block corresponding to the non-real eigenvalue classes of unit modulus has even multiplicity.
It is worth mentioning that Theorem 1.2 and Theorem 1.3, combined with [Reference Gongopadhyay, Lohan and MaityGLM3, Theorem 1.1], provide a complete list of the reversible and strongly reversible elements in the affine group
$\mathrm {GL}(n, \mathbb {H}) \ltimes \mathbb {H}^n$
.
Recall that an element
$g \in \mathrm {SL}(n,\mathbb {H})$
is called a skew-involution if
$ g^2 =-\mathrm {I}_n$
. We refer to [Reference Joven and ParasJP, Reference Paras and SalinasanPaSa] for the decomposition of matrices over a field as products of skew-involutions. Note that every reversible element of
$\mathrm {SL}(n,\mathbb {H})$
is not strongly reversible. However, we have the following result.
Theorem 1.4 An element of
$ \mathrm {SL }(n,\mathbb {H})$
is reversible if and only if it can be written as a product of two skew-involutions in
$\mathrm {SL }(n,\mathbb {H})$
.
In this paper, our approach uses the notion of Weyr canonical form of a matrix (see [Reference O’Meara, Clark and VinsonhalerOCV, Reference ShapiroSha]), and the structure of the reversing symmetry group or extended centralizer
$\mathcal {E}_{\mathrm {GL}(n,\mathbb {H})}(A) := \{ g \in \mathrm {GL}(n,\mathbb {H}) \mid gAg^{-1} = A \text { or } gAg^{-1} = A^{-1} \}$
for
$A \in \mathrm {GL}(n,\mathbb {H})$
; see [Reference Baake and RobertsBR], also [Reference O’Farrell and ShortOS, Section 2.1.4]. We classified reversibility in the group
$\mathrm {SL}(n,\mathbb {C})$
in [Reference Gongopadhyay, Lohan and MaityGLM2] and also described reversing symmetries for certain types of Jordan forms in
$\mathrm {GL}(n,\mathbb {C})$
; see [Reference Gongopadhyay, Lohan and MaityGLM2, Table 1]. In this article, an analog of [Reference Gongopadhyay, Lohan and MaityGLM2, Table 1] in the context of
$\mathrm {GL}(n,\mathbb {H})$
has been described in Table 1; see Section 3.2 for a proof of Table 1. We refer to Definition 2.2 and Definition 3.1 for the notations used in Table 1. Note that for a reversible element, the reversing symmetry group is a degree two extension of the centralizer, and hence Table 1 along with the Jordan decompositions provide us the structure of the reversing symmetry group for the reversible elements in
$\mathrm {SL}(n,\mathbb {H})$
.
Table 1 Reversing symmetries for Jordan forms in
$ \mathrm {SL}(n,\mathbb {H})$
.
Structure of the paper. In Section 2, we establish notations and recall some preliminary results. Theorem 1.3 is proved in Section 3 which classifies the strongly reversible elements in
$\mathrm {SL}(n,\mathbb {H})$
. Section 4 deals with products of two skew-involutions in
$\mathrm {SL}(n,\mathbb {H})$
and we prove Theorem 1.4. Finally, we investigate reversibility in
$\mathrm {PSL}(n,\mathbb {H})$
and prove Theorem 1.1 in Section 5.
2 Preliminaries
In this section, we fix some notation and recall some necessary background that will be used throughout this paper. Let
$\mathbb {H}:= \mathbb R + \mathbb R \mathbf {i} + \mathbb R \mathbf {j} + \mathbb R \mathbf {k}$
denote the division algebra of Hamilton’s quaternions, where
$\mathbf {i}^2=\mathbf {j}^2=\mathbf {k}^2=\mathbf {i} \mathbf {j} \mathbf {k} = -1$
. We consider
$\mathbb {H}^n$
as a right
$\mathbb {H}$
-module. We refer to [Reference RodmanRo] for an elaborate discussion on the linear algebra over the quaternions.
Definition 2.1 Let
$A \in \mathrm {M}(n,\mathbb {H})$
, the algebra of
$n \times n$
matrices over
$\mathbb {H}$
. A non-zero vector
$v \in \mathbb {H}^n $
is said to be a (right) eigenvector of A corresponding to a (right) eigenvalue
$\lambda \in \mathbb {H} $
if the equality
$ A v = v\lambda $
holds.
Eigenvalues of every matrix over quaternions occur in similarity classes, and each similarity class of eigenvalues contains a unique complex number with non-negative imaginary part. Here, instead of similarity classes of eigenvalues, we will consider the unique complex representatives with non-negative imaginary parts as eigenvalues unless specified otherwise. In places where we need to distinguish between the similarity class and a representative, we shall write the similarity class of an eigenvalue representative
$\lambda $
by
$[\lambda ]$
.
Definition 2.2 ([Reference RodmanRo, p. 94])
A Jordan block
$\mathrm {J}(\lambda ,m)$
is an
$m \times m (m>1)$
matrix with
$ \lambda \in \mathbb {H}$
on the diagonal entries,
$1$
on all of the super-diagonal entries and
$0$
elsewhere. For
$m=1$
,
$\mathrm {J}(\lambda ,1) \,:=\, (\lambda )$
. We will refer to a block diagonal matrix where each block is a Jordan block as Jordan form.
Definition 2.3 ([Reference RodmanRo, p. 113])
Let
$A \in \mathrm {M}(n,\mathbb {H})$
. Write
$ A = A_1 + A_2 \mathbf {j} $
, where
$ A_1, A_2 \in \mathrm {M}(n,\mathbb {C})$
. Consider the embedding
$ \Phi : \mathrm {M}(n,\mathbb {H}) \longrightarrow \mathrm {M}(2n,\mathbb {C})$
defined by
$$ \begin{align} \Phi(A) = \left(\begin{matrix} A_1 & A_2 \\ - \overline{A_2} & \overline{A_1} \\ \end{matrix}\right)\,, \end{align} $$
where each
$ \overline {A_i} $
denotes the complex conjugate of
$ A_i$
. The determinant of
$A \in \mathrm {M}(n,\mathbb {H})$
is defined as
$ \mathrm {det}(A):= \mathrm {det}(\Phi (A))$
. In view of the Skolem-Noether theorem, the above definition of the quaternionic determinant is independent of the choice of embedding
$ \Phi $
. Note that for
$A \in \mathrm {M}(n,\mathbb {H})$
,
$\mathrm {det(A)}$
is always a non-negative real number; see [Reference RodmanRo, Theorem 5.9.2].
We will consider the Lie groups
$ \mathrm {GL}(n,\mathbb {H}) := \{ g \in \mathrm {M}(n,\mathbb {H}) \mid \det (g) \neq 0 \}$
and
$ \mathrm {SL}(n,\mathbb {H}) := \{ g \in \mathrm {GL}(n,\mathbb {H}) \mid \det (g) = 1 \}$
. In the following lemma, we recall the Jordan decomposition in
$\mathrm {M}(n,\mathbb {H})$
; see [Reference RodmanRo, Theorem 5.5.3] for more details.
Lemma 2.4 ([Reference RodmanRo])
For every
$A \in \mathrm {M}(n,\mathbb {H})$
, there exists an invertible matrix
$S \in \mathrm {GL}(n,\mathbb {H})$
such that
$$ \begin{align} SAS^{-1} = \mathrm{J}(\lambda_1, m_1) \oplus \cdots \oplus \mathrm{J}(\lambda_k, m_k), \end{align} $$
where
$ \lambda _1, \dots , \lambda _k $
are complex numbers (not necessarily distinct) and have non-negative imaginary parts. The form (2.2) is uniquely determined by A up to a permutation of Jordan blocks.
2.1 Weyr canonical form
In this section, we will recall notations for partitioning a positive integer n and the notion of Weyr canonical form in
$\mathrm {M }(n,\mathbb {C})$
from [Reference Gongopadhyay, Lohan and MaityGLM2, Section 2].
Definition 2.5 ([Reference O’Meara, Clark and VinsonhalerOCV])
A partition of a positive integer n is a finite sequence
$(n_1,n_2,\dots , n_r)$
of positive integers such that
$n_1 + n_2 + \dots + n_r =n$
and
$n_1 \geq n_2 \geq \dots \geq n_r \geq 1$
. Moreover, the conjugate partition (or dual partition) of the partition
$(n_1,n_2,\dots , n_r)$
of n is the partition
$(m_1,m_2,\dots , m_{n_1})$
, where
$m_j = | \{i \mid n_i \geq j\}|$
, cardinality of the set
$\{i \mid n_i \geq j\}$
.
Definition 2.6 ([Reference Gongopadhyay and MaityGM, Section 3.3])
A partition of a positive integer n is an object of the form
$$ \begin{align*}{\mathbf{d}}(n) := [ d_1^{t_{d_1}}, \dots, d_s^{t_{d_s}} ],\end{align*} $$
where
$t_{d_i}, d_i \in \mathbb {N}, 1\leq i\leq s, $
such that
$ \sum _{i=1}^{s} t_{d_i} d_i = n, t_{d_i} \geq 1 $
and
$ d_1> \cdots > d_s > 0$
. Moreover, for a partition
${\mathbf {d}} (n)\, =\, [ d_1^{t_{d_1}},\, \ldots ,\, d_s^{t_{d_s}} ]$
of n, define
${\mathbb {N}}_{{\mathbf {d}}(n)} \,:=\, \{ d_i \,\mid \, 1 \,\leq \, i \,\leq \, s \}$
. Further, define
$$ \begin{align*}{\mathbb {E}}_{{\mathbf{d}}(n)} \,:=\, {\mathbb {N}}_{{\mathbf{d}}(n)} \cap (2\mathbb {N}), {\mathbb {O}}_{{\mathbf{d}}(n)} \,:=\, {\mathbb {N}}_{{\mathbf{d}}(n)}\setminus {\mathbb {E}}_{{\mathbf{d}}(n)}, \text{ and } \mathbb {E}_{{\mathbf{d}}(n)}^2 := \{ \eta \in \mathbb {E}_{{\mathbf{d}}(n)} \mid \eta \equiv 2\ \ \pmod {4} \}.\end{align*} $$
Here, we introduced two notations
$(n_1,n_2,\cdots , n_r)$
and
$ {\mathbf {d}}(n)$
for the partition of a positive integer n; see Definition 2.5 and Definition 2.6. Recall the following lemma from [Reference Gongopadhyay, Lohan and MaityGLM2], which gave the relationship between the partition
$ {\mathbf {d}}(n)$
and its conjugate partition
$ \overline {\mathbf {d}}(n)$
.
Lemma 2.7 ([Reference Gongopadhyay, Lohan and MaityGLM2, Lemma 2.2])
Let
$ {\mathbf {d}}(n) = [ d_1^{t_{d_1}}, \dots , d_s^{t_{d_s}} ]$
be a partition of a positive integer n. Then the conjugate partition
$ \overline {\mathbf {d}}(n)$
of
$ {\mathbf {d}}(n)$
has the following form:
$$ \begin{align*}\overline{\mathbf{d}}(n) = \Big[ (t_{d_1}+t_{d_2}+\cdots+t_{d_s})^{d_s}, (t_{d_1}+t_{d_2}+\cdots+t_{d_{s-1}})^{d_{s-1}-d_s}, \dots, (t_{d_1}+t_{d_2})^{d_2 -d_3},(t_{d_1})^{d_1 -d_2}\Big].\end{align*} $$
Now, we will recall the notion of Weyr canonical form in
$\mathrm {M}(n,\mathbb {C})$
from [Reference Gongopadhyay, Lohan and MaityGLM2, Section 2.4]. We refer to [Reference O’Meara, Clark and VinsonhalerOCV, Reference ShapiroSha] for an elaborate discussion on Weyr canonical forms.
Definition 2.8 ([Reference O’Meara, Clark and VinsonhalerOCV, Definition 2.1.1])
A basic Weyr matrix with eigenvalue
$\lambda $
is a matrix
$W \in \mathrm {M}(n,\mathbb {C})$
of the following form: there is a partition
$(n_1,n_2, \dots ,n_r)$
of n such that, when W is viewed as an
$r \times r$
blocked matrices
$(W_{ij})_{1 \leq i,j \leq r}$
, where the
$(i,j)$
-th block
$W_{ij}$
is an
$ n_i \times n_j$
matrix, the following three features are present.
-
(1) The main diagonal blocks
$W_{i,i}$
are the
$ n_i \times n_i$
scalar matrices
$\lambda \mathrm {I}_{n_i} $
for
$ i = 1,2, \dots , r$
. -
(2) The first super-diagonal blocks
$W_{i,{i+1}}$
are the
$ n_i \times n_{i+1}$
matrices in reduced row-echelon form (that is, an identity matrix followed by zero rows) for
$ i = 1,2, \dots , r-1$
. In other words, the rank of the reduced row-echelon matrix
$W_{i,{i+1}}$
is
$n_{i+1}$
for
$ i = 1,2, \dots , r-1$
. -
(3) All other blocks of W are zero (that is,
$W_{ij}=0$
when
$j \neq i, i+1)$
.
In this case, we say that W has Weyr structure
$(n_1,n_2, \dots ,n_r)$
.
Definition 2.9 ([Reference O’Meara, Clark and VinsonhalerOCV, Definition 2.1.5])
Let
$W \in \mathrm {M}(n,\mathbb {C})$
, and let
$\lambda _1, \lambda _2,\dots , \lambda _k$
be the distinct eigenvalues of W. We say that W is in Weyr form (or is a Weyr matrix) if W is a direct sum of basic Weyr matrices, one for each distinct eigenvalue. In other words, W has the following form:
$$ \begin{align*}W = W_1 \oplus W_2 \oplus \dots \oplus W_k,\end{align*} $$
where
$W_i $
is a basic Weyr matrix with eigenvalue
$\lambda _{i}$
for
$i = 1, 2, \dots ,k$
.
Remark 2.10 Note that a permutation transformation conjugates the Jordan and Weyr forms of a square matrix with complex entries. Moreover, for a given
$A \in \mathrm {M}(n,\mathbb {C})$
with a single eigenvalue
$\lambda \in \mathbb {C}$
, there is a duality between the partitions corresponding to the Jordan and Weyr form of A, respectively. In particular, if
${\mathbf {d}}(n)$
is a partition corresponding to Jordan form of
$A \in \mathrm {M}(n,\mathbb {C})$
, then the corresponding Weyr form
$A_W $
of A is represented by the conjugate partition
$\overline {\mathbf {d}}(n)$
, as given by Lemma 2.7; see [Reference O’Meara, Clark and VinsonhalerOCV, Theorem 2.4.1] and [Reference Gongopadhyay, Lohan and MaityGLM2, Section 2.5].
In the following result, we recall the centralizer of a basic Weyr matrix in
$\mathrm {M}(n,\mathbb {C})$
.
Proposition 2.11 ([Reference O’Meara, Clark and VinsonhalerOCV, Proposition 2.3.3])
Let
$W \in \mathrm {M}(n,\mathbb {C})$
be an
$n \times n$
basic Weyr matrix with the Weyr structure
$(n_1,\dots , n_r)$
,
$ r \geq 2$
. Let K be an
$n \times n$
matrix, blocked according to the partition
$(n_1,\dots , n_r)$
, and let
$K_{i,j}$
denote its
$(i, j)$
-th block (an
$n_i \times n_j$
matrix) for
$i, j \in \{1,\dots , r\} $
. Then W and K commute if and only if K is a block upper triangular matrix for which
$$ \begin{align*}K_{i,j}= \left(\begin{matrix} K_{i+1,j+1} & \ast \\ 0 & \ast \end{matrix}\right) \text{ for all } 1 \leq i \leq j \leq r-1.\end{align*} $$
Here, we have written
$K_{i,j}$
as a blocked matrix where the zero block is
$(n_i - n_{i+1}) \times n_{j+1}$
. The asterisk entries
$(\ast )$
indicate that there are no restrictions on the entries in that part of the matrix. The column of asterisks disappears if
$n_j = n_{j+1}$
, and the
$\left (\begin {smallmatrix} 0 & \ast \end {smallmatrix}\right )$
row disappears if
$n_i = n_{i+1}$
.
We refer to [Reference Gongopadhyay, Lohan and MaityGLM2, Example 2.11] for illustration of Proposition 2.11, which describes the centralizer of a Weyr matrix. In this article, for
$A \in \mathrm {M}(n,\mathbb {C})$
, we will use the notation
$A_W$
to denote the corresponding Weyr form.
In [Reference O’Meara, Clark and VinsonhalerOCV], the Weyr canonical forms of square matrices over algebraically closed fields are studied. Here, we will extend the notion of Weyr canonical form for matrices over the quaternions. In particular, in view of Lemma 2.4, we can write
$A\in \mathrm {M}(n,\mathbb {H})$
in the Weyr canonical form over the complex numbers.
2.2 Matrices commuting with Jordan blocks
In the following lemma, we recall the well-known Sylvester’s theorem on solutions to the matrix equation
$ AX= XB$
; see [Reference RodmanRo] for more details.
Lemma 2.12 ([Reference RodmanRo, Theorem 5.11.1])
Let
$A\in \mathrm {M}(n, \mathbb {H})$
and
$B\in \mathrm {M}(m, \mathbb {H})$
. Then the equation
$$ \begin{align*}AX= XB\end{align*} $$
has only the trivial solution if and only if A and B have no common eigenvalues.
The following lemma is useful in understanding the centralizer of a matrix in
$\mathrm {M}(n, \mathbb {H})$
.
Lemma 2.13 ([Reference O’Meara, Clark and VinsonhalerOCV, Proposition 3.1.1])
Let
$A = \left (\begin {smallmatrix} A_1 & \\ & A_2 \\ \end {smallmatrix}\right ) \in \mathrm {M}(n,\mathbb {H})$
, where
$A_1 \in \mathrm {M}(m,\mathbb {H})$
(resp.
$A_2 \in \mathrm {M}(n-m,\mathbb {H})$
) has a single eigenvalue
$\lambda _1$
(resp.
$\lambda _2$
) such that
$[\lambda _1] \neq [\lambda _2]$
. If
$B \in \mathrm {M}(n,\mathbb {H})$
such that
$B A = AB$
, then B has the following form
$$ \begin{align*}B = \left(\begin{matrix} B_1 & \\ & B_2 \\ \end{matrix}\right),\end{align*} $$
where
$B_1 \in \mathrm {M}(m,\mathbb {H})$
and
$B_2 \in \mathrm {M}(n-m,\mathbb {H})$
such that
$$ \begin{align*}B_1 A_1 = A_1B_1 \, \text{ and } \, B_2 A_2 = A_2B_2.\end{align*} $$
Proof Let
$B = \left (\begin {smallmatrix} B_{1,1} & B_{1,2} \\ B_{2,1} & B_{2,2} \end {smallmatrix}\right ) \in \mathrm {M}(n,\mathbb {H})$
be an element having the same block structure as A such that
$BA=AB$
. Then we have
$$ \begin{align*} \left(\begin{matrix} B_{1,1} & B_{1,2} \\ B_{2,1} & B_{2,2} \end{matrix}\right) \left(\begin{matrix} A_1 & \\ &A_2 \end{matrix}\right) = \left(\begin{matrix} A_1 & \\ &A_2 \end{matrix}\right)\left(\begin{matrix} B_{1,1} & B_{1,2} \\ B_{2,1} & B_{2,2} \end{matrix}\right) .\end{align*} $$
This implies that
$$ \begin{align*}\left(\begin{matrix} B_{1,1} A_1 & B_{1,2} A_2 \\ B_{2,1} A_1 & B_{2,2} A_2 \end{matrix}\right) = \left(\begin{matrix} A_1 B_{1,1} & A_1 B_{1,2}\\ A_2 B_{2,1} & A_2 B_{2,2} \end{matrix}\right) .\end{align*} $$
Thus, we have
$ B_{1,2} A_2 = A_1 B_{1,2} $
and
$B_{2,1} A_1 = A_2 B_{2,1}$
. Since
$A_1$
and
$A_2$
have no common eigenvalue, using Lemma 2.12, we conclude that
$B_{1,2}$
and
$B_{2,1}$
are zero matrices. Let
$B_1 = B_{1,1} $
and
$B_2 = B_{2,2} $
. Then, we have
$B_1 A_1 = A_1B_1 \, \text { and } \, B_2 A_2 = A_2B_2.$
This proves the lemma.
To formulate results related to matrices commuting with Jordan blocks in
$\mathrm {M}(n, \mathbb {H})$
, we need to recall the notation for upper triangular Toeplitz matrices.
Definition 2.14 ([Reference RodmanRo, p. 95])
For
$\mathbf {x}:=(x_{1},x_{2},\dots , x_{n}) \in \mathbb {H}^{n}$
, we define
$\mathrm {Toep}_{n}(\textbf {x}) \in \mathrm {M}(n, \mathbb {H})$
as
$$ \begin{align} \mathrm{Toep}_{n}(\mathbf{x}):= \left(\begin{matrix} x_{1} & x_{2} & \cdots & \cdots & \cdots & x_{n-1} & x_{n}\\ & x_{1} & x_{2} & \cdots & \cdots & x_{n-2}& x_{n-1}\\ & & x_{1} & x_{2} & \cdots & x_{n-3}& x_{n-2}\\ & & &\ddots & \ddots && \vdots\\ & & & & \ddots & \ddots & \vdots\\ & & & & & x_{1} & x_{2} \\ & & & & & & x_{1} \end{matrix}\right). \end{align} $$
We can also write
$\mathrm {Toep}_{n}(\textbf {x})$
as
$$ \begin{align} \mathrm{Toep}_{n}(\textbf{x}):= [x_{i,j}]_{n \times n} = \begin{cases} 0 & \text{if}\ i>j \\ x_{j-i+1}& \text{if}\ i \leq j\\ \end{cases}, \text{ where } 1 \leq i,j \leq n. \end{align} $$
In the following lemma, we recall a basic result that gives the centralizer of the Jordan blocks in
$\mathrm {M}(n, \mathbb {H})$
; see [Reference RodmanRo] for more details.
Lemma 2.15 ([Reference RodmanRo, Proposition 5.4.2])
Let
$B \in \mathrm {M}(n, \mathbb {H})$
be such that
$B \, \mathrm {J}(\lambda ,n)= \mathrm {J}(\lambda ,n) \,B$
. Then B has the following form:
$$ \begin{align*}B = \mathrm{Toep}_{n}(\mathbf{x}) \text{ for some }\mathbf{x} \in \begin{cases} \mathbb {H}^{n} & \text{ if }\lambda \in \mathbb R ,\\ \mathbb {C}^{n} & \text{ if } \lambda \in \mathbb {C} \setminus \mathbb R. \end{cases}\end{align*} $$
In particular, if
$B \in \mathrm {M}(n, \mathbb {H})$
such that
$B \, \mathrm {J}(e^{\mathbf {i} \theta },n)= \mathrm {J}(e^{\mathbf {i} \theta },n) \,B$
, where
$\theta \in (0, \pi )$
, then
$B = \mathrm {Toep}_{n}(\mathbf {x}) $
for some
$\mathbf {x} \in \mathbb {C}^{n}$
.
3 Strongly reversible elements in
$\mathrm {SL }(n,\mathbb {H})$
In this section, we will classify the strongly reversible elements in
$\mathrm {SL}(n,\mathbb {H})$
. First, we recall the following notation from [Reference Gongopadhyay, Lohan and MaityGLM2], which will be used to investigate reversing symmetries of reversible elements in
$\mathrm {SL}(n,\mathbb {H})$
.
Definition 3.1 ([Reference Gongopadhyay, Lohan and MaityGLM2, Definition 1.3])
For a non-zero
$\lambda \in \mathbb {C}$
, define the upper triangular matrix
$\Omega ( \lambda , n) := [ x_{i,j} ]_{ n \times n} \in \mathrm {GL}(n,\mathbb {C})$
such that:
-
(1)
$x_{i,j} = 0$
for all
$1\leq i,j \leq n$
such that
$i>j$
, -
(2)
$x_{i,n} = 0 $
for all
$1\leq i \leq n-1$
, -
(3)
$x_{n,n} = 1$
, -
(4) For
$ 1\leq i \leq j \leq n-1 $
, define (3.1)
$$ \begin{align} x_{i,j} = - \lambda^{-1} x_{i+1,j} - \lambda^{-2} x_{i+1,j+1}. \end{align} $$
Further, recall the following result from [Reference Gongopadhyay, Lohan and MaityGLM2, Section 3] which gives relationship between
$\Omega ( \lambda , n)$
,
$\Omega ( \lambda ^{-1}, n)$
and
$\mathrm {J}(\lambda , n)$
, where
$\lambda \neq 0$
.
Lemma 3.2 ([Reference Gongopadhyay, Lohan and MaityGLM2, Lemmas 3.2 and 3.3])
Let
$\Omega ( \lambda , n) \in \mathrm {GL }(n,\mathbb {C})$
be as defined in Definition 3.1. Then, the following statements are true.
-
(1)
$ \Omega ( \lambda , n) \, \mathrm {J}(\lambda ^{-1}, n) = \Big (\mathrm {J}(\lambda , n)\Big )^{-1} \, \Omega ( \lambda , n)$
. -
(2)
$\Big (\Omega ( \lambda , n)\Big )^{-1} = \Omega ( \lambda ^{-1}, n)$
.
In
$\mathrm {SL}(n,\mathbb {H})$
, there exist Jordan blocks that are reversible but not strongly reversible. For example, the element
$ \mathrm {J}(e^{\mathbf {i} \theta }, 1) = (e^{\mathbf {i} \theta }) \in \mathrm {SL }(1,\mathbb {H})$
, where
$ \theta \in (0,\pi )$
is reversible, since
$\mathbf {j} e^{\mathbf {i} \theta } = e^{-\mathbf {i} \theta } \mathbf {j}$
. Now if
$ (e^{\mathbf {i} \theta })$
is strongly reversible, then
$a e^{\mathbf {i} \theta } = e^{-\mathbf {i} \theta }a$
form some
$(a) \in \mathrm {SL }(1,\mathbb {H})$
with
$a^2=1$
. Writing
$a = x+ y \mathbf {j} \in \mathbb {H}$
,
$ x, y \in \mathbb {C}$
, it follows that
$a= y \mathbf {j}$
. Using the condition
$a^2=1$
, we get
$-|y|^2 =1$
, which is a contradiction. Thus,
$(e^{\mathbf {i} \theta })$
is reversible but not strongly reversible in
$\mathrm {SL }(1,\mathbb {H})$
.
We generalize the above example for an arbitrary n as follows.
Lemma 3.3 Let
$A:= \mathrm {J}(\alpha , n)$
be the Jordan block in
$ \mathrm {SL }(n,\mathbb {H})$
, where
$ \alpha \in \mathbb {C} \setminus \{- 1, +1\}$
with non-negative imaginary part such that
$|\alpha |= 1$
. Then A is reversible but not strongly reversible in
$\mathrm {SL }(n,\mathbb {H})$
.
Proof Write
$A = \mathrm {J}(e^{ \mathbf {i} \theta }, n) $
, where
$ \theta \in (0,\pi )$
. Since
$\mathbf {j} z = \bar {z} \mathbf {j}$
for all
$z \in \mathbb {C}$
, we have
$ \mathbf {j} \, P = \overline {P} \, \mathbf {j} $
for all
$P \in \mathrm {GL }(n,\mathbb {C})$
, where
$\overline {P}$
is the matrix obtained by taking conjugate of each entry of complex matrix P. This implies
$$ \begin{align} \mathbf {j} \, \Big( \mathrm{J}(e^{ \mathbf {i} \theta}, n) \Big) \, \mathbf {j}^{-1} = \overline{ \mathrm{J}(e^{ \mathbf {i} \theta}, n) }= \mathrm{J}(e^{ -\mathbf {i} \theta}, n). \end{align} $$
Consider
$\Omega (e^{ \mathbf {i} \theta } , n) \, \mathbf {j} \in \mathrm {SL}(n,\mathbb {H})$
, where
$\Omega (e^{ \mathbf {i} \theta }, n) \in \mathrm {GL}(n,\mathbb {C})$
is as defined in Definition 3.1. Then, using Lemma 3.2, we have
$$ \begin{align*} \Big(\Omega( e^{\mathbf {i} \theta}, n) \, \mathbf {j} \Big) A \Big(\Omega( e^{\mathbf {i} \theta}, n) \, \mathbf {j} \Big)^{-1}= A^{-1}. \end{align*} $$
Therefore, A is reversible in
$\mathrm {SL}(n,\mathbb {H})$
.
Suppose that A is strongly reversible in
$\mathrm {SL}(n,\mathbb {H})$
. Then there exists an involution
$g =[g_{i,j}]_{1\leq i,j \leq n} \in \mathrm {SL}(n,\mathbb {H})$
such that
$gAg^{-1}= A^{-1}$
. Note that the set of reversing elements of A is a right coset of the centralizer of A; see [Reference O’Farrell and ShortOS, Proposition 2.8]. Therefore, we have
$$ \begin{align*}g = f \Omega( e^{\mathbf {i} \theta}, n) \, \mathbf {j},\end{align*} $$
where
$f \in \mathrm {GL}(n,\mathbb {H})$
such that
$fA=Af$
. Now, using Lemma 2.15, we have
$$ \begin{align*}f = \mathrm{Toep}_{n}(\textbf{x}),\end{align*} $$
where
$\mathbf {x}:=(x_{1},x_{2},\dots , x_{n}) \in \mathbb {C}^{n}$
and
$\mathrm {Toep}_{n}(\textbf {x}) \in \mathrm {GL}(n, \mathbb {C})$
is as defined in Definition 2.14. This implies
$$ \begin{align*}g = \mathrm{Toep}_{n}(\textbf{x}) \Omega( e^{\mathbf {i} \theta}, n) \, \mathbf {j}.\end{align*} $$
Thus, we get
$g_{1,1} =z \mathbf {j}$
, where
$z = (-1)^{n-1} e^{-2\mathbf {i} (n-1) \theta } x_1 \in \mathbb {C}$
. Since g is an involution with an upper triangular form, we have
$(g_{1,1})^2 = 1$
. Therefore,
$|z|^2 = -1$
, which is a contradiction. Hence, A is not strongly reversible in
$\mathrm {SL}(n,\mathbb {H})$
. This completes the proof.
Although for every
$\theta \in (0,\pi )$
, the Jordan block
$\mathrm {J}(e^{\mathbf {i} \theta },n)$
is not strongly reversible in
$\mathrm {SL}(n,\mathbb {H})$
, Jordan forms in
$\mathrm {SL}(n,\mathbb {H})$
containing such Jordan blocks may still be strongly reversible.
Lemma 3.4 Let
$A:= \mathrm {J}(\alpha , n) \oplus \mathrm {J}(\alpha , n)$
be the Jordan form in
$\mathrm {SL }(2n,\mathbb {H})$
, where
$ \alpha \in \mathbb {C} \setminus \{-1, +1\}$
with non-negative imaginary part such that
$|\alpha |= 1$
. Then A is strongly reversible in
$\mathrm {SL }(2n,\mathbb {H})$
.
Proof Write
$A = \left (\begin {smallmatrix} \mathrm {J}(e^{ \mathbf {i} \theta }, n) & \\ & \mathrm {J}(e^{ \mathbf {i} \theta }, n) \end {smallmatrix}\right )$
, where
$ \theta \in (0,\pi )$
. Consider
$ \Omega (e^{ \mathbf {i} \theta }, n) \in \mathrm {GL}(n,\mathbb {C})$
as defined in Definition 3.1. Let
$g = \left (\begin {smallmatrix} & \Omega (e^{\mathbf {i} \theta }, n) \, \mathbf {j} \\ \Big ( \Omega (e^{\mathbf {i} \theta }, n) \, \mathbf {j} \Big )^{-1} & \end {smallmatrix}\right )$
. Note that
$gAg^{-1} = A^{-1}$
if and only if
$ \Big ( \Omega ( e^{ \mathbf {i} \theta }, n) \, \mathbf {j} \Big ) \, \Big ( \mathrm {J}(e^{ \mathbf {i} \theta }, n) \Big ) \, \Big ( \Omega ( e^{ \mathbf {i} \theta }, n) \, \mathbf {j} \Big )^{-1} = \Big (\mathrm {J}(e^{ \mathbf {i} \theta }, n)\Big )^{-1}$
. Moreover, g is an involution in
$ \mathrm {SL}(2n,\mathbb {H})$
. The proof now follows from Lemma 3.2 and Equation (3.2).
In the following result, we provide the necessary and sufficient conditions for the strong reversibility of elements of
$ \mathrm {SL}(n, \mathbb {H})$
that have only the eigenvalue
$ \alpha \in \mathbb {C} \setminus \{\pm 1\}$
with a non-negative imaginary part, where
$|\alpha |= 1$
. We used a similar line of argument as in the proof of [Reference Gongopadhyay, Lohan and MaityGLM2, Lemma 4.5], which is based on the notion of the Weyr canonical form and the structure of the set of reversing symmetries.
Proposition 3.5 Let
$A \in \mathrm {SL}(n, \mathbb {H})$
be an element having only eigenvalue
$e^{\mathbf {i} \theta }$
, where
$\theta \in (0,\pi )$
, and
$\mathbf {d}(n) = [d_1^{t_{d_1}}, \dots , d_s^{t_{d_s}}]$
be the corresponding partition in the Jordan decomposition of A. Then A is strongly reversible in
$\mathrm {SL}(n, \mathbb {H})$
if and only if
$t_{d_\ell }$
is even for all
$1 \leq \ell \leq s$
.
Proof (
$\Rightarrow $
) In view of Lemma 2.4, up to conjugacy, we can assume A in the Jordan form with complex entries given by Equation (2.2). Let
$A_{W}$
denote the Weyr form of
$A \in \mathrm {GL}(n,\mathbb {C})$
. Then
$A_{W} = \delta A \delta ^{-1}$
for some
$\delta \in \mathrm {GL}(n,\mathbb {C})$
. Using Lemma 2.7 and Remark 2.10, the partition
$\overline {{\mathbf {d}}}(n) $
representing the Weyr form
$A_{W}$
of A is given by:
$$ \begin{align*}\overline{\mathbf{d}}(n) = [ (t_{d_1}+t_{d_2}+\cdots+t_{d_s})^{d_s}, (t_{d_1}+t_{d_2}+\cdots+t_{d_{s-1}})^{d_{s-1}-d_s}, \cdots, (t_{d_1}+t_{d_2})^{d_2 -d_3},(t_{d_1})^{d_1 -d_2}].\end{align*} $$
Therefore,
$A_{W} \in \mathrm {GL}(n,\mathbb {C})$
is a block matrix with
$(d_1)^2$
many blocks and for all
$1\leq i \leq d_1$
, the size
$n_i$
of i-th diagonal block is given by
$$ \begin{align*}n_i = \begin{cases} t_{d_1}+t_{d_2}+\cdots+t_{d_s} & \text{if}\ 1 \leq i \leq d_s,\\ t_{d_1}+t_{d_2}+\cdots+t_{d_{s-r-1} }& \text{if}\ {d_{s-r}} +1 \leq i \leq {d_{s-r-1}}, \text{where}\ 0 \leq r \leq s-2. \end{cases}\end{align*} $$
This implies that
$(i,j)$
-th block of
$A_{W}$
has the size
$ n_i \times n_j$
; see [Reference Gongopadhyay, Lohan and MaityGLM2, Section 2.2]. Further,
$(i,j)$
-th block of the Weyr form
$A_{W}$
and its inverse
$(A_{W} )^{-1}$
can be given as follows:
$$ \begin{align*}(A_{W})_{i,j} &= \begin{cases} e^{\mathbf {i} \theta} \mathrm{I}_{n_i} & \text{if } j=i \\ \mathrm{I}_{n_i \times n_{i +1}} & \text{if } j =i+1\\ \mathrm{O}_{n_i \times n_{j}} & \text{otherwise} \end{cases}, \text{ and }\\ ((A_{W} )^{-1})_{i,j} &= \begin{cases} e^{-\mathbf {i} \theta}\mathrm{I}_{n_i} & \text{if } j=i \\ (-1)^k e^{-(k+1)\mathbf {i} \theta} \mathrm{I}_{n_i \times n_{i +k}} & \text{if } j =i+k, 1 \leq k \leq d_1 - i\\ \mathrm{O}_{n_i \times n_{j}} & \text{otherwise} \end{cases},\end{align*} $$
where
$1\leq i, j \leq d_1$
and
$\mathrm {O}_{n_i \times n_{j}}$
denotes the
$n_i \times n_{j}$
zero matrix. Consider
$\Omega _{W} := [ X_{i,j} ]_{d_1 \times d_1} \in \mathrm {GL}(n,\mathbb {C})$
such that
$$ \begin{align} X_{i,j} =\begin{cases} \mathrm{O}_{n_i \times n_{j}} & \text{if } i>j \\ \mathrm{O}_{n_i \times n_{j}} & \text{if } j =d_1, i \neq d_1\\ (-1)^{d_1-i} \, \Big( e^{-2(d_1-i) \mathbf {i} \theta}\Big) \, \mathrm{I}_{n_i}& \text{if } j=i \\ (-1)^{d_1-i} \, \binom{d_1-i-1}{j-i} \, \Big(e^{-(2d_1+i+j) \mathbf {i} \theta} \Big) \, \mathrm{I}_{n_i \times n_{j}} & \text{if } j>i, j \neq d_1 \end{cases}, \end{align} $$
where
$\binom {d_1-i-1}{j-i} $
denotes the binomial coefficient. Let
$\tau = \Omega _{W} \, \mathbf {j} \in \mathrm {GL}(n,\mathbb {H})$
. Then by using a similar argument as used in Lemma 3.3 and [Reference Gongopadhyay, Lohan and MaityGLM2, Lemma 3.2], we have
$$ \begin{align} \tau A_{W} \tau^{-1}=(A_{W} )^{-1}. \end{align} $$
Let
$f=[P_{i,j}]_{d_1 \times d_1} \in \mathrm {GL}(n,\mathbb {H})$
be an
$n \times n$
matrix commuting with Weyr form
$A_{W} \in \mathrm {GL}(n,\mathbb {C})$
, where both f and
$A_{W}$
are blocked according to the partition
$\overline {{\mathbf {d}}}(n) $
. Then, using a similar argument as in Lemma 2.15, we can conclude that f is a matrix with complex entries. Thus, we have
$f \in \mathrm {GL}(n,\mathbb {C})$
such that
$f (e^{\mathbf {i} \theta } \mathrm {I}_{n}) = (e^{\mathbf {i} \theta } \mathrm {I}_{n}) f$
. Then
$fA_W =A_W f$
implies that
$fN =Nf$
, where
$N= A_W - e^{\mathbf {i} \theta } \mathrm {I}_{n}$
is a nilpotent basic Weyr matrix given by the partition
$ \overline {\mathbf {d}}(n) $
. Therefore, using Proposition 2.11, we have that
$f \in \mathrm {GL}(n,\mathbb {C})$
is an upper triangular block matrix such that i-th diagonal block
$P_{i,i}$
of f is given as follows:
-
(1) if
$1 \leq i \leq d_s$
, then
$ P_{i,i}= \left (\begin {smallmatrix} {P}_{1} &\ast & \ast & \ast & \cdots & \ast \\ & {P}_{2} & \ast & \cdots & \cdots & \ast \\ & &\ddots & \ddots && \vdots \\ & & & \ddots & \ddots & \vdots \\ & & & & {P}_{{s-1}} & \ast \\ & & & & &{P}_{s} \end {smallmatrix}\right )$
, -
(2) if
${d_{s-r}} +1 \leq i \leq {d_{s-r-1}}$
, then
$ P_{i,i}= \left (\begin {smallmatrix} {P}_{1} &\ast & \ast & \ast & \cdots & \ast \\ & {P}_{2} & \ast & \cdots & \cdots & \ast \\ & &\ddots & \ddots && \vdots \\ & & & \ddots & \ddots & \vdots \\ & & & & {P}_{{s-r-2}} & \ast \\ & & & & &{P}_{s-r-1} \end {smallmatrix}\right ),$
-
(3) if
$d_2 +1 \leq i \leq d_1$
, then
$P_{i,i} = P_1$
,
where
$0 \leq r \leq s-3$
and
$P_k \in \mathrm {GL}(t_{d_k}, \mathbb {C})$
for all
$ 1 \leq k \leq s$
.
Since A is strongly reversible in
$\mathrm {SL}(n, \mathbb {H})$
, there exists an involution g in
$\mathrm {SL}(n,\mathbb {H})$
such that
$gAg^{-1} =A^{-1}$
. Consider
$h = [Y_{i,j}]_{d_1 \times d_1}:= \delta g \delta ^{-1}$
in
$\mathrm {SL}(n,\mathbb {H})$
. Then h is an involution in
$\mathrm {SL}(n,\mathbb {H})$
such that
$$ \begin{align} h A_{W} h^{-1} =(A_{W})^{-1}. \end{align} $$
Note that the set of reversing elements of
$A_W$
is a right coset of the centralizer of
$A_W$
. Therefore, using Equations (3.4) and (3.5), we have
$$ \begin{align*}h = f \tau.\end{align*} $$
This implies that
$h \in \mathrm {GL}(n,\mathbb {H})$
is an upper triangular block matrix, and the first diagonal block of h is given by
$$ \begin{align*}Y_{1, 1} = \left(\begin{matrix} {Q}_{1} \, \mathbf {j} &\ast & \ast & \ast & \cdots & \ast \\ & {Q}_{2} \, \mathbf {j} & \ast & \cdots & \cdots & \ast \\ & &\ddots & \ddots && \vdots \\ & & & \ddots & \ddots & \vdots \\ & & & & {Q}_{{s-1}} \, \mathbf {j} & \ast \\ & & & & &{Q}_{s} \, \mathbf {j} \end{matrix}\right),\end{align*} $$
where
$ Q_k= (-1)^{d_1-1} \, \Big ( e^{-2(d_1-1) \mathbf {i} \theta } \Big ) P_{k} \in \mathrm {GL}(t_{d_k}, \mathbb {C})$
for all
$1 \leq k \leq s$
. Since h is an involution, we have
$Y_{1, 1}$
, and hence
$Q_k \mathbf {j}$
is an involution for all
$1 \leq k \leq s$
. Then we have
$$ \begin{align*}Q_k \overline{Q_k}= -\mathrm{I}_{t_{d_k}}.\end{align*} $$
This implies that
$|\mathrm {det}( Q_k)|^2 = (-1)^{t_{d_k}}$
. Therefore,
$t_{d_k}$
is even for all
$1 \leq k \leq s$
.
(
$\Leftarrow $
) The proof of the converse part of the lemma follows from Lemma 3.4. This completes the proof.
3.1 Proof of Theorem 1.3
(
$\Leftarrow $
) Recall that if
$g \in \mathrm {GL }(n,\mathbb {H})$
is an involution, then
$ g \in \mathrm {SL }(n,\mathbb {H})$
; see Definition 2.3. The proof now follows from [Reference Gongopadhyay, Lohan, Maity and PapadopoulosGLM1, Theorem 5.4]
(
$\Rightarrow $
) Let A be a strongly reversible element in
$\mathrm {SL }(n,\mathbb {H})$
. If A has no non-real eigenvalues of unit modulus, the proof is complete. Now, assume that A has a non-real unit modulus eigenvalue
$\mu $
, with multiplicity
$m \geq 1$
. If
$m=n$
, then the proof follows from Proposition 3.5.
Assume that
$1\leq m <n$
. Write
$\mu = e^{\mathbf {i} \theta _o}$
for some
$\theta _o \in (0,\pi )$
. Using Lemma 2.4, we can express A as
$$ \begin{align*}A = \left(\begin{matrix} A_1 & \\ &A_2 \end{matrix}\right),\end{align*} $$
where
$A_1 \in \mathrm {GL}(m,\mathbb {H})$
and
$A_2 \in \mathrm {GL}(n-m,\mathbb {H})$
such that
$1\leq m <n$
. Moreover,
$A_1$
has a single eigenvalue
$e^{\mathbf {i} \theta _o}$
, and for each eigenvalue
$\lambda $
of
$A_2$
, we have
$[e^{\mathbf {i} \theta _o}] \neq [\lambda ]$
. Let
$B \in \mathrm {GL}(n,\mathbb {H})$
such that
$BA=AB$
. Then Lemma 2.13 implies that B has the following form:
$$ \begin{align*}B= \left(\begin{matrix} B_{1} & \\ & B_{2} \end{matrix}\right),\end{align*} $$
where
$ B_{1} \in \mathrm {GL}(m,\mathbb {H}) $
and
$B_{2} \in \mathrm {GL}(n-m,\mathbb {H})$
such that
$B_1A_1=A_1B_1$
and
$B_2A_2=A_2B_2$
. Since A is reversible, using Theorem 1.2, Lemma 3.3, and Table 1, we can find a reversing element h for A which has the form
$$ \begin{align*}h= \left(\begin{matrix} h_1 & \\ & h_2 \end{matrix}\right),\end{align*} $$
where
$ h_1 \in \mathrm {GL}(m,\mathbb {H}) $
and
$h_2 \in \mathrm {GL}(n-m,\mathbb {H})$
such that
$h_i A_i(h_i)^{-1}= (A_i)^{-1}$
for all
$ i \in \{1,2\} $
.
Let
$g \in \mathrm {SL}(n,\mathbb {H})$
be an involution such that
$gAg^{-1} = A^{-1}$
. Since the set of reversing elements of A is a right coset of the centralizer of A, we have that g has the following form
$$ \begin{align*}g= \left(\begin{matrix} g_1 & \\ & g_2 \end{matrix}\right),\end{align*} $$
where
$ g_1 \in \mathrm {GL}(m,\mathbb {H}) $
and
$g_2 \in \mathrm {GL}(n-m,\mathbb {H})$
are involutions such that
$g_i A_i(g_i)^{-1}= (A_i)^{-1}$
for
$ i \in \{1,2\} $
. Thus, we have an involution
$ g_1 \in \mathrm {GL}(m,\mathbb {H}) $
such that
$g_1A_1(g_1)^{-1}= (A_1)^{-1}$
. The proof of the theorem now follows from Proposition 3.5.
4 Product of two skew-involutions in
$\mathrm {SL }(n,\mathbb {H})$
In this section, we demonstrate that every reversible element in
$\mathrm {SL }(n,\mathbb {H})$
can be expressed as a product of two skew-involutions in
$\mathrm {SL }(n,\mathbb {H})$
. In view of Theorem 1.2 which classifies the reversible elements in
$\mathrm {SL }(n,\mathbb {H})$
, it is sufficient to consider certain Jordan forms in
$\mathrm {SL }(n,\mathbb {H})$
. Note the following two results, which will be used in proving Theorem 1.4.
Lemma 4.1 Let
$A:=\mathrm {J}(\mu , n)$
be the Jordan block in
$ \mathrm {SL }(n,\mathbb {H})$
, where
$ \mu \in \mathbb {C}$
with non-negative imaginary part such that
$|\mu |= 1$
. Then there exists a skew-involution
$g \in \mathrm {SL}(n,\mathbb {H}) $
such that
$g A g^{-1}= A^{-1}$
.
Proof Write
$A:=\mathrm {J}(e^{\mathbf {i} \theta }, n )$
, where
$\theta \in [0, \pi ]$
. Let
$g:= \Omega (e^{ \mathbf {i} \theta } , n) \, \mathbf {j} \in \mathrm {GL}(n,\mathbb {H})$
, where
$\Omega (e^{ \mathbf {i} \theta }, n) \in \mathrm {GL}(n,\mathbb {C})$
is as defined in Definition 3.1. Then, using Lemma 3.2 (1), we have
$gAg^{-1}= A^{-1}$
; see also Lemma 3.3. In view of Lemma 3.2 (2), we have
$$ \begin{align*}\Omega(e^{ \mathbf {i} \theta} , n) \Omega(e^{- \mathbf {i} \theta} , n) = \mathrm{I}_{n}.\end{align*} $$
This implies that
$$ \begin{align*}g^2 = \Omega(e^{ \mathbf {i} \theta} , n) \, \mathbf {j} \Omega(e^{ \mathbf {i} \theta} , n) \, \mathbf {j} = \Omega(e^{ \mathbf {i} \theta}) \overline{ \Omega(e^{ \mathbf {i} \theta} , n)} (\mathbf {j}^2) = - \Omega(e^{ \mathbf {i} \theta} , n) \Omega(e^{- \mathbf {i} \theta} , n) = -\mathrm{I}_{n}.\end{align*} $$
This proves the lemma.
Lemma 4.2 Let
$A:= \mathrm {J}(\lambda , n) \ \oplus \ \mathrm {J}(\lambda ^{-1}, n)$
be the Jordan form in
$ \mathrm {SL}(2n,\mathbb {H})$
, where
$\lambda \in \mathbb {C} \setminus \{0\} $
with non-negative imaginary part such that
$ |\lambda | \neq 1$
. Then there exists a skew-involution
$g $
in
$\mathrm {SL}(2n,\mathbb {H}) $
such that
$g A g^{-1}= A^{-1}$
.
Proof Write
$A= \left (\begin {smallmatrix} \mathrm {J}(\lambda , n) & \\ & \mathrm {J}(\lambda ^{-1}, n) \end {smallmatrix}\right ) \in \mathrm {SL}(2n,\mathbb {H})$
. Let
$g = \left (\begin {smallmatrix} & \Omega (\lambda , n) \\ - \Omega (\lambda ^{-1}, n) & \end {smallmatrix}\right ),$
where
$ \Omega (\lambda , n) \in \mathrm {GL}(n,\mathbb {C})$
is as defined in Definition 3.1. Then Lemma 3.2 (2) implies that g is a skew-involution in
$ \mathrm {SL}(2n,\mathbb {H})$
. Moreover,
$gAg^{-1} = A^{-1}$
if and only if
$ \Omega ( \lambda , n) \, \mathrm {J}(\lambda ^{-1}, n) = \Big (\mathrm {J}(\lambda , n)\Big )^{-1} \, \Omega ( \lambda , n).$
The proof now follows from Lemma 3.2 (1).
4.1 Proof of Theorem 1.4
Note that an element
$A \in \mathrm {SL }(n,\mathbb {H})$
can be written as a product of two skew-involutions if and only if there exists a skew-involution
$g \in \mathrm {SL}(n,\mathbb {H}) $
such that
$g A g^{-1}= A^{-1}$
. The proof now follows from Theorem 1.2, Lemma 2.4, Lemma 4.1, and Lemma 4.2
5 Reversibility in
$\mathrm {PSL}(n,\mathbb {H})$
In this section, we will investigate the reversibility problem in the quaternionic projective linear group
$\mathrm {PSL}(n,\mathbb {H}):= \mathrm {SL}(n,\mathbb {H})/\{\pm \mathrm {I}_{n}\}$
. Recall that for every
$g,h \in \mathrm {SL}(n,\mathbb {H})$
, we have
$$ \begin{align*}[g]=[h] \Leftrightarrow g=\pm h.\end{align*} $$
Moreover, every skew-involution in
$\mathrm {SL}(n,\mathbb {H})$
is an involution in
$\mathrm {PSL}(n,\mathbb {H})$
. The following result provides the relation between reversibility in the groups
$\mathrm {SL}(n,\mathbb {H})$
and
$\mathrm {PSL}(n,\mathbb {H}) $
, cf. [Reference Dutta, Gongopadhyay and LohanDGL, Lemma 4.1].
Lemma 5.1 An element
$[g] \in \mathrm {PSL}(n,\mathbb {H})$
is reversible if and only if there exists
$h \in \mathrm {SL}(n,\mathbb {H})$
such that either of the following conditions holds.
-
(1)
$hgh^{-1}= g^{-1}$
. -
(2)
$hgh^{-1}= -g^{-1}$
.
Now, we will investigate the equation
$g A g^{-1}= -A^{-1}$
, where
$A, g \in \mathrm {SL}(n,\mathbb {H}) $
. In [Reference Paras and SalinasanPaSa], authors did such investigation for matrices over an arbitrary field
$\mathbb {F}$
, and they gave necessary and sufficient conditions for
$A \in \mathrm {GL}(n, \mathbb {F})$
to be a product of an involution and a skew-involution; see [Reference Paras and SalinasanPaSa, Theorem 5]. The following result classify all elements
$A \in \mathrm {SL}(n,\mathbb {H}) $
such that A is conjugate to
$-A^{-1}$
in
$ \mathrm {SL}(n,\mathbb {H}) $
, cf. Theorem 1.2.
Theorem 5.2 An element
$A \in \mathrm {SL }(n,\mathbb {H})$
satisfies
$g A g^{-1}= -A^{-1}$
for some
$g \in \mathrm {SL}(n,\mathbb {H}) $
if and only if the Jordan blocks in the Jordan decomposition of A can be partitioned into pairs
$ \{ \mathrm {J}(\lambda , s),\mathrm {J}(-\lambda ^{-1}, s)\} $
or singletons
$\{\mathrm {J}(\mathbf {i}, t )\}$
, where
$\lambda \in \mathbb {C} \setminus \{0\}$
with non-negative imaginary parts and
$\lambda \neq \mathbf {i}$
.
Proof Note that
$g A g^{-1}= -A^{-1}$
for some
$g \in \mathrm {SL}(n,\mathbb {H}) $
if and only if A and
$-A^{-1}$
have the same Jordan form; see Lemma 2.4. Let
$a \in \mathbb {H} \setminus \{0\}$
. Recall that
$[a] =[-a^{-1}]$
if and only if
$\mathrm {Re}(a) = \mathrm {Re}(-a^{-1})$
and
$|a|= |-a^{-1}|$
; see [Reference RodmanRo, Theorem 2.2.6(5)]. Now, equation
$|a|= |-a^{-1}|$
implies that
$|a|=1$
. This implies that
$\mathrm {Re}(a) = \mathrm {Re}(-a^{-1}) = \mathrm {Re}(-\overline {a})$
. Therefore, we have
$[a] =[a^{-1}]$
if and only if
$\mathrm {Re}(a) =0$
and
$|a|=1$
. Hence, for
$\lambda \in \mathbb {C} \setminus \{0\}$
with non-negative imaginary parts, we have
$$ \begin{align*}[\lambda] =[-\lambda^{-1}] \Leftrightarrow \lambda =\mathbf {i}.\end{align*} $$
The proof now follows using a similar line of arguments as in [Reference Gongopadhyay, Lohan, Maity and PapadopoulosGLM1, Theorem 5.1]
Lemma 5.3 Let
$A:= \mathrm {J}(\lambda , n) \oplus \mathrm {J}(-\lambda ^{-1}, n)$
be the Jordan form in
$ \mathrm {SL }(2n,\mathbb {H})$
, where
$\lambda \in \mathbb {C} \setminus \{0\}$
with non-negative imaginary parts such that
$ \lambda \neq \mathbf {i}.$
Then there exists an involution
$g \in \mathrm {SL}(2n,\mathbb {H}) $
such that
$g A g^{-1}= -A^{-1}$
.
Proof Write
$A= \left (\begin {smallmatrix} \mathrm {J}(\lambda , n) & \\ & \mathrm {J}(-\lambda ^{-1}, n) \end {smallmatrix}\right ) \in \mathrm {SL}(2n,\mathbb {H})$
. Since
$ - \Big (\mathrm {J}(\lambda , n)\Big )^{-1}$
and
$\mathrm {J}(-\lambda ^{-1}, n)$
are conjugate in
$ \mathrm {GL}(n,\mathbb {C})$
, there exists an element
$P \in \mathrm {GL}(n,\mathbb {C})$
such that
$$ \begin{align} P \, \mathrm{J}(-\lambda^{-1}, n) \, P^{-1}= -\Big(\mathrm{J}(\lambda, n)\Big)^{-1}. \end{align} $$
Consider
$g = \left (\begin {smallmatrix} & P \\ P^{-1} & \end {smallmatrix}\right ) \in \mathrm {GL}(2n,\mathbb {C}) \subset \mathrm {SL}(2n,\mathbb {H})$
. Then g is an involution in
$ \mathrm {SL}(2n,\mathbb {H})$
; see Definition 2.3. Moreover,
$gAg^{-1} = -A^{-1}$
if and only if
$P \, \mathrm {J}(-\lambda ^{-1}, n) \, P^{-1}= -\Big (\mathrm {J}(\lambda , n)\Big )^{-1}.$
Hence, the proof follows.
Next we consider an example.
Example 5.4 Let
$A = \mathrm {J}(\mathbf {i}, 5 ) \in \mathrm {SL }(5,\mathbb {H})$
. Consider
$g= \left (\begin {smallmatrix} 1 & -3\mathbf {i} & -3 & \mathbf {i} &0 \\ & -1 & 2\mathbf {i} & 1 & 0\\ & & 1 & -\mathbf {i} &0 \\ & & & -1 &0 \\ & & & & 1 \end {smallmatrix}\right ) $
in
$ \mathrm {SL }(5,\mathbb {H})$
. Note that the following equations hold.
$$ \begin{align*}gA &= \left(\begin{matrix} 1 & -3\mathbf {i} & -3 & \mathbf {i} &0 \\ & -1 & 2\mathbf {i} & 1 & 0\\ & & 1 & -\mathbf {i} &0 \\ & & & -1 &0 \\ & & & & 1 \end{matrix}\right) \left(\begin{matrix} \mathbf {i}& 1 & 0 & 0 &0 \\ & \mathbf {i}& 1 & 0 & 0\\ & & \mathbf {i} & 1 &0 \\ & & & \mathbf {i}&1 \\ & & & &\mathbf {i} \end{matrix}\right) = \left(\begin{matrix} \mathbf {i}& 4 & -6 \mathbf {i} & 4& \mathbf {i} \\ & -\mathbf {i}& -3 & 3\mathbf {i} & 1\\ & & \mathbf {i} & 2 &-\mathbf {i} \\ & & &- \mathbf {i}&-1 \\ & & & &\mathbf {i} \end{matrix}\right), \text{ and }\\A^{-1}g &= \left(\begin{matrix} - \mathbf {i}& 1 & \mathbf {i} & -1 &-\mathbf {i} \\ & - \mathbf {i}& 1 & \mathbf {i} & -1\\ & & - \mathbf {i}& 1 & \mathbf {i} \\ & & & - \mathbf {i}& 1 \\ & & & & -\mathbf {i} \end{matrix}\right) \left(\begin{matrix} 1 & -3\mathbf {i} & -3 & \mathbf {i} &0 \\ & -1 & 2\mathbf {i} & 1 & 0\\ & & 1 & -\mathbf {i} &0 \\ & & & -1 &0 \\ & & & & 1 \end{matrix}\right) = \left(\begin{matrix} - \mathbf {i}& -4 & 6 \mathbf {i} & -4& -\mathbf {i} \\ & \mathbf {i}& 3 & -3\mathbf {i} & -1\\ & & -\mathbf {i} & -2 &\mathbf {i} \\ & & &\mathbf {i}&1 \\ & & & &-\mathbf {i} \end{matrix}\right).\end{align*} $$
Moreover,
$g^2 = \mathrm {I}_{5}.$
Therefore, g is an involution in
$ \mathrm {SL}(5,\mathbb {H}) $
such that
$g A g^{-1}= -A^{-1}$
.
In the following lemma, we will generalize Example 5.4.
Lemma 5.5 Let
$A:= \mathrm {J}(\mathbf {i}, n )$
be the Jordan block in
$ \mathrm {SL }(n,\mathbb {H})$
. Then there exists an involution g in
$\mathrm {SL}(n,\mathbb {H}) $
such that
$g A g^{-1}= -A^{-1}$
.
Proof Write
$ A = [a_{i,j}]_{ n \times n} $
and
$ A^{-1} = [b_{i,j}]_{ n \times n} $
, where
$$ \begin{align*} a_{i,j} = \begin{cases} \mathbf {i} & \text{if}\ j=i \\ 1 & \text{if}\ j =i+1\\ 0 & \text{otherwise} \end{cases}, \text{ and } b_{i,j} = \begin{cases} -\mathbf {i} & \text{if}\ j=i \\ - (\mathbf {i})^{j-i+1} & \text{if}\ j>i\\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
Consider the upper triangular matrix
$g := [ x_{i,j}]_{n \times n} \in \mathrm{GL}(n,\mathbb{C})$
, where
-
(1)
$x_{i,j} = 0$
for all
$1\leq i,j \leq n$
such that
$i>j$
, -
(2)
$x_{i,n} = 0 $
for all
$1\leq i \leq n-1$
, -
(3)
$x_{n,n} = 1$
, -
(4) for all
$ 1\leq i \leq j \leq n-1 $
, define (5.2)
$$ \begin{align} x_{i,j} = \mathbf {i} x_{i+1,j} - x_{i+1,j+1}. \end{align} $$
For more clarity, we can write
$g = [ x_{i,j} ]_{ 1\leq i, j \leq n} \in \mathrm {GL}(n,\mathbb {C})$
explicitly as follows:
$$ \begin{align} x_{i,j} =\begin{cases} 0 & \text{if}\ j <i \\ 0 & \text{if}\ j =n, i \neq n\\ (-1)^{n-i} & \text{if}\ j=i\\ (-1)^{n-i} \, \binom{n-i-1}{j-i} \, (-\mathbf {i})^{j-i}& \text{if}\ j>i, j \neq n \end{cases}, \end{align} $$
where
$\binom {n-i-1}{j-i} $
denotes the binomial coefficient. Observe that for all
$1\leq i <j\leq n$
, we have
$$ \begin{align} x_{i,j-1}= (i)^2 x_{i+1,j} + (i)^3 x_{i+2,j} + \dots + (i)^{j-i+1} x_{j,j} \end{align} $$
To prove the lemma, it suffices to establish the following two claims:
-
(1) Claim 1.
$gA = -A^{-1}g$
.Proof. Note that for all
$1\leq i \leq n$
, we have Since matrices under consideration are upper triangular, so it is enough to prove the following equality:
$$ \begin{align*}(gA)_{i,i} = - ( A^{-1} g)_{i,i} = (-1)^{n-i} \mathbf {i} = \mathbf {i} x_{i,i} .\end{align*} $$
To see this, note that for
$$ \begin{align*} (gA)_{i,j} = - ( A^{-1} g)_{i,j} = x_{i,j-1} + \mathbf {i} \, x_{i,j} \text { for all } 1 \leq i < j\leq n. \end{align*} $$
$1 \leq i < j\leq n$
, we have Further, for
$$ \begin{align*} (gA)_{i,j} = \sum_{k=1}^{n} (x_{i,k}) \, (a_{k,j}) = \sum_{k=i}^{j} (x_{i,k}) \, (a_{k,j})= x_{i,j-1} a_{j-1,j} + x_{i,j} a_{j,j}=x_{i,j-1} + \mathbf {i} \, x_{i,j}.\end{align*} $$
$1 \leq i < j\leq n$
, we have Using Equation (5.4), we get
$$ \begin{align*} ( A^{-1} g)_{i,j} & = \sum_{k=1}^{n} (b_{i,k}) (x_{k,j}) = \sum_{k=i}^{j} (b_{i,k}) (x_{k,j}) = b_{i,i} x_{i,j} + b_{i,i+1} x_{i+1,j}+ \dots + b_{i,j} x_{j,j} \\& =(-\mathbf {i} x_{i,j}) - \Big((i)^2 x_{i+1,j} + (i)^3 x_{i+2,j} + \dots + (i)^{j-i+1} x_{j,j} \Big). \end{align*} $$
Therefore, we have
$$ \begin{align*} ( A^{-1} g)_{i,j} = (-\mathbf {i} x_{i,j}) - (x_{i,j-1})= -( x_{i,j-1} +\mathbf {i} x_{i,j}) \text { for all } 1 \leq i < j\leq n. \end{align*} $$
$gA = -A^{-1}g$
.
-
(2) Claim 2.
$g^2= \mathrm {I}_n$
.Proof. Note that we have
$(g^2)_{i,i} =1$
for all
$1 \leq i \leq n$
. Moreover, for all
$1 \leq i < j \leq n$
, we have This implies that for all
$$ \begin{align*}(g^2)_{i,j} = \sum_{k=1}^{n} (x_{i,k}) \, (x_{k,j}) = \sum_{k=i}^{j} (x_{i,k}) \, (x_{k,j}) .\end{align*} $$
$1 \leq i < j \leq n$
, we have Therefore, for all
$$ \begin{align*}(g^2)_{i,j} = \sum_{k=i}^{j} (-1)^{n-i} \, \binom{n-i-1}{k-i } \, (-\mathbf {i})^{k-i} \, (-1)^{n-k} \, \binom{n-k-1}{j-k } \, (-\mathbf {i})^{j-k}.\end{align*} $$
$1 \leq i < j \leq n$
, we have (5.5)By substituting
$$ \begin{align} (g^2)_{i,j} = (-\mathbf {i})^{j-i} \, \sum_{k=i}^{j} (-1)^{(-i-k)} \, \binom{n-i-1}{k-i } \, \binom{n-k-1}{j-k }. \end{align} $$
$m = k-i$
in Equation (5.5), we get Now, recall the following well-known binomial identities concerning binomial coefficients from [Reference BurtonBu, Section 1.2]:
$$ \begin{align*} (g^2)_{i,j} = (-\mathbf {i})^{j-i} \, \sum_{m=0}^{j-i} (-1)^{(-2i-m)} \binom{n-i-1}{m } \binom{(n-i-1)-m}{(j-i) -m}. \end{align*} $$
-
(a) Newton’s identity:
$\binom {n}{k} \binom {k}{r}= \binom {n}{r} \binom {n-r}{k-r} $
for all
$ 0\leq r \leq k \leq n$
. -
(b) For
$n\geq 1$
,
$\sum _{k=0}^{n} (-1)^{k} \binom {n}{k}=0$
.
In view of the Newton’s identity (a) and identity (b), we get
Therefore,
$$ \begin{align*}(g^2)_{i,j} = (-\mathbf {i})^{j-i}\, \binom{n-i-1}{j-i } \, \sum_{r=0}^{j-i} \, (-1)^r \, \binom{j-i}{r } =0 \text { for all } 1\leq i < j \leq n.\end{align*} $$
$(g^2)= \mathrm {I}_n$
in
$\mathrm {GL }(n,\mathbb {C})$
.
-
Hence, the proof follows.
Theorem 5.6 Let
$A \in \mathrm {SL}(n,\mathbb {H}) $
. Then the following conditions are equivalent.
-
(1)
$g A g^{-1}= -A^{-1}$
for some
$g \in \mathrm {SL}(n,\mathbb {H}) $
. -
(2)
$h A h^{-1}= -A^{-1}$
for some involution
$h \in \mathrm {SL}(n,\mathbb {H}) $
.
The following result generalizes [Reference Dutta, Gongopadhyay and LohanDGL, Proposition 4.3] for an arbitrary n.
Proposition 5.7 Let
$A \in \mathrm {SL}(n,\mathbb {H}) $
be an element such that
$g A g^{-1}= -A^{-1}$
for some
$g \in \mathrm {SL}(n,\mathbb {H}) $
. Then A can be written as a product of an involution and a skew-involution in
$\mathrm {SL}(n,\mathbb {H}) $
.
Proof In view of the Theorem 5.6, there exists an involution
$h \in \mathrm {SL}(n,\mathbb {H}) $
such that
$hA h^{-1}= -A^{-1}$
. This implies that
$$ \begin{align*}A = (- h^{-1} A^{-1}) (h),\end{align*} $$
where
$(- h^{-1} A^{-1})^2 = -\mathrm {I}_n$
and
$h^{2}= \mathrm {I}_n$
. This completes the proof.
Acknowledgments
Gongopadhyay is partially supported by the SERB core research grant CRG/2022/003680. Lohan acknowledges the financial support from the IIT Kanpur Postdoctoral Fellowship. Maity is partially supported by the Seed Grant IISERBPR/RD/OO/2024/23.
