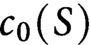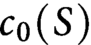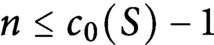1 Introduction
Le problème de Heawood consiste à déterminer le nombre chromatique des surfaces closes de genre non nul, c’est-à-dire la borne supérieure des nombres chromatiques des graphes qu’on peut plonger dans cette surface. Son étude a été amorcée par Heawood [Reference HeawoodHeawood, 1890] et Heffter [Reference HeffterHeffter, 1891], et sa résolution achevée trois quart de siècle plus tard par Ringel et Youngs [Reference Ringel and YoungsRingel et Youngs, 1968]: la valeur du nombre chromatique d’une surface S de caractéristique d’Euler
$\chi $
est
$c(S)=\lfloor \frac {7+\sqrt {49-24\chi }}2\rfloor $
, sauf pour la bouteille de Klein dont le nombre chromatique vaut 6. On peut consulter [Reference RingelRingel, 1974] pour la résolution complète du problème et un survol historique.
Ce nombre chromatique joue un rôle dans deux problèmes qui semblent a priori sans rapport. Le premier concerne les plongements polyédraux substantiels tendus de S dans
$\mathbb {R}^n$
(voir ci-dessous la Définition 3 d’un plongement tendu; un plongement dans
$\mathbb {R}^n$
est dit substantiel si son image n’est pas contenue dans un hyperplan affine ou, de manière équivalente, si le sous-espace affine engendré par l’image du plongement est
$\mathbb {R}^n$
). Il découle des travaux de Banchoff [Reference BanchoffBanchoff, 1965] et Kühnel [Reference KühnelKühnel, 1980] que la valeur maximale de la dimension n telle qu’un tel plongement existe est
$c(S)-1$
.
Le second problème touche au spectre des opérateurs de Schrödinger sur les surfaces. Colin de Verdière a conjecturé dans [Reference Colin de VerdièreColin de Verdière, 1987] que la multiplicité de la deuxième valeur propre d’un opérateur de Schrödinger sur S est majorée par
$c(S)-1$
, et il montre qu’une telle majoration serait optimale. Grâce aux travaux successifs de Cheng [Reference ChengCheng, 1976], Besson [Reference BessonBesson, 1980], Colin de Verdière [Reference Colin de VerdièreColin de Verdière, 1987] et Sévennec [Reference SévennecSévennec, 1994] [Reference SévennecSévennec, 2002], cette conjecture est démontrée pour les surfaces closes de caractéristique d’Euler supérieure ou égale à -3.
Récemment, ce problème de multiplicité de valeurs propres a été étudié pour le spectre de Steklov, qui est le spectre d’opérateurs de type Dirichlet-Neumann sur les variétés à bord (voir [Reference Fraser and SchoenFraser et Schoen, 2012], [Reference JammesJammes, 2014], [Reference Karpukhin, Kokarev and PolterovichKarpukhin et al., 2014]). Dans [Reference JammesJammes, 2014], la conjecture de Colin de Verdière est étendue au spectre de Steklov en remplaçant le nombre chromatique par un autre invariant, spécifique aux surfaces à bord et baptisé nombre chromatique relatif dans [Reference JammesJammes, 2016] (voir la Définition 2 ci-dessous). Le but du présent article est de montrer que ce nouvel invariant est pertinent pour l’étude des plongements polyédraux tendus de surfaces à bord, pour lesquels les résultats de [Reference KühnelKühnel, 1980] ne sont que partiels.
Rappelons et précisons quelques définitions. Le nombre chromatique relatif diffère du nombre chromatique usuel par le fait qu’on impose aux graphes plongés dans la surface d’avoir tous leurs sommets sur le bord :
Définition 1 Soient G un graphe fini et S une surface compacte à bord. Un plongement de G dans S sera appelé plongement propre si ce plongement envoie tous les sommets de G sur
$\partial S$
.
Définition 2 [Reference JammesJammes, 2016]
Si S est une surface compacte à bord, on appelle nombre chromatique relatif de S, noté
$c_0(S)$
, la borne supérieure des nombres chromatiques des graphes finis qui admettent un plongement propre dans S.
Contrairement au nombre chromatique usuel, la valeur du nombre chromatique relatif n’est connue que pour certaines surfaces de petit genre, ou sous des hypothèses sur le nombre de composantes connexes du bord en genre quelconque. On rappelera ce qu’on sait à son sujet au Paragraphe 2.1.
Les plongements tendus admettent plusieurs définitions qui ne sont pas équivalentes pour les surfaces à bord :
Définition 3 Un plongement
$\varphi :S\to \mathbb {R}^n$
est p-tendu si pour tout demi-espace affine ouvert E, le morphisme d’homologie
$H_p(\varphi (S)\cap E)\to H_p(\varphi (S))$
à coefficients dans
$\mathbb Z_2$
induit par l’inclusion est injectif. Le plongement est tendu s’il est p-tendu pour tout p.
On s’intéressera en particulier aux plongements tendus et 0-tendus. Ces deux priopriétés sont équivalentes pour les surfaces closes ([Reference KühnelKühnel, 1995], lemme 2.5), mais pas les surfaces à bord (voir les rappels de la section suivante, en particulier le Lemme 2.7). La propriété dite TPP (two pieces property), définie pour une partie de
$\mathbb {R}^n$
par le fait que tout hyperplan affine la sépare en au plus deux parties connexes, est équivalente pour l’image du plongement
$\varphi $
à la
$0$
-tension.
Remarque 1.1 Bien que ces propriétés soient généralement définies pour des plongements euclidiens ou affines, elles sont en fait projectives: elles sont préservées par changement de carte affine tant que l’image du plongement ne rencontre pas l’hyperplan à l’infini.
Ces précisions étant données, on peut énoncer les deux résultats de cet article. Le premier majore la dimension de l’espace dans lequel une surface à bord peut se plonger de manière polyédrale, substantielle et tendue. La borne obtenue est analogue à celle donnée dans [Reference BanchoffBanchoff, 1965] par Banchoff pour les surfaces closes.
Théorème 1.2 Si une surface compacte à bord S admet un plongement polyédral substantiel et tendu dans
$\mathbb {R}^n$
, alors
$n\leq c_0(S)-1$
.
Le second théorème montre que dans l’inégalité précédente, l’égalité est atteinte pour des surfaces de petit genre. En l’état actuel des connaissances, on ne peut pas espérer démontrer l’égalité pour toute surface comme dans le cas des surfaces closes. En effet, le résultat de W. Kühnel s’appuie de manière cruciale sur la résolution du problème de Heawood (plus précisément sur l’exhibition de plongement de graphes complets dans les surfaces). Or, ce problème n’est pas encore résolu pour le nombre chromatique relatif.
Pour une surface close S donnée, on notera
$S_p$
la surface obtenue en enlevant p disques disjoints à S. Rappelons que les travaux de Kühnel ([Reference KühnelKühnel, 1980], théorème D), reformulés à l’aide du nombre chromatique relatif (voir le Théorème 2.1 de la section suivante), donnent l’égalité dans le Théorème 1.2 pour les surfaces
$S_p$
vérifiant
$p=1$
ou
$p\geq c(S)/2$
, quelle que soit la surface close S.
Théorème 1.3 Si S est une surface close orientable de genre inférieur ou égal à 2, ou non orientable de genre inférieur ou égal à 3, alors pour tout entier
$p>0$
,
$S_p$
admet un plongement polyédral substantiel et tendu dans
$\mathbb {R}^{c_0(S_p)-1}$
dont tous les sommets sont sur
$\partial S$
.
Pour les surfaces de genre immédiatement supérieur à ceux couverts par ce théorème, la connaissance du nombre chromatique relatif commence à être lacunaire.
Remarque 1.4 La contrainte que tous les sommets du plongement soient sur le bord de la surface n’est pas indispensable pour montrer que le Théorème 1.2 est optimal, et elle n’était pas présente dans les travaux de Kühnel (avec entre autres conséquences qu’on ne peut pas toujours reprendre telles quelles les constructions de Kühnel pour démontrer le Théorème 1.3). Elle est toutefois motivée d’une part par l’analogie avec la Définition 1, et d’autre part par le fait que sous cette hypothèse les propriétés de tension et 0-tension sont équivalentes (voir Lemme 2.7).
On commencera par rappeler dans la Section 2 quelques résultats sur le nombre chromatique relatif et les plongements polyédraux tendus. La Section 3 sera consacrée à la démonstration du Théorème 1.2. Enfin, le Théorème 1.3 fera l’objet de la Section 4.
2 Rappels
2.1 Le nombre chromatique relatif
On rassemble ici les résultats connus sur le nombre chromatique relatif d’une surface compacte à bord. Rappelons qu’on note
$c(S)$
le nombre chromatique usuel d’une surface close,
$c_0(S)$
le nombre chromatique relatif d’une surface à bord,
$\chi (S)$
la caractéristique d’Euler d’une surface compacte (avec ou sans bord), et que si S est close, on note
$S_p$
la surface à bord obtenue en enlevant p disques disjoints à S.
Le théorème qui suit donne les résultats généraux sur
$c_0$
, notamment l’encadrement de
$c_0(S_p)$
en fonction de
$c(S)$
.
Théorème 2.1 ([Reference JammesJammes, 2016], théorème 3.1)
Le nombre chromatique relatif
$c_0(S_p)$
satisfait les propriétés suivantes:
(1) C’est une fonction croissante de p.
(2) Il vérifie les inégalités
(1)
$$ \begin{align} c(S)-1\leq c_0(S_p)\leq \inf\left(c(S),\frac{5+\sqrt{25-24\chi(S)+24p}}2\right). \end{align} $$
-
(3)
$c_0(S_p)$
est le nombre de sommets du plus grand graphe complet proprement plongeable dans
$S_p$
. -
(4) On a
$c_0(S_1)=c(S)-1$
et
$c_0(S_p)=c(S)$
si
$p\geq (c(S)-1)/2$
.
Dans [Reference JammesJammes, 2016] sont aussi calculées les valeurs particulières du nombre chromatique relatif sur les surfaces de petit genre. Les Tables 1 et 2 ci-dessous rassemblent les valeurs connues du nombre chromatique relatif (le numéro de la ligne correspondant au nombre p de composantes de bord).
Remarque 2.2 Dans tous ces exemples sauf
$\mathbb P_2^2$
et
$\mathbb K_1^2$
, on a égalité avec
$$ \begin{align*}\textsf{inf} \left\{c(S), \left\lfloor\frac{5+\sqrt{25-24\chi(S)+24p}}2\right\rfloor\right\}.\end{align*} $$
2.2 Quelques propriétés des plongements polyédraux tendus
On va rappeler ici divers résultats, établis essentiellement par Banchoff et Kühnel, sur les plongements polyédraux tendus de surfaces. Certains concernent aussi des graphes, pour lesquels la propriété de 0-tension (ou de manière équivalente la TPP) est bien définie; cette propriété implique en particulier que l’image de chaque arête du graphe par un plongement 0-tendu est un segment.
La démonstration des cinq lemmes qui suivent est rappelée dans le Chapitre 2 de [Reference KühnelKühnel, 1995]. Pour ne pas alourdir les énoncés, on identifiera les surfaces et les graphes à leur plongement.
Les deux premiers lemmes lient la 0-tension d’une surface polyédrale à un graphe, le squelette de son enveloppe convexe dans le premier et son propre squelette dans le second.
Table 1 Nombre chromatique relatif des surfaces orientables de petit genre.
$\mathbb S^2$
|
$\mathbb T^2$
|
$\mathbb T^2\#\mathbb T^2$
|
$\#3\mathbb T^2$
|
$\#4\mathbb T^2$
|
|
|---|---|---|---|---|---|
| 1 | 3 | 6 | 7 | 8 | 9 |
| 2 | 4 | 6 | 8 | ? | 9 |
| 3 | 4 | 7 | 8 | 9 | 10 |
| 4 | 4 | 7 | 8 | 9 | 10 |
Table 2 Nombre chromatique relatif des surfaces nonorientables de petit genre.
$\mathbb P^2$
|
$\mathbb K^2$
|
$\#3\mathbb P^2$
|
$\#4\mathbb P^2$
|
$\#5\mathbb P^2$
|
$\#6\mathbb P^2$
|
$\#7\mathbb P^2$
|
$\#8\mathbb P^2$
|
$\#9\mathbb P^2$
|
|
|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 5 | 6 | 7 | 8 | 8 | 9 | 9 | 9 |
| 2 | 5 | 6 | 7 | ? | 8 | ? | 9 | ? | ? |
| 3 | 6 | 6 | 7 | 8 | 9 | 9 | 9 | ? | 10 |
| 4 | 6 | 6 | 7 | 8 | 9 | 9 | 10 | 10 | 10 |
Lemme 2.3 ([Reference BanchoffBanchoff, 1965], lemme 3.1)
Une surface polyédrale 0-tendue contient le 1-squelette de son enveloppe convexe.
Remarque 2.4 Une surface polyédrale est contenue dans l’enveloppe convexe de ses sommets. L’enveloppe convexe de la surface est donc l’enveloppe convexe de ses sommets; en particulier, elle a une structure polyédrale et le 1-squelette de cette enveloppe est bien défini.
Lemme 2.5 ([Reference KühnelKühnel, 1980], lemme 1)
Une surface polyédrale à faces convexes est 0-tendue si et seulement si son 1-squelette est 0-tendu.
L’énoncé qui suit permet de caractériser les graphes 0-tendus.
Lemme 2.6 ([Reference KühnelKühnel, 1980], lemme 3)
Un graphe G est 0-tendu si et seulement s’il vérifie les deux conditions qui suivent:
-
(i) le graphe G contient le 1-squelette de son enveloppe convexe ;
-
(ii) tout sommet de G qui n’est pas un point extrême de l’enveloppe convexe de G est contenu dans l’enveloppe convexe de ses voisins.
Un autre résultat de W. Kühnel précise la distinction entre plongements tendus et 0-tendus d’une surface. C’est ce lemme qui garantira que les plongements du Théorème 1.3 sont tendus.
Lemme 2.7 ([Reference KühnelKühnel, 1980], lemme 7)
Pour toute surface polyédrale S à bord, les propositions suivantes sont équivalentes:
-
(i) la surface S est tendue ;
-
(ii) la surface S est 0-tendue et tous les points extrêmes de son enveloppe convexe sont situés sur son bord.
Ce lemme implique en particulier qu’une surface polyédrale tendue à bord est contenue dans l’enveloppe convexe de son bord.
Enfin, un dernier énoncé, dû à Grünbaum, permettra d’établir un lien entre la dimension de l’espace ambiant et les graphes plongés dans la surface.
Lemme 2.8 [Reference GrünbaumGrünbaum, 1965]
Le 1-squelette d’un polytope convexe de dimension d admet une subdivision du graphe complet
$K_{d+1}$
comme sous-graphe.
Une subdivision d’un graphe est un graphe obtenu par insertion de sommets sur les arêtes.
3 Borne sur la codimension des plongement tendus
L’objet de cette section est de démontrer le Théorème 1.2 en utilisant les résultats rappelés dans la section précédente.
Considérons une surface compacte à bord S plongée de manière polyédrale, tendue et substantielle dans un espace
$\mathbb {R}^n$
et notons G le 1-squelette de son enveloppe convexe. Le graphe G est contenu dans S selon le Lemme 2.3.
Le lemme 2.7 assure que les sommets de G sont situés sur le bord de S, c’est-à-dire que G se plonge proprement dans S.
Comme le plongement de S est substantiel, son enveloppe convexe est un polytope de dimension n. Le graphe G contient donc une subdivision du graphe complet à
$n+1$
sommets
$K_{n+1}$
d’après le Lemme 2.8. Ce graphe
$K_{n+1}$
est donc lui-aussi proprement plongé dans S.
Enfin, le Théorème 2.1 affirme que
$c_0(S)$
est le nombre du sommet du plus grand graphe complet qui se plonge proprement dans S. On en déduit que
$n+1\leq c_0$
, ce qui conclut la démonstration du Théorème 1.2.
4 Construction de plongements tendus
4.1 Trois méthodes générales
Ce paragraphe est consacré au rappel d’une méthode de construction de plongement tendu partant d’une triangulation de la surface par un graphe complet et à la démonstration de deux résultats sur la réalisation tendue d’opérations topologiques sur une surface.
Nous commençons avec la construction d’un plongement tendu d’une surface (avec ou sans bord) qu’on suppose triangulée par un graphe complet. Cette technique, que nous qualifierons de construction canonique était déjà à la base des constructions de W. Kühnel.
Théorème 4.1 Soit S une surface compacte triangulée par un graphe complet
$K_{n+1}$
. Si S a un bord, on suppose de plus que
$K_{n+1}$
est proprement plongé dans S. Alors S admet un plongement substantiel polyédral tendu dans
$\mathbb {R}^n$
.
Démonstration On considère un simplexe à
$n+1$
sommets dans
$\mathbb {R}^n$
. Son 1-squelette, qu’on identifiera au graphe
$K_{n+1}$
, est 0-tendu d’après le Lemme 2.6. On construit un plongement de S dans
$\mathbb {R}^n$
en envoyant chaque face de la triangulation induite par
$K_{n+1}$
sur la 2-face correspondante du simplexe. Le 1-squelette de ce plongement de S est le 1-squelette du simplexe. Le plongement est donc 0-tendu selon le Lemme 2.5. Si la surface est close, cela suffit à conclure que le plongement est tendu ([Reference KühnelKühnel, 1995], lemme 2.5). Si la surface a un bord, on remarque que l’enveloppe convexe de son plongement est exactement le simplexe. Comme le graphe
$K_{n+1}$
est proprement plongé, les points extrêmes de cette enveloppe convexe son sur le bord de la surface, et on conclut grâce au Lemme 2.7.
Nous en venons maintenant à la démonstration de deux résultats sur la construction d’un plongement tendu d’une surface à partir du plongement d’une autre surface. Le premier concerne les surfaces obtenues par adjonction d’une anse sur le bord. Le second s’applique aux surfaces obtenues par suppression d’un disque et sera utilisé systématiquement dans la démonstration du Théorème 1.3 pour les surfaces ayant un grand nombre de composantes de bord.
Proposition 4.2 Soient S une surface polyédrale et a, b, c et d quatre points distincts de S tels que
$[ab]$
et
$[cd]$
soient deux arêtes du bord de S.
Si le plongement de S est 0-tendu (resp. tendu) et que l’intérieur du tétraèdre
$abcd$
ne rencontre pas ce plongement, alors une surface
$S'$
obtenue par l’adjonction d’une anse entre
$[ab]$
et
$[cd]$
admet un plongement polyédral 0-tendu (resp. tendu) dans le même espace.
Si de plus le plongement polyédral de S a tous ses sommets sur son bord, alors le plongement de
$S'$
aussi.
Démonstration Le principe de la démonstration, illustré par la Figure 1, consiste à ajouter l’anse dans le tétraèdre
$abcd$
en ajoutant deux sommets et quatre triangles à la surface S. On va d’abord traiter le cas où S est 0-tendu, en indiquant ensuite comment le cas tendu s’en déduit.
Figure 1 adjonction d’anse.
Les deux nouveaux sommets e et f doivent être placés de manière à ce que la surface obtenue reste 0-tendue. On peut les définir précisément en donnant leurs coordonnées barycentriques dans la base affine
$(a,b,c,d)$
. Le point e sera donné par les poids
$(2,1,2,1)$
et le point f par les poids
$(1,2,1,2)$
. On peut vérifier que e est dans l’enveloppe convexe de a, c et f, et de même f dans l’enveloppe convexe de b, d et e. La surface obtenue est bien plongée puisque S ne rencontre pas l’intérieur de
$abcd$
, et d’après les Lemmes 2.5 et 2.6, ce plongement est 0-tendu.
Si la surface S est tendue, les points extrêmes de son enveloppe convexe sont sur son bord selon le Lemme 2.7. Comme l’adjonction d’anse qu’on vient de construire n’ajoute pas de point extrême et que les quatre points a, b, c et d restent sur le bord, le plongement obtenu vérifie la même propriété et le plongement est donc tendu.
Remarque 4.3 On peut changer la surface obtenue (en particulier son nombre de composantes de bord) en permutant le rôle de a et b. Par exemple, en partant du ruban de Möbius, on peut obtenir soit le plan projectif privé de deux disques, soit la bouteille de Klein privée d’un disque.
On rappelle que si S est une surface close, on note
$S_p$
la surface S privée de p disques disjoints.
Proposition 4.4 Soit S une surface close. Si
$S_p$
admet un plongement substantiel 0-tendu (resp. tendu) dans
$\mathbb {R}^n$
, alors
$S_{p+1}$
aussi. Si de plus le plongement polyédral de
$S_p$
a tous ses sommets sur son bord, alors le plongement de
$S_{p+1}$
aussi.
Démonstration Topologiquement, l’opération consiste à enlever un disque à la surface
$S_p$
. On la réalise sur le plongement en enlevant un triangle dans une face du plongement comme sur la Figure 2: en ajoutant trois sommets dans une face trianglulaire du plongement de
$S_p$
, on découpe cette face en sept triangles, puis on enlève le triangle central (si le plongement de
$S_p$
n’a pas de face triangulaire, on peut en créer une en ajoutant une arête dans une face quelconque).
Figure 2 création d’une composante de bord.
On obtient ainsi un plongement polyédral de
$S_{p+1}$
. En outre, il est clair que les nouveaux sommets sont dans l’enveloppe convexe de leurs voisins, ce plongement est donc 0-tendu d’après le Lemme 2.6. En outre, ces sommets sont sur le bord de
$S_{p+1}$
.
Le cas où le plongement de
$S_p$
est tendu se traite comme dans la proposition précédente.
4.2 Démonstration du théorème 1.3
Il s’agit maintenant d’exhiber des plongements tendus pour toutes les surfaces annoncées par le Théorème 1.3. On va traiter les différentes surfaces closes S par caractéristique d’Euler décroissante.
4.2.1 La sphère
$\mathbb S^2$
Comme
$\mathbb S_1^2$
est un disque et que
$c_0(\mathbb S_1^2)=3$
, il suffit de plonger
$\mathbb S^2_1$
dans
$\mathbb {R}^2$
sous la forme d’un triangle.
La surface
$\mathbb S^2_2$
est un cylindre, qu’on peut plonger de manière tendue dans
$\mathbb {R}^3$
en le décomposant en trois rectangles comme sur la Figure 4.
Figure 4 le cylindre.
Le cas des surfaces
$\mathbb S^2_p$
,
$p\geq 3$
se traite en appliquant la Proposition 4.4.
4.2.2 Le plan projectif
$\mathbb P^2$
La surface
$\mathbb P^2_1$
est le ruban de Möbius, qui est triangulé par le graphe
$K_5$
comme le montre la Figure 5.
Figure 5 le ruban de Möbius.
On peut donc mettre en œuvre la construction canonique du Théorème 4.1. On obtient un plongement polyédral substantiel tendu du ruban de Möbius dans
$\mathbb {R}^4$
, les sommets étant bien sur le bord de la surface, comme sur la Figure 5.
Le plongement tendu de
$\mathbb P^2_2$
dans
$\mathbb {R}^4$
se construit à partir de celui du ruban de Möbius en appliquant l’une des Propositions 4.2 (cf. remarque 4.3) ou 4.4.
Le plan projectif
$\mathbb P^2$
est triangulé par un plongement du graphe complet
$K_6$
(c’est la projectivisation de l’icosaèdre). On obtient donc un plongement tendu de
$\mathbb P^2_3$
dans
$\mathbb {R}^5$
en partant du plongement canonique de
$\mathbb P^2$
et en appliquant trois fois la Remarque 4.5. Les plongements tendus de
$\mathbb P^2_p$
,
$p\geq 4$
s’obtiennent grâce à la Proposition 4.4.
4.2.3 Le tore
$\mathbb T^2$
Le tore est triangulé par un plongement de
$K_7$
(cette observation semble remonter à Möbius [Reference MöbiusMöbius, 1886]). En enlevant un sommet et les faces adjacentes, on obtient une triangulation de
$\mathbb T^2_1$
par le graphe
$K_6$
. La construction canonique fournit un plongement tendu de
$\mathbb T^2_1$
dans
$\mathbb {R}^5$
, tous les sommets étant sur le bord.
La surface
$\mathbb T^2_2$
est traitée en appliquant l’une des Propositions 4.2 ou 4.4.
Pour les surfaces
$\mathbb T^2_p$
,
$p\geq 3$
, on part du plongement canonique de
$\mathbb T^2$
dans
$\mathbb {R}^6$
, on place six sommets sur le bord en enlevant deux faces et le septième en appliquant la Remarque 4.5. On peut ensuite appliquer la Proposition 4.4.
4.2.4 La bouteille de Klein
$\mathbb K^2$
La surface
$\mathbb K^2_1$
s’obtient par adjonction d’anse à partir du ruban de Möbius. Son plongement tendu dans
$\mathbb {R}^4$
est donc donné par la Proposition 4.2.
Le plongement tendu de
$\mathbb K^2_2$
dans
$\mathbb {R}^5$
va s’obtenir en plaçant tous les sommets sauf un sur un bord, puis en appliquant la Remarque 4.5. Le graphe complet
$K_6$
se plonge dans la bouteille de Klein, par exemple comme sur la Figure 6 (en ignorant le sommet 7 et les arêtes adjacentes). Ce plongement découpe la surface en 10 triangles et un hexagone 145346 ayant deux sommets identiques. En découpant le pentagone 14536 dans cet hexagone, on obtient une triangulation avec 5 sommets sur le bord de la surface mais on crée une arête 36 qui apparaît déjà ailleurs, on ne peut donc pas construire directement un plongement de cette manière. On ajoute donc un sommet 7 dans le triangle 346 de sorte que le bord du quadrilatère 3467 ne rencontre pas d’autre arête. La Remarque 4.5 permet de placer le sommet 2 sur un autre bord.
Figure 6 la bouteille de Klein.
Pour
$\mathbb K^2_p$
,
$p\geq 3$
, on fait encore appel à la Proposition 4.4.
4.2.5 La surface de caractéristique -1
En notant S la surface close de caractéristique d’Euler égale à -1, un plongement tendu de la surface
$S_1$
peut s’obtenir à partir de
$\mathbb T^2_1$
par adjonction d’une anse non orientable.
Le cas de
$S_2$
se base sur un plongement de
$K_7$
dans S (figure 7, inspirée de la figure 4, p. 20 de [Reference KühnelKühnel, 1995])Ce plongement découpe S en 14 triangles et un hexagone ayant deux sommets identiques. On procède alors comme pour
$\mathbb K^2_2$
: on applique la construction canonique à la surface S privée du pentagone 12573, on ajoute un sommet dans le triangle 237 de manière à obtenir un plongement et on enlève le triangle 246 de manière à ce que tous les sommets soient sur le bord.
Figure 7 la surface de caractéristique -1.
Le cas de
$S_p$
,
$p\geq 3$
se traite comme précédemment.
4.2.6 La surface orientable de genre 2
Pour traiter le cas de la surface
$S=\mathbb T^2\#\mathbb T^2$
, on va utiliser une description combinatoire d’un plongement de
$K_8$
dans cette surface tirée de [Reference RingelRingel, 1974] (section 2.2, p. 23). Cette description est donnée par la Table 3 qui se lit comme suit: chaque ligne commence par l’indice d’un des sommets du graphe et donne ensuite la liste de ses voisins ordonnée circulairement, le sens de l’ordre étant induit par l’orientation de la surface.
Table 3 plongement du graphe
$K_8$
dans
$\mathbb T^2\#\mathbb T^2$
.
| 0. | 2 | 7 | 3 | 1 | 4 | 5 | 6 |
| 2. | 4 | 1 | 5 | 3 | 6 | 7 | 0 |
| 4. | 6 | 3 | 7 | 5 | 0 | 1 | 2 |
| 6. | 0 | 5 | 2 | 7 | 2 | 3 | 4 |
| 1. | 7 | 6 | 5 | 2 | 4 | 0 | 3 |
| 3. | 1 | 0 | 7 | 4 | 6 | 2 | 5 |
| 5. | 3 | 2 | 1 | 6 | 0 | 4 | 7 |
| 7. | 5 | 4 | 3 | 0 | 2 | 6 | 1 |
On peut vérifier que ce plongement contient deux quadrilatères, de sommets 0246 et 1357, les autres faces étant des triangles. Cette remarque permet de conclure immédiatement pour les surfaces
$S_p$
,
$p\geq 2$
: si on enlève les deux quadrilatères, on obtient la surface
$S_2$
, qui est alors triangulée par le graphe
$K_8$
, tous les sommets étant sur le bord. On peut alors utiliser la construction canonique. Les valeurs supérieures de p sont couvertes par la Proposition 4.4.
Passons maintenant au cas
$p=1$
. Le sommet 0 est adjacent à six triangles et au quadrilatère 0246. Si on enlève ces 7 faces, deux problèmes empêchent d’appliquer la construction canonique: d’une part, le bord obtenu est l’octogone 27314564, où le sommet 4 apparaît deux fois; d’autre part, il reste une face qui n’est pas triangulaire, le quadrilatère 1357.
Le premier problème se traite comme dans le cas de la bouteille de Klein: on ajoute un sommet 8 dans le triangle 246 contenu dans le quadrilatère 0246. Au lieu d’enlever le quadrilatère 0246 dans son ensemble, on enlève seulement le quadrilatère 0286 qu’il contient.
Le second problème n’est pas apparu avec les surfaces précédentes. Pour le résoudre, on ajoute un sommet 9 à l’intérieur du quadrilatère 1357 de manière à le trianguler, et on enlève le triangle 139. Le plongement tendu est obtenu en appliquant la construction canonique en dehors des deux quadrilatères, on place le sommet 8 comme indiqué précédemment et on ajoute le sommet 9 à l’intérieur du tétraèdre 1357. Le bord est alors l’ennéagone 273914568. Les sommets 1 à 7 sont des points extrêmes de l’enveloppe convexe et les sommets 8 et 9 sont bien dans l’enveloppe convexe de leurs voisins. On obtient donc bien un plongement tendu.
