Published online by Cambridge University Press: 20 November 2018
It is known that any non-archimedean Fréchet space of countable type is isomorphic to a subspace of 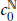 $c_{0}^{\mathbb{N}}$. In this paper we prove that there exists a non-archimedean Fréchet space
$c_{0}^{\mathbb{N}}$. In this paper we prove that there exists a non-archimedean Fréchet space 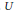 $U$ with a basis
$U$ with a basis 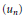 $({{u}_{n}})$ such that any basis
$({{u}_{n}})$ such that any basis 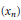 $({{x}_{n}})$ in a non-archimedean Fréchet space
$({{x}_{n}})$ in a non-archimedean Fréchet space 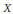 $X$ is equivalent to a subbasis
$X$ is equivalent to a subbasis 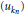 $({{u}_{kn}})$ of
$({{u}_{kn}})$ of 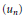 $({{u}_{n}})$. Then any non-archimedean Fréchet space with a basis is isomorphic to a complemented subspace of
$({{u}_{n}})$. Then any non-archimedean Fréchet space with a basis is isomorphic to a complemented subspace of 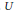 $U$. In contrast to this, we show that a non-archimedean Fréchet space
$U$. In contrast to this, we show that a non-archimedean Fréchet space 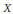 $X$ with a basis
$X$ with a basis 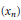 $({{x}_{n}})$ is isomorphic to a complemented subspace of
$({{x}_{n}})$ is isomorphic to a complemented subspace of 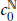 $c_{0}^{\mathbb{N}}$ if and only if
$c_{0}^{\mathbb{N}}$ if and only if 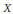 $X$ is isomorphic to one of the following spaces:
$X$ is isomorphic to one of the following spaces:  ${{c}_{0}},\,{{c}_{0}}\,\times \,{{\mathbb{K}}^{\mathbb{N}}},\,{{\mathbb{K}}^{\mathbb{N}}},\,c_{0}^{\mathbb{N}}$. Finally, we prove that there is no nuclear non-archimedean Fréchet space
${{c}_{0}},\,{{c}_{0}}\,\times \,{{\mathbb{K}}^{\mathbb{N}}},\,{{\mathbb{K}}^{\mathbb{N}}},\,c_{0}^{\mathbb{N}}$. Finally, we prove that there is no nuclear non-archimedean Fréchet space 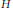 $H$ with a basis
$H$ with a basis 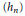 $({{h}_{n}})$ such that any basis
$({{h}_{n}})$ such that any basis 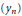 $({{y}_{n}})$ in a nuclear non-archimedean Fréchet space
$({{y}_{n}})$ in a nuclear non-archimedean Fréchet space 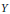 $Y$ is equivalent to a subbasis
$Y$ is equivalent to a subbasis 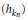 $({{h}_{kn}})$ of
$({{h}_{kn}})$ of 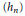 $({{h}_{n}})$.
$({{h}_{n}})$.