Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-07T00:22:03.593Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Uniqueness of Wave Operators Associated with Non-Trace Class Perturbations

Published online by Cambridge University Press:  20 November 2018

Jingbo Xia
Jingbo Xia*
Affiliation:
Department of Mathematics State University of New York at Buffalo Buffalo, New York 14260 USA, e-mail: jxia@acsu.buffalo.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Voiculescu has previously established the uniqueness of the wave operator for the problem of 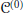${{\mathcal{C}}^{(0)}}$-perturbation of commuting tuples of self-adjoint operators in the case where the norm ideal 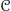$\mathcal{C}$ has the property 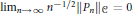${{\lim }_{n\,\to \,\infty }}\,{{n}^{-1/2}}\,\left\| {{P}_{n}} \right\|\mathcal{C}\,=\,0$, where 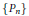$\{{{P}_{n}}\}$ is any sequence of orthogonal projections with rank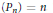$({{P}_{n}})\,=\,n$. We prove that the same uniqueness result holds true so long as 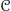$\mathcal{C}$ is not the trace class. (It is well known that there is no such uniqueness in the case of trace-class perturbation.)

Keywords

47A4047B10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 1 , 01 March 2004 , pp. 144 - 151
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Carey, R. and Pincus, J., Unitary equivalence modulo the trace class for self-adjoint operators. Amer. J. Math. 98 (1976), 481–514.Google Scholar
[2] Carey, R. and Pincus, J., Mosiacs, principal functions, and mean motion in von Neumann algebra. Acta Math. 138 (1977), 153–218.Google Scholar
[3] David, G. and Voiculescu, D., s-Numbers of singular integrals for the invariance of absolutely continuous spectra in fractional dimensions. J. Funct. Anal. 94 (1990), 14–26.Google Scholar
[4] Gohberg, I. and Krein, M., Introduction to the theory of linear nonselfadjoint operators. Amer.Math. Soc., Transl. Math.Monogr. 18, Providence, 1969.Google Scholar
[5] Kato, T., Perturbation of continuous spectra by trace class operators. Proc. Japan Acad. 33 (1957), 260–264.Google Scholar
[6] Kato, T., Perturbation theory for linear operators. Springer-Verlag, New York, 1976.Google Scholar
[7] Rosenblum, M., Perturbations of continuous spectrum and unitary equivalence. Pacific J. Math. 7 (1957), 997–1010.Google Scholar
[8] Reed, M. and Simon, B., Methods of modern mathematical physics, III, Scattering theory. Academic Press, New York, 1979.Google Scholar
[9] Voiculescu, D., Some results on norm-ideal perturbations of Hilbert space operators. J. Operator Theory 2 (1979), 3–37.Google Scholar
[10] Voiculescu, D., Some results on norm-ideal perturbations of Hilbert space operators. II. J. Operator Theory 5 (1981), 77–100.Google Scholar
[11] Voiculescu, D., On the existence of quasicentral approximate units relative to normed ideals. Part I. J. Funct. Anal. 91 (1990), 1–36.Google Scholar
[12] Xia, J., An analogue of the Kato-Rosenblum theorem for commuting tuples of self-adjoint operators. Comm. Math. Phys. 198 (1998), 187–197.Google Scholar
[13] Xia, J., Trace-class perturbation and strong convergence: wave operators revisited. Proc. Amer.Math. Soc. 128 (2000), 3519–3522.Google Scholar