Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-06T18:48:26.623Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Exponent of the NK0-Groups of Virtually Infinite Cyclic Groups

Published online by Cambridge University Press:  20 November 2018

Francis X. Connolly  and
Stratos Prassidis
Francis X. Connolly
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, IN 46556, USA, e-mail: connolly.1.@nd.edu
Stratos Prassidis
Affiliation:
Department of Mathematics & Statistics, Canisius College, Buffalo, NY 14208, USA, e-mail: prasside@canisius.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is known that the $K$-groups that appear in the calculation of the $K$-theory of a large class of groups can be computed from the $K$-theory of their virtually infinite cyclic subgroups. On the other hand, Nil-groups appear to be the obstacle in calculations involving the $K$-theory of the latter. The main difficulty in the calculation of Nil-groups is that they are infinitely generated when they do not vanish. We develop methods for computing the exponent of 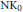$\text{N}{{\text{K}}_{0}}$-groups that appear in the calculation of the 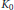${{K}_{0}}$-groups of virtually infinite cyclic groups.

Keywords

18F2519A31
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 2 , 01 June 2002 , pp. 180 - 195
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Bass, H., Algebraic K-theory. Benjamin, 1968.Google Scholar
[2] Bass, H., Unitary algebraic K-theory. Proceedings of the Conference in Algebraic K-theory (Battelle, 1972), Springer Lecture Notes in Math. 343 (1973), 343–1973.Google Scholar
[3] Carter, D. W., Localization in lower K-theory. Comm. Algebra 8 (1980), 8–1980.Google Scholar
[4] Cassou-Noguès, P., Groupe des classes de l’algèbre d’un groupe métacyclique. J. Algebra 41 (1976), 41–1976.Google Scholar
[5] Connolly, F. X. and daSilva, M. O. M., The groups NrK0(Zπ) are finitely generated Z[Nr]-modules if π is a finite group. K-theory 9 (1995), 9–1995.Google Scholar
[6] Connolly, F. X. and Kózniewski, T., Nil-groups in K-theory and surgery theory. Forum Math. 7 (1995), 7–1995.Google Scholar
[7] Connolly, F. X. and Prassidis, S., On the exponent of the equivariant topological K-groups. Preprint.Google Scholar
[8] Davis, J. F. and Vajiac, B., Algebraic K-theory of virtually cyclic groups. In preparation.Google Scholar
[9] Dicks, W. and Dunwoody, M. J., Groups acting on graphs. Cambridge Stud. Adv. Math. 17, Cambridge University Press, 1989.Google Scholar
[10] Farrell, F. T. and Hsiang, W. C., A formula for K1Rα[T]. Applications of Categorical Algebra, Proc. Symp. Pure Math. 17, Amer. Math. Soc., 1970, 192–218.Google Scholar
[11] Farrell, F. T. and Jones, J. E., Isomorphism conjectures in algebraic K-theory. J. Amer. Math. Soc. 6 (1993), 6–1993.Google Scholar
[12] Farrell, F. T. and Jones, J. E., The lower algebraic K-theory of virtually infinite cyclic groups. K-theory 9 (1995), 9–1995.Google Scholar
[13] Frölich, A., Keating, M. E. and Wilson, S. M. J., The class groups of quartenion and dihedral 2-groups. Mathematika 21, 64–71 (1974).Google Scholar
[14] Kervaire, M. A. and Murphy, M. P., On the projective class group of cyclic groups of prime power order. Comment. Math. Helv. 52 (1977), 52–1977.Google Scholar
[15] Munkholm, H. J. and Prassidis, S., Waldhausen's Nil-groups and continuously controlled K-theory. Fund. Math. 161(1999), 217–224.Google Scholar
[16] Munkholm, H. J. and Prassidis, S., On the vanishing of certain K-theory Nil-groups. Proceedings of BCAT 1998 (Barcelona, 1998), to appear.Google Scholar
[17] Pineda, D. J. and Prassidis, S., On the lower Waldhausen's Nil-groups. Forum Math., to appear.Google Scholar
[18] Prassidis, S., A split exact sequence of equivariant K-groups of virtually nilpotent groups. K-theory 11 (1997), 11–1997.Google Scholar
[19] Quillen, D., Higher algebraic K-theory. Springer Lecture Notes in Math. 341 (1973), 341–1973.Google Scholar
[20] Ranicki, A., Lower K- and L-Theory. Cambridge University Press, Cambridge, 1992.Google Scholar
[21] Serre, J.-P., Classes des corps cyclotomiques (d’après K. Iwasava). Séminaire Bourbaki 5, Exp. No. 174, Soc. Math. France, Paris, 1955, 83–93.Google Scholar
[22] Ullom, S. V., Fine structure of class groups of cyclic p-groups. J. Algebra 49 (1977), 49–1977.Google Scholar
[23] Waldhausen, F., Whitehead groups of generalized free products. Proceedings of the Conference in Algebraic K-theory (Battelle, 1972), Springer Lecture Notes in Mathematics 342, 1973.Google Scholar
[24] Waldhausen, F., Algebraic K-theory of generalized free products. Ann. of Math. 108 (1978), 108–1978.Google Scholar