Published online by Cambridge University Press: 20 November 2018
We recently introduced a weighted Banach algebra 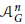 $\mathcal{A}_{G}^{n}$ of functions that are holomorphic on the unit disc
$\mathcal{A}_{G}^{n}$ of functions that are holomorphic on the unit disc 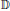 $\mathbb{D}$, continuous up to the boundary, and of the class
$\mathbb{D}$, continuous up to the boundary, and of the class 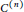 ${{C}^{\left( n \right)}}$ at all points where the function
${{C}^{\left( n \right)}}$ at all points where the function 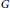 $G$ does not vanish. Here,
$G$ does not vanish. Here, 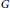 $G$ refers to a function of the disc algebra without zeros on
$G$ refers to a function of the disc algebra without zeros on 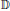 $\mathbb{D}$. Then we proved that all closed ideals in
$\mathbb{D}$. Then we proved that all closed ideals in 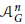 $\mathcal{A}_{G}^{n}$ with at most countable hull are standard. In this paper, on the assumption that
$\mathcal{A}_{G}^{n}$ with at most countable hull are standard. In this paper, on the assumption that 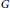 $G$ is an outer function in
$G$ is an outer function in 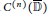 ${{C}^{\left( n \right)}}\,\left( {\bar{\mathbb{D}}} \right)$ having infinite roots in
${{C}^{\left( n \right)}}\,\left( {\bar{\mathbb{D}}} \right)$ having infinite roots in 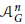 $\mathcal{A}_{G}^{n}$ and countable zero set
$\mathcal{A}_{G}^{n}$ and countable zero set 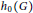 ${{h}_{o}}\left( G \right)$, we show that all the closed ideals
${{h}_{o}}\left( G \right)$, we show that all the closed ideals  $I$ with hull containing
$I$ with hull containing 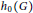 ${{h}_{o}}\left( G \right)$ are standard.
${{h}_{o}}\left( G \right)$ are standard.