Hostname: page-component-6bf8c574d5-h6jzd Total loading time: 0.001 Render date: 2025-02-14T10:01:37.229Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Theorem of Kawamoto on Normal Bases of Rings of Integers, II

Published online by Cambridge University Press:  20 November 2018

Humio Ichimura
Humio Ichimura*
Affiliation:
Faculty of Science, Ibaraki University, Bunkyo 2-1-1, Mito 310-8512, Japan e-mail: hichimur@mx.ibaraki.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 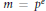$m={{p}^{e}}$ be a power of a prime number 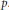$p$. We say that a number field 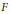$F$ satisfies the property 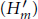$\left( {{H}^{'}}_{m} \right)$ when for any 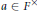$a\in {{F}^{\times }}$, the cyclic extension 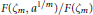$F\left( {{\zeta }_{m}},{{a}^{1/m}} \right)/F\left( {{\zeta }_{m}} \right)$ has a normal 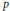$p$-integral basis. We prove that 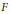$F$ satisfies 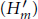$\left( {{H}^{'}}_{m} \right)$ if and only if the natural homomorphism 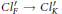$C{{l}^{'}}_{F}\to C{{l}^{'}}_{K}$ is trivial. Here 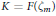$K=F\left( {{\zeta }_{m}} \right)$, and 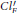$C{{l}^{'}}_{F}$ denotes the ideal class group of 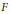$F$ with respect to the 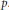$p$-integer ring o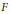f $F$.

Keywords

11R33
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 4 , 01 December 2005 , pp. 576 - 579
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Fröhlich, A. and Taylor, M. J., Algebraic Number Theory. Cambridge Studies in Advanced Mathematics 27, Cambridge Univ. Press, Cambridge, 1993.Google Scholar
[2] Ayala, E. J. Gómez, Bases normales d’entiers dans les extensions de Kummer de degré premier. J. Théor. Nombres Bordeaux 6(1994), 95–116.Google Scholar
[3] Greither, C., Cyclic Galois Extensions of Commutative Rings. Lecture Notes in Mathematics 1534, Springer-Verlag, Berlin, 1992.Google Scholar
[4] Ichimura, H., Note on the ring of integers of a Kummer extension of prime degree. II. Proc. Japan Acad. Ser A Math. Sci. 77(2001), 25–28.Google Scholar
[5] Ichimura, H., Note on the ring of integers of a Kummer extension of prime degree. IV. Proc. Japan Acad. Ser A Math. Sci. 77(2001), 92–94.Google Scholar
[6] Ichimura, H., On the ring of integers of a tame Kummer extension over a number field. J. Pure Appl. Algebra 87(2004), 169–182.Google Scholar
[7] Ichimura, H., On a theorem of Kawamoto on normal bases of rings of integers. Tokyo J. Math. 27(2004), 527–540.Google Scholar
[8] Ichimura, H., On the ring of p-integers of a cyclic p-extension over a number field. To appear in J. Théor. Nombres Bordeaux.Google Scholar
[9] Kawamoto, F., On normal integral bases. Tokyo J. Math. 7(1984), 221–231.Google Scholar
[10] Kawamoto, F., Remark on “On normal integral basis”. Tokyo J. Math. 8(1985), 275.Google Scholar