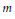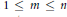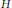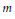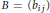Suppose $m$ and $n$ are integers such that $1\,\le \,m\,\le \,n$. For a subgroup $H$ of the symmetric group ${{S}_{m}}$ of degree $m$, consider the generalized matrix function on $m\,\times \,m$ matrices $B\,=\,\left( {{b}_{ij}} \right)$ defined by 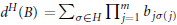${{d}^{H}}\left( B \right)\,=\,\sum{_{\sigma \in H}\,\prod{_{j=1}^{m}}\,{{b}_{j\sigma \left( j \right)}}}$ and the generalized numerical range of an $n\,\times \,n$ complex matrix 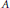$A$ associated with 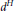${{d}^{H}}$ defined by

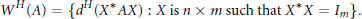$${{W}^{H}}\left( A \right)\,=\,\left\{ {{d}^{H}}\left( {{X}^{*}}\,AX \right)\,:\,X\,is\,n\,\times \,m\,\text{such}\,\text{that}\,{{X}^{*}}X\,\text{=}\,{{\text{I}}_{m}} \right\}$$

It is known that 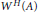${{W}^{H}}\left( A \right)$ is convex if 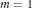$m\,=\,1$ or if 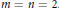$m\,=\,n\,=\,2$. We show that there exist normal matrices 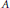$A$ for which 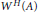${{W}^{H}}\left( A \right)$ is not convex if 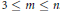$3\,\le \,m\,\le \,n$. Moreover, for 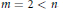$m\,=\,2\,<\,n$, we prove that a normal matrix 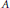$A$ with eigenvalues lying on a straight line has convex 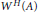${{W}^{H}}\left( A \right)$ if and only if 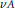$vA$ is Hermitian for some nonzero 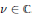$v\,\in \,\mathbb{C}$. These results extend those of Hu, Hurley and Tam, who studied the special case when 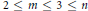$2\,\le \,m\,\le \,3\,\le \,n$ and 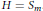$H\,=\,{{S}_{m}}$.