No CrossRef data available.
Article contents
A New Sufficient Condition for a Graph To Be (g, f, n)-Critical
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $G$ be a graph of order
$G$ be a graph of order  $p$, let
$p$, let  $a$,
$a$,  $b$, and
$b$, and  $n$ be nonnegative integers with
$n$ be nonnegative integers with 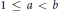 $1\,\le \,a\,<\,b$, and let
$1\,\le \,a\,<\,b$, and let  $g$ and
$g$ and  $f$ be two integer-valued functions defined on
$f$ be two integer-valued functions defined on 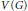 $V\left( G \right)$ such that
$V\left( G \right)$ such that 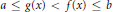 $a\,\le \,g\left( x \right)\,<\,f\left( x \right)\,\le \,b$ for all
$a\,\le \,g\left( x \right)\,<\,f\left( x \right)\,\le \,b$ for all 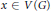 $x\,\in \,V\left( G \right)$. A
$x\,\in \,V\left( G \right)$. A 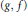 $\left( g,\,f \right)$-factor of graph
$\left( g,\,f \right)$-factor of graph  $G$ is a spanning subgraph
$G$ is a spanning subgraph  $F$ of
$F$ of  $G$ such that
$G$ such that 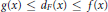 $g\left( x \right)\,\le \,{{d}_{F}}\left( x \right)\,\le \,f\left( x \right)$ for each
$g\left( x \right)\,\le \,{{d}_{F}}\left( x \right)\,\le \,f\left( x \right)$ for each 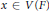 $x\,\in \,V\left( F \right)$. Then a graph
$x\,\in \,V\left( F \right)$. Then a graph  $G$ is called
$G$ is called  $\left( g,\,f,\,n \right)$-critical if after deleting any
$\left( g,\,f,\,n \right)$-critical if after deleting any  $n$ vertices of
$n$ vertices of  $G$ the remaining graph of
$G$ the remaining graph of  $G$ has a
$G$ has a 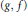 $\left( g,\,f \right)$-factor. The binding number
$\left( g,\,f \right)$-factor. The binding number 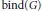 $\text{bind}\left( G \right)$ of
$\text{bind}\left( G \right)$ of  $G$ is the minimum value of
$G$ is the minimum value of 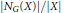 $\left| {{N}_{G}}\left( X \right) \right|/\left| X \right|$ taken over all non-empty subsets
$\left| {{N}_{G}}\left( X \right) \right|/\left| X \right|$ taken over all non-empty subsets 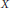 $X$ of
$X$ of 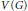 $V\left( G \right)$ such that
$V\left( G \right)$ such that  ${{N}_{G}}\left( X \right)\,\ne \,V\left( G \right)$. In this paper, it is proved that
${{N}_{G}}\left( X \right)\,\ne \,V\left( G \right)$. In this paper, it is proved that  $G$ is a
$G$ is a  $\left( g,\,f,\,n \right)$-critical graph if
$\left( g,\,f,\,n \right)$-critical graph if
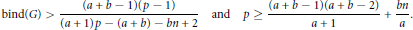 $$\text{bind}\left( G \right)\,>\,\frac{\left( a\,+\,b\,-\,1 \right)\left( p\,-\,1 \right)}{\left( a\,+\,1 \right)p\,-\,\left( a\,+b \right)\,-\,bn\,+\,2}\,\text{and}\,\text{p}\ge \,\frac{\left( a\,+\,b\,-\,1 \right)\left( a\,+\,b\,-2 \right)}{a\,+\,1}\,+\,\frac{bn}{a}.$$
$$\text{bind}\left( G \right)\,>\,\frac{\left( a\,+\,b\,-\,1 \right)\left( p\,-\,1 \right)}{\left( a\,+\,1 \right)p\,-\,\left( a\,+b \right)\,-\,bn\,+\,2}\,\text{and}\,\text{p}\ge \,\frac{\left( a\,+\,b\,-\,1 \right)\left( a\,+\,b\,-2 \right)}{a\,+\,1}\,+\,\frac{bn}{a}.$$
Furthermore, it is shown that this result is best possible in some sense.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010


