Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-11T00:20:22.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Local Complexity of Delone Sets and Crystallinity

Published online by Cambridge University Press:  20 November 2018

Jeffrey C. Lagarias  and
Peter A. B. Pleasants
Jeffrey C. Lagarias
Affiliation:
AT&T Labs—Research Florham Park, New Jersey 07932 U.S.A., e-mail: jcl@research.att.com
Peter A. B. Pleasants
Affiliation:
Department of Mathematics The University of Queensland QLD 4072 Australia, e-mail: pabp@maths.uq.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper characterizes when a Delone set $X$ in 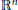${{\mathbb{R}}^{n}}$ is an ideal crystal in terms of restrictions on the number of its local patches of a given size or on the heterogeneity of their distribution. For a Delone set $X$, let 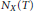${{N}_{X}}\left( T \right)$ count the number of translation-inequivalent patches of radius 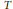$T$ in $X$ and let 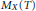${{M}_{X}}\left( T \right)$ be the minimum radius such that every closed ball of radius 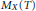${{M}_{X}}\left( T \right)$ contains the center of a patch of every one of these kinds. We show that for each of these functions there is a “gap in the spectrum” of possible growth rates between being bounded and having linear growth, and that having sufficiently slow linear growth is equivalent to $X$ being an ideal crystal.

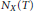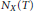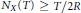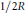Explicitly, for ${{N}_{X}}\left( T \right)$, if $R$ is the covering radius of $X$ then either ${{N}_{X}}\left( T \right)$ is bounded or ${{N}_{X}}\left( T \right)\,\ge \,T/2R$ for all $T\,>\,0$. The constant $1/2R$ in this bound is best possible in all dimensions.

For 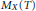${{M}_{X}}\left( T \right)$, either 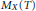${{M}_{X}}\left( T \right)$ is bounded or ${{M}_{X}}\left( T \right)\ge T/3$ for all $T\,>\,0$. Examples show that the constant 1/3 in this bound cannot be replaced by any number exceeding 1/2. We also show that every aperiodic Delone set $X$ has ${{M}_{X}}\left( T \right)\,\ge \,c\left( n \right)T$ for all $T\,>\,0$, for a certain constant $c\left( n \right)$ which depends on the dimension $n$ of $X$ and is $>\,1/3$ when $n\,>\,1$.

Keywords

52C2352C17aperiodic setDelone setpacking-covering constantsphere packing
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 4 , 01 December 2002 , pp. 634 - 652
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Alessandri, P. and Berthé, V., Three distance theorems and combinatorics on words. Enseign. Math. 44 (1998), 103–132.Google Scholar
[2] Berthé, V. and Vuillon, L., Tilings and rotations on the torus: a two-dimensional generalization of Sturmian sequences. Discrete Math. 223 (2000), 27–53.Google Scholar
[3] Berthé, V. and Vuillon, L., Suites doubles de basse complexité. J. Théorie Nombres, Bordeaux 12 (2000), 179–208.Google Scholar
[4] Conway, J. H. and Sloane, N. J. A., Sphere Packings, Lattices and Groups. Third Edition, Springer, New York, 1999.Google Scholar
[5] Coven, E. M. and Hedlund, G. A., Sequences with minimal block growth.Math. Systems Theory 7 (1973), 138–153.Google Scholar
[6] Delone, B. N. [Delaunay, B. N.], Dolbilin, N. P., Shtogrin, M. I. and Galiulin, R. V., A local criterion for regularity of a system of points. Sov. Math. Dokl. (2) 17 (1976), 319–322.Google Scholar
[7] Dolbilin, N. P., Lagarias, J. C. and Senechal, M., Multiregular point systems. Discrete Comput. Geom. 20 (1998), 477–498.Google Scholar
[8] Dolbilin, N. P. and Pleasants, P. A. B., Aperiodic sets with few isometry patches. in preparation.Google Scholar
[9] Engel, P., Geometric Crystallography. In: Handbook of Convex Geometry, Volume B, (eds. P. M. Gruber and J. M.Wills), North-Holland, Amsterdam, 1993, 989–1042.Google Scholar
[10] Epifanio, C., Koskas, M. and Mignosi, F., On a conjecture on bidimensional words. Theoret. Comput. Sci., (2002), to appear.Google Scholar
[11] Ferenczi, S., Rank and symbolic complexity. Ergodic Theory Dynam. Systems 16 (1996), 663–682.Google Scholar
[12] Gruber, P. M. and Lekkerkerker, C. G., Geometry of Numbers, Second Edition. North-Holland, Amsterdam 1987.Google Scholar
[13] Grünbaum, B. and Shephard, G. C., Tilings and Patterns. W. H. Freeman & Co., New York, 1987.Google Scholar
[14] Lagarias, J. C., Meyer's concept of quasicrystal and quasiregular sets. Comm. Math. Phys. 179 (1996), 365–376.Google Scholar
[15] Lagarias, J. C., Geometric models for quasicrystals I. Delone sets of finite type. Discrete Comput. Geom. 21 (1999), 161–191.Google Scholar
[16] Lagarias, J. C., Geometric models for quasicrystals II. Local rules under isometries. Discrete Comput. Geom. 21 (1999), 345–372.Google Scholar
[17] Lagarias, J. C. and Pleasants, P. A. B., Repetitive Delone Sets and Quasicrystals. Ergodic Theory Dynam. Systems, to appear.Google Scholar
[18] Lothaire, M., Combinatorics on Words. Cambridge Univ. Press, Cambridge, 1983.Google Scholar
[19] Moody, R. V., Meyer sets and their duals. In: [20], 1997, 403–441.Google Scholar
[20] Moody, R. V., Ed., The Mathematics of Long-Range Aperiodic Order. NATO ASI Series C 489, Kluwer, Dordrecht, 1997.Google Scholar
[21] Morse, M. and Hedlund, G. A., Symbolic dynamics. Amer. J. Math. 60 (1938), 815–866.Google Scholar
[22] Morse, M. and Hedlund, G. A., Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.Google Scholar
[23] Pleasants, P. A. B., Designer quasicrystals: cut-and-project sets with pre-assigned properties. In: Directions in Mathematical Quasicrystals, (eds. M. Baake and R. V. Moody), CRM Monograph Series, Amer. Math. Soc., Providence, Rhode Island, 2000, 95–141.Google Scholar
[24] Radin, C., Global order from local sources. Bull. Amer.Math. Soc. 25 (1991), 335–364.Google Scholar
[25] Radin, C. and Wolff, M., Space tilings and local isomorphism. Geom. Dedicata 42 (1992), 355–360.Google Scholar
[26] Ryshkov, S. S., Density of an (r, R)-system. Mat. Zametki 16 (1974), 447–454.Google Scholar
[27] Sander, J. W. and Tijdeman, R., The complexity of functions on lattices. Theoret. Comput. Sci. 246 (2000), 195–225.Google Scholar
[28] Sander, J. W. and Tijdeman, R., The rectangle complexity of functions on two-dimensional lattices. Theoret. Comput. Sci. 270 (2002), 857–863.Google Scholar
[29] Sander, J. W. and Tijdeman, R., Low complexity functions and convex sets in Zk . Math. Z. 233 (2000), 205–218.Google Scholar
[30] Senechal, M., Quasicrystals and Geometry. Cambridge University Press, Cambridge 1995, corrected reprint, 1996.Google Scholar
[31] Series, C., The geometry of Markoff numbers. Math. Intelligencer (3) 7 (1985), 20–29.Google Scholar
[32] Solomyak, B., Dynamics of self-similar tilings. Ergodic Theory Dynam. Systems 17 (1997), 695–738.Google Scholar
[33] Zong, C., Sphere packings. Springer, New York, 1999.Google Scholar