Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-06T07:55:12.223Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Maps on C*-Algebras Preserving the Set of Operators that are Invertible in

Published online by Cambridge University Press:  20 November 2018

Sang Og Kim  and
Choonkil Park
Sang Og Kim
Affiliation:
Department of Mathematics, Hallym University, Chuncheon 200-702, Republic of Koreae-mail: sokim@hallym.ac.kr
Choonkil Park
Affiliation:
Department of Mathematics, Hanyang University, Seoul 133-791, Republic of Koreae-mail: baak@hanyang.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For 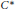${{C}^{*}}$-algebras 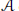$\mathcal{A}$ of real rank zero, we describe linear maps 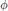$\phi $ on 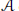$\mathcal{A}$ that are surjective up to ideals $\mathcal{J}$, and 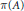$\text{ }\pi \text{ (}A\text{)}$ is invertible in 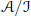$\mathcal{A}/\mathcal{J}$ if and only if 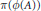$\text{ }\pi \text{ (}\phi (A))$ is invertible in 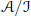$\mathcal{A}/\mathcal{J}$, where 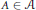$A\,\in \,\mathcal{A}$ and 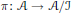$\text{ }\pi \text{ }\text{:}\mathcal{A}\to \mathcal{A}\text{/}\mathcal{J}$ is the quotient map. We also consider similar linear maps preserving zero products on the Calkin algebra.

Keywords

47B4847A1046H10preserversJordan automorphismsinvertible operatorszero products
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 1 , 01 March 2011 , pp. 141 - 146
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Aupetit, B., A primer on spectral theory. Universitext, Springer-Verlag, New York, 1991.Google Scholar
[2] Aupetit, B., Spectrum-preserving linear mappings between Banach algebras or Jordan-Banach algebras. J. London Math. Soc. 62(2000), no. 3, 917–924. doi:10.1112/S0024610700001514Google Scholar
[3] Brown, L. G. and Pedersen, G. K., C*-algebras of real rank zero. J. Funct. Anal. 99(1991), no. 1, 131–149. doi:10.1016/0022-1236(91)90056-BGoogle Scholar
[4] Chebotar, M. A., Ke, W.-F., Lee, P.-H., and Wong, N.-C., Mappings preserving zero products. Studia Math. 155(2003), no. 1, 77–94. doi:10.4064/sm155-1-6Google Scholar
[5] Dieudonné, J., Sur une généralisation du groupe orthogonal à quatre variables. Arch. Math. 1(1949), 282–287. doi:10.1007/BF02038756Google Scholar
[6] Farah, I., All automorphisms of the Calkin algebra are inner. arXiv:0705.3085v1 [math.OA].Google Scholar
[7] Guterman, A., Li, C.-K., and Šemrl, P., Some general techniques on linear preserver problems. Linear Algebra Appl. 315(2000), no. 1–3, 61–81. doi:10.1016/S0024-3795(00)00119-1Google Scholar
[8] Harrison, L. A. and Kadison, R. V., Affine mappings of invertible operators. Proc. Amer. Math. Soc. 124(1996), no. 8, 2415–2422. doi:10.1090/S0002-9939-96-03445-4Google Scholar
[9] Kaplansky, I., Algebraic and analytic aspects of operator algebras. Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics, 1, American Mathematical Society, Providence, RI, 1970.Google Scholar
[10] Marcus, M. and Purves, R., Linear transformations on algebras of matrices: the invariance of the elementary symmetric functions. Canad. J. Math. 11(1959), 383–396.Google Scholar
[11] Mbekhta, M., Linear maps preserving the set of Fredholm operators. Proc. Amer. Math. Soc. 135(2007), no. 11, 3613–3619. doi:10.1090/S0002-9939-07-08874-0Google Scholar
[12] Pearcy, C. and Topping, D., Sums of small numbers of idempotents. Michigan Math. J. 14(1967), 453–465. doi:10.1307/mmj/1028999848Google Scholar
[13] Phillips, N. C. and Weaver, W., The Calkin algebra has outer automorphisms. Duke Math. J. 139(2007), no. 1, 185–202. doi:10.1215/S0012-7094-07-13915-2Google Scholar
[14] Sourour, A. R., Invertibility preserving linear maps on ℒ(X) . Trans. Amer. Math. Soc. 348(1996), no. 1, 13–30. doi:10.1090/S0002-9947-96-01428-6Google Scholar