Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-06T03:37:57.727Z Has data issue: false hasContentIssue false
  • English
  • Français

Levi's Problem for Pseudoconvex Homogeneous Manifolds

Published online by Cambridge University Press:  20 November 2018

Bruce Gilligan
Bruce Gilligan*
Affiliation:
Dept. of Mathematics & Statistics, University of Regina, Regina, S4S 0A2 e-mail: gilligan@math.uregina.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose 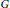$G$ is a connected complex Lie group and 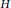$H$ is a closed complex subgroup. Then there exists a closed complex subgroup $J$ of 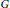$G$ containing 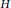$H$ such that the fibration $\pi :G/H\to $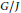$G/J$ is the holomorphic reduction of $G/H$i.e., 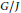$G/J$ is holomorphically separable and 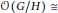$\mathcal{O}(G/H)\cong $${{\pi }^{*}}\mathcal{O}(G/J)$. In this paper we prove that if $G/H$ is pseudoconvex, i.e., if $G/H$ admits a continuous plurisubharmonic exhaustion function, then 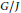$G/J$ is Stein and 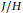$J/H$ has no non-constant holomorphic functions.

Keywords

32M1032U1032A1032Q28complex homogeneous manifoldplurisubharmonic exhaustion functionholomorphic reductionStein manifoldRemmert reductionHirschowitz annihilator
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 4 , 01 December 2017 , pp. 736 - 746
Creative Commons
Creative Common License - CCCreative Common License - BY
© Canadian Mathematical Society 2017 This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Akhiezer, D. N., Lie group actions in complex analysis. Aspects of Mathematics, E27, Friedr. Vieweg & Sohn, Braunschweig, 1995. http://dx.doi.org/10.1007/978-3-322-80267-5 Google Scholar
[2] Auslander, L., On radicals of discrete subgroups of Lie groups. Amer. J. Math. 85(1963), 145–150. http://dx.doi.org/10.2307/2373206 Google Scholar
[3] Auslander, L. and R. Tolimieri, On a conjecture of Mostow G. D. and the structure solvmanifolds. Bull. Amer. Math. Soc. 75(1969), 1330–1333. http://dx.doi.org/10.1090/S0002-9904-1969-12416-X Google Scholar
[4] Barth, W. and M. Otte, Uber fast-uniforme Untergruppen komplexer Liegruppen und auflosbare komplexe Mannigfaltigkeiten. Comment. Math. Helv. 44(1969), 269–281. http://dx.doi.org/10.1007/BF0256452 8 Google Scholar
[5] Barth, W., Invariante holomorphe Funktionen auf reduktiven Liegruppen. Math. Ann. 201(1973), 97–112. http://dx.doi.org/10.1007/BF01359787 Google Scholar
[6] Chevalley, C., Theorie des groupes deLie. Tome II. Groupes algebriques. Actualites Sci. Ind., 1152, Hermann & Cie., Paris, 1951. Google Scholar
[7] Coeure, G. and J.-J. Loeb, A counterexample to the Serre problem with a bounded domain ofC2 as fiber. Ann. of Math. (2) 122(1985), no. 2, 329–334. http://dx.doi.org/10.2307/1971305 Google Scholar
[8] Gilligan, B., Ends of complex homogeneous manifolds having nonconstant holomorphic functions. Arch. Math. (Basel) 37(1981), no. 6, 544–555. http://dx.doi.org/10.1007/BF01234393 Google Scholar
[9] Gilligan, B. and Huckleberry, A. T., On non-compact complex nil-manifolds. Math. Ann. 238(1978), no. 1, 39–49. http://dx.doi.org/10.1007/BF01351452 Google Scholar
[10] Gilligan, B., C. Miebach, and K. Oeljeklaus, Pseudoconvex domains spread over complex homogeneous manifolds. Manuscripta Math. 142(2013),35-59. http://dx.doi.org/10.1007/s00229-012-0592-8 Google Scholar
[11] Grauert, H., On Levi's problem and the imbedding of real-analytic manifolds. Ann. of Math. 68(1958), 460–472. http://dx.doi.org/10.2307/1970257 Google Scholar
[12] Hirschowitz, A., Le probleme de Levi pour les espaces homogenes. Bull. Soc. Math. France 103(1975), no. 2, 191–201. Google Scholar
[13] Huckleberry, A. T. and E. Oeljeklaus, Homogeneous spaces from a complex analytic view-point. In: Manifolds and Lie Groups (Notre Dame, Ind., 1980) Progr. Math., 14, Birkhauser, Boston, MA, 1981, pp. 159–186.Google Scholar
[14] Huckleberry, A. T., On holomorphically separable complex solv-manifolds. Ann. Inst. Fourier (Grenoble) 36(1986), no. 3, 57–65. http://dx.doi.org/10.5802/aif.1059 Google Scholar
[15] Jacobson, N., Lie algebras. Interscience Tracts in Pure and Applied Mathematics, 10, Interscience Publishers (a division of John Wiley & Sons), New York-London 1962. Google Scholar
[16] Kiselman, C. O., The partial Legendre transformation for plurisubharmonic functions. Invent. Math. 49(1978), 137–148. http://dx.doi.org/1 0.1007/BF01403083 Google Scholar
[17] Matsushima, Y., On the discrete subgroups and homogeneous spaces ofnilpotent Lie groups. Nagoya Math. J. 2(1951), 95–110. http://dx.doi.org/1 0.101 7/S0027763000010096 Google Scholar
[18] Matsushima, Y., Espaces homogenes de Stein des groupes de Lie complexes. Nagoya Math. J. 16(1960), 205–218. http://dx.doi.org/10.1017/S002 7763000007662 Google Scholar
[19] Matsushima, Y. and A. Morimoto, Sur certains espaces fibres holomorphes sur une variete de Stein. Bull. Soc. Math. France 88(1960), 137–155. Google Scholar
[20] Mostow, G. D., Factor spaces of solvable groups. Ann. of Math. (2) 60(1954), 1–27. http://dx.doi.org/10.2307/1969700 Google Scholar
[21] Mostow, G. D., Some applications of representative functions to solvmanifolds. Amer. J. Math. 93(1971), 11–32. http://dx.doi.org/10.2307/2373444 Google Scholar
[22] Narasimhan, R., The Levi problem for complex spaces. I, II, Math. Ann. 142(1961), 355–365; 146(1962), 195–216. http://dx.doi.org/10.1007/BF01470950 Google Scholar
[23] Narasimhan, R., The Levi problem in the theory of functions of several complex variables. Proc. Internat. Congr. Mathematicians (Stockholm, 1962), Inst. Mittag-Leffler, Djurholm, 1963, pp. 385–388. Google Scholar
[24] Onishchik, A., Complex hulls of compact homogeneous spaces. Dokl. Akad. Nauk SSSR 130 (1960 ), 726– 729 (Russian); translation in Soviet Math. Dokl. 1(1960), 88–91. Google Scholar
[25] Remmert, R., Sur les espaces analytiques holomorphiquement separables et holomorphiquement convexes. C. R. Acad. Sci. Paris 243(1956), 118–121. Google Scholar
[26] Serre, J.-P., Quelques problemes globaux relatifs aux varietes de Stein. In: Colloque sur les fonctions de plusieurs variables, tenu a Bruxelles, 1953, Georges Thone, Liege; Masson & Cie, Paris, 1953, pp. 57–68. Google Scholar
[27] Tits, J., Espaces homogenes complexes compacts. Comment. Math. Helv. 37(1962/1963), 111–120. http://dx.doi.org/10.1007/BF02566965 Google Scholar