No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
We introduce two Ramsey classes of finite relational structures. The first class contains finite structures of the form  $\left( A,\,\left( {{I}_{i}} \right)_{i=1}^{n},\le ,\left( {{\underline{\prec }}_{i}} \right)_{i=1}^{n} \right)$, where
$\left( A,\,\left( {{I}_{i}} \right)_{i=1}^{n},\le ,\left( {{\underline{\prec }}_{i}} \right)_{i=1}^{n} \right)$, where 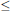 $\le$ is a total ordering on
$\le$ is a total ordering on 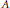 $A$ and
$A$ and  ${{\underline{\prec }}_{i}}$ is a linear ordering on the set
${{\underline{\prec }}_{i}}$ is a linear ordering on the set 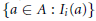 $\left\{ a\,\in \,A\,:\,{{I}_{i}}\left( a \right) \right\}$. The second class contains structures of the form a
$\left\{ a\,\in \,A\,:\,{{I}_{i}}\left( a \right) \right\}$. The second class contains structures of the form a 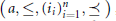 $\left( a,\le ,\left( {{i}_{i}} \right)_{i=1}^{n},\underline{\prec } \right)$, where
$\left( a,\le ,\left( {{i}_{i}} \right)_{i=1}^{n},\underline{\prec } \right)$, where 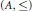 $\left( A,\,\le \right)$ is a weak ordering and
$\left( A,\,\le \right)$ is a weak ordering and 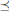 $\underline{\prec }$ is a linear ordering on
$\underline{\prec }$ is a linear ordering on 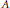 $A$ such that
$A$ such that 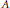 $A$ is partitioned by
$A$ is partitioned by 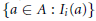 $\left\{ a\,\in \,A\,:\,{{I}_{i}}\left( a \right) \right\}$ into maximal chains in the partial ordering
$\left\{ a\,\in \,A\,:\,{{I}_{i}}\left( a \right) \right\}$ into maximal chains in the partial ordering 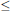 $\le$ and each
$\le$ and each 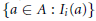 $\left\{ a\,\in \,A\,:\,{{I}_{i}}\left( a \right) \right\}$ is an interval with respect to
$\left\{ a\,\in \,A\,:\,{{I}_{i}}\left( a \right) \right\}$ is an interval with respect to 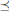 $\underline{\prec }$.
$\underline{\prec }$.