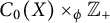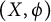1 Introduction and notation
The semicrossed product is a nonself-adjoint operator algebra which is constructed from a dynamical system. We recall the construction of the semicrossed product we will consider in this work. Let X be a locally compact Hausdorff space, and let
![]() $\phi :X\rightarrow X$
be a continuous and proper surjection (recall that a map
$\phi :X\rightarrow X$
be a continuous and proper surjection (recall that a map
![]() $\phi $
is proper if the inverse image
$\phi $
is proper if the inverse image
![]() $\phi ^{-1}(K)$
is compact for every compact
$\phi ^{-1}(K)$
is compact for every compact
![]() $K\subseteq X$
). The pair
$K\subseteq X$
). The pair
![]() $(X, \phi )$
is called a dynamical system. An action of
$(X, \phi )$
is called a dynamical system. An action of
![]() $\mathbb {Z}_+:=\mathbb N\cup \{0\}$
on
$\mathbb {Z}_+:=\mathbb N\cup \{0\}$
on
![]() $C_0(X)$
by isometric
$C_0(X)$
by isometric
![]() $*$
-endomorphisms
$*$
-endomorphisms
![]() $\alpha _n$
,
$\alpha _n$
,
![]() $n\in \mathbb {Z}_+$
is obtained by defining
$n\in \mathbb {Z}_+$
is obtained by defining
![]() $\alpha _n(f)=f\circ \phi ^n$
. We write the elements of the Banach space
$\alpha _n(f)=f\circ \phi ^n$
. We write the elements of the Banach space
![]() $\ell ^1({\mathbb Z}_+,C_0(X))$
as formal series
$\ell ^1({\mathbb Z}_+,C_0(X))$
as formal series
![]() $A=\sum _{n\in {\mathbb Z}_+}U^nf_n$
with the norm given by
$A=\sum _{n\in {\mathbb Z}_+}U^nf_n$
with the norm given by
![]() $\|A\|_1=\sum _{n\in {\mathbb Z}_+}\|f_n\|_{C_0(X)}$
. Multiplication on
$\|A\|_1=\sum _{n\in {\mathbb Z}_+}\|f_n\|_{C_0(X)}$
. Multiplication on
![]() $\ell ^1({\mathbb Z}_+,C_0(X))$
is defined by setting
$\ell ^1({\mathbb Z}_+,C_0(X))$
is defined by setting
and extending by linearity and continuity. With this multiplication,
![]() $\ell ^1({\mathbb Z}_+,C_0(X))$
is a Banach algebra.
$\ell ^1({\mathbb Z}_+,C_0(X))$
is a Banach algebra.
The Banach algebra
![]() $\ell ^1({\mathbb Z}_+,C_0(X))$
can be faithfully represented as a (concrete) operator algebra on a Hilbert space. This is achieved by assuming a faithful action of
$\ell ^1({\mathbb Z}_+,C_0(X))$
can be faithfully represented as a (concrete) operator algebra on a Hilbert space. This is achieved by assuming a faithful action of
![]() $C_0(X)$
on a Hilbert space
$C_0(X)$
on a Hilbert space
![]() $\mathcal {H}_0$
. Then we can define a faithful contractive representation
$\mathcal {H}_0$
. Then we can define a faithful contractive representation
![]() $\pi $
of
$\pi $
of
![]() $\ell _1({\mathbb Z}_+,C_0(X))$
on the Hilbert space
$\ell _1({\mathbb Z}_+,C_0(X))$
on the Hilbert space
![]() $\mathcal H=\mathcal {H}_0\otimes \ell ^2({\mathbb Z}_+)$
by defining
$\mathcal H=\mathcal {H}_0\otimes \ell ^2({\mathbb Z}_+)$
by defining
![]() $\pi (U^nf)$
as
$\pi (U^nf)$
as
The semicrossed product
![]() $C_0(X)\times _{\phi }{\mathbb Z}_+$
is the closure of the image of
$C_0(X)\times _{\phi }{\mathbb Z}_+$
is the closure of the image of
![]() $\ell ^1({\mathbb Z}_+,C_0(X))$
in
$\ell ^1({\mathbb Z}_+,C_0(X))$
in
![]() $\mathcal {B(H)}$
in the representation just defined. We will denote an element
$\mathcal {B(H)}$
in the representation just defined. We will denote an element
![]() $\pi (U^nf)$
of
$\pi (U^nf)$
of
![]() $C_0(X)\times _{\phi }{\mathbb Z}_+$
by
$C_0(X)\times _{\phi }{\mathbb Z}_+$
by
![]() $U^nf$
to simplify the notation.
$U^nf$
to simplify the notation.
For
![]() $A=\sum _{n\in {\mathbb Z}_+}U^nf_n\in \ell ^1({\mathbb Z}_+,C_0(X))$
, we call
$A=\sum _{n\in {\mathbb Z}_+}U^nf_n\in \ell ^1({\mathbb Z}_+,C_0(X))$
, we call
![]() $f_n\equiv E_n(A)$
the nth Fourier coefficient of A. The maps
$f_n\equiv E_n(A)$
the nth Fourier coefficient of A. The maps
![]() $E_n:\ell ^1({\mathbb Z}_+,C_0(X))\rightarrow C_0(X)$
are contractive in the (operator) norm of
$E_n:\ell ^1({\mathbb Z}_+,C_0(X))\rightarrow C_0(X)$
are contractive in the (operator) norm of
![]() $C_0(X)\times _{\phi }{\mathbb Z}_+$
, and therefore they extend to contractions
$C_0(X)\times _{\phi }{\mathbb Z}_+$
, and therefore they extend to contractions
![]() $E_n:C_0(X)\times _{\phi }{\mathbb Z}_+ \rightarrow C_0 (X)$
. An element A of the semicrossed product
$E_n:C_0(X)\times _{\phi }{\mathbb Z}_+ \rightarrow C_0 (X)$
. An element A of the semicrossed product
![]() $C_0(X)\times _{\phi }{\mathbb Z}_+$
is
$C_0(X)\times _{\phi }{\mathbb Z}_+$
is
![]() $0$
if and only if
$0$
if and only if
![]() $E_n(A)=0$
, for all
$E_n(A)=0$
, for all
![]() $n \in {\mathbb Z}_+$
, and thus A is completely determined by its Fourier coefficients. We will denote A by the formal series
$n \in {\mathbb Z}_+$
, and thus A is completely determined by its Fourier coefficients. We will denote A by the formal series
![]() $A=\sum _{n\in {\mathbb Z}_+}U^nf_n$
, where
$A=\sum _{n\in {\mathbb Z}_+}U^nf_n$
, where
![]() $f_n=E_n(A)$
. Note, however, that the series
$f_n=E_n(A)$
. Note, however, that the series
![]() $\sum _{n\in {\mathbb Z}_+}U^nf_n$
does not in general converge to A [Reference Peters6, II.9]. The kth arithmetic mean of A is defined to be
$\sum _{n\in {\mathbb Z}_+}U^nf_n$
does not in general converge to A [Reference Peters6, II.9]. The kth arithmetic mean of A is defined to be
![]() $\bar A_k=\frac {1}{k+1}\sum _{l=0}^k S_l(A)$
, where
$\bar A_k=\frac {1}{k+1}\sum _{l=0}^k S_l(A)$
, where
![]() $S_l(A)=\sum _{n=0}^l U^nf_n$
. Then, the sequence
$S_l(A)=\sum _{n=0}^l U^nf_n$
. Then, the sequence
![]() $\{\bar A_k\}_{k\in \mathbb {Z}_+}$
is norm convergent to A [Reference Peters6, Remark, p. 524]. We refer to [Reference Davidson, Fuller and Kakariadis3, Reference Donsig, Katavolos and Manoussos4, Reference Peters6] for more information about the semicrossed product.
$\{\bar A_k\}_{k\in \mathbb {Z}_+}$
is norm convergent to A [Reference Peters6, Remark, p. 524]. We refer to [Reference Davidson, Fuller and Kakariadis3, Reference Donsig, Katavolos and Manoussos4, Reference Peters6] for more information about the semicrossed product.
Let
![]() $\{X_n\}_{n=0}^{\infty }$
be a sequence of closed subsets of X satisfying
$\{X_n\}_{n=0}^{\infty }$
be a sequence of closed subsets of X satisfying
for all
![]() $n\in \mathbb N$
. Peters proved in [Reference Peters7] that the subspace
$n\in \mathbb N$
. Peters proved in [Reference Peters7] that the subspace
![]() $\mathcal I=\{A\in C_0(X)\times _{\phi }{\mathbb Z}_+:E_n(A)(X_n)=\{0\}\}$
is a closed two-sided ideal of
$\mathcal I=\{A\in C_0(X)\times _{\phi }{\mathbb Z}_+:E_n(A)(X_n)=\{0\}\}$
is a closed two-sided ideal of
![]() $C_0(X)\times _{\phi }{\mathbb Z}_+$
. We will write this as
$C_0(X)\times _{\phi }{\mathbb Z}_+$
. We will write this as
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
. We note that if
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
. We note that if
![]() $A\in \mathcal I\sim \{X_n\}_{n=0}^{\infty }$
, then
$A\in \mathcal I\sim \{X_n\}_{n=0}^{\infty }$
, then
![]() $U^nE_n(A)\in \mathcal I$
for all
$U^nE_n(A)\in \mathcal I$
for all
![]() $n\in {\mathbb Z}_+$
. Peters proved in [Reference Peters7] that there is a one-to-one correspondence between closed two-sided ideals
$n\in {\mathbb Z}_+$
. Peters proved in [Reference Peters7] that there is a one-to-one correspondence between closed two-sided ideals
![]() $\mathcal I\subseteq C_0(X)\times _{\phi }{\mathbb Z}_+$
and sequences
$\mathcal I\subseteq C_0(X)\times _{\phi }{\mathbb Z}_+$
and sequences
![]() $\{X_n\}_{n=0}^{\infty }$
of closed subsets of X satisfying (*), under the assumptions that X is metrizable and the dynamical system
$\{X_n\}_{n=0}^{\infty }$
of closed subsets of X satisfying (*), under the assumptions that X is metrizable and the dynamical system
![]() $(X,\phi )$
contains no periodic points. Moreover, he characterizes the maximal and prime ideals of the semicrossed product
$(X,\phi )$
contains no periodic points. Moreover, he characterizes the maximal and prime ideals of the semicrossed product
![]() $C_0(X)\times _{\phi }{\mathbb Z}_+$
in this case.
$C_0(X)\times _{\phi }{\mathbb Z}_+$
in this case.
Donsig, Katavolos, and Manousos obtained in [Reference Donsig, Katavolos and Manoussos4] a characterization of the Jacobson radical for the semicrossed product
![]() $C_0(X)\times _{\phi }{\mathbb Z}_+$
, where X is a locally compact metrizable space and
$C_0(X)\times _{\phi }{\mathbb Z}_+$
, where X is a locally compact metrizable space and
![]() $\phi :X\rightarrow X$
is a continuous and proper surjection. Andreolas, Anoussis, and the author characterized in [Reference Andreolas, Anoussis and Magiatis2] the ideal generated by the compact elements and in [Reference Andreolas, Anoussis and Magiatis1] the hypocompact and the scattered radical of the semicrossed product
$\phi :X\rightarrow X$
is a continuous and proper surjection. Andreolas, Anoussis, and the author characterized in [Reference Andreolas, Anoussis and Magiatis2] the ideal generated by the compact elements and in [Reference Andreolas, Anoussis and Magiatis1] the hypocompact and the scattered radical of the semicrossed product
![]() $C_0(X)\times _{\phi }{\mathbb Z}_+$
, where X is a locally compact Hausdorff space and
$C_0(X)\times _{\phi }{\mathbb Z}_+$
, where X is a locally compact Hausdorff space and
![]() $\phi :X\rightarrow X$
is a homeomorphism. All these ideals are of the form
$\phi :X\rightarrow X$
is a homeomorphism. All these ideals are of the form
![]() $\mathcal I\sim \{X_n\}_{n=0}^\infty $
for suitable families of closed subsets
$\mathcal I\sim \{X_n\}_{n=0}^\infty $
for suitable families of closed subsets
![]() $\{X_n\}_{n=0}^\infty $
.
$\{X_n\}_{n=0}^\infty $
.
In the present paper, we characterize the closed two-sided ideals
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
of
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
of
![]() $C_0(X)\times _\phi {\mathbb Z}_+$
with left (resp. right) approximate unit. As a consequence, we obtain a complete characterization of ideals with left (resp. right) approximate unit under the additional assumptions that X is metrizable and the dynamical system
$C_0(X)\times _\phi {\mathbb Z}_+$
with left (resp. right) approximate unit. As a consequence, we obtain a complete characterization of ideals with left (resp. right) approximate unit under the additional assumptions that X is metrizable and the dynamical system
![]() $(X,\phi )$
contains no periodic points.
$(X,\phi )$
contains no periodic points.
Recall that a left (resp. right) approximate unit of a Banach algebra
![]() $\mathcal A$
is a net
$\mathcal A$
is a net
![]() $\{u_\lambda \}_{\lambda \in \Lambda }$
of elements of
$\{u_\lambda \}_{\lambda \in \Lambda }$
of elements of
![]() $\mathcal A$
such that:
$\mathcal A$
such that:
-
(1) for some positive number r,
 $\|u_{\lambda }\|\leq r$
for all
$\|u_{\lambda }\|\leq r$
for all
 $\lambda \in \Lambda $
,
$\lambda \in \Lambda $
, -
(2)
 $\lim u_\lambda a=a$
(resp.
$\lim u_\lambda a=a$
(resp.
 $\lim au_\lambda =a$
), for all
$\lim au_\lambda =a$
), for all
 $a\in \mathcal A$
, in the norm topology of
$a\in \mathcal A$
, in the norm topology of
 $\mathcal A$
.
$\mathcal A$
.
A net which is both a left and a right approximate unit of
![]() $\mathcal A$
is called an approximate unit of
$\mathcal A$
is called an approximate unit of
![]() $\mathcal A$
. A left (resp. right) approximate unit
$\mathcal A$
. A left (resp. right) approximate unit
![]() $\{u_\lambda \}_{\lambda \in \Lambda }$
that satisfies
$\{u_\lambda \}_{\lambda \in \Lambda }$
that satisfies
![]() $\|u_{\lambda }\|\leq 1$
for all
$\|u_{\lambda }\|\leq 1$
for all
![]() $\lambda \in \Lambda $
is called a contractive left (resp. right) approximate unit.
$\lambda \in \Lambda $
is called a contractive left (resp. right) approximate unit.
We will say that an ideal
![]() $\mathcal I$
of a Banach algebra
$\mathcal I$
of a Banach algebra
![]() $\mathcal A$
has a left (resp. right) approximate unit if it has a left (resp. right) approximate unit as an algebra.
$\mathcal A$
has a left (resp. right) approximate unit if it has a left (resp. right) approximate unit as an algebra.
2 Ideals with approximate unit
In the following theorem, the ideals
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
with right approximate unit are characterized.
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
with right approximate unit are characterized.
Theorem 2.1 Let
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
be a nonzero ideal of
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
be a nonzero ideal of
![]() $C_0(X)\times _\phi {\mathbb Z}_+$
. The following are equivalent:
$C_0(X)\times _\phi {\mathbb Z}_+$
. The following are equivalent:
-
(1)
 $\mathcal I$
has a right approximate unit.
$\mathcal I$
has a right approximate unit. -
(2)
 $X_n=X_{n+1}$
, for all
$X_n=X_{n+1}$
, for all
 $n\in {\mathbb Z}_+$
.
$n\in {\mathbb Z}_+$
.
Proof We start by proving that (1)
![]() $\Rightarrow $
(2). Let
$\Rightarrow $
(2). Let
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
be an ideal with right approximate unit
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
be an ideal with right approximate unit
![]() $\{V_{\lambda }\}_{\lambda \in \Lambda }$
. We suppose that there exists
$\{V_{\lambda }\}_{\lambda \in \Lambda }$
. We suppose that there exists
![]() $n\in {\mathbb Z}_+$
such that
$n\in {\mathbb Z}_+$
such that
![]() $X_{n+1}\subsetneq X_{n}$
. Let
$X_{n+1}\subsetneq X_{n}$
. Let
![]() $x_0\in X_{n_0}\backslash X_{n_0+1}$
, and
$x_0\in X_{n_0}\backslash X_{n_0+1}$
, and
![]() $f\in C_0(X)$
such that
$f\in C_0(X)$
such that
![]() $f(x_0)=1$
,
$f(x_0)=1$
,
![]() $f(X_{n_0+1})=\{0\}$
, and
$f(X_{n_0+1})=\{0\}$
, and
![]() $\|f\|=1$
. Then, for
$\|f\|=1$
. Then, for
![]() $A=U^{n_0+1}f$
, we have
$A=U^{n_0+1}f$
, we have
![]() $A\in \mathcal I$
and
$A\in \mathcal I$
and
for all
![]() $\lambda \in \Lambda $
, since
$\lambda \in \Lambda $
, since
![]() $x_0\in X_{n_0}$
and
$x_0\in X_{n_0}$
and
![]() $E_0(V_{\lambda })(X_{n_0})=0$
, which is a contradiction. Therefore,
$E_0(V_{\lambda })(X_{n_0})=0$
, which is a contradiction. Therefore,
![]() $X_n=X_{n+1}$
for all
$X_n=X_{n+1}$
for all
![]() $n\in {\mathbb Z}_+$
.
$n\in {\mathbb Z}_+$
.
For (2)
![]() $\Rightarrow $
(1), assume that
$\Rightarrow $
(1), assume that
![]() $X_n=X_{n+1}$
for all
$X_n=X_{n+1}$
for all
![]() $n\in {\mathbb Z}_+$
. By (*), we get that
$n\in {\mathbb Z}_+$
. By (*), we get that
![]() $\phi (X_0)\subseteq X_0$
. We will show that if
$\phi (X_0)\subseteq X_0$
. We will show that if
![]() $\{u_{\lambda }\}_{\lambda \in \Lambda }$
is a contractive approximate unit of the ideal
$\{u_{\lambda }\}_{\lambda \in \Lambda }$
is a contractive approximate unit of the ideal
![]() $C_0(X\backslash X_0)$
of
$C_0(X\backslash X_0)$
of
![]() $C_0(X)$
, then
$C_0(X)$
, then
![]() $\{U^0u_{\lambda }\}_{\lambda \in \Lambda }$
is a right approximate unit of
$\{U^0u_{\lambda }\}_{\lambda \in \Lambda }$
is a right approximate unit of
![]() $\mathcal I$
. Since
$\mathcal I$
. Since
![]() $\|u_{\lambda }\|\leq 1$
, we have
$\|u_{\lambda }\|\leq 1$
, we have
![]() $\|U^0u_{\lambda }\|\leq 1$
.
$\|U^0u_{\lambda }\|\leq 1$
.
Let
![]() $A\in \mathcal I$
and
$A\in \mathcal I$
and
![]() $\varepsilon>0$
. Then there exists
$\varepsilon>0$
. Then there exists
![]() $k\in {\mathbb Z}_+$
such that
$k\in {\mathbb Z}_+$
such that
where
![]() $\bar A_k$
is the kth arithmetic mean of A. Since
$\bar A_k$
is the kth arithmetic mean of A. Since
![]() $X_n=X_0$
,
$X_n=X_0$
,
![]() $E_n(\bar A_k)\in C_0(X\backslash X_0)$
and
$E_n(\bar A_k)\in C_0(X\backslash X_0)$
and
![]() $\{u_{\lambda }\}_{\lambda \in \Lambda }$
is an approximate unit of
$\{u_{\lambda }\}_{\lambda \in \Lambda }$
is an approximate unit of
![]() $C_0(X\backslash X_0)$
, there exists
$C_0(X\backslash X_0)$
, there exists
![]() $\lambda _0\in \Lambda $
such that
$\lambda _0\in \Lambda $
such that
for all
![]() $l\leq k$
and
$l\leq k$
and
![]() $\lambda> \lambda _0$
. So, for
$\lambda> \lambda _0$
. So, for
![]() $\lambda>\lambda _0$
, we get that
$\lambda>\lambda _0$
, we get that
 $$ \begin{align*} \|AU^0u_\lambda-A\| & = \|AU^0u_\lambda-\bar A_kU^0u_\lambda+\bar A_kU^0u_\lambda-\bar A_k+\bar A_k-A\| \\ & \leq \|AU^0u_\lambda-\bar A_kU^0u_\lambda\|+\|\bar A_kU^0u_\lambda-\bar A_k\|+\|A-\bar A_k\| \\ & < \|\bar A_kU^0u_\lambda-\bar A_k\|+\frac{\varepsilon}{2}\\ &\leq \sum_{l=0}^k\|E_l(\bar A_k)u_\lambda -E_l(\bar A_k)\|+\frac{\varepsilon}{2}\\ &< \varepsilon, \end{align*} $$
$$ \begin{align*} \|AU^0u_\lambda-A\| & = \|AU^0u_\lambda-\bar A_kU^0u_\lambda+\bar A_kU^0u_\lambda-\bar A_k+\bar A_k-A\| \\ & \leq \|AU^0u_\lambda-\bar A_kU^0u_\lambda\|+\|\bar A_kU^0u_\lambda-\bar A_k\|+\|A-\bar A_k\| \\ & < \|\bar A_kU^0u_\lambda-\bar A_k\|+\frac{\varepsilon}{2}\\ &\leq \sum_{l=0}^k\|E_l(\bar A_k)u_\lambda -E_l(\bar A_k)\|+\frac{\varepsilon}{2}\\ &< \varepsilon, \end{align*} $$
which concludes the proof.
In the following theorem, the ideals
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
with left approximate unit are characterized.
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
with left approximate unit are characterized.
Theorem 2.2 Let
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
be a nonzero ideal of
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
be a nonzero ideal of
![]() $C_0(X)\times _\phi {\mathbb Z}_+$
. The following are equivalent:
$C_0(X)\times _\phi {\mathbb Z}_+$
. The following are equivalent:
-
(1)
 $\mathcal I$
has a left approximate unit.
$\mathcal I$
has a left approximate unit. -
(2)
 $X_0\subsetneq X$
and
$X_0\subsetneq X$
and
 $\phi ^{n}(X\backslash X_n)= X\backslash X_0$
, for all
$\phi ^{n}(X\backslash X_n)= X\backslash X_0$
, for all
 $n\in {\mathbb Z}_+$
.
$n\in {\mathbb Z}_+$
. -
(3)
 $\phi (X\backslash X_{1})= X\backslash X_{0}$
and
$\phi (X\backslash X_{1})= X\backslash X_{0}$
and
 $\phi (X_{n+1}\backslash X_{n+2})=X_{n}\backslash X_{n+1}$
, for all
$\phi (X_{n+1}\backslash X_{n+2})=X_{n}\backslash X_{n+1}$
, for all
 $n\in {\mathbb Z}_+$
.
$n\in {\mathbb Z}_+$
.
Proof We start by proving that (1)
![]() $\Rightarrow $
(2). Let
$\Rightarrow $
(2). Let
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
be an ideal with left approximate unit
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
be an ideal with left approximate unit
![]() $\{V_{\lambda }\}_{\lambda \in \Lambda }$
.
$\{V_{\lambda }\}_{\lambda \in \Lambda }$
.
First, we prove that
![]() $X_0\subsetneq X$
. We suppose that
$X_0\subsetneq X$
. We suppose that
![]() $X_0=X$
. Then
$X_0=X$
. Then
![]() $E_0(V_\lambda )=0$
, for all
$E_0(V_\lambda )=0$
, for all
![]() ${\lambda \in \Lambda }$
, and hence for every
${\lambda \in \Lambda }$
, and hence for every
![]() $U^nf\in \mathcal I$
, we have
$U^nf\in \mathcal I$
, we have
for all
![]() $\lambda \in \Lambda $
, which is a contradiction. Therefore,
$\lambda \in \Lambda $
, which is a contradiction. Therefore,
![]() $X_0\subsetneq X$
.
$X_0\subsetneq X$
.
Now, we prove that
![]() $\phi ^{n}(X\backslash X_n)= X\backslash X_0$
, for all
$\phi ^{n}(X\backslash X_n)= X\backslash X_0$
, for all
![]() $n\in {\mathbb Z}_+$
. We suppose that there exists
$n\in {\mathbb Z}_+$
. We suppose that there exists
![]() $n\in {\mathbb Z}_+$
such that
$n\in {\mathbb Z}_+$
such that
![]() $\phi ^{n}(X\backslash X_n)\not \subseteq X\backslash X_0$
and let
$\phi ^{n}(X\backslash X_n)\not \subseteq X\backslash X_0$
and let
The set
![]() $X\backslash X_{n_0}$
is nonempty, since
$X\backslash X_{n_0}$
is nonempty, since
![]() $X_{n_0}\subseteq X_0\subsetneq X$
. Then, there exist
$X_{n_0}\subseteq X_0\subsetneq X$
. Then, there exist
![]() $x_0\in X\backslash X_{n_0}$
such that
$x_0\in X\backslash X_{n_0}$
such that
![]() $\phi ^{n_0}(x_0)\in X_{0}$
and a function
$\phi ^{n_0}(x_0)\in X_{0}$
and a function
![]() $f\in C_0(X)$
such that
$f\in C_0(X)$
such that
![]() $f(x_0)=1$
,
$f(x_0)=1$
,
![]() $f(X_{n_0})=\{0\}$
, and
$f(X_{n_0})=\{0\}$
, and
![]() $\|f\|=1$
. If
$\|f\|=1$
. If
![]() $A=U^{n_0}f$
, by the choice of f, we have that
$A=U^{n_0}f$
, by the choice of f, we have that
![]() $A\in \mathcal I$
,
$A\in \mathcal I$
,
![]() $\|A\|=1$
and
$\|A\|=1$
and
 $$ \begin{align*} \|V_{\lambda}A-A\| & \ge \|E_{n_0}(V_{\lambda}A-A)\|\\ & = \|E_0(V_{\lambda})\circ\phi^{n_0}f-f\|\\ &\ge|(E_0(V_{\lambda})\circ\phi^{n_0}f-f)(x_0)|\\ &=1, \end{align*} $$
$$ \begin{align*} \|V_{\lambda}A-A\| & \ge \|E_{n_0}(V_{\lambda}A-A)\|\\ & = \|E_0(V_{\lambda})\circ\phi^{n_0}f-f\|\\ &\ge|(E_0(V_{\lambda})\circ\phi^{n_0}f-f)(x_0)|\\ &=1, \end{align*} $$
for all
![]() $\lambda \in \Lambda $
, since
$\lambda \in \Lambda $
, since
![]() $\phi ^{n_0}(x_0)\in X_0$
and
$\phi ^{n_0}(x_0)\in X_0$
and
![]() $E_0(V_{\lambda })(X_0)=\{0\}$
, which is a contradiction. Therefore,
$E_0(V_{\lambda })(X_0)=\{0\}$
, which is a contradiction. Therefore,
![]() $\phi ^{n}(X\backslash X_n)\subseteq X\backslash X_0$
. Furthermore, by (*), we get that
$\phi ^{n}(X\backslash X_n)\subseteq X\backslash X_0$
. Furthermore, by (*), we get that
![]() $\phi ^n(X_n)\subseteq X_0$
, for all
$\phi ^n(X_n)\subseteq X_0$
, for all
![]() $n\in {\mathbb Z}_+$
, and hence
$n\in {\mathbb Z}_+$
, and hence
Since
![]() $\phi ^{n}(X\backslash X_n)\subseteq X\backslash X_0$
and
$\phi ^{n}(X\backslash X_n)\subseteq X\backslash X_0$
and
![]() $\phi $
is surjective,
$\phi $
is surjective,
![]() $\phi ^n(X\backslash X_n)=X\backslash X_0$
, for all
$\phi ^n(X\backslash X_n)=X\backslash X_0$
, for all
![]() $n\in {\mathbb Z}_+$
.
$n\in {\mathbb Z}_+$
.
For (2)
![]() $\Rightarrow $
(1), assume that
$\Rightarrow $
(1), assume that
![]() $X_0\subsetneq X$
and
$X_0\subsetneq X$
and
![]() $\phi ^{n}(X\backslash X_n)= X\backslash X_0$
, for all
$\phi ^{n}(X\backslash X_n)= X\backslash X_0$
, for all
![]() $n\in {\mathbb Z}_+$
. We will show that if
$n\in {\mathbb Z}_+$
. We will show that if
![]() $\{u_{\lambda }\}_{\lambda \in \Lambda }$
is a contractive approximate unit of the ideal
$\{u_{\lambda }\}_{\lambda \in \Lambda }$
is a contractive approximate unit of the ideal
![]() $C_0(X\backslash X_0)$
of
$C_0(X\backslash X_0)$
of
![]() $C_0(X)$
, then
$C_0(X)$
, then
![]() $\{U^0u_{\lambda }\}_{\lambda \in \Lambda }$
is a left approximate unit of
$\{U^0u_{\lambda }\}_{\lambda \in \Lambda }$
is a left approximate unit of
![]() $\mathcal I$
. Since
$\mathcal I$
. Since
![]() $\|u_{\lambda }\|\leq 1$
, we have
$\|u_{\lambda }\|\leq 1$
, we have
![]() $\|U^0u_{\lambda }\|\leq 1$
.
$\|U^0u_{\lambda }\|\leq 1$
.
Let A be a norm-one element of
![]() $\mathcal I$
and
$\mathcal I$
and
![]() $\varepsilon>0$
. Then there exists
$\varepsilon>0$
. Then there exists
![]() $k\in {\mathbb Z}_+$
such that
$k\in {\mathbb Z}_+$
such that
where
![]() $\bar A_k$
is the kth arithmetic mean of A. For
$\bar A_k$
is the kth arithmetic mean of A. For
![]() $l\leq k$
, let
$l\leq k$
, let
 $$ \begin{align*} D_\varepsilon(E_l(\bar A_k))=\left\{x\in X: |E_l(\bar A_k)(x)|\ge\frac{\varepsilon}{4(k+1)} \right\}. \end{align*} $$
$$ \begin{align*} D_\varepsilon(E_l(\bar A_k))=\left\{x\in X: |E_l(\bar A_k)(x)|\ge\frac{\varepsilon}{4(k+1)} \right\}. \end{align*} $$
Since
![]() $A\in \mathcal I$
, we have
$A\in \mathcal I$
, we have
![]() $E_l(\bar A_k)(X_l)=\{0\}$
and hence
$E_l(\bar A_k)(X_l)=\{0\}$
and hence
![]() $D_\varepsilon (E_l(\bar A_k))\subseteq X\backslash X_l$
. Furthermore, since
$D_\varepsilon (E_l(\bar A_k))\subseteq X\backslash X_l$
. Furthermore, since
![]() $\phi ^{n}(X\backslash X_n)= X\backslash X_0$
, for all
$\phi ^{n}(X\backslash X_n)= X\backslash X_0$
, for all
![]() $n\in {\mathbb Z}_+$
, we have that
$n\in {\mathbb Z}_+$
, we have that
![]() $\phi ^{l}(D_\varepsilon (E_l(\bar A_k)))\subseteq X\backslash X_0$
. Moreover, the set
$\phi ^{l}(D_\varepsilon (E_l(\bar A_k)))\subseteq X\backslash X_0$
. Moreover, the set
![]() $D_\varepsilon (E_l(\bar A_k))$
is compact, since
$D_\varepsilon (E_l(\bar A_k))$
is compact, since
![]() $E_l(\bar A_k)\in C_0(X)$
, and hence the set
$E_l(\bar A_k)\in C_0(X)$
, and hence the set
![]() $\phi ^{l}(D_\varepsilon (E_l(\bar A_k)))$
is also compact. By Urysohn’s lemma for locally compact Hausdorff spaces [Reference Rudin8, p. 39], there is a norm-one function
$\phi ^{l}(D_\varepsilon (E_l(\bar A_k)))$
is also compact. By Urysohn’s lemma for locally compact Hausdorff spaces [Reference Rudin8, p. 39], there is a norm-one function
![]() $v_l\in C_0(X)$
such that
$v_l\in C_0(X)$
such that
 $$ \begin{align*} v_l(x)=\left\{\begin{array}{ll} 1, & x\in \phi^l(D_\varepsilon(E_l(\bar A_k))),\\ 0, & x\in X_0. \end{array} \right. \end{align*} $$
$$ \begin{align*} v_l(x)=\left\{\begin{array}{ll} 1, & x\in \phi^l(D_\varepsilon(E_l(\bar A_k))),\\ 0, & x\in X_0. \end{array} \right. \end{align*} $$
Then, there exists
![]() $\lambda _0\in \Lambda $
such that
$\lambda _0\in \Lambda $
such that
for all
![]() $l\leq k$
and
$l\leq k$
and
![]() $\lambda>\lambda _0$
, and hence
$\lambda>\lambda _0$
, and hence
for all
![]() $x\in \cup _{l=0}^k\phi ^{l}(D_\varepsilon (E_l(\bar A_k)))$
and
$x\in \cup _{l=0}^k\phi ^{l}(D_\varepsilon (E_l(\bar A_k)))$
and
![]() $\lambda>\lambda _0$
. Therefore, if
$\lambda>\lambda _0$
. Therefore, if
![]() $x\in \cup _{l=0}^k(D_\varepsilon (E_l(\bar A_k)))$
, then
$x\in \cup _{l=0}^k(D_\varepsilon (E_l(\bar A_k)))$
, then
![]() $\phi ^l(x)\in \cup _{l=0}^k\phi ^{l}(D_\varepsilon (E_l(\bar A_k)))$
and hence
$\phi ^l(x)\in \cup _{l=0}^k\phi ^{l}(D_\varepsilon (E_l(\bar A_k)))$
and hence
for all
![]() $l\leq k$
and
$l\leq k$
and
![]() $\lambda> \lambda _0$
. On the other hand, if
$\lambda> \lambda _0$
. On the other hand, if
![]() $x\not \in \cup _{l=0}^k(D_\varepsilon (E_l(\bar A_k)))$
, then
$x\not \in \cup _{l=0}^k(D_\varepsilon (E_l(\bar A_k)))$
, then
for all
![]() $l\leq k$
, and hence
$l\leq k$
, and hence
From what we said so far, we get that
 $$ \begin{align*} \|U^0u_\lambda A-A\| & < \|U^0u_\lambda\bar A_k-\bar A_k\|+\frac{\varepsilon}{2}\\ & \leq \sum_{l=0}^k\|(u_\lambda\circ\phi^l)E_l(\bar A_k)-E_l(\bar A_k)\|+\frac{\varepsilon}{2}\\ &< \varepsilon, \end{align*} $$
$$ \begin{align*} \|U^0u_\lambda A-A\| & < \|U^0u_\lambda\bar A_k-\bar A_k\|+\frac{\varepsilon}{2}\\ & \leq \sum_{l=0}^k\|(u_\lambda\circ\phi^l)E_l(\bar A_k)-E_l(\bar A_k)\|+\frac{\varepsilon}{2}\\ &< \varepsilon, \end{align*} $$
for all
![]() $\lambda>\lambda _0$
.
$\lambda>\lambda _0$
.
Now, we show that (2)
![]() $\Rightarrow $
(3). We assume that
$\Rightarrow $
(3). We assume that
![]() $\phi ^{n}(X\backslash X_{n})= X\backslash X_0$
, for all
$\phi ^{n}(X\backslash X_{n})= X\backslash X_0$
, for all
![]() $n\in {\mathbb Z}_+$
. Then,
$n\in {\mathbb Z}_+$
. Then,
![]() $\phi (X\backslash X_{n+2})\subseteq X\backslash X_{n+1}$
. Indeed, if
$\phi (X\backslash X_{n+2})\subseteq X\backslash X_{n+1}$
. Indeed, if
![]() $x\in X\backslash X_{n+2}$
and
$x\in X\backslash X_{n+2}$
and
![]() $\phi (x)\in X_{n+1}$
, then
$\phi (x)\in X_{n+1}$
, then
![]() ${\phi ^{n+2}(x)\in X_{0}}$
, by (*), which is a contradiction. Furthermore, by (*), we know that
${\phi ^{n+2}(x)\in X_{0}}$
, by (*), which is a contradiction. Furthermore, by (*), we know that
![]() $\phi (X_{n+1})\subseteq X_{n}$
and hence
$\phi (X_{n+1})\subseteq X_{n}$
and hence
![]() $\phi (X_{n+1}\backslash X_{n+2})\subseteq X_n\backslash X_{n+1}$
for all
$\phi (X_{n+1}\backslash X_{n+2})\subseteq X_n\backslash X_{n+1}$
for all
![]() $n\in {\mathbb Z}_+$
.
$n\in {\mathbb Z}_+$
.
To prove that
![]() $\phi (X_{n+1}\backslash X_{n+2})= X_n\backslash X_{n+1}$
for all
$\phi (X_{n+1}\backslash X_{n+2})= X_n\backslash X_{n+1}$
for all
![]() $n\in {\mathbb Z}_+$
, we suppose that there exists
$n\in {\mathbb Z}_+$
, we suppose that there exists
![]() $n\in {\mathbb Z}_+$
such that
$n\in {\mathbb Z}_+$
such that
![]() $\phi (X_{n+1}\backslash X_{n+2})\subsetneq X_n\backslash X_{n+1}$
. If
$\phi (X_{n+1}\backslash X_{n+2})\subsetneq X_n\backslash X_{n+1}$
. If
then
 $$ \begin{align*} \phi(X_{n_0+1}) & = \phi(X_{n_0+2}\cup(X_{n_0+1}\backslash X_{n_0+2}))\\ &= \phi(X_{n_0+2})\cup\phi(X_{n_0+1}\backslash X_{n_0+2})\\ & \subseteq X_{n_0+1}\cup\phi(X_{n_0+1}\backslash X_{n_0+2})\\ &\subsetneq X_{n_0+1}\cup(X_{n_0}\backslash X_{n_0+1})\\ &= X_{n_0}, \end{align*} $$
$$ \begin{align*} \phi(X_{n_0+1}) & = \phi(X_{n_0+2}\cup(X_{n_0+1}\backslash X_{n_0+2}))\\ &= \phi(X_{n_0+2})\cup\phi(X_{n_0+1}\backslash X_{n_0+2})\\ & \subseteq X_{n_0+1}\cup\phi(X_{n_0+1}\backslash X_{n_0+2})\\ &\subsetneq X_{n_0+1}\cup(X_{n_0}\backslash X_{n_0+1})\\ &= X_{n_0}, \end{align*} $$
and hence
 $$ \begin{align*} \phi(X) & = \phi(X_{n_0+1}\cup(X\backslash X_{n_0+1}))\\ &= \phi(X_{n_0+1})\cup\phi(X\backslash X_{n_0+1})\\ & \subseteq \phi(X_{n_0+1})\cup (X\backslash X_{n_0})\\ &\subsetneq X, \end{align*} $$
$$ \begin{align*} \phi(X) & = \phi(X_{n_0+1}\cup(X\backslash X_{n_0+1}))\\ &= \phi(X_{n_0+1})\cup\phi(X\backslash X_{n_0+1})\\ & \subseteq \phi(X_{n_0+1})\cup (X\backslash X_{n_0})\\ &\subsetneq X, \end{align*} $$
which is a contradiction, since
![]() $\phi $
is surjective. Therefore,
$\phi $
is surjective. Therefore,
![]() $\phi (X_{n+1}\backslash X_{n+2})= X_n\backslash X_{n+1}$
for all
$\phi (X_{n+1}\backslash X_{n+2})= X_n\backslash X_{n+1}$
for all
![]() $n\in {\mathbb Z}_+$
.
$n\in {\mathbb Z}_+$
.
Finally, we show that (3)
![]() $\Rightarrow $
(2). We assume that
$\Rightarrow $
(2). We assume that
![]() $\phi (X\backslash X_{1})= X\backslash X_{0}$
and
$\phi (X\backslash X_{1})= X\backslash X_{0}$
and
![]() $\phi (X_{n+1}\backslash X_{n+2})=X_{n}\backslash X_{n+1}$
, for all
$\phi (X_{n+1}\backslash X_{n+2})=X_{n}\backslash X_{n+1}$
, for all
![]() $n\in {\mathbb Z}_+$
. Then,
$n\in {\mathbb Z}_+$
. Then,
![]() $X_0\subsetneq X$
. Indeed, if
$X_0\subsetneq X$
. Indeed, if
![]() $X_0=X$
, then
$X_0=X$
, then
![]() $\mathcal I\equiv \{0\}$
, which is a contradiction. If
$\mathcal I\equiv \{0\}$
, which is a contradiction. If
![]() $n>1$
, we have that
$n>1$
, we have that
 $$ \begin{align*} \phi(X\backslash X_n)&=\phi\left[(X\backslash X_1)\cup(X_1\backslash X_2)\cup\dots\cup(X_{n-1}\backslash X_n)\right]\\ &=\phi(X\backslash X_1)\cup\phi(X_1\backslash X_2)\cup\dots\cup\phi(X_{n-1}\backslash X_n)\\ &=(X\backslash X_0)\cup(X_0\backslash X_1)\cup\dots\cup(X_{n-2}\backslash X_{n-1})\\ &=X\backslash X_{n-1} , \end{align*} $$
$$ \begin{align*} \phi(X\backslash X_n)&=\phi\left[(X\backslash X_1)\cup(X_1\backslash X_2)\cup\dots\cup(X_{n-1}\backslash X_n)\right]\\ &=\phi(X\backslash X_1)\cup\phi(X_1\backslash X_2)\cup\dots\cup\phi(X_{n-1}\backslash X_n)\\ &=(X\backslash X_0)\cup(X_0\backslash X_1)\cup\dots\cup(X_{n-2}\backslash X_{n-1})\\ &=X\backslash X_{n-1} , \end{align*} $$
and hence
![]() $\phi ^n(X\backslash X_n)=X\backslash X_{0}$
, for all
$\phi ^n(X\backslash X_n)=X\backslash X_{0}$
, for all
![]() $n\in {\mathbb Z}_+$
.
$n\in {\mathbb Z}_+$
.
Remark 2.3 It follows from the proofs of Theorems 2.1 and 2.2 that if
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
is an ideal of
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
is an ideal of
![]() $C_0(X)\times _\phi {\mathbb Z}_+$
with a left (resp. right) approximate unit, then it has a contractive left (resp. right) approximate unit of the form
$C_0(X)\times _\phi {\mathbb Z}_+$
with a left (resp. right) approximate unit, then it has a contractive left (resp. right) approximate unit of the form
![]() $\{U^0u_\lambda \}_{\lambda \in \Lambda }$
where
$\{U^0u_\lambda \}_{\lambda \in \Lambda }$
where
![]() $\{u_\lambda \}_{\lambda \in \Lambda }$
a contractive approximate unit of the ideal
$\{u_\lambda \}_{\lambda \in \Lambda }$
a contractive approximate unit of the ideal
![]() $C_0(X\backslash X_0)$
of
$C_0(X\backslash X_0)$
of
![]() $C_0(X)$
.
$C_0(X)$
.
By Theorem 2.2, if
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
is an ideal of
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
is an ideal of
![]() $C_0(X)\times _\phi {\mathbb Z}_+$
with a left approximate unit, then
$C_0(X)\times _\phi {\mathbb Z}_+$
with a left approximate unit, then
![]() $X_{n+1}= X_n$
or
$X_{n+1}= X_n$
or
![]() $X_{n+1}\subsetneq X_n$
for all
$X_{n+1}\subsetneq X_n$
for all
![]() $n\in {\mathbb Z}_+$
. If
$n\in {\mathbb Z}_+$
. If
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
and
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
and
![]() $X_{n+1}= X_n$
, for all
$X_{n+1}= X_n$
, for all
![]() $n\in {\mathbb Z}_+$
, we will write
$n\in {\mathbb Z}_+$
, we will write
![]() $\mathcal I\sim \{X_0\}$
. We obtain the following characterization.
$\mathcal I\sim \{X_0\}$
. We obtain the following characterization.
Corollary 2.4 Let
![]() $\mathcal I\sim \{X_0\}$
be a nonzero ideal of
$\mathcal I\sim \{X_0\}$
be a nonzero ideal of
![]() $C_0(X)\times _\phi {\mathbb Z}_+$
. The following are equivalent:
$C_0(X)\times _\phi {\mathbb Z}_+$
. The following are equivalent:
-
(1)
 $\mathcal I$
has a left approximate unit.
$\mathcal I$
has a left approximate unit. -
(2)
 $\phi (X_0)= X_0$
and
$\phi (X_0)= X_0$
and
 $\phi (X\backslash X_0)= X\backslash X_0$
.
$\phi (X\backslash X_0)= X\backslash X_0$
.
Proof By Theorem 2.2, we have
![]() $\phi (X\backslash X_0)= X\backslash X_0$
. By (*), we have
$\phi (X\backslash X_0)= X\backslash X_0$
. By (*), we have
![]() $\phi (X_0)\subseteq X_0$
, and since
$\phi (X_0)\subseteq X_0$
, and since
![]() $\phi $
is surjective, we get
$\phi $
is surjective, we get
![]() $\phi (X_0)= X_0$
.
$\phi (X_0)= X_0$
.
In the following proposition, the ideals
![]() $\mathcal I\sim \{X_n\}_{n=1}^\infty $
of
$\mathcal I\sim \{X_n\}_{n=1}^\infty $
of
![]() $C_0(X)\times _\phi {\mathbb Z}_+$
with a left approximate unit are characterized, when
$C_0(X)\times _\phi {\mathbb Z}_+$
with a left approximate unit are characterized, when
![]() $\phi $
is a homeomorphism.
$\phi $
is a homeomorphism.
Proposition 2.5 Let
![]() $\mathcal I\sim \{X_n\}_{n=1}^\infty $
be a nonzero ideal of
$\mathcal I\sim \{X_n\}_{n=1}^\infty $
be a nonzero ideal of
![]() $C_0(X)\times _\phi {\mathbb Z}_+$
, where
$C_0(X)\times _\phi {\mathbb Z}_+$
, where
![]() $\phi $
is a homeomorphism. The following are equivalent:
$\phi $
is a homeomorphism. The following are equivalent:
-
(1)
 $\mathcal I$
has a left approximate unit.
$\mathcal I$
has a left approximate unit. -
(2) There exist
 $S,W\subsetneq X$
such that S is closed and
$S,W\subsetneq X$
such that S is closed and
 $\phi (S)=S$
, the sets
$\phi (S)=S$
, the sets
 $\phi ^{-1}(W)$
,
$\phi ^{-1}(W)$
,
 $\phi ^{-2}(W),\dots $
are pairwise disjoint and
$\phi ^{-2}(W),\dots $
are pairwise disjoint and
 $\phi ^k(W)\cap S=\emptyset $
, for all
$\phi ^k(W)\cap S=\emptyset $
, for all
 $k\in {\mathbb Z}$
, and for all
$k\in {\mathbb Z}$
, and for all $$ \begin{align*} X_n=S\cup(\cup_{k=n}^{\infty}\phi^{-k}(W)), \end{align*} $$
$$ \begin{align*} X_n=S\cup(\cup_{k=n}^{\infty}\phi^{-k}(W)), \end{align*} $$
 $n\in {\mathbb Z}_+$
.
$n\in {\mathbb Z}_+$
.
Proof The second condition implies the second condition of Theorem 2.2 and hence the implication (2)
![]() $\Rightarrow $
(1) is immediate. We will prove the implication (1)
$\Rightarrow $
(1) is immediate. We will prove the implication (1)
![]() $\Rightarrow $
(2).
$\Rightarrow $
(2).
We set
![]() $S=\cap _{n=0}^\infty X_n$
. Clearly, the set S is closed and, by (*), we have
$S=\cap _{n=0}^\infty X_n$
. Clearly, the set S is closed and, by (*), we have
![]() $\phi (S)\subseteq S$
. We will prove that
$\phi (S)\subseteq S$
. We will prove that
![]() $\phi (S)=S$
. We suppose
$\phi (S)=S$
. We suppose
![]() $\phi (S)\subsetneq S$
. Since
$\phi (S)\subsetneq S$
. Since
![]() $\phi $
is surjective, there exists
$\phi $
is surjective, there exists
![]() $x\in X\backslash S$
such that
$x\in X\backslash S$
such that
![]() $\phi (x)\in S$
. Moreover,
$\phi (x)\in S$
. Moreover,
![]() $\phi ^n(x)\in S$
for all
$\phi ^n(x)\in S$
for all
![]() $n\ge 1$
. However, since
$n\ge 1$
. However, since
![]() $x\notin S$
, there exists
$x\notin S$
, there exists
![]() $n_0$
such that
$n_0$
such that
![]() $x\notin X_{n_0}$
and hence
$x\notin X_{n_0}$
and hence
![]() $\phi ^{n_0}(x)\in X\backslash X_0$
, by Theorem 2.2, which is a contradiction since
$\phi ^{n_0}(x)\in X\backslash X_0$
, by Theorem 2.2, which is a contradiction since
![]() $S\cap (X\backslash X_0)=\emptyset $
.
$S\cap (X\backslash X_0)=\emptyset $
.
By Theorem 2.2,
![]() $\phi (X_{n+1}\backslash X_{n+2})= X_n\backslash X_{n+1}$
for all
$\phi (X_{n+1}\backslash X_{n+2})= X_n\backslash X_{n+1}$
for all
![]() $n\in {\mathbb Z}_+$
and hence
$n\in {\mathbb Z}_+$
and hence
![]() $\phi ^n (X_{n}\backslash X_{n+1})= X_0\backslash X_{1}$
or equivalently
$\phi ^n (X_{n}\backslash X_{n+1})= X_0\backslash X_{1}$
or equivalently
![]() $ X_n\backslash X_{n+1}=\phi ^{-n} (X_{0}\backslash X_{1})$
since
$ X_n\backslash X_{n+1}=\phi ^{-n} (X_{0}\backslash X_{1})$
since
![]() $\phi $
is a homeomorphism. Furthermore, the sets
$\phi $
is a homeomorphism. Furthermore, the sets
![]() $\phi ^{-1}(X_0\backslash X_1),\phi ^{-2}(X_0\backslash X_1),\dots $
are pairwise disjoint.
$\phi ^{-1}(X_0\backslash X_1),\phi ^{-2}(X_0\backslash X_1),\dots $
are pairwise disjoint.
We set
![]() $W=X_0\backslash X_1$
. Clearly,
$W=X_0\backslash X_1$
. Clearly,
![]() $\phi ^k(W)\cap S=\emptyset $
for all
$\phi ^k(W)\cap S=\emptyset $
for all
![]() $k\in {\mathbb Z}$
, since
$k\in {\mathbb Z}$
, since
![]() $\phi (S)=S$
and
$\phi (S)=S$
and
![]() $\phi (W)\subseteq X\backslash X_0$
. Also,
$\phi (W)\subseteq X\backslash X_0$
. Also,
![]() $X_0=S\cup (X_0\backslash X_1)\cup (X_1\backslash X_2)\cup \cdots $
and hence
$X_0=S\cup (X_0\backslash X_1)\cup (X_1\backslash X_2)\cup \cdots $
and hence
Finally, for all
![]() $n\in {\mathbb Z}_+$
we have that
$n\in {\mathbb Z}_+$
we have that
and so
In the following corollary, the ideals with an approximate unit are characterized.
Corollary 2.6 Let
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
be a nonzero ideal of
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
be a nonzero ideal of
![]() $C_0(X)\times _\phi {\mathbb Z}_+$
. The following are equivalent:
$C_0(X)\times _\phi {\mathbb Z}_+$
. The following are equivalent:
-
(1)
 $\mathcal I$
has an approximate unit.
$\mathcal I$
has an approximate unit. -
(2)
 $X_n=X_{n+1}$
, for all
$X_n=X_{n+1}$
, for all
 $n\in {\mathbb Z}_+$
, and
$n\in {\mathbb Z}_+$
, and
 $\phi (X\backslash X_0)= X\backslash X_0$
.
$\phi (X\backslash X_0)= X\backslash X_0$
.
Proof (1)
![]() $\Rightarrow $
(2) is immediate from Theorem 2.1 and Corollary 2.4.
$\Rightarrow $
(2) is immediate from Theorem 2.1 and Corollary 2.4.
We show (2)
![]() $\Rightarrow $
(1). If
$\Rightarrow $
(1). If
![]() $X_n=X_{n+1}$
, by (*), we have
$X_n=X_{n+1}$
, by (*), we have
![]() $\phi (X_0)\subseteq X_0$
. Since
$\phi (X_0)\subseteq X_0$
. Since
![]() $\phi (X\backslash X_0)= X\backslash X_0$
and
$\phi (X\backslash X_0)= X\backslash X_0$
and
![]() $\phi $
surjective, we have
$\phi $
surjective, we have
![]() $\phi (X_0)= X_0$
. Theorem 2.1 and Corollary 2.4 conclude the proof.
$\phi (X_0)= X_0$
. Theorem 2.1 and Corollary 2.4 conclude the proof.
Let B be a Banach space, and let C be a subspace of B. The set of linear functionals that vanish on a subspace C of B is called the annihilator of C. A subspace C of a Banach space B is an M-ideal in B if its annihilator is the kernel of a projection P on
![]() $B^*$
such that
$B^*$
such that
![]() $\|y\|=\|P(y)\|+\|y-P(y)\|$
, for all y, where
$\|y\|=\|P(y)\|+\|y-P(y)\|$
, for all y, where
![]() $B^*$
is the dual space of B.
$B^*$
is the dual space of B.
Effros and Ruan proved that the M-ideals in a unital operator algebra are the closed two-sided ideals with an approximate unit [Reference Effros and Ruan5, Theorem 2.2]. Therefore, we obtain the following corollary about the M-ideals of a semicrossed product.
Corollary 2.7 Let
![]() $\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
be a nonzero ideal of
$\mathcal I\sim \{X_n\}_{n=0}^{\infty }$
be a nonzero ideal of
![]() $C(X)\times _\phi {\mathbb Z}_+$
, where X is compact. The following are equivalent:
$C(X)\times _\phi {\mathbb Z}_+$
, where X is compact. The following are equivalent:
-
(1)
 $\mathcal I$
is an M-ideal.
$\mathcal I$
is an M-ideal. -
(2)
 $\mathcal I$
has an approximate unit.
$\mathcal I$
has an approximate unit. -
(3)
 $X_n=X_{n+1}$
, for all
$X_n=X_{n+1}$
, for all
 $n\in {\mathbb Z}_+$
, and
$n\in {\mathbb Z}_+$
, and
 $\phi (X\backslash X_0)= X\backslash X_0$
.
$\phi (X\backslash X_0)= X\backslash X_0$
.
Acknowledgment
The author would like to thank M. Anoussis and D. Drivaliaris for their support and valuable remarks and comments.