Published online by Cambridge University Press: 20 November 2018
Let  $\mathcal{E}$ be an injectively resolving subcategory of left
$\mathcal{E}$ be an injectively resolving subcategory of left  $R$-modules. A left
$R$-modules. A left  $R$-module
$R$-module 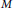 $M$ (resp. right
$M$ (resp. right  $R$-module
$R$-module 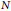 $N$) is called
$N$) is called  $\mathcal{E}$-injective (resp.
$\mathcal{E}$-injective (resp.  $\mathcal{E}$-flat) if
$\mathcal{E}$-flat) if  $\text{Ext}_{R}^{1}\left( G,\,M \right)\,=\,0$ (resp.
$\text{Ext}_{R}^{1}\left( G,\,M \right)\,=\,0$ (resp. 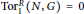 $\text{Tor}_{1}^{R}\left( N,\,G \right)\,=\,0$) for any
$\text{Tor}_{1}^{R}\left( N,\,G \right)\,=\,0$) for any 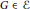 $G\,\in \,\mathcal{E}$. Let
$G\,\in \,\mathcal{E}$. Let  $\mathcal{E}$ be a covering subcategory. We prove that a left
$\mathcal{E}$ be a covering subcategory. We prove that a left  $R$-module
$R$-module 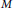 $M$ is
$M$ is  $\mathcal{E}$-injective if and only if
$\mathcal{E}$-injective if and only if 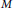 $M$ is a direct sum of an injective left
$M$ is a direct sum of an injective left  $R$-module and a reduced
$R$-module and a reduced  $\mathcal{E}$-injective left
$\mathcal{E}$-injective left  $R$-module. Suppose
$R$-module. Suppose 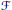 $\mathcal{F}$ is a preenveloping subcategory of right
$\mathcal{F}$ is a preenveloping subcategory of right  $R$-modules such that
$R$-modules such that 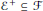 ${{\mathcal{E}}^{+}}\,\subseteq \,\mathcal{F}$ and
${{\mathcal{E}}^{+}}\,\subseteq \,\mathcal{F}$ and  ${{\mathcal{F}}^{+}}\,\subseteq \,\mathcal{E}$. It is shown that a finitely presented right
${{\mathcal{F}}^{+}}\,\subseteq \,\mathcal{E}$. It is shown that a finitely presented right  $R$-module
$R$-module 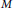 $M$ is
$M$ is  $\mathcal{E}$-flat if and only if
$\mathcal{E}$-flat if and only if 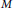 $M$ is a cokernel of an
$M$ is a cokernel of an 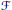 $\mathcal{F}$-preenvelope of a right
$\mathcal{F}$-preenvelope of a right  $R$-module. In addition, we introduce and investigate the
$R$-module. In addition, we introduce and investigate the  $\mathcal{E}$-injective and
$\mathcal{E}$-injective and  $\mathcal{E}$-flat dimensions of modules and rings. We also introduce
$\mathcal{E}$-flat dimensions of modules and rings. We also introduce  $\mathcal{E}$-(semi)hereditary rings and
$\mathcal{E}$-(semi)hereditary rings and  $\mathcal{E}$-von Neumann regular rings and characterize them in terms of
$\mathcal{E}$-von Neumann regular rings and characterize them in terms of  $\mathcal{E}$-injective and
$\mathcal{E}$-injective and  $\mathcal{E}$-flat modules.
$\mathcal{E}$-flat modules.