Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-10T10:13:24.585Z Has data issue: false hasContentIssue false
  • English
  • Français

Exponential Sums on Reduced Residue Systems

Published online by Cambridge University Press:  20 November 2018

W. K. A. Loh
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of this article is to obtain an upper bound for the exponential sums 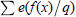$\sum{e(f(x)\,/\,q)}$, where the summation runs from 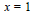$x=1$ to 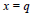$x=q$ with 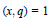$(x,q)=1$ and 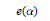$e(\alpha )$ denotes 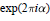$\exp (2\pi i\alpha )$.

We shall show that the upper bound depends only on the values of 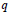$q$ and 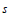$s$, where 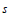$s$ is the number of terms in the polynomial 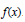$f(x)$.

Keywords

11L07
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 2 , 01 June 1998 , pp. 187 - 195
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Chalk, J. H. H., On Hua's Estimates for Exponential Sums, Mathematika (2) 34 (1987), 115–123.Google Scholar
2. Ding, Ping, An improvement to Chalk's Estimation of Exponential Sums, Acta Arith. LIX. 2 (1991), 149–155.Google Scholar
3. Ding, Ping, On Chalk's Estimation of Exponential Sums (II), Canad. Math. Bull., (1992), in the course of publication.Google Scholar
4. Hua, L. K., On an exponential sum, Chinese J. Math. 2 (1940), 301–312.Google Scholar
5. Hua, L. K., On exponential sums, Sci. Record (Peking) (N.S.) 1 (1957), 1–4.Google Scholar
6. Hua, L. K., Die Abschʺatzung von Exponentialsummen und ihre Anwendung in der Zahlentheorie, Enzyklop ʺadie Math. Wiss., Bd I2(1959), H.13, TI x13, S 41.Google Scholar
7. Hua, L. K., Additive Theory of Prime Numbers, Amer.Math. Soc. 1, Providence, 1965, 2–7.Google Scholar
8. Loh, W. K. A., Hua's Lemma, Bull. Austal. Math. Soc. (3) 50 (1994), 451–458.Google Scholar
9. Loxton, J. H. and Smith, R. A., On Hua's estimate of a complete exponential sums, J. London Math. Soc. (2) 26 (1982), 15–20.Google Scholar
10. Loxton, J. H. and Vaughan, R. C., The Estimation of Complete Exponential Sums, Canad. J. Math. (4) 28 (1985), 440–454.Google Scholar
11. Mordell, L. J., On a sum analogous to a Gauss's sum, Quart. J. Math. 3 (1932), 161–167.Google Scholar
12. Weil, A., On some exponential sums, Proc. Nat. Acad. Sci. U.S.A. 34 (1948), 204–207.Google Scholar