Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-04T19:03:51.302Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of Solutions to Poisson's Equation

Published online by Cambridge University Press:  20 November 2018

Mary Hanley
Mary Hanley*
Affiliation:
School of Mathematical Sciences, University College Dublin, Dublin 4, Ireland e-mail: maryhanley@maths.ucd.ie
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

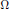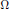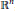Let $\Omega$ be a domain in ${{\mathbb{R}}^{n}}\,(n\,\ge \,2).$ We find a necessary and sufficient topological condition on $\Omega$ such that, for any measure $ $ on ${{\mathbb{R}}^{n}}$ , there is a function $u$ with specified boundary conditions that satisfies the Poisson equation $\Delta u\,=\,\mu$ on 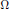$\Omega$ in the sense of distributions.

Keywords

31B25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 2 , 01 June 2008 , pp. 229 - 235
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Armitage, D. H. and Gardiner, S. J., Classical Potential Theory. Springer-Verlag, London, 2001.Google Scholar
[2] Gardiner, S. J., The Dirichlet problem with noncompact boundary. Math. Z. 213(1993), no. 1, 163–170.Google Scholar
[3] Gauthier, P. M., Tangential approximation by entire functions and functions holomorphic in a disc. Izv. Akad. Nauk Armjan. SSR Ser. Mat. 4(1969), no. 5, 319–326.Google Scholar
[4] Klimek, M., Pluripotential Theory. London Mathematical Society Monographs, New Series 6, Oxford University Press, Oxford, 1991.Google Scholar