Published online by Cambridge University Press: 20 November 2018
Assume that  $\Omega$ is a Hartogs domain in
$\Omega$ is a Hartogs domain in  ${{\mathbb{C}}^{1+n}}$, defined as
${{\mathbb{C}}^{1+n}}$, defined as 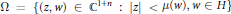 $\Omega =\left\{ \left( z,w \right)\,\in \,{{\mathbb{C}}^{1+n}}\,:\left| z \right|\,<\,\mu \left( w \right),w\,\in H \right\}$, where
$\Omega =\left\{ \left( z,w \right)\,\in \,{{\mathbb{C}}^{1+n}}\,:\left| z \right|\,<\,\mu \left( w \right),w\,\in H \right\}$, where 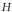 $H$ is an open set in
$H$ is an open set in 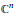 ${{\mathbb{C}}^{n}}$ and
${{\mathbb{C}}^{n}}$ and  $\mu$ is a continuous function with positive values in
$\mu$ is a continuous function with positive values in 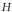 $H$ such that –ln
$H$ such that –ln  $\mu$ is a strongly plurisubharmonic function in
$\mu$ is a strongly plurisubharmonic function in 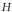 $H$. Let
$H$. Let 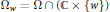 ${{\Omega }_{w}}=\Omega \cap \left( \mathbb{C}\times \left\{ w \right\} \right)$. For a given set
${{\Omega }_{w}}=\Omega \cap \left( \mathbb{C}\times \left\{ w \right\} \right)$. For a given set  $E$ contained in
$E$ contained in 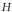 $H$ of the type
$H$ of the type 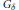 ${{G}_{\delta }}$ we construct a holomorphic function
${{G}_{\delta }}$ we construct a holomorphic function 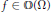 $f\in \mathbb{O}\left( \Omega \right)$ such that
$f\in \mathbb{O}\left( \Omega \right)$ such that
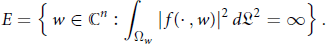 $$E=\left\{ w\in {{\mathbb{C}}^{n}}:\int\limits_{{{\Omega }_{w}}}{{{\left| f\left( \cdot ,w \right) \right|}^{2}}d{{\mathfrak{L}}^{2}}=\infty } \right\}.$$
$$E=\left\{ w\in {{\mathbb{C}}^{n}}:\int\limits_{{{\Omega }_{w}}}{{{\left| f\left( \cdot ,w \right) \right|}^{2}}d{{\mathfrak{L}}^{2}}=\infty } \right\}.$$