Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-06T14:01:29.572Z Has data issue: false hasContentIssue false
  • English
  • Français

A Dynamical Proof of Pisot's Theorem

Published online by Cambridge University Press:  20 November 2018

Jaroslaw Kwapisz
Jaroslaw Kwapisz*
Affiliation:
Department of Mathematical Sciences, Montana State University, Bozeman, MT 59717-2400, U.S.A. e-mail: jarek@math.montana.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

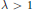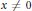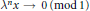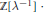We give a geometric proof of classical results that characterize Pisot numbers as algebraic $\text{ }\lambda \,>1$ for which there is $x\ne 0$ with $\text{ }\lambda {{\text{ }}^{n}}x\to 0\left( \,\bmod \,\,1 \right)$ and identify such $x$ as members of $\mathbb{Z}\left[ \text{ }\lambda {{\text{ }}^{-1}} \right]\cdot$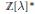$\mathbb{Z}{{\left[ \text{ }\!\!\lambda\!\!\text{ } \right]}^{*}}$ where 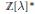$\mathbb{Z}{{\left[ \text{ }\!\!\lambda\!\!\text{ } \right]}^{*}}$ is the dual module of 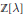$\mathbb{Z}\left[ \text{ }\!\!\lambda\!\!\text{ } \right]$.

Keywords

11R06
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 1 , 01 March 2006 , pp. 108 - 112
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Barge, M. and Kwapisz, J., Geometric theory of Pisot substitutions. In preparation; available at http://www.math.montana.edu/~jarek/papers.html.Google Scholar
[2] Bertin, M.-J., Decomps-Guilloux, A., Grandet-Hugot, M., Pathiaux-Delefosse, M., and Schreiber, J.-P., Pisot and Salem Numbers. Birkhäuser Verlag, Basel, 1992.Google Scholar
[3] Cassels, J. W. S., An Introduction to Diophantine Approximation. Cambridge Tracts in Mathematics and Mathematical Physics 45, Cambridge University Press, NY, 1957.Google Scholar
[4] Pisot, C., La répartition modulo 1 et les nombres algébriques. Ann. Scu. Norm. Sup. Pisa 27(1938), 205–248.Google Scholar
[5] Salem, R., Algebraic numbers and Fourier analysis. D. C. Heath, Boston, MA, 1963.Google Scholar
[6] Solomyak, B., Dynamics of self-similar tilings. Ergodic Theory Dynam. Systems 17(1997), 695–738.Google Scholar
[7] Vijayaraghavan, T., On the fractional parts of the powers of a number. II. Proc. Cambridge Philos. Soc. 37(1941), 349–357.Google Scholar
[8] Weiss, E., Algebraic Number Theory. Chelsea Publishing, New York, NY, 1976.Google Scholar