Published online by Cambridge University Press: 20 November 2018
In this paper we prove the following:
1. Let 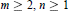 $m\ge 2,\,n\ge 1$ be integers and let
$m\ge 2,\,n\ge 1$ be integers and let  $G$ be a group such that
$G$ be a group such that  ${{(XY)}^{n}}\,=\,{{(YX)}^{n}}$ for all subsets
${{(XY)}^{n}}\,=\,{{(YX)}^{n}}$ for all subsets 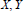 $X,Y$ of size
$X,Y$ of size 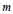 $m$ in
$m$ in  $G$. Then
$G$. Then
a)  $G$ is abelian or a
$G$ is abelian or a 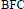 $\text{BFC}$-group of finite exponent bounded by a function of
$\text{BFC}$-group of finite exponent bounded by a function of 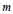 $m$ and
$m$ and 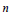 $n$.
$n$.
b) If 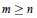 $m\ge n$ then
$m\ge n$ then  $G$ is abelian or
$G$ is abelian or  $|G|$ is bounded by a function of
$|G|$ is bounded by a function of 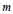 $m$ and
$m$ and 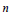 $n$.
$n$.
2. The only non-abelian group  $G$ such that
$G$ such that 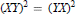 ${{(XY)}^{2}}\,=\,{{(YX)}^{2}}$ for all subsets
${{(XY)}^{2}}\,=\,{{(YX)}^{2}}$ for all subsets 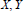 $X,Y$ of size 2 in
$X,Y$ of size 2 in  $G$ is the quaternion group of order 8.
$G$ is the quaternion group of order 8.
3. Let 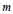 $m$,
$m$, 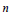 $n$ be positive integers and
$n$ be positive integers and  $G$ a group such that
$G$ a group such that 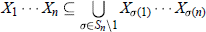 $${{X}_{1}}\cdot \cdot \cdot \,{{X}_{n}}\,\subseteq \,\bigcup\limits_{\sigma \in {{S}_{n}}\,\backslash \,1}{{{X}_{\sigma (1)}}\cdot \cdot \cdot \,{{X}_{\sigma (n)}}}$$
$${{X}_{1}}\cdot \cdot \cdot \,{{X}_{n}}\,\subseteq \,\bigcup\limits_{\sigma \in {{S}_{n}}\,\backslash \,1}{{{X}_{\sigma (1)}}\cdot \cdot \cdot \,{{X}_{\sigma (n)}}}$$
for all subsets 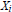 ${{X}_{i}}$ of size
${{X}_{i}}$ of size 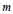 $m$ in
$m$ in  $G$. Then
$G$. Then  $G$ is
$G$ is 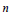 $n$-permutable or
$n$-permutable or  $|G|$ is bounded by a function of
$|G|$ is bounded by a function of 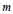 $m$ and
$m$ and 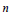 $n$.
$n$.